Sufficient signs of an extremum of a function. Signs of local increase and decrease of a function. Necessary and sufficient conditions for the existence of an extremum of a function at a point. A sufficient sign of the existence of an extremum

The function y = f(x) is called increasing (decreasing) in a certain interval, if for x 1< x 2 выполняется неравенство (f(x 1) < f (x 2) (f(x 1) >f(x 2)).

If the differentiable function y = f(x) increases (decreases) on an interval, then its derivative on this interval f " (x) > 0

(f" (x)< 0).

Dot x o called local maximum point (minimum) function f(x), if there is a neighborhood of the point x o, for all points of which the inequality f(x) ≤ f(x о) (f(x) ≥ f(x о)) is true.

The maximum and minimum points are called extremum points, and the values of the function at these points are its extremes.

Necessary conditions for an extremum. If the point x o is an extremum point of the function f(x), then either f " (x o) = 0, or f (x o) does not exist. Such points are called critical, and the function itself is defined at the critical point. The extrema of a function should be sought among its critical points.

The first sufficient condition. Let x o- critical point. If f "(x) when passing through a point x o changes the plus sign to minus, then at the point x o the function has a maximum, otherwise it has a minimum. If, when passing through the critical point, the derivative does not change sign, then at the point x o there is no extreme.

Second sufficient condition. Let the function f(x) have a derivative
f "(x) in the vicinity of the point x o and the second derivative at the point itself x o. If f "(x o) = 0, >0 (<0), то точка x o is the local minimum (maximum) point of the function f(x). If =0, then you need to either use the first sufficient condition or use higher derivatives.

On a segment, the function y = f(x) can reach its minimum or maximum value either at critical points or at the ends of the segment.

Studying conditions and plotting graphs.

Find the domain of a function

Find the intersection points of the graph with the coordinate axes

Find intervals of the sign of constancy

Examine for evenness, oddness

Find asymptotes of the graph of a function

Find intervals of monotonicity of a function

Find the extrema of the function

Find convexity intervals and inflection points

Asymptotes of function graphs. General scheme for studying and plotting function graphs. Examples.

Vertical

Vertical asymptote - a straight line, subject to the existence of a limit .

As a rule, when determining the vertical asymptote, they look for not one limit, but two one-sided ones (left and right). This is done in order to determine how the function behaves as it approaches the vertical asymptote from different directions. For example:

Note: pay attention to the infinity signs in these equalities.

[edit]Horizontal

Horizontal asymptote - a straight line, subject to the existence of a limit

[edit] Oblique

Oblique asymptote - a straight line, subject to the existence of limits

Example of an oblique asymptote

Note: a function can have no more than two oblique (horizontal) asymptotes!

Note: If at least one of the two limits mentioned above does not exist (or is equal to ), then the oblique asymptote at (or ) does not exist!

Relationship between oblique and horizontal asymptotes

If when calculating the limit , then it is obvious that the oblique asymptote coincides with the horizontal one. What is the connection between these two types of asymptotes?

The thing is, that the horizontal asymptote is a special case of the oblique at , and from the above comments it follows that

1. The function has either only one oblique asymptote, or one vertical asymptote, or one oblique and one vertical, or two oblique, or two vertical, or has no asymptotes at all.

2. The existence of the asymptotes indicated in paragraph 1.) is directly related to the existence of the corresponding limits.

Graph of a function with two horizontal asymptotes

]Finding asymptotes

The order of finding asymptotes

1. Finding vertical asymptotes.

2. Finding two limits

3. Finding two limits:

if in item 2.), then , and the limit is sought using the horizontal asymptote formula, .

The extremum point of a function is the point in the domain of definition of the function at which the value of the function takes on a minimum or maximum value. The values of the function at these points are called extrema (minimum and maximum) of the function.

Definition. Dot x1 function domain f(x) is called maximum point of the function , if the value of the function at this point is greater than the values of the function at points sufficiently close to it, located to the right and left of it (that is, the inequality holds f(x0 ) > f(x 0 + Δ x) x1 maximum.

Definition. Dot x2 function domain f(x) is called minimum point of the function, if the value of the function at this point is less than the values of the function at points sufficiently close to it, located to the right and left of it (that is, the inequality holds f(x0 ) < f(x 0 + Δ x) ). In this case we say that the function has at the point x2 minimum.

Let's say point x1 - maximum point of the function f(x) . Then in the interval up to x1 function increases, therefore the derivative of the function is greater than zero ( f "(x) > 0 ), and in the interval after x1 the function decreases, therefore, derivative of a function less than zero ( f "(x) < 0 ). Тогда в точке x1

Let us also assume that the point x2 - minimum point of the function f(x) . Then in the interval up to x2 the function is decreasing, and the derivative of the function is less than zero ( f "(x) < 0 ), а в интервале после x2 the function is increasing, and the derivative of the function is greater than zero ( f "(x) > 0 ). In this case also at the point x2 the derivative of the function is zero or does not exist.

Fermat's theorem (a necessary sign of the existence of an extremum of a function). If the point x0 - extremum point of the function f(x) then at this point the derivative of the function is equal to zero ( f "(x) = 0 ) or does not exist.

Definition. The points at which the derivative of a function is zero or does not exist are called critical points .

Example 1. Let's consider the function.

At the point x= 0 the derivative of the function is zero, therefore the point x= 0 is the critical point. However, as can be seen on the graph of the function, it increases throughout the entire domain of definition, so the point x= 0 is not the extremum point of this function.

Thus, the conditions that the derivative of a function at a point is equal to zero or does not exist are necessary conditions for an extremum, but not sufficient, since other examples of functions can be given for which these conditions are met, but the function does not have an extremum at the corresponding point. That's why there must be sufficient evidence, allowing one to judge whether there is an extremum at a particular critical point and what kind of extremum it is - maximum or minimum.

Theorem (the first sufficient sign of the existence of an extremum of a function). Critical point x0 f(x) if, when passing through this point, the derivative of the function changes sign, and if the sign changes from “plus” to “minus”, then it is a maximum point, and if from “minus” to “plus”, then it is a minimum point.

If near the point x0 , to the left and to the right of it, the derivative retains its sign, this means that the function either only decreases or only increases in a certain neighborhood of the point x0 . In this case, at the point x0 there is no extreme.

So, to determine the extremum points of the function, you need to do the following :

Find the derivative of the function.
Equate the derivative to zero and determine the critical points.
Mentally or on paper, mark the critical points on the number line and determine the signs of the derivative of the function in the resulting intervals. If the sign of the derivative changes from “plus” to “minus”, then the critical point is the maximum point, and if from “minus” to “plus”, then the minimum point.
Calculate the value of the function at the extremum points.

Example 2. Find the extrema of the function .

Solution. Let's find the derivative of the function:

Let's equate the derivative to zero to find the critical points:

Since for any values of “x” the denominator is not equal to zero, we equate the numerator to zero:

Got one critical point x= 3 . Let us determine the sign of the derivative in the intervals delimited by this point:

in the range from minus infinity to 3 - a minus sign, that is, the function decreases,

in the interval from 3 to plus infinity there is a plus sign, that is, the function increases.

That is, period x= 3 is the minimum point.

Let's find the value of the function at the minimum point:

Thus, the extremum point of the function is found: (3; 0), and it is the minimum point.

Theorem (the second sufficient sign of the existence of an extremum of a function). Critical point x0 is the extremum point of the function f(x) if the second derivative of the function at this point is not equal to zero ( f ""(x) ≠ 0 ), and if the second derivative is greater than zero ( f ""(x) > 0 ), then the maximum point, and if the second derivative is less than zero ( f ""(x) < 0 ), то точкой минимума.

Note 1. If at the point x0 If both the first and second derivatives vanish, then at this point it is impossible to judge the presence of an extremum based on the second sufficient criterion. In this case, you need to use the first sufficient criterion for the extremum of a function.

Remark 2. The second sufficient criterion for the extremum of a function is not applicable even when the first derivative does not exist at a stationary point (then the second derivative does not exist either). In this case, you also need to use the first sufficient sign of an extremum of a function.

Local nature of the extrema of the function

From the above definitions it follows that the extremum of a function is local in nature - it is the largest and smallest value of the function compared to nearby values.

Let's say you're looking at your earnings over a period of one year. If in May you earned 45,000 rubles, and in April 42,000 rubles and in June 39,000 rubles, then May earnings are the maximum of the earnings function compared to nearby values. But in October you earned 71,000 rubles, in September 75,000 rubles, and in November 74,000 rubles, so October earnings are the minimum of the earnings function compared to nearby values. And you can easily see that the maximum among the values of April-May-June is less than the minimum of September-October-November.

Generally speaking, on an interval a function can have several extrema, and it may turn out that some minimum of the function is greater than any maximum. So, for the function shown in the figure above, .

That is, one should not think that the maximum and minimum of a function are, respectively, its largest and smallest values on the entire segment under consideration. At the maximum point, the function has the greatest value only in comparison with those values that it has at all points sufficiently close to the maximum point, and at the minimum point it has the smallest value only in comparison with those values that it has at all points sufficiently close to the minimum point.

Therefore, we can clarify the above concept of extremum points of a function and call minimum points local minimum points, and maximum points local maximum points.

We look for the extrema of the function together

Example 3.

Solution: The function is defined and continuous on the entire number line. Its derivative also exists on the entire number line. Therefore, in this case, the critical points are only those at which, i.e. , from where and . Critical points and divide the entire domain of definition of the function into three intervals of monotonicity: . Let's select one control point in each of them and find the sign of the derivative at this point.

For the interval, the control point can be: find. Taking a point in the interval, we get, and taking a point in the interval, we have. So, in the intervals and , and in the interval . According to the first sufficient criterion for an extremum, there is no extremum at the point (since the derivative retains its sign in the interval), and at the point the function has a minimum (since the derivative changes sign from minus to plus when passing through this point). Let's find the corresponding values of the function: , a . In the interval the function decreases, since in this interval , and in the interval it increases, since in this interval .

To clarify the construction of the graph, we find the points of intersection of it with the coordinate axes. When we obtain an equation whose roots are and , i.e., two points (0; 0) and (4; 0) of the graph of the function are found. Using all the information received, we build a graph (see the beginning of the example).

For self-checking during calculations, you can use online derivative calculator .

Example 4. Find the extrema of the function and build its graph.

The domain of definition of a function is the entire number line, except for the point, i.e. .

To shorten the study, you can use the fact that this function is even, since . Therefore, its graph is symmetrical about the axis Oy and the study can only be performed for the interval.

Finding the derivative and critical points of the function:

1) ;

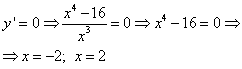2) ,

but the function suffers a discontinuity at this point, so it cannot be an extremum point.

Thus, the given function has two critical points: and . Taking into account the parity of the function, we will check only the point using the second sufficient criterion for an extremum. To do this, we find the second derivative and determine its sign at: we get . Since and , it is the minimum point of the function, and .

To get a more complete picture of the graph of a function, let’s find out its behavior at the boundaries of the domain of definition:

(here the symbol indicates the desire x to zero from the right, and x remains positive; similarly means aspiration x to zero from the left, and x remains negative). Thus, if , then . Next, we find

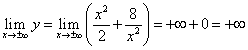those. if , then .

The graph of a function has no intersection points with the axes. The picture is at the beginning of the example.

For self-checking during calculations, you can use online derivative calculator .

We continue to search for extrema of the function together

Example 8. Find the extrema of the function.

Solution. Let's find the domain of definition of the function. Since the inequality must be satisfied, we obtain from .

Let's find the first derivative of the function.

To find the maxima and minima of a function, you can use any of the three sufficient signs of an extremum. Although the most common and convenient is the first one.

The first sufficient condition for an extremum.

Let the function y = f(x) is differentiable in a -neighborhood of the point, and is continuous at the point itself. Then

In other words:

Algorithm.

We find the domain of definition of the function.

We find the derivative of the function on the domain of definition.

We determine the zeros of the numerator, the zeros of the denominator of the derivative and the points of the domain of definition at which the derivative does not exist (these points are called points of possible extremum, passing through these points, the derivative can just change its sign).

These points divide the domain of definition of the function into intervals in which the derivative retains its sign. We determine the signs of the derivative on each of the intervals (for example, by calculating the value of the derivative of a function at any point in a particular interval).

We select points at which the function is continuous and, passing through which, the derivative changes sign.

Example. Find the extrema of the function.
Solution.
The domain of a function is the entire set of real numbers except x = 2.
Finding the derivative:

The zeros of the numerator are points x = -1 And x = 5, the denominator goes to zero at x = 2. Mark these points on the number axis

We determine the signs of the derivative at each interval; to do this, we calculate the value of the derivative at any of the points of each interval, for example, at the points x = -2, x = 0, x = 3 And x=6.

Therefore, on the interval the derivative is positive (in the figure we put a plus sign over this interval). Likewise

Therefore, we put a minus above the second interval, a minus above the third, and a plus above the fourth.

It remains to select points at which the function is continuous and its derivative changes sign. These are the extremum points.
At the point x = -1 the function is continuous and the derivative changes sign from plus to minus, therefore, according to the first sign of an extremum, x = -1 is the maximum point; the maximum of the function corresponds to it.
At the point x = 5 the function is continuous and the derivative changes sign from minus to plus, therefore, x = -1 is the minimum point; the minimum of the function corresponds to it.
Graphic illustration.

Answer: .

The second sufficient sign of an extremum of a function.
Let ,

if , then is the minimum point;

if , then is the maximum point.

As you can see, this criterion requires the existence of a derivative at least up to the second order at the point .
Example. Find the extrema of the function.
Solution.
Let's start with the domain of definition:

Let's differentiate the original function:

The derivative goes to zero at x = 1, that is, this is a point of possible extremum.
We find the second derivative of the function and calculate its value at x = 1:

Therefore, by the second sufficient condition for an extremum, x = 1- maximum point. Then - the maximum of the function.
Graphic illustration.

Answer: .
The third sufficient sign of an extremum of a function.
Let the function y = f(x) has derivatives up to n-th order in the -neighborhood of the point and derivatives up to n+1-th order at the point itself. Let it be.
Then,

End of work -

This topic belongs to the section:

Algebra and analytical geometry. The concept of a matrix, operations on matrices and their properties

The concept of a matrix is operations on matrices and their properties.. a matrix is a rectangular table made up of numbers that cannot be.. and matrix addition is an element-wise operation..

If you need additional material on this topic, or you did not find what you were looking for, we recommend using the search in our database of works:

What will we do with the received material:

If this material was useful to you, you can save it to your page on social networks:

All topics in this section:

Definition of differentiability
The operation of finding the derivative is called differentiation of a function. A function is said to be differentiable at some point if it has a finite derivative at that point, and

Rule of differentiation
Corollary 1. The constant factor can be taken out of the sign of the derivative:

Geometric meaning of derivative. Tangent equation
The angle of inclination of a straight line y = kx+b is the angle measured from the position

Geometric meaning of the derivative of a function at a point
Let us consider the secant AB of the graph of the function y = f(x) such that points A and B have coordinates, respectively

Solution
The function is defined for all real numbers. Since (-1; -3) is a point of tangency, then

Necessary conditions for an extremum and sufficient conditions for an extremum
Definition of an increasing function. The function y = f(x) increases on the interval X if for any

Conditions for monotonicity and constancy of a function
Condition for (nonstrict) monotonicity of a function on an interval. Let the function have a derivative in each

Definition of antiderivative
An antiderivative of a function f(x) on the interval (a; b) is a function F(x) such that the equality

Examination
To check the result, we differentiate the resulting expression: As a result, we get

The antiderivative of the product of a constant and a function is equal to the product of a constant and the antiderivative of a function
A sufficient condition for the existence of an antiderivative of a function given on an interval is

Definition
Let it be defined on

Geometric meaning
The definite integral is numerically equal to the area of the figure bounded by the abscissa axis and the straight lines

Properties of a definite integral
Basic properties of a definite integral. Property 1. The derivative of a definite integral with respect to the upper limit is equal to the integrand into which instead of a variable is integrated

Newton-Leibniz formula (with proof)
Newton-Leibniz formula. Let the function y = f(x) be continuous on an interval and F(x) be one of the antiderivatives of the function on this interval, then the equation

Theorem (the first sufficient condition for an extremum). Let the function be continuous at a point, and the derivative change sign when passing through the point. Then is the point of extremum: maximum if the sign changes from “+” to “–”, and minimum if from “–” to “+”.

Proof. Let at and at .

According to Lagrange's theorem , where .Then if , then ; that's why , hence, , or . If, then; that's why , hence, or .

Thus, it is proven that at any points near , i.e. – the maximum point of the function.

The proof of the theorem for the minimum point is carried out similarly. The theorem is proven.

If, when passing through a point, the derivative does not change sign, then there is no extremum at the point.

Theorem (second sufficient condition for extremum). Let the derivative of a twice differentiable function at a point be equal to 0 (), and its second derivative at this point be different from zero () and continuous in some neighborhood of the point. Then is the extremum point; at this is the minimum point, and at this is the maximum point.

An algorithm for finding extrema of a function using the first sufficient condition for an extremum.

1. Find the derivative.

2. Find the critical points of the function.

3. Investigate the sign of the derivative to the left and right of each critical point and draw a conclusion about the presence of extrema.

4. Find extreme values of the function.

An algorithm for finding extrema of a function using the second sufficient condition for an extremum.

1. Find the derivative.

2. Find the second derivative.

3. Find those points at which .

4. Determine the sign at these points.

5. Draw a conclusion about the existence and nature of extrema.

6. Find extreme values of the function.

Example. Let's consider . We'll find . Further, at and at . Let us study the critical points using the first sufficient condition for the extremum. We have that for and for , and for . At points and the derivative changes its sign: at from “+” to “–” and at at from “–” to “+”. This means that at a point the function has a maximum, and at a point it has a minimum; . For comparison, we study the critical points using the second sufficient condition for the extremum. Let's find the second derivative. We have: , and this means that at a point the function has a maximum, and at a point it has a minimum.

The concept of asymptote of a function graph. Horizontal, oblique and vertical asymptotes. Examples.

Definition. An asymptote of the graph of a function is a straight line that has the property that the distance from a point to this straight line tends to zero as the graph point moves indefinitely from the origin.

There are vertical (Fig. 6.6 a), horizontal (Fig. 6.6 b) and inclined (Fig. 6.6 c) asymptotes.

In Fig. 6.6a is shown vertical asymptote.

In Fig. 6.6b - horizontal asymptote.

In Fig. 6.6v – oblique asymptote.

Theorem 1. At points of vertical asymptotes (for example, ) the function suffers a discontinuity, its limit to the left and right of the point is equal to:

Theorem 2. Let the function be defined for sufficiently large and there are finite limits

AND .

Then the straight line is the oblique asymptote of the graph of the function.

Theorem 3. Let the function be defined for sufficiently large and there is a limit of the function. Then the straight line is the horizontal asymptote of the graph of the function.

The horizontal asymptote is a special case of the oblique asymptote, when . Therefore, if in any direction a curve has a horizontal asymptote, then in this direction there is no inclined one, and vice versa.

Example. Find the asymptotes of the graph of the function.

Solution. At the point the function is not defined, let’s find the limits of the function to the left and right of the point:

; .

Therefore, is a vertical asymptote.

General scheme for studying functions and constructing their graphs. Example.

General scheme of function research and plotting it.

1. Find the domain of definition.

2. Investigate the function for evenness - oddness.

3. Find vertical asymptotes and discontinuity points (if any).

4. Investigate the behavior of a function at infinity; find horizontal and oblique asymptotes (if any).

5. Find extrema and intervals of monotonicity of the function.

6. Find the points of intersection of the graph with the coordinate axes and, if necessary for schematic construction of the graph, find additional points.

7. Schematically draw a graph.

Detailed diagram of the function study and plotting .

1. Find the domain of definition .

a. If y has a denominator, it should not go to 0.

b. The radical expression of an even degree root must be non-negative (greater than or equal to zero).

c. The sublog expression must be positive.

2. Investigate the function for parity - oddness.

a. If , then the function is even.

b. If , then the function is odd.

c. If neither , nor , then is a function of general form.

3. Find vertical asymptotes and discontinuity points (if any).

a. A vertical asymptote can only occur at the boundary of the domain of definition of the function.

b. If ( or ), then is the vertical asymptote of the graph.

4. Investigate the behavior of a function at infinity; find horizontal and oblique asymptotes (if any).

a. If , then is the horizontal asymptote of the graph.

b. If , then the straight line is the inclined asymptote of the graph.

c. If the limits indicated in paragraphs a, b exist only when one-sided tends to infinity ( or ), then the resulting asymptotes will be one-sided: left-handed at and right-handed when .

5. Find extrema and intervals of monotonicity of the function.

a. Find the derivative.

b. Find critical points (those points where or where does not exist).

c. On the number axis, mark the domain of definition and its critical points.

d. On each of the resulting numerical intervals, determine the sign of the derivative.

e. Based on the signs of the derivative, draw a conclusion about the presence of extrema in y and their type.

f. Find extreme values.

g. Based on the signs of the derivative, draw conclusions about increasing and decreasing.

6. Find the points of intersection of the graph with the coordinate axes and, if necessary for schematic plotting of the graph, find additional points.

a. In order to find the points of intersection of the graph with the axis, it is necessary to solve the equation. The points where are zeros will be the points of intersection of the graph with the axis.

b. The point of intersection of the graph with the axis looks like . It exists only if the point is within the domain of the function.

8. Schematically draw a graph.

a. Construct a coordinate system and asymptotes.

b. Mark extreme points.

c. Mark the intersection points of the graph with the coordinate axes.

d. Schematically construct a graph so that it passes through the marked points and approaches the asymptotes.

Example. Explore the function and schematically construct its graph.

2. – function of general form.

3. Since and , then the lines and are vertical asymptotes; points are break points. , when is not included in the domain of definition of the function

Ticket No. 1

antiderivative functionTheoremProof indefinite integral

The point (X 0 ;Y 0) is called maximum point minimum point functions: for all points (x;y) different from (X 0 ;Y 0), from the δ-neighborhood of the point (X 0 ;Y 0) the inequality f(x;y)>f(X 0 ;Y 0) is satisfied .

Evidence:

Ticket No. 2

ProofGeometric meaning

private increment partial derivative Geometric meaning

Ticket No. 3

19. Determination of the maximum and minimum points of the function z=f(x,y). The point (X 0 ;Y 0) is called maximum point function z=f(x;y), if there is a δ-neighborhood of the point (X 0 ;Y 0) such that the inequality f(x;y) holds minimum point functions: for all points (x;y) different from (X 0 ;Y 0), from the δ-neighborhood of the point (X 0 ;Y 0) the inequality f(x;y)>f(X 0 ;Y 0) is satisfied . Let at a stationary point (X 0 ;Y 0) and some of its neighborhood the function f(x;y) have continuous partial derivatives up to the second order inclusive. Let us calculate at the point (X 0 ;Y 0) the values A=f"" xx (X 0 ;Y 0), B=f"" xy (X 0 ;Y 0), C=f"" yy (X 0 ;Y 0). Let us denote Δ=|AB; BC|=AC-B^2. Then: 1) if Δ><0; минимум, если A>0; 2) if Δ<0, то функция f(x;y) в точке (X 0 ;Y 0) экстремума не имеет. В случае Δ=0 экстремум в точке (X 0 ;Y 0) может быть, а может не быть. Необходимы дополнительные исследования.

Ticket No. 4 By a definite integral Properties Proof. at a point with coordinates (x;y;z).Δu/Δl=LimΔl→0(Δ l u/Δl)=(δu/δx)*cosα+(δu/δy)*cosβ+(δu/δz)*cosγ. Suppose that the function u(x;y;z) is continuous and has continuous derivatives with respect to its arguments in the domain D: Δu=(δu/δx)Δx+(δu/δy)Δy+(δu/δz)Δz+E 1 Δx+E 2 Δy+E 3 Δz, where E 1, E 2, E 3 tend to zero as Δl→0. Let us divide the entire equality by Δl. Δu/Δl=(δu/δx)(Δx/Δl)+(δu/δy)(Δy/Δl)+(δu/δz)(Δz/Δl)+E 1 (Δx/Δl)+E 2 (Δy/ Δl)+E 3 (Δz/Δl). Δx/Δl=cosα; Δy/Δl=cosβ; Δz/Δl=cosγ. The equality can be represented as follows: Δu/Δl=(δu/δx)cosα+(δu/δy)cosβ+(δu/δz)cosγ+E 1 cosα+E 2 cosβ+E 3 cosγ. Moving to the limit, we obtain Δu/Δl=LimΔl→0(Δ l u/Δl)=(δu/δx)*cosα+(δu/δy)*cosβ+(δu/δz)*cosγ.

Ticket No. 5

1. Antiderivative function. Theorem on the difference between two antiderivatives (with proof). Indefinite integral: definition The function F(x) is called antiderivative function f(x) on the interval (a;b), if for any x∈(a;b) the equality F"(x)=f(x) holds. Theorem. If the function F(x) is an antiderivative of the function f(x) on (a;b), then the set of all antiderivatives for f(x) is given by the formula F(x)+C, where C=const. Proof. The function F(x)+C is an antiderivative of f(x). Indeed, (F(x)+C)"=F"(x)=f(x). Let Ф(x) be some other antiderivative function f(x), different from F(x), i.e. Ф"(x)=f(x). Then for any x∈(a;b) we have (Ф(х)-F(x))"=Ф"(x)-F"(x)=f(x )-f(x)=0. And this means that Ф(x)-F(x)=C, C=const. Therefore, Ф(x)=F(x)+C. The set of all antiderivative functions F(x)+C for f(x) is called indefinite integral of the function f(x) and is denoted by the symbol ∫f(x)dx.

19. Determination of the maximum and minimum points of the function z=f(x,y). The point (X 0 ;Y 0) is called maximum point function z=f(x;y), if there is a δ-neighborhood of the point (X 0 ;Y 0) such that the inequality f(x;y) holds minimum point functions: for all points (x;y) different from (X 0 ;Y 0), from the δ-neighborhood of the point (X 0 ;Y 0) the inequality f(x;y)>f(X 0 ;Y 0) is satisfied . 20. A sufficient sign of the existence of an extremum of the function z=f(x;y). (wording). Let at a stationary point (X 0 ;Y 0) and some of its neighborhood the function f(x;y) have continuous partial derivatives up to the second order inclusive. Let us calculate at the point (X 0 ;Y 0) the values A=f"" xx (X 0 ;Y 0), B=f"" xy (X 0 ;Y 0), C=f"" yy (X 0 ;Y 0). Let us denote Δ=|AB; BC|=AC-B^2. Then: 1) if Δ>0, then the function f(x;y) at the point (X 0 ;Y 0) has an extremum: maximum if A<0; минимум, если A>0; 2) if Δ<0, то функция f(x;y) в точке (X 0 ;Y 0) экстремума не имеет. В случае Δ=0 экстремум в точке (X 0 ;Y 0) может быть, а может не быть. Необходимы дополнительные исследования.

Ticket No. 6

3. Calculation of a definite integral over a segment. Newton-Leibniz formula (derivation). If the function y=f(x) is continuous on an interval and F(x) is any of its antiderivatives on (F"(x)=f(x)), then the formula ∫(from a to b) f(x) holds )dx=F(b)-F(a). This formula is the Newton-Leibniz formula. Consider the identity: F(b)-F(a)=F(x n)-F(x 0)=(F(x n) -F(x n -1))+(f(x n -1)-F(x n -2))+…(F(x 2)-F(x 1))+(F(x 1)-F(x 0)). Let's transform each difference in brackets using the Lagrange formula: f(b)-f(a)=f'(c)*(b-a). We get F(b)-F(a)=F'(c n)( x n -x n -1)+F'(c n -1)(x n -1 -x n -2)+F'(c 2)(x 2 -x 1)+F'(c 1)(x 1 -x 0 )= ΣF'(Ci)ΔXi=Σf(Ci)ΔXi, that is, F(b)-F(a)= Σf(Ci)ΔXi, where Ci is some point of the interval (X i -1 ,X i). So since the function y=f(x) is continuous on , then it is integrable on . Therefore, there is a limit of the integral sum equal to the definite integral of f(x) on . Passing to the limit at λ=maxΔXi→0, we obtain F(b)-F( a)=lim Σf(Ci)ΔXi, that is, ∫(from a to b) f(x)dx=F(b)-F(a).

The function z=f(x;y) is called differentiable

11. Property of a differentiable function: connection between the differentiability of the function z=f(x;y) and the continuity of the function z=f(x;y) at a point (formulation, proof). If the function z=f(x;y) is differentiable at the point M(x;y), then it is continuous at this point and has partial derivatives at it. Proof. Let the function y=f(x) be differentiable at the point x 0 . At this point we give the argument an increment Δx. The function will receive an increment Δу. Let's find limΔx→0(Δy). limΔx→0(Δy)= limΔx→0((Δy*Δx)/Δx))= limΔx→0(Δy/Δx)* limΔx→0(Δx)=f"(x0)*0=0. Therefore, y =f(x) is continuous at the point x 0.

Ticket No. 7

A necessary sign of an extremum.

If a continuous function z=z(x,y) has an extremum at the point P0(x0,y0), then all its first-order partial derivatives at this point are either equal to zero or do not exist

Evidence: The partial derivative of the function z=f(x,y) with respect to x at the point P0(x0,y0) is the derivative of the function of one variable φ(x)=f(x,y0) at the point x-x0. But at this point the function φ(x) obviously has an extremum. Therefore, φ'(x0)=0. Since φ'(x0)=f'x(x0,y0), then f'x(x0,y0)=0 Similarly, it can be shown that f'y(x0,y0 )=0 . The theorem has been proven.

Ticket No. 8

6. The mean value theorem (formulation, proof, geometric meaning). If the function f(x) is continuous on the segment , then there is a point C∈ such that ∫(from a to b) f(x)dx=f(c)*(b-a). Proof. According to the Newton-Leibniz formula, we have ∫(from a to b) f(x)dx=F(x)|(from a to b)=F(b)-F(a), where F"(x)=f( x). Applying Lagrange's theorem (the theorem on the finite increment of a function) to the difference F(b)-F(a), we obtain F(b)-F(a)=F"(c)*(b-a)=f(c) *(b-a). Geometric meaning. The theorem for f(x)≥0 has a simple geometric meaning: the value of the definite integral is equal, for some C∈ (a;b), to the area of a rectangle with height f(c) and base b-a. The number f(c)=1/(b-a)∫(from a to b) f(x)dx is called the average value of the function f(x) on the segment.

8. Partial increments of the function z=f(x;y). Partial derivatives: definition and their geometric meaning. Let the function z=f(x;y) be given. Since x and y are independent variables, one of them can change while the other remains constant. Let's give the variable x an increment ∆x, keeping the value of the variable y unchanged. Then the function z will receive an increment, which we will call private increment z in x and denote ∆ x z. So, ∆ x z=f(x+∆x;y)–f(x;y). Similarly, we obtain the partial increment of z with respect to y: ∆ y z=f(x;у+∆y)–f(x;y).If there is a limit lim∆x→0(∆ x z/∆x)=lim∆x→0( (f(x+∆x;y)-f(x;y))/∆x), then it is called partial derivative function z=f(x;y) at the point M(x;y) in the variable x and is denoted by one of the symbols: z" x, δz/δx; f" x, δf/δx. Geometric meaning. The graph of the function z=f(x;y) is a certain surface. The graph of the function z=f(x 0 ;y 0) is the line of intersection of this surface with the plane y=y 0. Based on the geometric meaning of the derivative for a function of one variable, we conclude that f" x (x 0 ;y 0)=tgα, where α is the angle between the Ox axis and the tangent drawn to the curve z=f(x 0 ;y 0) in point M 0 (x 0 ;y 0 ;f(x 0 ;y 0)). Similar to f" y (x 0 ;y 0)=tgβ.

Ticket No. 9

Proof Geometric meaning

Tangent plane Normal to surface

Ticket No. 10

10. Definition of a differentiable function z=f(x;y) at a point. Definition of total differential dz and its form. The function z=f(x;y) is called differentiable at point M(x;y), if its total increment at this point can be represented as: ∆z=A*∆x+B*∆y+α*∆x+β*∆y, where α=α(∆ x;∆y)→0 and β=β(∆x;∆y)→0 for ∆x→0 and ∆y→0. The main part of the increment of the function z=f(x;y), linear with respect to ∆x and ∆y, is called full differential this function and is denoted by the symbol dz: dz=A*∆x+B*∆y. dz=(δz/δx)dx+(δz/δy)dy.

Ticket No. 11

4. Definition of a definite integral over a segment. Basic properties of a definite integral over a segment (with proof of one of them). By a definite integral over a segment of a function f(x), the limit of the integral sum Σf(c i)Δx i is called if this limit exists and does not depend either on the division of the segment into parts, or on the choice of points t inside each of the parts, provided that the length of the largest partial segments (∆xi) tends to zero, i.e. ∫(from a to b) f(x)dx=lim Δx i →0 Σf(c i)Δx i . Properties: 1) If c is a constant number and the function f(x) is integrable on , then ∫(from a to b) c*f(x)dx=c*∫(from a to b) f(x)dx.2) If the functions f 1 (x) b f 2 (x) are integrable on , then their sum is also integrable ∫(from a to b) (f 1 (x)+f 2 (x))dx=∫(from a to b) f 1 (x)dx+∫(from a to b) f 2 (x)dx. 3)∫(from a to b) f(x)dx= -∫(from b to a) f(x)dx. 4)If the function f(x) is integrable on and a

10. Definition of a differentiable function z=f(x;y) at a point. The function z=f(x;y) is called differentiable at point M(x;y), if its total increment at this point can be represented as: ∆z=A*∆x+B*∆y+α*∆x+β*∆y, where α=α(∆ x;∆y)→0 and β=β(∆x;∆y)→0 for ∆x→0 and ∆y→0.

12. Property of a differentiable function: connection between the differentiability of the function z=f(x,y) and the existence of partial derivatives at a point (formulation, proof). Theorem: If a function is differentiable at a point, then at this point there are finite partial derivatives, A and B are numerically equal Given: Δz=AΔx+BΔy+0(ρ) Prove: Ǝ(δz/δx(x 0 ;y 0)=A Proof: Let's give x 0 →Δx, y=y 0 =>Δ x z=(A*Δx+0(│x│). ρ=√(Δx 2 +Δy 2)=│Δx│. Δ x z/Δx=A +0(│x│)/Δx. LimΔx→0 (Δ x z/Δx)=lim=A. δz/Δx(x 0 ;y 0)=A. Similarly: Y 0 →Δy, x=x 0 => Δ y Z. δz/Δy(x 0 ;y 0)=B.

Ticket No. 12

Proof

Ticket No. 13

2. The problem of the area of a curvilinear trapezoid, leading to the concept of a definite integral over a segment. Definition of a definite integral over a segment. Let the function y=f(x)≥0 be given on the segment. A figure bounded above by the graph of the function y=f(x), below by the Ox axis, and on the side by straight lines x=a and x=b is called a curvilinear trapezoid. Let's find the area of this trapezoid. f(c 1)Δx 1 +f(c 2)Δx 2 +..+f(c n)Δx n =Σf(c i)Δx i =Sn. With a decrease in all values of Δx i, the accuracy of approximating a curvilinear trapezoid with a stepped figure and the accuracy of the resulting formula increase. Therefore, for the exact value of the area S of a curvilinear trapezoid, we take the limit S to which the area of the stepped figure Sn tends when n increases without limit so that λ=maxΔx i →0: S=lim n→∞ Sn=lim n→∞(λ→0 ) Σf(c i)Δx i , that is, S=∫(from a to b) f(x)dx. So, the definite integral of an indefinite function is numerically equal to the area of a curvilinear trapezoid. If the integral sum Sn has a limit I, which does not depend either on the method of dividing the segment into numerical segments or on the choice of points in them, then the number I is called the definite integral of the function y=f(x) on the segment and is denoted by ∫(from a to b) f(x)dx. Thus, ∫(from a to b) f(x)dx=lim n→∞(λ→0) Σf(c i)Δx i .

17. Tangent plane and normal to the surface (definition).Tangent plane to a surface at a point M, a plane passing through this point of the surface is called if the angle between this plane and the secant passing through the point M and any other point M 1 of the surface tends to zero as M tends to M 1. Normal to surface at a point M is a straight line passing through this point perpendicular to the tangent plane.

Ticket No. 14

5. Theorem on estimating a definite integral over a segment (formulation, proof, geometric meaning). Estimation of the integral. If m and M are, respectively, the smallest and largest values of the function y=f(x) on the segment , (a Proof. Since for any x∈ we have m≤f(x)≤M, then ∫(from a to b) mdx≤ ∫(from a to b) f(x)dx≤∫(from a to b) Mdx. We get: m(b-a)≤∫(from a to b) f(x)dx≤M(b-a). Geometric meaning. The area of a curvilinear trapezoid is enclosed between the areas of rectangles whose base is , and whose heights are m and M.

Ticket No. 15

Ticket No. 16

21. Derivative of the function u=u(x;y;z) in the direction l (definition). The limit LimΔl→0(Δu/Δl) is called derivative of the function u(x;y;z) in the direction of the vector l at a point with coordinates (x;y;z).

22. Gradient of the function u=u(x;y;z) at a point (definition). A vector with coordinates (δu/δx; δu/δy; δu/δz) is called

Ticket No. 17

7. Integral with a variable upper limit. Theorem on the derivative of an integral with a variable upper limit (formulation, proof). The derivative of a definite integral with respect to a variable upper limit is equal to the integrand in which the integration variable is replaced by this limit, that is, (∫(from a to x) f(t)dt)" x =f(x). Proof. According to the Newton-Leibniz formula, we have: ∫(from a to x) f(t)dt=F(t)|(from a to x)=F(x)-F(a). Therefore, (∫(from a to x) f(t)dt)" x =(F(x)-F(a))" x =F"(x)-0=f(x). This means that a definite integral with a variable upper limit is one of the antiderivatives of the integrand.

full increment continuous continuous

Ticket No. 18

1. Antiderivative function. Theorem on the difference between two antiderivatives (with proof). Indefinite integral: definition, simplest properties of the indefinite integral (with proof of one of them). The function F(x) is called antiderivative function f(x) on the interval (a;b), if for any x∈(a;b) the equality F"(x)=f(x) holds. Theorem. If the function F(x) is an antiderivative of the function f(x) on (a;b), then the set of all antiderivatives for f(x) is given by the formula F(x)+C, where C=const. Proof. The function F(x)+C is an antiderivative of f(x). Indeed, (F(x)+C)"=F"(x)=f(x). Let Ф(x) be some other antiderivative function f(x), different from F(x), i.e. Ф"(x)=f(x). Then for any x∈(a;b) we have (Ф(х)-F(x))"=Ф"(x)-F"(x)=f(x )-f(x)=0. And this means that Ф(x)-F(x)=C, C=const. Therefore, Ф(x)=F(x)+C. The set of all antiderivative functions F(x)+C for f(x) is called indefinite integral of the function f(x) and is denoted by the symbol ∫f(x)dx. Properties: 1) The differential of the indefinite integral is equal to the integrand, and the derivative of the indefinite integral is equal to the integrand d(∫f(x)dx)=f(x)dx, (∫f(x)dx)"=f(x).d (∫f(x)dx)=d(F(x)+C)=dF(x)+dC=F"(x)dx=f(x)dx. and (∫f(x)dx)"=(F(x)+C)"=F"(x)+0=f(x).2) The indefinite integral of the differential of some function is equal to the sum of this function and an arbitrary constant: ∫dF(x)=F(x)+C.∫dF(x)=F"(x)dx=∫f(x)dx=F(x)+C.3) The constant factor can be taken out of the integral sign: ∫af(x)dx=a∫f(x)dx.4) The indefinite integral of the algebraic sum of a finite number of continuous functions is equal to the algebraic sum of the integrals of the summands of the functions: ∫(f(x)±g(x))dx=∫f (x)dx±∫g(x)dx.5) (Invariance of the integration formula). If ∫f(x)dx=F(x)+C, then ∫f(u)du=F(u)+C, where u=φ(x) is an arbitrary function with a continuous derivative.

22. Gradient of the function u=u(x;y;z) at a point (definition, properties). Relationship between directional derivative and gradient of a function (rationale). A vector with coordinates (δu/δx; δu/δy; δu/δz) is called gradient of the function u=f(x;y;z) and is denoted by gradU=(δu/δx; δu/δy; δu/δz). gradU=(δu/δx)*i+(δu/δy)*j+(δu/δz)*k. Properties: 1)gradC=0; 2)grad(c*u)=c*gradU; 3)grad(u+v)=gradU+gradV; 4)grad(u*v)=u*gradV+v*gradU, where u*v are scalar products of vectors u and v. Connection. Let the function u=u(x;y;z) and the gradient field gradU=(δu/δx)*i+(δu/δy)*j+(δu/δz)*k be given. Then the derivative Δu/Δl in the direction of some vector l is equal to the projection of the vector GradU onto the vector l.

Ticket No. 19

4. Definition of a definite integral over a segment. Basic properties of a definite integral over a segment (with proof of one of them). By a definite integral over a segment of a function f(x), the limit of the integral sum Σf(c i)Δx i is called if this limit exists and does not depend either on the division of the segment into parts, or on the choice of points t inside each of the parts, provided that the length of the largest partial segments (∆xi) tends to zero, i.e. ∫(from a to b) f(x)dx=lim Δx i →0 Σf(c i)Δx i . Properties: 1) If c is a constant number and the function f(x) is integrable on , then ∫(from a to b) c*f(x)dx=c*∫(from a to b) f(x)dx. Proof. Let's compose the integral sum for the function c*f(x). We have Σс*f(c i)Δx i =с*Σf(c i)Δx i . Then lim n→∞ Σс*f(c i)Δx i =c*lim n→∞ f(c i)=с*∫(from a to b) f(x)dx. It follows that the function с*f(x) is integrable on and the formula ∫(from a to b) с*f(x)dx= с*∫(from a to b) f(x)dx.2) If the functions f 1 (x) b f 2 (x) are integrable on , then their sum is integrable and ∫(from a to b) (f 1 (x)+f 2 (x))dx=∫(from a to b) f 1 (x)dx+∫(from a to b) f 2 (x)dx. 3)∫(from a to b) f(x)dx= -∫(from b to a) f(x)dx. 4)If the function f(x) is integrable on and a

17. Tangent plane and normal to the surface (definition). Theorem on the existence of a tangent plane (formulation, proof). Tangent plane to a surface at a point M, a plane passing through this point of the surface is called if the angle between this plane and the secant passing through the point M and any other point M 1 of the surface tends to zero as M tends to M 1. Normal to surface at a point M is a straight line passing through this point perpendicular to the tangent plane. Theorem. If δF/δx; δF/δy; δF/δz are defined in the vicinity of the point Mo and are continuous at the point M 0 itself and at the same time do not vanish, then all the tangent lines to the lines on the surface lie in the same plane. Proof. L: system(x=x(t); y=y(t); z=z(t)). Tangent line (M 0 ;P) y=(x"(t 0); y"(t o); z"(t 0)). L∈Q (surface). F(x(t), y(t) , z(t))=0 is a complex function of the variable t. We use the rule of differentiability of a complex function: (δF/δx)*(dx/dt)+(δF/δy)*(dy/dt)+(δF/δz)*( dz/dt)=0; (δF(M 0)/δx)*x"(t 0)+(δF(M 0)/δy)*y"(t 0)+(δF(M 0)/δz) *z"(t 0)=0; g=(x"(t 0),y"(t 0),z"(t 0)); denote n=(δF(M 0)/δx; δF(M 0)/δy; δF(M 0) /δz); n⊥g. Since an infinite number of lines lying on the surface can be drawn through a given point, and an infinite number of tangent lines to them, therefore all tangent lines lie in the same plane.

Ticket No. 20

9. Full increment of the function z=f(x;y). Continuity of the function z=f(x;y) at a point (two definitions). Let the function z=f(x;y) be given. Let's give the independent variable x an increment ∆x, and the variable y an increment ∆y. Then full increment∆z of the function is determined by the equality: ∆z=f(x+∆x;y+∆y)-f(x;y). 1)The function z=f(x;y) is called continuous at the point M 0 (x 0 ;y 0)∈ D(z), if its limit at this point coincides with the value of the function at this point, i.e. limX→X 0 \Y→Y 0 (f(x;y))= f(x 0;y 0). 2) Function z=f(x;y) continuous on a set if it is continuous at every point of this set

Ticket No. 21

21. Derivative of the function u=u(x;y;z) in the direction l (definition, formula for calculation, derivation of the calculation formula). The limit LimΔl→0(Δu/Δl) is called derivative of the function u(x;y;z) in the direction of the vector l at a point with coordinates (x;y;z).Δu/Δl=LimΔl→0(Δ l u/Δl)=(δu/δx)*cosα+(δu/δy)*cosβ+(δu/δz)*cosγ. Suppose that the function u(x;y;z) is continuous and has continuous derivatives with respect to its arguments in the domain D: Δu=(δu/δx)Δx+(δu/δy)Δy+(δu/δz)Δz+E 1 Δx+E 2 Δy+E 3 Δz, where E 1, E 2, E 3 tend to zero as Δl→0. Let us divide the entire equality by Δl. Δu/Δl=(δu/δx)(Δx/Δl)+(δu/δy)(Δy/Δl)+(δu/δz)(Δz/Δl)+E 1 (Δx/Δl)+E 2 (Δy/ Δl)+E 3 (Δz/Δl). Δx/Δl=cosα; Δy/Δl=cosβ; Δz/Δl=cosγ. The equality can be represented as follows: Δu/Δl=(δu/δx)cosα+(δu/δy)cosβ+(δu/δz)cosγ+E 1 cosα+E 2 cosβ+E 3 cosγ. Moving to the limit, we obtain Δu/Δl=LimΔl→0(Δ l u/Δl)=(δu/δx)*cosα+(δu/δy)*cosβ+(δu/δz)*cosγ.

Ticket No. 22

20. A sufficient sign of the existence of an extremum of the function z=f(x;y). (wording). Let at a stationary point (X 0 ;Y 0) and some of its neighborhood the function f(x;y) have continuous partial derivatives up to the second order inclusive. Let us calculate at the point (X 0 ;Y 0) the values A=f"" xx (X 0 ;Y 0), B=f"" xy (X 0 ;Y 0), C=f"" yy (X 0 ;Y 0). Let us denote Δ=|AB; BC|=AC-B^2. Then: 1) if Δ>0, then the function f(x;y) at the point (X 0 ;Y 0) has an extremum: maximum if A<0; минимум, если A>0; 2) if Δ<0, то функция f(x;y) в точке (X 0 ;Y 0) экстремума не имеет. В случае Δ=0 экстремум в точке (X 0 ;Y 0) может быть, а может не быть. Необходимы дополнительные исследования.

Ticket No. 23

17. Tangent plane to a surface (definition).Tangent plane to a surface at a point M, a plane passing through this point of the surface is called if the angle between this plane and the secant passing through the point M and any other point M 1 of the surface tends to zero as M tends to M 1.

18. Equations of a tangent plane to a surface specified explicitlyObviously. z=f(x;y) at point Mo(Xo;Yo;Zo). K: (δz/δx)|M 0 (X-X 0)+(δz/δy)|M 0 (Y-Y 0)-(Z-Z 0)=0

Ticket No. 24