Integrale aus trigonometrische Funktionen.
Beispiele für Lösungen

In dieser Lektion betrachten wir Integrale trigonometrischer Funktionen, das heißt, die Füllung der Integrale besteht aus Sinus, Cosinus, Tangens und Kotangens in verschiedenen Kombinationen. Alle Beispiele werden detailliert analysiert, zugänglich und auch für eine Teekanne verständlich.

Um Integrale trigonometrischer Funktionen erfolgreich zu studieren, müssen Sie die einfachsten Integrale gut verstehen und einige Integrationstechniken beherrschen. Diese Materialien können Sie in Vorlesungen kennenlernen Unbestimmtes Integral. Beispiele für Lösungen Und .

Und jetzt brauchen wir: Tabelle der Integrale, Derivatetabelle Und Verzeichnis trigonometrischer Formeln. Alle methodische Handbücher finden Sie auf der Seite Mathematische Formeln und Tabellen. Ich empfehle, alles auszudrucken. Ich konzentriere mich besonders auf trigonometrische Formeln, Sie sollten vor Ihren Augen sein– ohne dies wird die Arbeitseffizienz spürbar sinken.

Aber zuerst geht es in diesem Artikel darum, was Integrale sind Nein. Es gibt keine Integrale der Form , - Kosinus, Sinus, multipliziert mit einem Polynom (seltener etwas mit Tangens oder Kotangens). Solche Integrale werden nach Teilen integriert. Um die Methode zu erlernen, besuchen Sie die Lektion Integration nach Teilen. Beispiele für Lösungen. Auch hier gibt es keine Integrale mit „Bögen“ – Arkustangens, Arkussinus usw., sie werden auch am häufigsten durch Teile integriert.

Beim Finden von Integralen trigonometrischer Funktionen werden verschiedene Methoden verwendet:

(4) Wir verwenden die tabellarische Formel Der einzige Unterschied besteht darin, dass wir anstelle von „X“ einen komplexen Ausdruck haben.

Beispiel 2

Beispiel 3

Finden Sie das unbestimmte Integral.

Ein Klassiker des Genres für diejenigen, die im Wettbewerb untergehen. Wie Sie wahrscheinlich bemerkt haben, gibt es in der Integraltabelle kein Integral von Tangens und Kotangens, aber dennoch können solche Integrale gefunden werden.

(1) Wir verwenden die trigonometrische Formel

(2) Wir bringen die Funktion unter das Differentialzeichen.

(3) Wir verwenden das Tabellenintegral .

Beispiel 4

Finden Sie das unbestimmte Integral.

Dies ist ein Beispiel für eine unabhängige Lösung. Die vollständige Lösung und Antwort finden Sie am Ende der Lektion.

Beispiel 5

Finden Sie das unbestimmte Integral.

Unsere Abschlüsse werden nach und nach steigen =).
Zuerst die Lösung:

(1) Wir verwenden die Formel

(2) Wir verwenden die trigonometrische Hauptidentität , woraus folgt .

(3) Teilen Sie den Zähler Term für Term durch den Nenner.

(4) Wir nutzen die Linearitätseigenschaft des unbestimmten Integrals.

(5) Wir integrieren mithilfe der Tabelle.

Beispiel 6

Finden Sie das unbestimmte Integral.

Dies ist ein Beispiel für eine unabhängige Lösung. Die vollständige Lösung und Antwort finden Sie am Ende der Lektion.

Es gibt auch Integrale von Tangenten und Kotangenten, die mehr sind hohe Abschlüsse. Das Integral des kubischen Tangens wird in der Lektion besprochen Wie berechnet man die Fläche einer flachen Figur? Integrale des Tangens (Kotangens) an die vierte und fünfte Potenz können auf der Seite ermittelt werden Komplexe Integrale.

Reduzierung des Integrandengrads

Diese Technik funktioniert, wenn die Integrandenfunktionen mit Sinus- und Cosinuswerten gefüllt sind sogar Grad. Um den Grad zu reduzieren, verwenden Sie trigonometrische Formeln , und , und die letzte Formel wird oft in die entgegengesetzte Richtung verwendet: .

Beispiel 7

Finden Sie das unbestimmte Integral.

Lösung:

Im Prinzip gibt es hier nichts Neues, außer dass wir die Formel angewendet haben (Erniedrigung des Integrandengrades). Bitte beachten Sie, dass ich die Lösung gekürzt habe. Mit zunehmender Erfahrung kann das Integral von mündlich gefunden werden; das spart Zeit und ist bei der Erledigung von Aufgaben durchaus akzeptabel. In diesem Fall ist es ratsam, die Regel nicht zu beschreiben , zuerst bilden wir verbal das Integral von 1, dann von .

Beispiel 8

Finden Sie das unbestimmte Integral.

Dies ist ein Beispiel für eine unabhängige Lösung. Die vollständige Lösung und Antwort finden Sie am Ende der Lektion.

Das ist die versprochene Abschlusssteigerung:

Beispiel 9

Finden Sie das unbestimmte Integral.

Erst die Lösung, dann die Kommentare:

(1) Bereiten Sie den Integranden vor, um die Formel anzuwenden .

(2) Wir wenden die Formel tatsächlich an.

(3) Wir quadrieren den Nenner und entnehmen aus dem Integralzeichen die Konstante. Es hätte etwas anders gemacht werden können, aber meiner Meinung nach war es bequemer.

(4) Wir verwenden die Formel

(5) Im dritten Term reduzieren wir den Grad erneut, verwenden jedoch die Formel .

(6) Wir präsentieren ähnliche Begriffe (hier habe ich Begriff für Begriff unterteilt). und machte die Addition).

(7) Eigentlich nehmen wir das Integral, die Linearitätsregel und die Methode zur Subsumierung einer Funktion unter dem Differentialzeichen wird mündlich durchgeführt.

(8) Kombination der Antwort.

! Bei einem unbestimmten Integral kann die Antwort oft auf verschiedene Arten geschrieben werden

In dem gerade betrachteten Beispiel hätte die endgültige Antwort auch anders geschrieben werden können – das Öffnen der Klammern und dies sogar vor der Integration des Ausdrucks, d. h. der folgende Abschluss des Beispiels ist durchaus akzeptabel:

Es ist durchaus möglich, dass diese Option noch bequemer ist, ich habe es nur so erklärt, wie ich es selbst gewohnt bin, es zu lösen. Hier ist ein weiteres typisches Beispiel für eine unabhängige Lösung:

Beispiel 10

Finden Sie das unbestimmte Integral.

Dieses Beispiel kann auf zwei Arten gelöst werden, und möglicherweise gelingt es Ihnen zwei völlig unterschiedliche Antworten(Genauer gesagt werden sie völlig anders aussehen, aber aus mathematischer Sicht sind sie gleichwertig). Höchstwahrscheinlich werden Sie nicht die rationalste Methode sehen und Probleme mit dem Öffnen von Klammern und der Verwendung anderer trigonometrischer Formeln haben. Die effektivste Lösung wird am Ende der Lektion angegeben.

Um den Absatz zusammenzufassen, schließen wir: jedes Integral der Form , wo und - sogar Zahlen, wird durch die Methode der Reduzierung des Integrandengrades gelöst.
In der Praxis stieß ich auf Integrale mit 8 und 10 Grad, und ich musste ihr schreckliches Durcheinander lösen, indem ich den Grad mehrmals verringerte, was zu langen, langen Antworten führte.

Variable Ersetzungsmethode

Wie im Artikel erwähnt Methode zur Variablenänderung im unbestimmten Integral Die Hauptvoraussetzung für die Verwendung der Ersetzungsmethode ist die Tatsache, dass es im Integranden eine bestimmte Funktion und deren Ableitung gibt:
(Funktionen sind nicht unbedingt im Produkt enthalten)

Beispiel 11

Finden Sie das unbestimmte Integral.

Wir schauen uns die Ableitungstabelle an und bemerken die Formeln, , das heißt, in unserem Integranden gibt es eine Funktion und ihre Ableitung. Wir sehen jedoch, dass sich bei der Differenzierung Kosinus und Sinus gegenseitig ineinander umwandeln, und es stellt sich die Frage: Wie führt man eine Änderung der Variablen durch und was verstehen wir unter Sinus oder Kosinus?! Die Frage kann durch wissenschaftliche Forschung gelöst werden: Wenn wir den Austausch falsch durchführen, wird nichts Gutes dabei herauskommen.

Eine allgemeine Richtlinie: In ähnlichen Fällen müssen Sie die Funktion angeben, die im Nenner steht.

Wir unterbrechen die Lösung und führen einen Ersatz durch

Im Nenner ist alles in Ordnung, alles hängt nur davon ab, jetzt bleibt abzuwarten, was daraus wird.
Dazu ermitteln wir das Differential:

Oder kurz gesagt:
Aus der resultierenden Gleichheit drücken wir unter Verwendung der Proportionsregel den Ausdruck aus, den wir benötigen:

Also:

Jetzt hängt unser gesamter Integrand nur noch davon ab und wir können mit der Lösung fortfahren

Bereit. Ich möchte Sie daran erinnern, dass der Zweck der Ersetzung darin besteht, den Integranden zu vereinfachen; in diesem Fall kam es auf die Integration an Power-Funktion laut Tabelle.

Es ist kein Zufall, dass ich dieses Beispiel so ausführlich beschrieben habe; dies geschah zum Zweck der Wiederholung und Vertiefung des Unterrichtsstoffs Methode zur Variablenänderung im unbestimmten Integral.

Und nun zwei Beispiele für Ihre eigene Lösung:

Beispiel 12

Finden Sie das unbestimmte Integral.

Beispiel 13

Finden Sie das unbestimmte Integral.

Vollständige Lösungen und Antworten am Ende der Lektion.

Beispiel 14

Finden Sie das unbestimmte Integral.

Auch hier gibt es im Integranden Sinus und Cosinus (eine Funktion mit Ableitung), aber im Produkt entsteht ein Dilemma: Was meinen wir mit Sinus oder Cosinus?

Sie können versuchen, einen Ersatz mit der wissenschaftlichen Methode durchzuführen, und wenn nichts funktioniert, dann kennzeichnen Sie ihn als eine andere Funktion, aber es gibt:

Allgemeine Richtlinie: Sie müssen die Funktion bezeichnen, die sich im übertragenen Sinne in einer „unbequemen Position“ befindet..

Wir sehen, dass in diesem Beispiel der Studentenkosinus unter dem Grad „leidet“ und der Sinus frei und für sich allein sitzt.

Machen wir deshalb einen Ersatz:

Wenn jemand immer noch Schwierigkeiten mit dem Algorithmus zum Ersetzen einer Variablen und zum Finden des Differentials hat, sollten Sie zur Lektion zurückkehren Methode zur Variablenänderung im unbestimmten Integral.

Beispiel 15

Finden Sie das unbestimmte Integral.

Lassen Sie uns den Integranden analysieren. Was sollte mit bezeichnet werden?
Erinnern wir uns an unsere Richtlinien:
1) Die Funktion liegt höchstwahrscheinlich im Nenner;
2) Die Funktion befindet sich in einer „unbequemen Position“.

Diese Richtlinien gelten übrigens nicht nur für trigonometrische Funktionen.

Da der Sinus beide Kriterien erfüllt (insbesondere das zweite), liegt ein Austausch nahe. Im Prinzip kann der Austausch bereits durchgeführt werden, aber zunächst wäre es schön herauszufinden, was man damit machen soll? Zuerst „kneifen“ wir einen Kosinus ab:

Wir reservieren für unsere „zukünftige“ Differenzierung

Und wir drücken es durch den Hauptsinus aus trigonometrische Identität:

Hier nun der Ersatz:

Allgemeine Regel: Wenn im Integranden eine der trigonometrischen Funktionen (Sinus oder Cosinus) enthalten ist seltsam Grad, dann müssen Sie eine Funktion vom ungeraden Grad „abbeißen“ und dahinter eine andere Funktion bezeichnen. Wir sprechen nur von Integralen, bei denen es Kosinus und Sinus gibt.

Im betrachteten Beispiel hatten wir einen Kosinus mit einer ungeraden Potenz, also haben wir einen Kosinus aus der Potenz genommen und ihn als Sinus bezeichnet.

Beispiel 16

Finden Sie das unbestimmte Integral.

Die Abschlüsse nehmen Fahrt auf =).
Dies ist ein Beispiel, das Sie selbst lösen können. Komplette Lösung und die Antwort am Ende der Lektion.

Universelle trigonometrische Substitution

Die universelle trigonometrische Substitution ist ein häufiger Fall der Variablenersetzungsmethode. Sie können versuchen, es zu verwenden, wenn Sie „nicht wissen, was Sie tun sollen“. Tatsächlich gibt es jedoch einige Richtlinien für die Anwendung. Typische Integrale, bei denen die universelle trigonometrische Substitution angewendet werden muss, sind die folgenden Integrale: , , , usw.

Beispiel 17

Finden Sie das unbestimmte Integral.

Die universelle trigonometrische Substitution wird in diesem Fall wie folgt implementiert. Ersetzen wir: . Ich verwende nicht den Buchstaben , aber der Buchstabe , das ist keine Regel, ich bin es nur gewohnt, Dinge auf diese Weise zu lösen.

Hier ist es bequemer, das Differential zu finden; dafür drücke ich aus der Gleichheit aus:
Ich füge an beide Teile einen Arcustangens an:

Arcustangens und Tangens heben sich gegenseitig auf:

Auf diese Weise:

In der Praxis muss man es nicht so ausführlich beschreiben, sondern einfach anwenden fertiges Ergebnis:

! Der Ausdruck ist nur gültig, wenn wir unter den Sinus- und Cosinuswerten einfach „X“ für das Integral haben (worüber wir später sprechen werden) Alles wird ein wenig anders sein!

Beim Ersetzen werden Sinus und Cosinus zu folgenden Brüchen:
, , diese Gleichungen basieren auf bekannten trigonometrischen Formeln: ,

Das endgültige Design könnte also so aussehen:

Führen wir eine universelle trigonometrische Substitution durch:

Im Detail werden Beispiele für partielle Integrallösungen betrachtet, deren Integrand das Produkt eines Polynoms mit einer Exponentialfunktion (e hoch x) oder mit einem Sinus (sin x) oder einem Cosinus (cos x) ist.

Inhalt

Siehe auch: Methode der partiellen Integration
Tabelle der unbestimmten Integrale
Methoden zur Berechnung unbestimmter Integrale
Grundlegende Elementarfunktionen und ihre Eigenschaften

Formel für die partielle Integration

Bei der Lösung der Beispiele in diesem Abschnitt wird die Formel für die partielle Integration verwendet:
;
.

Beispiele für Integrale, die das Produkt eines Polynoms und sin x, cos x oder e x enthalten

Hier sind Beispiele für solche Integrale:
, , .

Um solche Integrale zu integrieren, wird das Polynom mit u und der verbleibende Teil mit v dx bezeichnet. Als nächstes wenden Sie die Formel für die partielle Integration an.

Unten ist angegeben detaillierte Lösung diese Beispiele.

Beispiele für die Lösung von Integralen

Beispiel mit Exponent, e hoch x

Bestimmen Sie das Integral:
.

Führen wir den Exponenten unter dem Differentialzeichen ein:
e - x dx = - e - x d(-x) = - d(e - x).

Lassen Sie uns nach Teilen integrieren.

Hier
.
Wir integrieren auch das verbleibende Integral nach Teilen.
.
.
.
Endlich haben wir:
.

Ein Beispiel für die Definition eines Integrals mit Sinus

Berechnen Sie das Integral:
.

Lassen Sie uns den Sinus unter dem Differentialzeichen einführen:

Lassen Sie uns nach Teilen integrieren.

hier u = x 2 , v = cos(2 x+3), du = ( x 2 )′ dx

Wir integrieren auch das verbleibende Integral nach Teilen. Führen Sie dazu den Kosinus unter dem Differentialzeichen ein.


hier u = x, v = Sünde(2 x+3), du = dx

Endlich haben wir:

Beispiel für das Produkt eines Polynoms und eines Kosinus

Berechnen Sie das Integral:
.

Führen wir den Kosinus unter dem Differentialzeichen ein:

Lassen Sie uns nach Teilen integrieren.

hier u = x 2 + 3 x + 5, v = Sünde 2 x, du = ( x 2 + 3 x + 5 )′ dx

Tabelle der Stammfunktionen („Integrale“). Tabelle der Integrale. Tabellarische unbestimmte Integrale. (Die einfachsten Integrale und Integrale mit einem Parameter). Formeln für die partielle Integration. Newton-Leibniz-Formel.

Tabelle der Stammfunktionen („Integrale“). Tabellarische unbestimmte Integrale. (Die einfachsten Integrale und Integrale mit einem Parameter).
Integral einer Potenzfunktion.	Integral einer Potenzfunktion.
Ein Integral, das sich auf das Integral einer Potenzfunktion reduziert, wenn x unter dem Differentialvorzeichen gesteuert wird.
	Integral einer Exponentialfunktion, wobei a eine konstante Zahl ist.
Integraler Komplex Exponentialfunktion.	Integral einer Exponentialfunktion.
Ein Integral, das dem natürlichen Logarithmus entspricht.	Integral: „Langer Logarithmus“.
	Integral: „Langer Logarithmus“.
Integral: „Hoher Logarithmus“.	Ein Integral, bei dem x im Zähler unter dem Differentialzeichen steht (die Konstante unter dem Vorzeichen kann entweder addiert oder subtrahiert werden), ähnelt letztendlich einem Integral, das dem natürlichen Logarithmus entspricht.
Integral: „Hoher Logarithmus“.
Kosinusintegral.	Sinusintegral.
Integral gleich Tangens.	Integral gleich Kotangens.
Integral gleich Arkussinus und Arkuskosinus
Ein Integral, das sowohl Arkussinus als auch Arkuskosinus entspricht.	Ein Integral, das sowohl dem Arkustangens als auch dem Arkuskotangens entspricht.
Integral gleich Kosekans.	Integral gleich Sekante.
Integral gleich Arcsecants.	Integral gleich Arkuskosekant.
Integral gleich Arcsecants.	Integral gleich Arcsecants.
Integral gleich dem hyperbolischen Sinus.	Integral gleich dem hyperbolischen Kosinus.
Integral gleich dem hyperbolischen Sinus, wobei sinhx in der englischen Version der hyperbolische Sinus ist.	Integral gleich dem hyperbolischen Kosinus, wobei sinhx in der englischen Version der hyperbolische Sinus ist.
Integral gleich dem Tangens hyperbolicus.	Integral gleich dem hyperbolischen Kotangens.
Integral gleich der hyperbolischen Sekante.	Integral gleich dem hyperbolischen Kosekans.

Formeln für die partielle Integration. Integrationsregeln.

Formeln für die partielle Integration. Newton-Leibniz-Formel. Integrationsregeln.
Integrieren eines Produkts (einer Funktion) durch eine Konstante:
Integration der Funktionssumme:
unbestimmte Integrale:
Formel für die partielle Integration bestimmte Integrale:
Newton-Leibniz-Formel bestimmte Integrale:	Wobei F(a),F(b) die Werte der Stammfunktionen an den Punkten b bzw. a sind.

Tabelle der Derivate. Tabellarische Ableitungen. Derivat des Produkts. Ableitung des Quotienten. Ableitung einer komplexen Funktion.

Wenn x eine unabhängige Variable ist, dann:

Tabelle der Derivate. Tabellarische Ableitungen „Tabellenableitung“ – ja leider wird im Internet genau so danach gesucht
	Ableitung einer Potenzfunktion
	Ableitung des Exponenten
Ableitung einer komplexen Exponentialfunktion	Ableitung der Exponentialfunktion
Ableitung einer logarithmischen Funktion	Ableitung des natürlichen Logarithmus
	Ableitung des natürlichen Logarithmus einer Funktion
Ableitung des Sinus	Ableitung des Kosinus
Ableitung des Kosekans	Ableitung einer Sekante
Ableitung des Arkussinus	Ableitung des Arkuskosinus
Ableitung des Arkussinus	Ableitung des Arkuskosinus
Tangentenableitung	Ableitung des Kotangens
Ableitung des Arkustangens	Ableitung des Arcuskotangens
Ableitung des Arkustangens	Ableitung des Arcuskotangens
Ableitung von Arcsecant	Ableitung von Arkuskosekant
Ableitung von Arcsecant	Ableitung von Arkuskosekant
Ableitung des hyperbolischen Sinus Ableitung des hyperbolischen Sinus in der englischen Version	Ableitung des hyperbolischen Kosinus Ableitung des hyperbolischen Kosinus in der englischen Version
Ableitung des hyperbolischen Tangens	Ableitung des hyperbolischen Kotangens
Ableitung der hyperbolischen Sekante	Ableitung des hyperbolischen Kosekans

Differenzierungsregeln. Derivat des Produkts. Ableitung des Quotienten. Ableitung einer komplexen Funktion.
Ableitung eines Produkts (Funktion) durch eine Konstante:
Ableitung der Summe (Funktionen):
Ableitung von Produkt (Funktionen):
Ableitung des Quotienten (von Funktionen):
Ableitung einer komplexen Funktion:

Eigenschaften von Logarithmen. Grundformeln für Logarithmen. Dezimal (lg) und natürlicher Logarithmus (ln).

Grundlagen logarithmische Identität
Lassen Sie uns zeigen, wie jede Funktion der Form a b exponentiell gemacht werden kann. Da eine Funktion der Form e x dann exponentiell heißt
Jede Funktion der Form a b kann als Zehnerpotenz dargestellt werden

Natürlicher Logarithmus ln (Logarithmus zur Basis e = 2,718281828459045...) ln(e)=1; ln(1)=0

Taylor-Reihe. Taylorreihenentwicklung einer Funktion.

Es stellt sich heraus, dass die Mehrheit praktisch angetroffen Mathematische Funktionen können in der Nähe eines bestimmten Punktes mit beliebiger Genauigkeit in Form von Potenzreihen dargestellt werden, die Potenzen einer Variablen in aufsteigender Reihenfolge enthalten. Zum Beispiel in der Nähe des Punktes x=1:

Bei Verwendung von Serien namens Taylors Reihen Gemischte Funktionen, die beispielsweise algebraische, trigonometrische und exponentielle Funktionen enthalten, können als rein algebraische Funktionen ausgedrückt werden. Mithilfe von Reihen lassen sich Differenzierungen und Integrationen häufig schnell durchführen.

Die Taylor-Reihe in der Umgebung von Punkt a hat die Form:

1) , wobei f(x) eine Funktion ist, die Ableitungen aller Ordnungen bei x = a hat. R n – der Restterm in der Taylor-Reihe wird durch den Ausdruck bestimmt

2)

Der k-te Koeffizient (bei x k) der Reihe wird durch die Formel bestimmt

3) Ein Sonderfall der Taylor-Reihe ist die Maclaurin-Reihe (= McLaren-Reihe). (Die Erweiterung erfolgt um den Punkt a=0)

bei a=0

Mitglieder der Reihe werden durch die Formel bestimmt

Bedingungen für die Verwendung von Taylor-Reihen.

1. Damit die Funktion f(x) zu einer Taylor-Reihe auf dem Intervall (-R;R) entwickelt werden kann, ist es notwendig und ausreichend, dass der Restterm in der Taylor-Formel (Maclaurin (=McLaren)) hierfür verwendet wird Die Funktion tendiert gegen Null, wenn k →∞ im angegebenen Intervall (-R;R) ist.

2. Es ist notwendig, dass es Ableitungen für eine gegebene Funktion an dem Punkt gibt, in dessen Nähe wir die Taylor-Reihe konstruieren werden.

Eigenschaften der Taylor-Reihe.

Wenn f eine analytische Funktion ist, dann konvergiert ihre Taylor-Reihe an jedem Punkt a im Definitionsbereich von f gegen f in einer Umgebung von a.

Es gibt unendlich differenzierbare Funktionen, deren Taylor-Reihe konvergiert, sich aber gleichzeitig von der Funktion in jeder Umgebung von a unterscheidet. Zum Beispiel:

Taylor-Reihen werden in Näherung verwendet (Näherung - wissenschaftliche Methode, die darin besteht, einige Objekte durch andere zu ersetzen, die in gewisser Weise den ursprünglichen ähnlich sind, aber einfacher sind) Funktionen durch Polynome. Insbesondere die Linearisierung ((von linearis – linear), eine der Methoden zur Näherungsdarstellung geschlossener nichtlinearer Systeme, bei der die Untersuchung eines nichtlinearen Systems durch die Analyse eines linearen Systems ersetzt wird, das in gewissem Sinne dem ursprünglichen entspricht .) Gleichungen entstehen durch die Erweiterung zu einer Taylor-Reihe und das Abschneiden aller Terme oberhalb der ersten Ordnung.

Somit kann nahezu jede Funktion mit einer bestimmten Genauigkeit als Polynom dargestellt werden.

Beispiele einiger häufiger Entwicklungen von Potenzfunktionen in Maclaurin-Reihen (=McLaren, Taylor in der Nähe von Punkt 0) und Taylor in der Nähe von Punkt 1. Die ersten Terme von Entwicklungen der Hauptfunktionen in Taylor- und McLaren-Reihen.

Beispiele für einige gängige Entwicklungen von Potenzfunktionen in Maclaurin-Reihen (=McLaren, Taylor in der Nähe von Punkt 0)

Beispiele für einige gängige Taylor-Reihenentwicklungen in der Nähe von Punkt 1

Es wird auch Probleme geben, die Sie selbst lösen müssen und auf die Sie die Antworten sehen können.

Der Integrand kann vom Produkt trigonometrischer Funktionen in die Summe umgewandelt werden

Betrachten wir Integrale, bei denen der Integrand das Produkt von Sinus und Cosinus ersten Grades von x multipliziert mit verschiedenen Faktoren ist, also Integrale der Form

Bekanntes ausnutzen trigonometrische Formeln

(2)
(3)
(4)
man kann jedes der Produkte in Integrale der Form (31) umwandeln algebraische Summe und mithilfe der Formeln integrieren

(5)

(6)

Beispiel 1. Finden

Lösung. Nach Formel (2) bei

Beispiel 2. Finden Integral einer trigonometrischen Funktion

Lösung. Nach Formel (3) bei

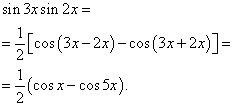
Beispiel 3. Finden Integral einer trigonometrischen Funktion

Lösung. Nach Formel (4) bei wir erhalten die folgende Transformation des Integranden:

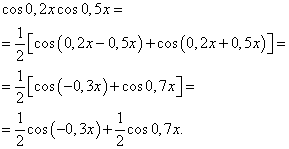
Wenn wir Formel (6) anwenden, erhalten wir

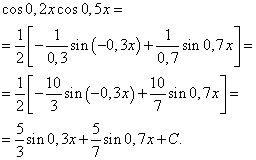
Integral des Produkts der Sinus- und Cosinuspotenzen desselben Arguments

Betrachten wir nun Integrale von Funktionen, die das Produkt von Sinus- und Cosinuspotenzen desselben Arguments sind, d. h.

(7)

In besonderen Fällen kann einer der Indikatoren ( M oder N) kann Null sein.

Bei der Integration solcher Funktionen wird davon ausgegangen, dass eine gerade Potenz des Kosinus durch den Sinus ausgedrückt werden kann und das Differential des Sinus gleich dem Kosinus ist xdx(oder sogar die Potenz des Sinus kann als Kosinus ausgedrückt werden, und das Differential des Kosinus ist gleich - sin xdx ) .

Es sind zwei Fälle zu unterscheiden: 1) mindestens einer der Indikatoren M Und N seltsam; 2) Beide Indikatoren sind gerade.

Lassen Sie den ersten Fall eintreten, nämlich den Indikator N = 2k+ 1 - ungerade. Dann, wenn man das bedenkt

Der Integrand wird so dargestellt, dass ein Teil davon nur eine Funktion des Sinus ist und der andere Teil das Differential des Sinus ist. Verwenden Sie jetzt die Variablenersetzung T= Sünde X Die Lösung reduziert sich auf die Integration des Polynoms bezüglich T. Wenn nur der Abschluss M seltsam ist, dann machen sie dasselbe und isolieren den Faktor Sünde X, der den Rest des Integranden in Form von cos ausdrückt X und glauben T=cos X. Diese Technik kann auch verwendet werden, wenn Integration der Quotientenpotenzen von Sinus und Cosinus , Wann Mindestens einer der Indikatoren ist seltsam . Der springende Punkt ist das der Quotient der Potenzen von Sinus und Cosinus ist besonderer Fall ihre Werke : Wenn eine trigonometrische Funktion im Nenner eines Integranden steht, ist ihr Grad negativ. Es gibt aber auch Fälle partieller trigonometrischer Funktionen, deren Potenzen nur gerade sind. Über sie - im nächsten Absatz.

Wenn beide Indikatoren M Und N– also sogar unter Verwendung trigonometrischer Formeln

Reduzieren Sie die Exponenten von Sinus und Cosinus, woraufhin ein Integral des gleichen Typs wie oben erhalten wird. Daher sollte die Integration nach dem gleichen Schema fortgesetzt werden. Wenn einer der geraden Exponenten negativ ist, also der Quotient gerader Potenzen von Sinus und Cosinus betrachtet wird, ist dieses Schema nicht geeignet . Dann wird eine Variablenänderung verwendet, je nachdem, wie der Integrand transformiert werden kann. Ein solcher Fall wird im nächsten Absatz behandelt.

Beispiel 4. Finden Integral einer trigonometrischen Funktion

Lösung. Der Kosinus-Exponent ist ungerade. Stellen wir uns daher vor

T= Sünde X(Dann dt=cos X dx ). Dann bekommen wir

Zurück zur alten Variablen finden wir endlich

Beispiel 5. Finden Integral einer trigonometrischen Funktion

.

Lösung. Der Kosinus-Exponent ist wie im vorherigen Beispiel ungerade, aber größer. Stellen wir uns vor

und nehmen Sie eine Änderung der Variablen vor T= Sünde X(Dann dt=cos X dx ). Dann bekommen wir

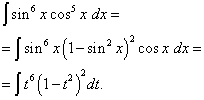
Öffnen wir die Klammern

und wir bekommen

Wenn wir zur alten Variablen zurückkehren, erhalten wir die Lösung

Beispiel 6. Finden Integral einer trigonometrischen Funktion

Lösung. Die Exponenten von Sinus und Cosinus sind gerade. Daher transformieren wir die Integrandenfunktion wie folgt:

Dann bekommen wir

Im zweiten Integral nehmen wir eine Änderung der Variablen Einstellung vor T= sin2 X. Dann (1/2)dt= cos2 X dx . Somit,

Endlich bekommen wir

Verwendung der Variablenersetzungsmethode

Variable Ersetzungsmethode Bei der Integration trigonometrischer Funktionen kann es in Fällen verwendet werden, in denen der Integrand nur Sinus oder nur Cosinus, das Produkt aus Sinus und Cosinus, bei dem entweder Sinus oder Cosinus im ersten Grad, Tangens oder Kotangens ist, sowie den Quotienten von enthält gerade Potenzen von Sinus und Cosinus ein und desselben Arguments. In diesem Fall ist es möglich, Permutationen durchzuführen, die nicht nur Sünde sind X = T und Sünde X = T, aber auch tg X = T und ctg X = T .

Beispiel 8. Finden Integral einer trigonometrischen Funktion

.

Lösung. Ändern wir die Variable: , then . Der resultierende Integrand kann mithilfe der Integraltabelle einfach integriert werden:

.

Beispiel 9. Finden Integral einer trigonometrischen Funktion

Lösung. Lassen Sie uns den Tangens in das Verhältnis von Sinus und Cosinus umwandeln:

Ändern wir die Variable: , then . Der resultierende Integrand ist Tabellenintegral mit Minuszeichen:

.

Zurück zur ursprünglichen Variablen erhalten wir schließlich:

.

Beispiel 10. Finden Integral einer trigonometrischen Funktion

Lösung. Ändern wir die Variable: , then .

Lassen Sie uns den Integranden transformieren, um die trigonometrische Identität anzuwenden :

Wir ändern die Variable und vergessen nicht, vor dem Integral ein Minuszeichen zu setzen (siehe oben, was gleich ist). dt). Als nächstes faktorisieren wir den Integranden und integrieren gemäß der Tabelle:

Zurück zur ursprünglichen Variablen erhalten wir schließlich:

.

Finden Sie selbst das Integral einer trigonometrischen Funktion und schauen Sie sich dann die Lösung an

Universelle trigonometrische Substitution

Universelle trigonometrische Substitution kann in Fällen verwendet werden, in denen der Integrand nicht unter die in den vorherigen Absätzen diskutierten Fälle fällt. Grundsätzlich gilt, wenn Sinus oder Cosinus (oder beide) im Nenner eines Bruchs stehen. Es wurde nachgewiesen, dass Sinus und Cosinus wie folgt durch einen anderen Ausdruck ersetzt werden können, der den Tangens des halben ursprünglichen Winkels enthält:

Beachten Sie jedoch, dass die universelle trigonometrische Substitution oft recht komplexe algebraische Transformationen mit sich bringt und daher am besten verwendet wird, wenn keine andere Methode funktioniert. Schauen wir uns Beispiele an, bei denen neben der universellen trigonometrischen Substitution auch die Substitution unter dem Differentialzeichen und die Methode der unbestimmten Koeffizienten verwendet werden.

Beispiel 12. Finden Integral einer trigonometrischen Funktion

.

Lösung. Lösung. Nutzen wir den Vorteil universelle trigonometrische Substitution. Dann
.

Wir multiplizieren die Brüche im Zähler und Nenner mit, nehmen die beiden heraus und stellen sie vor das Integralzeichen. Dann