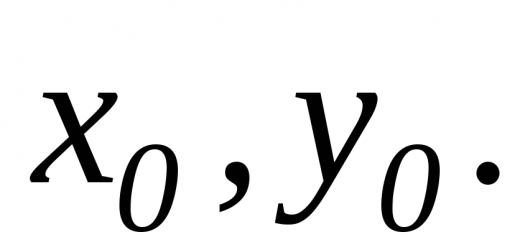تعريف: المجموعة w تسمى الفضاء الخطي وعنصره. -المتجهات إذا:

*القانون محدد (+) حسب القط. أي عنصرين x، y من w مرتبطان بعنصر يسمى. مجموعهم [س + ص]

* يتم إعطاء قانون (* للرقم أ)، وفقًا لعنصر القط x من w وa، تتم مقارنة عنصر من w، يسمى منتج x وa [ax]؛

* مكتمل

المتطلبات (أو البديهيات) التالية:

تتبع ج1. متجه صفر (ctv 0 1 و 0 2. بواسطة a3: 0 2 + 0 1 = 0 2 و 0 1 + 0 2 = 0 1. بواسطة a1 0 1 + 0 2 = 0 2 + 0 1 => 0 1 = 0 2.)

ج2. .(التلفزيون المركزي، A4)

ج3. 0 ناقل (a7)

ج4. أ(رقم)*0=0.(a6,c3)

ج5. x (*) -1 =0 متجه، مقابل x، أي. (-1)س = -س. (أ5،أ6)

ج6. في w، يتم تعريف إجراء الطرح: يسمى المتجه x الفرق بين المتجهات b وa، إذا كان x + a = b، ويشار إليه x = b - a.

رقم نمُسَمًّى البعد لين. العلاقات العامة أ ل ، إذا كان في ل هناك نظام نلين. nezav. المتجهات، وأي نظام من ن+1 ناقل - لين. متكل خافت ل= ن. فضاء ل تسمى ن الأبعاد.

مجموعة مرتبة من خطوط n. nezav. ناقلات ن الأبعاد مستقلة. فضاء - أساس

نظرية. يمكن تمثيل كل متجه X بطريقة فريدة كخط

دع (1) يكون أساس خطي ذو أبعاد n. العلاقات العامة فا الخامس، أي. مجموعة من المتجهات المستقلة خطيا. ستكون مجموعة المتجهات خطية. تعتمد، لأن هُم ن+ 1.

أولئك. هناك أرقام لا تساوي جميعها صفرًا في نفس الوقت، فما علاقة ذلك (وإلا (1) تعتمد خطيًا).

ثم أين هو تحلل المتجهات سعلى أساس (1) .

هذا التعبير فريد من نوعه، لأنه في حالة وجود تعبير آخر (**)

طرح المساواة (**) من (*)،

نحن نحصل

لأن مستقلة خطيا، إذن. تشتد

نظرية. إذا - لين. يمكن تمثيل المتجهات المستقلة للمساحة V وكل متجه x من V من خلال، ثم تشكل هذه المتجهات أساسًا لـ V

Doc: (1)-lin.independent =>تبقى الوثيقة مستقلة خطيًا. وفقا للاتفاقية يتم التعبير عن كل متجه a من خلال (1): ، ضع في اعتبارك، rang≤n => بين الأعمدة التي لا تزيد عن n مستقلة خطيًا، لكن أعمدة m > n=> m تعتمد خطيًا => s=1، n

أي أن المتجهات تعتمد على الخطية

وبالتالي، فإن الفضاء V هو ن البعد و(1) أساسه

№4مواطنه.المجموعة الفرعية L لين. الإنتاج الخامس يسمى لين. شرط. من هذه المساحة، إذا كان الفضاء الفرعي L، فيما يتعلق بالعمليات (+) و (*a) المحددة في V، عبارة عن مساحة خطية

النظرية المجموعة l من متجهات الفضاء V خطية. يتم تنفيذ مساحة فرعية من هذا الفضاء 

(تقدم) لنحقق (1) و (2)، لكي تكون L بسيطة. ويبقى إثبات أن جميع بديهيات لين مستوفاة. العلاقات العامة فا.

(-س): -س+س=0 د. أ(س + ص) = الفأس + المنعم يوسف;

(a-b) و(e-h) يترتب على صحة V؛ فلنثبت (c)

(الضرورة) لتكن اللام لين. الفضاء الجزئي لهذا الفضاء، فإن (1) و (2) يتم استيفاءهما بحكم تعريف الخطوط. العلاقات العامة فا

مواطنه.مجموعة من جميع أنواع الخطوط. مجموعات من بعض العناصر (x j) لين. المنتج يسمى قذيفة خطية

نظريةمجموعة تعسفية من جميع الخطوط. مجموعات من المتجهات V مع الحقيقية. المعامل هو لين سوببر V (قشرة خطية نظام معين من المتجهات لين. العلاقات العامة هي subpr الخطية لهذه العلاقات العامة. )

المساعدة الإنمائية الرسمية.مجموعة فرعية غير فارغة من ناقلات الخط L. الإنتاج الخامس يسمى لين. الفضاء الجزئي إذا:

أ) مجموع أي متجهات من L ينتمي إلى L

ب) حاصل ضرب كل متجه من L بأي رقم ينتمي إلى L

مجموع اثنين من الفضاءات الفرعيةلهو مرة أخرى مساحة فرعيةل

1) دع ص 1 + ص 2 (ل 1 + ل 2)<=>y 1 =x 1 +x 2, y 2 =x' 1 +x' 2, حيث (x 1,x' 1) L 1, (x 2,x' 2) L 2. ص 1 +ص 2 =(x 1 +x 2)+(x' 1 +x' 2)=(x 1 +x' 1)+(x 2 +x' 2)، حيث (x 1 +x' 1 ) L 1 , (x 2 +x' 2) L 2 => تم استيفاء الشرط الأول للمسافة الجزئية الخطية.

نعم 1 = الفأس 1 + الفأس 2، حيث (الفأس 1) L 1، (الفأس 2) L 2 => لأن (y 1 +y 2) (L 1 +L 2) , (ly 1) (L 1 +L 2) => استيفاء الشروط => L 1 +L 2 فضاء جزئي خطي.

تقاطع قسمينل 1 ول 2 لين. العلاقات العامة فال هو أيضًا بديل. هذه المساحة.

النظر في اثنين من المتجهات التعسفية س,ذ، تنتمي إلى تقاطع الفضاءات الجزئية، ورقمين عشوائيين أ,ب:.

وفقا لتعريف. تقاطعات المجموعات:

=> حسب تعريف الفضاء الجزئي للمساحة الخطية:،.

ناقلات المعارف التقليدية فأس + بواسطةينتمي للكثيرين ل 1، والعديد ل 2 فهو ينتمي بحكم التعريف إلى تقاطع هذه المجموعات. هكذا:

المساعدة الإنمائية الرسميةيقولون أن V هو المجموع المباشر لأقسامه. إذا و ب) هذا التحلل فريد من نوعه

ب")دعونا نبين أن ب) يعادل ب')

عندما ب) صحيح ب)

جميع أنواع (م, ن) من تتقاطع فقط على طول المتجه الصفري

دع ∃ ض ∈

عدل يعودل=

تناقض

نظرية ل (*) ضروري وكافي لاتحاد القواعد ( شكلت أساس الفضاء

(مطلوب)دع (*) والمتجهات تكون أساسًا لمجموعات فرعية. وهناك توسع في ; يتم توسيع x على الأساس L، من أجل الإشارة إلى أن ( تشكل أساسًا، من الضروري إثبات استقلالها الخطي؛ فكلها تحتوي على 0 0=0+...+0. نظرًا لتفرد توسيع 0 over : => بسبب الاستقلال الخطي للأساس => ( – base

(تحويلة.)دع ( يشكل أساس L تحللًا فريدًا (**) يوجد تحلل واحد على الأقل. حسب التفرد (*) => التفرد (**)

تعليق. البعد للمجموع المباشر يساوي مجموع أبعاد الفضاء الجزئي

يمكن لأي مصفوفة تربيعية غير مفردة أن تكون بمثابة مصفوفة انتقالية من أساس إلى آخر

واسمحوا في ن الأبعاد الفضاء الخطي V هناك قاعدتان و

(1) =A، حيث أن العنصرين * و ** ليسا أرقامًا، ولكننا سنوسع عمليات معينة على مصفوفة رقمية إلى هذه الصفوف.

لأن وإلا فإن المتجهات ** ستكون تابعة خطية

خلف.إذا كانت أعمدة A مستقلة خطيًا => فتشكل أساسًا

الإحداثيات و المرتبطة بالعلاقة ، أين عناصر المصفوفة الانتقالية

وليعلم تحلل عناصر الأساس "الجديد" إلى الأساس "القديم".

ثم المساواة صحيحة

ولكن إذا كانت المجموعة الخطية من العناصر المستقلة خطيًا تساوي 0، فإن =>

نظرية الاعتماد الخطي الأساسية

لو (*) يتم التعبير عنها خطيًا من خلال (**) الذي - التين<= م

دعونا نثبت عن طريق الحث على م

م = 1: النظام (*) يحتوي على 0 ولين. مدير - مستحيل

فليكن صحيحا بالنسبة لـ m=k-1

دعونا نثبت ل م = ك

قد يتبين أن 1) ، أي. v-ry (1) هي lin.comb. لين. في الخندق (2) النظام (1) خطي لا يمكن الاعتماد عليه، لأن هو جزء من lin.nezav. الأنظمة (*). لأن في النظام (2) لا يوجد سوى متجهات k-1، ثم من خلال فرضية الاستقراء نحصل على k+1

ليما 1 : إذا كان صف واحد (عمود) على الأقل في مصفوفة بالحجم n n يساوي صفرًا، فإن صفوف (أعمدة) المصفوفة تعتمد خطيًا.

دليل:ليكن السطر الأول صفرًا إذن

أين أ 1 0. هذا هو المطلوب.

تعريف: تسمى المصفوفة التي تكون عناصرها الواقعة أسفل القطر الرئيسي مساوية للصفر الثلاثي:

و اي = 0، أنا>ي.

ليما 2: محدد المصفوفة المثلثية يساوي حاصل ضرب عناصر القطر الرئيسي.

من السهل إجراء الإثبات عن طريق الحث على أبعاد المصفوفة.

نظرية يا الاستقلال الخطيثلاثة أبعاد.

أ)ضروري: تعتمد خطيا د = 0 .

دليل:دعهم يعتمدون خطيًا ، ي=,

أي أن هناك j لا يساوي الصفر، ي=،ماذا أ 1 أ 1 + أ 2 أ 2 + ... أ ن أ ن = , أ ي –أعمدة المصفوفة أ.دعونا، على سبيل المثال، ن¹0.

لدينا أ ي * = أ ي / أ ن , j £ n-1a 1 * أ 1 + أ 2 * أ 2 + ... أ ن -1 * أ ن -1 + أ ن = .

دعونا نستبدل العمود الأخير من المصفوفة أعلى

أ ن * = أ 1 * أ 1 + أ 2 * أ 2 + ... أ ن -1 أ ن -1 + أ ن = .

وفقًا لخاصية المحدد المثبتة أعلاه (لن تتغير إذا تمت إضافة عمود آخر مضروبًا برقم إلى أي عمود في المصفوفة)، فإن محدد المصفوفة الجديدة يساوي محدد المصفوفة الأصلية. لكن في المصفوفة الجديدة، عمود واحد يساوي صفرًا، وهو ما يعني أننا نحصل على توسيع المحدد فوق هذا العمود د = 0، Q.E.D.

ب)قدرة:مصفوفة الحجم ن نمع صفوف مستقلة خطيايمكن دائمًا اختزاله إلى شكل مثلث باستخدام التحويلات التي لا تغير القيمة المطلقة للمحدد. علاوة على ذلك، من استقلال صفوف المصفوفة الأصلية، يترتب على ذلك أن محددها يساوي صفرًا.

1. إذا كان في مصفوفة الحجم ن نمع عنصر الصفوف المستقلة خطيا 11يساوي الصفر، ثم العمود الذي عنصره أ 1 ي ¹ 0. وفقا لـ Lemma 1، يوجد مثل هذا العنصر. قد يختلف محدد المصفوفة المحولة عن محدد المصفوفة الأصلية فقط في الإشارة.

2. من الخطوط ذات الأرقام أنا>1اطرح السطر الأول مضروبًا في الكسر أ1/أ11. علاوة على ذلك، في العمود الأول من الصفوف بالأرقام أنا>1سينتج عنه صفر عناصر.

3. لنبدأ في حساب محدد المصفوفة الناتجة عن طريق التحلل على العمود الأول. وبما أن جميع العناصر فيه ما عدا الأول تساوي صفراً،

د جديد = أ 11 جديد (-1) 1+1 د 11 جديد،

أين د11 جديدهو المحدد لمصفوفة ذات حجم أصغر.

بعد ذلك، لحساب المحدد د 11كرر الخطوات 1، 2، 3 حتى يصبح المحدد الأخير هو محدد مصفوفة الحجم 1 1. بما أن الخطوة 1 تغير فقط إشارة محدد المصفوفة التي يتم تحويلها، والخطوة 2 لا تغير قيمة المحدد على الإطلاق، إذن، حتى الإشارة، سنحصل في النهاية على محدد المصفوفة الأصلية. في هذه الحالة، نظرًا للاستقلال الخطي لصفوف المصفوفة الأصلية، تكون الخطوة 1 راضية دائمًا، وستكون جميع عناصر القطر الرئيسي غير مساوية للصفر. وبالتالي، فإن المحدد النهائي، وفقا للخوارزمية الموصوفة، يساوي منتج العناصر غير الصفرية على القطر الرئيسي. ومن ثم، فإن محدد المصفوفة الأصلية لا يساوي صفرًا. Q.E.D.

الملحق 2

يتم استدعاء الوظائف مستقل خطيا،لو

(يُسمح فقط بمجموعة خطية تافهة من الوظائف التي تساوي الصفر). على النقيض من الاستقلال الخطي للمتجهات، فإن التركيبة الخطية هنا مطابقة للصفر، وليس المساواة. وهذا أمر مفهوم، حيث يجب تلبية مساواة المجموعة الخطية بالصفر لأي قيمة للوسيطة.

يتم استدعاء الوظائف تعتمد خطيا،إذا كانت هناك مجموعة غير صفرية من الثوابت (ليست كل الثوابت تساوي الصفر) بحيث (هناك مجموعة خطية غير تافهة من الوظائف تساوي الصفر).

نظرية.لكي تكون الوظائف معتمدة خطيًا، من الضروري والكافي أن يتم التعبير عن أي منها خطيًا من خلال الوظائف الأخرى (ممثلة كمجموعة خطية).

أثبت هذه النظرية بنفسك، فقد تم إثباتها بنفس طريقة إثبات نظرية مشابهة حول الاعتماد الخطي للمتجهات.

محدد فرونسكي.

يتم تقديم محدد Wronski للوظائف كمحدد تكون أعمدته مشتقات هذه الوظائف من الصفر (الوظائف نفسها) إلى الترتيب n-1st.

.

نظرية. إذا كانت الوظائف تعتمد خطيا، ثم

دليل. منذ الوظائف تعتمد خطيا، ثم يتم التعبير عن أي منها خطيا من خلال الآخرين، على سبيل المثال،

يمكن التمييز بين الهوية، لذلك

ثم يتم التعبير عن العمود الأول من محدد Wronski خطيًا من خلال الأعمدة المتبقية، وبالتالي فإن محدد Wronski يساوي الصفر.

نظرية.وذلك للحصول على حلول خطية متجانسة المعادلة التفاضليةكان الترتيب n يعتمد خطيًا، فمن الضروري والكافي ذلك.

دليل. الضرورة تتبع من النظرية السابقة.

قدرة. دعونا إصلاح بعض النقطة. نظرًا لأن أعمدة المحدد المحسوبة عند هذه النقطة هي متجهات تعتمد خطيًا.

، أن العلاقات راضية

بما أن المجموعة الخطية من الحلول لمعادلة خطية متجانسة هي حلها، فيمكننا تقديم حل بالصيغة

مجموعة خطية من الحلول لها نفس المعاملات.

لاحظ أن هذا الحل يحقق الشروط الأولية الصفرية، وهذا يتبع نظام المعادلات المكتوبة أعلاه. لكن الحل التافه للمعادلة الخطية المتجانسة يحقق أيضًا نفس الشروط الأولية الصفرية. لذلك، من نظرية كوشي يترتب على ذلك أن الحل المقدم يساوي تمامًا الحل التافه، وبالتالي،

وبالتالي فإن الحلول تعتمد خطيا.

عاقبة.إذا اختفى محدد ورونسكي، المبني على حلول معادلة خطية متجانسة، عند نقطة واحدة على الأقل، فإنه يساوي الصفر تمامًا.

دليل. إذا، فإن الحلول تعتمد خطيا، وبالتالي،.

نظرية.1. بالنسبة للاعتماد الخطي للحلول فهو ضروري وكافي(أو ).

2. من أجل الاستقلال الخطي للحلول، فهو ضروري وكافي.

دليل. البيان الأول يتبع من النظرية والنتيجة الطبيعية المثبتة أعلاه. يمكن إثبات العبارة الثانية بسهولة عن طريق التناقض.

دع الحلول تكون مستقلة خطيا. إذا كانت الحلول تعتمد خطيا. تناقض. لذلك، .

يترك . إذا كانت الحلول تعتمد خطيا، ثم , وبالتالي، تناقض. ولذلك، فإن الحلول مستقلة خطيا.

عاقبة.يعد اختفاء محدد ورونسكي عند نقطة واحدة على الأقل معيارًا للاعتماد الخطي للحلول على معادلة خطية متجانسة.

يعد الفرق بين محدد Wronski والصفر معيارًا للاستقلال الخطي لحلول المعادلة الخطية المتجانسة.

نظرية.بعد فضاء الحلول لمعادلة خطية متجانسة من الرتبة n يساوي n.

دليل.

أ) دعونا نبين أنه يوجد n حلول مستقلة خطيا لمعادلة تفاضلية متجانسة خطية من الرتبة n. دعونا نفكر في الحلول ، مستوفياً الشروط الأولية التالية:

...........................................................

مثل هذه الحلول موجودة. في الواقع، وفقًا لنظرية كوشي، من خلال النقطة يمر عبر منحنى متكامل واحد - الحل. من خلال النقطة الحل يمر عبر هذه النقطة

- الحل، من خلال نقطة - حل .

هذه الحلول مستقلة خطيا، منذ ذلك الحين .

ب) دعونا نوضح أن أي حل لمعادلة خطية متجانسة يتم التعبير عنه خطيًا من خلال هذه الحلول (هو مجموعها الخطي).

دعونا نفكر في حلين. واحد - حل تعسفي بشروط أولية . نسبة عادلة

النظرية 1. (حول الاستقلال الخطي للمتجهات المتعامدة). دعونا إذن يكون نظام المتجهات مستقلاً خطيًا.

لنقم بعمل تركيبة خطية ∑λ i x i =0 ونفكر في المنتج القياسي (x j , ∑lect i x i)=lect j ||x j || 2 =0، لكن ||x j || 2 ≠0⇒lect ي =0.

التعريف 1. نظام المتجهاتأو (e i ,e j)=δ ij - رمز كرونيكر، دعا متعامد (ONS).

التعريف 2. بالنسبة للعنصر التعسفي x للفضاء الإقليدي التعسفي لانهائي الأبعاد ونظام متعامد اعتباطي من العناصر، تسمى سلسلة فورييه للعنصر x فوق النظام بمجموع لا نهائي (سلسلة) مكون رسميًا من النموذج ، حيث الأعداد الحقيقية π i تسمى معاملات فورييه للعنصر x في النظام، حيث π i =(x,e i).

تعليق. (وبطبيعة الحال، يطرح السؤال حول تقارب هذه السلسلة. لدراسة هذه المسألة دعونا نثبت رقماً عشوائياً n ونكتشف ما يميزه ن الجزئيمجموع سلسلة فورييه لأي مجموعة خطية أخرى من العناصر n الأولى لنظام متعامد.)

النظرية 2. بالنسبة لأي رقم ثابت n، من بين جميع مجاميع النموذج، يكون للمجموع الجزئي n لسلسلة فورييه للعنصر أصغر انحراف عن العنصر x وفقًا لقاعدة الفضاء الإقليدي المحدد

مع الأخذ بعين الاعتبار التعامد الطبيعي للنظام وتعريف معامل فورييه، يمكننا الكتابة

يتم تحقيق الحد الأدنى من هذا التعبير عند c i = lecti، لأنه في هذه الحالة يختفي المجموع الأول غير السالب على الجانب الأيمن دائمًا، ولا تعتمد الحدود المتبقية على c i.

مثال. النظر في النظام المثلثي

في فضاء جميع دوال ريمان القابلة للتكامل f(x) على المقطع [-π,π]. من السهل التحقق من أن هذا هو ONS، ومن ثم فإن سلسلة فورييه للدالة f(x) لها الشكل حيث .

تعليق. (عادة ما يتم كتابة سلسلة فورييه المثلثية في النموذج ثم )

إن وجود ONS التعسفي في الفضاء الإقليدي ذي الأبعاد اللانهائية دون افتراضات إضافية، بشكل عام، ليس أساسًا لهذا الفضاء. على المستوى البديهي، دون إعطاء تعريفات صارمة، سنصف جوهر الأمر. في الفضاء الإقليدي العشوائي ذي الأبعاد اللانهائية E، خذ بعين الاعتبار ONS، حيث (e i ,e j)=δ j هو رمز كرونيكر. دع M يكون فضاءً فرعيًا للفضاء الإقليدي، و k=M ⊥ يكون فضاءً جزئيًا متعامدًا مع M بحيث يكون الفضاء الإقليدي E=M+M ⊥ . إسقاط المتجه x∈E على الفضاء الجزئي M هو المتجه ∈M، حيث

سنبحث عن قيم معاملات التمدد α k التي يكون لها المتبقي (المتبقي المربع) h 2 =||x-|| 2 سيكون الحد الأدنى:

ح 2 =||س-|| 2 =(x-,x-)=(x-∑α k e k ,x-∑α k e k)=(x,x)-2∑α k (x,e k)+(∑α k e k ,∑α k e k)= ||س|| 2 -2∑α ك (x,e k)+∑α k 2 +∑(x,e k) 2 -∑(x,e k) 2 =||x|| 2 +∑(α k -(x,e k)) 2 -∑(x,e k) 2 .

من الواضح أن هذا التعبير سيأخذ قيمة دنيا عند α k = 0، وهي قيمة تافهة، وعند α k =(x,e k). ثم ρ دقيقة =||x|| 2 -∑α ك 2 ≥0. من هنا نحصل على متباينة بسل ∑α k 2 ||x|| 2. عند ρ=0 يُطلق على النظام المتعامد الطبيعي للمتجهات (ONS) اسم النظام المتعامد الطبيعي الكامل بمعنى ستيكلوف (PONS).من هنا يمكننا الحصول على مساواة ستيكلوف-بارسيفال ∑α k 2 =||x|| 2- "نظرية فيثاغورس" للفراغات الإقليدية اللانهائية الأبعاد الكاملة بمعنى ستيكلوف. الآن سيكون من الضروري إثبات أنه لكي يتم تمثيل أي متجه في الفضاء بشكل فريد في شكل متسلسلة فورييه متقاربة إليه، فمن الضروري والكافي أن تكون المساواة بين ستيكلوف وبارسيفال صحيحة. نظام المتجهات pic = ""> أشكال ONB نظام المتجهات فكر في المجموع الجزئي للسلسلة ثم مثل ذيل سلسلة متقاربة. وبالتالي، فإن نظام المتجهات هو PONS ويشكل ONB.

مثال.النظام المثلثي

في فضاء جميع وظائف ريمان القابلة للتكامل f(x) على المقطع [-π,π] هو PONS ويشكل ONB.