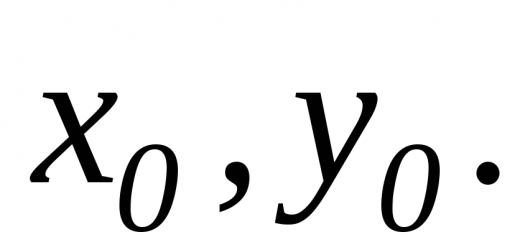The elektronički izvor izvrstan je materijal za dirigiranje interaktivno učenje V moderne škole. Napisan je korektno, ima jasnu strukturu i odgovara školskom planu i programu. Zahvaljujući detaljnim objašnjenjima, tema predstavljena u video lekciji postat će jasna što većem broju učenika u razredu. Učitelji moraju zapamtiti da nemaju svi učenici isti stupanj percepcije, brzinu razumijevanja ili bazu. Takvi materijali pomoći će vam da se nosite s poteškoćama i uhvatite korak s vršnjacima, poboljšate svoj akademski uspjeh. Uz njihovu pomoć, u mirnom kućnom okruženju, samostalno ili zajedno s mentorom, student može razumjeti pojedinu temu, proučavati teoriju i pogledati primjere praktična aplikacija jednu ili drugu formulu itd.
Ova video lekcija posvećena je temi "Sinus i kosinus razlike argumenata." Pretpostavlja se da su učenici već naučili osnove trigonometrije, upoznati s osnovnim funkcijama i njihovim svojstvima, duhovnim formulama i tablicama trigonometrijskih vrijednosti.

Također, prije nego što prijeđete na proučavanje ove teme, morate razumjeti sinus i kosinus zbroja argumenata, znati dvije osnovne formule i znati ih koristiti.
Na početku video lekcije spiker podsjeća učenike na ove dvije formule. Zatim se demonstrira prva formula - sinus razlike argumenata. Osim kako je sama formula izvedena, prikazano je kako je izvedena iz druge. Dakle, učenik neće morati pamtiti novu formulu a da je ne razumije, što je česta pogreška. Ovo je vrlo važno za učenike ovog razreda. Uvijek morate zapamtiti da možete dodati znak + ispred znaka minus, a minus na znaku plus će se na kraju pretvoriti u minus. Ovim jednostavnim korakom možete koristiti formulu za sinus zbroja i dobiti formulu za sinus razlike argumenata.
Formula za kosinus razlike izvodi se na sličan način iz formule za kosinus zbroja argumenata.
Govornik objašnjava sve korak po korak, a kao rezultat, na sličan način se izvodi opća formula za kosinus zbroja i razlike argumenata i sinusa.
Prvi primjer iz praktičnog dijela ove video lekcije sugerira pronalaženje kosinusa od Pi/12. Predlaže se prikazati ovu vrijednost u obliku određene razlike, u kojoj će minuend i subtrahend biti tablične vrijednosti. Zatim će se primijeniti formula kosinusa za razliku argumenata. Zamjenom izraza možete zamijeniti dobivene vrijednosti i dobiti odgovor. Spiker čita odgovor koji se prikazuje na kraju primjera.
Drugi primjer je jednadžba. I s desne i s lijeve strane vidimo kosinuse razlika argumenata. Govornik nalikuje formulama za lijevanje, koje se koriste za zamjenu i pojednostavljenje ovih izraza. Ove formule ispisane su s desne strane kako bi učenici mogli razumjeti odakle dolaze određene promjene.
Drugi primjer, treći, je određeni razlomak, gdje imamo i brojnik i nazivnik trigonometrijski izrazi, naime, razlike proizvoda.
I ovdje se pri rješavanju koriste redukcijske formule. Tako školarci mogu vidjeti da ako propuste jednu temu iz trigonometrije, bit će sve teže razumjeti ostale.
I na kraju, četvrti primjer. Ovo je također jednadžba u kojoj je potrebno koristiti nove naučene i stare formule pri rješavanju.
Možete detaljnije pogledati primjere dane u video tutorijalu i pokušati sami riješiti. Mogu se postaviti kao domaća zadaćaŠkolska djeca.
DEKODIRANJE TEKSTA:
Tema lekcije je "Sinus i kosinus razlike argumenata."
U prethodnom tečaju upoznali smo se s dvije trigonometrijske formule: sinus i kosinus zbroja argumenata.
sin(x + y) = sin x cos y + cos x sin y,
cos (x + y) = cos x cos y - sin x sin y.
sinus zbroja dva kuta jednak zbroju između umnoška sinusa prvog kuta i kosinusa drugog kuta i umnoška kosinusa prvog kuta i sinusa drugog kuta;
Kosinus zbroja dvaju kutova jednak je razlici umnoška kosinusa tih kutova i umnoška zbroja tih kutova.
Pomoću ovih formula izvest ćemo formule sinus i kosinus razlike argumenata.
Sinus razlike argumenata sin(x-y)

Dvije formule (sinus zbroja i sinus razlike) mogu se napisati kao:
grijeh (xy) = sin x cos ycos x sin y.
Slično, izvodimo formulu za kosinus razlike:
Prepišimo kosinus razlike između argumenata kao zbroj i primijenimo već poznatu formulu za kosinus zbroja: cos (x + y) = cosxcosy - sinxsiny.
samo za argumente x i -y. Zamjenom ovih argumenata u formulu dobivamo cosxcos(- y) - sinxsin(- y).
sin(- y)= - siny). te dobivamo konačni izraz cosxcosy + sinxsiny.
cos (x - y) = cos (x +(- y)) = cos xcos(- y) - sin x sin(- y)= cosx cos y + sin xsin y.
To znači cos (x - y) = cosxcos y + sin xsin y.
Kosinus razlike dvaju kutova jednak je zbroju umnoška kosinusa tih kutova i umnoška sinusa tih kutova.
Kombinirajući dvije formule (kosinus zbroja i kosinus razlike) u jednu, pišemo
cos(xy) = cosxcos y sin xsin y.
Podsjetimo se da se formule u praksi mogu primijeniti i slijeva na desno i obrnuto.
Pogledajmo primjere.
PRIMJER 1. Izračunajte cos (kosinus pi podijeljen s dvanaest).
Riješenje. Zapišimo pi podijeljeno s dvanaest kao razliku pi s tri i pi podijeljeno s četiri: = - .
Zamijenimo vrijednosti u formulu kosinusa razlike: cos (x - y) = cosxcosy + sinxsiny, dakle cos = cos (-) = cos cos + sin sin
Znamo da je cos = , cos = sin= , sin = . Prikaži tablicu vrijednosti.
Zamijenimo vrijednost sinusa i kosinusa brojčane vrijednosti i dobivamo ∙ + ∙ kada množimo razlomak s razlomkom, množimo brojnike i nazivnike, dobivamo
cos = cos (-) = cos cos + sin sin = ∙ + ∙ = = =.
Odgovor: cos =.

PRIMJER 2. Riješi cos jednadžba(2π - 5x) = cos(- 5x) (kosinus od dva pi minus pet x jednak je kosinus od pi za dva minus pet x).
Riješenje. Na lijevu i desnu stranu jednadžbe primjenjujemo redukcijske formule cos(2π - cos (kosinus dva pi minus alfa jednako je kosinus alfa) i cos(- = sin (kosinus pi dva minus alfa jednako je sinus alfa), dobivamo cos 5x = sin 5x, dajemo ga u obliku homogene jednadžbe prvog stupnja i dobivamo cos 5x - sin 5x = 0. Ovo je homogena jednadžba prvog stupnja. podijelimo obje strane člana jednadžbe s cos 5x. Imamo:
cos 5x: cos 5x - sin 5x: cos 5x = 0, jer cos 5x: cos 5x = 1, i sin 5x: cos 5x = tan 5x, tada dobivamo:
Budući da već znamo da jednadžba tgt = a ima rješenje t = arctga + πn, i budući da imamo t = 5x, a = 1, dobivamo
5x = arctan 1 + πn,
A arctg vrijednost 1, zatim tg 1= Prikaži tablicu
Zamijenite vrijednost u jednadžbu i riješite je:
Odgovor: x = +.
PRIMJER 3. Nađi vrijednost razlomka. (u brojniku je razlika umnoška kosinusa od sedamdeset pet stupnjeva i šezdeset pet stupnjeva i umnoška sinusa od sedamdeset pet stupnjeva i šezdeset pet stupnjeva, a u nazivniku je razlika umnoška sinusa od osamdeset i pet stupnjeva i kosinusa od trideset i pet stupnjeva i umnožak kosinusa od osamdeset i pet stupnjeva i sinusa od trideset i pet stupnjeva) .
Riješenje. U brojniku ovog razlomka razlika se može "skupiti" u kosinus zbroja argumenata 75° i 65°, au nazivniku se razlika može "skupiti" u sinus razlike između argumenata 85° i 35°. Dobivamo
Odgovor: - 1.
PRIMJER 4. Riješite jednadžbu: cos(-x) + sin(-x) = 1 (kosinus razlike pi za četiri i x plus sinus razlike pi za četiri i x je jednako jedan).
Riješenje. Primijenimo formule kosinus razlike i sinus razlike.
Pokazati opća formula razlika kosinusa
Tada je cos (-x) = cos cos x + sinsinh

Pokažite opću formulu za razliku sinusa
i sin (-h)= sin cosh - jer grijeh x
Zamijenite ove izraze u jednadžbu cos(-x) + sin(-x) = 1 i dobijete:
cos cos x + sinsin x + sin cos x - cos sin x = 1,
Budući da je cos= i sin= Pokaži tablici značenje sinusa i kosinusa
Dobivamo ∙ cos x + ∙ sinx + ∙ cos x - ∙ sinx = 1,
drugi i četvrti član su suprotni, stoga se poništavaju, ostavljajući:
∙ cos + ∙ cos = 1,
Odlučimo se dana jednadžba i to dobivamo
2∙ ∙ cos x= 1,
Pošto već znamo da jednadžba cos = a ima rješenje t = arcosa+ 2πk, a budući da imamo t=x, a =, dobivamo
x = arccos + 2πn,
a budući da je vrijednost arccos, tada je cos =
Formule za zbroj i razliku sinusa i kosinusa za dva kuta α i β omogućuju nam prijelaz sa zbroja ovih kutova na umnožak kutova α + β 2 i α - β 2. Odmah napominjemo da ne smijete brkati formule za zbroj i razliku sinusa i kosinusa s formulama za sinuse i kosinuse zbroja i razlike. U nastavku navodimo ove formule, dajemo njihove izvode i prikazujemo primjere primjene za specifične probleme.
Yandex.RTB R-A-339285-1
Formule za zbroj i razliku sinusa i kosinusa
Zapišimo kako izgledaju formule zbroja i razlike sinusa i kosinusa
Formule zbroja i razlike za sinuse
sin α + sin β = 2 sin α + β 2 cos α - β 2 sin α - sin β = 2 sin α - β 2 cos α + β 2
Formule zbroja i razlike za kosinuse
cos α + cos β = 2 cos α + β 2 cos α - β 2 cos α - cos β = - 2 sin α + β 2 cos α - β 2 , cos α - cos β = 2 sin α + β 2 · β - α 2
Ove formule vrijede za sve kutove α i β. Kutovi α + β 2 i α - β 2 nazivaju se poluzbroj odnosno polurazlika kutova alfa i beta. Navedimo formulaciju za svaku formulu.
Definicije formula za zbrojeve i razlike sinusa i kosinusa
Zbroj sinusa dvaju kutova jednak je dvostrukom umnošku sinusa poluzbroja ovih kutova i kosinusa polurazlike.
Razlika sinusa dvaju kutova jednak je dvostrukom umnošku sinusa polurazlike ovih kutova i kosinusa poluzbroja.
Zbroj kosinusa dvaju kutova jednak je dvostrukom umnošku kosinusa poluzbroja i kosinusa polurazlike ovih kutova.
Razlika kosinusa dvaju kutova jednak je dvostrukom umnošku sinusa poluzbroja i kosinusa polurazlike ovih kutova, uzetog s negativnim predznakom.
Izvođenje formula za zbroj i razliku sinusa i kosinusa
Za izvođenje formula za zbroj i razliku sinusa i kosinusa dvaju kutova koriste se formule zbrajanja. Nabrojimo ih u nastavku
sin (α + β) = sin α · cos β + cos α · sin β sin (α - β) = sin α · cos β - cos α · sin β cos (α + β) = cos α · cos β - sin α sin β cos (α - β) = cos α cos β + sin α sin β
Zamislimo i same kutove kao zbroj poluzbroja i polurazlike.
α = α + β 2 + α - β 2 = α 2 + β 2 + α 2 - β 2 β = α + β 2 - α - β 2 = α 2 + β 2 - α 2 + β 2
Nastavljamo izravno s izvođenjem formula zbroja i razlike za sin i cos.
Derivacija formule za zbroj sinusa
U zbroju sin α + sin β, zamjenjujemo α i β s izrazima za ove kutove danima gore. Dobivamo
sin α + sin β = sin α + β 2 + α - β 2 + sin α + β 2 - α - β 2
Sada na prvi izraz primjenjujemo formulu zbrajanja, a na drugi - formulu za sinus kutnih razlika (vidi formule iznad)
sin α + β 2 + α - β 2 = sin α + β 2 cos α - β 2 + cos α + β 2 sin α - β 2 sin α + β 2 - α - β 2 = sin α + β 2 cos α - β 2 - cos α + β 2 sin α - β 2 sin α + β 2 + α - β 2 + sin α + β 2 - α - β 2 = sin α + β 2 cos α - β 2 + cos α + β 2 sin α - β 2 + sin α + β 2 cos α - β 2 - cos α + β 2 sin α - β 2 Otvorite zagrade, dodajte slične članove i dobijte traženu formulu
sin α + β 2 cos α - β 2 + cos α + β 2 sin α - β 2 + sin α + β 2 cos α - β 2 - cos α + β 2 sin α - β 2 = = 2 sin α + β 2 cos α - β 2
Koraci za izvođenje preostalih formula su slični.
Izvod formule za razliku sinusa
sin α - sin β = sin α + β 2 + α - β 2 - sin α + β 2 - α - β 2 sin α + β 2 + α - β 2 - sin α + β 2 - α - β 2 = sin α + β 2 cos α - β 2 + cos α + β 2 sin α - β 2 - sin α + β 2 cos α - β 2 - cos α + β 2 sin α - β 2 = = 2 sin α - β 2 cos α + β 2
Derivacija formule za zbroj kosinusa
cos α + cos β = cos α + β 2 + α - β 2 + cos α + β 2 - α - β 2 cos α + β 2 + α - β 2 + cos α + β 2 - α - β 2 = cos α + β 2 cos α - β 2 - sin α + β 2 sin α - β 2 + cos α + β 2 cos α - β 2 + sin α + β 2 sin α - β 2 = = 2 cos α + β 2 cos α - β 2
Derivacija formule za razliku kosinusa
cos α - cos β = cos α + β 2 + α - β 2 - cos α + β 2 - α - β 2 cos α + β 2 + α - β 2 - cos α + β 2 - α - β 2 = cos α + β 2 cos α - β 2 - sin α + β 2 sin α - β 2 - cos α + β 2 cos α - β 2 + sin α + β 2 sin α - β 2 = = - 2 sin α + β 2 sin α - β 2
Primjeri rješavanja praktičnih problema
Prvo, provjerimo jednu od formula zamjenom određenih vrijednosti kuta u nju. Neka je α = π 2, β = π 6. Izračunajmo vrijednost zbroja sinusa tih kutova. Prvo, poslužimo se tablicom osnovnih vrijednosti trigonometrijske funkcije, a zatim primijenite formulu za zbroj sinusa.
Primjer 1. Provjera formule za zbroj sinusa dvaju kutova
α = π 2, β = π 6 sin π 2 + sin π 6 = 1 + 1 2 = 3 2 sin π 2 + sin π 6 = 2 sin π 2 + π 6 2 cos π 2 - π 6 2 = 2 sin π 3 cos π 6 = 2 3 2 3 2 = 3 2
Razmotrimo sada slučaj kada se vrijednosti kutova razlikuju od osnovnih vrijednosti prikazanih u tablici. Neka je α = 165°, β = 75°. Izračunajmo razliku sinusa ovih kutova.
Primjer 2. Primjena formule razlike sinusa
α = 165 °, β = 75 ° sin α - sin β = sin 165 ° - sin 75 ° sin 165 - sin 75 = 2 sin 165 ° - sin 75 ° 2 cos 165 ° + sin 75 ° 2 = = 2 sin 45 ° cos 120° = 2 2 2 - 1 2 = 2 2
Koristeći formule za zbroj i razliku sinusa i kosinusa, možete prijeći sa zbroja ili razlike na umnožak trigonometrijskih funkcija. Često se te formule nazivaju formulama za prijelaz sa zbroja na umnožak. Formule za zbroj i razliku sinusa i kosinusa naširoko se koriste u rješavanju trigonometrijske jednadžbe a kod pretvaranja trigonometrijskih izraza.
Ako primijetite grešku u tekstu, označite je i pritisnite Ctrl+Enter