ЕГОРОВА ВИКТОРИЯ ВАЛЕРИЕВНА

учител по математика

най-висока квалификационна категория

ТЕМА: „ИДЕНТИЧНА ТРАНСФОРМАЦИЯ

ЛОГАРИТМИЧНИ ИЗРАЖЕНИЯ"

Знания и умения, които учениците трябва да овладеят след изучаване на този урок:

познава дефиницията на логаритъм на число, основно логаритмично тъждество, свойства на логаритмите;

да може да извършва трансформации на изрази, съдържащи логаритми и да пресмята логаритми.

Литература:

1. Алимов Ш.А., Колягин Ю.М., Сидоров Ю.В. и др.Алгебра и началото на анализа: учебник за 10-11 клас образователни институции. – М.: Образование, 2001.

2. Кочагин В.В., Кочагина М.В., Интензивен курсподготовка за единен държавен изпит. – М.: Ексмо, 2009.

3. Merzlyak A.G., Polonsky V.B., Yakir M.S., Алгебричен симулатор: Наръчник за ученици и кандидати. – М.: Илекса, 2005.

4. Гусев В.А., Мордкович А.Г. Математика: Справочни материали: Книга за студенти. – М.: Образование, 2001.

План на урока:

Напредък на урока:

1) Логаритъм е гръцка дума, която се състои от 2 думи: "логос" - отношение, "аритмос" - число. Това означава, че логаритъмът е число, което измерва отношение. Публикация от 1614 г. съобщава, че Напиер е изобретил логаритмите. По-късно той съставя логаритмични таблици, които сега са ни известни като таблици на Брадис. За по-малко от един век таблиците се разпространиха по целия свят и се превърнаха в незаменим компютърен инструмент. Впоследствие те бяха, така да се каже, вградени в удобно устройство, което значително ускорява процеса на изчисление - слайд правило, което се използва до седемдесетте години на двадесети век.

Приложение 1.

2) Логаритъм положително числоbвъз основа на а, и и е по-голямо от нула и не е равно на единица,е степента, до която трябва да се повдигне дадено числоа за да получите номераb.

Това равенство, изразяващо дефиницията на логаритъм, се наричаосновно логаритмично тъждество .

В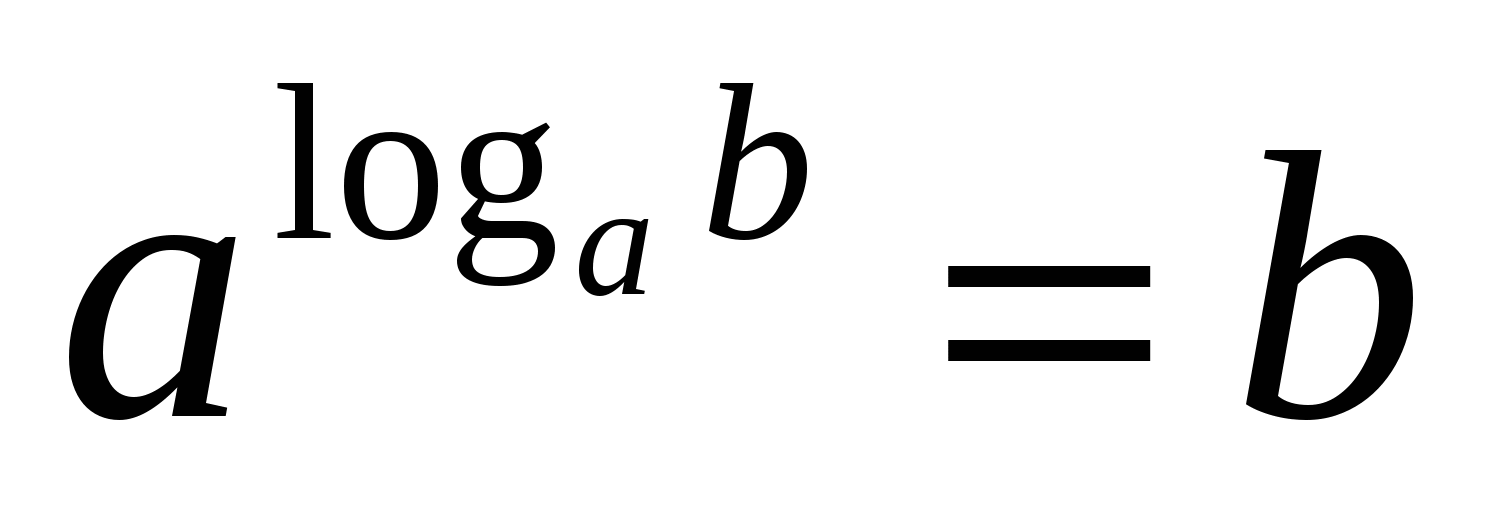

ИЛИ 1

П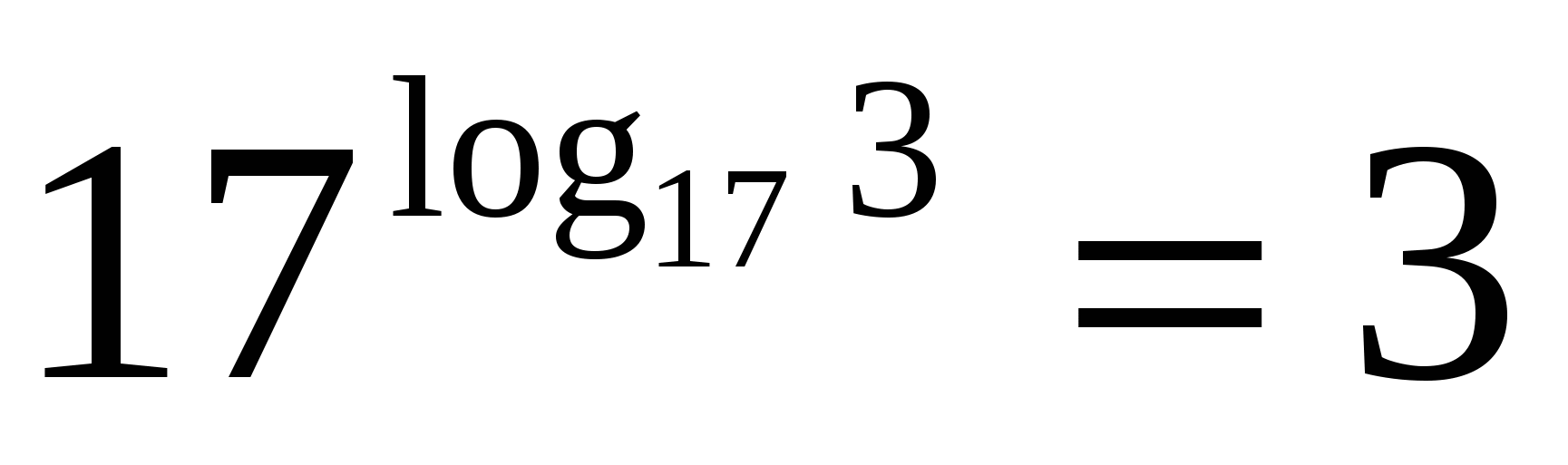

Основата на степента и основата на логаритъма са седемнадесет, което означава, че според основното логаритмично тъждество стойността на израза е три.

Да работим устно:

SCH
FIR-BELLE

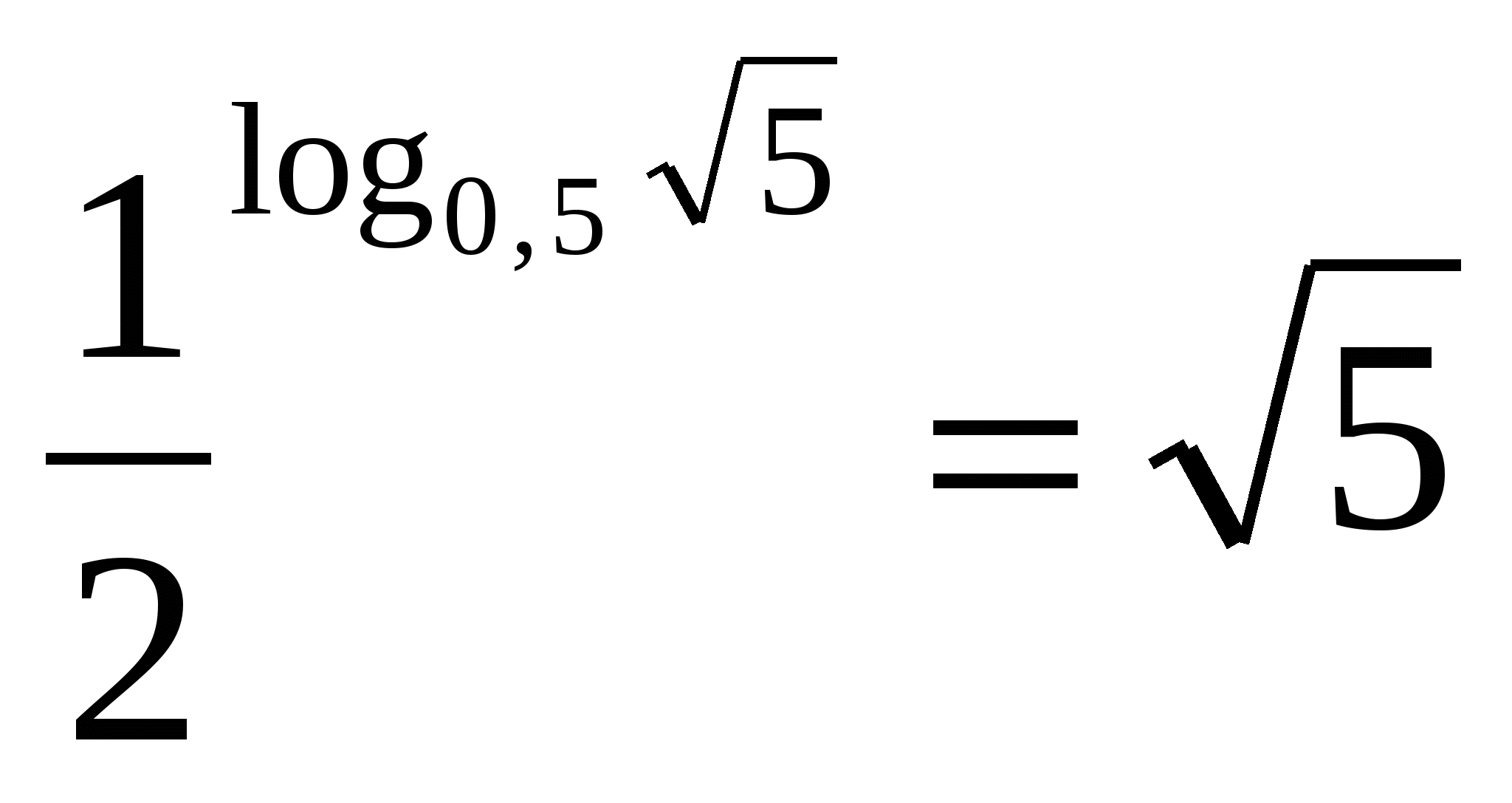
ЗА долната част на втората е равна на нула цяло пет, което означава, че изразът е равен на аритметичен корен квадратен от пет.

П

Приложение 2.

Равенство означава, че

От дефиницията на логаритъма се получават следните важни равенства:

Например:

П
Приложение 3.

Да преминем към Задачи за единен държавен изпит:

Приложение 4.

3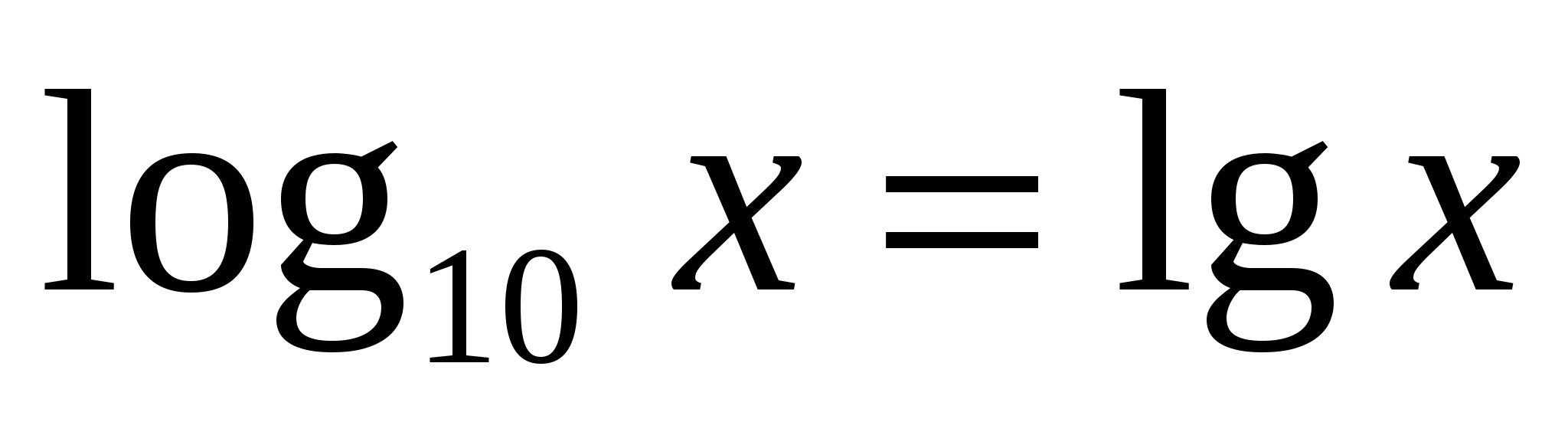
) Има специална нотация и име за логаритъм с основа десетдесетичен логаритъм .

Л
основен каларитъмд нареченнатурален логаритъм .

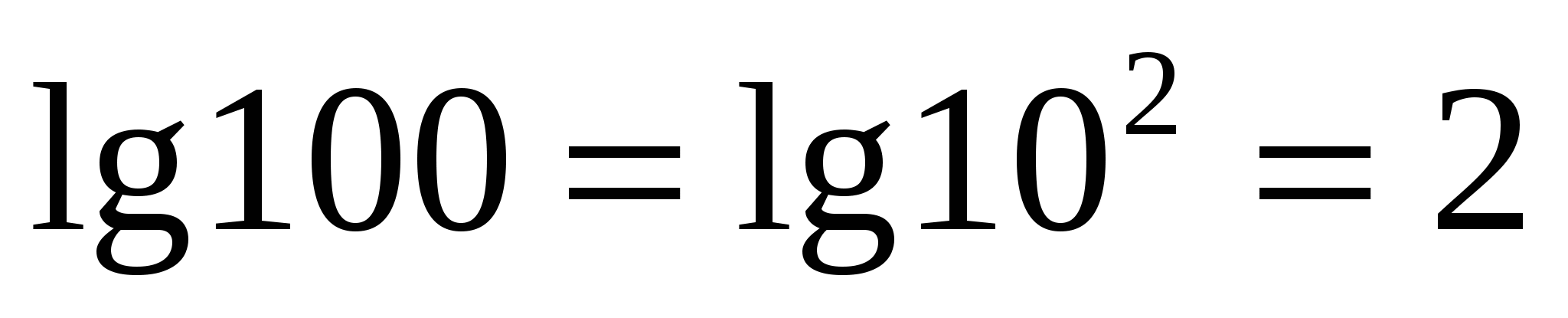
Н
например,

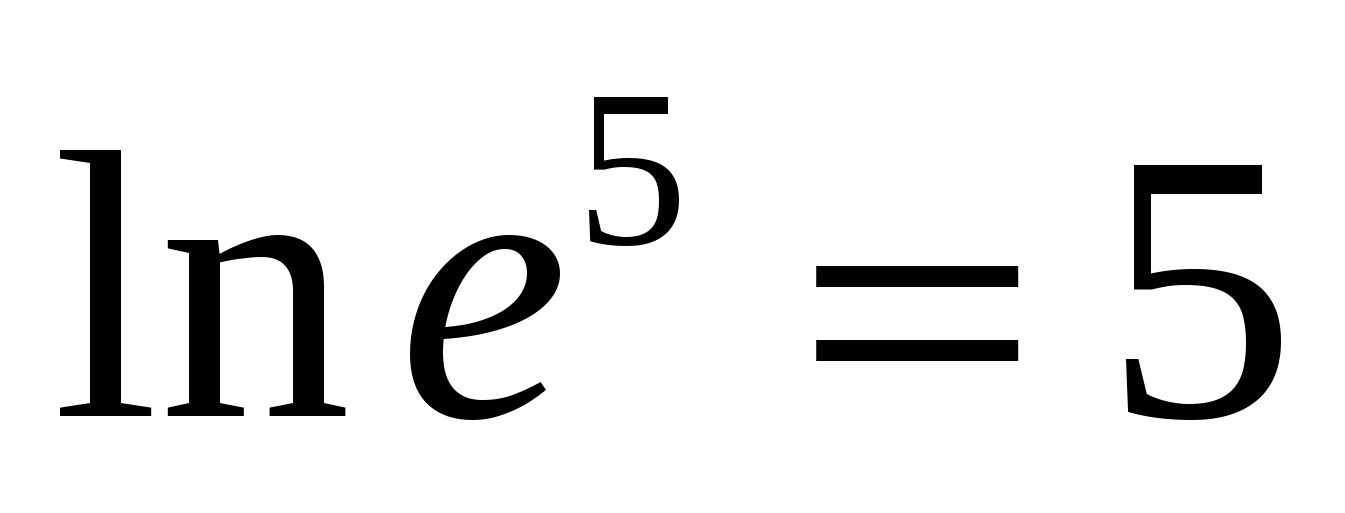
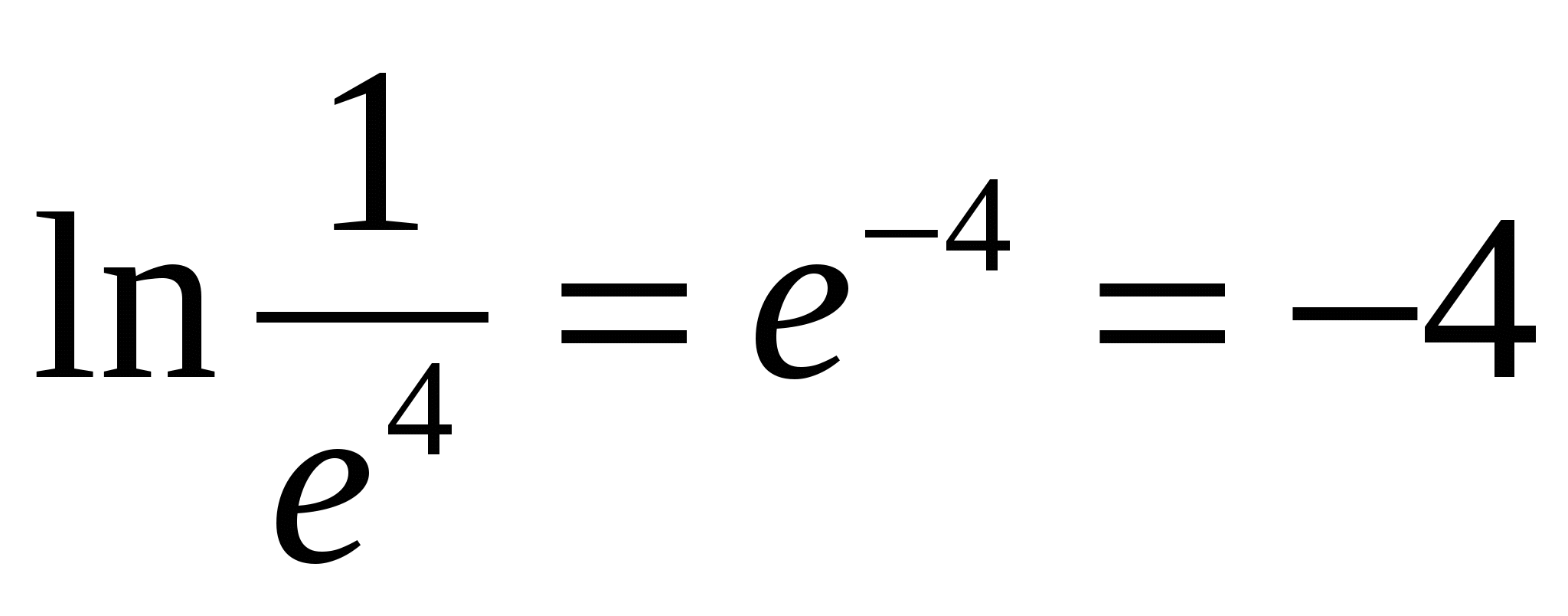
4) От дефиницията на логаритъм следват следните свойства. Всички свойства са формулирани и доказани само за положителни стойности на променливи, съдържащи се под знаците на логаритмите.

Логаритъм от произведението на две положителни числа към основата А равно на суматалогаритми на тези числа с една и съща основа.

ЦОР 2

например,

З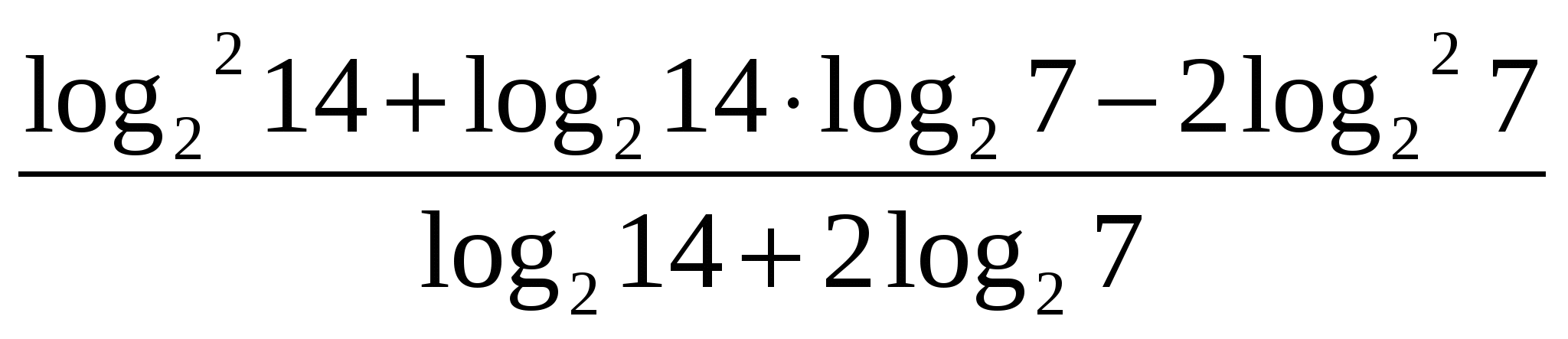
задача 1.

Задача 2.Опростете израза

IN
Нека използваме решението от предишния пример. Ние ще заменим

Моля, обърнете внимание, че логаритъма е на квадрат, така че сумата трябва да бъде на квадрат. Използвайки формулата за квадрат на сумата, отваряме скобите. Нека представим подобни термини.

5) Логаритъмът на частното е равен на разликата между логаритмите на делителя и делителя.

В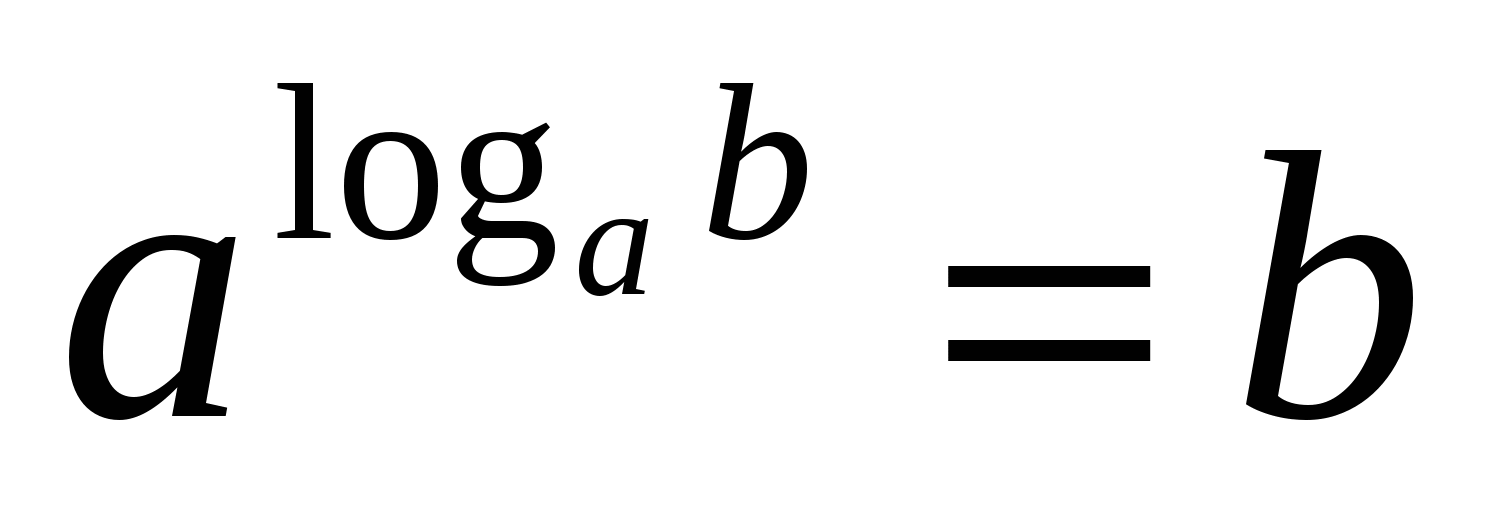

Обърнете внимание на основата на степента и основата на логаритъма - те са еднакви.

ИЛИ 3

Р

Нека да разгледаме приложението на тази формула с пример:

З
задача 1.Намерете стойността на израза if

Задача 2.Намерете стойността bчрез своя логаритъм

6) Логаритъм на степен спрямо основатаА , е равно на произведението на експонентата и логаритъма с една и съща основа.

ЦОР 4

например,

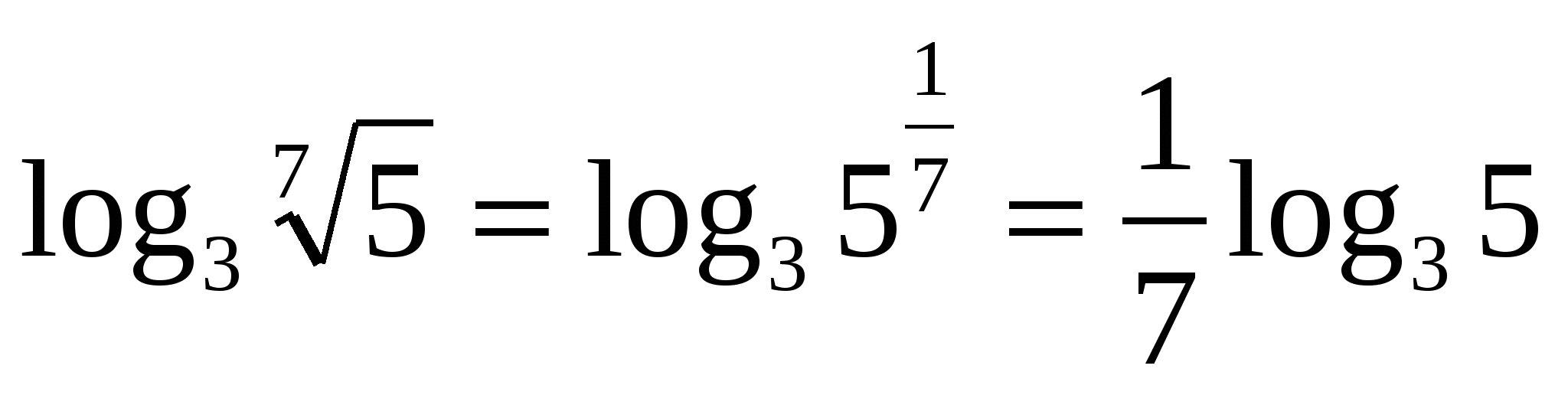
З
задача 1.Изчислете дали

Нека опростим израза

Формула

наречен формула за преминаване към нова основа.

З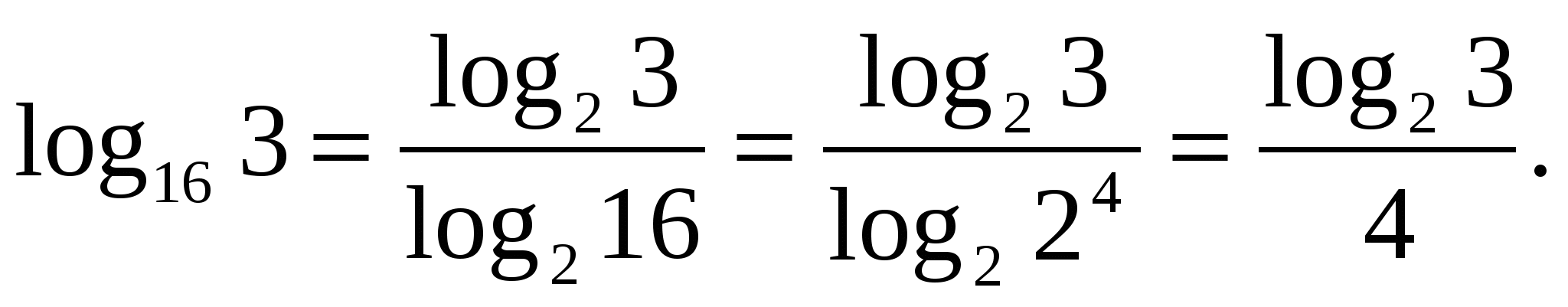

задача 1.Изразете с помощта на логаритъм с основа 2.

Задача 2.Изчислете

ЦОР 5

ЦОР 6

например,

З

задача 1.Изчислете

З
задача 2.Изчислете

9) Логаритмичните трансформации могат да бъдат стартирани само в случаите, когатоако помните всички свойства на логаритмите. След като ги повторим, ще разгледаме задачи за трансформация логаритмични изразиот другата страна.

За да преобразувате сумата или разликата на логаритмични изрази, понякога е достатъчно да използвате дефиницията на логаритъм и най-често свойствата на логаритъм от произведение или частно.

З
задача 1.Изчислете

Нека го решим по два начина.

1 начин, използвайки определението за логаритъм:

Метод 2, базиран насвойство на логаритъм от частно:

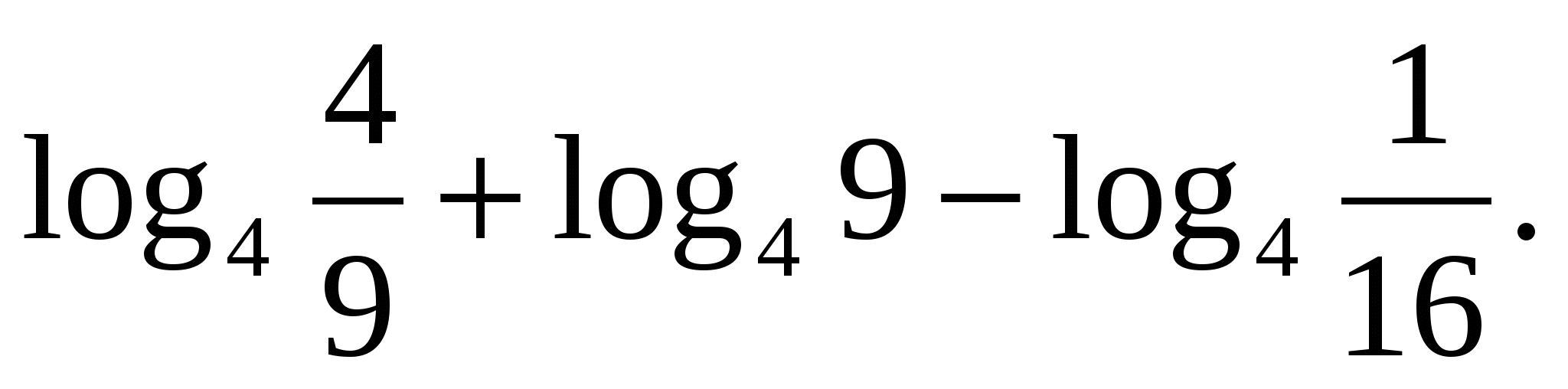
Задача 2.Намерете значението на израза

Нека първо приложим формулаталогаритъм на произведението, след това дефиницията на логаритъм.

Основната логаритмична идентичност се използва при преобразуване на изрази, съдържащи логаритъм като показател. Идеята на такива операции е да се получи равни основаниястепени и основи на логаритъма.

Понякога е необходимо да се трансформира изражениетоот свойствата на логаритъма и от свойствата на степента, също можете лесно да преминете от една база към друга, като използвате формулата за преход. В други случаи трябва да се приложат множество свойства.

З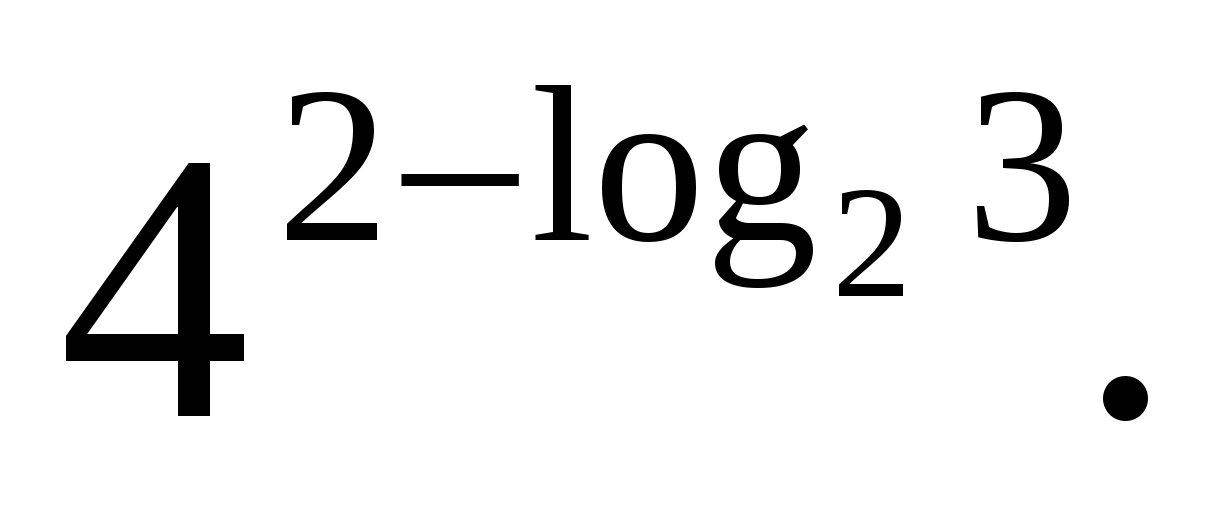
задача 3.Изчислете

З
задача 4.Намерете значението на израза

Задача 5.Намерете значението на израза

З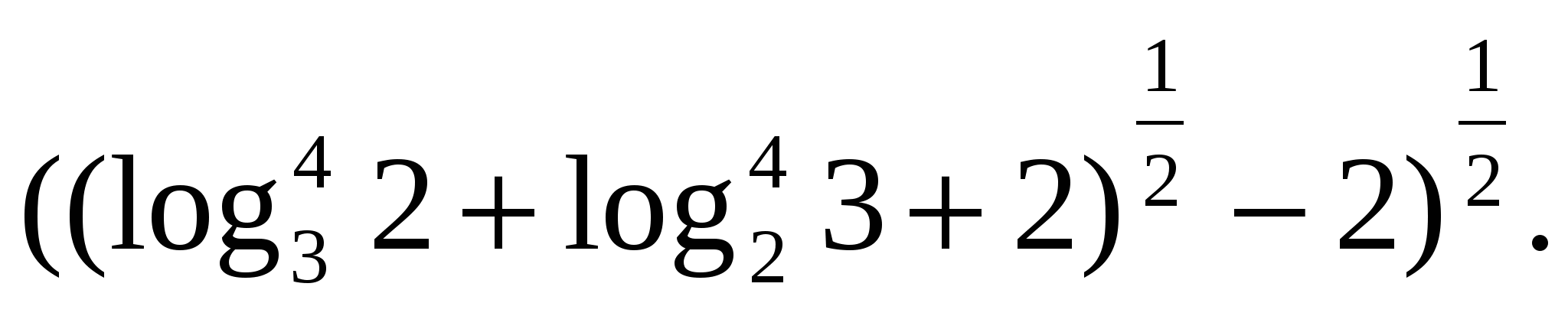
задача 6.Изразете го като разлика от логаритми

Н
Най-голямата трудност е при преобразуването на логаритмични изрази под радикала. В процеса на трансформации е необходимо да се разгледат модулите на логаритмичните изрази, за решаването на които е необходимо да се сравнят ирационални числа или рационално и ирационално число. Ще действаме последователно. Нека да разгледаме израза под вътрешния радикал.

Нека го заместим в оригиналния израз.

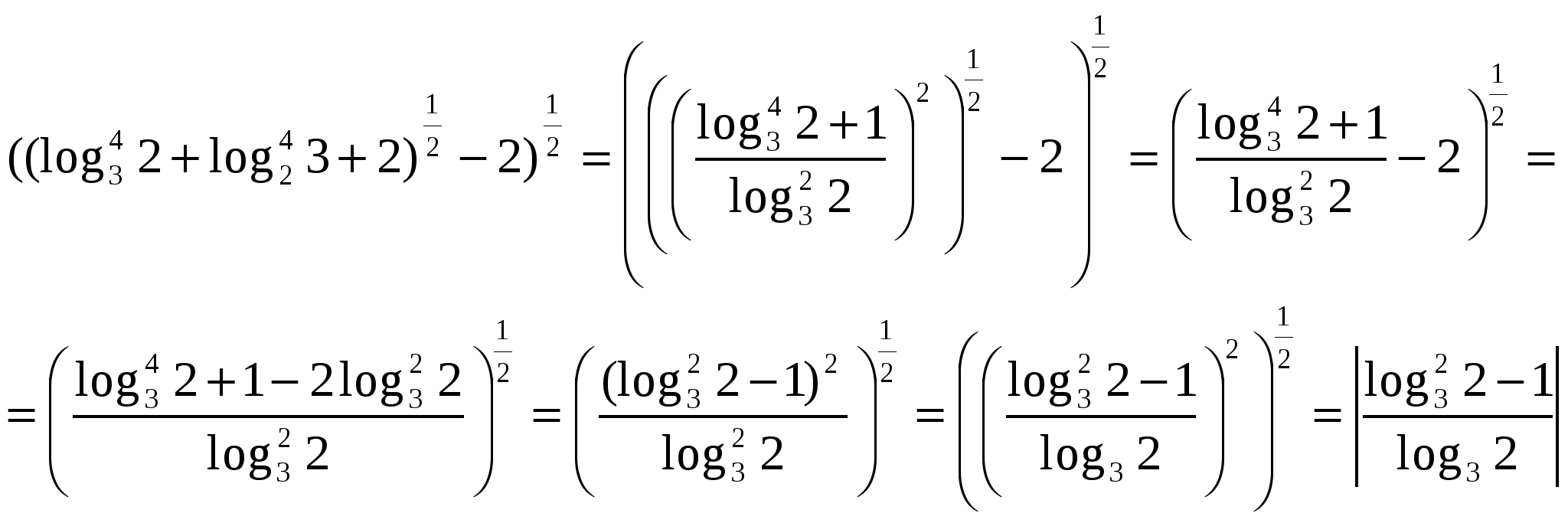Трябва да се отбележи, че преобразуването на логаритмични изрази може да се срещне и при решаване на уравнения и неравенства или изучаване на функции, поради което те могат да присъстват в имплицитна форма в задачи от групи B и C.

10) Обобщаващи въпроси:

Извиква се логаритъм при основа 10

основен логаритъм

главен логаритъм

натурален логаритъм

десетичен логаритъм

2) Какви стойности може да приеме?х в израза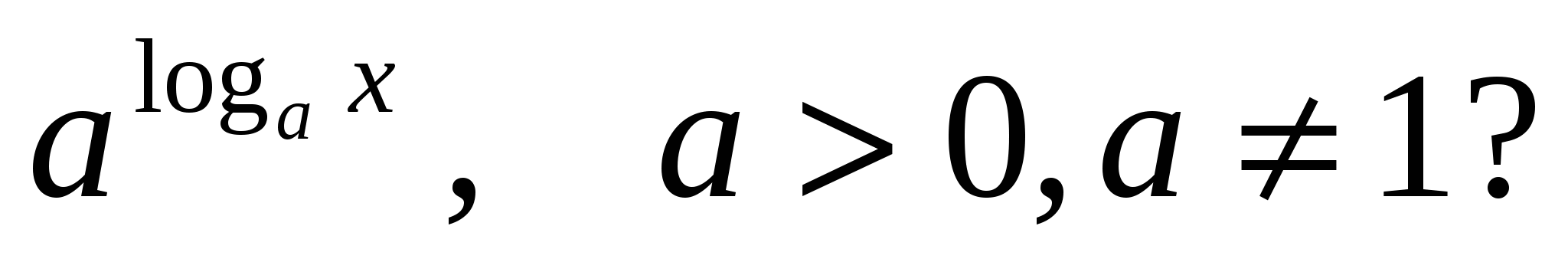

Стойността не е дефинирана

5) Дайте съотношение, което е вярно за всичких ≠ 0 .

6) Посочете правилното съотношение за формулата за преминаване към нова база.

7) Посочете правилното равенство за

11) Контролно изпитване.

Математика. Предметни тестове. Част II. Подготовка за Единния държавен изпит 2010 г. 10-11 клас. Изд. Лисенко F.F. - Ростов n/d .: Легион, 2009. - 176 с.

Математика. Единен държавен изпит 2009 г. Тематични тестове. Част II (B4-B8, C1-C2) Изд. Лисенко F.F. - Ростов н/Д: Легион, 2008 г. - 160 с.

Ръководството се състои от тестове по отделни теми, които са традиционни в курсовете по математика и следователно, като правило, са включени в Единния държавен изпит. Те покриват изцяло групи от задачи с повишено и високо ниво на сложност на Единния държавен изпит, с изключение на текстови задачи и задачи по геометрия. За всяка тема се предлагат един или повече комплекта тестове. Всеки комплект съдържа 10 теста, всеки тест съдържа 8 задачи.

Целта на тази книга е упражняване на задачи с кратък и дълъг отговор. Тестове за единен държавен изпит. Необходимо е предимно за завършилите, които очакват да получат a добра УПОТРЕБАоценяване, както и за ученици от 10 клас, които могат да затвърдят разгледаните теми от гледна точка на Единния държавен изпит. Предложеното ръководство може да бъде полезно за всички завършили, подготвящи се за Единния държавен изпит по математика, както и за учители, подготвящи ученици за Единния държавен изпит.

формат: djvu/zip (2009 , 176 стр.)

размер: 2,5 MB

Изтегляне / Изтегляне на файл 14

формат: pdf (2009 , 176 стр.)

размер: 8,6 MB

Изтегляне: 14 .12.2018 г., връзките премахнати по искане на издателство Легион (виж забележката)

формат: djvu/zip (2008 , 160-те.)

размер: 3 MB

Изтегляне / Изтегляне на файл 14 .12.2018 г., връзките премахнати по искане на издателство Легион (виж забележката)

формат: pdf (2008 , 160-те.)

размер: 9,9 MB

Изтегляне: 14 .12.2018 г., връзките премахнати по искане на издателство Легион (виж забележката)

Учебно-методически комплекс"Математика. Единен държавен изпит-2010" изд. Лисенко F.F. и Кулабухова С.Ю. включва уроци:
1. Математика. Подготовка за Единния държавен изпит 2010 г.
2. Решебник. Математика. Подготовка за Единния държавен изпит 2010 г.
3. Математика. Тематични тестове. Част I (базово ниво). Подготовка за Единния държавен изпит 2010 г. 10-11 клас.
4. Математика. Тематични тестове. Част II.
5. Подготовка за Единния държавен изпит 2010 г. 10-11 клас.
6. Математика. Тематични тестове: геометрия, текстови задачи.
7. Подготовка за Единния държавен изпит 2010 г. 10-11 клас.
8. Математика. Сборник тестове за единен държавен изпит 2001 - 2010 г.Математика. Подготовка за Единния държавен изпит 2010 г.

Образователни и тренировъчни тестове.
Джобен справочник
по математика.
Съдържание
От авторите 11
§ 1. Тъждествени преобразувания на логаритмични изрази 13
Вариант №1 13
Вариант № 2 13
Вариант №3 14
Вариант №4 14
Вариант №5 15
Вариант №6 15
Вариант №7 16
Вариант № 8 16
Вариант №9 17
Вариант № 10 17
§ 2. Тъждествени преобразувания на изрази, съдържащи степени на 18
Вариант №1 18
Вариант №2 19
Вариант №3 19
Вариант №4 20
Вариант №5 21
Вариант №6 21
Вариант №7 22
Вариант №8 23 Вариант №9 23 25
Вариант №10 24
§ 3. Трансформации на идентичността
ирационални изрази
Вариант №1 25
Вариант №2 25
Вариант № 3 26
Вариант №4 26
Вариант № 5 27
Вариант №6 28
Вариант №7 28
Вариант №8 29
Вариант №9 30
Вариант № 10 30
§ 4. Системи уравнения 31
Вариант №1 31
Вариант №2 32
Вариант № 3 33
Вариант № 4 33
Вариант № 5 34
Вариант № 6 35
Вариант №7 36
Вариант № 8 37 Вариант № 9 38Вариант № 10 39
§ 5.
Геометрично значение
производна 39
Вариант №1 39
Вариант №2 41
Вариант № 3 43
Вариант №4 44
Вариант № 5 46
Вариант №6 48
Вариант №7 50
Вариант № 8 52
Вариант №9 54
Вариант № 10 55
§ 6. Неравенства 56
Вариант №1 g 56
Вариант № 2 57
Вариант № 3 58
Вариант №4 58
Вариант № 5 59
Вариант №6 60
Вариант №7 60
Вариант № 8 61
Вариант №9 62
Вариант № 10 63
§ 7. Ирационални уравнения 63
Вариант №1 63
Вариант № 2 64
Вариант № 3 65
Вариант № 4 65
Вариант № 5 66
Вариант № 6 66
Вариант №7 67
Вариант № 8 67
Вариант №9 68
Вариант № Ю 68
§ 8. Тригонометрични уравнения 69
Вариант №1 69
Вариант № 2 69
Вариант № 3 70
Вариант № 4 70
Вариант № 5 71
Вариант № 6 72
Вариант № 7 72
Вариант № 8 73
Вариант №9 74
Вариант № 10 74
§ 9. Логаритмични уравнения 75
Вариант №1 75
Вариант № 2 75
Вариант № 3 76
Вариант № 4 76
Вариант № 5 77
Вариант № 6 77
Вариант № 7 78
Вариант №8*78
Вариант №9 79
Вариант № 10 79
§ 10. Показателни уравнения 80
Вариант №1 80
Вариант № 2 80
Вариант № 3 81
Вариант № 4 81
Вариант № 5 82
Вариант №6 82
Вариант № 7 83
Вариант № 8 83
Вариант №9 84
Вариант № 10 84
§11. Периодичност, четни и нечетни функции 85
Вариант №1 85
Вариант № 2 86
Вариант № 3 87
Вариант № 4 89
Вариант № 5 90
Вариант №6 91
Вариант № 7 92
Вариант № 8 93 Вариант № 9 94. Ограничена функция 97
Вариант № 1 97
Вариант № 2 97
Вариант № 3 98
Вариант № 4 98
Вариант № 5 99
Вариант № 6 99
Вариант № 7 100
Вариант № 8 100
Вариант № 9 101
Вариант № 10 101
§ 13. Област на дефиниране, множество от стойности, монотонност на функции 102
Вариант №1 102
Вариант № 2 102
Вариант № 3 103
Вариант №4 103
Вариант № 5 104
Вариант №6 104
Вариант № 7 105
Вариант № 8 105
Вариант № 9 106
Вариант № 10 107
§ 14. Екстремуми на функция. Най-големите и най-малките стойности на функцията 107
Вариант №1 107
Вариант № 2 108
Вариант №3 108
Вариант №4 109
Вариант № 5 109
Вариант №6 110
Вариант № 7 110
Вариант № 8 111
Вариант № 9 111
Вариант № 10 112
§ 15. Различни техники за решаване на логаритмични уравнения 113
Вариант №1 113
Вариант № 2 113
Вариант №3 114
Вариант №4 114
Вариант № 5 115
Вариант №6 115
Вариант № 7 116
Вариант № 8 116
Вариант № 9 117
Вариант № 10 117
§ 16. Различни техники за решаване тригонометрични уравнения 118
Вариант №1 118
Вариант № 2 118
Вариант №3 118
Вариант №4 119
Вариант № 5 119
Вариант №6 120
Вариант № 7 120
Вариант № 8 121
Вариант № 9 121
Вариант № 10 122
§ 17. Различни техники за решаване ирационални уравнения 123
Вариант №1 123
Вариант № 2 123
Вариант №3 124
Вариант №4 124
Вариант № 5 125
Вариант №6 125
Вариант №7 125
Вариант № 8 126
Вариант №9 126
Вариант № 10 127
§ 18. Уравнения, съдържащи променлива под знака на модула 127
Вариант №1 127
Вариант № 2 128
Вариант №3 128
Вариант №4 129
Вариант № 5 129
Вариант №6 130
Вариант № 7 130
Вариант № 8 131
Вариант № 9 131
Вариант № 10 131
§ 19. Различни техники за решаване експоненциални уравнения.132
Вариант №1 132
Вариант № 2 133
Вариант № 3 133
Вариант №4 134
Вариант № 5 134
Вариант №6 135
Вариант № 7 135
Вариант № 8 135
Вариант №9 136
Вариант № 10 136
§ 20. Различни техники за решаване на комбинирани уравнения 137
Вариант №1 137
Вариант № 2 137
Вариант №3 138
Вариант №4 138
Вариант № 5 139
Вариант №6 139
Вариант № 7 140
Вариант № 8 140
Вариант № 9 141
Вариант № 10 141
§ 21. Уравнения с параметър, съдържащ модул 142
Вариант №1 142
Вариант № 2 142
Вариант №3 143
Вариант №4 144
Вариант № 5 144
Вариант №6 145
Вариант № 7 146
Вариант № 8 146
Вариант № 9 147
Вариант № 10 148
Отговори 149
§ 1. Трансформации на идентичностталогаритмични изрази 149
§ 2. Тъждествени преобразувания на изрази, съдържащи степени на 150
§ 3. Тъждествени преобразувания на ирационални изрази 150
§ 4. Системи уравнения 151
§ 5. Геометричен смисъл на производната 151
§ 6. Неравенства 152
§ 7. Ирационални уравнения 152
§ 8. Тригонометрични уравнения 153
§ 9. Логаритмични уравнения 153
§ 10. Показателни уравнения 154
§11. Периодичност, четни и нечетни функции 154
§ 12. Нули на комплексна функция. Ограничена функция 155
§ 13. Област на дефиниране, множество от стойности, монотонност на функции 156
§ 14. Екстремуми на функция. Най-големите и най-малките стойности на функцията 158
§ 15. Различни техники за решаване на логаритмични уравнения 159
§ 16. Различни техники за решаване на тригонометрични уравнения 160
§ 17. Различни техники за решаване на ирационални уравнения 164
§ 18. Уравнения, съдържащи променлива под знака на модула 165
§ 19. Различни техники за решаване на експоненциални уравнения.166
§ 20. Различни техники за решаване на комбинирани уравнения 167
§ 21. Уравнения с параметър, съдържащ модул 169
Литература 170

Задача B7 дава някакъв израз, който трябва да бъде опростен. Резултатът трябва да бъде редовно число, което може да се запише във вашия лист за отговори. Всички изрази са условно разделени на три типа:

1. логаритмичен,
2. ориентировъчно,
3. Комбиниран.

Експоненциални и логаритмични изрази в тяхната чиста форма практически никога не се срещат. Въпреки това е абсолютно необходимо да знаете как се изчисляват.

Като цяло задача B7 се решава доста просто и е съвсем по силите на средния абитуриент. Липсата на ясни алгоритми се компенсира от неговата стандартизация и монотонност. Можете да се научите да решавате такива проблеми просто чрез голямо количествообучение.

Логаритмични изрази

По-голямата част от задачите на B7 включват логаритми под една или друга форма. Тази тема традиционно се счита за трудна, тъй като нейното изучаване обикновено се случва в 11-ти клас - ерата на масова подготовка за финални изпити. В резултат на това много завършили имат много неясно разбиране за логаритми.

Но в тази задача никой не изисква дълбоки теоретични познания. Ще срещнем само най-много прости изрази, които изискват просто разсъждение и лесно могат да бъдат усвоени самостоятелно. По-долу са основните формули, които трябва да знаете, за да се справите с логаритми:

Освен това трябва да можете да замествате корени и дроби със степени с рационален показател, в противен случай в някои изрази просто няма да има какво да се извади под знака за логаритъм. Формули за заместване:

Задача. Намерете значението на изразите:
log 6 270 − log 6 7.5
log 5 775 − log 5 6.2

Първите два израза се преобразуват като разлика на логаритми:
log 6 270 − log 6 7,5 = log 6 (270: 7,5) = log 6 36 = 2;
log 5 775 − log 5 6,2 = log 5 (775: 6,2) = log 5 125 = 3.

За да изчислите третия израз, ще трябва да изолирате степени - както в основата, така и в аргумента. Първо, нека намерим вътрешния логаритъм:

След това - външно:

Конструкциите на формата log a log b x изглеждат сложни и неразбрани за мнозина. Междувременно това е просто логаритъм от логаритъма, т.е. log a (log b x ). Първо се изчислява вътрешният логаритъм (поставете log b x = c), а след това външният: log a c.

Демонстративни изрази

Експоненциален израз ще наричаме всяка конструкция от вида a k, където числата a и k са произволни константи, а a > 0. Методите за работа с такива изрази са съвсем прости и се разглеждат в уроците по алгебра за 8 клас.

По-долу са основните формули, които определено трябва да знаете. Прилагането на тези формули на практика, като правило, не създава проблеми.

1. a n · a m = a n + m ;
2. a n / a m = a n − m;
3. (a n) m = a n · m;
4. (a · b) n = a n · b n;
5. (a : b ) n = a n : b n .

Ако попаднете на сложен израз със степени и не е ясно как да подходите към него, използвайте универсална техника - разлагане на прости фактори. В резултат на това големи числав основите на степените се заменят с прости и разбираеми елементи. След това остава само да приложите горните формули - и проблемът ще бъде решен.

Задача. Намерете стойностите на изразите: 7 9 · 3 11: 21 8, 24 7: 3 6: 16 5, 30 6: 6 5: 25 2.

Решение. Нека разложим всички основи на правомощията на прости фактори:
7 9 3 11: 21 8 = 7 9 3 11: (7 3) 8 = 7 9 3 11: (7 8 3 8) = 7 9 3 11: 7 8: 3 8 = 7 3 3 = 189.
24 7: 3 6: 16 5 = (3 2 3) 7: 3 6: (2 4) 5 = 3 7 2 21: 3 6: 2 20 = 3 2 = 6.
30 6: 6 5: 25 2 = (5 3 2) 6: (3 2) 5: (5 2) 2 = 5 6 3 6 2 6: 3 5: 2 5: 5 4 = 5 2 3 2 = 150 .

Комбинирани задачи

Ако знаете формулите, тогава всички експоненциални и логаритмични изрази могат да бъдат решени буквално в един ред. Въпреки това, в задача B7 степените и логаритмите могат да се комбинират, за да образуват доста силни комбинации.

приднестровски държавен университет

тях. Т.Г. Шевченко

Физико-математически факултет

Отдел математически анализ

и методи на обучение по математика

КУРСОВА РАБОТА

„Трансформации на идентичността

експоненциална и логаритмична

изрази"

Завършена работа:

ученик от _______ група

Физико-математически факултет

_________________________

Проверих работата:

_________________________

Тираспол, 2003 г

Въведение…………………………………………………………………………………2

Глава 1. Трансформации на идентичността и методи на преподаване в училищния курс по алгебра и началото на анализа………………………………………..4

§1. Формиране на умения за прилагане на специфични видове трансформации……………………………………………………………………………………….4

§2. Характеристики на организацията на система от знания при изучаването на трансформациите на идентичността.…….……………………………………..………….5

§3. Програма по математика………………………………………………………….11

Глава 2. Идентични преобразувания и изчисления на експоненциални и логаритмични изрази…………………………………………………13

§1. Обобщение на понятието степен……………………………………..13

§2. Експоненциална функция………………………………………………………..15

§3. Логаритмична функция…………………………………….16

Глава 3. Идентични преобразувания на експоненциални и логаритмични изрази на практика.................................................. ..............................................19

Заключение………………………………………………………………..24

Списък с литература………………………………………………………….25
Въведение

В това курсова работаЩе бъдат разгледани идентични преобразувания на експоненциални и логаритмични функции, ще бъде разгледана методиката за преподаването им в училищния курс по алгебра и началото на анализа.

Първата глава на тази работа описва методологията за преподаване на трансформации на идентичност в училищен курс по математика и също така включва програма по математика в курса „Алгебра и началото на анализа“ с изучаване на експоненциални и логаритмични функции.

Втората глава разглежда пряко самите експоненциални и логаритмични функции, техните основни свойства, използвани в трансформации на идентичност.

Третата глава е решаване на примери и задачи чрез идентични трансформации на експоненциални и логаритмични функции.

Изучаването на различни трансформации на изрази и формули заема значителна част от учебното време в курса училищна математика. Най-простите трансформации, базирани на свойства аритметични операции, вече се произвеждат в основно училищеи в IV–V клас. Но основната тежест за развиване на уменията и способностите за извършване на трансформации се носи от училищния курс по алгебра. Това се дължи както на рязкото увеличаване на броя и разнообразието на извършваните трансформации, така и на усложняването на дейностите по тяхното обосноваване и изясняване на условията за приложимост, на идентифицирането и изучаването на обобщените понятия за идентичност, идентична трансформация, еквивалентна трансформация, логическо следствие.

Културата на извършване на трансформации на идентичност се развива по същия начин като културата на изчисленията, основана на солидни познания за свойствата на операциите върху обекти (числа, вектори, полиноми и т.н.) и алгоритмите за тяхното изпълнение. Тя се проявява не само в способността за правилно обосноваване на трансформациите, но и в способността да се намери най-краткият път за преход от първоначалния аналитичен израз към израза, който най-много отговаря на целта на трансформацията, в способността да се наблюдават промените в областта на дефиниране на аналитични изрази във верига от идентични трансформации, в скоростта и точността на извършване на трансформациите.

сигурност висока култураизчисления и трансформации на идентичност представлява важен проблемпреподаване на математика. Този проблем обаче все още е далеч от задоволителното си решение. Доказателство за това са статистическите данни на властите обществено образование, в които грешки и ирационални методи на изчисления и трансформации, направени от ученици от различни класове при изпълнение тестове. Това се потвърждава от прегледи на старши образователни институцииза качеството на математическите знания и умения на кандидатите. Човек не може да не се съгласи с изводите на образователните органи и университетите, че не е достатъчно високо нивокултура на изчисления и трансформации на идентичността в гимназияе следствие от формализма в знанията на учениците, отделянето на теорията от практиката.

Идентични трансформации и методи на обучение

в училищния курс по алгебра и началото на анализа.

§1. Формиране на умения за прилагане

специфични видове трансформации.

Системата от техники и правила за извършване на трансформации, използвани на етапа на начална алгебра, има много широк спектър от приложения: използва се при изучаването на целия курс по математика. Въпреки това, именно поради ниската си специфичност, тази система изисква допълнителни трансформации, които отчитат структурните особености на трансформираните изрази и свойствата на нововъведените операции и функции. Усвояването на съответните видове трансформации започва с въвеждането на формули за съкратено умножение. След това трансформациите, свързани с операцията за степенуване, се разглеждат с различни класове елементарни функции– експоненциална, степенна, логаритмична, тригонометрична. Всеки от тези видове трансформации преминава през фаза на обучение, в която вниманието е насочено към овладяване на техните характерни черти.

Тъй като материалът се натрупва, става възможно да се изолират и общи чертивсички разглеждани трансформации и на тази основа въвеждат понятията тъждествени и еквивалентни трансформации.

Трябва да се отбележи, че концепцията за трансформация на идентичността е дадена в училищния курс по алгебра не в пълна обобщеност, а само в приложение към изрази. Трансформациите са разделени на два класа: тъждествените трансформации са трансформации на изрази, а еквивалентните трансформации са трансформации на формули. В случай, че има нужда от опростяване на една част от формулата, в тази формула се маркира израз, който служи като аргумент за приложената трансформация на идентичността. Съответният предикат се счита за непроменен.

Що се отнася до организацията на интегрална система от трансформации (синтез), нейната основна цел е да формира гъвкава и мощна; апарат, подходящ за използване при решаване на различни образователни задачи.

В курса по алгебра и започна анализ цялостна систематрансформации, вече оформени в основните си характеристики, продължава постепенно да се подобрява. Към него се добавят и някои нови видове трансформации, но те само го обогатяват, разширяват възможностите му, но не променят структурата му. Методологията за изучаване на тези нови трансформации практически не се различава от тази, използвана в курса по алгебра.

§2. Характеристики на организацията на системата от задачи

когато изучаваме трансформациите на идентичността.

Основният принцип за организиране на всяка система от задачи е да се представят от прости към сложни, като се вземе предвид необходимостта учениците да преодолеят възможни трудности и да създадат проблемни ситуации. Този основен принцип изисква спецификация във връзка с характеристиките на този учебен материал. За описание на различни системи от задачи в математическите методи се използва концепцията за цикъл от упражнения. Цикълът от упражнения се характеризира с комбинирането в последователност от упражнения на няколко аспекта на изучаване и техники за подреждане на материала. Във връзка с трансформациите на идентичността идеята за цикъл може да бъде дадена по следния начин.

Цикълът от упражнения е свързан с изучаването на една идентичност, около която се групират други идентичности, които са в естествена връзка с нея. Цикълът, наред с изпълнителните, включва задачи, които изискват разпознаване на приложимостта на въпросната идентичност. Изследваната идентичност се използва за извършване на изчисления в различни цифрови области. Отчита се спецификата на идентичността; по-специално, фигурите на речта, свързани с него, са организирани.

Задачите във всеки цикъл са разделени на две групи. Първият включва задачи, изпълнявани при първоначално запознаване с идентичността. Те служат учебен материалза няколко последователни урока, обединени от една тема. Втората група упражнения свързва изучаваната идентичност с различни приложения. Тази група не образува композиционно единство - упражненията тук са разпръснати по различни теми.

Описаната структура на цикъла се отнася до етапа на развитие на умения за прилагане на специфични видове трансформации. включено финален етап– на етапа на синтез циклите се модифицират. Първо, двете групи задачи се комбинират, за да образуват „разширен“ цикъл, а най-простите по отношение на формулировката или сложността на изпълнение на задачата се изключват от първата група. Останалите видове задачи стават по-сложни. На второ място, има сливане на цикли, свързани с различни идентичности, поради което се увеличава ролята на действията за разпознаване на приложимостта на определена идентичност.

Нека отбележим характеристиките на циклите на задачите, свързани с идентичностите за елементарни функции. Тези характеристики се дължат на факта, че, първо, съответните идентичности се изучават във връзка с изучаването на функционален материал и, второ, те се появяват по-късно от идентичностите от първата група и се изучават с помощта на вече формирани умения за извършване на трансформации на идентичността .

Всяка нововъведена елементарна функция драматично разширява диапазона от числа, които могат да бъдат обозначени и наименувани индивидуално. Следователно, първата група циклични задачи трябва да включва задачи за установяване на връзка между тези нови числови области и оригиналната област рационални числа. Нека дадем примери за такива задачи.

Пример 1. Изчислете:

До всеки израз е посочена идентичност, в циклите, за които могат да присъстват предложените задачи. Целта на такива задачи е да се овладеят характеристиките на записите, включително символи на нови операции и функции, и да се развият математически речеви умения.

Значителна част от използването на трансформации на идентичност, свързани с елементарни функции, се пада върху решаването на ирационални и трансцендентни уравнения. Циклите, свързани с асимилацията на идентичности, включват само най-много прости уравнения, но вече тук е препоръчително да се работи по овладяването на метода за решаване на такива уравнения: намаляването му чрез замяна на неизвестното с алгебрично уравнение.

Последователността от стъпки за това решение е следната:

а) намерете функцията, за която дадено уравнениепредставителен във формата ;

б) направете заместването и решете уравнението;

в) решаване на всяко от уравненията , където е множеството от корените на уравнението .

Когато се използва описаният метод, стъпка b) често се изпълнява имплицитно, без да се въвежда нотация за . Освен това учениците често предпочитат от различните пътища, водещи до намиране на отговор, да изберат този, който води до алгебричното уравнение по-бързо и по-лесно.

Пример 2. Решете уравнението.

Първи начин:

Втори начин:

а)

б)

Тук можете да видите, че с първия метод стъпка a) е по-трудна, отколкото с втората. Първият метод е „по-труден за започване“, въпреки че по-нататъшният ход на решението е много по-прост. От друга страна, вторият метод има предимствата на по-голяма лекота и по-голяма прецизност при научаването на редукция до алгебрично уравнение.

За училищен курсТипични са задачите по алгебра, при които преминаването към алгебрично уравнение е още по-просто, отколкото в този пример. Основното натоварване на такива задачи е свързано с идентифицирането на стъпка c) като независима част от процеса на решаване, свързана с използването на свойствата на елементарната функция, която се изучава.

Пример 3. Решете уравнението:

а) ; б) .

Тези уравнения се свеждат до уравненията: а) или ; б) или . Решаването на тези уравнения изисква познаване само на най-простите факти за експоненциална функция: неговата монотонност, диапазон от стойности. Подобно на предишния пример, уравнения a) и b) могат да бъдат класифицирани като първата група от поредица от упражнения за решаване на квадратни експоненциални уравнения.

Така стигаме до класификация на задачите в цикли, свързани с решаване на трансцендентни уравнения, които включват експоненциална функция:

1) уравнения, които се свеждат до уравнения от вида и имат прост общ отговор: ;

2) уравнения, които се свеждат до уравнения , където е цяло число, или , където ;

3) уравнения, които се свеждат до уравнения и изискват ясен анализ на формата, в която е написано числото.

Задачите за други елементарни функции могат да бъдат класифицирани по подобен начин.

В тях се доказват или поне се обясняват значителна част от тъждествата, изучавани в курсовете по алгебра и алгебра и принципи на анализ. Тази страна на изследването на идентичностите има голяма стойности за двата курса, тъй като доказателствените разсъждения в тях се извършват с най-голяма яснота и строгост именно по отношение на самоличностите. Извън този материал доказателствата обикновено са по-малко пълни; те не винаги се разграничават от използваната обосновка.

Свойствата на аритметичните операции се използват като основа, върху която се изграждат доказателства за идентичности.

Образователното въздействие на изчисленията и идентичните трансформации може да бъде насочено към развитието на логическото мислене, само ако учениците систематично се изискват да обосновават изчисленията и идентичните трансформации, както и към развитието на функционалното мислене, което се постига по различни начини. Значението на изчисленията и идентичните трансформации в развитието на волята, паметта, интелигентността, самоконтрола и творческата инициатива е съвсем очевидно.

Изискванията на ежедневната и индустриалната компютърна практика изискват от студентите да развият силни, автоматизирани умения за рационални изчисления и трансформации на идентичност. Тези умения се развиват в процеса на всяка изчислителна работа, но са необходими специални тренировъчни упражнения за бързи изчисления и трансформации.

Така че, ако урокът включва решаване на логаритмични уравнения с помощта на основния логаритмично тъждество, тогава е полезно да включите в плана на урока устни упражнения за опростяване или изчисляване на значенията на изрази: , , . Целта на упражненията винаги се съобщава на учениците. По време на упражнението може да се наложи да се изисква от учениците да обосноват отделни трансформации, действия или решението на цял проблем, дори ако това не е било планирано. Където е възможно различни начинирешавайки проблем, препоръчително е винаги да задавате въпроси: „Как беше решен проблемът?“, „Кой реши проблема по различен начин?“

Понятията тъждество и трансформация на тъждество са въведени изрично в курса по алгебра за VI клас. Самото определение идентични изразине може да се използва практически за доказване на идентичността на два израза и разбира, че същността на идентичните трансформации е да се приложат към израза дефинициите и свойствата на онези действия, които са посочени в израза, или да се добави към него израз, който е идентичен равно на 0, или да го умножим по израз, идентичен равно на едно. Но дори и да са усвоили тези разпоредби, учениците често не разбират защо тези трансформации ни позволяват да твърдим, че оригиналните и получените изрази са идентични, т.е. вземете едни и същи стойности за всякакви системи (набори) от променливи стойности.

Също така е важно да се гарантира, че учениците ясно разбират, че такива заключения от идентични трансформации са следствия от дефинициите и свойствата на съответните действия.

Апаратът за трансформации на идентичността, натрупан през предходните години, се разширява в VI клас. Това разширение започва с въвеждането на идентичност, изразяваща свойството на произведението на степени с еднакви бази: , където , са цели числа.

§3. Програма по математика. В училищния курс „Алгебра и началото на анализа“ учениците систематично изучават експоненциални и логаритмични функции и техните свойства, тъждествени преобразувания на логаритмични и експоненциални изрази и приложението им за решаване на съответните уравнения и неравенства и се запознават с основни понятия и твърдения . В 11 клас уроците по алгебра са 3 часа седмично, общо 102 часа годишно. Програмата отнема 36 часа за изучаване на експоненциални, логаритмични и степенни функции. Програмата включва разглеждане и изучаване на следните въпроси: Концепцията за степен с рационален показател. Решаване на ирационални уравнения. Експоненциална функция, нейните свойства и графика. Тъждествени трансформации на експоненциални изрази. Решаване на показателни уравнения и неравенства. Логаритъм на число. Основни свойства на логаритмите. Логаритмична функция, нейните свойства и графика. Решаване на логаритмични уравнения и неравенства. Производна на експоненциална функция. Номер и натурален логаритъм. Производна на степенна функция. Основната цел на раздела за експоненциална и логаритмична функция е да запознае учениците с експоненциална, логаритмична и степенна функция; учат учениците да решават експоненциални и логаритмични уравненияи неравенства. Понятията корен ти и степен с рационален показател са обобщение на понятията корен квадратен и степен с цяло число. Студентите трябва да обърнат внимание на факта, че свойствата на корените и степените с рационален показател, разглеждани тук, са подобни на тези свойства, притежавани от предишно изучени квадратни корении степени с цели числа. Необходимо е да се отдели достатъчно време за практикуване на свойствата на степени и развиване на умения за трансформация на идентичност. Понятие за степен c ирационален показателсе въвежда на визуална и интуитивна основа. Този материал играе спомагателна роля и се използва при въвеждане на експоненциалната функция. Изследването на свойствата на експоненциалните, логаритмичните и степенните функции е изградено в съответствие с приетата обща схема за изучаване на функциите. В този случай е даден преглед на свойствата в зависимост от стойностите на параметрите. Илюстративно и логаритмични неравенствасе решават въз основа на изучените свойства на функциите. Характерна особеностКурсът е систематизиране и обобщаване на знанията на учениците, консолидиране и развитие на уменията, придобити в курса по алгебра, което се извършва както при изучаване на нов материал, така и при провеждане на общо повторение.
Глава 2. Тъждествени преобразувания и пресмятания на експоненциални и логаритмични изрази

§1. Обобщение на понятието степен.

Определение: Коренът от чисто число е числото, чиято степен е равна на .

Според това определениеКоренът th от число е решението на уравнението. Броят на корените на това уравнение зависи от и. Нека разгледаме функцията. Както е известно, на интервала тази функция се увеличава за всяка стойност и взема всички стойности от интервала. Според теоремата за корена уравнението за всяко има неотрицателен корен и освен това само един. Нарича се аритметичен корен от степен th на число и се означава с ; числото се нарича радикален показател, а самото число се нарича радикален израз. Знакът се нарича още радикал.

Определение: Нарича се аритметичен корен на степен th на число неотрицателно число, чиято -та степен е равна на .

За четни числа функцията е четна. От това следва, че ако , то уравнението освен корен има и корен. Ако , тогава има един корен: ; ако , тогава това уравнение няма корени, тъй като дори степенвсяко число е неотрицателно.

За нечетни стойности функцията нараства по цялата числова линия; диапазонът му е множеството от всички реални числа. Прилагайки теоремата за корена, откриваме, че уравнението има един корен за всяко и по-специално за . Този корен за всяка стойност се означава с .

За корени от нечетна степен равенството е в сила. Всъщност, , т.е. числото е корен th от . Но такъв корен за нечетно е единственият. Следователно, .

Забележка 1: За всяко реално

Нека си припомним известните свойства на аритметичните корени от степен.

За всяко естествено число, цяло число и всички неотрицателни цели числа и равенствата са валидни:

1.

2.

3.

4.

Степен с рационален показател.

Изразът е дефиниран за всички и , с изключение на случая на . Нека си припомним свойствата на такива мощности.

За всякакви числа и всякакви цели числа и равенствата са валидни:

Също така отбелязваме, че ако , тогава за и за .. и

За учениците, полагащи Единния държавен изпит, учителите по математика в средно училище № 26 в Якутск използват списък с въпроси за съдържанието (кодификатор) за училищния курс по математика, чието владеене се тества при полагане на единния държавен изпит от 2007 г. Избираема дисциплинав подготовка за Обединеното Държавен изпитвъз основа на повторение, систематизиране и задълбочаване на предварително придобити знания. Занятията се провеждат под формата на безплатни...