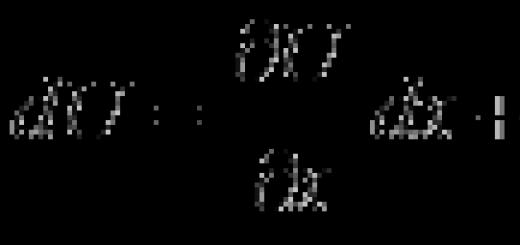القرن التاسع عشر هو بداية فترة رابعة جديدة في تاريخ الرياضيات - فترة الرياضيات الحديثة.

ونحن نعلم بالفعل أن أحد الاتجاهات الرئيسية في تطوير الرياضيات في الفترة الرابعة هو تعزيز صرامة البراهين في جميع الرياضيات، وخاصة إعادة هيكلة التحليل الرياضي على أساس منطقي. في النصف الثاني من القرن الثامن عشر. جرت محاولات عديدة لإعادة بناء التحليل الرياضي: تقديم تعريف النهاية (دالمبرت وآخرون)، تعريف المشتق باعتباره نهاية النسبة (أويلر وآخرون)، نتائج لاغرانج وكارنو. وما إلى ذلك، لكن هذه الأعمال كانت تفتقر إلى النظام، وفي بعض الأحيان لم تكن ناجحة. ومع ذلك، فقد مهدوا الأرضية التي قامت عليها البيريسترويكا في القرن التاسع عشر. يمكن تنفيذها. في القرن 19 أصبح هذا الاتجاه في تطور التحليل الرياضي هو الاتجاه الرائد. تم تناوله بواسطة O. Cauchy، B. Bolzano، K. Weierstrass وآخرين.

1. تخرج أوغسطين لويس كوشي (1789-1857) من كلية الفنون التطبيقية ومعهد الاتصالات في باريس. منذ عام 1816 عضو في أكاديمية باريس وأستاذ في مدرسة البوليتكنيك. في 1830-1838 خلال سنوات الجمهورية، كان في المنفى بسبب معتقداته الملكية. منذ عام 1848، أصبح كوشي أستاذا في جامعة السوربون - جامعة باريس. نشر أكثر من 800 ورقة بحثية حول التحليل الرياضي، والمعادلات التفاضلية، ونظرية دوال المتغير المركب، والجبر، ونظرية الأعداد، والهندسة، والميكانيكا، والبصريات، وما إلى ذلك. وكانت المجالات الرئيسية لاهتماماته العلمية هي التحليل الرياضي ونظرية دوال المتغير المركب. متغير معقد.

نشر كوشي محاضراته عن التحليل، التي ألقاها في مدرسة الفنون التطبيقية، في ثلاثة أعمال: "دورة التحليل" (1821)، "ملخص محاضرات حول حساب التفاضل والتكامل المتناهي الصغر" (1823)، "محاضرة عن تطبيقات التحليل على الهندسة"، في مجلدين. (1826، 1828). في هذه الكتب، ولأول مرة، تم بناء التحليل الرياضي على أساس نظرية الحدود. لقد شكلوا بداية إعادة هيكلة جذرية للتحليل الرياضي.

يعطي كوشي التعريف التالي لحد المتغير: “إذا كانت القيم المخصصة على التوالي لنفس المتغير تقترب من قيمة ثابتة إلى أجل غير مسمى، بحيث تختلف عنها في النهاية بأقل قدر ممكن، فإن الأخيرة تسمى الحد”. حد كل الآخرين." يتم التعبير عن جوهر الأمر جيدًا هنا، لكن الكلمات "القليل حسب الرغبة" نفسها تحتاج إلى تعريف، وبالإضافة إلى ذلك، تمت صياغة تعريف حد المتغير هنا، وليس حد الوظيفة. بعد ذلك، يثبت المؤلف خصائص النهايات المختلفة.

ثم يعطي كوشي التعريف التالي لاستمرارية الوظيفة: تسمى الوظيفة مستمرة (عند نقطة ما) إذا كانت الزيادة المتناهية الصغر في الوسيطة تولد زيادة متناهية الصغر في الوظيفة، أي في اللغة الحديثة

ثم لديه خصائص مختلفة للدوال المستمرة.

ويتناول الكتاب الأول أيضًا نظرية المتسلسلات: فيعطي تعريفًا لمجموع متسلسلة أعدادية باعتباره نهاية مجموعها الجزئي، ويقدم عددًا من المعايير الكافية لتقارب المتسلسلات العددية، وكذلك متسلسلات القوى والمنطقة لتقاربها - كل هذا في المجالات الحقيقية والمعقدة.

وقدم حساب التفاضل والتكامل في كتابه الثاني.

يعرّف كوشي مشتقة الدالة بأنها نهاية نسبة زيادة الدالة إلى زيادة الوسيط، عندما تميل زيادة الوسيط إلى الصفر، والتفاضل باعتباره نهاية النسبة ويترتب على ذلك أن. تتم مناقشة الصيغ المشتقة المعتادة بعد ذلك؛ في هذه الحالة، غالبًا ما يستخدم المؤلف نظرية القيمة المتوسطة لاغرانج.

في حساب التكامل، طرح كوشي أولاً التكامل المحدد كمفهوم أساسي. كما أنه يقدمها لأول مرة كحد للمجاميع التكاملية. هنا نثبت نظرية مهمة حول تكامل الوظيفة المستمرة. يتم تعريف تكامله غير المحدد على أنه دالة للوسيطة، بالإضافة إلى ذلك، يتم هنا النظر في توسعات الدوال في متسلسلة تايلور وماكلورين.

في النصف الثاني من القرن التاسع عشر. عدد من العلماء: B. Riemann، G. Darboux وآخرون وجدوا شروطًا جديدة لتكامل الوظيفة وحتى غيروا تعريف التكامل المحدد بحيث يمكن تطبيقه على تكامل بعض الوظائف المتقطعة.

في نظرية المعادلات التفاضلية، كان كوشي مهتمًا بشكل أساسي بإثباتات نظريات الوجود ذات الأهمية الأساسية: وجود حل لمعادلة تفاضلية عادية، أولًا من الدرجة الأولى ثم من الدرجة الرابعة؛ وجود حل لنظام خطي من المعادلات التفاضلية الجزئية.

في نظرية دوال المتغير المعقد، يعتبر كوشي هو المؤسس؛ العديد من مقالاته مخصصة لذلك. في القرن ال 18 وضع أويلر ودالمبيرت فقط بداية هذه النظرية. في الدورة الجامعية حول نظرية دوال المتغير المركب، نواجه باستمرار اسم كوشي: شروط كوشي - ريمان لوجود مشتق، تكامل كوشي، صيغة تكامل كوشي، وما إلى ذلك؛ العديد من النظريات حول بقايا الدالة ترجع أيضًا إلى كوشي. B. Riemann، K. Weierstrass، P. Laurent وآخرون حصلوا أيضًا على نتائج مهمة جدًا في هذا المجال.

دعنا نعود إلى المفاهيم الأساسية للتحليل الرياضي. وفي النصف الثاني من القرن، أصبح من الواضح أن العالم التشيكي برنارد بولزانو (1781 - 1848) قد فعل الكثير في مجال التحليل التثبتي قبل كوشي وفايرشتراس. قبل كوشي، قدم تعريفات للنهاية، واستمرارية الدالة وتقارب سلسلة الأعداد، وأثبت معيارًا لتقارب تسلسل رقمي، وأيضًا، قبل وقت طويل من ظهورها في Weierstrass، النظرية: إذا تم تعيين عدد يحدها من الأعلى (أدناه)، ثم لها حافة علوية محددة (حافة سفلية بالضبط. لقد نظر في عدد من خصائص الدوال المستمرة؛ دعونا نتذكر أنه في المقرر الجامعي للتحليل الرياضي هناك نظريات بولزانو-كوشي وبولزانو-فايرستراس حول الدوال المستمرة على فترة زمنية. قام بولزانو أيضًا بالبحث في بعض مسائل التحليل الرياضي، على سبيل المثال، قام ببناء المثال الأول لدالة متصلة على قطعة، ولكن ليس لها مشتقة في أي نقطة على القطعة. خلال حياته، لم يتمكن بولزانو من نشر سوى خمسة أعمال صغيرة، لذلك أصبحت نتائجه معروفة بعد فوات الأوان.

2. في التحليل الرياضي، أصبح الافتقار إلى تعريف واضح للدالة أكثر وضوحًا. مساهمة كبيرة في حل الخلاف حول المقصود بالوظيفة قدمها العالم الفرنسي جان فورييه. درس النظرية الرياضية للتوصيل الحراري في المواد الصلبة، وفيما يتعلق بهذا، استخدم المتسلسلة المثلثية (متسلسلة فورييه)

أصبحت هذه المتسلسلة فيما بعد مستخدمة على نطاق واسع في الفيزياء الرياضية، وهو العلم الذي يتعامل مع الطرق الرياضية لدراسة المعادلات التفاضلية الجزئية الموجودة في الفيزياء. أثبت فورييه أن أي منحنى مستمر، بغض النظر عن الأجزاء غير المتشابهة التي يتكون منها، يمكن تعريفه بتعبير تحليلي واحد - سلسلة مثلثية، ويمكن القيام بذلك أيضًا لبعض المنحنيات ذات الانقطاعات. أثارت دراسة فورييه لمثل هذه المتسلسلة مرة أخرى مسألة المقصود بالدالة. هل يمكن اعتبار مثل هذا المنحنى لتحديد الوظيفة؟ (هذا تجديد للنقاش القديم في القرن الثامن عشر حول العلاقة بين الوظيفة والصيغة على مستوى جديد.)

في عام 1837، قدم عالم الرياضيات الألماني P. Direchle لأول مرة تعريفًا حديثًا للدالة: "هي دالة لمتغير (على فترة زمنية إذا كانت كل قيمة (في هذه الفترة الزمنية) تتوافق مع قيمة محددة تمامًا، ولا يهم كيف" تم إنشاء هذا المراسلات - من خلال صيغة تحليلية، أو رسم بياني، أو جدول، أو حتى مجرد كلمات." ومن الجدير بالذكر الإضافة: "لا يهم كيف يتم إنشاء هذه المراسلات". وقد حظي تعريف ديركل باعتراف عام بسرعة كبيرة. ومع ذلك، فقد تم إثباته من المعتاد الآن أن نطلق على المراسلات نفسها وظيفة.

3. ظهر معيار الدقة الحديث في التحليل الرياضي لأول مرة في أعمال فايرستراس (1815-1897)، حيث عمل لفترة طويلة مدرسًا للرياضيات في صالات الألعاب الرياضية، وفي عام 1856 أصبح أستاذًا في جامعة برلين. قام مستمعو محاضراته بنشرها تدريجيا في شكل كتب منفصلة، ​​بفضل محتوى محاضرات Weierstrass أصبح معروفا جيدا في أوروبا. كان فايرستراس هو من بدأ في استخدام اللغة بشكل منهجي في التحليل الرياضي، فقد قدم تعريفًا لنهاية المتتابعة، وتعريفًا لنهاية الدالة في اللغة (والذي غالبًا ما يطلق عليه بشكل غير صحيح تعريف كوشي)، وأثبت نظريات النهايات بدقة وما يسمى بنظرية Weierstrass حول نهاية التسلسل الرتيب: التسلسل المتزايد (المتناقص) المحدود من الأعلى (من الأسفل) له حد محدود. بدأ في استخدام مفاهيم الحدود العليا والدنيا الدقيقة لمجموعة عددية، ومفهوم نقطة نهاية المجموعة، وأثبت النظرية (التي لها مؤلف آخر - بولزانو): المجموعة العددية المحدودة لها نقطة نهاية، وفحص بعض خواص الدوال المستمرة. خصص Weierstrass العديد من الأعمال لنظرية وظائف المتغير المعقد، وإثباتها بمساعدة متسلسلة القوى. كما درس حساب التفاضل والتكامل من الاختلافات والهندسة التفاضلية والجبر الخطي.

4. دعونا نتناول نظرية المجموعات اللانهائية. كان منشئها عالم الرياضيات الألماني كانتور. عمل جورج كانتور (1845-1918) لسنوات عديدة كأستاذ في جامعة هاله. نشر أعمالًا عن نظرية المجموعات بدءًا من عام 1870. لقد أثبت عدم إمكانية عد مجموعة الأعداد الحقيقية، وبالتالي أثبت وجود مجموعات لا نهائية غير متكافئة، وقدم المفهوم العام لقوة المجموعة، وأوضح مبادئ مقارنة القوى. بنى كانتور نظرية الأعداد اللامتناهية "غير الصحيحة"، ونسب أقل وأصغر عدد لانهائي إلى قوة مجموعة قابلة للعد (على وجه الخصوص، مجموعة الأعداد الطبيعية)، إلى قوة مجموعة الأعداد الحقيقية - أعلى، عدد أكبر لانهائي، وما إلى ذلك؛ وقد منحه هذا الفرصة لبناء عملية حسابية للأعداد اللامتناهية، على غرار الحساب العادي للأعداد الطبيعية. قام كانتور بتطبيق اللانهاية الفعلية بشكل منهجي، على سبيل المثال، إمكانية "استنفاد" السلسلة الطبيعية من الأعداد بشكل كامل، بينما سبقه في الرياضيات في القرن التاسع عشر. تم استخدام اللانهاية المحتملة فقط.

أثارت نظرية مجموعات كانتور اعتراضات العديد من علماء الرياضيات عند ظهورها، لكن الاعتراف بها جاء تدريجيًا عندما اتضحت أهميتها الهائلة لتبرير الطوبولوجيا ونظرية دوال المتغير الحقيقي. ولكن ظلت الفجوات المنطقية في النظرية نفسها، وعلى وجه الخصوص، تم اكتشاف مفارقات نظرية المجموعات. وهنا واحدة من المفارقات الأكثر شهرة. دعونا نشير بالمجموعة إلى كل هذه المجموعات التي ليست عناصر في حد ذاتها. هل يعتبر التضمين أيضًا عنصرًا وليس عنصرًا، لأنه، بشرط، يتم تضمين هذه المجموعات فقط كعناصر ليست عناصر في حد ذاتها؛ فإذا صح الشرط كان التضمين تناقضا في الحالتين.

وارتبطت هذه المفارقات بالتناقض الداخلي لبعض المجموعات. أصبح من الواضح أنه لا يمكن استخدام أي مجموعات في الرياضيات. تم التغلب على وجود المفارقات من خلال الخلق بالفعل في بداية القرن العشرين. نظرية المجموعات البديهية (E. Zermelo، A. Frenkel، D. Neumann، إلخ)، والتي، على وجه الخصوص، أجابت على السؤال: ما هي المجموعات التي يمكن استخدامها في الرياضيات؟ اتضح أنه يمكنك استخدام المجموعة الفارغة، واتحاد المجموعات المعطاة، ومجموعة جميع المجموعات الفرعية لمجموعة معينة، وما إلى ذلك.

تعتبر الفلسفة محور العلوم كلها، إذ شملت البراعم الأولى للأدب والفلك والأدب والعلوم الطبيعية والرياضيات وغيرها من المجالات. بمرور الوقت، تطور كل مجال بشكل مستقل، ولم تكن الرياضيات استثناءً. ويعتبر "التلميح" الأول للتحليل هو نظرية التحلل إلى كميات متناهية الصغر، والتي حاولت العديد من العقول الاقتراب منها، لكنها كانت غامضة وليس لها أي أساس. ويرجع ذلك إلى التمسك بمدرسة العلوم القديمة التي كانت صارمة في صياغاتها. لقد اقترب إسحاق نيوتن كثيرًا من تشكيل الأسس، ولكن بعد فوات الأوان. ونتيجة لذلك، فإن التحليل الرياضي يدين بظهوره كنظام منفصل للفيلسوف جوتفريد لايبنتز. كان هو الذي قدم للعالم العلمي مفاهيم مثل الحد الأدنى والحد الأقصى، ونقاط انعطاف وتحدب الرسم البياني للدالة، وصياغة أسس حساب التفاضل والتكامل. من هذه اللحظة فصاعدا، تم تقسيم الرياضيات رسميا إلى الابتدائية والعليا.

التحليل الرياضي. أيامنا

أي تخصص، سواء كان تقنيًا أو إنسانيًا، يتضمن التحليل أثناء الدراسة. يختلف عمق الدراسة، لكن الجوهر يبقى هو نفسه. ورغم كل «التجريد»، فهو أحد الركائز التي يرتكز عليها العلم الطبيعي بمفهومه الحديث. وبمساعدته تطورت الفيزياء والاقتصاد، وأصبح قادرًا على وصف أنشطة البورصة والتنبؤ بها، والمساعدة في بناء محفظة مثالية من الأسهم. تعتمد مقدمة التحليل الرياضي على مفاهيم أولية:

• الجموع.
• العمليات الأساسية على مجموعات؛
• خصائص العمليات على المجموعات؛
• الوظائف (والمعروفة باسم التعيينات)؛
• أنواع الوظائف؛
• تسلسلات؛
• خطوط الأعداد؛
• حد التسلسل
• خصائص الحدود.
• استمرارية الوظيفة.

يجدر تسليط الضوء بشكل منفصل على مفاهيم مثل المجموعة والنقطة والخط المستقيم والمستوى. وجميعها ليس لها تعريفات، لأنها المفاهيم الأساسية التي تبنى عليها كل الرياضيات. كل ما يمكن القيام به في هذه العملية هو شرح ما تعنيه بالضبط في الحالات الفردية.

الحد كاستمرار

تتضمن أساسيات التحليل الرياضي الحد. ومن الناحية العملية، فهي تمثل القيمة التي يسعى التسلسل أو الوظيفة إلى الوصول إليها، وتقترب من المطلوب، ولكنها لا تصل إليه. يُشار إليه بـ lim؛ فكر في حالة خاصة لحد الدالة: lim (x-1)= 0 لـ x→1. من هذا المثال الأبسط يتضح أنه عندما x → 1 فإن الدالة بأكملها تميل إلى 0، لأنه إذا قمنا باستبدال الحد في الدالة نفسها، نحصل على (1-1)=0. يتم تقديم معلومات أكثر تفصيلاً، من الحالات الخاصة الابتدائية إلى المعقدة، في نوع من "الكتاب المقدس" للتحليل - أعمال فيشتنهولتز. ويدرس التحليل الرياضي والحدود واشتقاقها وتطبيقها. على سبيل المثال، اشتقاق العدد e (ثابت أويلر) سيكون مستحيلا بدون نظرية النهايات. على الرغم من التجريد الديناميكي للنظرية، يتم استخدام الحدود بنشاط في الممارسة العملية في الاقتصاد وعلم الاجتماع. على سبيل المثال، بدونها، لا يمكنك الاستغناء عنها عند حساب الفائدة على الوديعة المصرفية.

إنجليزي:تعمل ويكيبيديا على جعل الموقع أكثر أمانًا. أنت تستخدم متصفح ويب قديمًا ولن يتمكن من الاتصال بويكيبيديا في المستقبل. يرجى تحديث جهازك أو الاتصال بمسؤول تكنولوجيا المعلومات لديك.

中文: لقد تخلصنا من هذه المشكلة. لقد تخلصنا من تكنولوجيا المعلومات.

الأسبانية:ويكيبيديا هي الموقع الأكثر أمانًا. يتم استخدام متصفح الويب القديم الذي لن يكون قادرًا على الاتصال بـ Wikipedia في المستقبل. قم بتشغيل جهازك أو اتصل بمسؤول المعلومات الخاص به. مزيد من المعلومات تحتوي على تحديث أطول وأكثر تقنية باللغة الإنجليزية.

ﺎﻠﻋﺮﺒﻳﺓ: ويكيبيديا تسعى لتأمين الموقع أكثر من ذي قبل. أنت تستخدم متصفح وب قديم لن يتمكن من الاتصال بموقع ويكيبيديا في المستقبل. يرجى تحديث جهازك أو الاتصال بغداري تقنية المعلومات الخاص بك. يوجد تحديث فني أطول ومغرق في التقنية باللغة الإنجليزية تاليا.

الفرنسية:تعمل ويكيبيديا على تعزيز أمان موقعها. أنت تستخدم بالفعل متصفح ويب قديمًا، والذي لا يمكنك الاتصال بويكيبيديا عندما يحدث ذلك. يرجى الرجوع إلى جهازك أو الاتصال بمسؤول المعلومات الخاص بك في هذا الوقت. المعلومات الإضافية بالإضافة إلى التقنيات واللغة الإنجليزية متاحة بسهولة.

日本語: ???????????????????????????????????????????????????????????????؟

ألمانية:ويكيبيديا erhöht die Sicherheit der Webseite. لا يمكنك استخدام متصفح ويب آخر، والذي لا يحتاج إلى المزيد من الوصول إلى ويكيبيديا. يمكنك تحديث الجهاز أو توفيره لمسؤول تكنولوجيا المعلومات. Ausführlicher (وتفصيل فني) Hinweise find Du unten باللغة الإنجليزية Sprache.

ايطالي:ويكيبيديا توفر موقعًا أكثر أمانًا. ابق على استخدام متصفح ويب لن تتمكن من التواصل مع ويكيبيديا في المستقبل. من أجل ذلك، قم بترقية جهازك أو الاتصال بمسؤول المعلومات الخاص بك. يمكن توفير المزيد من التفاصيل والتقنية باللغة الإنجليزية.

المجرية: Biztonságosabb ليز ويكيبيديا. من الجيد أن نخبرك أنه ليس من الممكن أن يكون لديك أي مشاكل أو مشاكل. لقد تم حل مشكلة الحداثة بشكل متكرر. Alább olvashatod a részletesebb magyarázatot (أنغولول).

سفينسكا:ويكيبيديا gör sidan mer säker. ستساعدك على نشر المزيد من صفحات الويب التجارية لتتمكن من استخدام ويكيبيديا وإطاراتها. قم بالتحديث من خلاله أو من خلال الاتصال بمسؤول تكنولوجيا المعلومات. هذه الفنلندية الطويلة والتقنية الأكثر تقدمًا في اللغة الإنجليزية الطويلة.

हिन्दी: विकिपीडिया साइट को और अधिक सुरक्षित बना रहा है। आप एक पुराने वेब ब्राउज़र का उपयोग कर रहे हैं जो भविष्य में विकिपीडिया से कनेक्ट नहीं हो पाएगा। कृपया अपना डिवाइस अपडेट करें या अपने आईटी व्यवस्थापक से संपर्क करें। नीचे अंग्रेजी में एक लंबा और अधिक तकनीकी अद्यतन है।

نحن نقوم بإزالة الدعم لإصدارات بروتوكول TLS غير الآمنة، وتحديدًا TLSv1.0 وTLSv1.1، والتي يعتمد عليها برنامج المتصفح الخاص بك للاتصال بمواقعنا. يحدث هذا عادةً بسبب المتصفحات القديمة أو الهواتف الذكية القديمة التي تعمل بنظام Android. أو قد يكون السبب تدخلاً من برنامج "Web Security" الخاص بالشركة أو الشخصية، مما يؤدي في الواقع إلى خفض مستوى أمان الاتصال.

يجب عليك ترقية متصفح الويب الخاص بك أو إصلاح هذه المشكلة للوصول إلى مواقعنا. ستبقى هذه الرسالة حتى 1 يناير 2020. وبعد ذلك التاريخ، لن يتمكن متصفحك من إنشاء اتصال بخوادمنا.

في تاريخ الرياضيات، يمكننا أن نميز تقريبًا بين فترتين رئيسيتين: الرياضيات الابتدائية والحديثة. كان المعلم الرئيسي الذي من المعتاد حساب عصر الرياضيات الجديدة (التي تسمى أحيانًا الرياضيات العليا) هو القرن السابع عشر - قرن ظهور التحليل الرياضي. بحلول نهاية القرن السابع عشر. I. Newton، G. Leibniz وأسلافهم أنشأوا جهاز حساب التفاضل والتكامل الجديد وحساب التفاضل والتكامل، والذي يشكل أساس التحليل الرياضي وحتى، ربما، الأساس الرياضي لجميع العلوم الطبيعية الحديثة.

التحليل الرياضي هو مجال واسع من الرياضيات مع موضوع مميز للدراسة (الكمية المتغيرة)، وطريقة بحث فريدة (التحليل عن طريق المتناهيات في الصغر أو عن طريق الممرات إلى الحدود)، ونظام معين من المفاهيم الأساسية (الوظيفة، الحد ، المشتق، التفاضلي، التكامل، المتسلسلة) وهو جهاز يتحسن باستمرار ويتطور، أساسه حساب التفاضل والتكامل.

دعونا نحاول إعطاء فكرة عن نوع الثورة الرياضية التي حدثت في القرن السابع عشر، وما الذي يميز الانتقال المرتبط بولادة التحليل الرياضي من الرياضيات الأولية إلى ما أصبح الآن موضوع البحث في التحليل الرياضي، وما الذي يفسره دور أساسي في النظام الحديث بأكمله للمعرفة النظرية والتطبيقية.

تخيل أن أمامك صورة ملونة تم تنفيذها بشكل جميل لموجة محيط عاصفة تندفع نحو الشاطئ: ظهر منحني قوي، وصدر شديد الانحدار ولكنه غائر قليلاً، ورأس مائل بالفعل إلى الأمام ومستعد للسقوط مع عرف رمادي يعذبه الماء. رياح. لقد توقفت في اللحظة، وتمكنت من اللحاق بالموجة، ويمكنك الآن دراستها بعناية بكل تفاصيلها دون تسرع. يمكن قياس الموجة، وباستخدام أدوات الرياضيات الأولية، يمكنك استخلاص العديد من الاستنتاجات المهمة حول هذه الموجة، وبالتالي جميع أخواتها في المحيطات. لكن بإيقاف الموجة حرمتها من الحركة والحياة. أصلها وتطورها وتشغيلها والقوة التي تضرب بها الشاطئ - كل هذا تبين أنه خارج مجال رؤيتك، لأنه ليس لديك حتى الآن لغة ولا جهاز رياضي مناسب للوصف والدراسة غير الثابتة، ولكن النامية والعمليات الديناميكية والمتغيرات وعلاقاتها.

"التحليل الرياضي ليس أقل شمولا من الطبيعة نفسها: فهو يحدد جميع العلاقات الملموسة، ويقيس الأزمنة، والمساحات، والقوى، ودرجات الحرارة." جي فورييه

الحركة والمتغيرات وعلاقاتها تحيط بنا في كل مكان. تشكل الأنواع المختلفة من الحركة وأنماطها الموضوع الرئيسي لدراسة علوم محددة: الفيزياء، والجيولوجيا، وعلم الأحياء، وعلم الاجتماع، وما إلى ذلك. لذلك، تبين أن اللغة الدقيقة والأساليب الرياضية المقابلة لوصف ودراسة الكميات المتغيرة ضرورية في جميع مجالات العلوم. المعرفة بنفس القدر تقريبًا مثل الأرقام والحساب ضرورية عند وصف العلاقات الكمية. لذلك يشكل التحليل الرياضي أساس اللغة والأساليب الرياضية لوصف المتغيرات والعلاقات بينها. في الوقت الحاضر، بدون تحليل رياضي، من المستحيل ليس فقط حساب المسارات الفضائية، وتشغيل المفاعلات النووية، وحركة أمواج المحيطات وأنماط تطور الأعاصير، ولكن أيضًا إدارة الإنتاج وتوزيع الموارد وتنظيم العمليات التكنولوجية اقتصاديًا، والتنبؤ بالمناخ. مسار التفاعلات الكيميائية أو التغيرات في عدد الأنواع المختلفة المترابطة في طبيعة الحيوانات والنباتات، لأن كل هذه العمليات هي عمليات ديناميكية.

كانت الرياضيات الابتدائية هي في الأساس رياضيات الكميات الثابتة، وقد درست بشكل أساسي العلاقات بين عناصر الأشكال الهندسية، والخصائص الحسابية للأعداد، والمعادلات الجبرية. يمكن مقارنة موقفه من الواقع إلى حد ما بدراسة متأنية، بل وشاملة، وكاملة لكل إطار ثابت من الفيلم الذي يصور العالم الحي المتغير والمتطور في حركته، والذي، مع ذلك، غير مرئي في إطار منفصل و والتي لا يمكن ملاحظتها إلا من خلال النظر إلى الشريط ككل. ولكن مثلما لا يمكن تصور السينما بدون التصوير الفوتوغرافي، فإن الرياضيات الحديثة مستحيلة دون ذلك الجزء الذي نسميه تقليديا الابتدائية، دون أفكار وإنجازات العديد من العلماء البارزين، مفصولة أحيانا بعشرات القرون.

الرياضيات متحدة، والجزء "الأعلى" منها مرتبط بالجزء "الابتدائي" بنفس الطريقة التي يرتبط بها الطابق التالي من منزل قيد الإنشاء بالطابق السابق، واتساع الآفاق التي تفتحها الرياضيات بالنسبة لنا في العالم من حولنا يعتمد على أي طابق من هذا المبنى تمكنا من الوصول إليه. ولد في القرن السابع عشر. لقد فتح التحليل الرياضي الفرص أمامنا للوصف العلمي والدراسة الكمية والنوعية للمتغيرات والحركة بالمعنى الواسع للكلمة.

ما هي شروط ظهور التحليل الرياضي؟

بحلول نهاية القرن السابع عشر. لقد نشأت الحالة التالية. أولاً، في إطار الرياضيات نفسها، تراكمت على مدى سنوات عديدة بعض الفئات المهمة من المسائل من نفس النوع (على سبيل المثال، مشاكل قياس مساحات وأحجام الأشكال غير القياسية، ومشاكل رسم مماسات المنحنيات) وطرق حلها. وقد ظهر حلها في مختلف الحالات الخاصة. ثانيًا، اتضح أن هذه المشكلات ترتبط ارتباطًا وثيقًا بمشاكل وصف الحركة الميكانيكية التعسفية (ليست بالضرورة موحدة)، وخاصة مع حساب خصائصها اللحظية (السرعة، والتسارع في أي وقت)، وكذلك مع إيجاد المسافة المقطوعة للحركة التي تحدث بسرعة متغيرة معينة. كان حل هذه المشاكل ضروريًا لتطوير الفيزياء وعلم الفلك والتكنولوجيا.

وأخيرا، ثالثا، بحلول منتصف القرن السابع عشر. وضعت أعمال R. Descartes و P. Fermat أسس الطريقة التحليلية للإحداثيات (ما يسمى بالهندسة التحليلية)، والتي مكنت من صياغة مشاكل هندسية وفيزيائية ذات أصل غير متجانس في لغة الأرقام العامة (التحليلية) والتبعيات العددية، أو كما نقول الآن، الدوال العددية.

أدى التقاء هذه الظروف إلى حقيقة أنه في نهاية القرن السابع عشر. نجح عالمان - نيوتن وج. لايبنتز - بشكل مستقل عن بعضهما البعض في إنشاء جهاز رياضي لحل هذه المشكلات، وتلخيص وتعميم النتائج الفردية لأسلافهما، بما في ذلك العالم القديم أرخميدس ومعاصري نيوتن ولايبنتز - ب. كافاليري، ب. باسكال، د. غريغوري، آي. بارو. شكل هذا الجهاز أساس التحليل الرياضي - وهو فرع جديد من الرياضيات يدرس العمليات النامية المختلفة، أي. العلاقات بين المتغيرات، والتي تسمى في الرياضيات بالتبعيات الوظيفية، أو بمعنى آخر، الوظائف. بالمناسبة، كان مصطلح "الوظيفة" نفسه مطلوبًا ونشأ بشكل طبيعي في القرن السابع عشر، والآن اكتسب ليس فقط أهمية رياضية عامة، ولكن أيضًا أهمية علمية عامة.

المعلومات الأولية حول المفاهيم الأساسية والأجهزة الرياضية للتحليل موجودة في المقالات "حساب التفاضل والتكامل" و"حساب التكامل".

في الختام، أود أن أتطرق إلى مبدأ واحد فقط من مبادئ التجريد الرياضي، وهو مشترك بين جميع الرياضيات وخاصية التحليل، وفي هذا الصدد أشرح كيف يدرس التحليل الرياضي المتغيرات وما هو سر هذه العالمية لأساليبه في الدراسة جميع أنواع عمليات التطوير المحددة والعلاقات المتبادلة بينها.

دعونا نلقي نظرة على بعض الأمثلة التوضيحية والقياسات.

في بعض الأحيان لم نعد ندرك أن، على سبيل المثال، علاقة رياضية مكتوبة ليس للتفاح أو الكراسي أو الفيلة، ولكن في شكل مجرد مجردة من أشياء محددة، هي إنجاز علمي متميز. وهذا قانون رياضي، كما تظهر التجربة، ينطبق على أشياء محددة مختلفة. وهذا يعني أنه من خلال دراسة الخصائص العامة للأرقام المجردة والمجردة في الرياضيات، فإننا ندرس العلاقات الكمية في العالم الحقيقي.

على سبيل المثال، من دورة الرياضيات المدرسية، من المعروف أنه في موقف معين يمكنك أن تقول: "إذا لم يعطوني شاحنتين قلابتين سعة ستة أطنان لنقل 12 طنًا من التربة، فيمكنني أن أطلب لثلاث شاحنات قلابة سعة أربعة أطنان وسيتم إنجاز العمل، وإذا أعطوني شاحنة قلابة واحدة فقط سعة أربعة أطنان، فسيتعين عليها القيام بثلاث رحلات جوية. وبالتالي، فإن الأرقام المجردة والأنماط العددية المألوفة لنا الآن ترتبط بمظاهرها وتطبيقاتها المحددة.

ترتبط قوانين التغيير في متغيرات محددة وعمليات الطبيعة النامية بنفس الطريقة تقريبًا بالوظيفة الشكلية المجردة التي تظهر فيها ويتم دراستها في التحليل الرياضي.

على سبيل المثال، قد تعكس النسبة المجردة اعتماد شباك التذاكر في السينما على عدد التذاكر المباعة، إذا كان 20 هو 20 كوبيل - سعر تذكرة واحدة. ولكن إذا كنا نركب دراجة هوائية على طريق سريع، ونسير بسرعة 20 كيلومترًا في الساعة، فيمكن تفسير هذه النسبة نفسها على أنها العلاقة بين الوقت (الساعات) لرحلتنا بالدراجة والمسافة المقطوعة خلال هذا الوقت (الكيلومترات). يمكنك قل دائمًا، على سبيل المثال، أن التغيير عدة مرات يؤدي إلى تغيير تناسبي (أي نفس عدد المرات) في قيمة، وإذا كان، فإن الاستنتاج المعاكس صحيح أيضًا. وهذا يعني، على وجه الخصوص، لمضاعفة شباك التذاكر لمسرح السينما، سيتعين عليك جذب ضعف عدد المتفرجين، ومن أجل السفر ضعف المسافة بالدراجة بنفس السرعة، سيتعين عليك ركوب ضعف المسافة .

تدرس الرياضيات كلاً من أبسط التبعيات وغيرها من التبعيات الأكثر تعقيدًا في شكل عام مجرد، مستخرج من تفسير معين. خصائص الوظيفة أو طرق دراسة هذه الخصائص المحددة في مثل هذه الدراسة ستكون ذات طبيعة تقنيات واستنتاجات وقوانين واستنتاجات رياضية عامة تنطبق على كل ظاهرة محددة تحدث فيها الوظيفة المدروسة بشكل مجرد، بغض النظر عن المجال من المعرفة تنتمي هذه الظاهرة .

لذلك، تم تشكيل التحليل الرياضي كفرع من الرياضيات في نهاية القرن السابع عشر. إن موضوع الدراسة في التحليل الرياضي (كما يظهر من المواقف الحديثة) هو الدوال، أو بمعنى آخر التبعيات بين الكميات المتغيرة.

مع ظهور التحليل الرياضي، أصبحت الرياضيات متاحة لدراسة وانعكاس العمليات النامية في العالم الحقيقي؛ الرياضيات شملت المتغيرات والحركة.

العصور القديمة

خلال العصر القديم ظهرت بعض الأفكار التي أدت فيما بعد إلى حساب التفاضل والتكامل، ولكن في ذلك العصر لم يتم تطوير هذه الأفكار بطريقة صارمة ومنهجية. يمكن العثور على حسابات الحجوم والمساحات، وهي أحد أغراض حساب التفاضل والتكامل، في بردية موسكو الرياضية من مصر (حوالي 1820 قبل الميلاد)، ولكن الصيغ أشبه بالتعليمات، دون أي إشارة إلى الطريقة، وبعضها ببساطة خاطئ. وفي عصر الرياضيات اليونانية، استخدم يودوكسوس (حوالي 408-355 قبل الميلاد) طريقة الاستنفاد لحساب المساحات والأحجام، وهو ما استبق مفهوم الحد، ولاحقًا تم تطوير هذه الفكرة على يد أرخميدس (حوالي 287-212 قبل الميلاد) اختراع الاستدلال الذي يشبه طرق حساب التفاضل والتكامل. تم اختراع طريقة الاستنفاد لاحقًا في الصين على يد ليو هوي في القرن الثالث الميلادي، والتي استخدمها لحساب مساحة الدائرة. في القرن الخامس الميلادي، طور زو تشونغزي طريقة لحساب حجم الكرة، والتي سُميت فيما بعد بمبدأ كافاليري.

العصور الوسطى

في القرن الرابع عشر، قدم عالم الرياضيات الهندي مادهافا سانجاماجراما ومدرسة كيرالا لعلم الفلك والرياضيات العديد من مكونات حساب التفاضل والتكامل، مثل متسلسلة تايلور، وتقريب المتسلسلة اللانهائية، واختبار التكامل للتقارب، والأشكال المبكرة للتمايز، والتكامل على حدة، الطرق التكرارية لحل المعادلات غير الخطية وتحديد المساحة تحت المنحنى التي تمثل تكاملها. يعتبر البعض أن كتاب يوكتبهاسا هو أول عمل في التحليل الرياضي.

العصر الحديث

في أوروبا، كان العمل الأساسي هو أطروحة بونافينتورا كافاليري، التي جادل فيها بأنه يمكن حساب الأحجام والمساحات كمجموع أحجام ومساحات مقطع رفيع للغاية. كانت الأفكار مشابهة لما أوجزه أرخميدس في طريقته، لكن هذه الأطروحة التي كتبها أرخميدس ضاعت حتى النصف الأول من القرن العشرين. لم يتم الاعتراف بعمل كافاليري لأن أساليبه يمكن أن تؤدي إلى نتائج خاطئة، كما أنه أعطى المتناهية الصغر سمعة مشكوك فيها.

كان البحث الرسمي في حساب التفاضل والتكامل المتناهي الصغر، والذي جمعه كافاليري مع حساب التفاضل والتكامل المحدود، يحدث في أوروبا في هذا الوقت تقريبًا. وقد قدم بيير فيرما، الذي زعم أنه استعاره من ديوفانتوس، مفهوم "شبه المساواة" (بالإنجليزية: adequality)، وهي المساواة حتى خطأ متناهي الصغر. كما قدم جون واليس وإسحاق بارو وجيمس جريجوري مساهمات كبيرة. وقد أثبتت المعادلتان الأخيرتان، حوالي عام 1675، النظرية الأساسية الثانية في حساب التفاضل والتكامل.

الأسباب

في الرياضيات، تشير الأسس إلى تعريف صارم لموضوع ما، بدءًا من البديهيات والتعاريف الدقيقة. في المرحلة الأولى من تطوير حساب التفاضل والتكامل، كان استخدام الكميات المتناهية الصغر يعتبر متساهلاً، وتعرض لانتقادات شديدة من قبل عدد من المؤلفين، أبرزهم ميشيل رول والأسقف بيركلي. وصف بيركلي بشكل ممتاز المتناهية الصغر بأنها "أشباح الكميات الميتة" في كتابه المحلل في عام 1734. لقد شغل تطوير أساس صارم لحساب التفاضل والتكامل علماء الرياضيات لأكثر من قرن بعد نيوتن ولايبنتز، ولا يزال إلى حد ما مجالًا نشطًا للبحث حتى اليوم.

حاول العديد من علماء الرياضيات، بما في ذلك ماكلورين، إثبات صحة استخدام المتناهيات الصغر، لكن هذا لم يتم إلا بعد 150 عامًا من خلال عمل كوشي وفايرستراس، اللذين وجدا أخيرًا طريقة للتهرب من "الأشياء الصغيرة" البسيطة للمتناهيات الصغر، و البدايات كانت حساب التفاضل والتكامل. نجد في كتابات كوشي مجموعة عالمية من المناهج الأساسية، بما في ذلك تعريف الاستمرارية من حيث المتناهيات في الصغر والنموذج الأولي (غير الدقيق إلى حد ما) لتعريف الحد (ε، δ) في تعريف التمايز. في عمله، يضفي فايرستراس طابعًا رسميًا على مفهوم الحد ويزيل الكميات المتناهية الصغر. بعد هذا العمل الذي قام به فايرستراس، أصبح الأساس العام لحساب التفاضل والتكامل هو الحدود، وليس الكميات المتناهية الصغر. استخدم بيرنهارد ريمان هذه الأفكار ليعطي تعريفًا دقيقًا للتكامل. بالإضافة إلى ذلك، خلال هذه الفترة، تم تعميم أفكار حساب التفاضل والتكامل على الفضاء الإقليدي وعلى المستوى المركب.

في الرياضيات الحديثة، يتم تضمين أساسيات حساب التفاضل والتكامل في فرع التحليل الحقيقي، الذي يحتوي على تعريفات وأدلة كاملة لنظريات حساب التفاضل والتكامل. لقد أصبح نطاق أبحاث حساب التفاضل والتكامل أوسع بكثير. طور هنري ليبيغ نظرية مجموعة المقاييس واستخدمها لتحديد تكاملات جميع الوظائف باستثناء الوظائف الأكثر غرابة. قدم لوران شوارتز الدوال المعممة، والتي يمكن استخدامها لحساب مشتقات أي دالة بشكل عام.

لم يكن إدخال الحدود هو النهج الصارم الوحيد لأساس حساب التفاضل والتكامل. والبديل سيكون، على سبيل المثال، تحليل أبراهام روبنسون غير القياسي. يستخدم نهج روبنسون، الذي تم تطويره في الستينيات، أدوات تقنية من المنطق الرياضي لتوسيع نظام الأعداد الحقيقية إلى الأعداد المتناهية الصغر والأعداد الكبيرة بلا حدود، كما هو الحال في مفهوم نيوتن-لايبنتز الأصلي. يمكن استخدام هذه الأرقام، التي تسمى الأرقام الحقيقية الفائقة، في القواعد العادية لحساب التفاضل والتكامل، تمامًا كما فعل لايبنتز.

أهمية

على الرغم من أن بعض أفكار حساب التفاضل والتكامل قد تم تطويرها سابقًا في مصر واليونان والصين والهند والعراق وبلاد فارس واليابان، إلا أن الاستخدام الحديث لحساب التفاضل والتكامل بدأ في أوروبا في القرن السابع عشر، عندما بنى إسحاق نيوتن وجوتفريد فيلهلم لايبنتز على أعمال حساب التفاضل والتكامل. علماء الرياضيات الأوائل للبناء على مبادئها الأساسية. اعتمد تطوير حساب التفاضل والتكامل على المفاهيم السابقة للحركة اللحظية والمساحة تحت المنحنى.

يتم استخدام حساب التفاضل والتكامل في الحسابات المتعلقة بالسرعة والتسارع، وانحدار المنحنى، والتحسين. تشمل تطبيقات حساب التفاضل والتكامل العمليات الحسابية التي تتضمن المساحات والأحجام وأطوال القوس ومراكز الكتلة والشغل والضغط. وتشمل التطبيقات الأكثر تعقيدًا حسابات متسلسلة الطاقة وسلسلة فورييه.

حساب التفاضل والتكامل [ ] يستخدم أيضًا للحصول على فهم أكثر دقة لطبيعة المكان والزمان والحركة. لعدة قرون، تصارع علماء الرياضيات والفلاسفة مع المفارقات المرتبطة بالقسمة على الصفر أو إيجاد مجموع سلسلة لا حصر لها من الأرقام. تطرح هذه الأسئلة عند دراسة الحركة وحساب المساحات. وقد أعطى الفيلسوف اليوناني القديم زينون الإيلي عدة أمثلة مشهورة لمثل هذه المفارقات. يوفر حساب التفاضل والتكامل أدوات لحل هذه المفارقات، ولا سيما النهايات والمتسلسلات اللانهائية.

الحدود والمتناهيات في الصغر

ملحوظات

1. موريس كلاين, الفكر الرياضي من القديم إلى الحديث، المجلد. أنا
2. أرخميدس, طريقة، في أعمال أرخميدسردمك 978-0-521-66160-7
3. دان، ليو؛ مروحة، داينيان؛ كوهين، ابن روبرتن.مقارنة بين دراسات أرشميدس وليو هوي حول الدوائر (الإنجليزية): مجلة. - سبرينغر، 1966. - المجلد. 130. - ص279. - ردمك 0-792-33463-9.، الفصل، ص. 279
4. زيل، دينيس G.؛ رايت، سكوت. رايت، وارن س.حساب التفاضل والتكامل: المتعالي المبكر (غير محدد). - 3. - تعلم جونز وبارتليت (إنجليزي)الروسية, 2009. - ص السابع والعشرون. - ردمك 0-763-75995-3.، مقتطف من الصفحة 27
5. الرياضيات الهندية
6. فون نيومان، "عالم الرياضيات"، في Heywood، R. B.، ed.، أعمال العقل، مطبعة جامعة شيكاغو، 1947، ص. 180-196. أعيد طبعه في Bródy, F., Vámos, T., eds., نيومان كومبيديومالشركة العالمية للنشر العلمي. بي تي إي. المحدودة، 1995، ISBN 9810222017، ص. 618-626.
7. أندريه ويل: نظرية الأعداد. نهج عبر التاريخ. من حمورابي إلى ليجيندر. بيركهاوزر بوسطن، شركة، بوسطن، ماساتشوستس، 1984، ISBN 0-8176-4565-9، ص. 28.
8. لايبنيز، جوتفريد فيلهلم. المخطوطات الرياضية المبكرة لايبنتز. شركة كوزيمو، 2008. الصفحة 228. نسخة
9. أونلو، أليف ماريا جايتانا أغنيسي (غير معرف) . كلية أغنيس سكوت (أبريل 1995). مؤرشفة من الأصلي في 5 أيلول (سبتمبر) 2012.

روابط

• رون لارسون، بروس هـ. إدواردز (2010). “حساب التفاضل والتكامل”، الطبعة التاسعة، بروكس كول سينجاج التعلم. ردمك 978-0-547-16702-2
• ماكواري، دونالد أ. (2003). الطرق الرياضية للعلماء والمهندسين، كتب العلوم الجامعية. ردمك 978-1-891389-24-5
• جيمس ستيوارت (2008). حساب التفاضل والتكامل: المتعالي المبكر، الطبعة السادسة، بروكس كول سينجاج التعلم.