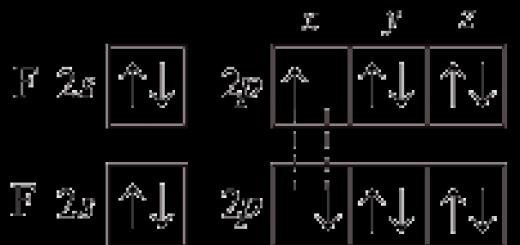
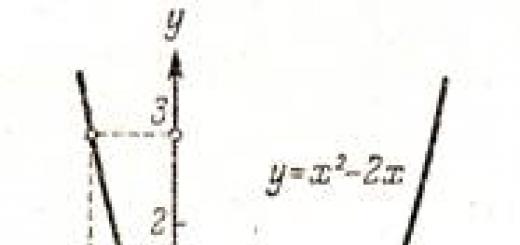Noaniq kvadratik shakl. Kvadrat shakllar shakllarning belgi aniqligi. Silvestr mezoni

Ushbu bo'limda biz ijobiy kvadratik shakllarning maxsus, ammo muhim sinfiga to'xtalamiz.

Ta'rif 3. Haqiqiy kvadratik shakl, agar o'zgaruvchilarning har qanday haqiqiy qiymatlari uchun manfiy bo'lmagan (musbat bo'lmagan) deyiladi.

. (35)

Bunday holda, koeffitsientlarning simmetrik matritsasi musbat yarim aniq (salbiy yarim aniq) deb ataladi.

Ta'rif 4. Haqiqiy kvadratik shakl musbat aniq (salbiy aniq) deb ataladi, agar o'zgaruvchilarning bir vaqtning o'zida nolga teng bo'lmagan har qanday haqiqiy qiymatlari uchun,

. (36)

Bunday holda, matritsa musbat aniq (salbiy aniq) deb ham ataladi.

Ijobiy aniq (salbiy aniq) shakllar sinfi inkor bo'lmagan (javob. nomusbat) shakllar sinfiga kiradi.

Salbiy bo'lmagan shakl berilsin. Keling, uni mustaqil kvadratlar yig'indisi sifatida tasavvur qilaylik:

. (37)

Ushbu tasvirda barcha kvadratlar ijobiy bo'lishi kerak:

. (38)

Haqiqatan ham, agar mavjud bo'lsa, unda bunday qiymatlarni tanlash mumkin edi

Ammo keyin, o'zgaruvchilarning ushbu qiymatlari bilan shakl salbiy qiymatga ega bo'ladi, bu shart bilan mumkin emas. Shubhasiz, aksincha, (37) va (38) dan shakl ijobiy ekanligi kelib chiqadi.

Shunday qilib, manfiy bo'lmagan kvadratik shakl tenglik bilan tavsiflanadi.

Keling, ijobiy aniq shakl bo'lsin. Keyin u salbiy bo'lmagan shakldir. Shuning uchun uni (37) ko'rinishda ifodalash mumkin, bu erda hammasi ijobiydir. Shaklning ijobiy aniqligidan kelib chiqadiki. Haqiqatan ham, bir vaqtning o'zida nolga teng bo'lmagan qiymatlarni tanlash mumkin bo'lsa, barchasi nolga aylanadi. Ammo keyin, (37) tufayli, (36) shartga zid keladi.

Ko'rish oson, aksincha, agar (37) da va hammasi ijobiy bo'lsa, u ijobiy aniq shakldir.

Boshqacha qilib aytadigan bo'lsak, inkor bo'lmagan shakl, agar u birlik bo'lmasa, ijobiy aniqlikdir.

Quyidagi teorema shakl koeffitsientlari qanoatlantirishi kerak bo'lgan tengsizliklar ko'rinishidagi shaklning ijobiy aniqligi mezonini beradi. Bunday holda, matritsaning ketma-ket asosiy voyaga etmaganlari uchun oldingi paragraflarda mavjud bo'lgan belgi qo'llaniladi:

Teorema 3. Kvadrat shakl musbat aniq bo‘lishi uchun tengsizliklar qanoatlantirilishi zarur va yetarlidir.

Isbot. (39) shartlarning etarliligi to'g'ridan-to'g'ri Yakobi formulasidan (28) kelib chiqadi. Shartlarning zarurligi (39) quyidagicha belgilanadi. Shaklning ijobiy aniqligidan "kesilgan" shakllarning ijobiy aniqligi kelib chiqadi

Ammo keyin bu shakllarning barchasi yagona bo'lmagan bo'lishi kerak, ya'ni.

Endi bizda Yakobi formulasidan (28) (da) foydalanish imkoniyati mavjud. Ushbu formulaning o'ng tomonida barcha kvadratlar ijobiy bo'lishi kerak

Bu tengsizliklarni bildiradi (39). Teorema isbotlangan.

Matritsaning har qanday asosiy minorini o'zgaruvchilarni to'g'ri qayta raqamlash bilan yuqori chap burchakda joylashtirish mumkin bo'lganligi sababli, bizda

Natija. Ijobiy aniq kvadratik shaklda koeffitsient matritsasining barcha asosiy kichiklari ijobiydir:

Izoh. Ketma-ket asosiy voyaga etmaganlarning noaniqligidan

shaklning salbiy emasligi ergashmaydi. Haqiqatan ham, shakl

unda , shartlarni qondiradi , lekin salbiy emas.

Biroq, quyidagi amal qiladi

Teorema 4. Kvadrat shakl manfiy bo‘lmasligi uchun uning koeffitsienti matritsasining barcha katta minorlari manfiy bo‘lmasligi zarur va yetarli:

Isbot. Yordamchi shaklini kiritaylik edi nomusbat, bu tengsizliklar sodir bo'lishi uchun zarur va etarli.

Kvadrat shakli n ta o‘zgaruvchining f(x 1, x 2,...,x n) yig‘indisi bo‘lib, uning har bir a’zosi o‘zgaruvchilardan birining kvadrati yoki ma’lum koeffitsient bilan olingan ikki xil o‘zgaruvchining ko‘paytmasi hisoblanadi: f. (x 1, x 2, ...,x n) = (a ij =a ji).

Bu koeffitsientlardan tuzilgan A matritsa kvadratik shakldagi matritsa deyiladi. Har doim shunday simmetrik matritsa (ya'ni asosiy diagonalga nisbatan simmetrik matritsa, a ij =a ji).

Matritsa yozuvida kvadratik shakl f(X) = X T AX, bu yerda

Haqiqatdan ham

Masalan, kvadrat shaklni matritsa shaklida yozamiz.

Buning uchun kvadrat shakldagi matritsani topamiz. Uning diagonal elementlari kvadrat o'zgaruvchilarning koeffitsientlariga, qolgan elementlari esa kvadrat shaklning mos keladigan koeffitsientlarining yarmiga teng. Shunung uchun

X o'zgaruvchilarning matritsa-ustunini Y matritsa-ustunining degenerativ bo'lmagan chiziqli o'zgarishi bilan olingan bo'lsin, ya'ni. X = CY, bu erda C - n-tartibdagi yagona bo'lmagan matritsa. U holda f(X) = X T AX = (CY) T A(CY) = (Y T C T)A(CY) =Y T (C T AC)Y kvadratik shakl.

Shunday qilib, degenerativ bo'lmagan chiziqli transformatsiya C bilan kvadrat shakldagi matritsa shaklni oladi: A * =C T AC.

Masalan, f(x 1, x 2) = 2x 1 2 + 4x 1 x 2 - 3x 2 2 kvadratik shakldan olingan f(y 1, y 2) kvadrat shaklini chiziqli aylantirish orqali topamiz.

Kvadrat shakl deyiladi kanonik(Bunda bor kanonik ko'rinish), agar i≠j uchun uning barcha koeffitsientlari ij = 0 bo'lsa, ya'ni f(x 1, x 2,...,x n) = a 11 x 1 2 + a 22 x 2 2 + … + a nn x n 2 =.

Uning matritsasi diagonaldir.

Teorema(bu erda dalil keltirilmagan). Har qanday kvadratik shaklni degenerativ bo'lmagan chiziqli transformatsiya yordamida kanonik shaklga keltirish mumkin.

Masalan, f(x 1, x 2, x 3) = 2x 1 2 + 4x 1 x 2 - 3x 2 2 – x 2 x 3 kvadrat shaklini kanonik shaklga keltiramiz.

Buning uchun avval x 1 o'zgaruvchisi bo'lgan to'liq kvadratni tanlang:

f(x 1, x 2, x 3) = 2(x 1 2 + 2x 1 x 2 + x 2 2) - 2x 2 2 - 3x 2 2 – x 2 x 3 = 2(x 1 + x 2) 2 - 5x 2 2 – x 2 x 3.

Endi biz x 2 o'zgaruvchisi bo'lgan to'liq kvadratni tanlaymiz:

f(x 1, x 2, x 3) = 2(x 1 + x 2) 2 – 5(x 2 2 – 2* x 2 *(1/10)x 3 + (1/100)x 3 2) - (5/100)x 3 2 = = 2(x 1 + x 2) 2 – 5(x 2 – (1/10)x 3) 2 - (1/20)x 3 2.

Keyin degenerativ bo'lmagan chiziqli transformatsiya y 1 = x 1 + x 2,y 2 = x 2 – (1/10)x 3 va y 3 = x 3 bu kvadrat shaklni kanonik ko'rinishga olib keladif(y 1,y 2, y 3) = 2y 1 2 - 5y 2 2 - (1/20)y 3 2 .

E'tibor bering, kvadrat shaklning kanonik shakli noaniq tarzda aniqlanadi (bir xil kvadrat shakl turli usullar bilan kanonik shaklga keltirilishi mumkin 1). Biroq, turli usullar bilan olingan kanonik shakllar bir qator umumiy xususiyatlarga ega. Xususan, kvadratik shaklning musbat (manfiy) koeffitsientlari bo'lgan hadlar soni shaklni ushbu shaklga qisqartirish usuliga bog'liq emas (masalan, ko'rib chiqilgan misolda har doim ikkita manfiy va bitta ijobiy koeffitsient bo'ladi). Bu xususiyat deyiladi kvadratik shakllarning inersiya qonuni.

Keling, bir xil kvadrat shaklni uning kanonik shakliga boshqa usulda keltirish orqali buni tasdiqlaylik. Transformatsiyani x 2:f(x 1, x 2, x 3) = 2x 1 2 + 4x 1 x 2 - 3x 2 2 – x 2 x 3 = -3x 2 2 – x 2 x 3 + o‘zgaruvchisi bilan boshlaylik. 4x 1 x 2 + 2x 1 2 = -3(x 2 2 – - 2* x 2 ((1/6) x 3 + (2/3)x 1) +((1/6) x 3 + (2) /3) x 1) 2) – 3((1/6) x 3 + (2/3)x 1) 2 + 2x 1 2 = = -3(x 2 – (1/6) x 3 - (2) /3) x 1) 2 – 3((1/6) x 3 + (2/3)x 1) 2 + 2x 1 2 =f(y 1 ,y 2 ,y 3) = -3y 1 2 - - 3y 2 2 + 2y 3 2 , bunda y 1 = - (2/3)x 1 + x 2 – (1/6) x 3 ,y 2 = (2/3)x 1 + (1/6) x 3 va y 3 = x 1. Bu erda y 3 uchun 2 ijobiy koeffitsient va y 1 va y 2 uchun ikkita manfiy koeffitsient (-3) mavjud (va boshqa usuldan foydalanib, biz y 1 uchun 2 ijobiy koeffitsientga ega bo'ldik - (-5) y 2 uchun va (-1/20) y 3 uchun).

Shuni ham ta'kidlash kerakki, kvadrat shakldagi matritsaning darajasi deyiladi kvadratik shakl darajasi, kanonik shaklning nolga teng bo'lmagan koeffitsientlari soniga teng va chiziqli transformatsiyalar ostida o'zgarmaydi.

f(X) kvadrat shakli deyiladi ijobiy(salbiy)aniq, agar bir vaqtning o'zida nolga teng bo'lmagan o'zgaruvchilarning barcha qiymatlari uchun u ijobiy bo'lsa, ya'ni f(X) > 0 (salbiy, ya'ni f(X)< 0).

Masalan, f 1 (X) = x 1 2 + x 2 2 kvadrat shakli musbat aniqlangan, chunki kvadratlar yig‘indisi bo‘lib, f 2 (X) = -x 1 2 + 2x 1 x 2 - x 2 2 kvadrat shakli manfiy aniqlangan, chunki ifodalaydi f 2 (X) = -(x 1 - x 2) 2 shaklida ifodalanishi mumkin.

Ko'pgina amaliy vaziyatlarda kvadrat shaklning aniq belgisini o'rnatish biroz qiyinroq, shuning uchun biz quyidagi teoremalardan birini ishlatamiz (ularni isbotsiz shakllantiramiz).

Teorema. Kvadrat shakl, agar uning matritsasining barcha xos qiymatlari ijobiy (salbiy) bo'lsa, ijobiy (salbiy) aniq hisoblanadi.

Teorema (Silvester mezoni). Kvadrat shakl musbat aniq bo'ladi, agar bu shakl matritsasining barcha yetakchi kichiklari ijobiy bo'lsa.

Asosiy (burchak) minor An-tartibdagi k-tartibli matritsalar A () matritsaning birinchi k qator va ustunlaridan tashkil topgan matritsaning determinanti deyiladi.

E'tibor bering, manfiy aniq kvadrat shakllar uchun asosiy kichiklarning belgilari almashinadi va birinchi darajali minor manfiy bo'lishi kerak.

Masalan, f(x 1, x 2) = 2x 1 2 + 4x 1 x 2 + 3x 2 2 kvadrat shaklini belgining aniqligi uchun tekshiramiz.

= (2 -)* *(3 -) – 4 = (6 - 2- 3+ 2) – 4 = 2 - 5+ 2 = 0;D= 25 – 8 = 17; . Demak, kvadratik shakl musbat aniqlangan.

2-usul. A matritsaning birinchi tartibli bosh minori  1 =a 11 = 2 > 0. Ikkinchi tartibli bosh minor  2 = = 6 – 4 = 2 > 0. Shuning uchun Silvestr mezoniga ko‘ra kvadratik shakl ijobiy aniqlangan.

Belgining aniqligi uchun boshqa kvadratik shaklni tekshiramiz, f(x 1, x 2) = -2x 1 2 + 4x 1 x 2 - 3x 2 2.

1-usul. A = kvadrat shakldagi matritsa quramiz. Xarakteristik tenglama shaklga ega bo'ladi = (-2 -)* *(-3 -) – 4 = (6 + 2+ 3+ 2) – 4 = 2 + 5+ 2 = 0;D= 25 – 8 = 17 ; . Demak, kvadratik shakl manfiy aniqlangan.

2-usul. A matritsaning birinchi tartibli bosh minori  1 =a 11 = = -2< 0. Главный минор второго порядка 2 = = 6 – 4 = 2 >0. Shuning uchun, Silvestr mezoniga ko'ra, kvadrat shakl salbiy aniqdir (minusdan boshlab katta kichiklarning belgilari almashinadi).

Yana bir misol sifatida, f(x 1, x 2) = 2x 1 2 + 4x 1 x 2 - 3x 2 2 belgisi bilan aniqlangan kvadrat shaklini ko'rib chiqamiz.

1-usul. A = kvadrat shakldagi matritsa quramiz. Xarakteristik tenglama shaklga ega bo'ladi = (2 -)* *(-3 -) – 4 = (-6 - 2+ 3+ 2) – 4 = 2 +- 10 = 0;D= 1 + 40 = 41; . Bu raqamlardan biri salbiy, ikkinchisi esa ijobiy. Xususiy qiymatlarning belgilari har xil. Binobarin, kvadratik shakl na manfiy, na ijobiy aniq bo'lishi mumkin, ya'ni. bu kvadrat shakl belgi-aniq emas (u har qanday belgining qiymatlarini qabul qilishi mumkin).

2-usul. A matritsaning birinchi tartibli bosh minori  1 =a 11 = 2 > 0. Ikkinchi tartibli bosh minor 2 = = -6 – 4 = -10< 0. Следовательно, по критерию Сильвестра квадратичная форма не является знакоопределенной (знаки главных миноров разные, при этом первый из них – положителен).

1Kvadrat shaklni kanonik ko'rinishga keltirishning ko'rib chiqilayotgan usuli o'zgaruvchilar kvadratlari bilan nolga teng bo'lmagan koeffitsientlar duch kelganda foydalanish uchun qulaydir. Agar ular bo'lmasa, konvertatsiya qilish hali ham mumkin, ammo siz boshqa usullardan foydalanishingiz kerak. Masalan, f(x 1, x 2) = 2x 1 x 2 = x 1 2 + 2x 1 x 2 + x 2 2 - x 1 2 - x 2 2 = bo'lsin.

= (x 1 + x 2) 2 - x 1 2 - x 2 2 = (x 1 + x 2) 2 – (x 1 2 - 2x 1 x 2 + x 2 2) - 2x 1 x 2 = (x 1 + x 2) 2 – - (x 1 - x 2) 2 - 2x 1 x 2 ; 4x 1 x 2 = (x 1 + x 2) 2 – (x 1 - x 2) 2 ;f(x 1, x 2) = 2x 1 x 2 = (1/2)* *(x 1 + x 2) ) 2 – (1/2)*(x 1 - x 2) 2 =f(y 1 ,y 2) = (1/2)y 1 2 – (1/2)y 2 2, bunda y 1 = x 1 + x 2, ay 2 = x 1 – x 2.

Kvadrat shakllar.
Shakllarning belgi aniqligi. Silvestr mezoni

"Kvadrat" sifati darhol bu erda biror narsa kvadrat (ikkinchi daraja) bilan bog'liqligini ko'rsatadi va tez orada biz bu "narsa" ni va uning shakli nima ekanligini bilib olamiz. Bu tilni o'giruvchi bo'lib chiqdi :)

Mening yangi darsimga xush kelibsiz va darhol isinish sifatida biz chiziqli shaklni ko'rib chiqamiz chiziqli. Chiziqli shakl o'zgaruvchilar chaqirdi bir hil 1-darajali polinom:

- ba'zi aniq raqamlar * (biz ulardan kamida bittasi nolga teng deb hisoblaymiz), a - ixtiyoriy qiymatlarni qabul qila oladigan o'zgaruvchilar.

* Ushbu mavzu doirasida biz faqat ko'rib chiqamiz haqiqiy raqamlar .

Biz allaqachon darsda "bir hil" atamasini uchratdik chiziqli tenglamalarning bir jinsli tizimlari, va bu holda ko'phadning ortiqcha doimiysi yo'qligini bildiradi.

Masalan: – ikki o‘zgaruvchining chiziqli shakli

Endi shakl kvadratikdir. Kvadrat shakli o'zgaruvchilar chaqirdi bir hil 2-darajali polinom, har bir atamasi yoki o'zgaruvchining kvadratini o'z ichiga oladi ikki barobar ortadi o'zgaruvchilar mahsuloti. Masalan, ikkita o'zgaruvchining kvadrat shakli quyidagi ko'rinishga ega:

Diqqat! Bu standart yozuv va bu haqda hech narsani o'zgartirishga hojat yo'q! "Qo'rqinchli" ko'rinishga qaramay, bu erda hamma narsa oddiy - doimiylarning ikkita pastki belgisi qaysi o'zgaruvchilar qaysi atamaga kiritilganligini bildiradi:
– bu atama hosilani o‘z ichiga oladi va (kvadrat);
- bu ish;
- va mana ish.

- Men koeffitsientning "minusini" yo'qotganda, bu atamaga tegishli ekanligini tushunmay, qo'pol xatoni darhol kutaman:

Ba'zan ruhda "maktab" dizayn varianti bor, lekin faqat ba'zan. Aytgancha, bu erda doimiylar bizga hech narsa aytmasligini unutmang, shuning uchun "oson belgini" eslab qolish qiyinroq. Ayniqsa, ko'proq o'zgaruvchilar mavjud bo'lganda.

Va uchta o'zgaruvchining kvadratik shakli allaqachon oltita atamani o'z ichiga oladi:

...nima uchun "ikki" omil "aralash" atamalarda joylashtirilgan? Bu qulay va nima uchun tez orada ma'lum bo'ladi.

Biroq, umumiy formulani yozamiz, uni "varaqda" yozish qulay:

- biz har bir qatorni diqqat bilan o'rganamiz - buning hech qanday yomon joyi yo'q!

Kvadrat shaklda o'zgaruvchilar kvadratlari bilan atamalar va ularning juftlashtirilgan mahsuloti bilan atamalar mavjud (sm. kombinatsion birikma formulasi) . Boshqa hech narsa yo'q - "yolg'iz X" va qo'shimcha konstanta yo'q (shunda siz kvadrat shaklga ega bo'lasiz, lekin heterojen 2-darajali polinom).

Kvadrat shaklning matritsa belgilari

Qiymatlarga qarab, ko'rib chiqilayotgan shakl ham ijobiy, ham manfiy qiymatlarni olishi mumkin va xuddi shu narsa har qanday chiziqli shaklga tegishli - agar uning koeffitsientlaridan kamida bittasi noldan farq qilsa, u ijobiy yoki salbiy bo'lishi mumkin (bo'lishi mumkin). qiymatlar).

Ushbu shakl deyiladi o'zgaruvchan belgi. Va agar chiziqli shaklda hamma narsa shaffof bo'lsa, kvadrat shaklda narsalar yanada qiziqarli bo'ladi:

Bu shakl har qanday belgining ma'nosini olishi mumkinligi aniq kvadratik shakl ham almashinishi mumkin.

Bu bo'lmasligi mumkin:

- har doim, agar bir vaqtning o'zida nolga teng bo'lmasa.

- har kim uchun vektor noldan tashqari.

Va umuman, agar kimdir uchun nolga teng bo'lmagan vektor , , keyin kvadratik shakl deyiladi ijobiy aniqlik; agar shunday bo'lsa salbiy aniqlik.

Va hamma narsa yaxshi bo'lar edi, lekin kvadratik shaklning aniqligi faqat oddiy misollarda ko'rinadi va bu ko'rinish engil murakkablik bilan ham yo'qoladi:
– ?

Shakl ijobiy aniqlangan deb taxmin qilish mumkin, lekin bu haqiqatan ham shundaymi? Agar u noldan kichik bo'lgan qiymatlar mavjud bo'lsa-chi?

a bor teorema: Agar hamma xos qiymatlar kvadratik shakldagi matritsalar musbat * , u holda u ijobiy aniqlikdir. Agar hammasi salbiy bo'lsa, unda salbiy.

* Haqiqiy simmetrik matritsaning barcha xos qiymatlari nazariy jihatdan isbotlangan. yaroqli

Yuqoridagi shaklning matritsasini yozamiz:
va tenglamadan. keling uni topamiz xos qiymatlar:

Keling, yaxshi eskilikni hal qilaylik kvadrat tenglama:

, bu shaklni bildiradi ijobiy ta'riflanadi, ya'ni. har qanday nolga teng bo'lmagan qiymatlar uchun u noldan katta.

Ko'rib chiqilgan usul ishlayotganga o'xshaydi, lekin bitta katta BUT bor. Allaqachon uch-uch matritsa uchun to'g'ri raqamlarni izlash uzoq va yoqimsiz vazifadir; yuqori ehtimollik bilan siz irratsional ildizlarga ega 3-darajali ko'phadni olasiz.

Nima qilishim kerak? Eng oson yo'li bor!

Silvestr mezoni

Yo'q, Silvestr Stallone emas :) Birinchidan, bu nima ekanligini eslatib o'taman burchakli voyaga etmaganlar matritsalar. Bu saralash uning yuqori chap burchagidan "o'sadi":

oxirgisi esa matritsaning determinantiga aynan teng.

Endi, aslida, mezon:

1) Kvadrat shakl aniqlangan ijobiy agar va faqat uning BARCHA burchak kichiklari noldan katta bo'lsa: .

2) Kvadrat shakl aniqlangan salbiy agar va faqat uning burchakli minorlari ishora bo‘yicha almashinsa, 1-chi minor noldan kichik bo‘lsa: , , agar – juft yoki , agar – toq.

Agar kamida bitta burchakli minor qarama-qarshi belgiga ega bo'lsa, u holda shakl o'zgaruvchan belgi. Agar burchakli voyaga etmaganlar "o'ng" belgisi bo'lsa-da, lekin ular orasida nollar bo'lsa, unda bu alohida holat bo'lib, men keng tarqalgan misollarni ko'rib chiqqandan keyin biroz keyinroq ko'rib chiqaman.

Keling, matritsaning burchakli minorlarini tahlil qilaylik :

Va bu darhol bizga shaklning salbiy ta'riflanmaganligini aytadi.

Xulosa: barcha burchak kichiklari noldan katta, ya'ni shakl ijobiy ta’riflanadi.

Xususiy qiymat usuli bilan farq bormi? ;)

dan shakl matritsasi yozamiz 1-misol:

birinchisi uning burchakli minori, ikkinchisi esa , shundan kelib chiqadiki, shakl belgisi bo'yicha almashinadi, ya'ni. qiymatlarga qarab, u ham ijobiy, ham salbiy qiymatlarni qabul qilishi mumkin. Biroq, bu allaqachon aniq.

dan shakl va uning matritsasini olamiz 2-misol:

Buni tushunmasdan aniqlashning iloji yo'q. Ammo Silvestrning mezoniga ko'ra, biz bunga ahamiyat bermaymiz:
, shuning uchun, shakl, albatta, salbiy emas.

, va albatta ijobiy emas (chunki barcha burchakli kichiklar ijobiy bo'lishi kerak).

Xulosa: shakli o'zgaruvchan.

O'z-o'zidan hal qilish uchun isitish misollari:

4-misol

Belgining aniqligi uchun kvadrat shakllarni o'rganing

Ushbu misollarda hamma narsa silliq (darsning oxiriga qarang), lekin aslida bunday vazifani bajarish uchun Silvestr mezoni etarli bo'lmasligi mumkin.

Gap shundaki, "chekka" holatlar mavjud, ya'ni: agar mavjud bo'lsa nolga teng bo'lmagan vektor, keyin shakl aniqlanadi salbiy bo'lmagan, agar - keyin salbiy. Ushbu shakllar mavjud nolga teng bo'lmagan Buning uchun vektorlar.

Bu erda siz quyidagi "akkordeon" dan iqtibos keltirishingiz mumkin:

Ajratish mukammal kvadrat, biz darhol ko'ramiz salbiy bo'lmaganlik shakl: , va koordinatalari teng bo'lgan har qanday vektor uchun u nolga teng, masalan: .

"Oyna" misoli salbiy ma'lum bir shakl:

va bundan ham ahamiyatsizroq misol:
– bu yerda shakl har qanday vektor uchun nolga teng , bu yerda ixtiyoriy son.

Salbiy bo'lmagan yoki ijobiy bo'lmagan shakllarni qanday aniqlash mumkin?

Buning uchun bizga kontseptsiya kerak katta voyaga etmaganlar matritsalar. Major minor - bu bir xil raqamlarga ega satrlar va ustunlar kesishmasida joylashgan elementlardan tashkil topgan minor. Shunday qilib, matritsada 1-tartibdagi ikkita asosiy kichik mavjud:
(element 1-qator va 1-ustun kesishmasida joylashgan);
(element 2-qator va 2-ustunning kesishmasida joylashgan),

va 2-tartibdagi bitta katta kichik:
– 1, 2-qator va 1, 2-ustun elementlaridan tuzilgan.

Matritsa "uchdan uchga" Yettita asosiy voyaga etmaganlar bor va bu erda siz bicepsingizni egishingiz kerak bo'ladi:
- uchta birinchi darajali voyaga etmaganlar,
uchta ikkinchi darajali voyaga etmaganlar:
– 1-, 2-qator va 1-, 2-ustun elementlaridan tuzilgan;
– 1, 3-qator va 1, 3-ustun elementlaridan tuzilgan;
- 2, 3-qator va 2, 3-ustun elementlaridan iborat;
va bitta uchinchi darajali kichik:
- 1, 2, 3-qator va 1, 2 va 3-ustun elementlaridan iborat.
Mashq qilish tushunish uchun: matritsaning barcha asosiy kichiklarini yozing .
Dars oxirida tekshiramiz va davom etamiz.

Shvartsenegger mezoni:

1) Nolga teng bo'lmagan* kvadrat shakl aniqlangan salbiy bo'lmagan agar va faqat uning barcha asosiy voyaga etmaganlari bo'lsa salbiy bo'lmagan(noldan katta yoki teng).

* Nol (degenerativ) kvadratik shakl barcha koeffitsientlar nolga teng.

2) Matritsali nolga teng bo'lmagan kvadratik shakl aniqlangan salbiy agar va faqat agar:
- 1-darajali voyaga etmaganlar ijobiy bo'lmagan(noldan kichik yoki teng);
- 2-tartibdagi katta voyaga etmaganlar salbiy bo'lmagan;
- 3-tartibdagi katta voyaga etmaganlar ijobiy bo'lmagan(almashtirish boshlandi);
…
– mayor-minor toifasi ijobiy bo'lmagan, agar - toq yoki salbiy bo'lmagan, agar – hatto.

Agar kamida bitta voyaga etmagan shaxs qarama-qarshi belgiga ega bo'lsa, unda shakl o'zgaruvchan belgidir.

Yuqoridagi misollarda mezon qanday ishlashini ko'rib chiqamiz:

Keling, shakl matritsasini yaratamiz va Birinchidan Keling, burchakli kichiklarni hisoblaylik - agar u ijobiy yoki salbiy aniqlansa nima bo'ladi?

Olingan qiymatlar Silvestr mezoniga javob bermaydi, lekin ikkinchi kichik salbiy emas, va bu 2-mezonni tekshirish zaruriyatini keltirib chiqaradi (2-mezon bo'lsa, avtomatik ravishda bajarilmaydi, ya'ni shaklning belgisini almashtirish to'g'risida darhol xulosa chiqariladi).

1-tartibdagi asosiy voyaga etmaganlar:
- ijobiy,
2-darajali minor:
- salbiy emas.

Shunday qilib, HAMMA katta voyaga etmaganlar salbiy emas, bu shaklni anglatadi salbiy bo'lmagan.

Shakl matritsasini yozamiz , buning uchun Silvestr mezoni aniq qoniqtirmaydi. Ammo biz qarama-qarshi belgilarni ham olmadik (chunki ikkala burchakli kichiklar ham nolga teng). Shuning uchun biz salbiy / ijobiy bo'lmagan mezonning bajarilishini tekshiramiz. 1-tartibdagi asosiy voyaga etmaganlar:
- ijobiy emas,
2-darajali minor:
- salbiy emas.

Shunday qilib, Shvartsenegger mezoniga ko'ra (2-band), shakl ijobiy aniqlanmagan.

Keling, yanada qiziqarli muammoni batafsil ko'rib chiqaylik:

5-misol

Belgining aniqligi uchun kvadrat shaklni tekshiring

Ushbu shakl har qanday haqiqiy raqamga teng bo'lishi mumkin bo'lgan "alfa" tartibi bilan bezatilgan. Ammo bu faqat qiziqarli bo'ladi qaror qilamiz.

Birinchidan, shakl matritsasini yozamiz, ehtimol ko'p odamlar buni og'zaki ravishda bajarishga o'rganib qolganlar: on; asosiy diagonali Biz kvadratchalar uchun koeffitsientlarni qo'yamiz va nosimmetrik joylarga mos keladigan "aralash" mahsulotlarning koeffitsientlarining yarmini qo'yamiz:

Keling, burchakli kichiklarni hisoblaylik:

Uchinchi determinantni 3-qatorda kengaytiraman:

Kvadrat shakl haqida tushuncha. Kvadrat shakl matritsasi. Kvadrat shaklning kanonik shakli. Lagrange usuli. Kvadrat shaklning normal ko'rinishi. Kvadrat shaklning darajasi, indeksi va imzosi. Ijobiy aniq kvadrat shakl. Kvadriklar.

Kvadrat shakl tushunchasi: vektor koordinatalarida ikkinchi darajali bir jinsli ko'phad bilan aniqlangan vektor fazodagi funksiya.

dan kvadrat shakl n noma'lum yig'indisi deyiladi, uning har bir a'zosi yoki bu noma'lumlardan birining kvadrati yoki ikki xil noma'lumning ko'paytmasi.

Kvadrat matritsa: Matritsa ma'lum asosda kvadrat shakldagi matritsa deb ataladi. Agar maydon xarakteristikasi 2 ga teng bo'lmasa, kvadrat shakldagi matritsa simmetrik, ya'ni, deb taxmin qilishimiz mumkin.

Kvadrat shakldagi matritsani yozing:

Demak,

Vektor matritsa shaklida kvadratik shakl:

A, qayerda

Kvadrat shaklning kanonik shakli: Kvadrat shakl, agar hammasi bo'lsa, kanonik deyiladi ya'ni

Har qanday kvadratik shakl chiziqli transformatsiyalar yordamida kanonik shaklga keltirilishi mumkin. Amalda odatda quyidagi usullar qo'llaniladi.

Lagrange usuli : to'liq kvadratlarni ketma-ket tanlash. Masalan, agar

Keyin kvadrat shakl bilan shunga o'xshash protsedura bajariladi va hokazo. Agar kvadrat shaklda hamma narsa lekin bo'lsa keyin dastlabki o'zgartirishdan so'ng masala ko'rib chiqilgan protseduraga tushadi. Shunday qilib, agar, masalan, biz taxmin qilamiz

Kvadrat shaklning normal shakli: Oddiy kvadratik shakl kanonik kvadratik shakl bo'lib, unda barcha koeffitsientlar +1 yoki -1 ga teng.

Kvadrat shaklning darajasi, indeksi va imzosi: Kvadrat shakl darajasi A matritsaning darajasi deyiladi A. Noma'lumlarning degenerativ bo'lmagan o'zgarishlarida kvadratik shaklning darajasi o'zgarmaydi.

Salbiy koeffitsientlar soni manfiy shakl indeksi deb ataladi.

Kanonik shakldagi musbat hadlar soni kvadratik shakldagi musbat inersiya indeksi, manfiy hadlar soni esa manfiy indeks deb ataladi. Ijobiy va manfiy indekslar orasidagi farq kvadrat shaklning imzosi deb ataladi

Ijobiy aniq kvadrat shakl: Haqiqiy kvadratik shakl Agar bir vaqtning o'zida nolga teng bo'lmagan o'zgaruvchilarning har qanday haqiqiy qiymatlari uchun, ijobiy aniq (salbiy aniq) deb ataladi.

. (36)

Bunday holda, matritsa musbat aniq (salbiy aniq) deb ham ataladi.

Ijobiy aniq (salbiy aniq) shakllar sinfi inkor bo'lmagan (javob. nomusbat) shakllar sinfiga kiradi.

Kvadriklar: Kvadrat - n- o'lchovli gipersurfa n+1-o'lchovli fazo, ikkinchi darajali ko'phadning nollar to'plami sifatida aniqlanadi. Agar siz koordinatalarni kiritsangiz ( x 1 , x 2 , x n+1 ) (evklid yoki affin fazoda), kvadratning umumiy tenglamasi

Ushbu tenglamani matritsa belgilarida ixchamroq qayta yozish mumkin:

bu erda x = ( x 1 , x 2 , x n+1 ) — qator vektori, x T - transpozitsiyalangan vektor, Q- o'lcham matritsasi ( n+1)×( n+1) (uning kamida bitta elementi nolga teng deb taxmin qilinadi), P qator vektoridir va R- doimiy. Haqiqiy yoki murakkab sonlar ustidagi kvadratiklar ko'pincha hisobga olinadi. Ta'rifni proyektiv fazoda kvadratlarga kengaytirish mumkin, pastga qarang.

Umuman olganda, polinom tenglamalar tizimining nollar to'plami algebraik xilma-xillik deb nomlanadi. Shunday qilib, kvadratik ikkinchi darajali (affin yoki proyektiv) algebraik xilma-xillik va 1 kod o'lchovidir.

Tekislik va fazoning o'zgarishi.

Tekislik transformatsiyasining ta'rifi. Harakatni aniqlash. harakat xususiyatlari. Harakatning ikki turi: birinchi turdagi harakat va ikkinchi turdagi harakat. Harakatlarga misollar. Harakatning analitik ifodasi. Tekislik harakatlarining tasnifi (qo'zg'almas nuqtalar va o'zgarmas chiziqlar mavjudligiga qarab). Samolyot harakatlari guruhi.

Tekislik transformatsiyasining ta'rifi: Ta'rifi. Nuqtalar orasidagi masofani saqlaydigan tekislik konvertatsiyasi deyiladi harakat samolyotning (yoki harakati). Tekislik konvertatsiyasi deyiladi affin, agar u bir toʻgʻrida yotgan har qanday uch nuqtani ham bir xil toʻgʻrida yotgan uchta nuqtaga aylantirsa va bir vaqtning oʻzida uch nuqtaning oddiy munosabatini saqlasa.

Harakat ta'rifi: Bu nuqtalar orasidagi masofani saqlaydigan shakl o'zgarishlari. Agar ikkita raqam harakat orqali bir-biriga aniq mos keladigan bo'lsa, unda bu raqamlar bir xil, tengdir.

Harakat xususiyatlari: Tekislikning har bir orientatsiyani saqlaydigan harakati parallel ko'chirish yoki aylanishdir; Harakatlanayotganda to'g'ri chiziq ustida yotgan nuqtalar to'g'ri chiziq ustida yotgan nuqtalarga aylanadi va ularning o'zaro joylashish tartibi saqlanadi. Harakatlanayotganda yarim chiziqlar orasidagi burchaklar saqlanib qoladi.

Ikki turdagi harakatlar: birinchi turdagi harakat va ikkinchi turdagi harakatlar: Birinchi turdagi harakatlar - bu ma'lum bir figuraning asoslari yo'nalishini saqlaydigan harakatlar. Ular doimiy harakatlar orqali amalga oshirilishi mumkin.

Ikkinchi turdagi harakatlar - bu asoslarning yo'nalishini teskari tomonga o'zgartiradigan harakatlar. Ularni doimiy harakatlar bilan amalga oshirish mumkin emas.

Birinchi turdagi harakatlarga to'g'ri chiziq atrofida aylantirish va aylanish, ikkinchi turdagi harakatlarga markaziy va oyna simmetriyalari misol bo'ladi.

Birinchi turdagi harakatlarning istalgan sonining tarkibi birinchi turdagi harakatdir.

Ikkinchi turdagi juft sonli harakatlar tarkibi 1-turdagi harakat, 2-turdagi toq sonli harakatlar tarkibi esa 2-turdagi harakatlardir.

Harakatlarga misollar:Parallel uzatish. Berilgan vektor a bo'lsin. a vektoriga parallel o'tkazish - bu tekislikning o'ziga xaritasi bo'lib, bunda har bir M nuqta M 1 nuqtaga tushiriladi, shuning uchun MM 1 vektor a vektoriga teng bo'ladi.

Parallel tarjima - bu harakat, chunki u masofalarni saqlagan holda tekislikning o'ziga xaritasi hisoblanadi. Ushbu harakatni vizual ravishda butun tekislikning berilgan a vektori yo'nalishi bo'yicha uzunligi bo'yicha siljishi sifatida tasvirlash mumkin.

Aylantirish. Tekislikdagi O nuqtani belgilaymiz ( burilish markazi) va burchakni o'rnating a ( burilish burchagi). Tekislikning O nuqta atrofida a burchak bilan aylanishi - bu tekislikning o'ziga xaritasi bo'lib, bunda har bir M nuqta M 1 nuqtaga tushiriladi, OM = OM 1 va MOM 1 burchagi a ga teng bo'ladi. Bunday holda, O nuqtasi o'z o'rnida qoladi, ya'ni u o'z-o'zidan xaritaga tushiriladi va boshqa barcha nuqtalar O nuqtasi atrofida bir xil yo'nalishda - soat yo'nalishi bo'yicha yoki soat sohasi farqli ravishda aylanadi (rasmda soat miliga teskari aylanish ko'rsatilgan).

Aylanish - bu harakat, chunki u masofalar saqlanib qolgan tekislikning o'ziga xaritasini ifodalaydi.

Harakatning analitik ifodasi: oldingi tasvir koordinatalari bilan nuqta tasviri orasidagi analitik bog`lanish (1) ko`rinishga ega bo`ladi.

Tekislik harakatlarining tasnifi (qo'zg'almas nuqtalar va o'zgarmas chiziqlar mavjudligiga qarab): Ta'rif:

Tekislikdagi nuqta o'zgarmas (qat'iy) hisoblanadi, agar u berilgan transformatsiya ostida o'ziga aylanadi.

Misol: Markaziy simmetriya bilan simmetriya markazining nuqtasi o'zgarmasdir. Burilish paytida aylanish markazining nuqtasi o'zgarmasdir. Eksenel simmetriya bilan o'zgarmas chiziq to'g'ri chiziqdir - simmetriya o'qi o'zgarmas nuqtalarning to'g'ri chizig'idir.

Teorema: Agar harakat bitta o'zgarmas nuqtaga ega bo'lmasa, u kamida bitta o'zgarmas yo'nalishga ega.

Misol: Parallel uzatish. Darhaqiqat, bu yo'nalishga parallel bo'lgan to'g'ri chiziqlar o'zgarmas nuqtalardan iborat bo'lmasa-da, bir butun sifatida invariantdir.

Teorema: Agar nur harakatlansa, nur o'ziga aylanadi, demak, bu harakat berilgan nurni o'z ichiga olgan to'g'ri chiziqqa nisbatan bir xil o'zgarish yoki simmetriyadir.

Shuning uchun, o'zgarmas nuqtalar yoki raqamlar mavjudligiga asoslanib, harakatlarni tasniflash mumkin.

Harakat nomi	Invariant nuqtalar	Invariant chiziqlar
Birinchi turdagi harakat.
1. - burilish	(markazda) - 0	Yo'q
2. Identifikatsiyani o'zgartirish	samolyotning barcha nuqtalari	hammasi to'g'ri
3. Markaziy simmetriya	nuqta 0 - markaz	0 nuqtadan o'tadigan barcha chiziqlar
4. Parallel uzatish	Yo'q	hammasi to'g'ri
Ikkinchi turdagi harakat.
5. Eksenel simmetriya.	nuqtalar to'plami	simmetriya o'qi (to'g'ri chiziq) barcha to'g'ri chiziqlar

Samolyot harakati guruhi: Geometriyada raqamlarning o'z-o'zidan tuzilgan guruhlari muhim rol o'ynaydi. Agar ma'lum bir figura tekislikda (yoki kosmosda) bo'lsa, unda biz tekislikning (yoki fazoning) barcha harakatlarining to'plamini ko'rib chiqishimiz mumkin, bunda bu raqam o'ziga aylanadi.

Ushbu to'plam guruhdir. Masalan, teng yonli uchburchak uchun uchburchakni o'ziga aylantiruvchi tekislik harakatlari guruhi 6 ta elementdan iborat: nuqta atrofida burchaklar orqali aylanishlar va uchta to'g'ri chiziq atrofidagi simmetriyalar.

Ular rasmda ko'rsatilgan. 1 qizil chiziqlar bilan. Muntazam uchburchakning o'z-o'zini tekislash guruhining elementlari boshqacha ko'rsatilishi mumkin. Buni tushuntirish uchun, keling, muntazam uchburchakning uchlarini 1, 2, 3 raqamlari bilan raqamlaymiz. Uchburchakning har qanday o'z-o'zini tekislashi 1, 2, 3 nuqtalarni bir xil nuqtalarga oladi, lekin boshqa tartibda olinadi, ya'ni. shartli ravishda quyidagi qavslardan biri shaklida yozilishi mumkin:

va hokazo.

bu erda 1, 2, 3 raqamlari ko'rib chiqilayotgan harakat natijasida 1, 2, 3 cho'qqilari kiradigan cho'qqilarning raqamlarini bildiradi.

Proyektiv fazolar va ularning modellari.

Proyektiv fazo tushunchasi va proyektiv fazo modeli. Proyektiv geometriyaning asosiy faktlari. Markazi O nuqtada joylashgan bir qator chiziqlar proyeksiyalovchi tekislikning modelidir. Proyektiv nuqtalar. Kengaytirilgan tekislik proyektiv tekislikning modelidir. Kengaytirilgan uch o'lchovli afin yoki Evklid fazosi proyektiv fazoning modelidir. Parallel dizayndagi tekis va fazoviy figuralarning tasvirlari.

Proyektiv fazo tushunchasi va proyektiv fazo modeli:

Maydon ustidagi proyektiv fazo - berilgan maydon ustidagi qandaydir chiziqli fazoning chiziqlaridan (bir o'lchovli pastki fazolardan) iborat bo'shliq. To'g'ridan-to'g'ri bo'shliqlar deyiladi nuqta proyektiv fazo. Ushbu ta'rifni ixtiyoriy tanaga umumlashtirish mumkin

Agar u o'lchamga ega bo'lsa, u holda proyektiv fazoning o'lchami raqam deb ataladi va proyektiv fazoning o'zi belgilanadi va bog'lanadi (buni ko'rsatish uchun belgi qabul qilinadi).

O'lchamning vektor fazosidan mos keladigan proyektiv fazoga o'tish deyiladi proyeksiyalash bo'sh joy.

Nuqtalarni bir hil koordinatalar yordamida tasvirlash mumkin.

Proyektiv geometriyaning asosiy faktlari: Proyektiv geometriya geometriyaning proyektiv tekislik va fazolarni o‘rganuvchi bo‘limidir. Proyektiv geometriyaning asosiy xususiyati - bu ko'plab dizaynlarga oqlangan simmetriya qo'shadigan ikkilik printsipi. Proyektiv geometriyani ham sof geometrik nuqtai nazardan, ham analitik (bir hil koordinatalardan foydalangan holda) va salgebraik nuqtai nazardan, proyektiv tekislikni maydon ustidagi struktura sifatida ko'rib chiqish mumkin. Ko'pincha va tarixan, haqiqiy proyektiv tekislik "abadiy chiziq" qo'shilishi bilan Evklid tekisligi hisoblanadi.

Holbuki, Evklid geometriyasi shug'ullanadigan figuralarning xususiyatlari metrik(burchaklar, segmentlar, maydonlarning o'ziga xos qiymatlari) va raqamlarning ekvivalenti ularga teng muvofiqlik(ya'ni, metrik xususiyatlarni saqlab qolgan holda, figuralarni harakat orqali bir-biriga aylantirish mumkin bo'lsa), geometrik figuralarning "chuqur yotuvchi" xususiyatlari harakatga qaraganda ko'proq umumiy turdagi transformatsiyalarda saqlanadi. Proyektiv geometriya sinf bo'yicha o'zgarmas bo'lgan figuralarning xususiyatlarini o'rganish bilan shug'ullanadi proyektiv transformatsiyalar, shuningdek, bu o'zgarishlarning o'zi.

Proyektiv geometriya Evklid geometriyasini to'ldiradi, bu bilan parallel chiziqlar mavjudligi bilan murakkab bo'lgan ko'plab masalalarga chiroyli va oddiy echimlar beradi. Konus kesimlarining proyektiv nazariyasi ayniqsa sodda va nafisdir.

Proyektiv geometriyaning uchta asosiy yondashuvi mavjud: mustaqil aksiomatizatsiya, Evklid geometriyasini to'ldirish va maydon bo'yicha tuzilish.

Aksiomatizatsiya

Proyektiv fazoni boshqa aksiomalar to'plami yordamida aniqlash mumkin.

Coxeter quyidagilarni ta'minlaydi:

1. To'g'ri chiziq bor va unda bo'lmagan nuqta bor.

2. Har bir chiziqda kamida uchta nuqta bor.

3. Ikki nuqta orqali siz aniq bitta to'g'ri chiziq chizishingiz mumkin.

4. Agar A, B, C, Va D- turli nuqtalar va AB Va CD keyin kesishadi A.C. Va BD kesishadi.

5. Agar ABC tekislik bo'lsa, unda tekislikda bo'lmagan kamida bitta nuqta bor ABC.

6. Ikki xil tekislik kamida ikkita nuqtani kesishadi.

7. To'liq to'rtburchakning uchta diagonal nuqtasi kollinear emas.

8. Agar uchta nuqta bir chiziqda bo'lsa X X

Proyektiv tekislik (uchinchi o'lchamsiz) biroz boshqacha aksiomalar bilan belgilanadi:

1. Ikki nuqta orqali siz aniq bitta to'g'ri chiziq chizishingiz mumkin.

2. Har qanday ikkita chiziq kesishadi.

3. To'rtta nuqta bor, ulardan uchtasi to'g'ri kelmaydi.

4. To'liq to'rtburchaklarning uchta diagonal nuqtasi kollinear emas.

5. Agar uchta nuqta bir chiziqda bo'lsa X ph ning proektsiyasiga nisbatan o'zgarmasdir, keyin barcha nuqtalar ustida X ph ga nisbatan invariant.

6. Dezarg teoremasi: Agar ikkita uchburchak nuqta orqali perspektiv bo‘lsa, ular chiziq orqali perspektiv bo‘ladi.

Uchinchi o'lchov mavjudligida Dezarg teoremasini ideal nuqta va chiziq kiritmasdan isbotlash mumkin.

Kengaytirilgan tekislik - proyektiv tekislik modeli: A3 affin fazoda markazi O nuqtada bo'lgan S(O) chiziqlar to'plamini va to'plam markazidan o'tmaydigan P tekislikni olamiz: O 6∈ N. Affin fazodagi chiziqlar to'plami proyektiv tekislikning modelidir. Keling, n tekislik nuqtalari to'plamining S bog'lovchining to'g'ri chiziqlar to'plamiga xaritasini aniqlaylik (Juda, agar sizda bu savol bo'lsa, meni kechiring)

Kengaytirilgan uch o'lchovli afin yoki Evklid fazosi - proektiv fazoning modeli:

Xaritani syurektiv qilish uchun biz affin tekislikni n proyektiv tekislikka rasmiy ravishda kengaytirish jarayonini takrorlaymiz va n tekislikni noto'g'ri nuqtalar to'plami (M∞) bilan to'ldiramiz, shunday qilib: ((M∞)) = P0(O). Xaritada S(O) tekisliklar toʻplamining har bir tekisligining teskari tasviri d tekislikdagi chiziq boʻlgani uchun choʻzilgan tekislikning barcha notoʻgʻri nuqtalari toʻplami: n = Π ∩ (M∞) aniq koʻrinadi. , (M∞), cho'zilgan tekislikning noto'g'ri d∞ chizig'ini ifodalaydi, bu yakka tekislikning teskari tasviri n0: (d∞) = P0(O) (= n0). (I.23) Keling, bu erda va bundan buyon biz oxirgi tenglikni P0(O) = n0 nuqtalar to'plamining tengligi ma'nosida tushunamiz, degan fikrga qo'shilamiz, lekin boshqa tuzilishga ega. Affin tekislikni noto'g'ri chiziq bilan to'ldirish orqali biz xaritalash (I.21) kengaytirilgan tekislikning barcha nuqtalari to'plamida ikki tomonlama bo'lishini ta'minladik:

Parallel dizayn paytida tekis va fazoviy figuralarning rasmlari:

Stereometriyada fazoviy figuralar o'rganiladi, lekin chizmada ular tekis figuralar sifatida tasvirlanadi. Samolyotda fazoviy figurani qanday tasvirlash kerak? Odatda geometriyada buning uchun parallel dizayn qo'llaniladi. p qandaydir samolyot bo'lsin, l- uni kesib o'tuvchi to'g'ri chiziq (1-rasm). Ixtiyoriy nuqta orqali A, qatorga tegishli emas l, chiziqqa parallel chiziq chizish l. Bu chiziqning p tekislik bilan kesishgan nuqtasi nuqtaning parallel proyeksiyasi deyiladi A to'g'ri chiziq yo'nalishi bo'yicha p tekislikka l. Uni belgilaylik A". Agar nuqta A qatoriga kiradi l, keyin parallel proyeksiya orqali A chiziqning kesishish nuqtasi p tekislikda deb hisoblanadi l samolyot bilan p.

Shunday qilib, har bir nuqta A fazoda uning proyeksiyasi solishtiriladi A" p tekislikka. Bu moslik p tekislikka to'g'ri chiziq yo'nalishi bo'yicha parallel proyeksiya deyiladi. l.

Proyektiv transformatsiyalar guruhi. Muammoni hal qilish uchun dastur.

Tekislikning proyektiv o'zgarishi tushunchasi. Tekislikning proyektiv o'zgarishlariga misollar. Proyektiv transformatsiyalarning xossalari. Gomologiya, gomologiyaning xossalari. Proyektiv transformatsiyalar guruhi.

Tekislikning proyektiv o'zgarishi tushunchasi: Proyektiv transformatsiya tushunchasi markaziy proyeksiya tushunchasini umumlashtiradi. Agar a tekislikning qandaydir a 1 tekislikka markaziy proyeksiyasini bajarsak, u holda a 1 ning a 2 ga, a 2 ning a 3, ... ga proyeksiyasi va nihoyat, qandaydir a tekislik proyeksiyasi amalga oshiriladi. n yana a 1 bo'yicha, u holda barcha bu proyeksiyalarning tarkibi a tekislikning proyektiv o'zgarishi; Bunday zanjirga parallel proyeksiyalarni ham kiritish mumkin.

Proyektiv tekislik o'zgarishlariga misollar: Tugallangan tekislikning proyektiv o'zgarishi - bu uning o'ziga birma-bir xaritalashi, bunda nuqtalarning kollinearligi saqlanib qoladi yoki boshqacha aytganda, har qanday chiziqning tasviri to'g'ri chiziqdir. Har qanday proyektiv transformatsiya markaziy va parallel proyeksiyalar zanjirining tarkibidir. Affin transformatsiya - bu cheksizlikdagi chiziq o'ziga aylanadigan proyektiv transformatsiyaning alohida holati.

Proyektiv o'zgarishlarning xususiyatlari:

Proyektiv o'zgartirish jarayonida to'g'ri chiziqda yotmagan uchta nuqta chiziqda yotmaydigan uchta nuqtaga aylanadi.

Proyektiv transformatsiya jarayonida ramka ramkaga aylanadi.

Proyektiv transformatsiya paytida chiziq to'g'ri chiziqqa, qalam esa qalamga o'tadi.

Gomologiya, gomologiyaning xossalari:

O'zgarmas nuqtalar chizig'iga ega bo'lgan tekislikning proektiv o'zgarishi, shuning uchun o'zgarmas chiziqlar qalami homologiya deb ataladi.

1. Mos kelmaydigan mos keladigan gomologik nuqtalardan o'tuvchi chiziq o'zgarmas chiziqdir;

2. Bir-biriga to'g'ri kelmaydigan mos keladigan gomologik nuqtalardan o'tadigan chiziqlar bir xil qalamga tegishli bo'lib, uning markazi o'zgarmas nuqtadir.

3. Nuqta, uning tasviri va gomologiya markazi bir xil to'g'ri chiziqda yotadi.

Proyektiv o'zgarishlar guruhi: P 2 proyeksiyalovchi tekislikning o'ziga proyektiv xaritalanishini, ya'ni bu tekislikning proyektiv o'zgarishini (P 2 ' = P 2) ko'rib chiqaylik.

Avvalgidek, P 2 proyektiv tekisligining f 1 va f 2 proyektiv o'zgarishlarining f tarkibi f 1 va f 2 o'zgarishlarning ketma-ket bajarilishi natijasidir: f = f 2 °f 1.

1-teorema: P 2 proyeksiyalovchi tekislikning barcha proyektiv o'zgarishlarining H to'plami proyeksiyalovchi o'zgarishlar tarkibiga nisbatan guruhdir.

Kvadrat shakllar

Bu koeffitsientlardan tuzilgan A matritsa kvadratik shakldagi matritsa deyiladi. Har doim shunday simmetrik matritsa (ya'ni asosiy diagonalga nisbatan simmetrik matritsa, a ij = a ji).

Matritsa yozuvida kvadratik shakl f(X) = X T AX, bu yerda

Haqiqatdan ham

Masalan, kvadrat shaklni matritsa shaklida yozamiz.

X o'zgaruvchilarning matritsa-ustunini Y matritsa-ustunining degenerativ bo'lmagan chiziqli o'zgarishi bilan olingan bo'lsin, ya'ni. X = CY, bu erda C - n-tartibdagi yagona bo'lmagan matritsa. Keyin kvadrat shakl
f(X) = X T AX = (CY) T A(CY) = (Y T C T)A(CY) = Y T (C T AC)Y.

Shunday qilib, degenerativ bo'lmagan chiziqli transformatsiya C bilan kvadrat shaklning matritsasi shaklni oladi: A * = C T AC.

Masalan, f(x 1, x 2) = 2x 1 2 + 4x 1 x 2 - 3x 2 2 kvadratik shakldan olingan f(y 1, y 2) kvadrat shaklini chiziqli aylantirish orqali topamiz.

Kvadrat shakl deyiladi kanonik(Bunda bor kanonik ko'rinish), agar uning barcha koeffitsientlari i ≠ j uchun a ij = 0 bo'lsa, ya'ni.
f(x 1, x 2,...,x n) = a 11 x 1 2 + a 22 x 2 2 + … + a nn x n 2 =.

Uning matritsasi diagonaldir.

Teorema(bu erda dalil keltirilmagan). Har qanday kvadratik shaklni degenerativ bo'lmagan chiziqli transformatsiya yordamida kanonik shaklga keltirish mumkin.

Masalan, kvadrat shaklni kanonik shaklga keltiramiz
f(x 1, x 2, x 3) = 2x 1 2 + 4x 1 x 2 - 3x 2 2 – x 2 x 3.

Buning uchun avval x 1 o'zgaruvchisi bo'lgan to'liq kvadratni tanlang:

f(x 1, x 2, x 3) = 2(x 1 2 + 2x 1 x 2 + x 2 2) - 2x 2 2 - 3x 2 2 – x 2 x 3 = 2(x 1 + x 2) 2 - 5x 2 2 – x 2 x 3.

Endi biz x 2 o'zgaruvchisi bo'lgan to'liq kvadratni tanlaymiz:

f(x 1, x 2, x 3) = 2(x 1 + x 2) 2 – 5(x 2 2 – 2* x 2 *(1/10)x 3 + (1/100)x 3 2) - (5/100)x 3 2 =
= 2(x 1 + x 2) 2 – 5(x 2 – (1/10)x 3) 2 - (1/20)x 3 2.

Keyin degenerativ bo'lmagan chiziqli transformatsiya y 1 = x 1 + x 2, y 2 = x 2 – (1/10) x 3 va y 3 = x 3 bu kvadrat shaklni f(y 1, y 2) kanonik ko'rinishga keltiradi. , y 3) = 2y 1 2 - 5y 2 2 - (1/20)y 3 2 .

E'tibor bering, kvadrat shaklning kanonik shakli noaniq tarzda aniqlanadi (bir xil kvadrat shakl turli usullar bilan kanonik shaklga keltirilishi mumkin). Biroq, turli usullar bilan olingan kanonik shakllar bir qator umumiy xususiyatlarga ega. Xususan, kvadratik shaklning musbat (manfiy) koeffitsientlari bo'lgan hadlar soni shaklni ushbu shaklga qisqartirish usuliga bog'liq emas (masalan, ko'rib chiqilgan misolda har doim ikkita manfiy va bitta ijobiy koeffitsient bo'ladi). Bu xususiyat deyiladi kvadratik shakllarning inersiya qonuni.

Keling, bir xil kvadrat shaklni kanonik shaklga boshqa usulda keltirish orqali buni tasdiqlaylik. Transformatsiyani x 2 o'zgaruvchisi bilan boshlaylik:
f(x 1, x 2, x 3) = 2x 1 2 + 4x 1 x 2 - 3x 2 2 – x 2 x 3 = -3x 2 2 – x 2 x 3 + 4x 1 x 2 + 2x 1 2 = - 3(x 2 2 –
- 2* x 2 ((1/6) x 3 + (2/3)x 1) +((1/6) x 3 + (2/3)x 1) 2) – 3((1/6) x 3 + (2/3)x 1) 2 + 2x 1 2 =
= -3(x 2 – (1/6) x 3 - (2/3)x 1) 2 – 3((1/6) x 3 + (2/3)x 1) 2 + 2x 1 2 = f (y 1 , y 2 , y 3) = -3y 1 2 -
-3y 2 2 + 2y 3 2, bunda y 1 = - (2/3)x 1 + x 2 – (1/6) x 3, y 2 = (2/3)x 1 + (1/6) x 3 va y 3 = x 1. Bu erda y 3 da 2 ijobiy koeffitsient va y 1 va y 2 da ikkita manfiy koeffitsient (-3) mavjud (va boshqa usul yordamida biz y 1 da 2 ijobiy koeffitsientni va ikkita manfiy koeffitsientni oldik - (-5) da. y 2 va (-1 /20) y 3 da).

f(X) kvadrat shakli deyiladi ijobiy (salbiy) aniq, agar bir vaqtning o'zida nolga teng bo'lmagan o'zgaruvchilarning barcha qiymatlari uchun u ijobiy bo'lsa, ya'ni. f(X) > 0 (salbiy, ya'ni.
f(X)< 0).

Masalan, f 1 (X) = x 1 2 + x 2 2 kvadrat shakli musbat aniqlangan, chunki kvadratlar yig‘indisi bo‘lib, f 2 (X) = -x 1 2 + 2x 1 x 2 - x 2 2 kvadrat shakli manfiy aniqlangan, chunki ifodalaydi, uni f 2 (X) = -(x 1 - x 2) 2 shaklida ifodalash mumkin.

Ko'pgina amaliy vaziyatlarda kvadrat shaklning aniq belgisini o'rnatish biroz qiyinroq, shuning uchun biz quyidagi teoremalardan birini ishlatamiz (ularni isbotsiz shakllantiramiz).

Teorema. Kvadrat shakl, agar uning matritsasining barcha xos qiymatlari ijobiy (salbiy) bo'lsa, ijobiy (salbiy) aniq hisoblanadi.

Teorema (Silvester mezoni). Kvadrat shakl musbat aniq bo'ladi, agar bu shakl matritsasining barcha yetakchi kichiklari ijobiy bo'lsa.

Asosiy (burchak) minor n-tartibli A k-tartibli matritsa A () matritsaning birinchi k qator va ustunlaridan tashkil topgan matritsaning determinanti deyiladi.

E'tibor bering, manfiy aniq kvadrat shakllar uchun asosiy kichiklarning belgilari almashinadi va birinchi darajali minor salbiy bo'lishi kerak.

Masalan, f(x 1, x 2) = 2x 1 2 + 4x 1 x 2 + 3x 2 2 kvadrat shaklini belgining aniqligi uchun tekshiramiz.

= (2 - l)*
*(3 - l) – 4 = (6 - 2l - 3l + l 2) – 4 = l 2 - 5l + 2 = 0; D = 25 – 8 = 17;
. Demak, kvadratik shakl musbat aniqlangan.

2-usul. A D 1 = a 11 = 2 > 0 ikkinchi tartibli matritsaning bosh minori D 2 = = 6 – 4 = 2 > 0. Shuning uchun Silvestr mezoniga ko‘ra kvadratik shakl. ijobiy aniqlik.

Belgining aniqligi uchun boshqa kvadratik shaklni tekshiramiz, f(x 1, x 2) = -2x 1 2 + 4x 1 x 2 - 3x 2 2.

1-usul. A = kvadrat shakldagi matritsa quramiz. Xarakteristik tenglama shaklga ega bo'ladi = (-2 - l)*
*(-3 - l) – 4 = (6 + 2l + 3l + l 2) – 4 = l 2 + 5l + 2 = 0; D = 25 – 8 = 17;
. Demak, kvadratik shakl manfiy aniqlangan.