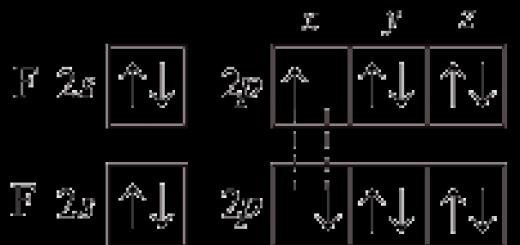
Kompleks sonlar haqiqiy sonlar toʻplamining kengaytmasi boʻlib, odatda bilan belgilanadi. Har qanday kompleks sonni rasmiy yig'indi sifatida ko'rsatish mumkin, bu erda va haqiqiy sonlar va xayoliy birlikdir.
Kompleks sonni , , shaklida yozish kompleks sonning algebraik shakli deyiladi.
Kompleks sonlarning xossalari. Kompleks sonning geometrik talqini.
Algebraik shaklda berilgan kompleks sonlar ustida amallar:
Kompleks sonlar ustida arifmetik amallarni bajarish qoidalarini ko‘rib chiqamiz.
Agar a = a + bi va b = c + di ikkita kompleks son berilsa, u holda
a + b = (a + bi) + (c + di) = (a + c) + (b + d)i,
a – b = (a + bi) – (c + di) = (a – c) + (b – d)i. (o'n bir)
Bu ikki tartibli juft haqiqiy sonlarni qoʻshish va ayirish amallarini aniqlashdan kelib chiqadi ((1) va (3) formulalarga qarang). Kompleks sonlarni qo‘shish va ayirish qoidalarini oldik: ikkita kompleks sonni qo‘shish uchun ularning haqiqiy qismlarini va shunga mos ravishda xayoliy qismlarini alohida qo‘shishimiz kerak; Bitta murakkab sondan boshqasini ayirish uchun mos ravishda ularning haqiqiy va xayoliy qismlarini ayirish kerak.
– a = – a – bi songa a = a + bi sonining teskarisi deyiladi. Bu ikki sonning yig'indisi nolga teng: - a + a = (- a - bi) + (a + bi) = (-a + a) + (-b + b)i = 0.
Murakkab sonlarni ko'paytirish qoidasini olish uchun biz (6) formuladan foydalanamiz, ya'ni i2 = -1. Bu munosabatni hisobga olib, (a + bi)(c + di) = ac + adi + bci + bdi2 = ac + (ad + bc)i - bd, ya'ni topamiz.
(a + bi)(c + di) = (ac - bd) + (ad + bc)i . (12)
Bu formula (2) formulaga to'g'ri keladi, bu esa tartiblangan juft haqiqiy sonlarni ko'paytirishni aniqladi.
E'tibor bering, ikkita murakkab konjugat sonning yig'indisi va mahsuloti haqiqiy sonlardir. Haqiqatan ham, a = a + bi, = a – bi bo'lsa, a = (a + bi)(a - bi) = a2 – i2b2 = a2 + b2 , a + = (a + bi) + (a - bi) = ( a + a) + (b - b)i= 2a, ya'ni.
a + = 2a, a = a2 + b2. (13)
Ikkita kompleks sonni algebraik ko‘rinishda bo‘lishda bo‘linishning bir xil turdagi son bilan ham ifodalanishini kutish kerak, ya’ni a/b = u + vi, bu yerda u, v R. Kompleks sonlarni bo‘lish qoidasini chiqaramiz. . a = a + bi, b = c + di raqamlari berilsin va b ≠ 0, ya'ni c2 + d2 ≠ 0. Oxirgi tengsizlik c va d bir vaqtning o'zida yo'q bo'lib ketmasligini bildiradi (c = 0 bo'lganda holat istisno qilinadi) , d = 0). (12) va ikkinchi (13) tenglik formulalarini qo'llagan holda, biz quyidagilarni topamiz:
Shunday qilib, ikkita kompleks sonning nisbati quyidagi formula bilan aniqlanadi:
formula (4) ga mos keladi.
b = c + di soni uchun olingan formuladan foydalanib, uning teskari soni b-1 = 1/b ni topish mumkin. (14) formulada a = 1, b = 0 deb faraz qilsak, hosil qilamiz
Bu formula noldan boshqa berilgan kompleks sonning teskarisini aniqlaydi; bu raqam ham murakkab.
Masalan: (3 + 7i) + (4 + 2i) = 7 + 9i;
(6 + 5i) – (3 + 8i) = 3 – 3i;
(5 – 4i)(8 – 9i) = 4 – 77i;
Algebraik shaklda kompleks sonlar ustida amallar.
55. Kompleks sonning argumenti. Kompleks sonni yozishning trigonometrik shakli (hosil qilish).
Arg.com.raqamlari. – haqiqiy X o‘qining musbat yo‘nalishi va berilgan sonni ifodalovchi vektor o‘rtasida.
Trigon formulasi. Raqamlar: ,
TA’RIF
Kompleks sonning algebraik shakli \(\z\) kompleks sonni \(\z=x+i y\) ko'rinishida yozishdan iborat bo'lib, bu erda \(\x\) va \(\y\) haqiqiy sonlardir. , \(\i\ ) - \(\i^(2)=-1\) munosabatini qanoatlantiruvchi xayoliy birlik.
\(\ x \) soni \(\ z \) kompleks sonning haqiqiy qismi deyiladi va \(\ x=\operatorname(Re) z \) bilan belgilanadi.
\(\y\) soni \(\z\) kompleks sonning xayoliy qismi deyiladi va \(\y=\operator nomi(Im) z\) bilan belgilanadi.
Masalan:
Kompleks son \(\ z=3-2 i \) va uning qoʻshma soni \(\ \overline(z)=3+2 i \) algebraik shaklda yoziladi.
Xayoliy miqdor \(\ z=5 i \) algebraik shaklda yoziladi.
Bundan tashqari, siz hal qilayotgan masalaga qarab, murakkab sonni trigonometrik yoki eksponensial songa aylantirishingiz mumkin.
\(\z=\frac(7-i)(4)+13\) sonni algebraik shaklda yozing, uning haqiqiy va xayoliy qismlarini, shuningdek konjugat sonini toping.
Kasrlarni bo'lish atamasi va kasrlarni qo'shish qoidasidan foydalanib, biz quyidagilarni olamiz:
\(\z=\frac(7-i)(4)+13=\frac(7)(4)+13-\frac(i)(4)=\frac(59)(4)-\frac( 1)(4)i\)
Demak, \(\ z=\frac(5 g)(4)-\frac(1)(4) i \) kompleks sonning haqiqiy qismi \(\ x=\operatorname(Re) z= sondir. \frac(59) (4) \) , xayoliy qism soni \(\ y=\operatorname(Im) z=-\frac(1)(4) \)
Konjugat raqami: \(\ \overline(z)=\frac(59)(4)+\frac(1)(4) i \)
\(\ z=\frac(59)(4)-\frac(1)(4) i \), \(\ \operator nomi(Re) z=\frac(59)(4) \), \(\ \operatorname(Im) z=-\frac(1)(4) \), \(\ \overline(z)=\frac(59)(4)+\frac(1)(4) i \)
Kompleks sonlarning algebraik shakldagi harakatlari taqqoslash
Ikkita kompleks son \(\ z_(1)=x_(1)+i y_(1) \) teng deyiladi, agar \(\ x_(1)=x_(2) \), \(\ y_(1) boʻlsa )= y_(2) \) ya'ni. Ularning haqiqiy va xayoliy qismlari tengdir.
\(\ z_(1)=13+y i \) va \(\ z_(2)=x+5 i \) ikkita kompleks sonlar qaysi x va y uchun teng ekanligini aniqlang.
Ta'rifga ko'ra, ikkita murakkab son, agar ularning haqiqiy va xayoliy qismlari teng bo'lsa, ya'ni. \(\x=13\), \(\y=5\).
qo'shimcha
Kompleks sonlarni qo‘shish \(\z_(1)=x_(1)+i y_(1)\) haqiqiy va xayoliy qismlarni to‘g‘ridan-to‘g‘ri yig‘ish orqali amalga oshiriladi:
\(\ z_(1)+z_(2)=x_(1)+i y_(1)+x_(2)+i y_(2)=\chap(x_(1)+x_(2)\o‘ng) +i\chap(y_(1)+y_(2)\o'ng) \)
\(\ z_(1)=-7+5 i \), \(\ z_(2)=13-4 i \) kompleks sonlar yigʻindisini toping.
Kompleks sonning haqiqiy qismi \(\ z_(1)=-7+5 i \) sondir \(\ x_(1)=\operatorname(Re) z_(1)=-7 \) , xayoliy son. qismi soni \( \ y_(1)=\mathrm(Im) \), \(\ z_(1)=5 \) . \(\ z_(2)=13-4 i \) kompleks sonning haqiqiy va xayoliy qismlari \(\ x_(2)=\operatorname(Re) z_(2)=13 \) va \( ga teng. \ y_(2) mos ravishda )=\operator nomi(Im) z_(2)=-4 \) .
Shunday qilib, kompleks sonlar yig'indisi:
\(\ z_(1)+z_(2)=\chap(x_(1)+x_(2)\o‘ng)+i\chap(y_(1)+y_(2)\o‘ng)=(-7+ 13)+i(5-4)=6+i \)
\(\ z_(1)+z_(2)=6+i \)
Murakkab raqamlarni qo'shish haqida batafsil ma'lumotni alohida maqolada o'qing: Kompleks sonlarni qo'shish.
Ayirish
\(\z_(1)=x_(1)+i y_(1)\) va \(\z_(2)=x_(2)+i y_(2)\) kompleks sonlarni ayirish toʻgʻridan-toʻgʻri ayirish yoʻli bilan bajariladi. Haqiqiy va xayoliy qismlar:
\(\ z_(1)-z_(2)=x_(1)+i y_(1)-\chap(x_(2)+i y_(2)\oʻng)=x_(1)-x_(2) +\left(i y_(1)-i y_(2)\o'ng)=\left(x_(1)-x_(2)\o'ng)+i\left(y_(1)-y_(2)\o'ng ) \)
kompleks sonlar ayirmasini toping \(\ z_(1)=17-35 i \), \(\ z_(2)=15+5 i \)
Kompleks sonlarning haqiqiy va xayoliy qismlarini toping \(\ z_(1)=17-35 i \), \(\ z_(2)=15+5 i \) :
\(\ x_(1)=\operator nomi(Re) z_(1)=17, x_(2)=\operator nomi(Re) z_(2)=15 \)
\(\ y_(1)=\operator nomi(Im) z_(1)=-35, y_(2)=\operator nomi(Im) z_(2)=5 \)
Shunday qilib, kompleks sonlarning farqi:
\(\ z_(1)-z_(2)=\chap(x_(1)-x_(2)\o'ng)+i\chap(y_(1)-y_(2)\o'ng)=(17-15 )+i(-35-5)=2-40 i \)
\(\ z_(1)-z_(2)=2-40 i \) koʻpaytirish
\(\ z_(1)=x_(1)+i y_(1) \) va \(\ z_(2)=x_(2)+i y_(2) \) kompleks sonlarni koʻpaytirish toʻgʻridan-toʻgʻri hosil qilish orqali bajariladi. Xayoliy birlikning xususiyatini hisobga olgan holda algebraik shakldagi raqamlar \(\i^(2)=-1\) :
\(\ z_(1) \cdot z_(2)=\left(x_(1)+i y_(1)\o‘ng) \cdot\left(x_(2)+i y_(2)\o‘ng)=x_ (1) \cdot x_(2)+i^(2) \cdot y_(1) \cdot y_(2)+\left(x_(1) \cdot i y_(2)+x_(2) \cdot i y_(1)\o'ng)=\)
\(\ =\left(x_(1) \cdot x_(2)-y_(1) \cdot y_(2)\right)+i\left(x_(1) \cdot y_(2)+x_(2) ) \cdot y_(1)\o'ng) \)
Kompleks sonlar koʻpaytmasini toping \(\ z_(1)=1-5 i \)
Kompleks sonlar majmuasi:
\(\ z_(1) \cdot z_(2)=\left(x_(1) \cdot x_(2)-y_(1) \cdot y_(2)\o'ng)+i\left(x_(1) \cdot y_(2)+x_(2) \cdot y_(1)\right)=(1 \cdot 5-(-5) \cdot 2)+i(1 \cdot 2+(-5) \cdot 5 )=15-23 i\)
\(\ z_(1) \cdot z_(2)=15-23 i \) boʻlinish
Kompleks sonlarning koeffitsienti \(\z_(1)=x_(1)+i y_(1)\) va \(\z_(2)=x_(2)+i y_(2)\) koʻpaytirish yoʻli bilan aniqlanadi. ayiruvchi va maxrajni maxrajli qo‘shma songa:
\(\ \frac(z_(1))(z_(2))=\frac(x_(1)+i y_(1))(x_(2)+i y_(2))=\frac(\chap) (x_(1)+i y_(1)\o'ng)\left(x_(2)-i y_(2)\o'ng))(\left(x_(2)+i y_(2)\o'ng)\chap (x_(2)-i y_(2)\o'ng))=\frac(x_(1) \cdot x_(2)+y_(1) \cdot y_(2))(x_(2)^(2) +y_(2)^(2))+i \frac(x_(2) \cdot y_(1)-x_(1) \cdot y_(2))(x_(2)^(2)+y_(2) )^(2)) \)
1 sonni kompleks songa bo'lish uchun \(\z=1+2i\).
Haqiqiy 1 raqamining xayoliy qismi nolga teng bo'lgani uchun omil:
\(\ \frac(1)(1+2 i)=\frac(1 \cdot 1)(1^(2)+2^(2))-i \frac(1 \cdot 2)(1^( 2)+2^(2))=\frac(1)(5)-i \frac(2)(5)\)
\(\ \frac(1)(1+2 i)=\frac(1)(5)-i \frac(2)(5) \)
Kompleks sonlar haqida kerakli ma'lumotlarni eslaylik.
Kompleks raqam shaklning ifodasidir a + bi, Qayerda a, b haqiqiy sonlar va i- deb atalmish xayoliy birlik, kvadrati –1 ga teng bo'lgan belgi, ya'ni i 2 = –1. Raqam a chaqirdi haqiqiy qismi, va raqam b - xayoliy qism murakkab son z = a + bi. Agar b= 0, keyin o'rniga a + 0i oddiygina yozadilar a. Haqiqiy raqamlar ekanligini ko'rish mumkin maxsus holat murakkab sonlar.
Kompleks sonlar ustidagi arifmetik amallar haqiqiy sonlar bilan bir xil: ularni bir-biriga qo‘shish, ayirish, ko‘paytirish va bo‘lish mumkin. Qo'shish va ayirish qoidaga muvofiq amalga oshiriladi ( a + bi) ± ( c + di) = (a ± c) + (b ± d)i, va ko'paytirish qoidaga amal qiladi ( a + bi) · ( c + di) = (ac – bd) + (reklama + mil. avv)i(bu erda shunday ishlatiladi i 2 = –1). Raqam = a – bi chaqirdi murakkab konjugat Kimga z = a + bi. Tenglik z · = a 2 + b 2 sizga bitta murakkab sonni boshqa (nol bo'lmagan) kompleks songa qanday ajratishni tushunishga imkon beradi:
(Masalan, 
.)
Murakkab sonlar qulay va vizual geometrik tasvirga ega: raqam z = a + bi koordinatalari bo'lgan vektor bilan ifodalanishi mumkin ( a; b) Dekart tekisligida (yoki, bu deyarli bir xil narsa, nuqta - bu koordinatalarga ega vektorning oxiri). Bunday holda, ikkita kompleks sonning yig'indisi mos keladigan vektorlarning yig'indisi sifatida tasvirlangan (buni parallelogramma qoidasi yordamida topish mumkin). Pifagor teoremasiga ko'ra vektor uzunligi koordinatali ( a; b) ga teng. Bu miqdor deyiladi modul murakkab son z = a + bi va | bilan belgilanadi z|. Bu vektorning x o'qining musbat yo'nalishi (soat miliga teskari hisoblangan) bilan hosil qiladigan burchak deyiladi dalil murakkab son z va Arg bilan belgilanadi z. Argument yagona aniqlangan emas, faqat 2 ga karra qo'shilishigacha π
radianlar (yoki gradus bilan hisoblansa, 360 °) - axir, boshlanish atrofida bunday burchak bilan aylanish vektorni o'zgartirmasligi aniq. Ammo uzunlik vektori bo'lsa r burchak hosil qiladi φ
x o'qining musbat yo'nalishi bilan uning koordinatalari ( ga teng bo'ladi. r cos φ
; r gunoh φ
). Bu erdan chiqadi trigonometrik belgilar murakkab raqam: z = |z| · (cos(Arg z) + i gunoh (Arg z)). Ko'pincha bu shaklda murakkab raqamlarni yozish qulay, chunki u hisob-kitoblarni sezilarli darajada osonlashtiradi. Trigonometrik shaklda murakkab sonlarni ko'paytirish juda oddiy: z 1 · z 2 = |z 1 | · | z 2 | · (cos(Arg z 1 + Arg z 2) + i gunoh (Arg z 1 + Arg z 2)) (ikkita kompleks sonni ko'paytirishda ularning modullari ko'paytiriladi va argumentlari qo'shiladi). Bu yerdan kuzatib boring Moivre formulalari: z n = |z|n· (chunki n· (Arg z)) + i gunoh( n· (Arg z))). Ushbu formulalardan foydalanib, murakkab sonlardan istalgan darajadagi ildizlarni ajratib olishni o'rganish oson. Ildiz n-daraja z raqamidan- bu murakkab raqam w, Nima w n = z. Bu aniq 
, qayerda k to'plamdan istalgan qiymatni qabul qilishi mumkin (0, 1, ..., n- 1). Bu har doim aniq borligini anglatadi n ildizlar n kompleks sonning th darajasi (tekislikda ular muntazamning uchlarida joylashgan n-gon).
Kvadrat tenglamani ko'rib chiqing.
Keling, uning ildizlarini aniqlaylik.
Kvadrati -1 bo'lgan haqiqiy son yo'q. Lekin operatorni formula bilan aniqlasak i xayoliy birlik sifatida, u holda bu tenglamaning yechimini quyidagicha yozish mumkin 
. Qayerda 
Va 
- kompleks sonlar, bunda -1 haqiqiy qism, 2 yoki ikkinchi holatda -2 xayoliy qismdir. Xayoliy qism ham haqiqiy sondir. Xayoliy qismning xayoliy birlikka ko'paytirilishi allaqachon degan ma'noni anglatadi xayoliy raqam.
Umuman olganda, kompleks son shaklga ega
z = x + iy ,
Qayerda x, y– haqiqiy sonlar, – xayoliy birlik. Bir qator amaliy fanlarda, masalan, elektrotexnika, elektronika, signallar nazariyasida xayoliy birlik quyidagicha belgilanadi. j. Haqiqiy raqamlar x = Re(z) Va y =men(z) chaqiriladi haqiqiy va xayoliy qismlar raqamlar z. ifoda deyiladi algebraik shakl murakkab sonni yozish.
Har qanday haqiqiy son shakldagi kompleks sonning maxsus holatidir 
. Xayoliy son ham murakkab sonning alohida holidir 
.
Kompleks sonlar to'plamining ta'rifi C
Bu ibora quyidagicha o'qiladi: set BILAN, shunday elementlardan iborat x Va y haqiqiy sonlar to‘plamiga tegishli R va xayoliy birlikdir. E'tibor bering, va hokazo.
Ikkita murakkab raqam 
Va 
ularning haqiqiy va xayoliy qismlari teng bo'lgan taqdirdagina teng bo'ladi, ya'ni. Va .
Kompleks sonlar va funksiyalar fan va texnikada, xususan, mexanika, oʻzgaruvchan tok zanjirlarini tahlil qilish va hisoblash, analog elektronika, nazariya va signallarni qayta ishlash, nazariya fanlarida keng qoʻllaniladi. avtomatik boshqaruv va boshqa amaliy fanlar.
- Kompleks sonlar arifmetikasi
Ikki kompleks sonni qo'shish ularning haqiqiy va qo'shilishidan iborat xayoliy qismlar, ya'ni.
Shunga ko'ra, ikkita kompleks sonning farqi
Kompleks raqam 
chaqirdi har tomonlama konjugat raqam z =x+iy.
z va z * murakkab konjugat raqamlari xayoliy qismning belgilarida farqlanadi. Bu aniq
.
O'rtasidagi har qanday tenglik murakkab ifodalar hamma joyda bu tenglik bo'lsa, o'z kuchida qoladi i bilan almashtirildi -
i, ya'ni. konjugat sonlarning tengligiga o'ting. Raqamlar i Va –
i chunki algebraik jihatdan farqlanmaydi 
.
Ikkita kompleks sonning mahsulotini (ko'paytirish) quyidagicha hisoblash mumkin:
Ikki kompleks sonning bo'linishi:
Misol:
- Murakkab samolyot
Kompleks sonni to‘g‘ri to‘rtburchak koordinatalar tizimida grafik ko‘rinishda ifodalash mumkin. Keling, tekislikda to'rtburchaklar koordinatalar tizimini aniqlaylik (x, y).
Eksa bo'yicha ho'kiz biz haqiqiy qismlarni joylashtiramiz x, deyiladi haqiqiy (haqiqiy) o'q, o'qda Oy- xayoliy qismlar y murakkab sonlar. Bu deyiladi xayoliy o'q. Bunday holda, har bir kompleks son tekislikning ma'lum bir nuqtasiga to'g'ri keladi va bunday tekislik deyiladi murakkab tekislik. Nuqta A murakkab tekislik vektorga mos keladi O.A.
Raqam x chaqirdi abscissa kompleks son, son y – ordinata.
Murakkab konjugat sonlar juftligi haqiqiy o'q atrofida nosimmetrik joylashgan nuqtalar bilan ifodalanadi.
 |
Agar samolyotda bo'lsak qutbli koordinatalar tizimi, keyin har bir kompleks son z qutb koordinatalari bilan aniqlanadi. Qayerda modul raqamlar 
nuqtaning qutb radiusi va burchakdir 
- uning qutb burchagi yoki kompleks son argumenti z.
Kompleks sonning moduli 
har doim salbiy emas. Kompleks sonning argumenti yagona aniqlanmaydi. Argumentning asosiy qiymati shartni qondirishi kerak 
. Murakkab tekislikning har bir nuqtasi ham mos keladi umumiy ma'no dalil. 2p ning karrali bilan farq qiladigan argumentlar teng hisoblanadi. Nol soni argumenti aniqlanmagan.
Argumentning asosiy qiymati quyidagi iboralar bilan aniqlanadi:
Bu aniq
Qayerda
, 
.
Kompleks sonlarni ifodalash z sifatida
chaqirdi trigonometrik shakl murakkab son.
Misol.
- Kompleks sonlarning ko'rsatkichli shakli
Ichida parchalanish Maclaurin seriyasi Haqiqiy argument funktsiyalari uchun 
shaklga ega:
Murakkab argumentli eksponensial funksiya uchun z parchalanish shunga o'xshash
.
Xayoliy argumentning eksponensial funktsiyasi uchun Maklaurin seriyasining kengayishi quyidagicha ifodalanishi mumkin.
Olingan identifikatsiya deyiladi Eyler formulasi.
Salbiy dalil uchun u shaklga ega
Ushbu ifodalarni birlashtirib, siz sinus va kosinus uchun quyidagi iboralarni belgilashingiz mumkin
.
Eyler formulasidan foydalanib, kompleks sonlarni ifodalashning trigonometrik shaklidan
mavjud indikativ Kompleks sonning (eksponensial, qutbli) shakli, ya'ni. shaklda uning ifodalanishi
,
Qayerda 
- to'rtburchaklar koordinatali nuqtaning qutb koordinatalari ( x,y).
Kompleks sonning konjugati ko'rsatkichli shaklda quyidagicha yoziladi.
Eksponensial shakl uchun uni aniqlash oson quyidagi formulalar kompleks sonlarni ko'paytirish va bo'lish
Ya'ni, ko'rsatkichli shaklda kompleks sonlarning ko'paytmasi va bo'linishi algebraik shaklga qaraganda oddiyroqdir. Ko'paytirishda omillarning modullari ko'paytiriladi va argumentlar qo'shiladi. Ushbu qoida har qanday omillar uchun amal qiladi. Xususan, murakkab sonni ko'paytirishda z yoqilgan i vektor z soat miliga teskari 90 aylanadi
Bo‘lishda payning moduli maxrajning moduliga bo‘linadi va maxrajning argumenti hisobning argumentidan ayiriladi.
Kompleks sonlarning eksponensial shaklidan foydalanib, biz taniqli trigonometrik identifikatsiyalar uchun ifodalarni olishimiz mumkin. Masalan, shaxsdan
Eyler formulasidan foydalanib yozishimiz mumkin
Haqiqiy va xayoliy qismlarni tenglashtirish bu ifoda, biz burchaklar yig'indisining kosinus va sinusi uchun ifodalarni olamiz
- Kompleks sonlarning darajalari, ildizlari va logarifmlari
Kompleks sonni ga oshirish tabiiy daraja n formula bo'yicha ishlab chiqariladi
Misol. Keling, hisoblaylik 
.
Keling, bir raqamni tasavvur qilaylik trigonometrik shaklda
’
Eksponentsiya formulasini qo'llash orqali biz olamiz
Qiymatni ifodaga qo'yish orqali r= 1, biz shunday deb ataladigan narsani olamiz Moivre formulasi, uning yordamida siz bir nechta burchaklarning sinuslari va kosinuslari uchun ifodalarni aniqlashingiz mumkin.
Ildiz n-kompleks sonning darajasi z Unda bor n ifoda bilan belgilanadigan turli qiymatlar
Misol. Keling, topamiz.
Buning uchun kompleks sonni () trigonometrik shaklda ifodalaymiz
.
Kompleks sonning ildizini hisoblash formulasidan foydalanib, biz olamiz
Kompleks sonning logarifmi z- bu raqam w, buning uchun. Tabiiy logarifm kompleks songa ega cheksiz to'plam qiymatlar va formula yordamida hisoblanadi
Haqiqiy (kosinus) va xayoliy (sinus) qismdan iborat. Bu kuchlanish uzunlik vektori sifatida ifodalanishi mumkin Um , boshlang'ich bosqichi(burchak) burchak tezligi bilan aylanish ω .
Bundan tashqari, agar murakkab funktsiyalar qo'shilsa, ularning haqiqiy va xayoliy qismlari qo'shiladi. Agar murakkab funktsiya doimiy yoki haqiqiy funktsiyaga ko'paytirilsa, uning haqiqiy va xayoliy qismlari bir xil ko'rsatkichga ko'paytiriladi. Bunday murakkab funktsiyani differentsiallash/integratsiyalash haqiqiy va xayoliy qismlarning differentsiatsiyasi/integratsiyasiga to'g'ri keladi.
Masalan, murakkab stress ifodasini farqlash
ga ko'paytirishdir iō f(z) funksiyaning haqiqiy qismi va 
– funksiyaning xayoliy qismi. Misollar: 
.
Ma'nosi z kompleks z tekisligidagi nuqta va unga mos qiymat bilan ifodalanadi w- murakkab tekislikdagi nuqta w. Ko'rsatilganda w = f(z) tekis chiziqlar z tekis chiziqlarga aylantiriladi w, bir tekislikning raqamlarini boshqasining raqamlariga aylantiradi, lekin chiziqlar yoki raqamlarning shakllari sezilarli darajada o'zgarishi mumkin.
Dars rejasi.
1. Tashkiliy moment.
2. Materialni taqdim etish.
3. Uy vazifasi.
4. Darsni yakunlash.
Darslar davomida
I. Tashkiliy moment.
II. Materialning taqdimoti.
Motivatsiya.
Haqiqiy sonlar to'plamining kengayishi haqiqiy sonlarga yangi raqamlarni (xayoliy) qo'shishdan iborat. Ushbu raqamlarning kiritilishi haqiqiy sonlar to'plamida manfiy sonning ildizini ajratib olishning iloji yo'qligi bilan bog'liq.
Kompleks son tushunchasi bilan tanishtirish.
Haqiqiy sonlarni to'ldiruvchi xayoliy sonlar shaklda yoziladi bi, Qayerda i xayoliy birlikdir va i 2 = - 1.
Bunga asoslanib, kompleks sonning quyidagi ta’rifini olamiz.
Ta'rif. Kompleks son shaklning ifodasidir a+bi, Qayerda a Va b- haqiqiy raqamlar. Bunday holda, quyidagi shartlar bajariladi:
a) Ikkita kompleks son a 1 + b 1 i Va a 2 + b 2 i teng va faqat agar a 1 = a 2, b 1 = b 2.
b) Kompleks sonlarning qo‘shilishi quyidagi qoida bilan aniqlanadi:
(a 1 + b 1 i) + (a 2 + b 2 i) = (a 1 + a 2) + (b 1 + b 2) i.
c) Kompleks sonlarni ko'paytirish qoida bilan aniqlanadi:
(a 1 + b 1 i) (a 2 + b 2 i) = (a 1 a 2 - b 1 b 2) + (a 1 b 2 - a 2 b 1) i.
Kompleks sonning algebraik shakli.
Kompleks sonni shaklda yozish a+bi kompleks sonning algebraik shakli deyiladi, bu erda A- haqiqiy qism, bi xayoliy qismdir va b- haqiqiy raqam.
Kompleks raqam a+bi Agar uning haqiqiy va xayoliy qismlari nolga teng bo'lsa, nolga teng deb hisoblanadi: a = b = 0
Kompleks raqam a+bi da b = 0 haqiqiy son bilan bir xil deb hisoblanadi a: a + 0i = a.
Kompleks raqam a+bi da a = 0 sof xayoliy deyiladi va belgilanadi bi: 0 + bi = bi.
Ikkita murakkab raqam z = a + bi Va = a - bi, faqat xayoliy qismning belgisi bilan farqlanadi, konjugat deyiladi.
Algebraik shaklda kompleks sonlar ustida amallar.
Kompleks sonlar ustida quyidagi amallarni algebraik shaklda bajarish mumkin.
1) qo'shimcha.
Ta'rif. Kompleks sonlar yig'indisi z 1 = a 1 + b 1 i Va z 2 = a 2 + b 2 i kompleks son deyiladi z, uning haqiqiy qismi haqiqiy qismlar yig'indisiga teng z 1 Va z 2, va xayoliy qism sonlarning xayoliy qismlari yig'indisidir z 1 Va z 2, ya'ni z = (a 1 + a 2) + (b 1 + b 2)i.
Raqamlar z 1 Va z 2 atamalar deb ataladi.
Kompleks sonlarni qo'shish quyidagi xususiyatlarga ega:
1º. Kommutativlik: z 1 + z 2 = z 2 + z 1.
2º. Assotsiativlik: (z 1 + z 2) + z 3 = z 1 + (z 2 + z 3).
3º. Kompleks raqam –a –bi kompleks sonning teskarisi deyiladi z = a + bi. Kompleks son, kompleks songa qarama-qarshi z, belgilangan -z. Kompleks sonlar yig'indisi z Va -z nolga teng: z + (-z) = 0
1-misol: Qo'shishni bajaring (3 – i) + (-1 + 2i).
(3 – i) + (-1 + 2i) = (3 + (-1)) + (-1 + 2) i = 2 + 1i.
2) ayirish.
Ta'rif. Kompleks sondan ayirish z 1 murakkab son z 2 z, Nima z + z 2 = z 1.
Teorema. Kompleks sonlar orasidagi farq mavjud va noyobdir.
2-misol: ayirish amalini bajaring (4 – 2i) - (-3 + 2i).
(4 – 2i) - (-3 + 2i) = (4 - (-3)) + (-2 - 2) i = 7 – 4i.
3) ko'paytirish.
Ta'rif. Kompleks sonlar mahsuloti z 1 =a 1 +b 1 i Va z 2 =a 2 +b 2 i kompleks son deyiladi z, tenglik bilan belgilanadi: z = (a 1 a 2 – b 1 b 2) + (a 1 b 2 + a 2 b 1)i.
Raqamlar z 1 Va z 2 omillar deyiladi.
Kompleks sonlarni ko'paytirish quyidagi xususiyatlarga ega:
1º. Kommutativlik: z 1 z 2 = z 2 z 1.
2º. Assotsiativlik: (z 1 z 2)z 3 = z 1 (z 2 z 3)
3º. Ko'paytirishning qo'shishga nisbatan taqsimlanishi:
(z 1 + z 2) z 3 = z 1 z 3 + z 2 z 3.
4º. z = (a + bi)(a – bi) = a 2 + b 2- haqiqiy raqam.
Amalda kompleks sonlarni ko'paytirish yig'indini yig'indiga ko'paytirish va haqiqiy va xayoliy qismlarni ajratish qoidasiga muvofiq amalga oshiriladi.
Quyidagi misolda murakkab sonlarni ikki usulda ko‘paytirishni ko‘rib chiqamiz: qoida bo‘yicha va yig‘indini yig‘indiga ko‘paytirish.
3-misol: Ko'paytirishni bajaring (2 + 3i) (5 – 7i).
1 yo'l. (2 + 3i) (5 – 7i) = (2× 5 – 3× (- 7)) + (2× (- 7) + 3× 5)i = = (10 + 21) + (- 14 + 15) )i = 31 + i.
2-usul. (2 + 3i) (5 – 7i) = 2× 5 + 2× (- 7i) + 3i× 5 + 3i× (- 7i) = = 10 – 14i + 15i + 21 = 31 + i.
4) Bo'lim.
Ta'rif. Kompleks sonni ajrating z 1 murakkab songa z 2, shunday kompleks sonni topishni bildiradi z, Nima z · z 2 = z 1.
Teorema. Kompleks sonlar bo'limi mavjud va yagona bo'lsa z 2 ≠ 0 + 0i.
Amalda kompleks sonlarning bo‘linmasi ayiruvchi va maxrajni maxrajning konjugatiga ko‘paytirish yo‘li bilan topiladi.
Mayli z 1 = a 1 + b 1 i, z 2 = a 2 + b 2 i, Keyin
.
Quyidagi misolda biz sonning maxrajga konjugati bilan ko'paytirish formulasi va qoidasi yordamida bo'linishni bajaramiz.
4-misol. Ko‘rsatkichni toping 
.
5) Ijobiy butun kuchga ko'tarilish.
a) Xayoliy birlikning kuchlari.
Tenglikdan foydalanish i 2 = -1, xayoliy birlikning istalgan musbat butun kuchini aniqlash oson. Bizda ... bor:
i 3 = i 2 i = -i,
i 4 = i 2 i 2 = 1,
i 5 = i 4 i = i,
i 6 = i 4 i 2 = -1,
i 7 = i 5 i 2 = -i,
i 8 = i 6 i 2 = 1 va hokazo.
Bu daraja qiymatlarini ko'rsatadi men n, Qayerda n– musbat butun son, vaqti-vaqti bilan indikator ortishi bilan takrorlanadi 4 .
Shuning uchun, raqamni oshirish uchun i musbat butun kuchga, biz ko'rsatkichni ga bo'lishimiz kerak 4 va qurish i ko'rsatkichi bo'linishning qolgan qismiga teng bo'lgan darajaga.
5-misol: Hisoblang: (i 36 + i 17) i 23.
i 36 = (i 4) 9 = 1 9 = 1,
i 17 = i 4 × 4+1 = (i 4) 4 × i = 1 · i = i.
i 23 = i 4 × 5+3 = (i 4) 5 × i 3 = 1 · i 3 = - i.
(i 36 + i 17) · i 23 = (1 + i) (- i) = - i + 1= 1 – i.
b) Kompleks sonni musbat butun darajaga ko'tarish binomialni mos darajaga ko'tarish qoidasiga muvofiq amalga oshiriladi, chunki bu bir xil kompleks omillarni ko'paytirishning maxsus holatidir.
6-misol: Hisoblang: (4 + 2i) 3
(4 + 2i) 3 = 4 3 + 3× 4 2 × 2i + 3× 4× (2i) 2 + (2i) 3 = 64 + 96i – 48 – 8i = 16 + 88i.
