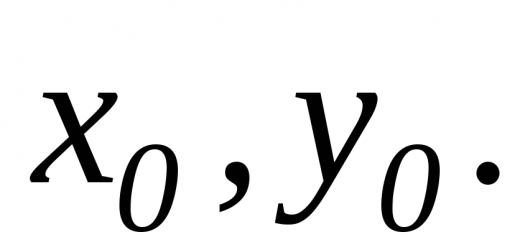Limitlar barcha matematika talabalariga juda ko'p muammolarni keltirib chiqaradi. Cheklovni hal qilish uchun, ba'zida siz juda ko'p hiyla-nayranglardan foydalanishingiz va turli xil echim usullaridan ma'lum bir misol uchun mos keladiganini tanlashingiz kerak.

Ushbu maqolada biz sizning imkoniyatlaringiz chegaralarini tushunishga yoki nazorat chegaralarini tushunishga yordam bermaymiz, lekin biz savolga javob berishga harakat qilamiz: oliy matematikada chegaralarni qanday tushunish kerak? Tushunish tajriba bilan birga keladi, shuning uchun biz bir nechtasini beramiz batafsil misollar tushuntirishlar bilan chegaralar yechimlari.

Matematikada limit tushunchasi

Birinchi savol: bu chegara nima va nimaning chegarasi? Raqamli ketma-ketliklar va funksiyalarning chegaralari haqida gapirish mumkin. Bizni funktsiyaning chegarasi tushunchasi qiziqtiradi, chunki o'quvchilar ko'p uchraydigan narsa. Lekin birinchi navbatda, chegaraning eng umumiy ta'rifi:

Aytaylik, o'zgaruvchan qiymat bor. Agar o'zgarish jarayonida bu qiymat cheksiz ravishda ma'lum bir raqamga yaqinlashsa a , Bu a - bu qiymatning chegarasi.

Muayyan intervalda aniqlangan funksiya uchun f(x)=y bunday raqam chegara deb ataladi A , bu funksiya qachonga intiladi X , ma'lum bir nuqtaga moyil A . Nuqta A funksiya aniqlangan intervalga tegishli.

Bu og'ir tuyuladi, lekin u juda oddiy yozilgan:

Lim- ingliz tilidan chegara- chegara.

Chegarani aniqlashning geometrik tushuntirishi ham mavjud, ammo bu erda biz nazariyani chuqur o'rganmaymiz, chunki biz masalaning nazariy tomoniga emas, balki amaliy tomoniga ko'proq qiziqamiz. Buni aytganda X ba'zi qiymatga intiladi, bu o'zgaruvchining raqam qiymatini olmasligini, lekin unga cheksiz yaqinlashishini bildiradi.

beraylik aniq misol. Vazifa chegarani topishdir.

Ushbu misolni hal qilish uchun biz qiymatni almashtiramiz x=3 funksiyaga aylanadi. Biz olamiz:

Aytgancha, agar siz matritsalar bo'yicha asosiy operatsiyalarga qiziqsangiz, ushbu mavzu bo'yicha alohida maqolani o'qing.

Misollarda X har qanday qiymatga moyil bo'lishi mumkin. Bu har qanday raqam yoki cheksizlik bo'lishi mumkin. Mana bir misol qachon X cheksizlikka intiladi:

Nima ekanligi intuitiv ravishda aniq kattaroq raqam maxrajda funksiya qabul qiladigan qiymat qanchalik kichik bo'lsa. Shunday qilib, cheksiz o'sish bilan X ma'nosi 1/x kamayadi va nolga yaqinlashadi.

Ko'rib turganingizdek, chegarani hal qilish uchun siz faqat funktsiyaga intiladigan qiymatni almashtirishingiz kerak. X . Biroq, bu eng oddiy holat. Ko'pincha chegarani topish unchalik aniq emas. Chegaralar ichida turning noaniqliklari mavjud 0/0 yoki cheksizlik/cheksizlik . Bunday hollarda nima qilish kerak? Fokuslarga murojaat qiling!

Ichidagi noaniqliklar

Infinity/infinity shaklining noaniqligi

Cheklov bo'lsin:

Funktsiyada cheksizlikni almashtirishga harakat qilsak, biz sonda ham, maxrajda ham cheksizlikka ega bo'lamiz. Umuman olganda, bunday noaniqliklarni hal qilishda san'atning ma'lum bir elementi borligini aytish kerak: siz noaniqlik yo'qolishi uchun funktsiyani qanday o'zgartirishingiz mumkinligini payqashingiz kerak. Bizning holatlarimizda biz hisoblagich va maxrajni ajratamiz X oliy darajadagi. Nima bo'ladi?

Yuqorida muhokama qilingan misoldan bilamizki, maxrajda x ni o'z ichiga olgan atamalar nolga moyil bo'ladi. Keyin chegaraning yechimi:

Turi noaniqliklarini hal qilish uchun cheksizlik/cheksizlik son va maxrajni ga bo'ling X eng yuqori darajada.

Aytmoqchi! O'quvchilarimiz uchun endi 10% chegirma mavjud har qanday ish turi

Boshqa turdagi noaniqlik: 0/0

Har doimgidek, funktsiyaga qiymatlarni almashtirish x=-1 beradi 0 son va maxrajda. Bir oz ko'proq diqqat bilan qarang va buni bizning numeratorimizda ko'rasiz kvadrat tenglama. Keling, ildizlarni topamiz va yozamiz:

Keling, kamaytiramiz va olamiz:

Shunday qilib, agar siz noaniqlik turiga duch kelsangiz 0/0 – son va maxrajni ko‘paytiruvchi.

Misollarni echishni osonlashtirish uchun biz ba'zi funktsiyalar chegaralari bilan jadvalni taqdim etamiz:

L'Hopital qoidasi ichida

Ikkala turdagi noaniqlikni bartaraf etishning yana bir kuchli usuli. Usulning mohiyati nimada?

Agar chegarada noaniqlik mavjud bo'lsa, noaniqlik yo'qolguncha pay va maxrajning hosilasini oling.

L'Hopital qoidasi quyidagicha ko'rinadi:

Muhim nuqta : ayiruvchi va maxrajning hosilalari boʻluvchi va ayiruvchi oʻrniga turish chegarasi mavjud boʻlishi kerak.

Va endi - haqiqiy misol:

Oddiy noaniqlik mavjud 0/0 . Numerator va maxrajning hosilalarini olaylik:

Voila, noaniqlik tez va oqlangan tarzda hal qilinadi.

Umid qilamizki, siz ushbu ma'lumotni amalda qo'llay olasiz va "Oliy matematikada chegaralarni qanday hal qilish kerak" degan savolga javob topasiz. Agar siz ketma-ketlik chegarasini yoki bir nuqtada funktsiya chegarasini hisoblashingiz kerak bo'lsa va bu ish uchun mutlaqo vaqt yo'q bo'lsa, tez va batafsil yechim uchun professional talabalar xizmatiga murojaat qiling.

Ta'rif berilgan yakuniy chegara ketma-ketliklar. Tegishli xususiyatlar va ekvivalent ta'riflar muhokama qilinadi. A nuqta ketma-ketlikning chegarasi emasligi ta'rifi berilgan. Ta'rif yordamida chegaraning mavjudligi isbotlangan misollar ko'rib chiqiladi.

Tarkib

Shuningdek qarang: Ketma-ketlik chegarasi - asosiy teoremalar va xususiyatlar
Tengsizliklarning asosiy turlari va ularning xossalari

Bu erda biz ketma-ketlikning chekli chegarasining ta'rifini ko'rib chiqamiz. Ketma-ketlikning cheksizlikka yaqinlashish holati "Cheksiz katta ketma-ketlikning ta'rifi" sahifasida muhokama qilinadi.

Har qanday musbat e soni uchun ketma-ketlikning chegarasi a if sonidir > 0 shunday narsa bor natural son N e ga qarab shunday bo'lsinki, barcha natural n > N e uchun tengsizlik
| x n - a|< ε .
Bu yerda x n - n sonli ketma-ketlikning elementi. Ketma-ketlik chegarasi quyidagicha ifodalanadi:
.
Yoki da.

Tengsizlikni o'zgartiramiz:
;
;
.

e - nuqtaning qo'shnisi a - ochiq oraliq (a - e, a + e). Konvergent ketma-ketlik chegarasi bo'lgan ketma-ketlikdir. Shuningdek, ketma-ketligi aytiladi birlashadi a ga. Divergent ketma-ketlik chegarasi bo'lmagan ketma-ketlikdir.

Ta'rifdan kelib chiqadiki, agar ketma-ketlik a chegarasiga ega bo'lsa, u holda biz a nuqtaning qaysi e-qo'shnisini tanlamaylik, faqat yakuniy raqam ketma-ketlik elementlari yoki umuman yo'q ( bo'sh to'plam). Va har qanday e-mahalla cheksiz sonli elementlarni o'z ichiga oladi. Haqiqatan ham, ma'lum bir e sonini berganimizdan so'ng, biz raqamga ega bo'lamiz. Shunday qilib, raqamlar bilan ketma-ketlikning barcha elementlari, ta'rifiga ko'ra, a nuqtaning e - qo'shnisida joylashgan. Birinchi elementlar har qanday joyda joylashgan bo'lishi mumkin. Ya'ni, e-mahalladan tashqarida elementlardan ortiq bo'lishi mumkin emas - ya'ni chekli son.

Shuni ham ta'kidlaymizki, farq monoton ravishda nolga moyil bo'lishi shart emas, ya'ni har doim kamayishi kerak. U monoton bo'lmagan holda nolga moyil bo'lishi mumkin: u mahalliy maksimallarga ega bo'lgan ortishi yoki kamayishi mumkin. Biroq, bu maksimallar, n ortishi bilan, nolga moyil bo'lishi kerak (ehtimol monoton emas).

Borliq va universallikning mantiqiy belgilaridan foydalanib, chegara ta’rifini quyidagicha yozish mumkin:
(1) .

A ekanligini aniqlash chegara emas

Endi a soni ketma-ketlikning chegarasi emasligi haqidagi qarama-qarshi gapni ko'rib chiqing.

Raqam a ketma-ketlikning chegarasi emas, agar shunday bo'lsa, har qanday natural n soni uchun shunday natural m mavjud > n, Nima
.

Bu gapni mantiqiy belgilar yordamida yozamiz.
(2) .

Bayonot a raqami ketma-ketlikning chegarasi emas, shuni anglatadiki
siz shunday e - a nuqtaning qo'shnisini tanlashingiz mumkin, uning tashqarisida ketma-ketlikning cheksiz sonli elementlari bo'ladi..

Keling, bir misolni ko'rib chiqaylik. Umumiy elementli ketma-ketlik berilsin
(3)
Nuqtaning har qanday qo'shnisi cheksiz sonli elementlarni o'z ichiga oladi. Biroq, bu nuqta ketma-ketlikning chegarasi emas, chunki nuqtaning har qanday qo'shnisi ham cheksiz sonli elementlarni o'z ichiga oladi. Keling, e - nuqtaning e = bo'lgan qo'shnisini olaylik 1 . Bu interval bo'ladi (-1, +1) . Juft n ga ega bo'lgan birinchi elementdan tashqari barcha elementlar ushbu intervalga tegishli. Lekin toq n bo'lgan barcha elementlar bu oraliqdan tashqarida, chunki ular x n tengsizlikni qanoatlantiradi > 2 . Toq elementlarning soni cheksiz bo'lgani uchun, tanlangan mahalladan tashqarida cheksiz sonli elementlar bo'ladi. Shuning uchun nuqta ketma-ketlikning chegarasi emas.

Endi biz (2) bayonotiga qat'iy rioya qilgan holda buni ko'rsatamiz. Nuqta (3) ketma-ketlikning chegarasi emas, chunki har qanday natural n uchun tengsizlik o'rinli bo'lgan g'alati nuqta mavjud bo'ladi.
.

Har qanday a nuqta bu ketma-ketlikning chegarasi bo'la olmasligini ham ko'rsatish mumkin. Biz har doim a nuqtaning 0-nuqtasini ham, 2-nuqtasini ham o'z ichiga olmaydi e - qo'shniligini tanlashimiz mumkin. Va keyin tanlangan mahalladan tashqarida ketma-ketlikning cheksiz sonli elementlari bo'ladi.

Ketma-ketlik chegarasining ekvivalent ta'rifi

E - mahalla tushunchasini kengaytirsak, ketma-ketlik chegarasining ekvivalent ta'rifini berishimiz mumkin. Agar e-mahalla oʻrniga a nuqtaning istalgan qoʻshnisi boʻlsa, biz ekvivalent taʼrifni olamiz. Nuqtaning qo'shnisi - bu nuqtani o'z ichiga olgan har qanday ochiq oraliq. Matematik jihatdan nuqta qo'shnisi quyidagicha aniqlanadi: , bu yerda e 1 va e 2 - ixtiyoriy ijobiy sonlar.

Keyin chegaraning ekvivalent ta'rifi quyidagicha bo'ladi.

Ketma-ketlikning chegarasi a soni bo'lib, agar uning har qanday qo'shnisi uchun N natural son mavjud bo'lsa, sonli ketma-ketlikning barcha elementlari shu mahallaga tegishli bo'ladi.

Ushbu ta'rif kengaytirilgan shaklda ham taqdim etilishi mumkin.

Ketma-ketlik chegarasi har qanday musbat sonlar uchun a if soni bo'lib, unga bog'liq bo'lgan N natural soni mavjud bo'lib, tengsizliklar barcha natural sonlar uchun amal qiladi.
.

Ta'riflarning ekvivalentligini isbotlash

Yuqorida keltirilgan ketma-ketlik chegarasining ikkita ta'rifi ekvivalent ekanligini isbotlaylik.

Birinchi ta'rifga ko'ra a soni ketma-ketlikning chegarasi bo'lsin. Bu shuni anglatadiki, har qanday musbat e soni uchun quyidagi tengsizliklar bajariladigan funktsiya mavjud:
(4) da .

Ikkinchi ta'rif bilan a soni ketma-ketlikning chegarasi ekanligini ko'rsatamiz. Ya'ni, har qanday musbat sonlar uchun e bo'ladigan shunday funksiya borligini ko'rsatishimiz kerak 1 va e 2 quyidagi tengsizliklar qanoatlantiriladi:
(5) da .

Keling, ikkita ijobiy raqamga ega bo'lamiz: e 1 va e 2 . Ularning eng kichigi e bo'lsin: . Keyin; ; . Buni (5) da ishlatamiz:
.
Lekin tengsizliklar uchun qanoatlantiriladi. U holda (5) tengsizliklar uchun ham bajariladi.

Ya'ni, har qanday musbat e sonlar uchun (5) tengsizliklar qanoatlantiriladigan funksiya topdik. 1 va e 2 .
Birinchi qism isbotlangan.

Endi a soni ikkinchi ta'rifga ko'ra ketma-ketlikning chegarasi bo'lsin. Bu shuni anglatadiki, har qanday musbat sonlar uchun e bo'ladigan funksiya mavjud 1 va e 2 quyidagi tengsizliklar qanoatlantiriladi:
(5) da .

Birinchi ta'rif bo'yicha a soni ketma-ketlikning chegarasi ekanligini ko'rsatamiz. Buning uchun siz qo'yishingiz kerak. Keyin quyidagi tengsizliklar bajarilganda:
.
Bu bilan birinchi ta'rifga mos keladi.
Ta'riflarning ekvivalentligi isbotlangan.

Misollar

1-misol

Buni isbotlang.

(1) .
Bizning holatda;
.

.
Tengsizliklar xossalaridan foydalanamiz. Keyin agar va bo'lsa, keyin
.

.
Keyin
da .
Bu raqam berilgan ketma-ketlikning chegarasi ekanligini anglatadi:
.

2-misol

Ketma-ketlik chegarasining ta'rifidan foydalanib, buni isbotlang
.

Keling, ketma-ketlik chegarasining ta'rifini yozamiz:
(1) .
Bizning holatda,;
.

Ijobiy raqamlarni kiriting va:
.
Tengsizliklar xossalaridan foydalanamiz. Keyin agar va bo'lsa, keyin
.

Ya'ni, har qanday musbat uchun biz har qanday natural sondan katta yoki teng olishimiz mumkin:
.
Keyin
da .
.

3-misol

.

Biz belgini kiritamiz, .
Keling, farqni o'zgartiramiz:
.
Tabiiy n uchun = 1, 2, 3, ... bizda ... bor:
.

Keling, ketma-ketlik chegarasining ta'rifini yozamiz:
(1) .
Ijobiy raqamlarni kiriting va:
.
Keyin agar va bo'lsa, keyin
.

Ya'ni, har qanday musbat uchun biz har qanday natural sondan katta yoki teng olishimiz mumkin:
.
Qayerda
da .
Bu raqam ketma-ketlikning chegarasi ekanligini anglatadi:
.

4-misol

Ketma-ketlik chegarasining ta'rifidan foydalanib, buni isbotlang
.

Keling, ketma-ketlik chegarasining ta'rifini yozamiz:
(1) .
Bizning holatda,;
.

Ijobiy raqamlarni kiriting va:
.
Keyin agar va bo'lsa, keyin
.

Ya'ni, har qanday musbat uchun biz har qanday natural sondan katta yoki teng olishimiz mumkin:
.
Keyin
da .
Bu raqam ketma-ketlikning chegarasi ekanligini anglatadi:
.

Adabiyotlar:
L.D. Kudryavtsev. Matematik tahlil kursi. 1-jild. Moskva, 2003 yil.
SM. Nikolskiy. Matematik tahlil kursi. 1-jild. Moskva, 1983 yil.

Shuningdek qarang:

Geyne (ketma-ketliklar orqali) va Koshi bo‘yicha (epsilon va delta mahallalari orqali) funksiya chegarasining ta’riflari berilgan. Ta'riflar universal shaklda berilgan bo'lib, ular cheklangan va cheksiz uzoq nuqtalarda ikki tomonlama va bir tomonlama chegaralarga nisbatan qo'llaniladi. a nuqta funktsiyaning chegarasi emasligi ta'rifi ko'rib chiqiladi. Geyne va Koshi ta'riflarining ekvivalentligini isbotlash.

Tarkib

Shuningdek qarang: Bir nuqtaning qo'shnisi
Funksiyaning oxirgi nuqtadagi chegarasini aniqlash
Funksiyaning cheksizlikdagi chegarasini aniqlash

Funktsiya chegarasining birinchi ta'rifi (Geyne bo'yicha)

(x) x nuqtada 0 :
,
Agar
1) x nuqtaning shunday teshilgan qo'shnisi bor 0
2) har qanday ketma-ketlik uchun (xn), x ga yaqinlashish 0 :
, uning elementlari mahallaga tegishli,
keyingi ketma-ketlik (f(xn)) ga birlashadi:
.

Bu erda x 0 a esa chekli sonlar yoki cheksizlikdagi nuqtalar bo‘lishi mumkin. Mahalla ikki tomonlama yoki bir tomonlama bo'lishi mumkin.

.

Funktsiya chegarasining ikkinchi ta'rifi (Koshi bo'yicha)

a soni f funksiyaning chegarasi deyiladi (x) x nuqtada 0 :
,
Agar
1) x nuqtaning shunday teshilgan qo'shnisi bor 0 , bunda funksiya aniqlanadi;
2) har qanday musbat son e uchun > 0 d e shunday raqam mavjud > 0 , e ga qarab, teshilgan d e ga tegishli barcha x uchun x nuqtaning qo'shnisi 0 :
,
funktsiya qiymatlari f (x) a nuqtaning e-mahallasiga tegishli:
.

X ball 0 a esa chekli sonlar yoki cheksizlikdagi nuqtalar bo‘lishi mumkin. Mahalla ham ikki tomonlama yoki bir tomonlama bo'lishi mumkin.

Keling, mavjudlik va universallikning mantiqiy belgilaridan foydalanib, ushbu ta'rifni yozamiz:
.

Ushbu ta'rifda uchlari bir xil masofada joylashgan mahallalar qo'llaniladi. Ekvivalent ta'rif nuqtalarning ixtiyoriy qo'shnilari yordamida berilishi mumkin.

O'zboshimchalik bilan qo'shnilar yordamida ta'rif
a soni f funksiyaning chegarasi deyiladi (x) x nuqtada 0 :
,
Agar
1) x nuqtaning shunday teshilgan qo'shnisi bor 0 , bunda funksiya aniqlanadi;
2) har qanday mahalla U uchun (a) a nuqtaning x nuqtasining shunday teshilgan qo'shnisi bor 0 bu x nuqtaning teshilgan qo'shnisiga tegishli barcha x uchun 0 :
,
funktsiya qiymatlari f (x) U mahallasiga tegishli (a) a nuqtalari:
.

Borliq va universallikning mantiqiy belgilaridan foydalanib, bu ta’rifni quyidagicha yozish mumkin:
.

Bir tomonlama va ikki tomonlama chegaralar

Yuqoridagi ta'riflar universaldir, chunki ular har qanday turdagi mahalla uchun ishlatilishi mumkin. Agar biz oxirgi nuqtaning chap qirrali teshilgan qo'shnisi sifatida foydalansak, biz chap tomonli chegaraning ta'rifini olamiz. Agar biz cheksizlikdagi nuqtaning qo'shniligini qo'shni sifatida ishlatsak, cheksizlikdagi chegara ta'rifini olamiz.

Geyne chegarasini aniqlash uchun bu ga yaqinlashuvchi ixtiyoriy ketma-ketlikka qo'shimcha cheklov qo'yilganligidan kelib chiqadi: uning elementlari nuqtaning mos keladigan teshilgan qo'shnisiga tegishli bo'lishi kerak.

Koshi chegarasini aniqlash uchun har bir holatda nuqta qo'shnisining tegishli ta'riflaridan foydalangan holda ifodalarni va tengsizliklarga aylantirish kerak.
"Nuqtaning qo'shnisi" ga qarang.

Bu a nuqtani aniqlash funksiyaning chegarasi emas

Ko'pincha a nuqtasi funksiyaning chegarasi emas, degan shartdan foydalanish kerak bo'ladi. Keling, yuqoridagi ta'riflarga inkorlar tuzamiz. Ularda f funksiyasi deb faraz qilamiz (x) x nuqtaning ba'zi bir teshilgan qo'shnisida aniqlanadi 0 . a va x nuqtalari 0 chekli sonlar yoki cheksiz masofali bo'lishi mumkin. Quyida aytilganlarning barchasi ikki tomonlama va bir tomonlama chegaralarga taalluqlidir.

Geynega ko'ra.
Raqam a emas funktsiya chegarasi f (x) x nuqtada 0 : ,
agar bunday ketma-ketlik mavjud bo'lsa (xn), x ga yaqinlashish 0 :
,
uning elementlari mahallaga tegishli bo'lsa,
ketma-ketligi qanday (f(xn)) ga yaqinlashmaydi:
.
.

Koshiga ko'ra.
Raqam a emas funktsiya chegarasi f (x) x nuqtada 0 :
,
agar shunday ijobiy raqam bo'lsa e > 0 , shuning uchun har qanday musbat d soni uchun > 0 , x nuqtasining teshilgan d-mahallasiga tegishli x mavjud. 0 :
,
funktsiyaning qiymati f (x) a nuqtaning e-mahallasiga tegishli emas:
.
.

Albatta, agar a nuqta funksiyaning chegarasi bo'lmasa, bu uning chegarasi bo'lishi mumkin emas degani emas. Cheklov bo'lishi mumkin, lekin u a ga teng emas. Funktsiya nuqtaning teshilgan qo'shnisida aniqlangan bo'lishi ham mumkin, lekin chegarasi yo'q.

Funktsiya f(x) = sin(1/x) x → 0 kabi chegarasi yo'q.

Misol uchun, funktsiya da belgilangan, lekin hech qanday chegara yo'q. Buni isbotlash uchun keling, ketma-ketlikni olaylik. Bir nuqtaga yaqinlashadi 0 : . Chunki, keyin.
Keling, ketma-ketlikni olaylik. Shuningdek, u nuqtaga yaqinlashadi 0 : . Lekin o'shandan beri.
U holda chegara hech qanday a soniga teng bo'lishi mumkin emas. Darhaqiqat, uchun , qaysi bilan ketma-ketlik bor. Shuning uchun, nolga teng bo'lmagan har qanday raqam chegara emas. Ammo bu ham chegara emas, chunki ketma-ketlik mavjud.

Limitning Geyne va Koshi ta'riflarining ekvivalentligi

Teorema
Funksiya chegarasining Geyn va Koshi ta’riflari ekvivalentdir.

Isbot

Isbotda biz funktsiya nuqtaning ba'zi bir teshilgan qo'shnisida (cheklangan yoki cheksizlikda) aniqlangan deb faraz qilamiz. A nuqtasi ham chekli yoki cheksiz bo'lishi mumkin.

Geynning isboti ⇒ Koshining isboti

Birinchi ta'rifga ko'ra (Geyne bo'yicha) funktsiya nuqtada a chegarasiga ega bo'lsin. Ya'ni, nuqtaning teshilgan qo'shnisiga tegishli va chegaraga ega bo'lgan har qanday ketma-ketlik uchun
(1) ,
ketma-ketlikning chegarasi:
(2) .

Funktsiyaning bir nuqtada Koshi chegarasi borligini ko'rsataylik. Ya'ni, hamma uchun hamma uchun nimadir bor.

Buning aksini faraz qilaylik. (1) va (2) shartlar bajarilsin, lekin funksiya Koshi chegarasiga ega emas. Ya'ni, har kim uchun mavjud bo'lgan narsa bor, shuning uchun
.

ni olaylik, bu yerda n natural son. Keyin mavjud va
.
Shunday qilib, ga yaqinlashuvchi ketma-ketlikni tuzdik, lekin ketma-ketlikning chegarasi a ga teng emas. Bu teorema shartlariga ziddir.

Birinchi qism isbotlangan.

Koshining isboti ⇒ Geynning isboti

Funksiya ikkinchi ta'rifga ko'ra (Koshi bo'yicha) nuqtada a chegarasiga ega bo'lsin. Ya'ni, har kim uchun bu mavjud
(3) Barcha uchun .

Funktsiyaning Geynega ko'ra nuqtada a chegarasi borligini ko'rsataylik.
Keling, ixtiyoriy raqamni olaylik. Koshi ta'rifiga ko'ra, raqam mavjud, shuning uchun (3) o'rinli.

Teshilgan mahallaga tegishli va ga yaqinlashuvchi ixtiyoriy ketma-ketlikni olaylik. Konvergent ketma-ketlikning ta'rifiga ko'ra, har qanday kishi uchun bu mavjud
da .
Keyin (3) dan shunday keladi
da .
Chunki bu har kimga tegishli
.

Teorema isbotlangan.

Adabiyotlar:
L.D. Kudryavtsev. Matematik tahlil kursi. 1-jild. Moskva, 2003 yil.

Shuningdek qarang:

Bugun sinfda biz ko'rib chiqamiz qat'iy ketma-ketlik Va funktsiya chegarasining qat'iy ta'rifi, shuningdek, nazariy xarakterdagi dolzarb masalalarni yechishni o'rganadi. Maqola, birinchi navbatda, matematik tahlil nazariyasini o'rganishni boshlagan va oliy matematikaning ushbu bo'limini tushunishda qiyinchiliklarga duch kelgan tabiiy fanlar va muhandislik mutaxassisliklarining birinchi kurs talabalari uchun mo'ljallangan. Bundan tashqari, material o'rta maktab o'quvchilari uchun juda qulay.

Sayt mavjud bo'lgan yillar davomida menga taxminan quyidagi mazmundagi o'nlab xatlar keldi: "Men matematik tahlilni yaxshi tushunmayapman, nima qilishim kerak?", "Men matematikani umuman tushunmayman, men o'qishni to'xtatish haqida o'ylash" va boshqalar. Darhaqiqat, birinchi mashg'ulotdan keyin talabalar guruhini tez-tez yupqalashtiradigan matandir. Nima uchun bu shunday? Chunki mavzu tasavvur qilib bo'lmaydigan darajada murakkabmi? Umuman yo'q! Matematik tahlil nazariyasi o'ziga xos bo'lganidek qiyin emas. Va siz uni kimligi uchun qabul qilishingiz va sevishingiz kerak =)

Eng qiyin holatdan boshlaylik. Birinchi va eng muhimi, siz o'qishdan voz kechishingiz shart emas. To'g'ri tushuning, siz har doim ham ketishingiz mumkin;-) Albatta, agar bir yoki ikki yildan keyin siz tanlagan mutaxassisligingizdan kasal bo'lib qolsangiz, ha, bu haqda o'ylashingiz kerak. (va g'azablanmang!) faoliyatning o'zgarishi haqida. Ammo hozircha buni davom ettirishga arziydi. Iltimos, "Men hech narsani tushunmayapman" iborasini unuting - siz umuman hech narsani tushunmaysiz.

Agar nazariya yomon bo'lsa, nima qilish kerak? Aytgancha, bu nafaqat matematik tahlilga tegishli. Agar nazariya yomon bo'lsa, birinchi navbatda siz amaliyotga jiddiy e'tibor qaratishingiz kerak. Bunday holda, bir vaqtning o'zida ikkita strategik vazifa hal qilinadi:

– Birinchidan, muhim ulush nazariy bilim amaliyot orqali yuzaga kelgan. Va shuning uchun ko'p odamlar nazariyani ... orqali tushunishadi - bu to'g'ri! Yo'q, yo'q, siz bu haqda o'ylamaysiz =)

- Va, ikkinchidan, amaliy ko'nikmalar sizni imtihondan o'tkazishi mumkin, hattoki ... lekin bu qadar hayajonlanmaylik! Hamma narsa haqiqiy va hamma narsani juda qisqa vaqt ichida "ko'tarish" mumkin. Matematik tahlil - bu oliy matematikaning eng sevimli bo'limi, shuning uchun men sizga yordam qo'lini bermay qo'ya olmadim:

1-semestr boshida, odatda, ketma-ketlik chegaralari va funktsiyalar chegaralari qoplanadi. Bu nima ekanligini tushunmayapsizmi va ularni qanday hal qilishni bilmayapsizmi? Maqola bilan boshlang Funktsiya chegaralari, unda kontseptsiyaning o'zi "barmoqlarda" ko'rib chiqiladi va eng oddiy misollar tahlil qilinadi. Keyinchalik, mavzu bo'yicha boshqa darslar, jumladan, haqida dars bilan ishlang ketma-ketliklar ichida, Men aslida qat'iy ta'rifni ishlab chiqqanman.

Tengsizlik belgilari va moduldan tashqari qanday belgilarni bilasiz?

- uzun vertikal tayoq quyidagicha o'qiydi: "bunday", "bunday", "bunday" yoki "bunday", bizning holatlarimizda, aniqki, biz raqam haqida gapiramiz - shuning uchun "bunday";

– dan katta bo‘lgan barcha “en” uchun;

– modul belgisi masofani bildiradi, ya'ni. Ushbu yozuv bizga qiymatlar orasidagi masofa epsilondan kamroq ekanligini aytadi.

Xo'sh, bu halokatli qiyinmi? =)

Amaliyotni o'zlashtirgandan so'ng, sizni keyingi paragrafda ko'rishni orziqib kutaman:

Va aslida, keling, bir oz o'ylab ko'raylik - ketma-ketlikning qat'iy ta'rifini qanday shakllantirish kerak? ...Dunyoda birinchi bo‘lib aqlga kelgan narsa amaliy dars: "ketma-ketlik chegarasi - ketma-ketlik a'zolari cheksiz yaqinlashadigan son."

Mayli, yozamiz keyingi ketma-ketlik :

Buni tushunish qiyin emas keyingi ketma-ketlik –1 soniga cheksiz yaqinlik va juft sonli hadlar - "bir" ga.

Yoki ikkita chegara bormi? Ammo nega hech qanday ketma-ketlikda ulardan o'n yoki yigirmatasi bo'lishi mumkin emas? Siz bu yo'ldan uzoqqa borishingiz mumkin. Shu munosabat bilan, deb taxmin qilish mantiqan to'g'ri keladi agar ketma-ketlik chegarasiga ega bo'lsa, u yagonadir.

Eslatma : ketma-ketlikning chegarasi yo'q, lekin undan ikkita kichik ketma-ketlikni ajratish mumkin (yuqoriga qarang), ularning har biri o'z chegarasiga ega.

Shunday qilib, yuqoridagi ta'rif asossiz bo'lib chiqadi. Ha, u kabi holatlar uchun ishlaydi (amaliy misollarning soddalashtirilgan tushuntirishlarida men unchalik to'g'ri foydalanmadim), lekin endi biz qat'iy ta'rifni topishimiz kerak.

Ikkinchi urinish: "ketma-ketlik chegarasi - bu ketma-ketlikning BARCHA a'zolari yaqinlashadigan raqam, ehtimol ularning sonidan tashqari. final miqdorlar." Bu haqiqatga yaqinroq, ammo baribir to'liq aniq emas. Shunday qilib, masalan, ketma-ketlik atamalarning yarmi umuman nolga yaqinlashmaydi - ular shunchaki unga teng =) Aytgancha, "miltillovchi chiroq" odatda ikkita sobit qiymatni oladi.

Formulyatsiyani aniqlashtirish qiyin emas, lekin keyin yana bir savol tug'iladi: ta'rifni qanday yozish kerak matematik belgilar? Ilmiy dunyo Vaziyatni hal qilgunimcha, men bu muammo bilan uzoq vaqt kurashdim mashhur maestro, bu mohiyatan klassik matematik tahlilni butun jiddiyligi bilan rasmiylashtirgan. Koshi jarrohlik amaliyotini taklif qildi atrof-muhit , bu nazariyani sezilarli darajada ilgari surdi.

Ba'zi bir nuqtani ko'rib chiqing va uning o'zboshimchalik bilan-atrof:

"Epsilon" qiymati har doim ijobiydir va bundan tashqari, uni o'zimiz tanlashga haqlimiz. Faraz qilaylik, bu mahallada ko'plab a'zolar bor (hammasi shart emas) ba'zi ketma-ketlik. Masalan, o'ninchi davr mahallada ekanligini qanday yozish kerak? Uning o'ng tomonida bo'lsin. Keyin nuqtalar orasidagi masofa va "epsilon" dan kam bo'lishi kerak: . Biroq, agar "x o'ninchi" "a" nuqtasining chap tomonida joylashgan bo'lsa, farq salbiy bo'ladi va shuning uchun unga belgi qo'shilishi kerak. modul: .

Ta'rif: agar raqam ketma-ketlikning chegarasi deyiladi har qanday uchun uning atrofi (oldindan tanlangan) BUNDAY natural son bor HAMMA Yuqori raqamlarga ega bo'lgan ketma-ketlik a'zolari mahalla ichida bo'ladi:

Yoki qisqasi: agar

Boshqacha qilib aytganda, “epsilon” qiymati qanchalik kichik bo'lmasin, ertami-kechmi ketma-ketlikning “cheksiz dumi” TO'LIMI shu mahallada bo'ladi.

Misol uchun, ketma-ketlikning "cheksiz dumi" nuqtaning har qanday o'zboshimchalik bilan kichik mahallasiga to'liq kiradi. Demak, bu qiymat ta'rif bo'yicha ketma-ketlikning chegarasidir. Eslatib o'taman, chegarasi nolga teng bo'lgan ketma-ketlik chaqiriladi cheksiz kichik.

Shuni ta'kidlash kerakki, ketma-ketlik uchun endi "cheksiz dum" deyish mumkin emas. kirib keladi“- toq sonli a’zolar aslida nolga teng va “hech qaerga bormang” =) Shuning uchun ta’rifda “paydo bo’ladi” fe’li ishlatilgan. Va, albatta, bu kabi ketma-ketlik a'zolari ham "hech qaerga bormaydilar". Aytgancha, raqam uning chegarasi yoki yo'qligini tekshiring.

Endi biz ketma-ketlikning chegarasi yo'qligini ko'rsatamiz. Misol uchun, nuqta qo'shnisini ko'rib chiqing. Ma'lum bir mahallada BARCHA atamalar tugaydigan bunday raqam yo'qligi aniq - toq atamalar har doim "minus bir" ga "sakrab chiqadi". Xuddi shunday sababga ko'ra, nuqtada hech qanday chegara yo'q.

Keling, materialni amaliyot bilan birlashtiramiz:

1-misol

Ketma-ketlik chegarasi nolga teng ekanligini isbotlang. Nuqtaning istalgan kichik mahallasida ketma-ketlikning barcha a'zolariga kafolat beriladigan raqamni ko'rsating.

Eslatma : Ko'p ketma-ketliklar uchun kerakli natural son qiymatga bog'liq - shuning uchun yozuv .

Yechim: o'ylab ko'ring o'zboshimchalik bilan bormi raqam - shunday qilib, raqamlari yuqori bo'lgan HAMMA a'zolar shu mahallada bo'ladi:

Kerakli sonning mavjudligini ko'rsatish uchun uni orqali ifodalaymiz.

“en” ning istalgan qiymati uchun modul belgisi olib tashlanishi mumkin:

Biz sinfda takrorlagan tengsizliklar bilan "maktab" harakatlaridan foydalanamiz Chiziqli tengsizliklar Va Funktsiya domeni. Bunday holda, "epsilon" va "en" ijobiy bo'lishi muhim holat:

Chapda biz natural sonlar haqida gapiramiz, va o'ng qism V umumiy holat kasr bo'lsa, uni yaxlitlash kerak:

Eslatma : ba'zan xavfsiz tomonda bo'lish uchun o'ngga birlik qo'shiladi, lekin aslida bu ortiqcha. Nisbatan aytganda, agar yaxlitlash orqali natijani zaiflashtirsak, eng yaqin mos raqam ("uch") asl tengsizlikni qondiradi.

Endi biz tengsizlikni ko'rib chiqamiz va dastlab nimani ko'rib chiqqanimizni eslaymiz o'zboshimchalik bilan-mahalla, ya'ni. "epsilon" ga teng bo'lishi mumkin har kim ijobiy raqam.

Xulosa: nuqtaning har qanday ixtiyoriy kichik -qo'shnisi uchun qiymat topildi . Shunday qilib, raqam ta'rifi bo'yicha ketma-ketlikning chegarasidir. Q.E.D.

Aytgancha, olingan natijadan tabiiy naqsh aniq ko'rinadi: mahalla qanchalik kichik bo'lsa, raqam shunchalik katta bo'ladi, shundan so'ng ketma-ketlikning HAMMA a'zolari shu mahallada bo'ladi. Ammo "epsilon" qanchalik kichik bo'lmasin, har doim ichida "cheksiz dum" bo'ladi va tashqarida - hatto katta bo'lsa ham, lekin final a'zolar soni.

Taassurotlaringiz qanday? =) Men bu biroz g'alati ekanligiga qo'shilaman. Lekin qat'iy! Iltimos, qayta o'qing va hamma narsani yana o'ylab ko'ring.

Keling, shunga o'xshash misolni ko'rib chiqaylik va boshqalar bilan tanishamiz texnik usullar:

2-misol

Yechim: ketma-ketlikning ta'rifi bilan buni isbotlash kerak (baland ovozda ayting!!!).

Keling, ko'rib chiqaylik o'zboshimchalik bilan-punkt va chekning qo'shniligi; mavjudmi natural son - shundayki, barcha katta sonlar uchun quyidagi tengsizlik amal qiladi:

Bundaylarning mavjudligini ko'rsatish uchun siz "epsilon" orqali "en" ni ifodalashingiz kerak. Modul belgisi ostidagi ifodani soddalashtiramiz:

Modul minus belgisini yo'q qiladi:

Maxraj har qanday "en" uchun ijobiydir, shuning uchun tayoqlarni olib tashlash mumkin:

Aralash:

Endi biz chiqarib olishimiz kerak Kvadrat ildiz, lekin ushlash shundaki, ba'zi "epsilon" uchun o'ng tomon salbiy bo'ladi. Ushbu muammodan qochish uchun mustahkamlaymiz modul bo'yicha tengsizlik:

Nima uchun buni qilish mumkin? Agar nisbatan aytganda, shunday bo'lib chiqsa, u holda shart ham qondiriladi. Modul mumkin shunchaki oshiring kerakli raqam va bu bizga ham mos keladi! Taxminan aytganda, agar yuzinchi mos bo'lsa, ikki yuzinchi ham mos keladi! Ta'rifga ko'ra, siz ko'rsatishingiz kerak raqamning mavjudligi haqiqati(hech bo'lmaganda ba'zi), shundan keyin ketma-ketlikning barcha a'zolari -mahallada bo'ladi. Aytgancha, shuning uchun biz o'ng tomonni yuqoriga qarab yakuniy yaxlitlashdan qo'rqmaymiz.

Ildizni ajratib olish:

Va natijani aylantiring:

Xulosa: chunki "epsilon" qiymati o'zboshimchalik bilan tanlangan, keyin nuqtaning har qanday o'zboshimchalik bilan kichik qo'shnisi uchun qiymat topilgan. , shunday qilib, barcha katta raqamlar uchun tengsizlik o'rinli bo'ladi . Shunday qilib, a-prior. Q.E.D.

maslahat beraman ayniqsa tengsizliklarning kuchayishi va zaiflashishini tushunish matematik tahlilda odatiy va juda keng tarqalgan texnikadir. Kuzatishingiz kerak bo'lgan yagona narsa - bu yoki boshqa harakatning to'g'riligi. Masalan, tengsizlik hech qanday sharoitda mumkin emas bo'shatmoq, ayirish, aytaylik, bir:

Shunga qaramay, shartli ravishda: agar raqam to'liq mos kelsa, avvalgisi endi mos kelmasligi mumkin.

Mustaqil yechim uchun quyidagi misol:

3-misol

Ketma-ketlik ta'rifidan foydalanib, buni isbotlang

Dars oxirida qisqacha yechim va javob.

Agar ketma-ketlik cheksiz katta, u holda chegaraning ta'rifi shunga o'xshash tarzda tuziladi: nuqta ketma-ketlikning chegarasi deb ataladi, agar mavjud bo'lsa, xohlaganingizcha katta soni, shunday raqam borki, barcha katta raqamlar uchun tengsizlik qondiriladi. Raqam chaqiriladi "ortiqcha cheksizlik" nuqtasiga yaqinlik:

Boshqacha aytganda, nima bo'lishidan qat'iy nazar katta ahamiyatga ega Nima bo'lishidan qat'iy nazar, ketma-ketlikning "cheksiz dumi" albatta nuqtaning qo'shni qismiga kiradi va chap tomonda faqat cheklangan sonli atamalar qoladi.

Standart misol:

Va qisqartirilgan belgi: , agar

Vaziyat uchun ta'rifni o'zingiz yozing. To'g'ri versiya dars oxirida.

Amaliy misollar bilan tanishganingizdan va ketma-ketlik chegarasining ta'rifini aniqlaganingizdan so'ng, siz hisob bo'yicha adabiyotlarga va/yoki ma'ruza daftaringizga murojaat qilishingiz mumkin. Men Bohanning 1 jildini yuklab olishni tavsiya qilaman (oddiyroq - sirtqi talabalar uchun) va Fichtenholtz (batafsilroq va batafsil). Boshqa mualliflar qatorida men Piskunovni tavsiya qilaman, uning kursi texnik universitetlarga qaratilgan.

Ketma-ketlik chegarasi, ularning dalillari, oqibatlariga tegishli teoremalarni vijdonan o'rganishga harakat qiling. Dastlab, nazariya "bulutli" bo'lib tuyulishi mumkin, ammo bu normal holat - siz shunchaki ko'nikishingiz kerak. Va ko'pchilik buning ta'mini his qiladi!

Funktsiya chegarasining qat'iy ta'rifi

Keling, xuddi shu narsadan boshlaylik - bu kontseptsiyani qanday shakllantirish kerak? Funktsiya chegarasining og'zaki ta'rifi ancha sodda tarzda ifodalangan: "agar "x" ga moyil bo'lsa, son - bu funktsiyaning chegarasi. (chap va o'ng), mos keladigan funktsiya qiymatlari » (rasmga qarang). Hamma narsa normaldek tuyuladi, lekin so'zlar - so'zlar, ma'no - ma'no, piktogramma - bu piktogramma va etarli darajada qattiq matematik belgilar mavjud emas. Va ikkinchi xatboshida biz ushbu masalani hal qilishning ikkita yondashuvi bilan tanishamiz.

Funktsiya ma'lum bir oraliqda aniqlansin, mumkin bo'lgan nuqtadan tashqari. IN o'quv adabiyoti funksiya borligi umumiy qabul qilingan Yo'q belgilangan:

Bu tanlov ta'kidlaydi funksiya chegarasining mohiyati: "x" cheksiz yaqin yondashuvlar va funksiyaning mos qiymatlari cheksiz yaqin ga. Boshqacha qilib aytadigan bo'lsak, chegara tushunchasi nuqtalarga "aniq yondashuv" ni anglatmaydi, balki aniq cheksiz yaqinlik, funktsiyaning nuqtada aniqlangan yoki aniqlanmaganligi muhim emas.

Funktsiya chegarasining birinchi ta'rifi, ajablanarli emas, ikkita ketma-ketlik yordamida tuzilgan. Birinchidan, tushunchalar o'zaro bog'liq, ikkinchidan, funktsiyalar chegaralari odatda ketma-ketlik chegaralaridan keyin o'rganiladi.

Ketma-ketlikni ko'rib chiqing ball (chizmada emas), intervalga tegishli Va dan farqli, qaysi birlashadi ga. Keyin mos keladigan funktsiya qiymatlari ham a'zolari ordinata o'qida joylashgan sonli ketma-ketlikni hosil qiladi.

Geyne bo'yicha funksiya chegarasi har qanday uchun nuqtalar ketma-ketligi (tegishli va undan farqli) nuqtaga yaqinlashadigan , funktsiya qiymatlarining mos keladigan ketma-ketligi ga yaqinlashadi.

Eduard Geyne - nemis matematiki. ...Bunday o'ylashning hojati yo'q, Evropada faqat bitta gey bor - Gey-Lyussak =)

Limitning ikkinchi ta'rifi yaratildi... ha, ha, siz haqsiz. Lekin birinchi navbatda uning dizaynini tushunaylik. Nuqtaning o'zboshimchalik bilan qo'shniligini ko'rib chiqing ("qora" mahalla). Oldingi paragrafga asoslanib, yozuv shuni anglatadiki ba'zi qiymat funksiya "epsilon" mahallasida joylashgan.

Endi berilgan -mahallaga mos keladigan -mahallani topamiz (qora nuqtali chiziqlarni aqliy ravishda chapdan o'ngga, so'ngra yuqoridan pastga qarating). E'tibor bering, qiymat tanlangan kichikroq segmentning uzunligi bo'ylab, bu holda - qisqaroq chap segmentning uzunligi bo'ylab. Bundan tashqari, "malina" - nuqtaning qo'shnisi hatto qisqartirilishi mumkin, chunki quyidagi ta'rifda mavjudligi haqiqatining o'zi muhimdir bu mahalla. Va shunga o'xshab, belgi "delta" mahallasida qandaydir qiymat mavjudligini anglatadi.

Koshi funktsiyasi chegarasi: son funksiyaning nuqtadagi chegarasi deyiladi if har qanday uchun oldindan tanlangan Turar joy dahasi (siz xohlagancha kichik), mavjud- nuqta qo'shnisi, BUNDAY, bu: FAQAT qadriyatlar sifatida (tegishli) ushbu hududga kiritilgan: (qizil o'qlar)- SHUNDAN DARXOL mos funksiya qiymatlari qo'shni hududga kirishi kafolatlanadi: (ko'k o'qlar).

Men sizni ogohlantirishim kerakki, tushunarli bo'lishi uchun men biroz improvizatsiya qildim, shuning uchun ortiqcha ishlatmang =)

Qisqa yozuv: , agar

Ta'rifning mohiyati nimada? Majoziy ma'noda, qo'shnichilikni cheksiz kamaytirish orqali biz funktsiya qiymatlariga o'z chegarasigacha "hamrohlik qilamiz" va ularga boshqa joyga yaqinlashishga muqobil bo'lmaymiz. Juda g'ayrioddiy, lekin yana qat'iy! Fikrni to'liq tushunish uchun so'zlarni qayta o'qing.

! Diqqat: agar siz faqat shakllantirishingiz kerak bo'lsa Geyne ta'rifi yoki shunchaki Koshi ta'rifi iltimos unutmang muhim dastlabki mulohazalar: "Ma'lum bir oraliqda aniqlangan funktsiyani ko'rib chiqing, ehtimol nuqtadan tashqari". Men buni boshida bir marta aytdim va har safar takrorlamadim.

Matematik tahlilning tegishli teoremasiga ko'ra, Geyn va Koshi ta'riflari ekvivalentdir, ammo ikkinchi variant eng mashhurdir. (hali ham bo'lardi!), bu "til chegarasi" deb ham ataladi:

4-misol

Limit ta'rifidan foydalanib, buni isbotlang

Yechim: funktsiya nuqtadan tashqari butun son chizig'ida aniqlanadi. Ta'rifdan foydalanib, biz berilgan nuqtada chegara mavjudligini isbotlaymiz.

Eslatma : "delta" mahallasining qiymati "epsilon" ga bog'liq, shuning uchun belgilash

Keling, ko'rib chiqaylik o'zboshimchalik bilan-atrof. Vazifa bu qiymatdan foydalanish yoki yo'qligini tekshirishdir mavjudmi-atrof, BUNDAY, bu tengsizlikdan tengsizlik kelib chiqadi .

deb faraz qilsak, oxirgi tengsizlikni o'zgartiramiz:
(kvadrat uchburchakni kengaytirdi)

Ta'rif 1. Mayli E- cheksiz son. Agar biron bir mahalla to'plamning nuqtalarini o'z ichiga olsa E, nuqtadan farq qiladi A, Bu A chaqirdi yakuniy to'plamning nuqtasi E.

Ta'rif 2. (Genrix Geyne (1821-1881)). Funktsiyaga ruxsat bering
to'plamda aniqlanadi X Va A chaqirdi chegara funktsiyalari
nuqtada (yoki qachon
, agar argument qiymatlarining har qanday ketma-ketligi uchun
, ga yaqinlashish , funktsiya qiymatlarining mos keladigan ketma-ketligi raqamga yaqinlashadi A. Ular yozadilar:
.

Misollar. 1) Funktsiya
ga teng chegaraga ega Bilan, raqamlar chizig'ining istalgan nuqtasida.

Darhaqiqat, har qanday nuqta uchun va argument qiymatlarining har qanday ketma-ketligi
, ga yaqinlashish va boshqa raqamlardan iborat , funktsiya qiymatlarining mos keladigan ketma-ketligi shaklga ega
, va biz bilamizki, bu ketma-ketlik ga yaqinlashadi Bilan. Shunung uchun
.

2) Funktsiya uchun

.

Bu aniq, chunki agar
, keyin
.

3) Dirixle funktsiyasi
hech qanday nuqtada chegarasi yo'q.

Haqiqatan ham, ruxsat bering
Va
, va hammasi - ratsional sonlar. Keyin
Barcha uchun n, Shunung uchun
. Agar
va tamom ular irratsional sonlardir
Barcha uchun n, Shunung uchun
. 2-ta'rifning shartlari qoniqtirilmaganligini ko'ramiz
mavjud emas.

4)
.

Haqiqatan ham, keling, ixtiyoriy ketma-ketlikni olaylik
, ga yaqinlashish

soni 2. Keyin . Q.E.D.

Ta'rif 3. (Koshi (1789-1857)). Funktsiyaga ruxsat bering
to'plamda aniqlanadi X Va bu to'plamning chegara nuqtasidir. Raqam A chaqirdi chegara funktsiyalari
nuqtada (yoki qachon
, agar mavjud bo'lsa
bo'ladi
, shunday qilib, argumentning barcha qiymatlari uchun X, tengsizlikni qondirish

,

tengsizlik haqiqatdir

.

Ular yozadilar:
.

Koshining ta'rifi mahallalar yordamida ham berilishi mumkin, agar shuni ta'kidlasak, a:

funksiyasiga ruxsat bering
to'plamda aniqlanadi X Va bu to'plamning chegara nuqtasidir. Raqam A chegara deb ataladi funktsiyalari
nuqtada , agar mavjud bo'lsa - nuqta qo'shnisi A
teshilgani bor - nuqta qo'shnisi
,shu kabi
.

Ushbu ta'rifni chizma bilan tasvirlash foydalidir.

Misol 5.
.

Haqiqatan ham, olaylik
tasodifiy va toping
, hamma uchun shunday X, tengsizlikni qondirish
tengsizlik mavjud
. Oxirgi tengsizlik tengsizlikka teng
, shuning uchun biz olish uchun etarli ekanligini ko'ramiz
. Bayonot isbotlangan.

Yarmarka

Teorema 1. Geyne va Koshi bo'yicha funksiya limitining ta'riflari ekvivalentdir.

Isbot. 1) Mayli
Koshiga ko'ra. Xuddi shu son Geynega ko'ra chegara ekanligini isbotlaylik.

Keling, olamiz
o'zboshimchalik bilan. 3-ta'rifga ko'ra mavjud
, hamma uchun shunday
tengsizlik mavjud
. Mayli
– shunday ixtiyoriy ketma-ketlik
da
. Keyin raqam bor N hamma uchun shunday
tengsizlik mavjud
, Shunung uchun
Barcha uchun
, ya'ni.

Geynega ko'ra.

2) Keling
Geynega ko'ra. Keling, buni isbotlaylik
va Koshiga ko'ra.

Keling, buning aksini faraz qilaylik, ya'ni. Nima
Koshiga ko'ra. Keyin bor
har kim uchun shunday
bo'ladi
,
Va
. Ketma-ketlikni ko'rib chiqing
. Belgilanganlar uchun
va har qanday n mavjud

Va
. Bu shuni anglatadiki
, Garchi
, ya'ni. raqam A chegara emas
nuqtada Geynega ko'ra. Biz qarama-qarshilikni qo'lga kiritdik, bu bayonotni tasdiqlaydi. Teorema isbotlangan.

Teorema 2 (chegaraning o'ziga xosligi bo'yicha). Agar biror nuqtada funktsiya chegarasi mavjud bo'lsa , keyin u yagona.

Isbot. Agar Geyne bo'yicha chegara aniqlangan bo'lsa, unda uning o'ziga xosligi ketma-ketlik chegarasining yagonaligidan kelib chiqadi. Agar chegara Koshi bo'yicha aniqlangan bo'lsa, uning o'ziga xosligi Koshi va Geyne bo'yicha chegara ta'riflarining ekvivalentligidan kelib chiqadi. Teorema isbotlangan.

Ketma-ketliklar uchun Koshi mezoniga o'xshab, funktsiya chegarasining mavjudligi uchun Koshi mezoni amal qiladi. Uni shakllantirishdan oldin, keling

Ta'rif 4. Funktsiya deb aytishadi
nuqtadagi Koshi shartini qanoatlantiradi , agar mavjud bo'lsa
mavjud

, shu kabi
Va
, tengsizlik amal qiladi
.

Teorema 3 (Chekning mavjudligi uchun Koshi mezoni). Funktsiyani bajarish uchun
nuqtada bor edi chekli chegara, bu nuqtada funksiya Koshi shartini qondirishi zarur va etarli.

Isbot.Zaruriyat. Mayli
. Biz buni isbotlashimiz kerak
nuqtada qanoatlantiradi Koshi holati.

Keling, olamiz
o'zboshimchalik bilan va qo'yish
. Cheklov ta'rifi bo'yicha mavjud
, har qanday qiymatlar uchun shunday
, tengsizliklarni qondirish
Va
, tengsizliklar qanoatlantiriladi
Va
. Keyin

Ehtiyoj isbotlangan.

Adekvatlik. Funktsiyaga ruxsat bering
nuqtada qanoatlantiradi Koshi holati. Biz bu nuqtada borligini isbotlashimiz kerak yakuniy chegara.

Keling, olamiz
o'zboshimchalik bilan. Ta'rifga ko'ra 4 ta mavjud
, shundayki, tengsizliklardan
,
shunga amal qiladi
- bu berilgan.

Avval buni har qanday ketma-ketlik uchun ko'rsatamiz
, ga yaqinlashish , ketma-ketlik
funksiya qiymatlari yaqinlashadi. Haqiqatan ham, agar
, keyin, ketma-ketlik chegarasining ta'rifi tufayli, berilgan uchun
raqam bor N, har qanday uchun shunday

Va
. Chunki
nuqtada Koshi shartini qanoatlantiradi, bizda bor
. Keyin, ketma-ketliklar uchun Koshi mezoniga ko'ra, ketma-ketlik
birlashadi. Keling, bunday ketma-ketliklarning barchasini ko'rsatamiz
bir xil chegaraga yaqinlashadi. Keling, buning aksini faraz qilaylik, ya'ni. ketma-ketliklar nima
Va
,
,
, shu kabi. Keling, ketma-ketlikni ko'rib chiqaylik. ga yaqinlashishi aniq , shuning uchun yuqorida isbotlanganidek, ketma-ketlik yaqinlashadi, bu mumkin emas, chunki pastki ketma-ketliklar
Va
turli chegaralarga ega Va . Olingan qarama-qarshilik shundan dalolat beradi =. Shuning uchun, Geynning ta'rifiga ko'ra, funktsiya nuqtada mavjud yakuniy chegara. Yetarlilik va demak, teorema isbotlangan.