Намалюйте схему системи та позначте на ній центр тяжіння.Якщо знайдений центр ваги знаходиться поза системою об'єктів, ви отримали неправильну відповідь. Можливо, ви виміряли відстань від різних точок відліку. Повторіть виміри.
- Наприклад, якщо на гойдалках сидять діти, центр ваги буде десь між дітьми, а не праворуч чи ліворуч від гойдалок. Також центр ваги ніколи не збігатиметься з точкою, де сидить дитина.
- Ці міркування вірні у двовимірному просторі. Намалюйте квадрат, де помістяться всі об'єкти системи. Центр тяжкості повинен знаходитись усередині цього квадрата.
Перевірте математичні обчислення, якщо ви отримали невеликий результат.Якщо точка відліку знаходиться на одному кінці системи, маленький результат поміщає центр тяжіння біля кінця системи. Можливо, це правильна відповідь, але в переважній більшості випадків такий результат свідчить про помилку. Коли ви обчислювали моменти, ви перемножували відповідні ваги та відстані? Якщо замість множення ви склали ваги та відстані, ви отримаєте набагато менший результат.
Виправте помилку, якщо ви знайшли кілька центрів ваги.Кожна система має лише один центр важкості. Якщо ви знайшли кілька центрів важкості, швидше за все, ви не склали всі моменти. Центр тяжкості дорівнює відношенню «сумарного» моменту до «сумарної» ваги. Не потрібно ділити "кожний" момент на "кожну" вагу: так ви знайдете положення кожного об'єкта.
Перевірте точку відліку, якщо відповідь відрізняється на певне значення.У прикладі відповідь дорівнює 3,4 м. Припустимо, ви отримали відповідь 0,4 м чи 1,4 м, чи інше число, що закінчується на «,4». Це тому, що як точка відліку ви вибрали не лівий кінець дошки, а точку, яка розташована правіше на цілу величину. Насправді, ваша відповідь вірна, незалежно від того, яку точку відліку ви обрали! Просто запам'ятайте: точка відліку завжди знаходиться в положенні x = 0. Ось приклад:
- У нашому прикладі точка відліку знаходилася на лівому кінці дошки, і ми знайшли, що центр ваги знаходиться на відстані 3,4 м від цієї точки відліку.
- Якщо в якості точки відліку вибрати точку, яка розташована на відстані 1 м праворуч від лівого кінця дошки, ви отримаєте відповідь 2,4 м. Тобто центр ваги знаходиться на відстані 2,4 м від нової точки відліку, яка, у свою чергу, знаходиться на відстані 1 м від лівого кінця дошки. Таким чином, центр ваги знаходиться на відстані 2,4+1=3,4 м від лівого кінця дошки. Вийшла стара відповідь!
- Примітка: при вимірі відстані пам'ятайте, що відстань до «лівої» точки відліку є негативною, а до «правої» – позитивною.
Вимірюйте відстані по прямих лініях.Припустимо, на гойдалках дві дитини, але одна дитина набагато вища за іншу, або одна дитина висить під дошкою, а не сидить на ній. Проігноруйте таку різницю та виміряйте відстані по прямій лінії дошки. Вимір відстаней під кутами призведе до близьких, але не зовсім точних результатів.
- У разі завдання з гойдалками-дошкою пам'ятайте, що центр ваги знаходиться між правим і лівим кінцями дошки. Пізніше ви навчитеся обчислювати центр тяжкості складніших двовимірних систем.
Лекція 4. Центр тяжкості.
У цій лекції розглядаються такі питання
1. Центр важкості твердого тіла.
2. Координати центрів тяжкості неоднорідних тіл.
3. Координати центрів тяжкості однорідних тіл.
4. Методи визначення координат центрів тяжкості.
5. Центри тяжкості деяких однорідних тіл.
Вивчення даних питань необхідно надалі вивчення динаміки руху тіл з урахуванням тертя ковзання і тертя кочення, динаміки руху центру мас механічної системи, кінетичних моментів, на вирішення завдань у дисципліні «Опір матеріалів».
Наведення паралельних сил.
Після того, як було розглянуто приведення до центру плоскої системи та довільної просторової системи сил, ми знову повертаємося до розгляду окремого випадку системи паралельних сил.
Приведення двох паралельних сил.
У ході розгляду такої системи сил можливі три наступні випадки приведення.
1. Система двох колінеарних сил. Розглянемо систему двох паралельних та спрямованих в один бік сил Pі Q, доданих у точках Аі У. Вважатимемо, що сили перпендикулярні до цього відрізка (рис.1, а).
З, що належить відрізку АВі задовільну умову:
АС/СВ = Q/P.(1)
Головний вектор системи R C = P + Qпо модулюравний сумі цих сил: R C = P + Q.
Зз урахуванням (1) дорівнює нулю:MC = P ∙ АС- Q∙ СВ = 0.
Таким чином, у результаті наведення ми отримали: R C ≠ 0, MC= 0. Це означає, що головний вектор еквівалентний рівнодіючої, що проходить через центр приведення, тобто:
Рівнодійна колінеарна сила дорівнює за модулем їх сумі, а її лінія дії ділить відрізок, що з'єднує точки їх застосування, обернено пропорційно модулям цих сил внутрішнім чином.
Зазначимо, що положення точки Зне зміниться, якщо сили Рі Qповернути на кутα. Крапка З, Що має таку властивість називається центром паралельних сил.
2. Система двох антиколінеарнихі не рівних за модулем сил. Нехай сили Pі Q, додані в точках Аі У, паралельні, спрямовані у протилежні сторони і по модулю не рівні (рис.1, б).
Виберемо як центр приведення точку З, що задовольняє як і раніше співвідношенню (1) і лежить на тій же прямій, але за межами відрізка АВ.
Головний вектор цієї системи R C = P + Qпо модулю тепер дорівнюватиме різниці модулів векторів: R C = Q - P.
Головний момент щодо центру Зяк і дорівнює нулю:MC = P ∙ АС- Q∙ СВ= 0, тому
Рівнодійна антиколінеарнихі не рівних за модулем сил дорівнює їх різниці, спрямована у бік більшої сили, а її лінія дії ділить відрізок, що з'єднує точки їх застосування, обернено пропорційно модулям цих сил зовнішнім образом.
Рис.1
3. Система двох антиколінеарнихта рівних за модулем сил. Візьмемо вихідний попередній випадок приведення. Зафіксуємо силу Р, а силу Qспрямуємо по модулю до сили Р.
Тоді при Q → Р у формулі (1) відношення АС/СВ → 1. Це означає, що АС → СВ, тобто відстань АС →∞ .
При цьому модуль головного вектора R C → 0, а модуль головного моменту не залежить від положення центру приведення і залишається рівним первісному значенню:
MC = P ∙ АС- Q∙ СВ = P ∙ ( АС- СВ) =P ∙ АB.
Отже, у межі ми отримали систему сил, для якої R C = 0, MC≠ 0, а центр приведення видалений у нескінченність, яку не можна замінити рівнодією. У цій системі неважко дізнатися пару сил, тому пара сил рівнодіючої не має.
Центр системи паралельних сил.
Розглянемо систему nсил P i, доданих у точкахA і (x i , y i , z i)і паралельних осіOv з ортом l(Рис.2).
Якщо заздалегідь виключити випадок системи, еквівалентній парі сил, неважко на підставі попереднього параграфа довести існування її рівнодіючоїR.
Визначимо координати центруC(x c, y c, z c) паралельних сил, тобто координати точки докладання рівнодіючої цієї системи.
Скористаємося з цією метою теорема Варіньйона, на підставі якої:
M 0 (R) = Σ M 0(P i).

Рис.2
Вектор-момент сили можна подати у вигляді векторного твору, тому:
М 0 (R) = r c× R = Σ М0i(P i) = Σ ( r i× P i ).
Враховуючи, що R = R v ∙ l, а P i = P vi ∙ l та скориставшись властивостями векторного твору, отримаємо:
r c × R v ∙ l = Σ ( r i × P vi ∙ l),
r c ∙ R v × l = Σ ( r i ∙ P vi × l) = Σ ( r i ∙ P vi ) × l,
або:
[ r c R v - Σ ( r i P vi )] × l= 0.
Останній вираз справедливий тільки в тому випадку, якщо вираз у квадратних дужках дорівнює нулю. Тому, опускаючи індексvта враховуючи, що рівнодіючаR = Σ P i , звідси отримаємо:
r c = (Σ P i r i )/(Σ P i ).
Проектуючи останню векторну рівність на осі координат, отримаємо шукане вираз координат центру паралельних сил:
x c = (Σ P i x i)/(Σ P i );
y c = (Σ P i y i )/(Σ P i );(2)
z c = (Σ P i z i )/(Σ P i ).
Центр тяжкості тел.
Координати центрів тяжкості однорідного тіла.
Розглянемо тверде тіло вагою Pта обсягом Vу системі координат Oxyzде осі xі yпов'язані з поверхнею землі, а вісь zнаправлена в зеніт.
Якщо розбити тіло на елементарні частини об'ємом∆ V i , то на кожну його частину діятиме сила тяжіння∆ P iнаправлена до центру Землі. Припустимо, що розміри тіла значно менші за розміри Землі, тоді систему сил, прикладених до елементарних частин тіла можна вважати не схожою, а паралельною (рис.3), і до неї застосовні всі висновки попереднього розділу.

Рис.3
Визначення . Центром важкості твердого тіла називається центр паралельних сил важкості елементарних частин цього тіла.
Нагадаємо, що питомою вагоюелементарної частини тіла називається відношення її ваги∆ P iдо обсягу ∆ V i : γ i = ∆ P i/ ∆ V i . Для однорідного тіла ця величина є постійною:γ i = γ = P/ V.
Підставляючи у (2) ∆ P i = γ i ∙∆ V i замість P i, враховуючи останнє зауваження та скорочуючи чисельник та знаменник наg, отримаємо вирази координат центру тяжкості однорідного тіла:
x c = (Σ ∆ V i∙ x i)/(Σ ∆ V i);
y c = (Σ ∆ V i∙ y i )/(Σ ∆ V i);(3)
z c = (Σ ∆ V i∙ z i )/(Σ ∆ V i).
При визначенні центру важкості корисні кілька теорем.
1) Якщо однорідне тіло має площину симетрії, то центр ваги його знаходиться у цій площині.
Якщо осі хі урозташувати в цій площині симетрії, то для кожної точки з координатами. І координата по (3), дорівнюватиме нулю, т.к. у сумівсе члени, що мають протилежні знаки, попарно знищуються. Значить центр ваги розташованийу площині симетрії.
2) Якщо однорідне тіло має вісь симетрії, центр тяжкості тіла знаходиться на цій осі.
Справді, у разі, якщо вісьzпровести по осі симетрії, для кожної точки з координатамиможна знайти точку з координатамиі координати та , Обчислені за формулами (3), виявляться рівними нулю.
Аналогічно підтверджується і третя теорема.
3) Якщо однорідне тіло має центр симетрії, центр тяжкості тіла знаходиться в цій точці.
І ще кілька зауважень.
Перше. Якщо тіло можна розділити на частини, у яких відома вага та положення центру тяжіння, то нема чого розглядати кожну точку, а у формулах (3) P i – визначати як вагу відповідної частини та- Як координати її центру тяжкості.
Друге. Якщо тіло однорідне, то вага окремої частини його, де - питома вага матеріалу, з якого зроблено тіло, а V i - Обсяг цієї частини тіла. І формули (3) набудуть більш зручного вигляду. Наприклад,
І аналогічно, де - Обсяг всього тіла.
Третє зауваження. Нехай тіло має вигляд тонкої платівки площею Fта завтовшки t, що лежить у площині Oxy. Підставляючи (3)∆ V i =t ∙ ∆ F i , отримаємо координати центру ваги однорідної платівки:
x c = (Σ ∆ F i∙ x i) / (Σ ∆ F i);
y c = (Σ ∆ F i∙ y i ) / (Σ ∆ F i).
z c = (Σ ∆ F i∙ z i ) / (Σ ∆ F i).
де - Координати центру тяжкості окремих пластин;- Загальна площа тіла.
Четверте зауваження. Для тіла у вигляді тонкого криволінійного стрижня завдовжки Lз площею поперечного перерізу aелементарний обсяг∆ V i = a ∙∆ L i тому координати центру важкості тонкого криволінійного стрижнябудуть рівні:
x c = (Σ ∆ L i∙ x i)/(Σ ∆ L i);
y c = (Σ ∆ L i∙ y i )/(Σ ∆ L i);(4)
z c = (Σ ∆ L i∙ z i )/(Σ ∆ L i).
де – координати центру важкостіi-ї ділянки; .
Зазначимо, що згідно з визначенням центр ваги – це точка геометрична; вона може лежати і поза даного тіла (наприклад, для кільця).
Примітка.
У цьому розділі курсу ми не робимо різниці між силою тяжіння, силою тяжіння та вагою тіла. Насправді сила тяжіння є різницею між силою тяжіння Землі і відцентровою силою, викликаної її обертанням.
Координати центрів важкості неоднорідних тіл.
Координати центру важкості неоднорідного твердого тіла(рис.4) у вибраній системі відліку визначаються таким чином:

Рис.4



де - вага одиниці об'єму тіла (питома вага)
![]() -вага всього тіла.
-вага всього тіла.
неоднорідну поверхню(рис.5), то координати центру тяжкості у вибраній системі відліку визначаються таким чином:

Рис.5
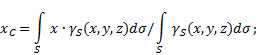

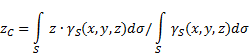
де - вага одиниці площі тіла,
![]() -вага всього тіла.
-вага всього тіла.
Якщо тверде тіло є неоднорідну лінію(рис.6), то координати центру тяжкості у вибраній системі відліку визначаються таким чином:

Рис.6

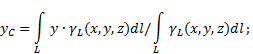

де - вага одиниці довжини тіла,
Вага всього тіла.
Способи визначення координат центру важкості.
Виходячи з отриманих вище загальних формул, можна вказати конкретні способи визначення координат центрів тяжіння тіл.
1. Симетрія.Якщо однорідне тіло має площину, вісь чи центр симетрії (мал.7), його центр ваги лежить відповідно у площині симетрії, осі симетрії чи центрі симетрії.

Рис.7
2. Розбиття.Тіло розбивається на кінцеве число частин (рис.8), кожної з яких становище центру тяжкості і площа відомі.

Рис.8
S = S1 + S2.
3.Метод негативних площ.Окремий випадок способу розбиття (рис.9). Він застосовується до тіл, що мають вирізи, якщо центри ваги тіла без вирізу та вирізаної частини відомі. Тіло у вигляді пластинки з вирізом є комбінацією суцільної пластинки (без вирізу) з площею S 1 та площі вирізаної частини S2.

Рис.9
S = S1-S2.
4.Метод угруповання.Є добрим доповненням двох останніх методів. Після розбиття фігури на складові елементи частина їх зручно об'єднати знову, щоб потім спростити рішення шляхом обліку симетрії цієї групи.
Центри тяжкості деяких однорідних тіл.
1) Центр тяжкості дуги кола.Розглянемо дугу АВрадіусуR з центральним кутом. Через симетрію центр тяжкості цієї дуги лежить на осіOx(Рис. 10).

Рис.10
Знайдемо координатуза формулою . Для цього виділимо на дузі АВелемент ММ ’ довжиною, положення якого визначається кутом. Координата хелемента ММ’буде. Підставляючи ці значення хі d l і маючи на увазі, що інтеграл має бути поширений на всю довжину дуги, отримаємо:
![]()
де L - Довжина дуги АВ, рівна.
Звідси остаточно знаходимо, що центр тяжіння дуги кола лежить на її осі симетрії на відстані від центруО, рівному
де кут вимірюється у радіанах.
2) Центр тяжкості площі трикутника. Розглянемо трикутник, що лежить у площині Oxyкоординати вершин якого відомі: A і (x i,y i ), (i= 1,2,3). Розбиваючи трикутник на вузькі смужки, паралельні стороні А 1 А 2 , дійдемо висновку, що центр тяжіння трикутника повинен належати медіані А 3 М 3 (рис.11).

Рис.11
Розбиваючи трикутник на смужках, паралельні стороні А 2 А 3 можна переконатися, що він повинен лежати на медіані А 1 М 1 . Таким чином, центр тяжкості трикутника лежить у точці перетину його медіан, Яка, як відомо, відокремлює від кожної медіани третину, рахуючи від відповідної сторони.
Зокрема, для медіани А 1 М 1 отримаємо, враховуючи, що координати точки М 1 - це середнє арифметичне координат вершин А 2 та А 3 :
x c = x 1 + (2/3) ∙ (xМ 1 - x 1 ) = x 1 + (2/3) ∙ [(x 2 + x 3 )/2 - x 1 ] = (x 1 + x 2 + x 3 )/3.
Таким чином, координати центру тяжкості трикутника є середнім арифметичним з координат його вершин:
x c =(1/3) Σ x i ; y c =(1/3) Σ y i .
3) Центр ваги площі кругового сектора.Розглянемо сектор кола радіусу Rз центральним кутом 2α , розташований симетрично щодо осі Ox (рис.12).
Очевидно, що y c = 0, а відстань від центру кола, з якого вирізаний цей сектор, до центру тяжкості можна визначити за формулою:

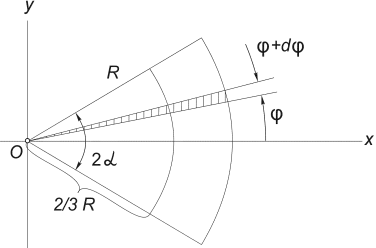
Рис.12
Найпростіше цей інтеграл обчислити, розбиваючи область інтегрування на елементарні сектори з кутом dφ . З точністю до нескінченно малих першого порядку такий сектор можна замінити трикутником з основою, що дорівнює R × dφ та заввишки R. Площа такого трикутника dF =(1/2)R 2 ∙ dφ , а його центр тяжіння знаходиться на відстані 2/3 Rвід вершини, тому в (5) покладемо x = (2/3)R∙ cosφ. Підставляючи (5) F= α R 2, отримаємо:

За допомогою останньої формули обчислимо, зокрема, відстань до центру ваги півкола.
Підставляючи (2) α = π /2, отримаємо: x c = (4 R)/(3 π ) ≅ 0,4 R .
приклад 1.Визначимо центр тяжкості однорідного тіла, зображеного на рис. 13.

Рис.13
Рішення.Тіло однорідне, що складається із двох частин, що мають симетричну форму. Координати центрів тяжкості їх:
Обсяги їх:
Тому координати центру тяжкості тіла
приклад 2. Знайдемо центр ваги пластини зігнутої під прямим кутом. Розміри – на кресленні (рис.14).

Рис.14
Рішення. Координати центрів тяжкості:
0.
Площі:
Тому:
приклад 3.
У квадратного листа
см вирізаний квадратний отвір
див (рис.15). Знайдемо центр тяжкості аркуша.приклад 4. Знайти положення центру ваги платівки, представленої на рис. 16. Розміри наведені в сантиметрах.

Рис.16
Рішення. Розділимо платівку на фігури (рис. 17), центритяжкості яких відомі.
Площі цих фігур та координати їх центрів тяжіння:
1) прямокутник зі сторонами 30 і 40 см,S 1 =30 ∙ 40 = 1200 см 2 ; х 1= 15 см; у 1 = 20 см.
2) прямокутний трикутник із основою 50 см і висотою 40 см;S 2 =0,5 ∙ 50 ∙ 40 = 1000 см 2 ; х 2 = 30 +50/3 = 46,7 см; у 2 =40/3 =13,3 див;
3) половина кола кола радіусу r = 20 см;S 3 =0,5 ∙π∙ 20 2 = 628 см 2 ; х 3 =4 R /3 π =8,5 див; у
Рішення. Нагадаємо, що у фізиці щільність тілаρ та його питома вагаgпов'язані співвідношенням:γ = ρ g , деg - прискорення вільного падіння. Щоб знайти масу такого однорідного тіла потрібно щільність помножити на його об'єм.

Рис.19
Термін "лінійна" або "погонна" щільність означає, що для визначення маси стрижня ферми потрібно погонну щільність помножити на довжину цього стрижня.
Для вирішення задачі можна скористатися методом розбиття. Представивши задану ферму у вигляді суми 6 окремих стрижнів, отримаємо:
деL i довжинаi -го стрижня ферми, аx i , y i - координати його центру тяжкості.
Вирішення цього завдання можна спростити, якщо згрупувати 5 останніх стрижнів ферми. Неважко бачити, що вони утворюють фігуру, що має центр симетрії, розташований посередині четвертого стрижня, де знаходиться центр тяжкості цієї групи стрижнів.
Таким чином, задану ферму можна подати комбінацією всього двох груп стрижнів.
Перша група складається з першого стрижня, для неїL 1 = 4 м,x 1 = 0 м,y 1 = 2 м. Друга група стрижнів складається з п'яти стрижнів, для неїL 2 = 20 м,x 2 = 3 м,y 2 = 2 м.
Координати центру тяжкості ферми знаходимо за такою формулою:
x c = (L 1 ∙ x 1 + L 2 ∙ x 2 )/(L 1 + L 2 ) = (4∙0 + 20∙3)/24 = 5/2 м;
y c = (L 1 ∙ y 1 + L 2 ∙ y 2 )/(L 1 + L 2 ) = (4∙2 + 20∙2)/24 = 2 м.
Зазначимо, що центр З лежить на прямій, що з'єднує З 1 і З 2 і ділить відрізок З 1 З 2 щодо: З 1 З/СС 2 = (x c - x 1 )/(x 2 - x c ) = L 2 / L 1 = 2,5/0,5.
Запитання для самоперевірки
– Що називається центром паралельних сил?
– Як визначаються координати центру паралельних сил?
- Як визначити центр паралельних сил, рівнодіюча яких дорівнює нулю?
- Яку властивість має центр паралельних сил?
– За якими формулами обчислюються координати центру паралельних сил?
- Що називається центром тяжкості тіла?
- Чому сили тяжіння Землі, що діють на точку тіла, можна прийняти за систему паралельних сил?
- Запишіть формулу визначення положення центру тяжкості неоднорідних і однорідних тіл, формулу визначення положення центру тяжкості плоских перерізів?
- Запишіть формулу для визначення положення центру ваги простих геометричних фігур: прямокутника, трикутника, трапеції та половини кола?
– Що називають статичним моментом площі?
- Наведіть приклад тіла, центр ваги якого розташований поза тілом.
- Як використовуються властивості симетрії щодо центрів тяжкості тіл?
- У чому полягає суть способу негативних ваг?
- Де розташований центр тяжіння дуги кола?
- Якою графічною побудовою можна знайти центр тяжіння трикутника?
- Запишіть формулу, яка визначає центр ваги кругового сектора.
- Використовуючи формули, що визначають центри тяжіння трикутника та кругового сектора, виведіть аналогічну формулу для кругового сегмента.
- За якими формулами обчислюються координати центрів ваги однорідних тіл, плоских фігур та ліній?
- Що називається статичним моментом площі плоскої фігури щодо осі, як він обчислюється та яку розмірність має?
- Як визначити положення центру тяжкості площі, якщо відоме положення центрів тяжкості окремих її частин?
- Якими допоміжними теоремами користуються щодо положення центру тяжкості?
Автор: Візьмемо тіло довільної форми Чи можна підвісити його на нитки так, щоб воно після підвішування зберегло своє положення (тобто не стало повертатися) при будь-якийпочаткової орієнтації (рис. 27.1)?
Іншими словами, чи існує така точка, щодо якої сума моментів сил тяжіння, що діють на різні частини тіла, дорівнювала б нулю при будь-якийорієнтації тіла у просторі?
Читач: По-моєму, так Така точка називається центром важкості тіла.
Доказ.Для простоти розглянемо тіло як плоскої пластини довільної форми довільним чином орієнтоване у просторі (рис. 27.2). Візьмемо систему координат х 0уз початком у центрі мас – точці Зтоді х З = 0, у С = 0.
 Представимо це тіло у вигляді сукупності великої кількості точкових мас m i, положення кожної з яких задається радіусом-вектором.
Представимо це тіло у вигляді сукупності великої кількості точкових мас m i, положення кожної з яких задається радіусом-вектором.
За визначенням центру мас , а координата х З = .
Так як у прийнятій нами системі координат х З= 0, то. Помножимо цю рівність на gі отримаємо
Як видно із рис. 27.2, | x i| - Це плече сили. Причому якщо х i> 0, то момент сили M i> 0, а якщо х j < 0, то M j < 0, поэтому с учетом знака можно утверждать, что для любого x iмомент сили дорівнюватиме M i = m i g x i.Тоді рівність (1) еквівалентна рівності , де M i- Момент сили тяжіння. А це означає, що при довільній орієнтації тіла сума моментів сил тяжіння, що діють на тіло, дорівнюватиме нулю щодо його центру мас.
Щоб тіло, яке ми розглядаємо, знаходилося в рівновазі, до нього необхідно прикласти в точці Зсилу Т = mg, спрямовану вертикально догори. Момент цієї сили щодо точки Здорівнює нулю.
Оскільки наші міркування аж ніяк не залежали від того, як саме орієнтоване тіло в просторі, ми довели, що центр тяжкості збігається з центром мас, що потрібно було довести.
Завдання 27.1.Знайти центр ваги невагомого стрижня довжини l, на кінцях якого укріплено дві точкові маси т 1 і т 2 .
| т 1 т 2 l | Рішення. Будемо шукати не центр тяжкості, а центр мас (оскільки це одне й те саме). Введемо вісь х(Рис. 27.3). |
| х З =? | |
Відповідь: на відстані від маси т 1 .
СТОП! Вирішіть самостійно: В1–В3.
Твердження 1 . Якщо однорідне плоске тіло має вісь симетрії, центр ваги знаходиться на цій осі.
Дійсно, для будь-якої точкової маси m i, розташованої праворуч від осі симетрії, знайдеться така сама точкова маса , розташована симетрично щодо першої (рис. 27.4). При цьому сума моментів сил.
Оскільки все тіло можна уявити розбитим на подібні пари точок, то сумарний момент сил тяжіння щодо будь-якої точки, що лежить на осі симетрії дорівнює нулю, а отже, на цій осі знаходиться центр тяжіння тіла. Звідси випливає важливий висновок: якщо тіло має кілька осей симетрії, то центр тяжіння лежить на перетині цих осей(Рис. 27.5).
Мал. 27.5 
Твердження 2. Якщо два тіла масами т 1 і т 2 з'єднані в одне, то центр тяжіння такого тіла лежатиме на відрізку прямої, що з'єднує центри тяжіння першого і другого тіла (рис. 27.6).
Мал. 27.6 ![]() Мал. 27.7
Мал. 27.7
Доказ.Розташуємо складове тіло так, щоб відрізок, що з'єднує центри ваги тіл, був вертикальним. Тоді сума моментів сил тяжіння першого тіла щодо точки З 1 дорівнює нулю, і сума моментів сил тяжіння другого тіла щодо точки З 2 дорівнює нулю (рис. 27.7).
Зауважимо, що плечесили тяжіння будь-якої точкової маси т iодне й те саме щодо будь-якої точки, що лежить на відрізку З 1 З 2 , а значить, і момент сили тяжіння щодо будь-якої точки, що лежить на відрізку З 1 З 2 , той самий. Отже, сил тяжіння всього тіла дорівнює нулю щодо будь-якої точки відрізка З 1 З 2 . Таким чином, центр ваги складеного тіла лежить на відрізку З 1 З 2 .
Зі твердження 2 випливає важливий практичний висновок, який чітко сформульований у вигляді інструкції.
Інструкція,
як шукати центр тяжкості твердого тіла, якщо його можна розбити
на частини, положення центрів тяжкості кожної з яких відомо
1. Слід замінити кожну частину масою, розташованою у центрі тяжкості цієї частини.
2. Знайти центр мас(а це те саме, що і центр тяжіння) отриманої системи точкових мас, вибравши зручну систему координат х 0у, За формулами:
Справді, розташуємо складове тіло так, щоб відрізок З 1 З 2 був горизонтальним, і підвісимо його на нитках у точках З 1 і З 2 (рис. 27.8, а). Зрозуміло, що тіло перебуватиме у рівновазі. І ця рівновага не порушиться, якщо ми замінимо кожне тіло точковими масами т 1 і т 2 (рис. 27.8, б).
 Мал. 27.8
Мал. 27.8
СТОП! Вирішіть самостійно: С3.
Завдання 27.2.У двох вершинах рівностороннього трикутника вміщено кульки маси ткожен. У третій вершині поміщена кулька маси 2 т(Рис. 27.9, а). Сторона трикутника а. Визначити центр важкості цієї системи.
| т 2т а |  Мал. 27.9 Мал. 27.9 |
| х З = ? у С = ? | |
Рішення. Введемо систему координат х 0у(Рис. 27.9, б). Тоді
![]() ,
,
 .
.
Відповідь: х З = а/2; ; центр ваги лежить на половині висоти АD.
Підручник для 7 класу
§ 25.3. Як знайти центр ваги тіла?
Нагадаємо, що центром тяжкості називають точку застосування сили тяжіння. Розглянемо, як знайти на досвіді положення центру тяжкості плоского тіла – скажімо, вирізаної з картону фігури довільної форми (див. лабораторну роботу №12).
Підвісимо картонну фігуру за допомогою шпильки або цвяха так, щоб вона могла вільно обертатися навколо горизонтальної осі, що проходить через точку О (рис. 25.4 а). Тоді цю фігуру можна як важіль з точкою опори Про.
Мал. 25.4. Як знайти на досвіді центр ваги плоскої фігури
Коли фігура знаходиться в рівновазі, сили, що діють на неї, врівноважують одна одну. Це сила тяжіння F т, прикладена в центрі тяжкості фігури Т, і сила пружності F упр, прикладена в точці (ця сила прикладена з боку шпильки або цвяха).
Ці дві сили врівноважують одна одну лише за умови, що точки застосування цих сил (точки Т і О) лежать на одній вертикалі (див. рис. 25.4, а). В іншому випадку сила тяжіння повертатиме фігуру навколо точки О (рис. 25.4, б).
Отже, коли фігура знаходиться в рівновазі, центр ваги лежить на одній вертикалі з точкою підвісу О. Це дозволяє визначити положення центру тяжіння фігури. Проведемо за допомогою схилу вертикаль, що проходить через точку підвісу (синя лінія на рис. 25.4, в). На проведеній лінії лежить центр ваги тіла. Повторимо цей досвід за іншого положення точки підвісу. У результаті отримаємо другу лінію, де лежить центр тяжкості тіла (зелена лінія на рис. 25.4, г). Отже, на перетині цих ліній знаходиться центр тяжкості тіла, що шукається (червона точка Г на рис. 25.4, г).
В інженерній практиці трапляється, що виникає необхідність обчислити координати центру важкості складної плоскої фігури, що складається з простих елементів, для яких розташування центру важкості відоме. Таке завдання є частиною завдання визначення...
Геометричних характеристик складових поперечних перерізів балок та стрижнів. Часто з подібними питаннями доводиться стикатися інженерам-конструкторам вирубних штампів при визначенні координат центру тиску, розробникам схем навантаження різного транспорту при розміщенні вантажів, проектувальникам будівельних металевих конструкцій при доборі перерізів елементів і, звичайно, студентам при вивченні дисциплін «Теоретична механіка» та « ».
Бібліотека елементарних постатей.

Для симетричних плоских фігур центр ваги збігається із центром симетрії. До симетричної групи елементарних об'єктів належать: коло, прямокутник (зокрема квадрат), паралелограм (зокрема ромб), правильний багатокутник.
З десяти фігур, представлених малюнку вище, лише дві є базовими. Тобто, використовуючи трикутники та сектори кіл, можна скомбінувати майже будь-яку фігуру, яка має практичний інтерес. Будь-які довільні криві можна, розбивши на ділянки, замінити дугами кіл.
Вісім фігур, що залишилися, є найпоширенішими, тому вони і були включені в цю своєрідну бібліотеку. У нашій класифікації ці елементи є базовими. Прямокутник, паралелограм та трапецію можна скласти із двох трикутників. Шестикутник – це сума із чотирьох трикутників. Сегмент кола – це різниця сектора кола та трикутника. Кільцевий сектор кола – різниця двох секторів. Коло – це сектор кола з кутом α=2*π=360˚. Півколо – це, відповідно, сектор кола з кутом α=π=180˚.
Розрахунок у Excel координат центру важкості складеної фігури.
Передавати та сприймати інформацію, розглядаючи приклад, завжди легше, ніж вивчати питання на суто теоретичних викладках. Розглянемо розв'язання задачі "Як знайти центр тяжкості?" на прикладі складової фігури, зображеної малюнку, розташованому нижче цього тексту.

Складовий переріз є прямокутником (з розмірами a1 =80 мм, b1 =40 мм), до якого зліва зверху додали рівнобедрений трикутник (з розміром основи a2 =24 мм та висотою h2 =42 мм) і з якого праворуч зверху вирізали півколо (з центром у точці з координатами x03 =50 мм та y03 =40 мм, радіусом r3 = 26 мм).
На допомогу для виконання розрахунку залучимо програму MS Excel або програму OOo Calc . Будь-яка з них легко впорається із нашим завданням!
У осередках з жовтою заливкою виконаємо допоміжні попередні розрахунки .
У осередках зі світло-жовтою заливкою вважаємо результати.
Синій шрифт – це вихідні дані .
Чорний шрифт – це проміжні результати розрахунків .
Червоний шрифт – це остаточні результати розрахунків .
Починаємо розв'язання задачі – починаємо пошук координат центру тяжкості перерізу.
Вихідні дані:
1. Назви елементарних фігур, що утворюють складовий переріз, впишемо відповідно
в комірку D3: Прямокутник
в комірку E3: Трикутник
в комірку F3: Півколо
2. Користуючись представленою в цій статті «Бібліотекою елементарних фігур», визначимо координати центрів ваги елементів складеного перерізу xciі yciв мм щодо довільно вибраних осей 0x і 0y і запишемо
у комірку D4: =80/2 = 40,000
xc 1 = a 1 /2
у комірку D5: =40/2 =20,000
yc 1 = b 1 /2
у комірку E4: =24/2 =12,000
xc 2 = a 2 /2
у комірку E5: =40+42/3 =54,000
yc 2 = b 1 + h 2 /3
у комірку F4: =50 =50,000
xc 3 = x03
у комірку F5: =40-4*26/3/ПІ() =28,965
yc 3 = y 03 -4* r3 /3/ π
3. Розрахуємо площі елементів F 1 , F 2 , F3 у мм2, скориставшись знову формулами з розділу "Бібліотека елементарних фігур"
у комірці D6: =40*80 =3200
F1 = a 1 * b1
у комірці E6: =24*42/2 =504
F2 = a2 *h2 /2
у комірці F6: =-ПІ()/2*26^2 =-1062
F3 =-π/2*r3 ^2
Площа третього елемента – півкола – негативна тому, що це виріз – пусте місце!

Розрахунок координат центру тяжкості:
4. Визначимо загальну площу підсумкової фігури F0 в мм2
в об'єднаному осередку D8E8F8: =D6+E6+F6 =2642
F0 = F 1 + F 2 + F3
5. Обчислимо статичні моменти складової фігури Sxі Syв мм3 щодо вибраних осей 0x та 0y
в об'єднаному осередку D9E9F9: =D5*D6+E5*E6+F5*F6 =60459
Sx = yc1 * F1 + yc2 * F2 + yc3 * F3
в об'єднаному осередку D10E10F10: =D4*D6+E4*E6+F4*F6 =80955
Sy = xc1 * F1 + xc2 * F2 + xc3 * F3
6. І на завершення розрахуємо координати центру важкості складеного перерізу Xcі Ycмм в обраній системі координат 0x - 0y
в об'єднаному осередку D11E11F11: =D10/D8 =30,640
Xc = Sy / F0
в об'єднаному осередку D12E12F12: =D9/D8 =22,883
Yc = Sx / F0
Завдання вирішено, розрахунок в Excel виконано - знайдено координати центру тяжкості перерізу, складеного при використанні трьох простих елементів!
Висновок.
Приклад у статті був обраний дуже простим для того, щоб легше було розібратися в методології розрахунків центру важкого перетину. Метод полягає в тому, що будь-яку складну фігуру слід розбити на прості елементи з відомими місцями розташування центрів тяжіння і зробити підсумкові обчислення для перерізу.
Якщо перетин складено з прокатних профілів – куточків та швелерів, то їх немає необхідності розбивати на прямокутники та квадрати з вирізаними круговими «π/2» секторами. Координати центрів тяжкості цих профілів наведені в таблицях ГОСТів, тобто і куточок і швелер будуть у ваших розрахунках складових перерізів базовими елементарними елементами (про двотаври, труби, прути і шестигранники говорити немає сенсу - це центрально симетричні перерізи).
Розташування осей координат на положення центру ваги фігури, звісно, не впливає! Тому вибирайте систему координат, що спрощує розрахунки. Якщо, наприклад, я розгорнув би в нашому прикладі систему координат на 45 за годинниковою стрілкою, то обчислення координат центрів тяжкості прямокутника, трикутника і півкола перетворилося б на ще один окремий і громіздкий етап розрахунків, який «в розумі» не виконаєш.
Поданий нижче розрахунковий файл Excel у разі програмою не є. Швидше - це малюнок калькулятора, алгоритм, шаблон за яким слідує в кожному конкретному випадку складати свою послідовність формул для осередків з яскравою жовтою заливкою.
Отже, як знайти центр тяжіння будь-якого перетину, ви тепер знаєте! Повний розрахунок всіх геометричних характеристик довільних складних перерізів буде розглянуто в одній з найближчих статей у рубриці « ». Слідкуйте за новинами на блозі.
Для отримання інформації про вихід нових статей і для скачування робочих файлів програм прошу вас підписатися на анонси у вікні, розташованому наприкінці статті або у вікні вгорі сторінки.
Після введення адреси своєї електронної пошти та натискання на кнопку «Отримувати анонси статей» НЕ ЗАБУДЬТЕ ПІДТВЕРДЖУВАТИ ПЕРЕДПЛАТУ кліком за посиланням у листі, який відразу прийде до вас на вказану пошту (іноді - в папку « Спам » )!
Кілька слів про келих, монету та дві виделки, які зображені на «значку-ілюстрації» на самому початку статті. Багатьом із вас, безумовно, знайомий цей «трюк», який викликає захоплені погляди дітей та непосвячених дорослих. Тема цієї статті – центр тяжкості. Саме він і точка опори, граючи з нашою свідомістю та досвідом, просто дурять наш розум!
Центр ваги системи «вилки+монета» завжди розташовується на фіксованомувідстані по вертикалі внизвід краю монети, що у свою чергу є точкою опори. Це становище стійкої рівноваги!Якщо похитати вилки, то відразу стає очевидним, що система прагне зайняти своє старе стійке становище! Уявіть маятник – точка закріплення (=точка опори монети на кромку келиха), стрижень-вісь маятника (=у нашому випадку вісь віртуальна, оскільки маса двох вилок розведена в різні боки простору) і вантаж внизу осі (=центр тяжіння всієї системи «вилки» +монета»). Якщо почати відхиляти маятник від вертикалі в будь-який бік (вперед, назад, ліворуч, праворуч), то він неминуче під дією сили тяжіння повертатиметься у вихідне стійкий стан рівноваги(це ж саме відбувається і з нашими вилками та монетою)!
Хто не зрозумів, але хоче зрозуміти – розберіться самостійно. Адже це дуже цікаво «доходити» самому! Додам, що цей самий принцип використання стійкої рівноваги реалізований і в іграшці ванька-встань-ка. Тільки центр ваги у цієї іграшки розташований вище точки опори, але нижче центру півсфери опорної поверхні.
Завжди радий вашим коментарям, шановні читачі!
Прошу, Шановна працю автора, завантажувати файл ПІСЛЯ ПЕРЕДПЛАТИ на новини статей.










