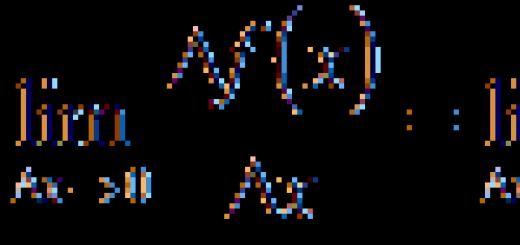A vektorok skaláris szorzata (a továbbiakban SP). Kedves barátaim! A matematika vizsga egy vektoros megoldási feladatcsoportot tartalmaz. Néhány problémát már megvizsgáltunk. A „Vektorok” kategóriában láthatja őket. Általában véve a vektorok elmélete nem bonyolult, a lényeg az, hogy következetesen tanulmányozzuk. A számítások és a vektorokkal végzett műveletek az iskolai matematika tanfolyamon egyszerűek, a képletek nem bonyolultak. Vessünk egy pillantást. Ebben a cikkben a vektorok SP-vel kapcsolatos problémákat elemezzük (amelyek szerepelnek az Egységes Államvizsgában). Most „merülés” az elméletben:

H Egy vektor koordinátáinak meghatározásához ki kell vonni a vektor végének koordinátáitorigójának megfelelő koordinátáit

És tovább:

*A vektorhossz (modulus) a következőképpen kerül meghatározásra:

Ezeket a képleteket emlékezni kell!!!

Mutassuk meg a vektorok közötti szöget:

Nyilvánvaló, hogy 0 és 180 0 között változhat(vagy radiánban 0-tól Pi-ig).

A skalárszorzat előjelére vonatkozóan levonhatunk néhány következtetést. A vektorok hosszának pozitív értéke van, ez nyilvánvaló. Ez azt jelenti, hogy a skaláris szorzat előjele a vektorok közötti szög koszinuszának értékétől függ.

Lehetséges esetek:

1. Ha a vektorok közötti szög hegyes (0 0 és 90 0 között), akkor a szög koszinusza pozitív értékű lesz.

2. Ha a vektorok közötti szög tompaszögű (90 0 és 180 0 között), akkor a szög koszinusza negatív értékű lesz.

*Nulla fokon, azaz ha a vektorok iránya azonos, a koszinusz egyenlő eggyel, és ennek megfelelően az eredmény pozitív lesz.

180 o-nál, vagyis amikor a vektorok ellentétes irányúak, a koszinusz egyenlő mínusz eggyel,és ennek megfelelően az eredmény negatív lesz.

Most a FONTOS PONT!

90 o-nál, azaz amikor a vektorok merőlegesek egymásra, a koszinusz egyenlő nullával, és ezért az SP egyenlő nullával. Ezt a tényt (következményt, következtetést) számos olyan probléma megoldásában használják fel, ahol a vektorok egymáshoz viszonyított helyzetéről beszélünk, beleértve a matematikai feladatok nyitott bankjában szereplő feladatokat is.

Fogalmazzuk meg az állítást: a skaláris szorzat akkor és csak akkor egyenlő nullával, ha ezek a vektorok merőleges egyeneseken fekszenek.

Tehát az SP vektorok képletei:

Ha ismerjük a vektorok koordinátáit vagy a kezdeti és végpontjuk koordinátáit, akkor mindig megtaláljuk a vektorok közötti szöget:

Nézzük a feladatokat:

27724 Határozza meg az a és b vektor skaláris szorzatát!

A vektorok skaláris szorzatát két képlet egyikével találhatjuk meg:

A vektorok közötti szög ismeretlen, de könnyen megkereshetjük a vektorok koordinátáit, majd az első képletet használhatjuk. Mivel mindkét vektor origója egybeesik a koordináták origójával, ezeknek a vektoroknak a koordinátái megegyeznek a végük koordinátáival, azaz

A vektor koordinátáinak megtalálása a következő részben található:

Kiszámoljuk:

Válasz: 40

Keressük meg a vektorok koordinátáit, és használjuk a képletet:

Egy vektor koordinátáinak megtalálásához ki kell vonni a kezdetének megfelelő koordinátáit a vektor végének koordinátáiból, ami azt jelenti, hogy

Kiszámoljuk a skalárszorzatot:

Válasz: 40

Határozzuk meg az a és b vektorok közötti szöget! Válaszát fokokban adja meg.

Legyen a vektorok koordinátái a következő formában:

A vektorok közötti szög meghatározásához a vektorok skaláris szorzatának képletét használjuk:

A vektorok közötti szög koszinusza:

Ennélfogva:

Ezeknek a vektoroknak a koordinátái egyenlőek:

Helyettesítsük be őket a képletbe:

A vektorok közötti szög 45 fok.

Válasz: 45

Így a vektor hosszát a koordinátáinak négyzetösszegének négyzetgyökeként számítjuk ki
. Hasonló módon számítjuk ki egy n-dimenziós vektor hosszát is
. Ha emlékezünk arra, hogy egy vektor minden koordinátája a vége és a kezdet koordinátái közötti különbség, akkor megkapjuk a szakasz hosszának képletét, azaz. A pontok közötti euklideszi távolság.

Skaláris szorzat két vektor egy síkon e vektorok hosszának és a köztük lévő szög koszinuszának a szorzata:
. Bizonyítható, hogy két vektor skaláris szorzata = (x 1, x 2) és = (y 1 , y 2) egyenlő ezen vektorok megfelelő koordinátáinak szorzatának összegével:
= x 1 * y 1 + x 2 * y 2 .

Az n-dimenziós térben az X= (x 1, x 2,...,x n) és Y= (y 1, y 2,...,y n) vektorok skaláris szorzata a szorzatok összege. a megfelelő koordinátáik: X*Y = x 1 * y 1 + x 2 * y 2 + ... + x n * y n.

A vektorok egymással való szorzása hasonló a sormátrix és az oszlopmátrix szorzásához. Hangsúlyozzuk, hogy az eredmény szám lesz, nem vektor.

A vektorok skaláris szorzata a következő tulajdonságokkal (axiómákkal) rendelkezik:

1) Kommutatív tulajdonság: X*Y=Y*X.

2) Az összeadásra vonatkozó eloszlási tulajdonság: X(Y+Z) =X*Y+X*Z.

3) Bármely valós számra 
.

4)
, haX nem nulla vektor;
ifX egy nulla vektor.

Egy lineáris vektorteret, amelyben adott a vektorok skaláris szorzata, amely kielégíti a négy megfelelő axiómát, ún. Euklideszi lineáris vektorhely.

Könnyen belátható, hogy ha bármely vektort megszorozunk önmagával, megkapjuk a hosszának négyzetét. Szóval ez más hossz egy vektor a skalárnégyzetének négyzetgyökeként definiálható:.

A vektor hossza a következő tulajdonságokkal rendelkezik:

1) |X| = 0Х = 0;

2) |X| = ||*|X|, ahol egy valós szám;

3) |X*Y||X|*|Y| ( Cauchy-Bunyakovsky egyenlőtlenség);

4) |X+Y||X|+|Y| ( háromszög egyenlőtlenség).

Az n-dimenziós térben a vektorok közötti  szöget a skaláris szorzat fogalma alapján határozzuk meg. Sőt, ha
, Azt
. Ez a tört nem nagyobb egynél (a Cauchy-Bunyakovsky egyenlőtlenség szerint), így innen -t találhatunk.

A két vektort ún ortogonális vagy merőleges, ha skalárszorzatuk nulla. A skaláris szorzat definíciójából az következik, hogy a nulla vektor ortogonális bármely vektorra. Ha mindkét ortogonális vektor nem nulla, akkor cos= 0, azaz=/2 = 90 o.

Nézzük újra a 7.4. ábrát. Az ábráról látható, hogy a vektor vízszintes tengelyhez viszonyított hajlásszögének  koszinusza kiszámítható
, és a vektor függőleges tengelyhez viszonyított szögénekhajlásának koszinusza
. Ezeket a számokat általában hívják irány koszinuszokat. Könnyen ellenőrizhető, hogy az iránykoszinuszok négyzetösszege mindig egyenlő eggyel: cos 2 +cos 2 = 1. Hasonlóképpen bevezethető az iránykoszinusz fogalma nagyobb méretű terekre is.

Vektor tér alapja

A vektorok esetében definiálhatjuk a fogalmakat lineáris kombináció,lineáris függőségÉs függetlenség hasonlóan ahhoz, ahogy ezeket a fogalmakat bevezették a mátrixsorokhoz. Az is igaz, hogy ha a vektorok lineárisan függőek, akkor legalább az egyik a többivel lineárisan kifejezhető (azaz ezek lineáris kombinációja). Ennek a fordítottja is igaz: ha az egyik vektor a többi lineáris kombinációja, akkor ezek a vektorok együtt lineárisan függenek.

Vegyük észre, hogy ha az a l , a 2 ,...a m vektorok között van egy nulla vektor, akkor ez a vektorhalmaz szükségszerűen lineárisan függő. Valójában  l a l + 2 a 2 +...+ m a m = 0-t kapunk, ha például a nullavektornál lévő j együtthatót eggyel, az összes többi együtthatót pedig nullával egyenlővé tesszük. Ebben az esetben nem minden együttható egyenlő nullával ( j ≠ 0).

Ezen túlmenően, ha egy vektorhalmazból származó vektorok egy része lineárisan függő, akkor ezek a vektorok mindegyike lineárisan függő. Valójában, ha egyes vektorok egy nulla vektort adnak a lineáris kombinációjukban olyan együtthatókkal, amelyek nem mind nullák, akkor a fennmaradó vektorokat a nulla együtthatókkal megszorozva hozzáadhatjuk ehhez a szorzatösszeghez, és ez továbbra is nulla vektor lesz.

Hogyan állapítható meg, hogy a vektorok lineárisan függenek-e?

Például vegyünk három vektort: ​​a 1 = (1, 0, 1, 5), a 2 = (2, 1, 3, -2) és a 3 = (3, 1, 4, 3). Készítsünk belőlük egy mátrixot, amelyben oszlopok lesznek:

Ekkor a lineáris függés kérdése ennek a mátrixnak a rangjának meghatározására redukálódik. Ha kiderül, hogy három, akkor mindhárom oszlop lineárisan független, és ha kevesebbnek bizonyul, akkor ez a vektorok lineáris függését jelzi.

Mivel a rang 2, a vektorok lineárisan függenek.

Vegyük észre, hogy a probléma megoldása kezdődhet olyan érveléssel is, amely a lineáris függetlenség definícióján alapul. Nevezetesen hozzunk létre egy  l a l + 2 a 2 + 3 a 3 = 0 vektoregyenletet, amely a következő formában lesz:  l *(1, 0, 1, 5) + 2 *(2, 1, 3, - 2) + 3 *(3, 1, 4, 3) = (0, 0, 0, 0). Ekkor kapunk egy egyenletrendszert:

Ennek a rendszernek a Gauss-módszerrel történő megoldása ugyanazon lépésmátrix megszerzésére redukálódik, csak még egy oszlop nélküli kifejezése lesz. Mindegyik nulla lesz, mivel a nullák lineáris transzformációja nem vezethet eltérő eredményhez. A transzformált egyenletrendszer a következőképpen alakul:

Ennek a rendszernek a megoldása a (-с;-с; с), ahol с tetszőleges szám; például (-1;-1;1). Ez azt jelenti, hogy ha  l = -1; 2 =-1 és 3 = 1, akkor l a l + 2 a 2 + 3 a 3 = 0, azaz. a vektorok valójában lineárisan függenek.

A megoldott példából világossá válik, hogy ha a tér dimenziójánál nagyobb vektorok számát vesszük, akkor azok szükségszerűen lineárisan függenek. Valójában, ha ebben a példában öt vektort vennénk, egy 4 x 5-ös mátrixot kapnánk, amelynek a rangja nem lehet nagyobb négynél. Azok. a lineárisan független oszlopok maximális száma továbbra sem lehet több négynél. Két, három vagy négy négydimenziós vektor lehet lineárisan független, de öt vagy több nem. Ebből következően legfeljebb két vektor lehet lineárisan független a síkon. A kétdimenziós térben bármely három vektor lineárisan függ. A háromdimenziós térben bármely négy (vagy több) vektor mindig lineárisan függ. Stb.

Ezért dimenzió a teret a benne található lineárisan független vektorok maximális számaként határozhatjuk meg.

Az R n-dimenziós tér n lineárisan független vektorának halmazát nevezzük alapján ezt a teret.

Tétel. A lineáris tér minden vektora bázisvektorok lineáris kombinációjaként ábrázolható, és egyedi módon.

Bizonyíték. Legyen az e l , e 2 ,...e n vektorok egy R bázisdimenziós teret. Bizonyítsuk be, hogy bármely X vektor ezen vektorok lineáris kombinációja. Mivel az X vektorral együtt a vektorok száma (n +1) lesz, ezek az (n +1) vektorok lineárisan függőek lesznek, azaz. vannak  l , 2 ,..., n , számok, amelyek egyidejűleg nem egyenlők nullával, így

 l e l + 2 e 2 +...+ n e n +Х = 0

Ebben az esetben 0, mert különben  l e l + 2 e 2 +...+ n e n = 0, ahol nem minden együttható l , 2 ,..., n egyenlő nullával. Ez azt jelenti, hogy a bázisvektorok lineárisan függőek lennének. Ezért az első egyenlet mindkét oldalát oszthatjuk:

( l /)e l + ( 2 /)e 2 +...+ ( n /)e n + X = 0

Х = -( l /)e l - ( 2 /)e 2 -...- ( n /)e n

Х = x l e l +x 2 e 2 +...+x n e n,

ahol x j = -( j /),
.

Most bebizonyítjuk, hogy egy ilyen lineáris kombináció formájában történő ábrázolás egyedülálló. Tegyük fel az ellenkezőjét, pl. hogy van egy másik ábrázolás:

Х = y l e l +y 2 e 2 +...+y n e n

Vonjuk ki belőle tagonként az előzőleg kapott kifejezést:

0 = (y l – x 1)e l + (y 2 – x 2)e 2 +...+ (y n – x n)e n

Mivel a bázisvektorok lineárisan függetlenek, azt kapjuk, hogy (y j - x j) = 0,
, azaz y j = x j . Így a kifejezés ugyanaznak bizonyult. A tétel bizonyítást nyert.

Az X = x l e l +x 2 e 2 +...+x n e n kifejezést ún. bomlás X vektor e l, e 2,...e n és x l, x 2,...x n számok alapján - koordináták x vektor ehhez a bázishoz viszonyítva, vagy ebben a bázisban.

Bizonyítható, hogy ha egy n-dimenziós euklideszi tér nonzero vektorai páronként merőlegesek, akkor bázist alkotnak. Valójában szorozzuk meg a l e l + 2 e 2 +...+ n e n = 0 egyenlőség mindkét oldalát tetszőleges e i vektorral.  l (e l *е i) +  2 (e 2 *е i) +...+  n (e n *е i) = 0   i (e i *е i) = 0   i = 0  i-re.

Az n-dimenziós euklideszi térforma e l , e 2 ,...e n vektorai ortonormális alap, ha ezek a vektorok páronként merőlegesek és mindegyik normája eggyel egyenlő, azaz. ha e i *e j = 0 i≠j и |е i | esetén = 1 fori.

Tétel (nincs bizonyíték). Minden n-dimenziós euklideszi térben van egy ortonormális alap.

Az ortonormális bázisra példa egy n egységvektorból álló e i rendszer, amelynél az i-edik komponens egyenlő eggyel, a többi komponens pedig nulla. Minden ilyen vektort ún ort. Például az (1, 0, 0), (0, 1, 0) és (0, 0, 1) vektorvektorok képezik a háromdimenziós tér alapját.

Szög vektorok között

Tekintsünk két megadott vektort: ​​$\overrightarrow(a)$ és $\overrightarrow(b)$. Vonjuk ki a $\overrightarrow(a)=\overrightarrow(OA)$ és a $\overrightarrow(b)=\overrightarrow(OB)$ vektorokat egy tetszőlegesen kiválasztott $O$ pontból, ekkor a $AOB$ szöget a szög a $\overrightarrow( a)$ és $\overrightarrow(b)$ vektorok között (1. ábra).

1. kép

Itt jegyezzük meg, hogy ha a $\overrightarrow(a)$ és a $\overrightarrow(b)$ vektorok egyirányúak, vagy az egyik a nulla vektor, akkor a vektorok közötti szög $0^0$.

Jelölés: $\widehat(\overrightarrow(a),\overrightarrow(b))$

A vektorok pontszorzatának fogalma

Matematikailag ez a definíció a következőképpen írható fel:

A pontszorzat két esetben lehet nulla:

Ha az egyik vektor nulla vektor (Azóta a hossza nulla).

Ha a vektorok egymásra merőlegesek (azaz $cos(90)^0=0$).

Vegye figyelembe azt is, hogy a skaláris szorzat nagyobb nullánál, ha a vektorok közötti szög hegyes (mivel $(cos \left(\widehat(\overrightarrow(a),\overrightarrow(b))\right)\ ) >0$) , és nullánál kisebb, ha a vektorok közötti szög tompaszögű (mivel $(cos \left(\widehat(\overrightarrow(a),\overrightarrow(b))\right)\ )

A skalárszorzat fogalmához kapcsolódik a skalárnégyzet fogalma.

2. definíció

A $\overrightarrow(a)$ vektor skalárnégyzete ennek a vektornak önmagával való skaláris szorzata.

Azt találjuk, hogy a skaláris négyzet egyenlő

\[\overrightarrow(a)\overrightarrow(a)=\left|\overrightarrow(a)\right|\left|\overrightarrow(a)\right|(cos 0^0\ )=\left|\overrightarrow(a) )\right|\left|\overrightarrow(a)\right|=(\left|\overrightarrow(a)\right|)^2\]

A pontszorzat kiszámítása vektorkoordinátákból

A skalárszorzat értékének meghatározásának a definícióból következő szokásos módszere mellett van egy másik módszer is.

Vegyük fontolóra.

Legyen a $\overrightarrow(a)$ és $\overrightarrow(b)$ $\left(a_1,b_1\right)$ és $\left(a_2,b_2\right)$ koordinátája.

1. tétel

A $\overrightarrow(a)$ és $\overrightarrow(b)$ vektorok skaláris szorzata egyenlő a megfelelő koordináták szorzatának összegével.

Matematikailag ez a következőképpen írható fel

\[\overrightarrow(a)\overrightarrow(b)=a_1a_2+b_1b_2\]

Bizonyíték.

A tétel bizonyítást nyert.

Ennek a tételnek számos következménye van:

1. következmény: A $\overrightarrow(a)$ és a $\overrightarrow(b)$ vektorok akkor és csak akkor merőlegesek, ha $a_1a_2+b_1b_2=0$

2. következmény: A vektorok közötti szög koszinusza: $cos\alpha =\frac(a_1a_2+b_1b_2)(\sqrt(a^2_1+b^2_1)\cdot \sqrt(a^2_2+b^2_2))$

A vektorok skaláris szorzatának tulajdonságai

Bármely három vektorra és egy valós számra $k$ igaz:

$(\overrightarrow(a))^2\ge 0$

Ez a tulajdonság a skalárnégyzet definíciójából következik (2. definíció).

Utazási törvény:$\overrightarrow(a)\overrightarrow(b)=\overrightarrow(b)\overrightarrow(a)$.

Ez a tulajdonság a skalárszorzat definíciójából következik (1. definíció).

Elosztási törvény:

$\left(\overrightarrow(a)+\overrightarrow(b)\right)\overrightarrow(c)=\overrightarrow(a)\overrightarrow(c)+\overrightarrow(b)\overrightarrow(c)$. \end(felsorol)

Az 1. Tétel szerint a következőket kapjuk:

\[\left(\overrightarrow(a)+\overrightarrow(b)\right)\overrightarrow(c)=\left(a_1+a_2\right)a_3+\left(b_1+b_2\right)b_3=a_1a_3+a_2a_3+ b_1b_3 +b_2b_3==\overrightarrow(a)\overrightarrow(c)+\overrightarrow(b)\overrightarrow(c)\]

Kombinációs törvény:$\left(k\overrightarrow(a)\right)\overrightarrow(b)=k(\overrightarrow(a)\overrightarrow(b))$. \end(felsorol)

Az 1. Tétel szerint a következőket kapjuk:

\[\left(k\overrightarrow(a)\right)\overrightarrow(b)=ka_1a_2+kb_1b_2=k\left(a_1a_2+b_1b_2\right)=k(\overrightarrow(a)\overrightarrow(b))\]

Példa a vektorok skaláris szorzatának kiszámítására vonatkozó feladatra

1. példa

Keresse meg a $\overrightarrow(a)$ és $\overrightarrow(b)$ vektorok skaláris szorzatát, ha $\left|\overrightarrow(a)\right|=3$ és $\left|\overrightarrow(b)\right |= 2$, és a köztük lévő szög egyenlő: $((30)^0,\ 45)^0,\ (90)^0,\ (135)^0$.

Megoldás.

Az 1. definíciót használva azt kapjuk

$(30)^0:$-ért

\[\overrightarrow(a)\overrightarrow(b)=6(cos \left((30)^0\right)\ )=6\cdot \frac(\sqrt(3))(2)=3\sqrt( 3)\]

$(45)^0:$-ért

\[\overrightarrow(a)\overrightarrow(b)=6(cos \left((45)^0\right)\ )=6\cdot \frac(\sqrt(2))(2)=3\sqrt( 2)\]

$(90)^0:$-ért

\[\overrightarrow(a)\overrightarrow(b)=6(cos \left((90)^0\right)\ )=6\cdot 0=0\]

$(135)^0:$-ért

\[\overrightarrow(a)\overrightarrow(b)=6(cos \left((135)^0\right)\ )=6\cdot \left(-\frac(\sqrt(2))(2)\ jobb)=-3\sqrt(2)\]

Előadás: vektor koordináták; vektorok skaláris szorzata; vektorok közötti szög

Vektor koordináták

Tehát, mint korábban említettük, a vektor egy irányított szegmens, amelynek saját kezdete és vége van. Ha a kezdetet és a végét bizonyos pontok ábrázolják, akkor ezeknek saját koordinátái vannak a síkon vagy a térben.

Ha minden pontnak megvannak a saját koordinátái, akkor megkaphatjuk a teljes vektor koordinátáit.

Tegyük fel, hogy van egy vektorunk, amelynek kezdete és vége a következő jelölésekkel és koordinátákkal rendelkezik: A(A x ; Ay) és B(B x ; By)

Egy adott vektor koordinátáinak megszerzéséhez ki kell vonni a kezdet megfelelő koordinátáit a vektor végének koordinátáiból:

Egy vektor térbeli koordinátáinak meghatározásához használja a következő képletet:

Vektorok pontszorzata

A skaláris szorzat fogalmát kétféleképpen lehet meghatározni:

• Geometriai módszer. Eszerint a skaláris szorzat egyenlő ezen modulok értékeinek és a köztük lévő szög koszinuszának szorzatával.

• Algebrai jelentés. Az algebra szempontjából két vektor skaláris szorzata egy bizonyos mennyiség, amelyet a megfelelő vektorok szorzatainak összegeként kapunk.

Ha a vektorok térben vannak megadva, akkor hasonló képletet kell használni:

Tulajdonságok:

• Ha két azonos vektort skalárisan megszorozunk, akkor a skalárszorzatuk nem lesz negatív:

• Ha két azonos vektor skaláris szorzata nullával egyenlő, akkor ezeket a vektorokat nullának tekintjük:

• Ha egy bizonyos vektort megszorozunk önmagával, akkor a skaláris szorzat egyenlő lesz a modulusának négyzetével:

• A skalárszorzatnak kommunikatív tulajdonsága van, vagyis a skalárszorzat nem változik, ha a vektorokat átrendezzük:

• A nullától eltérő vektorok skaláris szorzata csak akkor lehet nulla, ha a vektorok merőlegesek egymásra:

• A vektorok skaláris szorzatára a kommutatív törvény akkor érvényes, ha az egyik vektort megszorozzuk egy számmal:

• Skaláris szorzattal a szorzás eloszlási tulajdonságát is használhatja:

Szög vektorok között

Síkfeladat esetén az a = (a x; a y) és b = (b x; b y) vektorok skaláris szorzata a következő képlettel kereshető meg:

a b = a x b x + a y b y

A vektorok skaláris szorzatának képlete térbeli problémákhoz

Térbeli probléma esetén az a = (a x; a y; a z) és b = (b x; b y; b z) vektorok skaláris szorzata a következő képlettel kereshető meg:

a b = a x b x + a y b y + a z b z

Az n-dimenziós vektorok skaláris szorzatának képlete

Egy n-dimenziós tér esetén az a = (a 1; a 2; ...; a n) és b = (b 1; b 2; ...; b n) vektorok skaláris szorzatát a segítségével találhatjuk meg. a következő képlet:

a b = a 1 b 1 + a 2 b 2 + ... + a n b n

A vektorok skaláris szorzatának tulajdonságai

1. Egy vektor skaláris szorzata önmagával mindig nagyobb vagy egyenlő nullával:

2. Egy vektor skaláris szorzata önmagával akkor és csak akkor egyenlő nullával, ha a vektor egyenlő a nulla vektorral:

a · a = 0<=>a = 0

3. Egy vektor skaláris szorzata önmagával egyenlő a modulusának négyzetével:

4. A skaláris szorzás művelete kommunikatív:

5. Ha két nem nulla vektor skaláris szorzata egyenlő nullával, akkor ezek a vektorok merőlegesek:

a ≠ 0, b ≠ 0, a b = 0<=>a ┴ b

6. (αa) b = α(a b)

7. A skaláris szorzás művelete disztributív:

(a + b) c = a c + b c

Példák a vektorok skaláris szorzatának kiszámításához szükséges feladatokra

Példák vektorok skaláris szorzatának kiszámítására síkfeladatokhoz

Határozzuk meg az a = (1; 2) és b = (4; 8) vektorok skaláris szorzatát!

Megoldás: a · b = 1 · 4 + 2 · 8 = 4 + 16 = 20.

Határozzuk meg az a és b vektorok skaláris szorzatát, ha azok hossza |a| = 3, |b| = 6, és a vektorok közötti szög 60˚.

Megoldás: a · b = |a| · |b| cos α = 3 · 6 · cos 60˚ = 9.

Határozzuk meg a p = a + 3b és q = 5a - 3 b vektorok skaláris szorzatát, ha hosszuk |a| = 3, |b| = 2, és az a és b vektorok közötti szög 60˚.

Megoldás:

p q = (a + 3b) (5a - 3b) = 5 a a - 3 a b + 15 b a - 9 b b =

5 |a| 2 + 12 a · b - 9 |b| 2 = 5 3 2 + 12 3 2 cos 60˚ - 9 2 2 = 45 +36 -36 = 45.

Példa a vektorok skaláris szorzatának kiszámítására térbeli problémákra

Határozzuk meg az a = (1; 2; -5) és b = (4; 8; 1) vektorok skaláris szorzatát!

Megoldás: a · b = 1 · 4 + 2 · 8 + (-5) · 1 = 4 + 16 - 5 = 15.

Példa az n-dimenziós vektorok pontszorzatának kiszámítására

Határozzuk meg az a = (1; 2; -5; 2) és b = (4; 8; 1; -2) vektorok skaláris szorzatát!

Megoldás: a · b = 1 · 4 + 2 · 8 + (-5) · 1 + 2 · (-2) = 4 + 16 - 5 -4 = 11.

13. A vektorok és egy vektor keresztszorzatát ún harmadik vektor , a következőképpen definiálva:

2) merőleges, merőleges. (1"")

3) a vektorok orientációja ugyanúgy történik, mint a teljes tér alapja (pozitív vagy negatív).

Kijelölés: .

A vektorszorzat fizikai jelentése

— az O ponthoz viszonyított erőnyomaték; - sugár - az erő alkalmazási pontjának vektora, akkor

Sőt, ha az O pontba mozgatjuk, akkor a hármast bázisvektorként kell orientálni.