A függvény szélsőértékének elegendő jele. A funkció helyi növekedésének és csökkenésének jelei. Egy függvény szélsőértékének egy pontban való létezésének szükséges és elégséges feltételei.

Az y = f(x) függvényt meghívjuk növekvő (csökkenő) egy bizonyos intervallumban, ha x 1-re< x 2 выполняется неравенство (f(x 1) < f (x 2) (f(x 1) >f(x 2)).

Ha az y = f(x) differenciálható függvény növekszik (csökken) egy intervallumon, akkor a deriváltja ezen az intervallumon f " (x) > 0

(f" (x)< 0).

Pont x o hívott helyi maximum pont (minimális) f(x) függvény, ha van a pont szomszédsága x o, minden olyan pontra igaz, amelynek f(x) ≤ f(x о) (f(x) ≥ f(x о)) egyenlőtlenség igaz.

A maximum és minimum pontokat hívjuk szélsőséges pontok, és a függvény értékei ezeken a pontokon az ő szélsőségek.

Az extrémumhoz szükséges feltételek. Ha a lényeg x o az f(x) függvény szélsőpontja, akkor vagy f " (x o) = 0, vagy f (x o) nem létezik. Az ilyen pontokat ún. kritikai, maga a függvény pedig a kritikus pontban van definiálva. Egy függvény szélsőpontját a kritikus pontjai között kell keresni.

Az első elégséges feltétel. Hadd x o- kritikus pont. Ha f "(x) ponton való áthaladáskor x o módosítja a plusz jelet mínuszra, majd a pontra x o a függvénynek van maximuma, egyébként minimuma. Ha a kritikus ponton áthaladva a derivált nem vált előjelet, akkor a pontban x o nincs szélsőség.

Második elégséges feltétel. Legyen az f(x) függvénynek deriváltja
f "(x) a pont közelében x o a második derivált pedig magában a pontban x o. Ha f "(x o) = 0, >0 (<0), то точка x o az f(x) függvény lokális minimum (maximum) pontja. Ha =0, akkor vagy az első elégséges feltételt kell használnia, vagy magasabb származékokat kell használnia.

Egy szakaszon az y = f(x) függvény akár a kritikus pontokon, akár a szakasz végén elérheti minimális vagy maximum értékét.

Tanulmányozási feltételek és grafikonok ábrázolása.

Keresse meg egy függvény tartományát

Keresse meg a grafikon és a koordinátatengelyek metszéspontjait

Keresse meg az állandóság jelének intervallumait!

Vizsgálja meg az egyenletességet, a páratlanságot

Keresse meg egy függvény gráfjának aszimptotáit

Keresse meg egy függvény monotonitási intervallumait

Keresse meg a függvény szélsőértékét

Konvexitási intervallumok és inflexiós pontok keresése

Függvénygráfok aszimptotái. A függvénygráfok tanulmányozásának és ábrázolásának általános sémája. Példák.

Függőleges

Függőleges aszimptota - egyenes vonal, határérték fennállása esetén .

A függőleges aszimptota meghatározásakor általában nem egy határt, hanem két egyoldalút (bal és jobb) keresnek. Ennek célja annak meghatározása, hogy a függvény hogyan viselkedik, amikor különböző irányokból megközelíti a függőleges aszimptotát. Például:

Megjegyzés: ügyeljen ezekben az egyenlőségekben a végtelen jeleire.

[szerkesztés]Vízszintes

Vízszintes aszimptota - egyenes vonal, határérték fennállása esetén

[szerkesztés] Ferde

Ferde aszimptota - egy egyenes vonal, a határok meglététől függően

Példa egy ferde aszimptotára

Megjegyzés: egy függvénynek legfeljebb két ferde (vízszintes) aszimptotája lehet!

Megjegyzés: Ha a fent említett két határérték közül legalább az egyik nem létezik (vagy egyenlő azzal), akkor a (vagy ) pontban lévő ferde aszimptóta nem létezik!

A ferde és vízszintes aszimptoták kapcsolata

Ha a határérték kiszámításakor , akkor nyilvánvaló, hogy a ferde aszimptota egybeesik a vízszintessel. Mi a kapcsolat a két aszimptotatípus között?

A dolog, hogy a vízszintes aszimptota a ferde speciális esete nál nél , és a fenti megjegyzésekből az következik

1. A függvénynek vagy csak egy ferde aszimptotája van, vagy egy függőleges aszimptotája, vagy egy ferde és egy függőleges, vagy két ferde, vagy két függőleges, vagy egyáltalán nincs aszimptotája.

2. Az 1.) bekezdésben megjelölt aszimptoták megléte közvetlenül összefügg a megfelelő határértékek meglétével.

Egy függvény grafikonja két vízszintes aszimptotával

]Aszimptoták keresése

Az aszimptoták megtalálásának sorrendje

1. Függőleges aszimptoták keresése.

2. Két határ megtalálása

3. Két határ megtalálása:

ha a 2.), akkor , és a határértéket a horizontális aszimptota képlet segítségével kell keresni, .

A függvény szélsőpontja a függvény definíciós tartományának az a pontja, ahol a függvény értéke minimum vagy maximum értéket vesz fel. A függvény értékeit ezeken a pontokon a függvény szélsőértékének (minimum és maximum) nevezzük.

Meghatározás. Pont x1 függvény tartomány f(x) nak, nek hívják a függvény maximális pontja , ha a függvény értéke ezen a ponton nagyobb, mint a függvény értékei a hozzá kellően közeli pontokban, amelyek tőle jobbra és balra helyezkednek el (azaz az egyenlőtlenség fennáll f(x0 ) > f(x 0 + Δ x) x1 maximális.

Meghatározás. Pont x2 függvény tartomány f(x) nak, nek hívják a függvény minimális pontja, ha a függvény értéke ezen a ponton kisebb, mint a függvény értékei a hozzá kellően közeli pontokban, amelyek tőle jobbra és balra helyezkednek el (azaz az egyenlőtlenség fennáll f(x0 ) < f(x 0 + Δ x) ). Ebben az esetben azt mondjuk, hogy a függvénynek a pontja van x2 minimális.

Mondjuk pont x1 - a függvény maximális pontja f(x) . Majd az intervallumban ig x1 funkciója növekszik ezért a függvény deriváltja nagyobb nullánál ( f "(x) > 0 ), és az azt követő intervallumban x1 a funkció csökken, ezért függvény deriváltja nullánál kisebb ( f "(x) < 0 ). Тогда в точке x1

Tegyük fel azt is, hogy a lényeg x2 - a függvény minimális pontja f(x) . Majd az intervallumban ig x2 a függvény csökkenőben van, és a függvény deriváltja kisebb, mint nulla ( f "(x) < 0 ), а в интервале после x2 a függvény növekszik, és a függvény deriváltja nagyobb, mint nulla ( f "(x) > 0). Ebben az esetben is a ponton x2 a függvény deriváltja nulla vagy nem létezik.

Fermat-tétel (egy függvény szélsőértékének szükséges jele). Ha a lényeg x0 - a függvény szélsőpontja f(x) akkor ezen a ponton a függvény deriváltja egyenlő nullával ( f "(x) = 0 ) vagy nem létezik.

Meghatározás. Meghívjuk azokat a pontokat, ahol egy függvény deriváltja nulla vagy nem létezik kritikus pontok .

1. példa Tekintsük a függvényt.

Azon a ponton x= 0 a függvény deriváltja nulla, ezért a pont x= 0 a kritikus pont. Azonban, mint a függvény grafikonján látható, az egész definíciós tartományban növekszik, tehát a lényeg x A = 0 nem ennek a függvénynek a szélsőpontja.

Tehát azok a feltételek, hogy egy függvény deriváltja egy pontban egyenlő nullával, vagy nem létezik, szükséges feltételek egy szélsőséghez, de nem elégségesek, hiszen más példákat is lehet adni olyan függvényekre, amelyekre ezek a feltételek teljesülnek, de a függvény nincs szélső értéke a megfelelő pontban. Ezért elegendő bizonyítéknak kell lennie, amely lehetővé teszi annak megítélését, hogy van-e szélsőség egy adott kritikus ponton, és milyen szélsőségről van szó - maximum vagy minimum.

Tétel (egy függvény szélsőértéke létezésének első elégséges jele). Kritikus pont x0 f(x) ha ezen a ponton áthaladva a függvény deriváltja előjelet vált, és ha az előjel „plusz”-ról „mínuszra” változik, akkor az maximum pont, ha pedig „mínusz”-ról „pluszra”, akkor ez egy minimum pont.

Ha a pont közelében x0 , tőle balra és jobbra a derivált megtartja előjelét, ez azt jelenti, hogy a függvény vagy csak csökken, vagy csak a pont egy bizonyos környezetében nő. x0 . Ebben az esetben a ponton x0 nincs szélsőség.

Így, a függvény szélsőpontjainak meghatározásához a következőket kell tennie :

Keresse meg a függvény deriváltját!
Egyenlítse a derivált nullával, és határozza meg a kritikus pontokat.
Gondolatban vagy papíron jelölje be a kritikus pontokat a számegyenesen, és határozza meg a függvény deriváltjának előjeleit a kapott intervallumokban! Ha a derivált előjele „pluszról” mínuszra változik, akkor a kritikus pont a maximum pont, ha pedig „mínusz”-ról „pluszra”, akkor a minimumpont.
Számítsa ki a függvény értékét a szélsőpontokban!

2. példa Keresse meg a függvény szélsőértékét .

Megoldás. Keressük meg a függvény deriváltját:

Tegyük egyenlővé a derivált nullával, hogy megtaláljuk a kritikus pontokat:

Mivel az „x” bármely értékénél a nevező nem egyenlő nullával, a számlálót nullával egyenlővé tesszük:

Van egy kritikus pont x= 3. Határozzuk meg a derivált előjelét az e pont által határolt intervallumokban:

a mínusz végtelentől 3-ig terjedő tartományban - mínusz jel, vagyis a függvény csökken,

a 3-tól a plusz végtelenig terjedő intervallumban van egy pluszjel, vagyis a függvény növekszik.

Vagyis pont x= 3 a minimumpont.

Keressük meg a függvény értékét a minimum pontban:

Így a függvény szélsőpontja: (3; 0), és ez a minimumpont.

Tétel (a függvény szélsőértékének létezésének második elégséges jele). Kritikus pont x0 a függvény szélsőpontja f(x) ha a függvény második deriváltja ebben a pontban nem egyenlő nullával ( f ""(x) ≠ 0), és ha a második derivált nagyobb, mint nulla ( f ""(x) > 0 ), akkor a maximális pont, és ha a második derivált kisebb, mint nulla ( f ""(x) < 0 ), то точкой минимума.

Megjegyzés 1. Ha azon a ponton x0 Ha az első és a második derivált is eltűnik, akkor ezen a ponton lehetetlen a szélsőség meglétét megítélni a második elégséges kritérium alapján. Ebben az esetben az első elégséges kritériumot kell használnia egy függvény szélsőértékéhez.

Megjegyzés 2. A függvény szélsőértékére vonatkozó második elégséges feltétel akkor sem alkalmazható, ha az első derivált egy stacionárius pontban nem létezik (akkor a második derivált sem létezik). Ebben az esetben a függvény szélsőértékének első elégséges jelét is kell használni.

A függvény szélsőértékének lokális jellege

A fenti definíciókból az következik, hogy egy függvény szélsőértéke lokális jellegű - ez a függvény legnagyobb és legkisebb értéke a közeli értékekhez képest.

Tegyük fel, hogy egy éves időszakra tekinti a bevételeit. Ha májusban 45 000 rubelt, áprilisban 42 000 rubelt és júniusban 39 000 rubelt keresett, akkor a májusi bevétel a bevételi függvény maximuma a közeli értékekhez képest. De októberben 71 000 rubelt, szeptemberben 75 000 rubelt, novemberben 74 000 rubelt keresett, tehát az októberi bevétel a kereseti függvény minimuma a közeli értékekhez képest. És könnyen belátható, hogy az április-május-június értékek között a maximum kevesebb, mint a szeptember-október-november minimum.

Általánosságban elmondható, hogy egy intervallumon egy függvénynek több szélsősége is lehet, és kiderülhet, hogy a függvény valamely minimuma nagyobb bármely maximumnál. Tehát a fenti ábrán látható függvényhez .

Vagyis nem szabad azt gondolni, hogy egy függvény maximuma és minimuma a legnagyobb és legkisebb értéke a teljes vizsgált szegmensben. A maximum ponton a függvénynek csak azokhoz az értékekhez viszonyítva van a legnagyobb értéke, amelyek minden pontjában kellően közel vannak a maximum ponthoz, a minimum ponton pedig csak ezekkel az értékekkel összehasonlítva a legkisebb értéke. hogy minden pontján kellően közel legyen a minimumponthoz.

Ezért tisztázhatjuk a függvény szélsőpontjainak fenti fogalmát, és a minimumpontokat helyi minimumpontoknak, a maximumpontokat pedig lokális maximumpontoknak nevezhetjük.

Együtt keressük a függvény szélsőértékét

3. példa

Megoldás: A függvény definiált és folytonos a teljes számegyenesen. A származéka a teljes számegyenesen is létezik. Ezért ebben az esetben csak azok a kritikus pontok, amelyeknél, pl. , honnan és . A kritikus pontok és a függvény teljes definíciós tartományát három monotonitási intervallumra osztjuk: . Válasszunk ki mindegyikben egy-egy vezérlőpontot, és keressük meg a derivált előjelét ezen a ponton.

Az intervallumhoz a vezérlőpont lehet: find. Ha egy pontot veszünk az intervallumban, akkor azt kapjuk, és az intervallumban egy pontot veszünk. Tehát az intervallumokban és , és az intervallumban. A szélsőség első elégséges kritériuma szerint a pontban nincs szélsőérték (mivel a derivált az intervallumban megtartja előjelét), a pontban pedig a függvénynek van minimuma (mivel a derivált mínuszból plusz előjelet vált átadáskor ezen a ponton keresztül). Keressük meg a függvény megfelelő értékeit: , a . Az intervallumban a függvény csökken, mivel ebben az intervallumban , az intervallumban pedig nő, mivel ebben az intervallumban .

A gráf felépítésének tisztázása érdekében megkeressük annak metszéspontjait a koordinátatengelyekkel. Ha olyan egyenletet kapunk, amelynek gyöke és, azaz a függvény grafikonjának két (0; 0) és (4; 0) pontja található. Az összes kapott információ felhasználásával grafikont készítünk (lásd a példa elejét).

A számítások során végzett önellenőrzéshez használhatja online származékkalkulátor .

4. példa Keresse meg a függvény szélsőértékét, és készítse el a grafikonját.

Egy függvény definíciós tartománya a teljes számegyenes, kivéve a pontot, azaz. .

A tanulmány lerövidítésére használhatja azt a tényt, hogy ez a függvény páros, mivel . Ezért a grafikonja szimmetrikus a tengelyre Oyés a vizsgálat csak az intervallumra végezhető el.

A származék megkeresése és a funkció kritikus pontjai:

1) ;

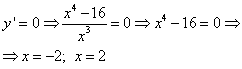2) ,

de a függvény ezen a ponton diszkontinuitást szenved, így nem lehet szélsőpont.

Így az adott függvénynek két kritikus pontja van: és . Figyelembe véve a függvény paritását, csak a pontot fogjuk ellenőrizni a szélsőség második elégséges feltételével. Ehhez megtaláljuk a második származékot és határozzuk meg az előjelét: kapunk . Mivel és , ez az és függvény minimális pontja .

Ahhoz, hogy teljesebb képet kapjunk egy függvény gráfjáról, nézzük meg a viselkedését a definíciós tartomány határain:

(itt a szimbólum a vágyat jelzi x jobbról nullára, és x pozitív marad; hasonlóképpen törekvést jelent x balról nullára, és x negatív marad). Így ha , akkor . Ezután megtaláljuk

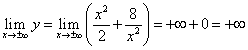azok. ha akkor .

Egy függvény grafikonjának nincs metszéspontja a tengelyekkel. A kép a példa elején található.

A számítások során végzett önellenőrzéshez használhatja online származékkalkulátor .

Továbbra is közösen keressük a függvény szélsőségeit

8. példa. Keresse meg a függvény szélsőértékét.

Megoldás. Keressük meg a függvény definíciós tartományát. Mivel az egyenlőtlenségnek teljesülnie kell, ebből kapjuk.

Keressük meg a függvény első deriváltját.

Egy függvény maximumának és minimumának meghatározásához használhatja a szélsőség három elégséges jelét. Bár a leggyakoribb és legkényelmesebb az első.

Az első elégséges feltétel az extrémumhoz.

Legyen a függvény y = f(x) differenciálható a pont szomszédságában, és magában a pontban folytonos. Akkor

Más szavakkal:

Algoritmus.

Megtaláljuk a függvény definíciós tartományát.

A függvény deriváltját a definíciós tartományon találjuk.

Meghatározzuk a számláló nulláit, a derivált nevezőjének nulláit és a definíciós tartomány azon pontjait, ahol a derivált nem létezik (ezeket a pontokat ún. lehetséges szélsőpontok, ezeken a pontokon áthaladva a derivált éppen előjelét változtathatja).

Ezek a pontok a függvény definíciós tartományát olyan intervallumokra osztják, amelyekben a derivált megtartja előjelét. Meghatározzuk a derivált előjeleit az egyes intervallumokon (például úgy, hogy egy függvény deriváltjának értékét kiszámítjuk egy adott intervallum bármely pontján).

Kijelöljük azokat a pontokat, ahol a függvény folytonos, és amelyeken áthaladva a derivált előjelet vált.

Példa. Keresse meg a függvény szélsőértékét.
Megoldás.
Egy függvény tartománya a valós számok teljes halmaza, kivéve x = 2.
A származék megkeresése:

A számláló nullái pontok x = -1És x = 5, akkor a nevező nullára megy x = 2. Jelölje be ezeket a pontokat a számtengelyen

Minden intervallumban meghatározzuk a derivált előjeleit, ehhez kiszámítjuk a derivált értékét az egyes intervallumok bármelyik pontjában, például a pontokban x = -2, x = 0, x = 3És x=6.

Ezért az intervallumon a derivált pozitív (az ábrán pluszjelet teszünk erre az intervallumra). Hasonlóképpen

Ezért a második intervallum fölé mínuszt, a harmadik fölé mínuszt, a negyedik fölé pedig pluszt teszünk.

Marad a pontok kiválasztása, ahol a függvény folytonos és deriváltja előjelet vált. Ezek az extrém pontok.
Azon a ponton x = -1 a függvény folytonos és a derivált az előjelet pluszról mínuszra változtatja, ezért a szélsőség első jele szerint x = -1 a maximum pont, a függvény maximuma ennek felel meg.
Azon a ponton x = 5 a függvény folytonos és a derivált előjelet mínuszról pluszra változtat, ezért x = -1 a minimumpont, a függvény minimuma ennek felel meg.
Grafikus illusztráció.

Válasz: .

A függvény szélsőértékének második elégséges jele.
hagyd,

ha , akkor a minimum pont;

ha , akkor a maximális pont.

Amint láthatja, ez a feltétel megköveteli, hogy a pontban legalább a másodrendű derivált létezzen.
Példa. Keresse meg a függvény szélsőértékét.
Megoldás.
Kezdjük a definíció tartományával:

Különböztessük meg az eredeti függvényt:

A derivált nullára megy at x = 1, vagyis ez egy lehetséges szélsőpont.
Megkeressük a függvény második deriváltját, és kiszámítjuk az értékét x = 1:

Ezért a második elégséges feltétel egy szélsőséghez, x = 1- maximum pont. Ezután - a függvény maximuma.
Grafikus illusztráció.

Válasz: .
A függvény szélsőértékének harmadik elégséges jele.
Legyen a függvény y = f(x) ig származékai vannak n-edik sorrend a pont szomszédságában és deriváltak ig n+1-edik sorrend magán a ponton. Hadd legyen.
Akkor,

Munka vége -

Ez a téma a következő részhez tartozik:

Algebra és analitikus geometria. A mátrix fogalma, műveletek mátrixokon és tulajdonságaik

A mátrix fogalma a mátrixokon végzett műveletek és tulajdonságaik. A mátrix egy téglalap alakú táblázat, amely olyan számokból áll, amelyek nem lehetnek.. a mátrixösszeadás pedig egy elemenkénti művelet.

Ha további anyagra van szüksége ebben a témában, vagy nem találta meg, amit keresett, javasoljuk, hogy használja a munkaadatbázisunkban található keresést:

Mit csinálunk a kapott anyaggal:

Ha ez az anyag hasznos volt az Ön számára, elmentheti az oldalára a közösségi hálózatokon:

Az összes téma ebben a részben:

A differenciálhatóság definíciója
A derivált megtalálásának műveletét függvény differenciálásának nevezzük. Egy függvényt egy bizonyos ponton differenciálhatónak mondunk, ha abban a pontban véges deriváltja van, és

A megkülönböztetés szabálya
Következmény 1. A konstans tényező kivehető a derivált előjeléből:

A származék geometriai jelentése. Érintőegyenlet
Az y = kx+b egyenes dőlésszöge a helyzettől mért szög

Egy függvény deriváltjának geometriai jelentése egy pontban
Tekintsük az y = f(x) függvény grafikonjának AB szekánsát úgy, hogy az A és B pont koordinátái legyenek.

Megoldás
A függvény minden valós számra definiálva van. Mivel (-1; -3) egy érintési pont, akkor

Az extrémumhoz szükséges feltételek és a szélsőséghez elegendő feltételek
Növekvő függvény definíciója. Az y = f(x) függvény növekszik az X intervallumon, ha van ilyen

Egy függvény monotonitásának és állandóságának feltételei
Egy függvény (nem szigorú) monotonitásának feltétele egy intervallumon. Legyen a függvénynek mindegyikben deriváltja

Az antiderivatív definíciója
Egy f(x) függvény antideriváltja az (a; b) intervallumon egy olyan F(x) függvény, hogy az egyenlőség

Vizsgálat
Az eredmény ellenőrzéséhez megkülönböztetjük a kapott kifejezést: Ennek eredményeként azt kapjuk

Egy konstans és egy függvény szorzatának antideriváltája egyenlő egy állandó és egy függvény antideriváltjának szorzatával
Egy intervallumon adott függvény antideriváltja létezésének elégséges feltétele az

Meghatározás
Legyen definiálva

Geometriai jelentés
A határozott integrál numerikusan egyenlő az ábra abszcissza tengelye és az egyenesek által határolt területével

Határozott integrál tulajdonságai
Határozott integrál alapvető tulajdonságai. Tulajdonság 1. Egy határozott integrál deriváltja a felső határhoz képest egyenlő azzal az integrandusszal, amelybe változó helyett integrálunk

Newton-Leibniz képlet (bizonyítással)
Newton-Leibniz képlet. Legyen az y = f(x) függvény folytonos egy intervallumon és F(x) a függvény egyik antideriváltja ezen az intervallumon, akkor az egyenlet

Tétel (az első elégséges feltétel a szélsőséghez). Legyen a függvény folytonos egy pontban, és a derivált változás előjele a ponton való áthaladáskor. Ekkor a szélsőség pontja: maximum, ha a jel „+”-ról „–”-ra változik, és minimum, ha „–”-ról „+”-ra változik.

Bizonyíték. Legyen a és at .

Lagrange tétele szerint , ahol .Akkor ha , akkor ; ezért , ennélfogva, , vagy . Ha akkor; ezért , ennélfogva, vagy .

Így bebizonyosodott, hogy a közeli pontokon, pl. – a függvény maximális pontja.

A tétel bizonyítása a minimumpontra hasonlóan történik. A tétel bebizonyosodott.

Ha egy ponton áthaladva a derivált nem változtat előjelet, akkor a pontban nincs szélsőség.

Tétel (szélsőség második elégséges feltétele). Legyen egy pontban egy kétszer differenciálható függvény deriváltja 0 (), és legyen a második deriváltja ebben a pontban nullától () eltérő, és a pont valamely környezetében folytonos. Ekkor a szélsőpont; ez a minimum pont, és ez a maximum pont.

Algoritmus egy függvény szélsőértékének meghatározására a szélsőség első elégséges feltételével.

1. Keresse meg a származékot.

2. Keresse meg a függvény kritikus pontjait!

3. Vizsgálja meg minden kritikus ponttól balra és jobbra a derivált előjelét, és vonjon le következtetést a szélsőségek jelenlétére!

4. Keresse meg a függvény szélső értékeit.

Algoritmus egy függvény szélsőértékének meghatározására a szélsőség második elégséges feltételével.

1. Keresse meg a származékot.

2. Keresse meg a második deriváltot.

3. Keresse meg azokat a pontokat, ahol .

4. Határozza meg az előjelet ezeken a pontokon.

5. Vonjon le következtetést a szélsőségek létezéséről és természetéről!

6. Keresse meg a függvény szélső értékeit.

Példa. Mérlegeljük . meg fogjuk találni . Továbbá a és a . Tanulmányozzuk a kritikus pontokat a szélsőség első elégséges feltételével. Megvan ez érte és érte , és érte . A pontokban és a derivált megváltoztatja az előjelét: at „+”-ról „–”-ra, és at at „–”-ról „+”-ra. Ez azt jelenti, hogy egy ponton a függvénynek van maximuma, egy ponton pedig minimuma; . Összehasonlításképpen a kritikus pontokat a szélsőség második elégséges feltételével vizsgáljuk. Keressük a második származékot. Van: , és ez azt jelenti, hogy egy ponton a függvénynek van maximuma, egy ponton pedig minimuma.

A függvénygráf aszimptotájának fogalma. Vízszintes, ferde és függőleges aszimptoták. Példák.

Meghatározás. Egy függvény grafikonjának aszimptotája egy olyan egyenes, amelynek az a tulajdonsága, hogy egy pont és az egyenes közötti távolság nullára hajlik, amikor a gráfpont korlátlanul elmozdul az origótól.

Vannak függőleges (6.6. ábra a), vízszintes (6.6. b ábra) és ferde (6.6. c. ábra) aszimptoták.

ábrán. 6.6a látható függőleges aszimptota.

A 6.6b ábrán - vízszintes aszimptota.

ábrán. 6,6 V - ferde aszimptota.

1. tétel. A függőleges aszimptoták pontjain (például ) a függvény folytonossági hiányt szenved, a ponttól balra és jobbra eső határértéke egyenlő:

2. tétel. Legyen a függvény kellően nagyra definiálva, és vannak véges határok

ÉS .

Ekkor az egyenes a függvény grafikonjának ferde aszimptotája.

3. tétel. Legyen a függvény kellően nagyra definiálva, és a függvénynek van korlátja. Ekkor az egyenes a függvény grafikonjának vízszintes aszimptotája.

A vízszintes aszimptota a ferde aszimptota speciális esete, amikor . Ezért, ha bármely irányban egy görbének van vízszintes aszimptotája, akkor ebben az irányban nincs ferde, és fordítva.

Példa. Keresse meg a függvény grafikonjának aszimptotáit!

Megoldás. Abban a pontban, ahol a függvény nincs definiálva, keressük meg a ponttól balra és jobbra eső függvény határait:

; .

Ezért ez egy függőleges aszimptota.

A függvények tanulmányozásának és grafikonjainak felépítésének általános sémája. Példa.

A függvénykutatás általános sémája és megtervezi azt.

1. Keresse meg a definíciós tartományt.

2. Vizsgálja meg az egyenlőség - páratlanság függvényét.

3. Keresse meg a függőleges aszimptotákat és a folytonossági pontokat (ha vannak).

4. Vizsgálja meg egy függvény viselkedését a végtelenben; keresse meg a vízszintes és a ferde aszimptotákat (ha vannak).

5. Határozza meg a függvény monotonságának szélsőértékeit és intervallumait!

6. Keresse meg a gráf és a koordinátatengelyek metszéspontjait, és ha szükséges a gráf sematikus felépítéséhez, keressen további pontokat!

7. Rajzoljon sematikusan egy grafikont.

A függvénytanulmány részletes diagramja és az összerajzolás .

1. Keresse meg a definíció tartományát .

a. Ha y-nak van nevezője, akkor nem szabad 0-ra mennie.

b. A páros fokú gyök gyök kifejezésének nem negatívnak kell lennie (nullánál nagyobb vagy egyenlő).

c. Az alblog kifejezésnek pozitívnak kell lennie.

2. Vizsgáljuk meg a paritás - páratlanság függvényét.

a. Ha , akkor a függvény páros.

b. Ha , akkor a függvény páratlan.

c. Ha egyik sem, sem , akkor az általános forma függvénye.

3. Keressen függőleges aszimptotákat és megszakítási pontokat (ha vannak).

a. Függőleges aszimptota csak a függvény definíciós tartományának határán fordulhat elő.

b. Ha ( vagy ), akkor a grafikon függőleges aszimptotája.

4. Vizsgálja meg egy függvény viselkedését a végtelenben; keresse meg a vízszintes és a ferde aszimptotákat (ha vannak).

a. Ha , akkor a gráf vízszintes aszimptotája.

b. Ha , akkor az egyenes a gráf ferde aszimptotája.

c. Ha az a, b bekezdésekben jelzett határértékek csak akkor léteznek, ha az egyoldaliság a végtelenbe hajlik (vagy ), akkor az eredményül kapott aszimptoták egyoldalúak lesznek: balkezesek és jobbkezesek, amikor .

5. Keresse meg a függvény monotonitás szélsőségeit és intervallumait.

a. Keresse meg a származékot.

b. Keresse meg a kritikus pontokat (azokat a pontokat, ahol vagy ahol nem léteznek).

c. A számtengelyen jelölje be a definíciós tartományt és annak kritikus pontjait.

d. A kapott numerikus intervallumok mindegyikén határozza meg a derivált előjelét.

e. A derivált jelei alapján vonjon le következtetést az y-ban lévő szélsőségek jelenlétéről és típusáról!

f. Keressen szélsőséges értékeket.

g. A derivált jelei alapján vonjon le következtetéseket a növekedésről és a csökkenésről!

6. Keresse meg a grafikon és a koordinátatengelyek metszéspontjait, és ha szükséges a grafikon sematikus ábrázolásához, keressen további pontokat.

a. A gráf tengellyel való metszéspontjainak megtalálásához meg kell oldani az egyenletet. Azok a pontok, ahol nullák, a grafikon és a tengely metszéspontjai lesznek.

b. A grafikon és a tengely metszéspontja így néz ki. Csak akkor létezik, ha a pont a függvény tartományán belül van.

8. Rajzoljon sematikusan egy grafikont.

a. Szerkesszünk koordinátarendszert és aszimptotákat!

b. Jelölje meg a szélsőséges pontokat.

c. Jelölje be a grafikon metszéspontjait a koordinátatengelyekkel.

d. Készítsen sematikusan egy gráfot úgy, hogy az áthaladjon a megjelölt pontokon, és megközelítse az aszimptotákat.

Példa. Fedezze fel a függvényt, és vázolja fel a grafikonját.

2. – általános forma funkciója.

3. Mivel és , akkor a és vonalak függőleges aszimptoták; pontok töréspontok. , amikor nem szerepel a függvény definíciós tartományában

1. számú jegy

antiderivatív funkcióTételBizonyíték határozatlan integrál

Az (X 0 ;Y 0) pontot hívjuk maximális pont minimum pont függvények: minden (X 0 ;Y 0) ponttól eltérő (x;y) pontra az (X 0 ;Y 0) pont δ-szomszédságából az f(x;y)>f(X 0 ;Y) egyenlőtlenség 0) elégedett.

Bizonyíték:

Jegy 2. sz

BizonyítékGeometriai jelentés

magán növekmény részleges származéka Geometriai jelentés

Jegy 3. sz

19. A z=f(x,y) függvény maximum és minimum pontjainak meghatározása. Az (X 0 ;Y 0) pontot hívjuk maximális pont z=f(x;y) függvény, ha az (X 0 ;Y 0) pontnak van olyan δ-szomszédsága, amelyre az f(x;y) egyenlőtlenség teljesül minimum pont függvények: minden (X 0 ;Y 0) ponttól eltérő (x;y) pontra az (X 0 ;Y 0) pont δ-szomszédságából az f(x;y)>f(X 0 ;Y) egyenlőtlenség 0) elégedett. Legyen egy stacionárius pontban (X 0 ;Y 0) és a szomszédságában az f(x;y) függvénynek folytonos parciális deriváltjai a második rendig bezárólag. Számítsuk ki az (X 0 ;Y 0) pontban az A=f"" xx (X 0 ;Y 0), B=f"" xy (X 0 ;Y 0), C=f"" yy (X 0 ;Y 0). Jelöljük Δ=|AB; BC|=AC-B^2. Ekkor: 1) ha Δ><0; минимум, если A>0; 2) ha Δ<0, то функция f(x;y) в точке (X 0 ;Y 0) экстремума не имеет. В случае Δ=0 экстремум в точке (X 0 ;Y 0) может быть, а может не быть. Необходимы дополнительные исследования.

4. sz. jegy Határozott integrállal Tulajdonságok Bizonyíték. egy pontban koordinátákkal (x;y;z).Δu/Δl=LimΔl→0(Δl u/Δl)=(δu/δx)*cosα+(δu/δy)*cosβ+(δu/δz)*cosγ Tegyük fel, hogy az u(x;y;z) függvény folytonos és folytonos deriváltjai vannak a D tartománybeli argumentumaihoz képest: Δu=(δu/δx)Δx+(δu/δy)Δy+(δu/δz)Δz+ E 1 Δx+E 2 Δy+E 3 Δz, ahol E 1, E 2, E 3 nullára hajlik, mint Δl→0. Osszuk el a teljes egyenlőséget Δl-lel. Δu/Δl=(δu/δx)(Δx/Δl)+(δu/δy)(Δy/Δl)+(δu/δz) (Δz/Δl)+E 1 (Δx/Δl)+E 2 (Δy/ Δl)+E3 (Δz/Δl). Δx/Δl=cosα; Δy/Δl=cosβ; Δz/Δl=cosγ. Az egyenlőség a következőképpen ábrázolható: Δu/Δl=(δu/δx)cosα+(δu/δy)cosβ+(δu/δz)cosγ+E 1 cosα+E 2 cosβ+E 3 cosγ. A határértékre haladva megkapjuk a Δu/Δl=LimΔl→0(Δ l u/Δl)=(δu/δx)*cosα+(δu/δy)*cosβ+(δu/δz)*cosγ.

5. sz. jegy

1. Antiderivatív funkció. Tétel két antiderivált különbségéről (bizonyítással). Határozatlan integrál: definíció Az F(x) függvényt meghívjuk antiderivatív funkció f(x) az (a;b) intervallumon, ha bármely x∈(a;b) esetén teljesül az F"(x)=f(x) egyenlőség. Tétel. Ha az F(x) függvény az (a;b) f(x) függvény antideriváltja, akkor f(x) összes antideriváltjának halmazát az F(x)+C képlet adja meg, ahol C= const. Bizonyíték. Az F(x)+C függvény az f(x) antideriváltja. Valóban, (F(x)+C)"=F"(x)=f(x). Legyen Ф(x) valamilyen másik, az F(x-től eltérő f(x) antiderivatív függvény, azaz. Ф"(x)=f(x). Ekkor bármely x∈(a;b) esetén van (Ф(х)-F(x))"=Ф"(x)-F"(x)=f( x )-f(x)=0. Ez pedig azt jelenti, hogy Ф(x)-F(x)=C, C=állandó. Ezért Ф(x)=F(x)+C. Az F(x)+C antiderivatív függvények halmazát f(x)-re ún. határozatlan integrál az f(x) függvényből, és ∫f(x)dx szimbólummal jelöljük.

19. A z=f(x,y) függvény maximum és minimum pontjainak meghatározása. Az (X 0 ;Y 0) pontot hívjuk maximális pont z=f(x;y) függvény, ha az (X 0 ;Y 0) pontnak van olyan δ-szomszédsága, amelyre az f(x;y) egyenlőtlenség teljesül minimum pont függvények: minden (X 0 ;Y 0) ponttól eltérő (x;y) pontra az (X 0 ;Y 0) pont δ-szomszédságából az f(x;y)>f(X 0 ;Y) egyenlőtlenség 0) elégedett . 20. A z=f(x;y) függvény szélsőértéke létezésének elégséges jele. (megfogalmazás). Legyen egy stacionárius pontban (X 0 ;Y 0) és a szomszédságában az f(x;y) függvénynek folytonos parciális deriváltjai a második rendig bezárólag. Számítsuk ki az (X 0 ;Y 0) pontban az A=f"" xx (X 0 ;Y 0), B=f"" xy (X 0 ;Y 0), C=f"" yy (X 0 ;Y 0). Jelöljük Δ=|AB; BC|=AC-B^2. Ekkor: 1) ha Δ>0, akkor az f(x;y) függvénynek az (X 0 ;Y 0) pontban van egy szélsőértéke: maximum, ha A<0; минимум, если A>0; 2) ha Δ<0, то функция f(x;y) в точке (X 0 ;Y 0) экстремума не имеет. В случае Δ=0 экстремум в точке (X 0 ;Y 0) может быть, а может не быть. Необходимы дополнительные исследования.

Jegy 6. sz

3. Határozott integrál számítása szakaszon. Newton-Leibniz formula (származtatás). Ha az y=f(x) függvény folytonos egy intervallumon, és F(x) bármely antideriváltja az (F"(x)=f(x) ponton), akkor az ∫(a-tól b-ig) f( x) teljesül )dx=F(b)-F(a). Ez a képlet a Newton-Leibniz képlet. Tekintsük az azonosságot: F(b)-F(a)=F(x n)-F(x 0)= (F(xn)-F(xn-1))+(f(xn-1)-F(xn-2))+…(F(x2)-F(x1))+(F(x1) )-F(x 0)). Alakítsuk át az egyes különbségeket zárójelben a Lagrange-képlet segítségével: f(b)-f(a)=f'(c)*(b-a). F(b)-F(a) )=F'(c n)(xn-xn-1)+F'(cn-1)(xn-1-xn-2)+F'(c 2)(x 2-x 1)+F'(c) 1)(x 1 -x 0 )= ΣF'(Ci)ΔXi=Σf(Ci)ΔXi, azaz F(b)-F(a)= Σf(Ci)ΔXi, ahol Ci az intervallum valamely pontja (X i -1 ,X i) Tehát mivel az y=f(x) függvény folytonos -on, akkor integrálható -on. Ezért van az integrálösszegnek egy határa, amely megegyezik az f(x) határozott integráljával. A λ=maxΔXi→0 határértékre átlépve F(b)-F( a)=lim Σf(Ci)ΔXi, azaz ∫(a-ból b-be) f(x)dx=F( b)-F(a).

A z=f(x;y) függvényt meghívjuk megkülönböztethető

11. Differenciálható függvény tulajdonsága: kapcsolat a z=f(x;y) függvény differenciálhatósága és a z=f(x;y) függvény egy pontban való folytonossága között (megfogalmazás, bizonyítás). Ha a z=f(x;y) függvény az M(x;y) pontban differenciálható, akkor ebben a pontban folytonos és parciális deriváltjai vannak. Bizonyíték. Legyen az y=f(x) függvény az x 0 pontban differenciálható. Ezen a ponton az argumentumnak Δx növekményt adunk. A függvény Δу növekményt kap. Keressük limΔx→0(Δy). limΔx→0(Δy)= limΔx→0((Δy*Δx)/Δx))= limΔx→0(Δy/Δx)* limΔx→0(Δx)=f"(x0)*0=0. Ezért y =f(x) folytonos az x 0 pontban.

Jegy 7. sz

Az extrémum szükséges jele.

Ha egy z=z(x,y) folytonos függvénynek szélsőértéke van a P0(x0,y0) pontban, akkor ebben a pontban az összes elsőrendű parciális deriváltja vagy egyenlő nullával, vagy nem létezik

Bizonyíték: A z=f(x,y) függvény parciális deriváltja x-hez képest a P0(x0,y0) pontban az egyik φ(x)=f(x,y0) változó függvényének a deriváltja a pontban. x-x0. De ezen a ponton a φ(x) függvénynek nyilvánvalóan van szélső értéke. Ezért φ'(x0)=0. Mivel φ'(x0)=f'x(x0,y0), akkor f'x(x0,y0)=0 Hasonlóképpen kimutatható, hogy f'y(x0, y0 )=0 . A tétel bizonyítást nyert.

Jegy 8. sz

6. Az átlagérték tétele (megfogalmazás, bizonyítás, geometriai jelentés). Ha az f(x) függvény folytonos a szakaszon, akkor van olyan C∈ pont, hogy ∫(a-tól b-ig) f(x)dx=f(c)*(b-a). Bizonyíték. A Newton-Leibniz képlet szerint ∫(a-ból b-be) f(x)dx=F(x)|(a-ból b)=F(b)-F(a), ahol F"(x) )=f( x). A Lagrange-tételt (a függvény véges növekményére vonatkozó tételt) az F(b)-F(a) különbségre alkalmazva F(b)-F(a)=F"(c) )*(b-a)=f(c) *(b-a). Geometriai jelentés. Az f(x)≥0 tételnek egyszerű geometriai jelentése van: a határozott integrál értéke bizonyos C∈ (a;b) esetén egyenlő egy f(c) magasságú és alappal rendelkező téglalap területével. b-a. Az f(c)=1/(b-a)∫(a-tól b-ig) f(x)dx számot az f(x) függvény átlagértékének nevezzük a szakaszon.

8. A z=f(x;y) függvény részleges növekményei. Parciális származékok: meghatározás és geometriai jelentésük. Legyen adott a z=f(x;y) függvény. Mivel x és y független változók, az egyik változhat, míg a másik állandó marad. Adjunk meg az x változónak egy ∆x növekményt úgy, hogy az y változó értéke változatlan marad. Ekkor a z függvény növekményt kap, amit meg fogunk hívni magán növekmény z x-ben és jelölje ∆ x z. Tehát ∆ x z=f(x+∆x;y)–f(x;y). Hasonlóképpen megkapjuk z részleges növekményét y-hoz képest: ∆ y z=f(x;у+∆y)–f(x;y). Ha van határérték lim∆x→0(∆ x z/∆x )=lim∆x→0( (f(x+∆x;y)-f(x;y))/∆x), akkor ún. részleges származéka z=f(x;y) függvény az x változó M(x;y) pontjában, és a következő szimbólumok egyikével jelöljük: z" x, δz/δx; f" x, δf/δx. Geometriai jelentés. A z=f(x;y) függvény gráfja egy bizonyos felület. A z=f(x 0 ;y 0) függvény grafikonja ennek a felületnek az y=y 0 síkkal való metszésvonala. Az egyik változó függvényének deriváltjának geometriai jelentése alapján arra a következtetésre jutunk, hogy f" x (x 0 ;y 0)=tgα, ahol α az Ox tengely és a z=f görbe érintője közötti szög (x 0 ;y 0) az M 0 pontban (x 0 ;y 0 ;f(x 0 ;y 0)). Hasonló: f" y (x 0 ;y 0)=tgβ.

Jegy 9. sz

Bizonyíték Geometriai jelentés

Érintő sík Normál felületre

10. sz. jegy

10. Egy pontban z=f(x;y) differenciálható függvény definíciója. A dz teljes differenciál definíciója és formája. A z=f(x;y) függvényt meghívjuk megkülönböztethető az M(x;y) pontban, ha ennek teljes növekménye ebben a pontban a következőképpen ábrázolható: ∆z=A*∆x+B*∆y+α*∆x+β*∆y, ahol α=α(∆ x;∆y)→0 és β=β(∆x;∆y)→0 ∆x→0 és ∆y→0 esetén. A z=f(x;y) függvény ∆x-hez és ∆y-hez képest lineáris növekményének fő részét ún. teljes differenciálmű ezt a függvényt és a dz szimbólummal jelöljük: dz=A*∆x+B*∆y. dz=(δz/δx)dx+(δz/δy)dy.

Jegy 11. sz

4. Határozott integrál definíciója egy szakaszon. Egy szegmens feletti határozott integrál alaptulajdonságai (az egyik bizonyításával). Határozott integrállal egy f(x) függvény szegmensén az Σf(c i)Δx i integrálösszeg határértékét hívjuk meg, ha ez a határ létezik, és nem függ sem a szakasz részekre osztásától, sem a t pontok megválasztásától. az egyes részeken belül, feltéve, hogy a legnagyobb részszakaszok hossza (∆xi) nullára hajlik, azaz ∫(a-tól b-ig) f(x)dx=lim Δx i →0 Σf(c i)Δx i . Tulajdonságok: 1) Ha c egy állandó szám, és az f(x) függvény integrálható -ra, akkor ∫(a-tól b-ig) c*f(x)dx=c*∫(a-tól b-ig) f(x)dx .2) Ha az f 1 (x) b f 2 (x) függvények integrálhatók -ra, akkor az összegük is integrálható ∫(a-tól b-ig) (f 1 (x)+f 2 (x))dx=∫( a-tól b-ig) f 1 (x)dx+∫(a-tól b-ig) f 2 (x)dx. 3)∫(a-tól b-ig) f(x)dx= -∫(b-től a-ig) f(x)dx. 4)Ha az f(x) függvény integrálható és a

10. Egy pontban z=f(x;y) differenciálható függvény definíciója. A z=f(x;y) függvényt meghívjuk megkülönböztethető az M(x;y) pontban, ha ennek teljes növekménye ebben a pontban a következőképpen ábrázolható: ∆z=A*∆x+B*∆y+α*∆x+β*∆y, ahol α=α(∆ x;∆y)→0 és β=β(∆x;∆y)→0 ∆x→0 és ∆y→0 esetén.

12. Differenciálható függvény tulajdonsága: kapcsolat a z=f(x,y) függvény differenciálhatósága és a parciális deriváltak egy pontban való létezése között (megfogalmazás, bizonyítás). Tétel: Ha egy függvény egy pontban differenciálható, akkor ebben a pontban véges parciális deriváltak vannak, A és B numerikusan egyenlő Adott: Δz=AΔx+BΔy+0(ρ) Bizonyítsuk be: Ǝ(δz/δx(x 0 ; y 0)=A Bizonyítás: Adjuk meg x 0 →Δx, y=y 0 =>Δ x z=(A*Δx+0(│x│). ρ=√(Δx 2 +Δy 2)=│Δx│. Δxz/Δx=A +0(│x│)/Δx. LimΔx→0 (Δ x z/Δx)=lim=A. δz/Δx(x 0 ;y 0)=A. Hasonlóan: Y 0 →Δy, x=x 0 => Δ y Z. δz/Δy(x 0 ;y 0)=B.

Jegy 12. sz

Bizonyíték

Jegy 13. sz

2. A görbe vonalú trapéz területének problémája, ami egy szegmens feletti határozott integrál fogalmához vezet. Határozott integrál definíciója egy szakaszon. Legyen adott az y=f(x)≥0 függvény a szakaszon. Görbe trapéznek nevezzük azt az ábrát, amelyet fent az y=f(x) függvény grafikonja, lent az Ox tengely, oldalt pedig az x=a és x=b egyenesek határolnak. Keressük meg ennek a trapéznak a területét. f(c 1)Δx 1 +f(c 2)Δx 2 +..+f(c n)Δx n =Σf(c i)Δx i =Sn. A Δx i összes értékének csökkenésével nő a görbe vonalú trapéz lépcsőzetes ábrával történő közelítésének pontossága és a kapott képlet pontossága. Ezért egy görbe vonalú trapéz S területének pontos értékéhez azt az S határértéket vesszük, amelyre az Sn lépcsős alakzat területe hajlik, amikor n korlátlanul növekszik, így λ=maxΔx i →0: S=lim n →∞ Sn=lim n→∞(λ→0 ) Σf(c i)Δx i, azaz S=∫(a-tól b-ig) f(x)dx. Tehát egy határozatlan függvény határozott integrálja numerikusan egyenlő egy görbe vonalú trapéz területével. Ha az Sn integrálösszegnek van egy határértéke I, ami nem függ sem a szakasz numerikus szakaszokra osztásának módjától, sem a pontok kiválasztása bennük, akkor az I számot az y=f(x) függvény meghatározott integráljának nevezzük a szakaszon, és ∫(a-tól b-ig) f(x)dx jelöli. Így ∫(a-tól b-ig) f(x)dx=lim n→∞(λ→0) Σf(c i)Δx i .

17. A felület érintősíkja és merőlegese (definíció).Érintő sík egy M pontban lévő felületre, a felület ezen pontján átmenő síkot akkor nevezzük, ha e sík és az M ponton átmenő szekáns és a felület bármely másik M 1 pontja közötti szög zérusra hajlik, míg M az M-re. 1. Normál felületre egy M pontban ezen a ponton átmenő egyenes az érintősíkra merőlegesen.

Jegy 14. sz

5. Tétel egy meghatározott integrál becslésére egy szakaszon (megfogalmazás, bizonyítás, geometriai jelentés). Az integrál becslése. Ha m és M az y=f(x) függvény legkisebb és legnagyobb értéke a szakaszon, (a Bizonyíték. Mivel bármely x∈ esetén m≤f(x)≤M, akkor ∫(a-tól b-ig) mdx≤ ∫(a-tól b-ig) f(x)dx≤∫(a-tól b-ig) Mdx. A következőt kapjuk: m(b-a)≤∫(a-tól b-ig) f(x)dx≤M(b-a). Geometriai jelentés. A görbe vonalú trapéz területe olyan téglalapok területei közé van zárva, amelyek alapja , és amelyek magassága m és M.

Jegy 15. sz

Jegy 16. sz

21. Az u=u(x;y;z) függvény deriváltja l irányban (definíció). A LimΔl→0(Δu/Δl) határértéket nevezzük az u(x;y;z) függvény deriváltja az l vektor irányában egy pontban koordinátákkal (x;y;z).

22. Az u=u(x;y;z) függvény gradiense egy pontban (definíció). A koordinátákkal (δu/δx; δu/δy; δu/δz) rendelkező vektort ún.

Jegy 17. sz

7. Integrál változó felső határral. Tétel egy változó felső határú integrál deriváltjáról (formulálás, bizonyítás). Egy meghatározott integrál deriváltja egy változó felső határához képest egyenlő azzal az integrandusszal, amelyben az integrációs változót ezzel a határértékkel helyettesítjük, azaz (∫(a-tól x-ig) f(t)dt)" x =f (x). Bizonyíték. A Newton-Leibniz képlet szerint: ∫(a-tól x-ig) f(t)dt=F(t)|(a-tól x-ig)=F(x)-F(a). Ezért (∫(a-tól x-ig) f(t)dt)" x =(F(x)-F(a))" x =F"(x)-0=f(x). Ez azt jelenti, hogy a a változó felső határú határozott integrál az integrandus egyik antideriváltja.

teljes növekmény folyamatos folyamatos

Jegy 18. sz

1. Antiderivatív funkció. Tétel két antiderivált különbségéről (bizonyítással). Határozatlan integrál: definíció, a határozatlan integrál legegyszerűbb tulajdonságai (az egyik bizonyításával). Az F(x) függvényt meghívjuk antiderivatív funkció f(x) az (a;b) intervallumon, ha bármely x∈(a;b) esetén teljesül az F"(x)=f(x) egyenlőség. Tétel. Ha az F(x) függvény az (a;b) f(x) függvény antideriváltja, akkor f(x) összes antideriváltjának halmazát az F(x)+C képlet adja meg, ahol C= const. Bizonyíték. Az F(x)+C függvény az f(x) antideriváltja. Valóban, (F(x)+C)"=F"(x)=f(x). Legyen Ф(x) valamilyen másik, az F(x-től eltérő f(x) antiderivatív függvény, azaz. Ф"(x)=f(x). Ekkor bármely x∈(a;b) esetén van (Ф(х)-F(x))"=Ф"(x)-F"(x)=f( x )-f(x)=0. Ez pedig azt jelenti, hogy Ф(x)-F(x)=C, C=állandó. Ezért Ф(x)=F(x)+C. Az F(x)+C antiderivatív függvények halmazát f(x)-re ún. határozatlan integrál az f(x) függvényből, és ∫f(x)dx szimbólummal jelöljük. Tulajdonságok: 1) A határozatlan integrál differenciálja egyenlő az integrandusszal, a határozatlan integrál deriváltja pedig egyenlő a d(∫f(x)dx)=f(x)dx, (∫f(x)dx )"=f(x).d (∫f(x)dx)=d(F(x)+C)=dF(x)+dC=F"(x)dx=f(x)dx. és (∫f(x)dx)"=(F(x)+C)"=F"(x)+0=f(x).2) Valamely függvény differenciáljának határozatlan integrálja egyenlő az összeggel ennek a függvénynek és egy tetszőleges állandónak: ∫dF(x)=F(x)+C.∫dF(x)=F"(x)dx=∫f(x)dx=F(x)+C.3) A konstans tényező kivehető az integrál előjelből: ∫af(x)dx=a∫f(x)dx.4) Véges számú folytonos függvény algebrai összegének határozatlan integrálja egyenlő a függvény algebrai összegével. a függvények összegzőinek integráljai: ∫(f(x)±g(x))dx=∫f (x)dx±∫g(x)dx.5) (Az integrációs képlet invarianciája). Ha ∫f(x)dx=F(x)+C, akkor ∫f(u)du=F(u)+C, ahol u=φ(x) tetszőleges függvény folytonos deriválttal.

22. Az u=u(x;y;z) függvény gradiense egy pontban (definíció, tulajdonságok). Egy függvény irányderiváltja és gradiense közötti kapcsolat (ráció). A koordinátákkal (δu/δx; δu/δy; δu/δz) rendelkező vektort ún. az u=f(x;y;z) függvény gradienseés gradU=(δu/δx; δu/δy; δu/δz) jelöli. gradU=(δu/δx)*i+(δu/δy)*j+(δu/δz)*k. Tulajdonságok: 1)gradC=0; 2)grad(c*u)=c*gradU; 3)grad(u+v)=gradU+gradV; 4)grad(u*v)=u*gradV+v*gradU, ahol u*v az u és v vektorok skaláris szorzatai. Kapcsolat. Legyen adott az u=u(x;y;z) függvény és a gradU=(δu/δx)*i+(δu/δy)*j+(δu/δz)*k gradiens mező. Ekkor a Δu/Δl derivált valamely l vektor irányában egyenlő a GradU vektor l vektorra való vetületével.

Jegy 19. sz

4. Határozott integrál definíciója egy szakaszon. Egy szegmens feletti határozott integrál alaptulajdonságai (az egyik bizonyításával). Határozott integrállal egy f(x) függvény szegmensén az Σf(c i)Δx i integrálösszeg határértékét hívjuk meg, ha ez a határ létezik, és nem függ sem a szakasz részekre osztásától, sem a t pontok megválasztásától. az egyes részeken belül, feltéve, hogy a legnagyobb részszakaszok hossza (∆xi) nullára hajlik, azaz ∫(a-tól b-ig) f(x)dx=lim Δx i →0 Σf(c i)Δx i . Tulajdonságok: 1) Ha c egy állandó szám, és az f(x) függvény integrálható -ra, akkor ∫(a-tól b-ig) c*f(x)dx=c*∫(a-tól b-ig) f(x)dx . Bizonyíték.Állítsuk össze a c*f(x) függvény integrálösszegét. Van Σс*f(c i)Δx i =с*Σf(c i)Δx i. Ekkor lim n→∞ Σс*f(c i)Δx i =c*lim n→∞ f(c i)=с*∫(a-tól b-ig) f(x)dx. Ebből következik, hogy az с*f(x) függvény integrálható és a képlet ∫(a-tól b-ig) с*f(x)dx= с*∫(a-tól b-ig) f(x)dx.2) Ha az f 1 (x) b f 2 (x) függvények integrálhatók -ra, akkor az összegük integrálható és ∫(a-tól b-ig) (f 1 (x)+f 2 (x))dx=∫(a-tól b-ig ) f 1 (x)dx+∫(a-tól b-ig) f 2 (x)dx. 3)∫(a-tól b-ig) f(x)dx= -∫(b-től a-ig) f(x)dx. 4)Ha az f(x) függvény integrálható és a

17. A felület érintősíkja és merőlegese (definíció). Tétel érintősík létezéséről (megfogalmazás, bizonyítás). Érintő sík egy M pontban lévő felületre, a felület ezen pontján átmenő síkot akkor nevezzük, ha e sík és az M ponton átmenő szekáns és a felület bármely másik M 1 pontja közötti szög zérusra hajlik, míg M az M-re. 1. Normál felületre egy M pontban ezen a ponton átmenő egyenes az érintősíkra merőlegesen. Tétel. Ha δF/δx; δF/δy; A δF/δz az Mo pont közelében definiált, és magában az M 0 pontban folytonosak, és ugyanakkor nem tűnnek el, akkor a felületen lévő egyenesek összes érintője ugyanabban a síkban van. Bizonyíték. L: rendszer(x=x(t); y=y(t); z=z(t)). Érintővonal (M 0 ;P) y=(x"(t 0); y"(t o); z"(t 0)). L∈Q (felület). F(x(t), y(t) , z(t))=0 a t változó komplex függvénye.. A komplex függvény differenciálhatóságának szabályát alkalmazzuk: (δF/δx)*(dx/dt)+(δF/δy)*(dy/dt )+(δF/δz)*( dz/dt)=0; (δF(M 0)/δx)*x"(t 0)+(δF(M 0)/δy)*y"(t 0)+ (δF(M0)/δz) *z"(t 0)=0; g=(x"(t 0),y"(t 0),z"(t 0)); jelölje n=(δF(M 0)/δx; δF(M 0)/δy; δF(M 0) /δz); n⊥g. Mivel egy adott ponton végtelen számú, a felületen fekvő egyenes húzható át, és végtelen számú érintő egyenes, ezért minden érintővonal ugyanabban a síkban van.

20. sz. jegy

9. A z=f(x;y) függvény teljes növekménye. A z=f(x;y) függvény folytonossága egy pontban (két definíció). Legyen adott a z=f(x;y) függvény. Adjunk az x független változónak ∆x, az y változónak pedig ∆y növekményt. Akkor teljes növekmény A függvény ∆z értékét a következő egyenlőség határozza meg: ∆z=f(x+∆x;y+∆y)-f(x;y). 1) A z=f(x;y) függvényt meghívjuk folyamatos az M 0 (x 0 ;y 0)∈ D(z) pontban, ha a határértéke ebben a pontban egybeesik a függvény értékével ebben a pontban, azaz. limX → X 0 \Y → Y 0 (f(x;y))= f(x 0; y 0). 2) z=f(x;y) függvény folyamatos halmazon, ha ennek a halmaznak minden pontjában folytonos

Jegy 21. sz

21. Az u=u(x;y;z) függvény származéka l irányban (definíció, számítási képlet, számítási képlet származtatása). A LimΔl→0(Δu/Δl) határértéket nevezzük az u(x;y;z) függvény deriváltja az l vektor irányában egy pontban koordinátákkal (x;y;z).Δu/Δl=LimΔl→0(Δl u/Δl)=(δu/δx)*cosα+(δu/δy)*cosβ+(δu/δz)*cosγ Tegyük fel, hogy az u(x;y;z) függvény folytonos és folytonos deriváltjai vannak a D tartománybeli argumentumaihoz képest: Δu=(δu/δx)Δx+(δu/δy)Δy+(δu/δz)Δz+ E 1 Δx+E 2 Δy+E 3 Δz, ahol E 1, E 2, E 3 nullára hajlik, mint Δl→0. Osszuk el a teljes egyenlőséget Δl-lel. Δu/Δl=(δu/δx)(Δx/Δl)+(δu/δy)(Δy/Δl)+(δu/δz) (Δz/Δl)+E 1 (Δx/Δl)+E 2 (Δy/ Δl)+E3 (Δz/Δl). Δx/Δl=cosα; Δy/Δl=cosβ; Δz/Δl=cosγ. Az egyenlőség a következőképpen ábrázolható: Δu/Δl=(δu/δx)cosα+(δu/δy)cosβ+(δu/δz)cosγ+E 1 cosα+E 2 cosβ+E 3 cosγ. A határértékre haladva megkapjuk a Δu/Δl=LimΔl→0(Δ l u/Δl)=(δu/δx)*cosα+(δu/δy)*cosβ+(δu/δz)*cosγ.

Jegy 22. sz

20. A z=f(x;y) függvény szélsőértéke létezésének elégséges jele. (megfogalmazás). Legyen egy stacionárius pontban (X 0 ;Y 0) és a szomszédságában az f(x;y) függvénynek folytonos parciális deriváltjai a második rendig bezárólag. Számítsuk ki az (X 0 ;Y 0) pontban az A=f"" xx (X 0 ;Y 0), B=f"" xy (X 0 ;Y 0), C=f"" yy (X 0 ;Y 0). Jelöljük Δ=|AB; BC|=AC-B^2. Ekkor: 1) ha Δ>0, akkor az f(x;y) függvénynek az (X 0 ;Y 0) pontban van egy szélsőértéke: maximum, ha A<0; минимум, если A>0; 2) ha Δ<0, то функция f(x;y) в точке (X 0 ;Y 0) экстремума не имеет. В случае Δ=0 экстремум в точке (X 0 ;Y 0) может быть, а может не быть. Необходимы дополнительные исследования.

Jegy 23. sz

17. Felület érintősíkja (definíció).Érintő sík egy M pontban lévő felületre, a felület ezen pontján átmenő síkot akkor nevezzük, ha e sík és az M ponton átmenő szekáns és a felület bármely másik M 1 pontja közötti szög zérusra hajlik, míg M az M-re. 1.

18. Explicit módon meghatározott felület érintősíkjának egyenleteiMagától értetődően. z=f(x;y) az Mo(Xo;Yo;Zo) pontban. K: (δz/δx)|M 0 (X-X 0)+(δz/δy)|M 0 (Y-Y 0)-(Z-Z 0)=0

Jegy 24. sz