Rajzolja fel a rendszer diagramját, és jelölje meg rajta a súlypontot. Ha a talált súlypont az objektumrendszeren kívül van, akkor helytelen választ kapott. Lehet, hogy különböző referenciapontoktól mért távolságot. Ismételje meg a méréseket.
- Például, ha gyerekek ülnek a hintán, a súlypont valahol a gyerekek között lesz, és nem a hintától jobbra vagy balra. Ezenkívül a súlypont soha nem esik egybe azzal a ponttal, ahol a gyermek ül.
- Ezek az érvek kétdimenziós térben érvényesek. Rajzolj egy négyzetet, amely a rendszer összes objektumát tartalmazza. A súlypontnak ezen a négyzeten belül kell lennie.
Ellenőrizze a matematikát, ha kis eredményt kap. Ha a referenciapont a rendszer egyik végén van, egy kis eredmény a súlypontot a rendszer végéhez közel helyezi. Lehet, hogy ez a helyes válasz, de az esetek túlnyomó többségében ez az eredmény hibára utal. Amikor kiszámította a pillanatokat, megszorozta a megfelelő súlyokat és távolságokat? Ha a szorzás helyett összeadná a súlyokat és a távolságokat, sokkal kisebb eredményt kapna.
Javítsa ki a hibát, ha több súlypontot talált. Minden rendszernek csak egy súlypontja van. Ha több súlypontot talált, valószínűleg nem adta össze az összes pillanatot. A súlypont egyenlő a „teljes” nyomaték és a „teljes” tömeg arányával. Nem kell „minden” pillanatot „minden” súllyal elosztani: így megtalálja az egyes tárgyak helyzetét.
Ellenőrizze a referenciapontot, ha a válasz valamilyen egész értékkel eltér. Példánkban a válasz 3,4 m. Tegyük fel, hogy a válasz 0,4 m vagy 1,4 m, vagy egy másik „.4”-re végződő szám. Ennek az az oka, hogy nem a tábla bal végét választottad kiindulási pontnak, hanem egy olyan pontot, amely egész jobbra található. Valójában a válaszod helyes, függetlenül attól, hogy melyik referenciapontot választod! Ne feledje: a referenciapont mindig az x = 0 pozícióban van. Íme egy példa:
- Példánkban a referenciapont a tábla bal oldalán volt, és azt találtuk, hogy a súlypont 3,4 m-re van ettől a referenciaponttól.
- Ha olyan pontot választunk referenciapontnak, amely a tábla bal végétől 1 m-re van jobbra, akkor a választ 2,4 m-re kapja, vagyis a súlypont 2,4 m-re van az új referenciaponttól, ami , viszont a tábla bal végétől 1 m-re található. Így a súlypont 2,4 + 1 = 3,4 m távolságra van a tábla bal végétől. Régi válasznak bizonyult!
- Megjegyzés: a távolságok mérésekor ne feledje, hogy a „bal” referenciapont távolsága negatív, a „jobb” referenciapont távolsága pedig pozitív.
Mérje meg a távolságokat egyenes vonalakban. Tegyük fel, hogy két gyerek van egy hintán, de az egyik gyerek sokkal magasabb, mint a másik, vagy az egyik gyerek a deszka alatt lóg, nem pedig ül rajta. Hagyja figyelmen kívül ezt a különbséget, és mérje meg a távolságokat a tábla egyenes vonala mentén. A távolságok szögben történő mérése közeli, de nem teljesen pontos eredményeket ad.
- A libikókalap probléma esetén ne feledje, hogy a súlypont a tábla jobb és bal vége között van. Később megtanulod kiszámítani a bonyolultabb kétdimenziós rendszerek súlypontját.
4. előadás. Súlypont.
Ez az előadás a következő kérdéseket fedi le
1. Szilárd test súlypontja.
2. Inhomogén testek súlypontjainak koordinátái.
3. Homogén testek súlypontjainak koordinátái.
4. A súlypontok koordinátáinak meghatározására szolgáló módszerek.
5. Néhány homogén test súlypontja.
Ezeknek a kérdéseknek a tanulmányozása a jövőben szükséges a testek mozgásának dinamikájának tanulmányozásához a csúszási és gördülési súrlódás figyelembevételével, a mechanikai rendszer tömegközéppontjának mozgásának dinamikájával, a mozgási nyomatékokkal, a problémák megoldása érdekében. „Anyagok szilárdsága” tudományág.
Párhuzamos erők hozása.
Miután megfontoltuk egy síkrendszer és egy tetszőleges térbeli erőrendszer középpontba helyezését, ismét visszatérünk a párhuzamos erőrendszer speciális esetéhez.
Két párhuzamos erőt hozva.
Egy ilyen erőrendszer mérlegelése során a következő három csökkentési eset lehetséges.
1. Két kollineáris erő rendszere. Tekintsünk két párhuzamos, egy irányba ható erő rendszerét PÉs K pontokon alkalmazva AÉs BAN BEN. Feltételezzük, hogy az erők merőlegesek erre a szakaszra (1. ábra, A).
VAL VEL szegmenshez tartozó ABés megfelel a feltételnek:
AC/NE = K/P.(1)
A rendszer fővektora R C = P + K modulusa egyenlő ezen erők összegével: R C = P + K.
VAL VEL figyelembe véve (1) egyenlő nullával:MC = P ∙ AC- K∙ CB = 0.
Így a casting eredményeként a következőket kaptuk: R C ≠ 0, MC= 0. Ez azt jelenti, hogy a fővektor ekvivalens a redukciós középponton áthaladó eredővel, azaz:
A kollineáris erők eredője modulusában egyenlő az összegükkel, és hatásvonala felosztja az alkalmazásuk pontjait összekötő szakaszt, fordított arányban ezen erők modulusaival belső módon.
Vegye figyelembe, hogy a pont helyzete VAL VEL nem fog változni, ha az erők RÉs K szöget fordítaniα. Pont VAL VEL, amely rendelkezik ezzel a tulajdonsággal, az úgynevezett párhuzamos erők középpontja.
2. Kettős rendszer antikollineárisés nem egyenlő nagyságú erők. Legyen az erő PÉs K pontokon alkalmazva AÉs BAN BEN, párhuzamos, ellentétes irányú és nem egyenlő nagyságú (1. ábra, b).
Válasszunk egy pontot redukciós középpontnak VAL VEL, amely még mindig kielégíti az (1) relációt, és ugyanazon a vonalon fekszik, de a szegmensen kívül AB.
Ennek a rendszernek a fő vektora R C = P + K a modulus most egyenlő lesz a vektorok modulusai közötti különbséggel: R C = K - P.
A fő szempont a központtal kapcsolatban VAL VEL még mindig nulla:MC = P ∙ AC- K∙ NE= 0, tehát
Eredő antikollineáris a nem egyenlő nagyságú erők pedig egyenlők a különbségükkel, a nagyobb erő felé irányulnak, és ennek hatásvonala osztja fel az alkalmazási pontokat összekötő szakaszt, fordított arányban ezen erők külső modulusaival.
1. ábra
3. Kettős rendszer antikollineárisés egyenlő nagyságú erők. Vegyük kezdeti esetnek a redukció előző esetét. Rögzítsük az erőt R, és erőt K irányítsuk a modulust az erőre R.
Aztán at K → R az (1) képletben az összefüggést AC/NE → 1. Ez azt jelenti AC → NE, vagyis a távolság AC →∞ .
Ebben az esetben a fővektor modulja R C → 0, és a főnyomaték modulusa nem függ a redukciós középpont helyzetétől, és egyenlő marad az eredeti értékkel:
MC = P ∙ AC- K∙ NE = P ∙ ( AC- NE) =P ∙ AB.
Tehát a határértékben olyan erőrendszert kaptunk, amelyre R C = 0, MC≠ 0, és a redukciós középpont a végtelenbe kerül, ami nem helyettesíthető az eredővel. Nem nehéz felismerni néhány erőt ebben a rendszerben, így egy erőpárnak nincs eredője.
A párhuzamos erők rendszerének középpontja.
Fontolja meg a rendszert n erő P i pontokon alkalmazvaA i (x i , y i , z i) és párhuzamos a tengellyelOv orth-al l(2. ábra).
Ha előzetesen kizárjuk egy erőpárral ekvivalens rendszer esetét, akkor az előző bekezdés alapján nem nehéz bizonyítani eredőjének létezését.R.
Határozzuk meg a középpont koordinátáitC(x c, y c, z c) párhuzamos erők, vagyis ennek a rendszernek az eredője alkalmazási pontjának koordinátái.
Erre a célra a Varignon-tételt használjuk, amely alapján:
M0 (R) = Σ M0(P i).

2. ábra
Egy erő vektor-nyomatéka vektorszorzatként ábrázolható, ezért:
M 0 (R) = r c× R = Σ M0i(P i) = Σ ( r i× P i ).
Tekintve, hogy R = Rv ∙ l, A P i = Pvi ∙ l és a vektorszorzat tulajdonságait felhasználva kapjuk:
r c × Rv ∙ l = Σ ( r i × Pvi ∙ l),
r c ∙ R v× l = Σ ( r i ∙ Pvi × l) = Σ ( r i ∙ Pvi ) × l,
vagy:
[ r c R v - Σ ( r i Pvi )] × l= 0.
Az utolsó kifejezés csak akkor érvényes, ha a szögletes zárójelben lévő kifejezés nulla. Ezért az index elhagyásavés figyelembe véve, hogy az eredőR = Σ P i , innen kapjuk:
r c = (Σ P i r i )/(Σ P i ).
Az utolsó vektoregyenlőséget a koordinátatengelyre vetítve megkapjuk a szükségeset párhuzamos erők középpontjának koordinátáinak kifejezése:
x c = (Σ P i x i)/(Σ P i );
y c = (Σ P i y i )/(Σ P i );(2)
z c = (Σ P i z i )/(Σ P i ).
A testek súlypontja.
Egy homogén test súlypontjainak koordinátái.
Vegyünk egy merev testsúlyt Pés hangerőt V a koordinátarendszerben Oxyz, hol vannak a tengelyek xÉs y kapcsolódik a föld felszínéhez és a tengelyhez z a zenitet célozta meg.
Ha a testet elemi részekre bontjuk egy hangerővel∆ V én , akkor a vonzás ereje hatni fog annak minden részére∆ P i, a Föld közepe felé irányítva. Tegyük fel, hogy a test méretei lényegesen kisebbek, mint a Föld méretei, akkor a test elemi részeire ható erőrendszer nem konvergálónak, hanem párhuzamosnak tekinthető (3. ábra), és ebből az összes következtetés. az előző fejezetben foglaltak vonatkoznak rá.

3. ábra
Meghatározás . A szilárd test tömegközéppontja ennek a testnek az elemi részei párhuzamos gravitációs erőinek középpontja.
Emlékezzünk erre fajsúly egy elemi testrész tömegének arányának nevezzük∆ P i hangerőre ∆ V én : γ én = ∆ P i/ ∆ V én . Homogén test esetén ez az érték állandó:γ én = γ = P/ V.
∆ helyettesítése (2) P i = γ én ∙∆ V én ahelyett P i, figyelembe véve az utolsó megjegyzést és csökkentve a számlálót és a nevezőtg, kapunk homogén test súlypontjának koordinátáinak kifejezései:
x c = (Σ ∆ V i∙ x i)/(Σ ∆ V i);
y c = (Σ ∆ V i∙ y i )/(Σ ∆ V i);(3)
z c = (Σ ∆ V i∙ z i )/(Σ ∆ V i).
Számos tétel hasznos a súlypont meghatározásában.
1) Ha egy homogén testnek van szimmetriasíkja, akkor a súlypontja ebben a síkban van.
Ha a tengelyek xÉs nál nél ebben a szimmetriasíkban elhelyezkedő, akkor minden pontra koordinátákkal. És a koordináta (3) szerint nullával egyenlő lesz, mert összesen Minden ellentétes előjelű tagok páronként megsemmisülnek. Ez azt jelenti, hogy a súlypont található a szimmetria síkjában.
2) Ha egy homogén testnek van szimmetriatengelye, akkor a test súlypontja ezen a tengelyen van.
Valóban, ebben az esetben, ha a tengelyzrajzoljon a szimmetriatengely mentén, minden pontra koordinátákkalkoordinátákkal találhat egy pontotés koordináták és , amelyet a (3) képletekkel számítunk ki, egyenlő lesz nullával.
A harmadik tételt hasonló módon bizonyítjuk.
3) Ha egy homogén testnek van szimmetriaközéppontja, akkor a test súlypontja ezen a ponton van.
És még néhány megjegyzés.
Első. Ha a test olyan részekre osztható, amelyekhez ismert a tömeg és a súlypont helyzete, akkor nem kell minden pontot figyelembe venni, és a (3) képletekben P i – a megfelelő alkatrész súlyaként meghatározva és– súlypontjának koordinátáiként.
Második. Ha a test homogén, akkor annak egy-egy részének súlya, Ahol - annak az anyagnak a fajsúlya, amelyből a test készült, és V i - ennek a testrésznek a térfogata. És a (3) képletek kényelmesebb formát öltenek. Például,
És hasonlóképpen hol - az egész test térfogata.
Harmadik megjegyzés. Legyen a test egy vékony lemez alakú, egy területtel Fés vastagsága t, a repülőben fekve Oxy. Csere a (3)-ban∆ V én =t ∙ ∆F én , megkapjuk egy homogén lemez súlypontjának koordinátáit:
x c = (Σ ∆ F i∙ x i) / (Σ ∆ F i);
y c = (Σ ∆ F i∙ y i ) / (Σ ∆ F i).
z c = (Σ ∆ F i∙ z én ) / (Σ ∆ F i).
Ahol – az egyes lemezek súlypontjának koordinátái;– teljes testfelület.
Negyedik megjegyzés. Vékony ívelt hosszúságú rúd formájú testhez L keresztmetszeti területtel a elemi kötet∆ V én = a ∙∆ L én , Ezért vékony ívelt rúd súlypontjának koordinátái egyenlő lesz:
x c = (Σ ∆ L i∙ x i)/(Σ ∆ L i);
y c = (Σ ∆ L i∙ y i )/(Σ ∆ L i);(4)
z c = (Σ ∆ L i∙ z i )/(Σ ∆ L i).
Ahol – a súlypont koordinátáién-edik szakasz; .
Figyeljük meg, hogy a definíció szerint a súlypont egy geometriai pont; adott test határain kívül is feküdhet (például egy gyűrű esetében).
Jegyzet.
A tanfolyam ezen szakaszában nem teszünk különbséget gravitáció, gravitáció és testsúly között. A valóságban a gravitáció a Föld gravitációs ereje és a forgásából eredő centrifugális erő közötti különbség.
Inhomogén testek súlypontjainak koordinátái.
A súlypont koordinátái inhomogén szilárd anyag(4. ábra) a kiválasztott referenciarendszerben az alábbiak szerint határozzák meg:

4. ábra



Ahol - a test térfogategységére jutó tömeg (fajsúly)
![]() - teljes testtömeg.
- teljes testtömeg.
nem egyenletes felület(5. ábra), akkor a kiválasztott vonatkoztatási rendszerben a súlypont koordinátáit a következőképpen határozzuk meg:

5. ábra
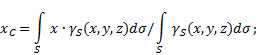

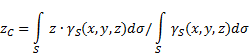
Ahol - testfelület egységenkénti súlya,
![]() - teljes testtömeg.
- teljes testtömeg.
Ha a szilárd nem egységes vonal(6. ábra), akkor a kiválasztott vonatkoztatási rendszerben a súlypont koordinátáit a következőképpen határozzuk meg:

6. ábra

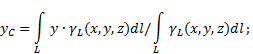

Ahol - súly testhosszonként,
Teljes testtömeg.
A súlypont koordinátáinak meghatározására szolgáló módszerek.
A fent kapott általános képletek alapján lehetőség van konkrét módszerek megjelölésére testek súlypontjainak koordinátáinak meghatározása.
1. Szimmetria. Ha egy homogén testnek van síkja, tengelye vagy szimmetriaközéppontja (7. ábra), akkor a súlypontja rendre a szimmetriasíkban, a szimmetriatengelyben vagy a szimmetriaközéppontban van.

7. ábra
2. Hasítás. A test véges számú részre van osztva (8. ábra), amelyek mindegyikénél ismert a súlypont és a terület helyzete.

8. ábra
S =S 1 + S 2.
3.Negatív terület módszer. A particionálási módszer speciális esete (9. ábra). Kivágásokkal rendelkező testekre vonatkozik, ha a kivágás és a kivágás nélküli test súlypontja ismert. A kivágással ellátott lemez alakú testet egy tömör lemez (kivágás nélkül) kombinációja ábrázolja egy területtel S 1 és a vágott rész területe S2.

9. ábra
S = S 1 - S 2.
4.Csoportosítási módszer. Jó kiegészítője az utolsó két módszernek. Miután az ábrát felosztottuk alkotóelemeire, célszerű néhányat újra kombinálni, hogy azután leegyszerűsítsük a megoldást a csoport szimmetriájának figyelembevételével.
Egyes homogén testek súlypontjai.
1) Egy körív súlypontja. Tekintsük az ívet AB sugárR központi szöggel. A szimmetria miatt ennek az ívnek a súlypontja a tengelyen fekszikÖkör(10. ábra).

10. ábra
Keressük a koordinátát képlet szerint . Ehhez válassza ki az íven AB elem MM ’ hossz, amelynek helyzetét a szög határozza meg. Koordináta x elem MM' akarat. Ezeket az értékeket helyettesítve xÉs d l és szem előtt tartva, hogy az integrált az ív teljes hosszára ki kell terjeszteni, így kapjuk:
![]()
ahol L az AB ív hossza, egyenlő .
Innentől végre azt találjuk, hogy egy körív súlypontja a szimmetriatengelyén van a középponttól távol.Ó egyenlő
hol van a szög radiánban mérve.
2) A háromszög területének súlypontja. Tekintsünk egy háromszöget, amely a síkban fekszik Oxy, melynek csúcsainak koordinátái ismertek: A i (x i,y i ), (én= 1,2,3). A háromszög oldalával párhuzamos keskeny csíkokra bontása A 1 A A 2. ábrán arra a következtetésre jutunk, hogy a háromszög súlypontjának a mediánhoz kell tartoznia A 3 M 3 (11. ábra).

11. ábra
Háromszög feltörése oldalával párhuzamos csíkokra A 2 A 3, ellenőrizhetjük, hogy a mediánon kell feküdnie A 1 M 1 . És így, a háromszög súlypontja a mediánjainak metszéspontjában van, amely, mint ismeretes, minden mediántól egy harmadik részt választ el, a megfelelő oldaltól számítva.
Különösen a medián esetében A 1 M 1 kapjuk, figyelembe véve, hogy a pont koordinátái M 1 - ez a csúcsok koordinátáinak számtani átlaga A 2 és A 3 :
x c = x 1 + (2/3) ∙ (xM 1 - x 1 ) = x 1 + (2/3) ∙ [(x 2 + x 3 )/2 - x 1 ] = (x 1 + x 2 + x 3 )/3.
Így a háromszög súlypontjának koordinátái a csúcsok koordinátáinak számtani átlagai:
x c =(1/3) Σ x i ; y c =(1/3) Σ y i .
3) Egy kör alakú szektor területének súlypontja. Tekintsük egy kör sugarú szektorát R középső szöggel 2α , amely szimmetrikusan helyezkedik el a tengely körül Ökör (12. ábra) .
Ez nyilvánvaló y c = 0, és a távolság annak a körnek a középpontjától, amelyből ez a szektor el van vágva a súlypontig, a következő képlettel határozható meg:

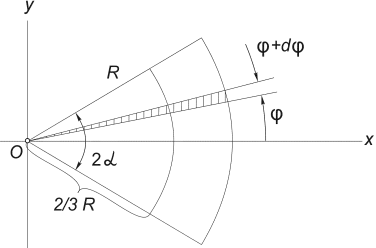
12. ábra
Ezt az integrált a legegyszerűbben úgy számíthatjuk ki, hogy az integrációs tartományt szöggel elemi szektorokra osztjuk dφ . Az első rendű infinitezimálisok pontosságával egy ilyen szektor helyettesíthető egy háromszöggel, amelynek alapja egyenlő R × dφ és magasság R. Egy ilyen háromszög területe dF =(1/2)R 2 ∙ dφ , és a súlypontja 2/3 távolságra van R a csúcsból, ezért az (5)-ben feltesszük x = (2/3)R∙ cosφ. Behelyettesítés (5) F= α R 2, kapjuk:

Az utolsó képlet segítségével kiszámítjuk különösen a súlypont távolságát félkör.
Ha α = π /2-t behelyettesítjük (2-be), a következőt kapjuk: x c = (4 R)/(3π) ≅ 0,4 R .
1. példaHatározzuk meg az ábrán látható homogén test súlypontját! 13.

13. ábra
Megoldás.A test homogén, két szimmetrikus formájú részből áll. Súlypontjuk koordinátái:
Köteteik:
Ezért a test súlypontjának koordinátái
2. példa Keressük meg egy derékszögben meghajlított lemez súlypontját. A méretek a rajzon találhatók (14. ábra).

14. ábra
Megoldás. A súlypontok koordinátái:
0.
Területek:
Ezért:
3. példa
Egy négyzet alakú lapon
cm-es négyzet alakú lyuk kivágása
cm (15. ábra). Keressük meg a lap súlypontját. 4. példa Határozza meg a lemez súlypontjának helyzetét az ábrán látható módon. 16. A méretek centiméterben vannak megadva.

16. ábra
Megoldás. Osszuk fel a táblát ábrákra (17. ábra), központok amelynek súlyossága ismert.
Ezen ábrák területei és súlypontjaik koordinátái:
1) egy téglalap 30 és 40 cm-es oldalakkal,S 1 =30 ∙ 40=1200 cm 2 ; x 1=15 cm; nál nél 1 = 20 cm.
2) derékszögű háromszög, amelynek alapja 50 cm és magassága 40 cm;S 2 =0,5 ∙ 50 ∙ 40 = 1000 cm 2 ; x 2 =30+50/3=46,7 cm; y 2 =40/3 =13,3 cm;
3) félkör sugarú kör r = 20 cm;S 3 =0,5 ∙π∙ 20 2 =628 cm 2 ; x 3 =4 R /3 π =8,5 cm; nál nél
Megoldás. Emlékezzünk vissza, hogy a fizikában a test sűrűségeρ és fajsúlyagösszefüggésben állnak egymással:γ = ρ g , Aholg - a gravitáció gyorsulása. Egy ilyen homogén test tömegének meghatározásához meg kell szoroznia a sűrűséget a térfogatával.

19. ábra
A „lineáris” vagy „lineáris” sűrűség kifejezés azt jelenti, hogy a rácsos rúd tömegének meghatározásához a lineáris sűrűséget meg kell szorozni a rúd hosszával.
A probléma megoldásához használhatja a particionálási módszert. Ha egy adott rácsot 6 különálló rúd összegeként ábrázolunk, a következőket kapjuk:
AholL i hosszén th rácsos rúd, ésx i , y i - súlypontjának koordinátáit.
A probléma megoldása leegyszerűsíthető a rácsos tartó utolsó 5 rúdjának csoportosításával. Könnyen belátható, hogy a negyedik rúd közepén elhelyezkedő szimmetriaközéppontú alakzatot alkotnak, ahol ennek a rúdcsoportnak a súlypontja található.
Így egy adott rácsos tartó csak két rúdcsoport kombinációjával ábrázolható.
Az első csoport az első rúdból állL 1 = 4 m,x 1 = 0 m,y 1 = 2 m. A második rúdcsoport öt rúdból áll, ehhezL 2 = 20 m,x 2 = 3 m,y 2 = 2 m.
A rácsos súlypont koordinátáit a következő képlet segítségével találjuk meg:
x c = (L 1 ∙ x 1 + L 2 ∙ x 2 )/(L 1 + L 2 ) = (4∙0 + 20∙3)/24 = 5/2 m;
y c = (L 1 ∙ y 1 + L 2 ∙ y 2 )/(L 1 + L 2 ) = (4∙2 + 20∙2)/24 = 2 m.
Vegye figyelembe, hogy a központ VAL VEL az összekötő egyenesen fekszik VAL VEL 1 és VAL VEL 2, és felosztja a szakaszt VAL VEL 1 VAL VEL 2 kapcsolatban: VAL VEL 1 VAL VEL/SS 2 = (x c - x 1 )/(x 2 - x c ) = L 2 / L 1 = 2,5/0,5.
Önellenőrző kérdések
- Mit nevezünk párhuzamos erők középpontjának?
- Hogyan határozzák meg a párhuzamos erők középpontjának koordinátáit?
- Hogyan határozzuk meg azoknak a párhuzamos erőknek a középpontját, amelyek eredője nulla?
- Milyen tulajdonságokkal rendelkezik a párhuzamos erők középpontja?
- Milyen képletekkel számítják ki a párhuzamos erők középpontjának koordinátáit?
- Hogy hívják egy test súlypontját?
- Miért tekinthetők párhuzamos erőrendszernek a Föld egy test pontjára ható gravitációs erői?
- Írja fel az inhomogén és homogén testek súlypontjának meghatározására szolgáló képletet, a síkszelvények súlypontjának meghatározására szolgáló képletet?
- Írja fel az egyszerű geometriai alakzatok súlypontjának meghatározására szolgáló képletet: téglalap, háromszög, trapéz és fél kör?
- Mit nevezünk terület statikus momentumának?
- Mondjon példát olyan testre, amelynek súlypontja a testen kívül található!
- Hogyan használják fel a szimmetria tulajdonságait a testek súlypontjainak meghatározásában?
- Mi a lényege a negatív súlyozás módszerének?
- Hol található egy körív súlypontja?
- Milyen grafikus konstrukcióval lehet megkeresni a háromszög súlypontját?
- Írja fel a képletet, amely meghatározza egy körszektor súlypontját!
- A háromszög és a körszektor súlypontját meghatározó képletek segítségével származtassanak hasonló képletet egy körszakaszra.
- Milyen képletekkel számítják ki a homogén testek, sík alakok és egyenesek súlypontjainak koordinátáit?
- Mit nevezünk egy sík alakzat területének statikus nyomatékának a tengelyhez viszonyítva, hogyan számítják ki és milyen méretei vannak?
- Hogyan határozható meg egy terület súlypontjának helyzete, ha ismert az egyes részei súlypontjainak helyzete?
- Milyen segédtételekkel határozzuk meg a súlypont helyzetét?
Szerző: Vegyünk egy tetszőleges alakú testet. Fel lehet-e akasztani egy cérnára úgy, hogy a felakasztás után megtartsa a helyzetét (azaz ne kezdjen el forogni), amikor Bármi kezdeti tájolás (27.1. ábra)?
Más szóval, van-e olyan pont, amelyhez képest a test különböző részein ható gravitációs nyomatékok összege nullával egyenlő lenne Bármi testorientáció a térben?
Olvasó: Szerintem igen. Ezt a pontot hívják a test súlypontja.
Bizonyíték. Az egyszerűség kedvéért tekintsünk egy tetszőleges alakú, térben tetszőlegesen orientált lapos lemez formájú testet (27.2. ábra). Vegyük a koordináta-rendszert x 0nál nél kezdetével a tömegközéppontban - pont VAL VEL, Akkor x C = 0, C-nél = 0.
 Képzeljük el ezt a testet nagyszámú ponttömeg gyűjteményének m i, amelyek mindegyikének helyzetét a sugárvektor határozza meg.
Képzeljük el ezt a testet nagyszámú ponttömeg gyűjteményének m i, amelyek mindegyikének helyzetét a sugárvektor határozza meg.
Definíció szerint a tömegközéppont , és a koordináta x C = .
Mivel az általunk elfogadott koordináta-rendszerben x C= 0, akkor . Ezt az egyenlőséget szorozzuk meg vele gés megkapjuk
ábrából látható. 27.2, | x i| - ez a hatalom válla. És ha x i> 0, akkor az erőnyomaték M i> 0, és ha x j < 0, то Mj < 0, поэтому с учетом знака можно утверждать, что для любого x i az erőnyomaték egyenlő lesz M i = m i gx i . Ekkor az (1) egyenlőség egyenlő az egyenlőséggel, ahol M i– gravitációs nyomaték. Ez azt jelenti, hogy a test tetszőleges tájolásával a testre ható gravitációs nyomatékok összege a tömegközépponthoz képest nullával egyenlő.
Ahhoz, hogy az általunk vizsgált test egyensúlyban legyen, a ponton kell rá alkalmazni VAL VEL Kényszerítés T = mg, függőlegesen felfelé irányítva. Ennek az erőnek a ponthoz viszonyított nyomatéka VAL VEL egyenlő nullával.
Mivel az okfejtésünk semmilyen módon nem függött attól, hogy a test pontosan hogyan tájolódik a térben, bebizonyítottuk, hogy a tömegközéppont egybeesik a tömegközépponttal, ezt kellett bizonyítanunk.
27.1 probléma. Keresse meg egy súlytalan hosszúságú rúd súlypontját l, melynek végein két ponttömeg van rögzítve T 1 és T 2 .
| T 1 T 2 l | Megoldás. Nem a súlypontot fogjuk keresni, hanem a tömegközéppontot (mivel ezek ugyanazok). Mutassuk be a tengelyt x(27.3. ábra). |
| x C =? | |
Válasz: a tömegtől távol T 1 .
ÁLLJ MEG! Döntse el Ön: B1–B3.
1. állítás . Ha egy homogén lapos testnek van szimmetriatengelye, akkor ezen a tengelyen van a súlypont.
Valójában bármilyen ponttömegre m i, amely a szimmetriatengelytől jobbra helyezkedik el, ugyanaz a ponttömeg található szimmetrikusan az elsőhöz képest (27.4. ábra). Ebben az esetben az erőnyomatékok összege .
Mivel az egész testet hasonló pontpárokra osztva ábrázolhatjuk, a szimmetriatengelyen fekvő bármely ponthoz viszonyított összsúlynyomaték nulla, ami azt jelenti, hogy a test súlypontja ezen a tengelyen helyezkedik el. . Ez egy fontos következtetéshez vezet: ha egy testnek több szimmetriatengelye van, akkor a súlypont ezeknek a tengelyeknek a metszéspontjában van(27.5. ábra).
Rizs. 27.5 
2. állítás. Ha két testnek tömege van T 1 és T A 2. ábrán látható testek tömegközéppontja az első és a második test súlypontját összekötő egyenes szakaszon lesz (27.6. ábra).
Rizs. 27.6 ![]() Rizs. 27.7
Rizs. 27.7
Bizonyíték. Helyezzük el az összetett testet úgy, hogy a testek súlypontjait összekötő szakasz függőleges legyen. Ekkor az első test ponthoz viszonyított nehézségi nyomatékainak összege VAL VEL 1 egyenlő nullával, és a második test gravitációs nyomatékainak összege a ponthoz képest VAL VEL 2 egyenlő nullával (27.7. ábra).
vegye észre, az váll bármely ponttömeg gravitációja t i ugyanez a szakaszon fekvő bármely pontra vonatkozóan VAL VEL 1 VAL VEL 2, és ezért a gravitációs nyomaték a szakasz bármely pontjához viszonyítva VAL VEL 1 VAL VEL 2, ugyanaz. Következésképpen az egész test gravitációs ereje a szakasz bármely pontjához képest nulla VAL VEL 1 VAL VEL 2. Így az összetett test súlypontja a szegmensen fekszik VAL VEL 1 VAL VEL 2 .
Fontos gyakorlati következtetés következik a 2. állításból, amely egyértelműen utasítások formájában van megfogalmazva.
Utasítás,
hogyan lehet megtalálni a szilárd test súlypontját, ha az eltörhető
részekre, amelyek mindegyikének súlypontjainak helyzete ismert
1. Minden alkatrészt ki kell cserélni az adott alkatrész súlypontjában elhelyezkedő tömeggel.
2. Keresse meg a tömeg közepe(és ez megegyezik a súlyponttal) a kapott tömegpontrendszerből, egy kényelmes koordináta-rendszer kiválasztásával x 0nál nél, a képletek szerint:
Valójában rendezzük el az összetett testet úgy, hogy a szegmens VAL VEL 1 VAL VEL 2 vízszintes volt, és akassza fel a szálakra a pontokon VAL VEL 1 és VAL VEL 2 (27.8. ábra, A). Nyilvánvaló, hogy a test egyensúlyban lesz. És ez az egyensúly nem fog felborulni, ha minden testet ponttömegekkel helyettesítünk T 1 és T 2 (27.8. ábra, b).
 Rizs. 27.8
Rizs. 27.8
ÁLLJ MEG! Döntse el Ön: C3.
27.2 probléma. Tömeggolyókat helyezünk egy egyenlő oldalú háromszög két csúcsára T minden. A harmadik csúcsba 2 tömegű golyót helyezünk T(27.9. ábra, A). Háromszög oldal A. Határozza meg ennek a rendszernek a súlypontját.
| T 2T A |  Rizs. 27.9 Rizs. 27.9 |
| x C = ? C-nél = ? | |
Megoldás. Mutassuk be a koordinátarendszert x 0nál nél(27.9. ábra, b). Akkor
![]() ,
,
 .
.
Válasz: x C = A/2; ; súlypontja félmagasságban van HIRDETÉS.
Tankönyv 7. osztálynak
§ 25.3. Hogyan lehet megtalálni a test súlypontját?
Emlékezzünk vissza, hogy a súlypont az a pont, ahol a gravitáció érvényesül. Gondoljuk át, hogyan lehet kísérletileg meghatározni egy lapos test súlypontjának helyzetét - mondjuk egy kartonból kivágott tetszőleges alakú figura (lásd 12. számú laboratóriumi munka).
A kartonfigurát tűvel vagy szöggel felakasztjuk, hogy az O ponton átmenő vízszintes tengely körül szabadon foroghasson (25.4. ábra, a). Akkor ez a szám egy O támaszpontú karnak tekinthető.
Rizs. 25.4. Hogyan találjuk meg kísérletileg egy lapos alak súlypontját
Ha egy figura egyensúlyban van, a rá ható erők kiegyenlítik egymást. Ez a T ábra súlypontjában fellépő F t gravitációs erő és az O pontban kifejtett F exr rugalmassági erő (ezt az erőt egy csap vagy szög felől fejtik ki).
Ez a két erő csak akkor egyensúlyozza ki egymást, ha ezen erők alkalmazási pontjai (T és O pontok) ugyanazon a függőlegesen helyezkednek el (lásd 25.4. ábra, a). Ellenkező esetben a gravitáció elforgatja az ábrát az O pont körül (25.4. ábra, b).
Tehát amikor az ábra egyensúlyban van, a súlypont ugyanazon a függőlegesen helyezkedik el, mint az O felfüggesztési pont. Ez lehetővé teszi számunkra, hogy meghatározzuk az ábra súlypontjának helyzetét. Egy függővonal segítségével a felfüggesztési ponton áthaladó függőleges vonalat húzunk (kék vonal a 25.4. ábrán c). A test súlypontja a megrajzolt vonalon fekszik. Ismételjük meg ezt a kísérletet a felfüggesztési pont másik helyzetével. Ennek eredményeként egy második vonalat kapunk, amelyen a test súlypontja fekszik (zöld vonal a 25.4. ábrán, d). Következésképpen ezen vonalak metszéspontjában van a test kívánt súlypontja (a 25.4. ábrán a piros G pont, d).
A mérnöki gyakorlatban előfordul, hogy olyan egyszerű elemekből álló összetett lapos alakzat súlypontjának koordinátáit kell kiszámítani, amelyeknél ismert a tömegközéppont helye. Ez a feladat része annak a feladatnak, hogy meghatározzuk...
Gerendák és rudak kompozit keresztmetszeteinek geometriai jellemzői. Gyakran hasonló kérdésekkel kell szembesülniük a vágószerszámok tervezőinek a nyomásközéppont koordinátáinak meghatározásakor, a különféle járművek rakodási sémáinak kidolgozóinak a rakomány elhelyezésekor, a fémszerkezetek tervezőinek az elemek keresztmetszete kiválasztásakor és természetesen a hallgatók az „Elméleti mechanika” és az „Anyagok szilárdsága” tudományágak tanulmányozása során.
Elemi figurák könyvtára.

Szimmetrikus síkfigurák esetén a súlypont egybeesik a szimmetria középpontjával. Az elemi objektumok szimmetrikus csoportjába tartozik: kör, téglalap (beleértve a négyzetet is), paralelogramma (a rombusz is), szabályos sokszög.
A fenti ábrán bemutatott tíz ábra közül csak kettő alapvető. Vagyis háromszögek és körágak segítségével szinte bármilyen gyakorlati érdeklődésre számot tartó figurát kombinálhat. Bármely tetszőleges görbe szakaszokra osztható és körívekkel helyettesíthető.
A maradék nyolc figura a leggyakoribb, ezért kerültek be ebbe az egyedülálló könyvtárba. Osztályozásunkban ezek az elemek nem alapvetőek. Két háromszögből téglalap, paralelogramma és trapéz alkotható. A hatszög négy háromszög összege. A körszakasz a kör szektora és a háromszög közötti különbség. A kör gyűrű alakú szektora két szektor különbsége. A kör egy kör olyan szektora, amelynek szöge α=2*π=360˚. A félkör ennek megfelelően egy α=π=180˚ szögű kör szektora.
Összetett ábra súlypontjának koordinátáinak kiszámítása Excelben.
Mindig könnyebb egy példán keresztül információt átadni és felfogni, mint pusztán elméleti számításokkal tanulmányozni a kérdést. Nézzük meg a „Hogyan találjuk meg a súlypontot?” probléma megoldását. a szöveg alatti ábrán látható összetett ábra példájával.

Az összetett szakasz egy téglalap (méretekkel a1 = 80 mm, b1 =40 mm), amelyhez egy egyenlő szárú háromszög került a bal felsőbe (az alap méretével a2 =24 mm és magasság h2 =42 mm) és amelyből jobbról felülről egy félkört vágtunk ki (a középponttal a koordinátákkal ellátott pontban) x03 =50 mm és y03 =40 mm, sugár r3 =26 mm).
A számítások elvégzéséhez egy programot fogunk használni MS Excel vagy program OOo Calc . Bármelyikük könnyedén megbirkózik a feladatunkkal!
A cellákban sárga megtöltjük segédelőzetes számításokat .
Az eredményeket világossárga kitöltésű cellákban számítjuk ki.
Kék betűtípus az kezdeti adatok .
Fekete betűtípus az közbülső számítási eredmények .
Piros betűtípus az végső számítási eredmények .
Elkezdjük a probléma megoldását - elkezdjük keresni a szakasz súlypontjának koordinátáit.
Kiinduló adatok:
1. Ennek megfelelően írjuk fel az összetett szakaszt alkotó elemi alakzatok nevét
D3 cellába: Téglalap
az E3 cellához: Háromszög
az F3 cellába: Félkör
2. A jelen cikkben bemutatott „Elemi figurák könyvtára” segítségével meghatározzuk az összetett metszet elemeinek súlypontjainak koordinátáit. xciÉs yci mm-ben a tetszőlegesen kiválasztott 0x és 0y tengelyekhez képest, és írja be
a D4 cellához: =80/2 = 40,000
xc 1 = a 1 /2
a D5 cellához: =40/2 =20,000
yc 1 = b 1 /2
az E4 cellához: =24/2 =12,000
xc 2 = a 2 /2
az E5 cellába: =40+42/3 =54,000
yc 2 = b 1 + h 2 /3
az F4 cellába: =50 =50,000
xc 3 = x03
az F5 cellába: =40-4*26/3/PI() =28,965
yc 3 = y 03 -4* r3 /3/ π
3. Számítsuk ki az elemek területét! F 1 , F 2 , F3 mm2-ben, ismét az „Elemi ábrák könyvtára” szakasz képleteivel
a D6 cellában: =40*80 =3200
F1 = a 1 * b1
az E6 cellában: =24*42/2 =504
F2 = a2 *h2 /2
az F6 cellában: =-PI()/2*26^2 =-1062
F3 =-π/2*r3 ^2
A harmadik elem - a félkör - területe negatív, mert ez egy kivágás - egy üres hely!

A súlypont koordinátáinak kiszámítása:
4. Határozza meg a végső szám teljes területét F0 mm2-ben
a D8E8F8 egyesített cellában: =D6+E6+F6 =2642
F0 = F 1 + F 2 + F3
5. Számítsuk ki egy összetett ábra statikus momentumait SxÉs Sy mm3-ben a kiválasztott 0x és 0y tengelyekhez képest
a D9E9F9 egyesített cellában: =D5*D6+E5*E6+F5*F6 =60459
Sx = yc1 * F1 + yc2 *F2 + yc3 *F3
az egyesített D10E10F10 cellában: =D4*D6+E4*E6+F4*F6 =80955
Sy = xc1 * F1 + xc2 *F2 + xc3 *F3
6. Végül pedig számítsuk ki az összetett szakasz súlypontjának koordinátáit XcÉs Yc mm-ben a kiválasztott koordinátarendszerben 0x - 0y
a D11E11F11 egyesített cellában: =D10/D8 =30,640
Xc = Sy / F0
az egyesített D12E12F12 cellában: =D9/D8 =22,883
Yc =Sx/F0
A probléma megoldva, a számítás Excelben elkészült - a szakasz súlypontjának három egyszerű elem segítségével összeállított koordinátáit megtaláltuk!
Következtetés.
A cikkben szereplő példát nagyon egyszerűnek választottuk, hogy könnyebben érthető legyen egy összetett szakasz súlypontjának kiszámításának módszere. A módszer az, hogy minden összetett ábrát egyszerű elemekre kell osztani, amelyekben ismert a súlypontok elhelyezkedése, és végső számításokat kell végezni a teljes szakaszra.
Ha a szakasz hengerelt profilokból - szögekből és csatornákból áll, akkor nem kell azokat téglalapokra és négyzetekre osztani, kivágott kör alakú „π/2” szektorokkal. Ezeknek a profiloknak a súlypontjának koordinátáit a GOST táblázatok adják meg, vagyis mind a szög, mind a csatorna lesz az alapvető elemi elem az összetett metszetek számításaiban (nincs értelme I-gerendákról beszélni, csövek, rudak és hatszögek – ezek központilag szimmetrikus szakaszok).
A koordinátatengelyek elhelyezkedése természetesen nem befolyásolja az ábra súlypontjának helyzetét! Ezért válasszon olyan koordináta-rendszert, amely leegyszerűsíti a számításokat. Ha például példánkban a koordinátarendszert az óramutató járásával megegyező irányban 45˚-kal elforgatnám, akkor egy téglalap, háromszög és félkör súlypontjainak koordinátáinak kiszámítása egy másik különálló és nehézkes számítási szakaszba fordulna, amelyet nem lehet elvégezni. a fejben".
Az alábbiakban bemutatott Excel számítási fájl ebben az esetben nem program. Inkább egy számológép vázlata, egy algoritmus, egy sablon, amely minden konkrét esetben követi hozza létre saját képletsorozatát az élénksárga kitöltésű cellákhoz.
Tehát most már tudja, hogyan találja meg bármely szakasz súlypontját! A tetszőleges összetett összetett metszet összes geometriai jellemzőjének teljes kiszámítását a „” szakasz egyik következő cikkében tárgyaljuk. Kövesse a híreket a blogon.
Mert fogadása információk az új cikkek megjelenéséről és azért működő programfájlok letöltése Kérem, hogy iratkozzon fel a közleményekre a cikk végén található ablakban vagy az oldal tetején található ablakban.
Miután megadta e-mail címét és a „Cikkhirdetések fogadása” gombra kattintott NE FELEJTSD EL ERŐSÍTSD EL ELŐFIZETÉSÉT a linkre kattintva levélben, amely azonnal megérkezik a megadott e-mail címre (néha a mappában « Levélszemét » )!
Néhány szó az üvegről, az érméről és a két villáról, amelyek a cikk elején található „illusztrációs ikonban” láthatók. Bizonyára sokan ismeritek ezt a „trükköt”, amely gyönyörködtető pillantásokat vált ki gyerekekből és avatatlan felnőttekből. A cikk témája a súlypont. Ő és a támaszpont, akik a tudatunkkal és tapasztalatunkkal játszanak, egyszerűen becsapják az elménket!
A „villa+érme” rendszer súlypontja mindig a következőn található rögzített távolság függőlegesen lefelé az érme szélétől, ami viszont a támaszpont. Ez egy stabil egyensúlyi helyzet! Ha megrázzuk a villákat, azonnal nyilvánvalóvá válik, hogy a rendszer igyekszik elfoglalni korábbi stabil pozícióját! Képzeljünk el egy ingát - rögzítési pontot (= egy érme támaszpontja az üveg szélén), az inga rúdtengelyét (= esetünkben a tengely virtuális, mivel a két villa tömege a tér különböző irányaiban szétterítve) és a tengely alján lévő teher (= a teljes „villa” rendszer súlypontja + érme”). Ha elkezdi az ingát bármilyen irányba eltéríteni a függőlegestől (előre, hátra, balra, jobbra), akkor a gravitáció hatására elkerülhetetlenül visszatér eredeti helyzetébe. állandó egyensúlyi állapot(ugyanez történik a villáinkkal és az érméinkkel is)!
Ha nem érted, de érteni akarod, találd ki magad. Nagyon érdekes "odajutni" magad! Hozzáteszem, hogy ugyanez a stabil egyensúly használatának elve érvényesül a Vanka-stand-up játékban is. Ennek a játéknak csak a súlypontja található a támaszpont felett, de a tartófelület félgömbjének középpontja alatt.
Mindig örömmel látom a hozzászólásaitokat, kedves olvasók!!!
Kérdez, TISZTELETT szerzői mű, letölthető fájl ELŐFIZETÉS UTÁN cikkhirdetésekre.










