EGOROVA VICTORIA VALERIEVNA

Matematika tanár

legmagasabb minősítési kategória

TÉMA: „AZ IDENTÁLIS ÁTALAKULÁS

LOGARITMIKUS KIFEJEZÉSEK"

Azok az ismeretek és készségek, amelyeket a tanulóknak el kell sajátítaniuk a leckét követően:

ismeri egy szám logaritmusának definícióját, a logaritmus alapvető azonosságát, a logaritmus tulajdonságait;

legyen képes logaritmusokat tartalmazó kifejezések transzformációira és logaritmusszámítására.

Irodalom:

1. Alimov Sh.A., Kolyagin Yu.M., Sidorov Yu.V. és mások Az algebra és az elemzés kezdetei: tankönyv 10-11 oktatási intézmények. – M.: Oktatás, 2001.

2. Kochagin V.V., Kochagina M.V., Intenzív felkészítő tanfolyam az egységes államvizsgára. – M.: Eksmo, 2009.

3. Merzlyak A.G., Polonsky V.B., Yakir M.S., Algebrai szimulátor: kézikönyv iskolásoknak és jelentkezőknek. – M.: Ilexa, 2005.

4. Gusev V.A., Mordkovich A.G. Matematika: Referencia anyagok: Könyv diákoknak. – M.: Oktatás, 2001.

Tanterv:

Az órák alatt:

1) A logaritmus egy görög szó, amely 2 szóból áll: „logos” - arány, „aritmosz” - szám. Ez azt jelenti, hogy a logaritmus olyan szám, amely egy arányt mér. Egy 1614-es publikáció arról számolt be, hogy Napier feltalálta a logaritmusokat. Később logaritmikus táblákat állított össze, amelyeket ma Bradis-tábláknak nevezünk. Kevesebb mint egy évszázad alatt a táblázatok az egész világon elterjedtek, és nélkülözhetetlen számítástechnikai eszközzé váltak. Ezt követően, úgymond, egy kényelmes eszközbe építették be, amely nagyban felgyorsítja a számítási folyamatot - egy csúszdaszabályba, amelyet a huszadik század hetvenes éveiig használtak.

1. számú melléklet.

2) Logaritmus pozitív számb alapján a, és és nagyobb nullánál és nem egyenlő eggyel,az a kitevő, amelyre egy számot emelni kella hogy megkapja a számotb.

Ezt az egyenlőséget, amely a logaritmus definícióját fejezi ki, únalapvető logaritmikus azonosság .

C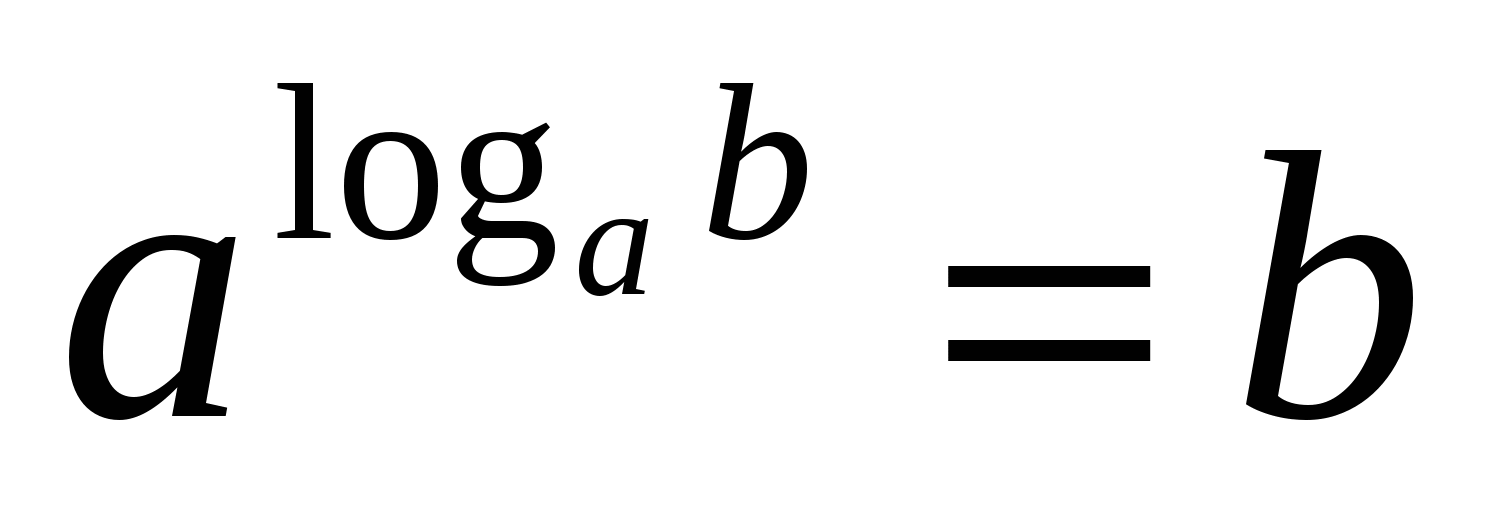

VAGY 1

P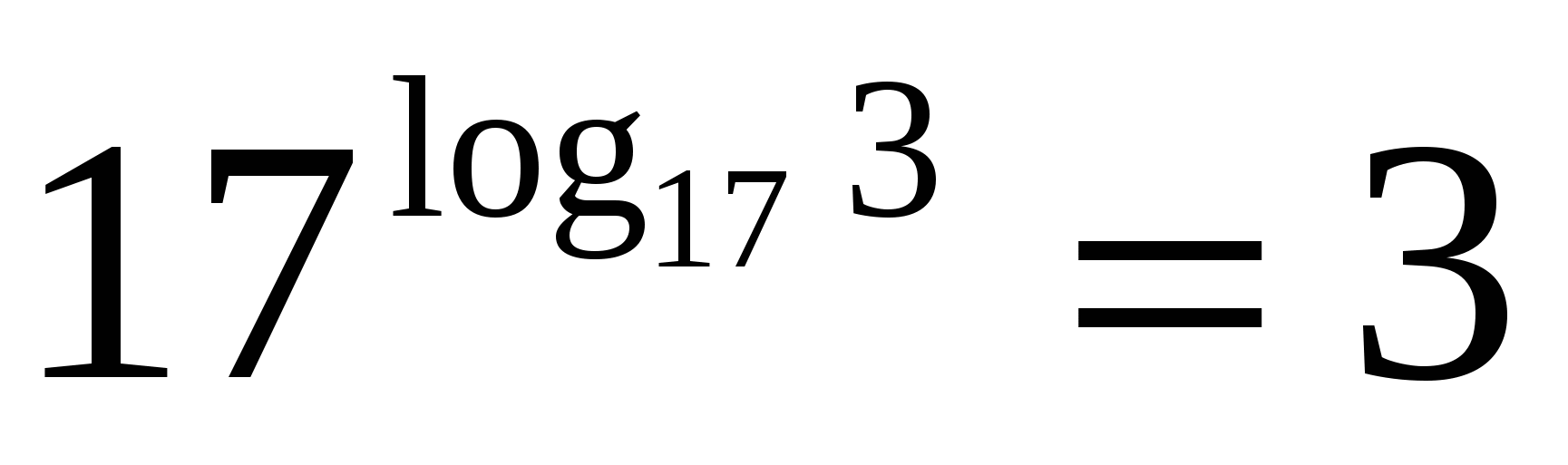

A hatvány és a logaritmus alapja tizenhét, ami azt jelenti, hogy a logaritmikus alapazonosság szerint a kifejezés értéke három.

Dolgozzuk ki szóban:

SCH
FIR-BELLE

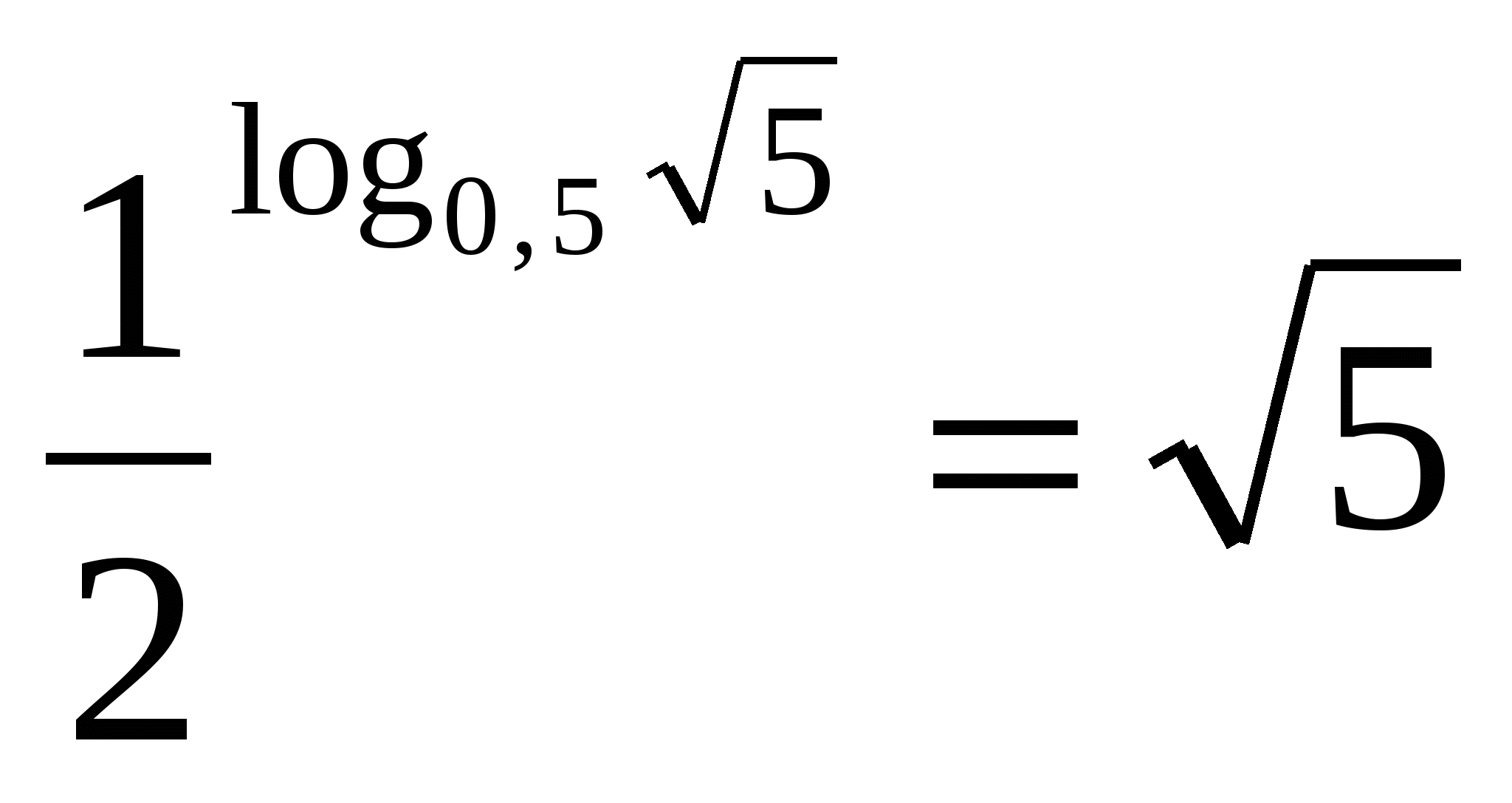
RÓL RŐL a második alja egyenlő nulla pont öttel, ami azt jelenti, hogy a kifejezés egyenlő az öt számtani négyzetgyökével.

P

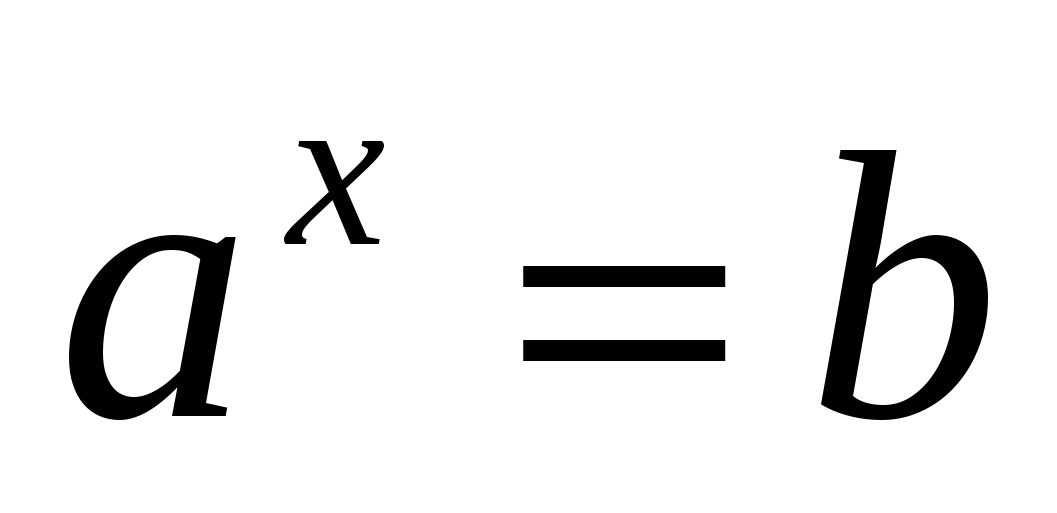2. függelék.

Egyenlőség azt jelenti, hogy

A logaritmus definíciójából a következő fontos egyenlőségeket kapjuk:

Például:

P
3. függelék.

Menjünk tovább Egységes államvizsga-feladatok:

4. függelék.

3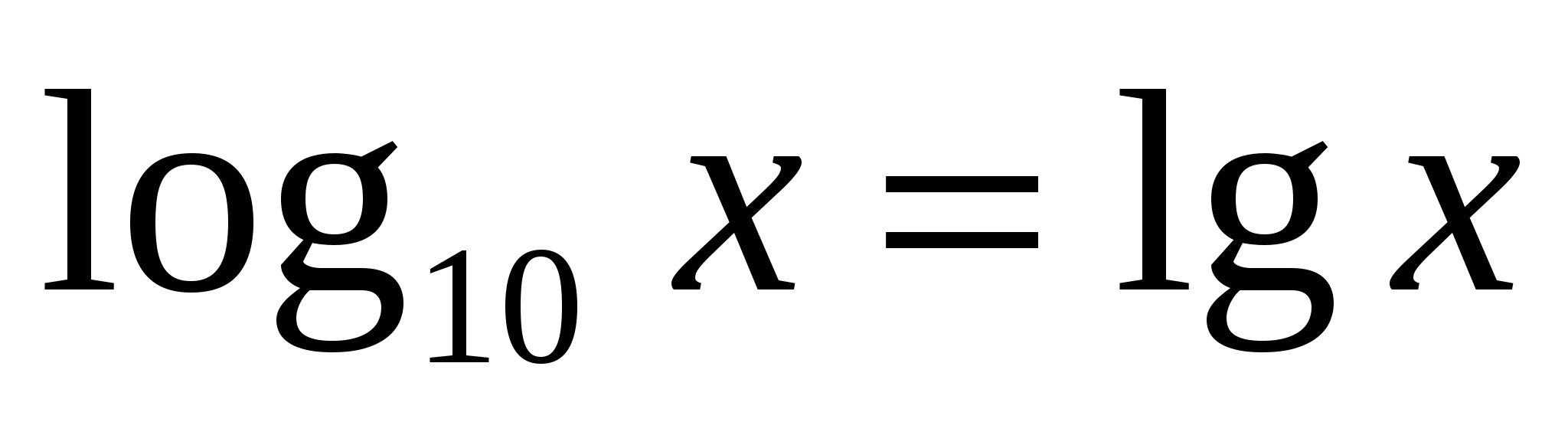
) A tízes alapú logaritmusnak van egy speciális jelölése és nevedecimális logaritmus .

L
alapkalaritmuse hívotttermészetes logaritmus .

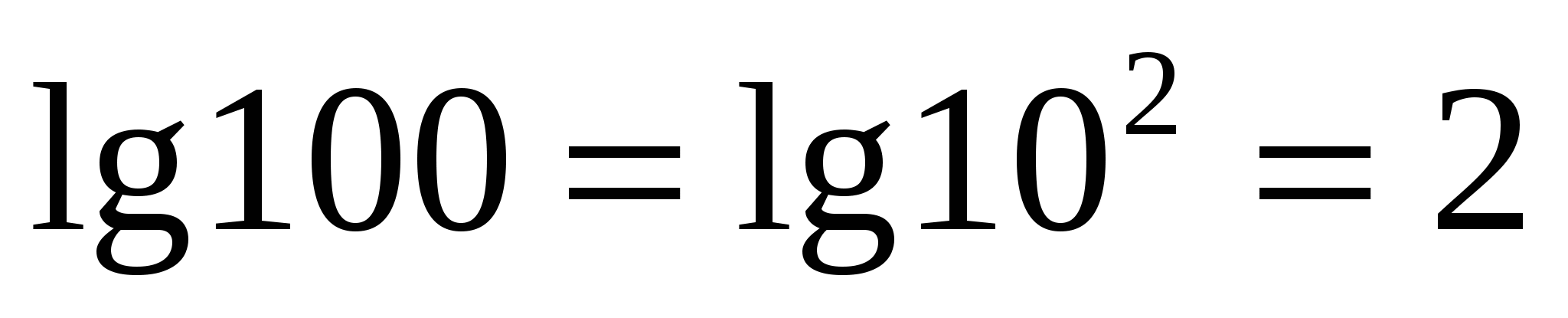
N
például,

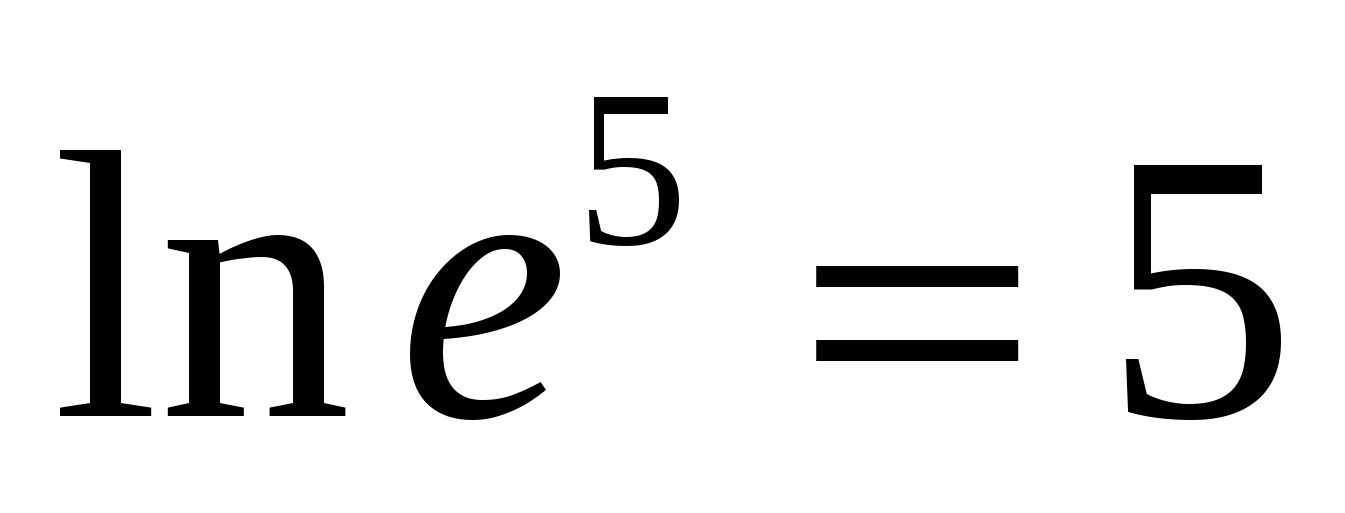
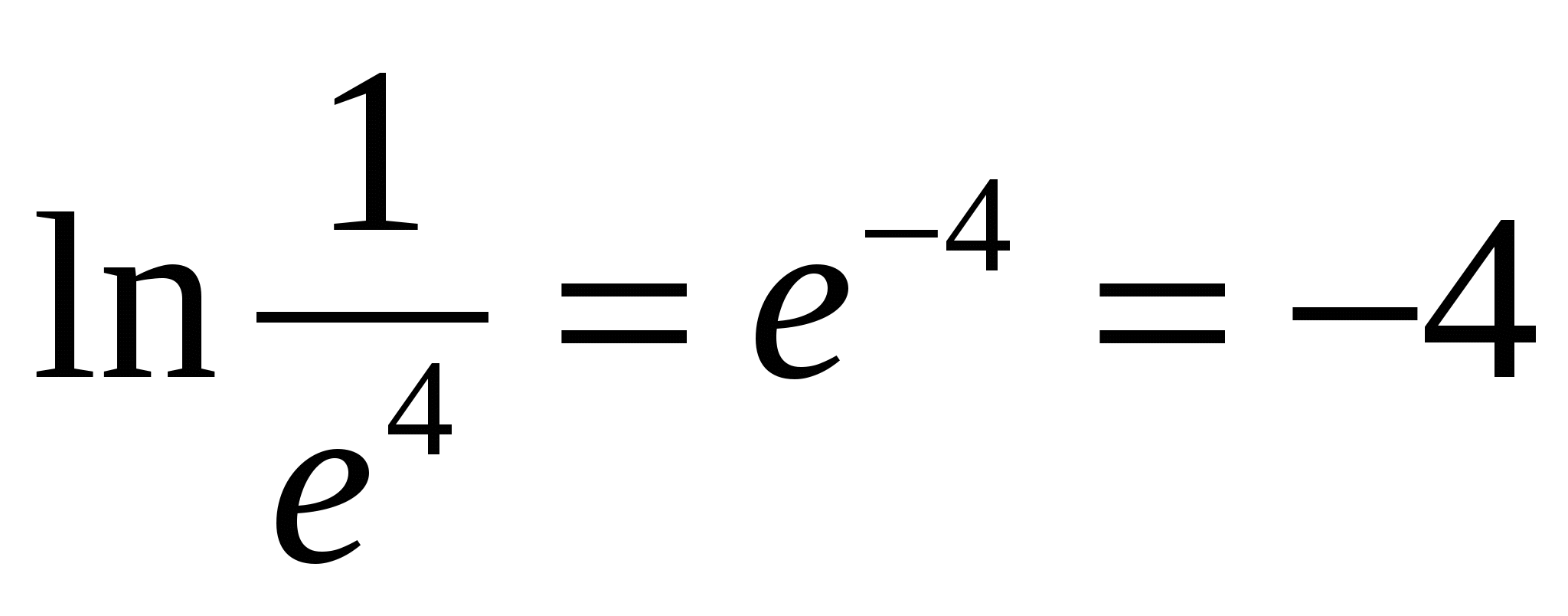
4) A következő tulajdonságok következnek a logaritmus definíciójából. Minden tulajdonság csak a logaritmusjelek alatt lévő változók pozitív értékeire van megfogalmazva és bizonyított.

Két pozitív szám bázishoz viszonyított szorzatának logaritmusa A egyenlő az összeggel ezeknek a számoknak az azonos bázisú logaritmusa.

TsOR 2

Például,

Z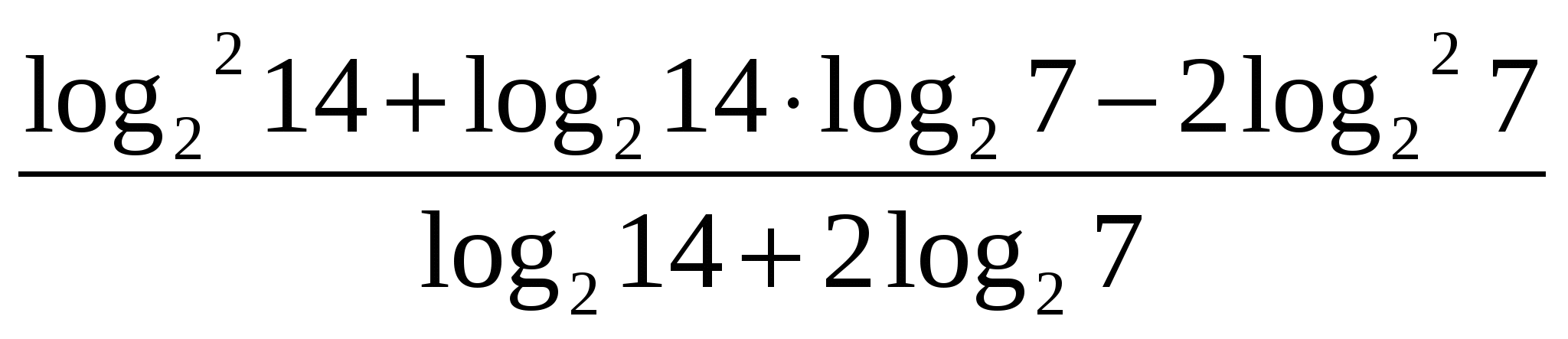
feladat 1.

2. feladat. Egyszerűsítse a kifejezést

BAN BEN
Használjuk az előző példa megoldását. Cseréljük

Kérjük, vegye figyelembe, hogy a logaritmus négyzet, tehát az összeget négyzetre kell számítani. Az összeg négyzetének képletével kinyitjuk a zárójeleket. Mutassunk be hasonló kifejezéseket.

5) A hányados logaritmusa megegyezik az osztó és az osztó logaritmusa közötti különbséggel.

C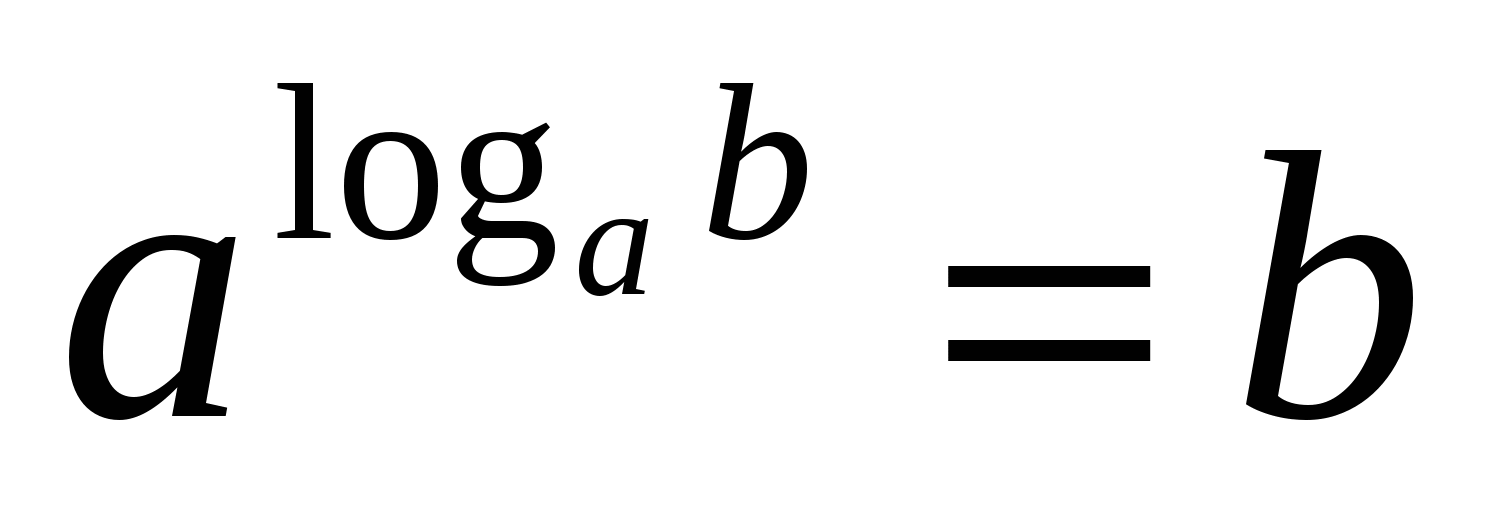

Ügyeljen a hatvány alapjára és a logaritmus alapjára - ezek ugyanazok.

VAGY 3

R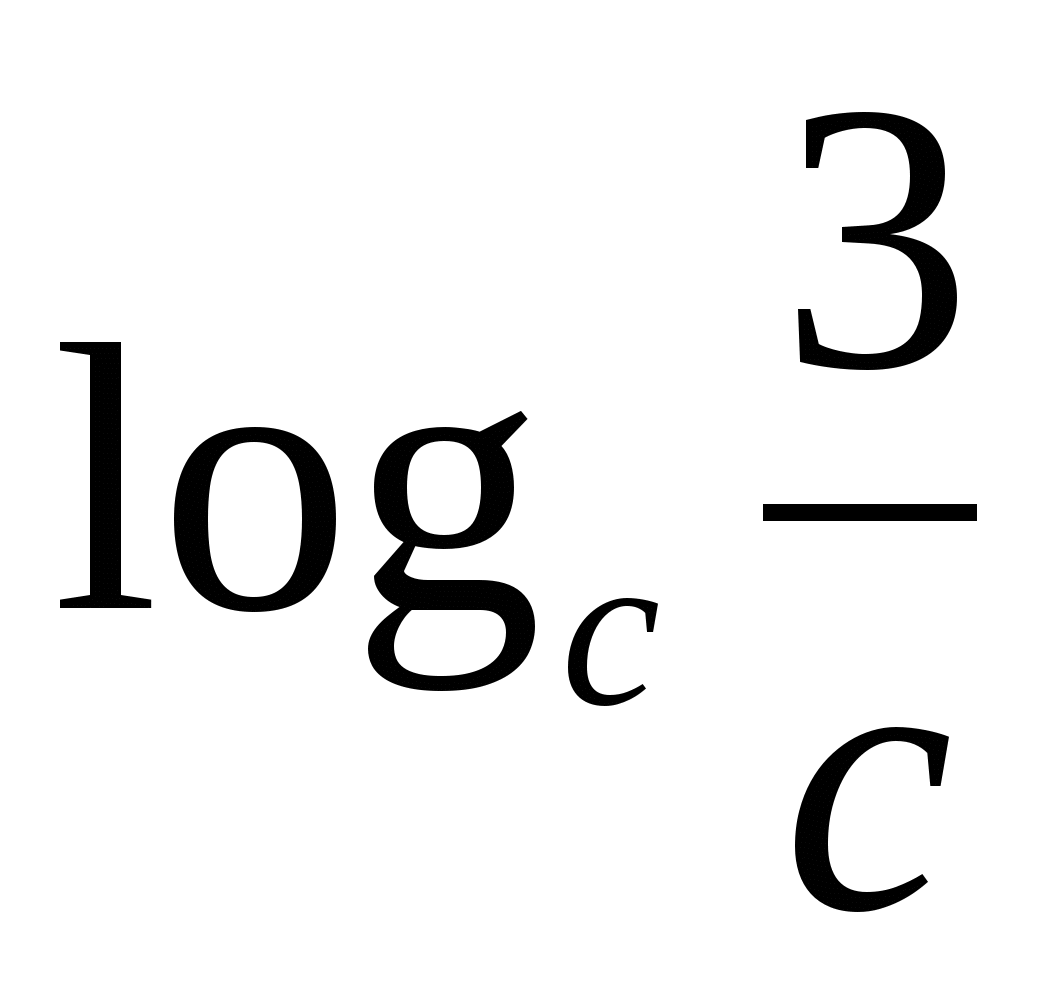

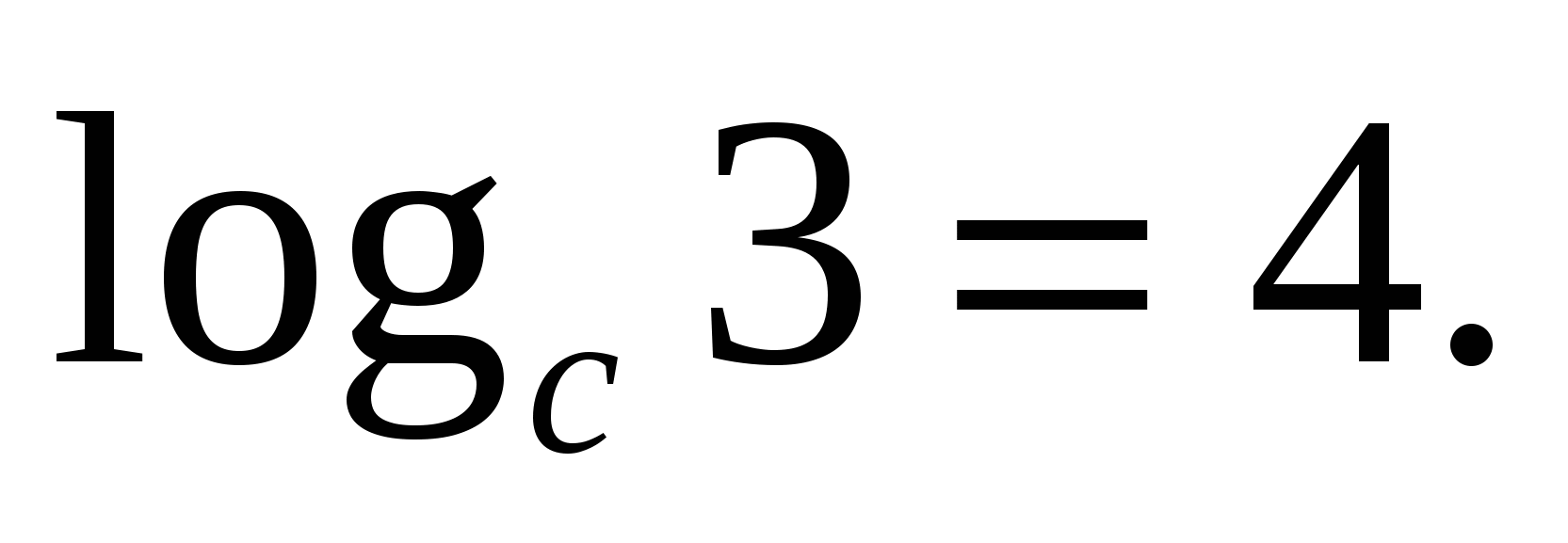Nézzük meg ennek a képletnek az alkalmazását egy példa segítségével:

Z
feladat 1. Keresse meg az if kifejezés értékét

2. feladat. Keresse meg az értéket b logaritmusa alapján

6) Hatvány logaritmusa a bázishozA , egyenlő a kitevő és a logaritmus szorzatával, ugyanazt az alapot használva.

TsOR 4

Például,

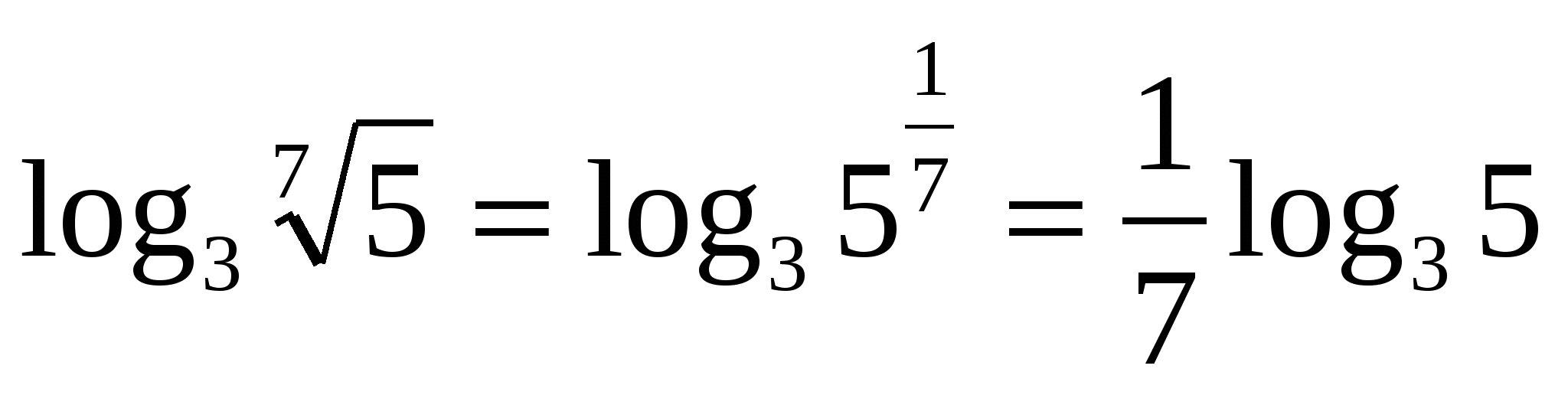
Z
feladat 1. Számold ki, ha

Egyszerűsítsük a kifejezést

Képlet

hívott képlet az új alapra való áttéréshez.

Z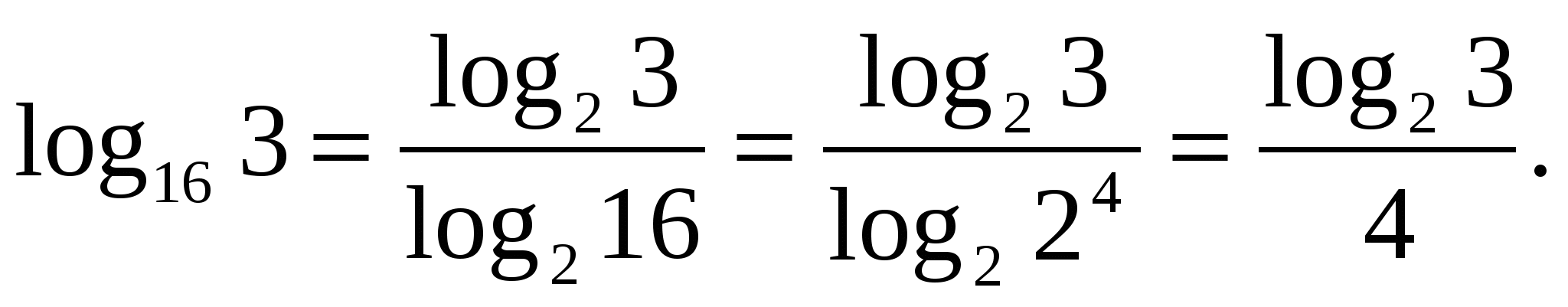

feladat 1. Fejezd ki 2-es bázisú logaritmussal.

2. feladat. Kiszámítja

TsOR 5

TsOR 6

Például,

Z

feladat 1. Kiszámítja

Z
feladat 2. Kiszámítja

9) A logaritmikus transzformáció csak olyan esetekben indítható el, amikor ha emlékszel a logaritmusok összes tulajdonságára. Ezeket megismételve átgondoljuk az átalakítási feladatokat logaritmikus kifejezések a másik oldalon.

A logaritmikus kifejezések összegének vagy különbségének konvertálásához néha elegendő egy logaritmus definícióját használni, és leggyakrabban egy szorzat vagy hányados logaritmusának tulajdonságait.

Z
feladat 1. Kiszámítja

Kétféleképpen oldjuk meg.

1 módon, a logaritmus definíciójával:

2. módszer alapján hányados logaritmusának tulajdonsága:

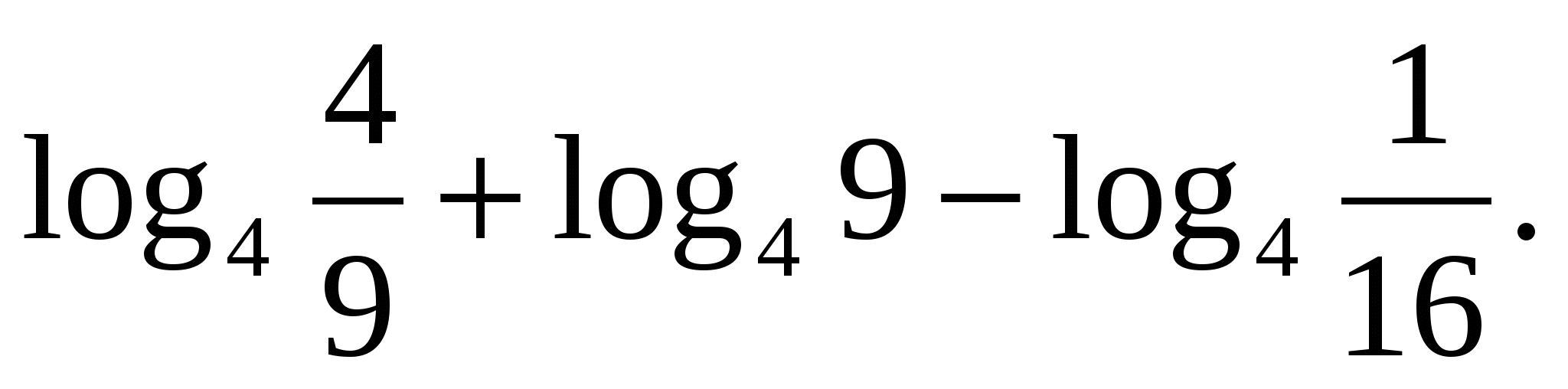
2. feladat. Keresse meg a kifejezés jelentését

Először alkalmazzuk a képletet a szorzat logaritmusa, majd a logaritmus definíciója.

Az alapvető logaritmikus azonosságot a logaritmust kitevőként tartalmazó kifejezések konvertálásakor használjuk. Az ilyen műveletek ötlete az, hogy megszerezzük egyenlő alapon a logaritmus hatványai és alapjai.

Néha szükség van a kifejezés átalakítására a logaritmus tulajdonságaival és a fok tulajdonságaival is az átmeneti képlet segítségével könnyedén léphet egyik alapról a másikra. Más esetekben több tulajdonságot kell alkalmazni.

Z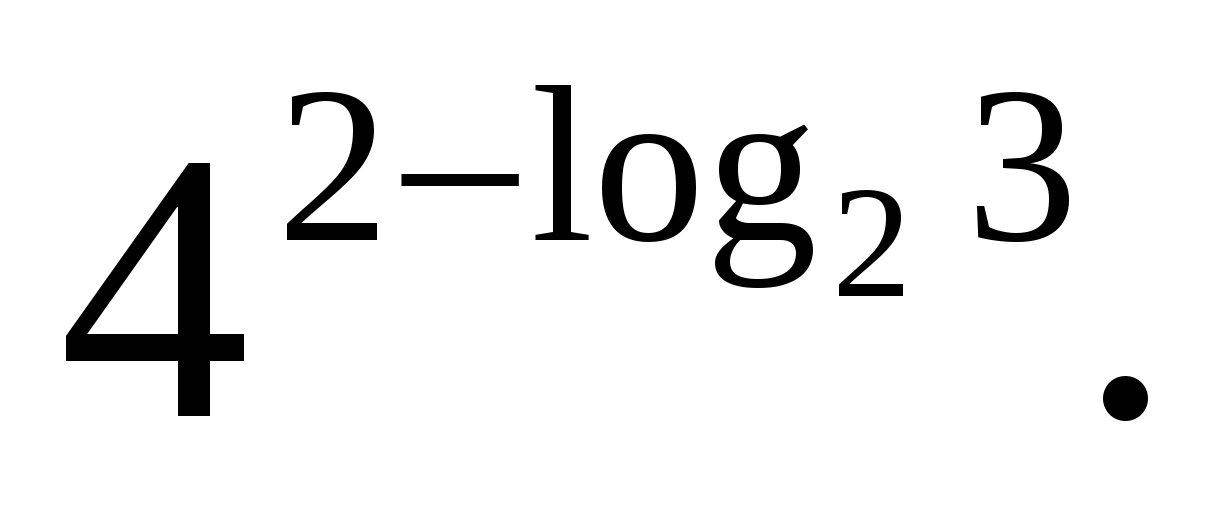
feladat 3. Kiszámítja

Z
feladat 4. Keresse meg a kifejezés jelentését

5. feladat. Keresse meg a kifejezés jelentését

Z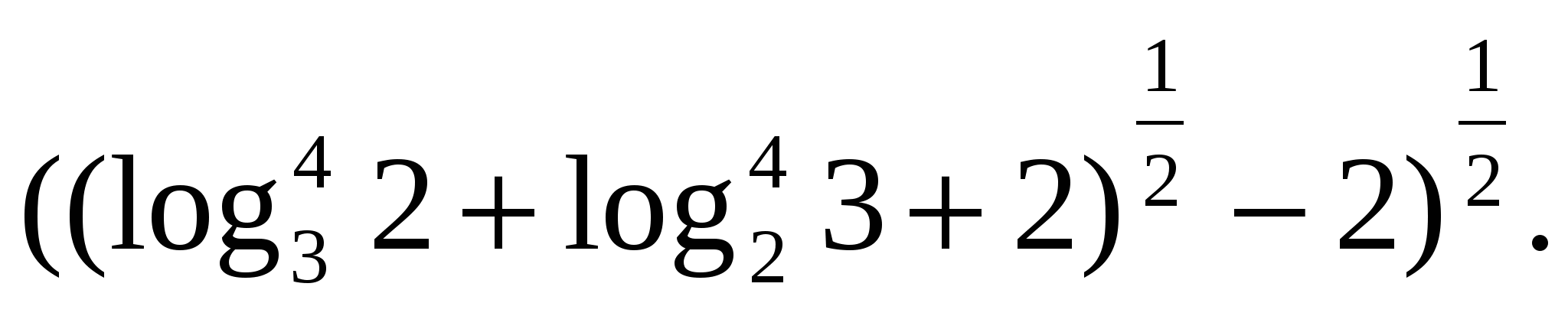
feladat 6. Fejezd ki logaritmusok különbségeként!

N
A legnagyobb nehézséget a logaritmikus kifejezések gyökbe konvertálása jelenti. A transzformációk során figyelembe kell venni a logaritmikus kifejezések moduljait, amelyek megoldásához az irracionális számok vagy egy racionális és egy irracionális szám összehasonlítása szükséges. Következetesen fogunk cselekedni. Nézzük a belső gyök alatti kifejezést.

Helyettesítsük az eredeti kifejezéssel.

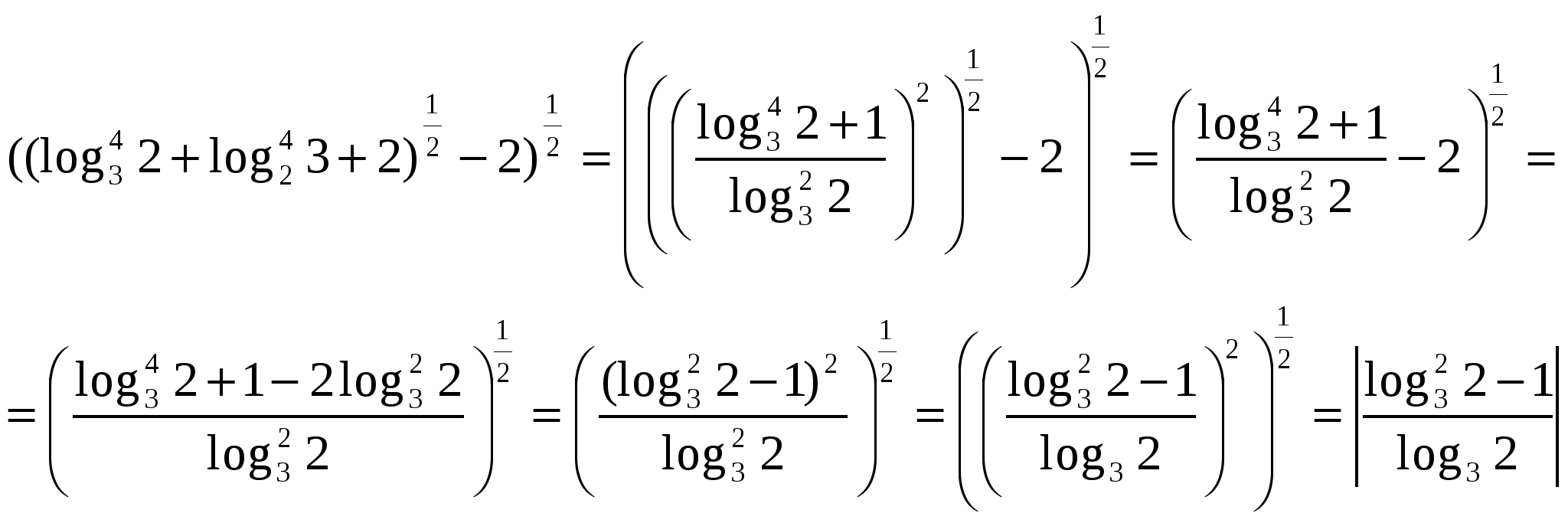Megjegyzendő, hogy a logaritmikus kifejezések transzformációjával egyenletek és egyenlőtlenségek megoldásánál, függvények tanulmányozásánál is találkozhatunk, ezért implicit formában jelen lehetnek a B és C csoport feladataiban.

10) Összegzés. Kérdések:

A 10-es bázis logaritmusát nevezzük

alap logaritmus

fő logaritmus

természetes logaritmus

decimális logaritmus

2) Milyen értékeket vehet fel?x kifejezésében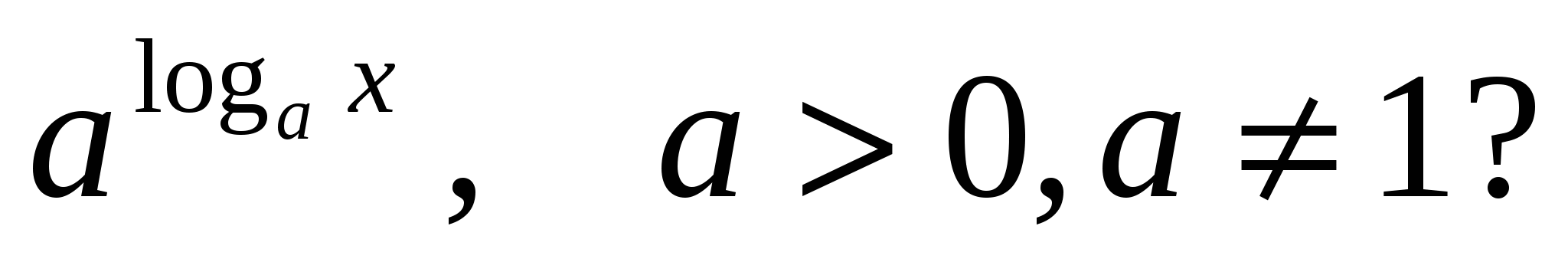

Az érték nincs megadva

5) Adjon meg egy mindenkire igaz arányt!x ≠ 0 .

6) Adja meg az új alapra költözés képletének helyes arányát.

7) Adja meg a megfelelő egyenlőséget

11) Ellenőrző tesztelés.

Matematika. Tantárgyi tesztek. rész II. Felkészülés a 2010-es egységes államvizsgára. 10-11 évfolyam. Szerk. Lysenko F.F. - Rostov n/d.: Légió, 2009. - 176 p.

Matematika. Egységes államvizsga 2009. Tematikus tesztek. II. rész (B4-B8, C1-C2) Szerk. Lysenko F.F. - Rostov n/D: Légió, 2008 - 160 p.

A kézikönyv a matematika kurzusokban hagyományosnak számító, és ezért rendszerint az Egységes Államvizsga részét képező, egyedi témakörökre vonatkozó tesztekből áll. Teljes mértékben lefedik az egységes államvizsga fokozott és összetettebb feladatcsoportjait, kivéve a szöveges és geometriai feladatokat. Minden témához egy vagy több tesztsorozatot kínálunk. Minden készlet 10 tesztet tartalmaz, minden teszt 8 feladatot tartalmaz.

A könyv célja rövid és hosszú válaszokat tartalmazó feladatok gyakorlása. Egységes államvizsga tesztek. Elsősorban a végzettek számára szükséges, akik elvárják, hogy megkapják a jó HASZNÁLATértékelést, valamint a 10. évfolyamos tanulók számára, akik az Egységes Államvizsga szemszögéből tudják megszilárdítani a felvett témákat. A javasolt kézikönyv hasznos lehet minden matematika egységes államvizsgára készülő végzős, valamint az egységes államvizsgára felkészítő tanár számára.

Formátum: djvu/zip (2009 , 176 o.)

Méret: 2,5 MB

Fájl letöltése / letöltése 14

Formátum: pdf (2009 , 176 o.)

Méret: 8,6 MB

Letöltés: 14 .12.2018, a linkek a Legion kiadó kérésére eltávolítva (lásd a megjegyzést)

Formátum: djvu/zip (2008 , 160-as évek.)

Méret: 3 MB

Fájl letöltése / letöltése 14 .12.2018, a linkek a Legion kiadó kérésére eltávolítva (lásd a megjegyzést)

Formátum: pdf (2008 , 160-as évek.)

Méret: 9,9 MB

Letöltés: 14 .12.2018, a linkek a Legion kiadó kérésére eltávolítva (lásd a megjegyzést)

Képzési és módszertani komplexum"Matematika. Egységes államvizsga-2010" szerk. Lysenko F.F. és Kulabukhova S.Yu. oktatóanyagokat tartalmaz:
1. Matematika. Felkészülés a 2010-es egységes államvizsgára.
2. Reshebnik. Matematika. Felkészülés a 2010-es egységes államvizsgára.
3. Matematika. Tematikus tesztek. I. rész (alapszint). Felkészülés a 2010-es egységes államvizsgára. 10-11 évfolyam.
4. Matematika. Tematikus tesztek. rész II. Felkészülés a 2010-es egységes államvizsgára. 10-11 évfolyam.
5. Matematika. Tematikus tesztek: geometria, szöveges feladatok. Felkészülés a 2010-es egységes államvizsgára. 10-11 évfolyam.
6. Matematika. Egységes államvizsga-tesztek gyűjteménye 2001-2010.
7. Matematika. Felkészülés a 2010-es egységes államvizsgára. Oktatási és képzési tesztek.
8. Pocket Guide matematika.

Tartalomjegyzék
A szerzőktől 11
1. § Logaritmikus kifejezések azonos transzformációi 13
1. lehetőség 13
2. lehetőség 13
3. lehetőség 14
4. lehetőség 14
5. lehetőség 15
6. lehetőség 15
7. lehetőség 16
8. lehetőség 16
9. számú lehetőség 17
10. számú lehetőség 17
2. § A 18-as hatványokat tartalmazó kifejezések azonos átalakításai
1. lehetőség 18
2. lehetőség 19
3. lehetőség 19
4. lehetőség 20
5. lehetőség 21
6. lehetőség 21
7. lehetőség 22
8. lehetőség 23
9. számú lehetőség 23
10 24. számú lehetőség
3. § Identitásátalakítások irracionális kifejezések 25
1. számú lehetőség 25
2. lehetőség 25
3. lehetőség 26
4. lehetőség 26
5. számú lehetőség 27
6. lehetőség 28
7. lehetőség 28
8. lehetőség 29
9. számú lehetőség 30
10 30. számú lehetőség
4. § Egyenletrendszerek 31
1. számú lehetőség 31
2. lehetőség 32
3. lehetőség 33
4. számú lehetőség 33
5. számú lehetőség 34
6. számú lehetőség 35
7. számú lehetőség 36
8. számú lehetőség 37
9. számú lehetőség 38
10 39. számú lehetőség
5. §. Geometriai jelentés származéka 39
1. számú lehetőség 39
2. lehetőség 41
3. lehetőség 43
4. számú lehetőség 44
5. lehetőség 46
6. lehetőség 48
7 50. számú lehetőség
8 52. számú lehetőség
9 54. számú lehetőség
10 55. számú lehetőség
6. § Egyenlőtlenségek 56
1. számú opció g 56
2. lehetőség 57
3. lehetőség 58
4. lehetőség 58
5. számú lehetőség 59
6. számú lehetőség 60
7 60. számú lehetőség
8 61. számú lehetőség
9 62. számú lehetőség
10 63. számú lehetőség
7. § Irracionális egyenletek 63
1. számú lehetőség 63
2. lehetőség 64
3. lehetőség 65
4. lehetőség 65
5. lehetőség 66
6. számú lehetőség 66
7. lehetőség 67
8 67. számú lehetőség
9 68. számú lehetőség
Yu 68 számú opció
8. § Trigonometrikus egyenletek 69
1. számú lehetőség 69
2. lehetőség 69
3. lehetőség 70
4. számú lehetőség 70
5. számú lehetőség 71
6 72. számú lehetőség
7. számú lehetőség 72
8 73. számú lehetőség
9 74. számú lehetőség
10 74. számú lehetőség
9. § Logaritmikus egyenletek 75
1. számú lehetőség 75
2. lehetőség 75
3. lehetőség 76
4. számú lehetőség 76
5. számú lehetőség 77
6 77. számú lehetőség
7. számú lehetőség 78
8. * 78. számú lehetőség
9 79. számú lehetőség
10 79. számú lehetőség
10. § Exponenciális egyenletek 80
1. számú opció 80
2. lehetőség 80
3. lehetőség 81
4. lehetőség 81
5. számú opció 82
6 82. számú lehetőség
7 83. számú lehetőség
8. számú opció 83
9 84. számú lehetőség
10 84. számú lehetőség
§tizenegy. Periodikus, páros és páratlan függvények 85
1. számú lehetőség 85
2. lehetőség 86
3. lehetőség 87
4. lehetőség 89
5. számú lehetőség 90
6 91. számú lehetőség
7 92. számú lehetőség
8 93. számú lehetőség
9 94. számú lehetőség
10 95. számú opció
12. § Nullák összetett funkció. Korlátozott funkció 97
1 97. számú lehetőség
2. lehetőség 97
3. lehetőség 98
4 98. számú lehetőség
5 99. számú lehetőség
6 99. számú lehetőség
7 100. számú lehetőség
8 100. számú lehetőség
9 101. számú lehetőség
10 101. számú lehetőség
13. § Meghatározási terület, értékkészlet, függvények monotonitása 102
1 102. számú lehetőség
2. lehetőség 102
3. lehetőség 103
4 103. számú lehetőség
5 104. számú lehetőség
6 104. számú lehetőség
7 105. számú lehetőség
8 105. számú lehetőség
9 106. számú lehetőség
10 107. számú lehetőség
14. § Egy funkció szélsősége. A 107-es függvény legnagyobb és legkisebb értéke
1. számú lehetőség 107
2. lehetőség 108
3. lehetőség 108
4 109. számú lehetőség
5 109. számú lehetőség
6 110. számú lehetőség
7 110. számú lehetőség
8 111. számú lehetőség
9 111. számú lehetőség
10 112 számú opció
15. § Különféle technikák logaritmikus egyenletek megoldására 113
1 113. számú lehetőség
2. lehetőség 113
3 114. számú lehetőség
4 114. számú lehetőség
5 115. számú lehetőség
6 115. számú lehetőség
7 116. számú lehetőség
8 116. számú lehetőség
9 117. számú lehetőség
10 117. számú lehetőség
16. § Különféle megoldási technikák trigonometrikus egyenletek 118
1 118. számú lehetőség
2. lehetőség 118
3. lehetőség 118
4 119. számú lehetőség
5 119. számú lehetőség
6 120. számú lehetőség
7 120. számú lehetőség
8 121. számú lehetőség
9 121. számú lehetőség
10 122 számú opció
17. § Különféle megoldási technikák irracionális egyenletek 123
1 123. számú lehetőség
2. lehetőség 123
3 124. számú lehetőség
4 124. számú lehetőség
5 125. számú lehetőség
6 125. számú lehetőség
7 125. számú lehetőség
8 126. számú lehetőség
9 126. számú lehetőség
10 127. számú lehetőség
18. § Modulusjel alatt változót tartalmazó egyenletek 127
1 127. számú lehetőség
2. lehetőség 128
3. lehetőség 128
4 129. számú lehetőség
5 129. számú lehetőség
6 130. számú lehetőség
7 130. számú lehetőség
8 131. számú lehetőség
9 131. számú lehetőség
10 131. számú lehetőség
19. § Különféle megoldási technikák exponenciális egyenletek.132
1 132. számú lehetőség
2. lehetőség 133
3. lehetőség 133
4 134. számú lehetőség
5 134. számú lehetőség
6 135. számú lehetőség
7 135. számú lehetőség
8 135. számú lehetőség
9 136. számú lehetőség
10 136. számú lehetőség
20. § Különféle technikák kombinált egyenletek megoldására 137
1 137. számú lehetőség
2. lehetőség 137
3. lehetőség 138
4 138. számú lehetőség
5 139. számú lehetőség
6 139. számú lehetőség
7 140. számú lehetőség
8 140. számú lehetőség
9 141. számú lehetőség
10 141 számú lehetőség
21. § Egyenletek a 142. modult tartalmazó paraméterrel
1 142. számú lehetőség
2. lehetőség 142
3. lehetőség 143
4 144. számú lehetőség
5 144. számú lehetőség
6 145. számú lehetőség
7 146. számú lehetőség
8 146. számú lehetőség
9 147. számú lehetőség
10 148 számú lehetőség
Válaszok 149
1. §. Identitás transzformációk logaritmikus kifejezések 149
2. § A 150-es hatványokat tartalmazó kifejezések azonos transzformációi
3. § Irracionális kifejezések azonos transzformációi 150
4. § Egyenletrendszerek 151
5. § A származék geometriai jelentése 151
6. § Egyenlőtlenségek 152
7. § Irracionális egyenletek 152
8. § Trigonometrikus egyenletek 153
9. § Logaritmikus egyenletek 153
10. § Exponenciális egyenletek 154
§tizenegy. Periodikus, páros és páratlan függvények 154
12. § Összetett függvény nullái. Korlátozott funkció 155
13. § Meghatározási terület, értékkészlet, függvények monotonitása 156
14. § Egy funkció szélsősége. A 158-as függvény legnagyobb és legkisebb értéke
15. § Különféle technikák logaritmikus egyenletek megoldására 159
16. § Különféle technikák trigonometrikus egyenletek megoldására 160
17. § Különféle technikák irracionális egyenletek megoldására 164
18. § Modulusjel alatt változót tartalmazó egyenletek 165
19. § Különféle technikák az exponenciális egyenletek megoldására.166
20. § Különféle technikák kombinált egyenletek megoldására 167
21. § Egyenletek a 169. modult tartalmazó paraméterrel
Irodalom 170

A B7 feladat olyan kifejezést ad, amelyet le kell egyszerűsíteni. Az eredmény egy szabályos szám legyen, amelyet fel lehet írni a válaszlapra. Az összes kifejezést hagyományosan három típusra osztják:

1. Logaritmikus,
2. tájékoztató jellegű,
3. Kombinált.

Az exponenciális és logaritmikus kifejezések tiszta formájukban gyakorlatilag soha nem találhatók. Számításuk módjának ismerete azonban feltétlenül szükséges.

Általánosságban elmondható, hogy a B7 problémát meglehetősen egyszerűen megoldják, és az átlagos diplomás képességein belül van. Az egyértelmű algoritmusok hiányát a szabványosítás és a monotónia kompenzálja. Egyszerűen megtanulhatja az ilyen problémák megoldását nagy mennyiség kiképzés.

Logaritmikus kifejezések

A B7 feladatok túlnyomó többsége valamilyen formában logaritmusokat tartalmaz. Ezt a témát hagyományosan nehéznek tekintik, mivel általában a 11. évfolyamon - a záróvizsgákra való tömeges felkészítés korszakában - folyik a tanulmányozása. Ennek eredményeként sok diplomás nagyon homályosan érti a logaritmusokat.

De ebben a feladatban senki sem igényel mély elméleti ismereteket. Csak a legtöbbet fogjuk találkozni egyszerű kifejezések, amelyek egyszerű érvelést igényelnek, és önállóan is könnyen elsajátíthatók. Az alábbiakban felsoroljuk azokat az alapvető képleteket, amelyeket ismernie kell a logaritmus kezeléséhez:

Ezenkívül képesnek kell lennie arra, hogy a gyököket és a törteket hatványokkal helyettesítse racionális mutató, különben egyes kifejezésekben egyszerűen nem lesz mit kivenni a logaritmusjel alól. Csere képletek:

Feladat. Keresse meg a kifejezések jelentését:
log 6 270 − log 6 7.5
log 5 775 − log 5 6.2

Az első két kifejezést a rendszer a logaritmusok különbségeként konvertálja:
log 6 270 − log 6 7,5 = log 6 (270: 7,5) = log 6 36 = 2;
log 5 775 − log 5 6,2 = log 5 (775: 6,2) = log 5 125 = 3.

A harmadik kifejezés kiszámításához el kell különítenie a hatványokat - mind az alapban, mind az argumentumban. Először keressük meg a belső logaritmust:

Aztán - külső:

A log a log b x konstrukció sokak számára bonyolultnak és félreérthetőnek tűnik. Eközben ez csak a logaritmus logaritmusa, azaz. log a (log b x ). Először a belső logaritmust számítjuk ki (log b x = c), majd a külsőt: log a c.

Demonstratív kifejezések

Exponenciális kifejezésnek fogunk nevezni minden olyan a k alakú konstrukciót, ahol az a és k számok tetszőleges állandók, és a > 0. Az ilyen kifejezésekkel való munkamódszer meglehetősen egyszerű, és a 8. osztály algebrai óráin tárgyaljuk őket.

Az alábbiakban felsoroljuk azokat az alapvető képleteket, amelyeket feltétlenül tudnod kell. E képletek gyakorlati alkalmazása általában nem okoz problémát.

1. a n · a m = a n + m ;
2. a n / a m = a n − m ;
3. (a n ) m = a n · m ;
4. (a · b ) n = a n · b n ;
5. (a : b ) n = a n : b n .

Ha egy összetett, erõs kifejezéssel találkozik, és nem világos, hogyan kell megközelíteni, használjon egy univerzális technikát - az egyszerû tényezõkre való bontást. Ennek eredményeként nagy számok a fokozatok alapjaiban egyszerű és érthető elemek váltják fel. Ezután már csak a fenti képleteket kell alkalmazni - és a probléma megoldódik.

Feladat. Keresse meg a következő kifejezések értékét: 7 9 · 3 11: 21 8, 24 7: 3 6: 16 5, 30 6: 6 5: 25 2.

Megoldás. Bontsuk fel a hatványok összes alapját egyszerű tényezőkre:
7 9 3 11: 21 8 = 7 9 3 11: (7 3) 8 = 7 9 3 11: (7 8 3 8) = 7 9 3 11: 7 8: 3 8 = 7 3 3 = 189.
24 7: 3 6: 16 5 = (3 2 3) 7: 3 6: (2 4) 5 = 3 7 2 21: 3 6: 2 20 = 3 2 = 6.
30 6: 6 5: 25 2 = (5 3 2) 6: (3 2) 5: (5 2) 2 = 5 6 3 6 2 6: 3 5: 2 5: 5 4 = 5 2 3 2 = 150 .

Kombinált feladatok

Ha ismeri a képleteket, akkor minden exponenciális és logaritmikus kifejezés szó szerint egy sorban megoldható. A B7 feladatban azonban a hatványok és a logaritmusok kombinálhatók, hogy meglehetősen erős kombinációkat alkossanak.

Dnyeszteren túli Állami Egyetem

őket. T.G. Sevcsenko

Fizikai és Matematikai Kar

Matematikai Elemzés Tanszék

és a matematikatanítás módszerei

TANFOLYAM MUNKA

"Identitás átalakulások

exponenciális és logaritmikus

kifejezések"

Elkészült munka:

a _______ csoport tanulója

Fizikai és Matematikai Kar

_________________________

Megnéztem a munkát:

_________________________

Tiraszpol, 2003

Bevezetés…………………………………………………………………………………2

1. fejezet Identitástranszformációk és tanítási módszerek az algebra iskolai kurzusában és az elemzés kezdete………………………………………..4

§1. Az átalakítások meghatározott típusainak alkalmazásához szükséges készségek kialakítása…………………………………………………………………………………………….4

§2. A tudásrendszer szerveződésének jellemzői az identitás-transzformációk vizsgálatában.…….…………………………………………..………….

§3. Matematika program………………………………………………………….11

2. fejezet Exponenciális és logaritmikus kifejezések azonos transzformációi és számításai…………………………………………………13

§1. A fokozat fogalmának általánosítása……………………………………..13

§2. Exponenciális függvény………………………………………………………..15

§3. Logaritmikus függvény…………………………………….16

3. fejezet Exponenciális és logaritmikus kifejezések azonos transzformációi a gyakorlatban................................... ...................................................19

Következtetés………………………………………………………………..24

Hivatkozások listája…………………………………………………………….25
Bevezetés

Ebben tanfolyami munka Figyelembe kell venni az exponenciális és logaritmikus függvények azonos transzformációit, az iskolai algebratanfolyamon való tanítás módszertanát és az elemzés kezdetét.

A munka első fejezete leírja az identitástranszformációk tanításának módszertanát egy iskolai matematika kurzusban, valamint tartalmaz egy matematikai programot az „Algebra és az elemzés kezdetei” kurzusban, exponenciális és logaritmikus függvények tanulmányozásával.

A második fejezet közvetlenül magát az exponenciális és logaritmikus függvényeket, az identitástranszformációk során használt alapvető tulajdonságaikat vizsgálja.

A harmadik fejezet példák és problémák megoldása exponenciális és logaritmikus függvények azonos transzformációival.

A kifejezések és képletek különféle transzformációinak tanulmányozása a tantárgy tanítási idejének jelentős részét foglalja el iskolai matematika. A tulajdonságokon alapuló legegyszerűbb átalakítások aritmetikai műveletek, már ben gyártják Általános Iskolaévfolyamon pedig a IV–V. De az átalakítások végrehajtásához szükséges készségek és képességek fejlesztésének fő terhét az iskolai algebratanfolyam viseli. Ennek oka egyrészt az elvégzendő átalakítások számának és változatosságának meredek növekedése, másrészt az azokat alátámasztó, az alkalmazhatóság feltételeit tisztázó tevékenységek bonyolultsága, az identitás, az azonos átalakulás általánosított fogalmainak azonosítása és tanulmányozása, ekvivalens transzformáció, logikai következmény.

Az identitástranszformációk végrehajtásának kultúrája ugyanúgy fejlődik, mint a számítások kultúrája, amely az objektumokon végzett műveletek tulajdonságainak (számok, vektorok, polinomok stb.) és a végrehajtásukhoz szükséges algoritmusok szilárd ismeretén alapul. Nemcsak a transzformációk helyes alátámasztásának képességében nyilvánul meg, hanem abban is, hogy megtaláljuk a legrövidebb utat az átmenethez az eredeti analitikus kifejezésről a transzformáció céljának leginkább megfelelő kifejezésre, a változások nyomon követésének képességében is. az analitikus kifejezések meghatározásának tartománya azonos transzformációk láncolatában, a transzformációk végrehajtásának gyorsaságában és pontosságában.

Biztonság magas kultúra számításokat és azonosságtranszformációkat ábrázol fontos probléma matematika tanítása. Ez a probléma azonban még messze van a kielégítő megoldástól. Ennek bizonyítéka a hatóságok statisztikai adatai közoktatás, amelyben a különböző osztályok tanulói által végzett hibák és irracionális számítási módszerek és átalakítások tesztek. Ezt megerősítik az idősebbek véleményei oktatási intézmények a jelentkezők matematikai tudásának és készségeinek minőségéről. Nem lehet egyet érteni a közoktatási hatóságok és az egyetemek azon következtetéseivel, hogy ez nem elég magas szint számítások és identitásátalakítások kultúrája in Gimnázium a formalizmus következménye a hallgatók tudásában, az elmélet és a gyakorlat elválasztása.

Azonos átalakítások és tanítási módszerek

az algebra iskolai kurzusában és az elemzés kezdetén.

§1. Alkalmazási készségek kialakítása

specifikus típusú transzformációk.

Az átalakítások végrehajtására szolgáló technikák és szabályok rendszere, amelyet az algebra kezdeti szakaszában használnak, nagyon széles körű alkalmazási körrel rendelkezik: a teljes matematika kurzus tanulmányozásában használják. Ez a rendszer azonban éppen alacsony specifitása miatt további átalakításokat igényel, amelyek figyelembe veszik a transzformálandó kifejezések szerkezeti sajátosságait és az újonnan bevezetett műveletek és függvények tulajdonságait. A megfelelő típusú transzformációk elsajátítása a rövidített szorzóképletek bevezetésével kezdődik. Ezután a hatványozás műveletéhez kapcsolódó transzformációkat különböző osztályokkal vizsgáljuk elemi függvények– exponenciális, hatvány, logaritmikus, trigonometrikus. Az ilyen típusú átalakítások mindegyike egy tanulási fázison megy keresztül, amelyben a figyelem a jellemző tulajdonságaik elsajátítására összpontosul.

Az anyag felhalmozódásával lehetővé válik az összes vizsgált transzformáció közös jellemzőinek kiemelése, és ennek alapján az azonos és egyenértékű transzformációk fogalmának bevezetése.

Megjegyzendő, hogy az identitástranszformáció fogalmát az iskolai algebra kurzusban nem teljes általánosságban adjuk meg, hanem csak kifejezésekre vonatkoztatva. A transzformációk két osztályba sorolhatók: az azonos transzformációk kifejezések transzformációi, az ekvivalens transzformációk pedig képletek transzformációi. Abban az esetben, ha a képlet egy részének egyszerűsítésére van szükség, ebben a képletben egy kifejezést emelünk ki, amely argumentumként szolgál az alkalmazott azonosságtranszformációhoz. A megfelelő predikátumot változatlannak tekintjük.

Ami az átalakítások (szintézis) integrált rendszerének megszervezését illeti, annak fő célja egy rugalmas és erőteljes; különféle megoldásokra alkalmas készülékek oktatási feladatokat.

Az algebra és az elemzés kezdete során a főbb jellemzőiben már kialakult holisztikus transzformációs rendszer fokozatosan tovább fejlődik. Néhány új típusú átalakítás is hozzáadódik hozzá, de ezek csak gazdagítják, bővítik a képességeit, de nem változtatnak a szerkezetén. Az új transzformációk tanulmányozásának módszertana gyakorlatilag nem különbözik az algebra kurzusban használt módszertől.

§2. A feladatrendszer felépítésének jellemzői

az identitástranszformációk tanulmányozása során.

Bármilyen feladatrendszer megszervezésének alapelve, hogy az egyszerűtől a bonyolultig mutassuk be azokat, figyelembe véve a tanulók számára, hogy leküzdjék a megvalósítható nehézségeket és alkossanak. problémás helyzetek. Ez az alapelv pontosítást igényel az oktatási anyag jellemzőivel kapcsolatban. A matematikai módszerek különböző feladatrendszereinek leírására a gyakorlati ciklus fogalmát használjuk. A gyakorlati ciklust a tanulás több aspektusának és az anyag elrendezésének technikáinak gyakorlati sorozatban történő kombinációja jellemzi. Az identitás-transzformációk kapcsán a ciklus fogalma a következőképpen adható meg.

A gyakorlatok ciklusa egy identitás vizsgálatához kapcsolódik, amely köré csoportosulnak a vele természetes kapcsolatban álló további identitások. A ciklus a végrehajtókkal együtt olyan feladatokat tartalmaz, amelyek megkövetelik a kérdéses identitás alkalmazhatóságának felismerését. A vizsgált identitás különféle numerikus tartományokra vonatkozó számítások elvégzésére szolgál. Az identitás sajátosságait figyelembe veszik; különösen a hozzá kapcsolódó beszédfigurák szerveződnek.

Az egyes ciklusok feladatai két csoportra oszlanak. Az elsőbe az identitás első megismerése során elvégzett feladatok tartoznak. Szolgálnak oktatási anyag több egymást követő órára, amelyeket egy téma egyesít. A gyakorlatok második csoportja a vizsgált identitást kapcsolja össze különféle alkalmazásokkal. Ez a csoport nem alkot kompozíciós egységet - a gyakorlatok itt szétszórva vannak különböző témákban.

A leírt ciklusstruktúra az adott típusú transzformációk alkalmazásának képességeinek fejlesztési szakaszára vonatkozik. Tovább végső szakasz– a szintézis szakaszában a ciklusok módosulnak. Először is, mindkét feladatcsoport egy „kibővített” ciklust alkot, és a megfogalmazás vagy a feladat elvégzésének bonyolultsága szempontjából a legegyszerűbbek kimaradnak az első csoportból. A többi feladattípus összetettebbé válik. Másodszor, a különböző identitáshoz kapcsolódó ciklusok összeolvadása következik be, aminek következtében megnő az adott identitás alkalmazhatóságát felismerő cselekvések szerepe.

Jegyezzük meg az elemi függvények azonosságához kapcsolódó feladatciklusok jellemzőit. Ezek a jellemzők abból a tényből adódnak, hogy egyrészt a megfelelő identitásokat a funkcionális anyag tanulmányozása során tanulmányozzák, másrészt később jelennek meg, mint az első csoport identitásai, és a már kialakult identitástranszformációk végrehajtásához szükséges készségekkel tanulmányozzák őket. .

Minden újonnan bevezetett elemi függvény drámaian kibővíti az egyedileg kijelölhető és elnevezhető számok körét. Ezért a ciklusfeladatok első csoportjának olyan feladatokat kell tartalmaznia, amelyek az új számszerű területek és az eredeti terület közötti kapcsolatot teremtik meg racionális számok. Mondjunk példákat ilyen feladatokra.

1. példa Számítsa ki:

Minden kifejezés mellett egy azonosság van feltüntetve, azokban a ciklusokban, amelyekhez a javasolt feladatok jelen lehetnek. Az ilyen feladatok célja a rekordok jellemzőinek elsajátítása, beleértve az új műveletek és funkciók szimbólumait, valamint a matematikai beszédkészség fejlesztését.

Az elemi függvényekhez kapcsolódó identitástranszformációk használatának jelentős része irracionális és transzcendentális egyenletek megoldására esik. Az identitások asszimilációjával kapcsolatos ciklusok csak a legtöbbet tartalmazzák egyszerű egyenletek, de már itt is célszerű munkát végezni az ilyen egyenletek megoldási módszerének elsajátításán: csökkenteni az ismeretlent helyettesítve algebrai egyenlet.

A megoldás lépéseinek sorrendje a következő:

a) keresse meg a függvényt, amelyhez adott egyenlet formában ábrázolható ;

b) végezze el a behelyettesítést és oldja meg az egyenletet;

c) oldja meg az egyes egyenleteket, ahol az egyenlet gyökeinek halmaza.

A leírt módszer alkalmazásakor a b) lépést gyakran implicit módon hajtják végre, anélkül, hogy jelölést vezetnének be. Emellett a tanulók gyakran a válaszkereséshez vezető különféle utak közül azt választják, amelyik gyorsabban és könnyebben vezet az algebrai egyenlethez.

2. példa Oldja meg az egyenletet!

Első út:

Második út:

A)

b)

Itt látható, hogy az első módszerrel az a) lépés nehezebb, mint a másodiknál. Az első módszerrel „nehezebb kezdeni”, bár a megoldás további menete sokkal egyszerűbb. Másrészt a második módszer előnye, hogy könnyebb és pontosabb az algebrai egyenletre való redukálás megtanulása.

Mert iskolai tanfolyam Jellemzőek azok az algebrai feladatok, amelyekben az algebrai egyenletre való átmenet még egyszerűbb, mint ebben a példában. Az ilyen feladatok fő terhelése a c) lépés azonosítása, mint a megoldási folyamat önálló része, amely a vizsgált elemi függvény tulajdonságainak felhasználásához kapcsolódik.

3. példa Oldja meg az egyenletet:

A) ; b) .

Ezeket az egyenleteket a következő egyenletekre redukáljuk: a) vagy ; b) vagy . Ezen egyenletek megoldásához csak a legegyszerűbb tények ismerete szükséges exponenciális függvény: monotóniája, értéktartománya. Az előző példához hasonlóan az a) és b) egyenlet a másodfokú exponenciális egyenletek megoldására szolgáló gyakorlatok első csoportjába sorolható.

Így eljutunk a feladatok ciklusok szerinti osztályozásához, amelyek az exponenciális függvényt tartalmazó transzcendentális egyenletek megoldásához kapcsolódnak:

1) olyan egyenletek, amelyek a következő alakú egyenletekre redukálódnak, és amelyeknek egyszerű, általános válaszuk van: ;

2) egyenletek, amelyek egyenletekre redukálódnak, ahol egy egész szám, vagy , ahol ;

3) olyan egyenletek, amelyek egyenletekre redukálódnak, és megkövetelik a szám írásbeli alakjának explicit elemzését.

Hasonlóan osztályozhatók a többi elemi függvény feladatai is.

Az algebrában és az algebrában tanult identitások és az elemzési kurzusok alapelvei jelentős része bennük bizonyított, vagy legalábbis kifejtésre kerül. Az identitások tanulmányozásának ez az oldala nagyon fontos mindkét kurzus esetében, mivel ezekben a bizonyítási érvelés éppen az identitások vonatkozásában történik a legnagyobb világossággal és szigorúsággal. Ezen az anyagon túlmenően a bizonyítékok általában kevésbé teljesek, nem mindig különböztetik meg a felhasznált bizonyítékoktól.

Az aritmetikai műveletek tulajdonságait használjuk támaszként, amelyre az azonosságok bizonyítása épül.

A számítások és az azonos átalakítások nevelési hatása a logikus gondolkodás fejlesztésére irányulhat, ha csak a tanulóktól szisztematikusan megkövetelik a számítások és az azonos átalakítások indoklását, valamint a funkcionális gondolkodás fejlesztését, amely többféleképpen valósul meg. A számítások és az azonos átalakítások jelentősége az akarat, a memória, az intelligencia, az önuralom és a kreatív kezdeményezőkészség fejlesztésében teljesen nyilvánvaló.

A mindennapi és ipari számítástechnikai gyakorlat követelményei megkövetelik a hallgatóktól, hogy erős, automatizált készségeket fejlesszenek ki a racionális számítások és identitásátalakítások terén. Ezeket a készségeket bármilyen számítási munka során fejlesztik, azonban a gyors számítások és átalakítások speciális gyakorlatai szükségesek.

Tehát, ha az óra logaritmikus egyenletek megoldását foglalja magában az alapvető logaritmikus azonosság használatával, akkor hasznos az óratervbe szóbeli gyakorlatokat beépíteni a kifejezések értékének egyszerűsítésére vagy kiszámítására: , , . A gyakorlatok célját mindig közöljük a tanulókkal. A gyakorlat során szükség lehet arra, hogy a tanulók megindokolják az egyéni átalakításokat, cselekvéseket, vagy egy teljes probléma megoldását, még akkor is, ha ez nem volt tervezett. Ahol lehetséges különböző módokon egy probléma megoldása során célszerű mindig kérdéseket feltenni: „Hogyan oldották meg a problémát?”, „Ki oldotta meg másképp a problémát?”

Az identitás és az identitástranszformáció fogalmát a VI. osztályos algebrai kurzus kifejezetten bemutatja. Maga a meghatározás azonos kifejezések gyakorlatilag nem használható két kifejezés azonosságának bizonyítására, és értse meg, hogy az azonos transzformációk lényege, hogy a kifejezésre alkalmazzuk a kifejezésben feltüntetett cselekvések definícióit és tulajdonságait, vagy hozzáadunk egy olyan kifejezést, amely azonos. egyenlő 0-val, vagy kifejezéssel szorozva, azonos egyenlő eggyel. De a tanulók még e rendelkezések elsajátítása után is gyakran nem értik, hogy ezek az átalakítások miért teszik lehetővé számunkra annak állítását, hogy az eredeti és a kapott kifejezések azonosak, pl. vegye ugyanazokat az értékeket bármely változóérték-rendszerhez (halmazhoz).

Azt is fontos biztosítani, hogy a tanulók világosan megértsék, hogy az azonos transzformációk ilyen következtetései a megfelelő cselekvések definícióinak és tulajdonságainak következményei.

évfolyamon bővül az identitásátalakítások korábbi években felhalmozott apparátusa. Ez a kiterjesztés egy olyan azonosság bevezetésével kezdődik, amely az azonos bázisú hatványok szorzatának tulajdonságát fejezi ki: , ahol , egész számok.

§3. Matematika program. Az „Algebra és az elemzés kezdetei” iskolai kurzuson a hallgatók szisztematikusan tanulmányozzák az exponenciális és logaritmikus függvényeket és tulajdonságaikat, a logaritmikus és exponenciális kifejezések azonos transzformációit és alkalmazásukat a megfelelő egyenletek és egyenlőtlenségek megoldására, megismerkednek az alapfogalmakkal és állításokkal. . A 11. évfolyamon heti 3 órát vesznek igénybe az algebra órák, összesen évi 102 órában. A program 36 órát vesz igénybe az exponenciális, logaritmikus és hatványfüggvények tanulmányozására. A program a következő kérdések megfontolását és tanulmányozását tartalmazza: A diploma fogalma racionális kitevővel. Irracionális egyenletek megoldása. Exponenciális függvény, tulajdonságai és grafikonja. Exponenciális kifejezések azonos transzformációi. Exponenciális egyenletek és egyenlőtlenségek megoldása. Egy szám logaritmusa. A logaritmusok alapvető tulajdonságai. Logaritmikus függvény, tulajdonságai és grafikonja. Logaritmikus egyenletek és egyenlőtlenségek megoldása. Exponenciális függvény deriváltja. Szám és természetes logaritmus. Hatványfüggvény származéka. Az exponenciális és logaritmikus függvény rész fő célja, hogy a tanulókat megismertesse az exponenciális, logaritmikus és hatványfüggvényekkel; tanítsa meg a tanulókat az exponenciális és logaritmikus egyenletekés egyenlőtlenségek. A th gyök és a fok fogalma racionális kitevővel a négyzetgyök és az egész kitevővel rendelkező fok fogalmának általánosítása. A tanulóknak figyelniük kell arra, hogy az itt vizsgált racionális kitevővel rendelkező gyökök és hatványok tulajdonságai hasonlóak a korábban vizsgált tulajdonságokkal. négyzetgyök fokokat pedig egész kitevőkkel. Elegendő időt kell szánni a fokozatok tulajdonságainak gyakorlására, az identitástranszformációs készségek fejlesztésére. fokozat fogalma c irracionális mutató vizuális és intuitív alapon kerül bevezetésre. Ez az anyag segéd szerepet játszik, és az exponenciális függvény bevezetésekor használják. Az exponenciális, logaritmikus és hatványfüggvények tulajdonságainak vizsgálata a függvénytanulmányozás elfogadott általános sémája szerint történik. Ebben az esetben a tulajdonságok áttekintése a paraméterértékek függvényében történik. Szemléltető és logaritmikus egyenlőtlenségek függvények vizsgált tulajdonságai alapján oldják meg. Jellemző tulajdonság A kurzus a hallgatók tudásának rendszerezése, általánosítása, az algebratanfolyamon elsajátított készségek megszilárdítása, fejlesztése, amely mind az új tananyag tanulmányozása, mind az általánosított ismétlés elvégzése során valósul meg.
2. fejezet Exponenciális és logaritmikus kifejezések azonos transzformációi és számításai

§1. A fokozat fogalmának általánosítása.

Definíció: Egy tiszta szám th gyöke az a szám, amelynek th hatványa egyenlő -vel.

Alapján ezt a meghatározást Egy szám gyöke az egyenlet megoldása. Ennek az egyenletnek a gyökeinek száma függ és. Nézzük a függvényt. Mint ismeretes, az intervallumon ez a függvény bármely értéknél növekszik, és az összes értéket az intervallumból veszi. A gyöktétel szerint a tetszőleges egyenletnek nemnegatív gyöke van, ráadásul csak egy. Ezt a szám th-edik fokának aritmetikai gyökének nevezik, és jelölése ; a számot radikális kitevőnek, magát a számot pedig radikális kifejezésnek nevezzük. A jelet radikálisnak is nevezik.

Definíció: Egy szám hatványának számtani gyökerét nevezzük nem negatív szám, amelynek -edik foka egyenlő a .

Páros számok esetén a függvény páros. Ebből következik, hogy ha , akkor az egyenletnek a gyökön kívül gyöke is van. Ha , akkor egy gyök van: ; ha , akkor ennek az egyenletnek nincs gyöke, hiszen páros fokozat bármely szám nem negatív.

Páratlan értékek esetén a függvény a teljes számegyenesen növekszik; tartománya az összes valós szám halmaza. A gyöktételt alkalmazva azt találjuk, hogy az egyenletnek egy gyöke van bármely és különösen -ra. Ezt a gyökeret bármely értéknél a jelöli.

A páratlan fokú gyökerekre az egyenlőség igaz. Valójában , azaz. szám a th gyöke. De a páratlan ilyen gyöke az egyetlen. Ennélfogva, .

1. megjegyzés: Bármilyen valódi

Emlékezzünk vissza a th-edik fokú aritmetikai gyökök ismert tulajdonságaira.

Bármilyen természetes számra, egész számra és bármely nemnegatív egészre érvényesek, és az egyenlőségek érvényesek:

1.

2.

3.

4.

Fokozat racionális kitevővel.

A kifejezés az összes és -re van definiálva, kivéve az esetet. Emlékezzünk vissza az ilyen erők tulajdonságaira.

Bármilyen számra , tetszőleges egész számra és az egyenlőségek érvényesek:

Azt is megjegyezzük, hogy ha , akkor for és for .. és

Az egységes államvizsgát letevő tanulók számára a jakutszki 26-os középiskola matematikatanárai egy tartalmi kérdéslistát (kódolót) használnak az iskolai matematika kurzushoz, amelynek elsajátítását a 2007-es egységes államvizsga letételekor tesztelik. Választható tárgy az Egységesre való felkészülésről Államvizsga a korábban megszerzett ismeretek ismétlése, rendszerezése, elmélyítése alapján. A foglalkozásokat ingyenes formában tartjuk...