Az érintő x négyzet integrálja. Trigonometrikus függvények integrálása. Nem szabványos módszerek a trigonometrikus függvények integrálására

Integrálok innen trigonometrikus függvények.
Példák megoldásokra

Ebben a leckében a trigonometrikus függvények integráljait nézzük meg, vagyis az integrálok kitöltése szinuszok, koszinuszok, érintők és kotangensek lesznek különböző kombinációkban. Az összes példát részletesen elemzik, még egy teáskanna számára is hozzáférhető és érthető.

A trigonometrikus függvények integráljainak sikeres tanulmányozásához jól kell ismernie a legegyszerűbb integrálokat, valamint el kell sajátítania néhány integrációs technikát. Ezekkel az anyagokkal előadásokon ismerkedhet meg Határozatlan integrál. Példák megoldásokraÉs .

És most szükségünk van: Integrálok táblázata, Származékos táblázatÉs A trigonometrikus képletek könyvtára. Minden módszertani kézikönyvek oldalon találhatók Matematikai képletek és táblázatok. Azt javaslom, hogy nyomtasson ki mindent. Különösen a trigonometrikus képletekre koncentrálok, a szemed előtt kell lenniük– e nélkül a munka hatékonysága érezhetően csökken.

De először arról, hogy milyen integrálok vannak ebben a cikkben Nem. Az alaknak nincsenek integráljai, - koszinusz, szinusz, szorozva valamilyen polinommal (ritkábban érintővel vagy kotangenssel). Az ilyen integrálokat részenként integráljuk, a módszer elsajátításához pedig látogassa meg az Integrálás részenként leckét. Példák a megoldásokra Itt sincsenek „íves” integrálok - arctangens, arcsine stb., ezeket is legtöbbször részekkel integrálják.

A trigonometrikus függvények integráljainak megtalálásakor számos módszert alkalmaznak:

(4) A táblázatos képletet használjuk , az egyetlen különbség az, hogy „X” helyett összetett kifejezésünk van.

2. példa

3. példa

Keresse meg a határozatlan integrált.

A műfaj klasszikusa azoknak, akik belefulladnak a versenybe. Mint valószínűleg észrevette, az integrálok táblázatában nincs érintő és kotangens integrálja, de ennek ellenére megtalálhatók ilyen integrálok.

(1) A trigonometrikus képletet használjuk

(2) A függvényt a differenciáljel alá visszük.

(3) A táblázatintegrált használjuk .

4. példa

Keresse meg a határozatlan integrált.

Ez egy példa egy önálló megoldásra, a teljes megoldás és a válasz a lecke végén található.

5. példa

Keresse meg a határozatlan integrált.

Fokozataink fokozatosan emelkednek =).
Először a megoldás:

(1) A képletet használjuk

(2) A fő trigonometrikus azonosságot használjuk , amiből az következik .

(3) Osszuk el a számlálót a nevező tagjával!

(4) A határozatlan integrál linearitási tulajdonságát használjuk.

(5) A táblázat segítségével integrálunk.

6. példa

Keresse meg a határozatlan integrált.

Ez egy példa egy önálló megoldásra, a teljes megoldás és a válasz a lecke végén található.

Vannak érintők és kotangensek integráljai is, amelyek többben vannak magas fokok. A tangens kocka integrálját tárgyaljuk a leckében Hogyan lehet kiszámítani egy lapos alak területét? A negyedik és ötödik hatvány érintőjének (kotangensének) integráljai megtalálhatók az oldalon Komplex integrálok.

Az integrandus fokának csökkentése

Ez a technika akkor működik, ha az integrand függvények szinuszokkal és koszinuszokkal vannak kitöltve még fokon. A mérték csökkentéséhez használjon trigonometrikus képleteket , és , és az utolsó képletet gyakran az ellenkező irányba használják: .

7. példa

Keresse meg a határozatlan integrált.

Megoldás:

Elvileg nincs itt semmi új, azon kívül, hogy alkalmaztuk a képletet (az integrandus mértékének csökkentése). Kérjük, vegye figyelembe, hogy lerövidítettem a megoldást. A tapasztalatszerzés során az integrál szóban is megtalálható, ez időt takarít meg, és teljesen elfogadható a feladatok elvégzésekor. Ebben az esetben tanácsos nem leírni a szabályt , először szóban vesszük 1 integrálját, majd .

8. példa

Keresse meg a határozatlan integrált.

Ez egy példa egy önálló megoldásra, a teljes megoldás és a válasz a lecke végén található.

Ez az ígért fokozatemelés:

9. példa

Keresse meg a határozatlan integrált.

Először a megoldás, aztán a megjegyzések:

(1) Készítse elő az integrandust a képlet alkalmazásához .

(2) Valójában alkalmazzuk a képletet.

(3) Négyzetre emeljük a nevezőt, és kivesszük az integráljelből a konstanst. Kicsit másképp is meg lehetett volna csinálni, de véleményem szerint kényelmesebb volt.

(4) A képletet használjuk

(5) A harmadik tagban ismét csökkentjük a fokozatot, de a képlet segítségével .

(6) Hasonló kifejezéseket mutatunk be (itt terminusonként osztottam fel és elvégezte a kiegészítést).

(7) Valójában az integrált, a linearitási szabályt vesszük és a függvény különbségi jel alá vonásának módját szóban hajtjuk végre.

(8) A válasz összefésülése.

! A határozatlan integrálban a válasz sokszor többféleképpen is írható

Az imént vizsgált példában a végső választ másként is megírhatták volna - a zárójelek megnyitásával és akár a kifejezés integrálása előtt is, vagyis a példa következő befejezése teljesen elfogadható:

Lehetséges, hogy ez a lehetőség még kényelmesebb, csak úgy magyaráztam el, ahogyan magam szoktam megoldani). Íme egy másik tipikus példa egy független megoldásra:

10. példa

Keresse meg a határozatlan integrált.

Ezt a példát kétféleképpen lehet megoldani, és sikerrel járhat két teljesen különböző válasz(pontosabban teljesen máshogy néznek ki, de matematikai szempontból egyenértékűek lesznek). Valószínűleg nem a legracionálisabb módszert fogja látni, és szenvedni fog a zárójelek megnyitásával és más trigonometrikus képletek használatával. A leghatékonyabb megoldást a lecke végén adjuk meg.

Összefoglalva a bekezdést, levonjuk a következtetést: az űrlap bármely integrálja , hol és - még számok, az integrandus fokának csökkentésének módszerével oldjuk meg.
A gyakorlatban 8 és 10 fokos integrálokkal találkoztam, amelyek iszonyatos zűrzavarát többszöri fokozatcsökkentéssel kellett megoldanom, aminek eredményeként hosszú-hosszú válaszok születtek.

Változócsere módszere

Ahogy a cikkben is említettük Változómódosítási módszer határozatlan integrálban, a helyettesítési módszer használatának fő feltétele az, hogy az integrandusban van egy bizonyos függvény és annak deriváltja:
(a funkciók nem feltétlenül szerepelnek a termékben)

11. példa

Keresse meg a határozatlan integrált.

Megnézzük a derivált táblázatot, és észrevesszük a képleteket, , vagyis az integrandusunkban van egy függvény és annak deriváltja. Látjuk azonban, hogy a differenciálás során a koszinusz és a szinusz kölcsönösen egymásba alakul át, és felvetődik a kérdés: hogyan kell végrehajtani egy változóváltást és mit értünk szinuszon vagy koszinuszon?! Tudományos piszkálással megoldható a kérdés: ha rosszul hajtjuk végre a cserét, abból semmi jó nem sül ki.

Általános irányelv: hasonló esetekben meg kell jelölni azt a függvényt, amely a nevezőben van.

Megszakítjuk a megoldást és cserét végzünk

A nevezőben minden rendben van, minden csak a -n múlik, most már csak azt kell kideríteni, mi lesz belőle.
Ehhez megtaláljuk a különbséget:

Vagy röviden:
A kapott egyenlőségből az arányszabály segítségével fejezzük ki a szükséges kifejezést:

Így:

Most az egész integránsunk csak azon múlik, és folytathatjuk a megoldást

Kész. Hadd emlékeztessem önöket, hogy a csere célja az integrandus egyszerűsítése, ebben az esetben minden az integrációra dőlt el. teljesítmény funkció táblázat szerint.

Nem véletlen, hogy ezt a példát ilyen részletesen leírtam, ez az órai anyagok ismétlése és megerősítése céljából történt. Változómódosítási módszer határozatlan integrálban.

És most két példa a saját megoldásodra:

12. példa

Keresse meg a határozatlan integrált.

13. példa

Keresse meg a határozatlan integrált.

Teljes megoldások és válaszok a lecke végén.

14. példa

Keresse meg a határozatlan integrált.

Az integrandusban itt is van szinusz és koszinusz (függvény deriválttal), de egy szorzatban felmerül a dilemma - mit értünk szinuszon vagy koszinuszon?

Megpróbálhatja tudományos módszerrel végrehajtani a cserét, és ha semmi sem működik, akkor jelölje ki másik funkcióként, de van:

Általános irányelv: meg kell jelölni azt a funkciót, amely képletesen szólva „kényelmetlen” helyzetben van..

Azt látjuk, hogy ebben a példában a hallgatói koszinusz „szenvedi” a fokozatot, a szinusz pedig szabadon, önállóan ül.

Ezért cseréljünk:

Ha valakinek továbbra is nehézségei vannak a változó lecserélésének és a differenciál megtalálásának algoritmusával, akkor térjen vissza a leckéhez Változómódosítási módszer határozatlan integrálban.

15. példa

Keresse meg a határozatlan integrált.

Elemezzük az integrandust, mit kell jelölni?
Emlékezzünk az irányelveinkre:
1) A függvény nagy valószínűséggel a nevezőben van;
2) A funkció „kényelmetlen” helyzetben van.

Egyébként ezek az irányelvek nem csak a trigonometrikus függvényekre érvényesek.

A szinusz mindkét kritériumnak megfelel (különösen a másodiknak), ezért a csere önmagát javasolja. Elvileg a csere már elvégezhető, de előbb jó lenne kitalálni, hogy mihez kezdjünk vele? Először „lecsípünk” egy koszinust:

Fenntartjuk a „jövő” differenciálművünket

És szinuszon keresztül fejezzük ki a main segítségével trigonometrikus azonosság:

Most itt a csere:

Általános szabály: Ha az integrandusban az egyik trigonometrikus függvény (szinusz vagy koszinusz) benne van páratlan fokozatot, akkor a páratlan fokozatból „le kell harapni” egy függvényt, és ki kell jelölni mögé egy másik függvényt. Csak olyan integrálokról beszélünk, ahol koszinuszok és szinuszok vannak.

A vizsgált példában páratlan hatványú koszinuszunk volt, ezért kivontunk egy koszinuszot a hatványból, és szinusznak jelöltük.

16. példa

Keresse meg a határozatlan integrált.

Felszállnak a fokok =).
Ez egy példa, amelyet egyedül kell megoldania. Komplett megoldásés a válasz a lecke végén.

Univerzális trigonometrikus helyettesítés

Az univerzális trigonometrikus helyettesítés a változó helyettesítési módszer gyakori esete. Megpróbálhatja használni, ha „nem tudja, mit tegyen”. De valójában van néhány irányelv az alkalmazására. Tipikus integrálok, ahol az univerzális trigonometrikus helyettesítést kell alkalmazni, a következő integrálok: , , , stb.

17. példa

Keresse meg a határozatlan integrált.

Az univerzális trigonometrikus helyettesítés ebben az esetben a következő módon valósítható meg. Cseréljük ki: . Nem a betűt használom, hanem a betűt, ez nem valamiféle szabály, hanem megint csak én szoktam így megoldani a dolgokat.

Itt kényelmesebb megtalálni a különbséget, erre az egyenlőségből a következőket fejezem ki:
Mindkét részhez csatolok egy arctangenst:

Az arktangens és az érintő kioltják egymást:

És így:

A gyakorlatban nem kell ilyen részletesen leírni, hanem egyszerűen használni kész eredmény:

! A kifejezés csak akkor érvényes, ha a szinuszok és koszinuszok alatt egyszerűen csak „X” van, az integrálra (amiről majd később) minden kicsit másképp lesz!

Cserekor a szinuszok és koszinuszok a következő törtekké alakulnak:
, , ezek az egyenlőségek jól ismert trigonometrikus képleteken alapulnak: ,

Tehát a végső terv így nézhet ki:

Végezzünk el egy univerzális trigonometrikus helyettesítést:

Részletesen megvizsgáljuk az integrálok részenkénti megoldására vonatkozó példákat, amelyek integrandusa egy polinom exponenciális (e az x hatványhoz) vagy egy szinusz (sin x) vagy koszinusz (cos x) szorzata.

Tartalom

Lásd még: Alkatrészenkénti integráció módja
Határozatlan integrálok táblázata
Határozatlan integrálok számítási módszerei
Alapvető elemi függvények és tulajdonságaik

Alkatrészenkénti integráció képlete

Ebben a részben a példák megoldása során a részenkénti integráció képletet használjuk:
;
.

Példák egy polinom és sin x, cos x vagy e x szorzatát tartalmazó integrálokra

Íme néhány példa az ilyen integrálokra:
, , .

Az ilyen integrálok integrálásához a polinomot u, a fennmaradó részt v dx-el jelöljük. Ezután alkalmazza a részenkénti integráció képletét.

Az alábbiakban megadjuk részletes megoldás ezeket a példákat.

Példák integrálok megoldására

Példa kitevővel, e x hatványára

Határozza meg az integrált:
.

Vezessük be a differenciáljel alatti kitevőt:
e - x dx = - e - x d(-x) = - d(e - x).

Integráljuk részenként.

Itt
.
A fennmaradó integrált is részenként integráljuk.
.
.
.
Végül nálunk van:
.

Példa a szinuszos integrál meghatározására

Számítsa ki az integrált:
.

Vezessük be a szinust a differenciáljel alá:

Integráljuk részenként.

itt u = x 2, v = cos (2 x+3), du = ( x 2 )′ dx

A fennmaradó integrált is részenként integráljuk. Ehhez vezesse be a koszinust a differenciáljel alá.

itt u = x, v = bűn(2x+3), du = dx

Végül nálunk van:

Példa polinom és koszinusz szorzatára

Számítsa ki az integrált:
.

Vezessük be a differenciáljel alatti koszinust:

Integráljuk részenként.

itt u = x 2 + 3 x + 5, v = bűn 2 x, du = ( x 2 + 3 x + 5 )′ dx

Az antiderivatívek ("integrálok") táblázata. Integrálok táblázata. Táblázatos határozatlan integrálok. (A legegyszerűbb integrálok és paraméteres integrálok). Képletek alkatrészenkénti integrációhoz. Newton-Leibniz képlet.

Az antiderivatívek ("integrálok") táblázata. Táblázatos határozatlan integrálok. (A legegyszerűbb integrálok és paraméteres integrálok).
Teljesítményfüggvény integrálja.	Teljesítményfüggvény integrálja.
Integrál, amely egy hatványfüggvény integráljára redukálódik, ha x-et a differenciáljel alatt hajtjuk.

	Exponenciális integrál, ahol a egy állandó szám.
Integrált komplexum exponenciális függvény.	Exponenciális függvény integrálja.

A természetes logaritmussal egyenlő integrál.	Integrál: "Hosszú logaritmus".
	Integrál: "Hosszú logaritmus".
Integrál: "Magas logaritmus".	Egy integrál, ahol a számlálóban x a differenciáljel alá kerül (az előjel alatti konstans összeadható vagy kivonható), végső soron hasonló a természetes logaritmussal egyenlő integrálhoz.
Integrál: "Magas logaritmus".

Koszinusz integrál.	Szinusz integrál.
Integrál egyenlő az érintővel.	Integrál egyenlő a kotangenssel.

Integrál egyenlő mind az arcszinusz, mind az arkoszinusz
Egy integrál egyenlő az arcszinuszral és az arkoszinusszal.	Egy integrál egyenlő az arctangenssel és az arkkotangenssel.

Integrál egyenlő a koszekánssal.	Integrál egyenlő a szekánssal.
Integrál egyenlő íves.	Az arccosekantal egyenlő integrál.
Integrál egyenlő íves.	Integrál egyenlő íves.

Integrál egyenlő a hiperbolikus szinuszával.	A hiperbolikus koszinusznak megfelelő integrál.

A hiperbolikus szinusz integrálja, ahol sinhx a hiperbolikus szinusz az angol változatban.	Integrál egyenlő a hiperbolikus koszinusszal, ahol sinhx a hiperbolikus szinusz az angol változatban.
Integrál egyenlő a hiperbolikus érintővel.	Integrál egyenlő a hiperbolikus kotangenssel.
Integrál egyenlő a hiperbolikus szekánssal.	Integrál egyenlő a hiperbolikus koszekánssal.

Képletek alkatrészenkénti integrációhoz. Integrációs szabályok.

Képletek alkatrészenkénti integrációhoz. Newton-Leibniz formula, az integráció szabályai.
Termék (függvény) integrálása konstanssal:
A függvények összegének integrálása:
határozatlan integrálok:
Alkatrészenkénti integráció képlete határozott integrálok:
Newton-Leibniz képlet határozott integrálok:	Ahol F(a), F(b) az antiderivatívek értékei a b és a pontban.

Származékok táblázata. Táblázatos származékok. A termék származéka. A hányados származéka. Komplex függvény származéka.

Ha x független változó, akkor:

Származékok táblázata. Táblázatos származékok."táblázati származék" - igen, sajnos pontosan így keresik őket az interneten
	Hatványfüggvény származéka

	A kitevő származéka
Komplex exponenciális függvény deriváltja	Az exponenciális függvény deriváltja

Logaritmikus függvény deriváltja	A természetes logaritmus származéka
	Függvény természetes logaritmusának deriváltja

A szinusz származéka	A koszinusz származéka
A koszekáns származéka	Szekáns származéka
Az arcszinusz származéka	Az ív koszinusz származéka
Az arcszinusz származéka	Az ív koszinusz származéka
Érintő derivált	A kotangens származéka
Az arctangens származéka	Az ívkotangens származéka
Az arctangens származéka	Az ívkotangens származéka
Az arcsekant származéka	Az arccosecant származéka
Az arcsekant származéka	Az arccosecant származéka

A hiperbolikus szinusz származéka A hiperbolikus szinusz származéka az angol változatban	A hiperbolikus koszinusz származéka A hiperbolikus koszinusz származéka angol változatban
A hiperbolikus érintő származéka	A hiperbolikus kotangens származéka
A hiperbolikus szekáns származéka	A hiperbolikus koszekáns származéka

A megkülönböztetés szabályai. A termék származéka. A hányados származéka. Komplex függvény származéka.
Egy szorzat (függvény) származéka konstanssal:
Az összeg származéka (függvények):
A termék származéka (függvények):
A (függvények) hányadosának deriváltja:
Egy összetett függvény származéka:

A logaritmusok tulajdonságai. A logaritmusok alapképletei. Tizedes (lg) és természetes logaritmus (ln).

Alapok logaritmikus azonosság
Mutassuk meg, hogyan tehető exponenciálissá az a b alak bármely függvénye. Mivel az e x alakú függvényt exponenciálisnak nevezzük, akkor
Bármely a b alakú függvény tíz hatványaként ábrázolható

Természetes logaritmus ln (logaritmus e bázishoz = 2,718281828459045...) ln(e)=1; ln(1)=0

Taylor sorozat. Egy függvény Taylor sorozatának bővítése.

Kiderült, hogy a többség gyakorlatilag találkoztunk A matematikai függvények egy adott pont közelében tetszőleges pontossággal ábrázolhatók egy változó hatványait növekvő sorrendben tartalmazó hatványsorok formájában. Például az x=1 pont közelében:

ún. sorozat használatakor Taylor sorai mondjuk algebrai, trigonometrikus és exponenciális függvényeket tartalmazó vegyes függvények tisztán algebrai függvényekként fejezhetők ki. A sorozatok használatával gyakran gyorsan elvégezhető a differenciálás és az integráció.

A Taylor-sorozat az a pont szomszédságában a következő formában van:

1) , ahol f(x) egy olyan függvény, amelynek minden rendjének deriváltja van x = a helyen. R n - a Taylor-sorozat maradék tagját a kifejezés határozza meg

A sorozat k-edik együtthatóját (x k-nél) a képlet határozza meg

3) A Taylor sorozat speciális esete a Maclaurin (=McLaren) sorozat (a tágulás az a=0 pont körül történik)

a=0-nál

a sorozat tagjait a képlet határozza meg

A Taylor sorozat használatának feltételei.

1. Ahhoz, hogy az f(x) függvény Taylor-sorozattá bővüljön a (-R;R) intervallumon, szükséges és elegendő, hogy a Taylor (Maclaurin (=McLaren)) képletben a maradék tag ehhez függvény nullára hajlik, mint k →∞ a megadott intervallumon (-R;R).

2. Szükséges, hogy egy adott függvénynek legyenek deriváltjai abban a pontban, amelynek közelében a Taylor-sort megszerkesztjük.

A Taylor sorozat tulajdonságai.

Ha f egy analitikus függvény, akkor a Taylor-sora f definíciós tartományának bármely a pontjában konvergál f-hez az a szomszédságában.

Vannak végtelenül differenciálható függvények, amelyek Taylor-sora konvergál, ugyanakkor eltér a bármely szomszédságában lévő függvénytől. Például:

A Taylor sorozatokat közelítésben használjuk (közelítés - tudományos módszer, amely abból áll, hogy egyes objektumokat másokkal helyettesítünk, amelyek bizonyos értelemben közel állnak az eredetiekhez, de egyszerűbb) függvényeket polinomokkal. Különösen a linearizálás ((linearis - lineáris), a zárt nemlineáris rendszerek közelítő ábrázolásának egyik módszere, amelyben a nemlineáris rendszer tanulmányozását egy lineáris rendszer elemzése váltja fel, bizonyos értelemben egyenértékű az eredetivel .) egyenletek úgy lépnek fel, hogy Taylor sorozattá bővülnek, és az összes elsőrendű tagot levágják.

Így szinte minden függvény adott pontossággal polinomként ábrázolható.

Példák a hatványfüggvények néhány gyakori kiterjesztésére a Maclaurin sorozatban (=McLaren, Taylor a 0. pont közelében) és Taylor az 1. pont közelében. A Taylor és McLaren sorozatok fő függvényeinek kiterjesztésének első feltételei.

Példák a hatványfüggvények néhány gyakori kiterjesztésére a Maclaurin sorozatban (=McLaren, Taylor a 0. pont közelében)

Példák néhány gyakori Taylor sorozat bővítésre az 1. pont közelében

Lesznek önálló megoldandó problémák is, amelyekre láthatod a válaszokat.

Az integrandus a trigonometrikus függvények szorzatából összegezhető

Tekintsünk olyan integrálokat, amelyekben az integrandus az x első fokú szinuszainak és koszinuszainak szorzata különböző tényezőkkel, vagyis az alak integráljai

Kihasználva az ismert trigonometrikus képletek

(2)
(3)
(4)
a (31) alakú integrálokban lévő termékek mindegyikét átalakíthatjuk olyanra algebrai összegés integráljuk a képletek segítségével

(5)

(6)

1. példa megtalálja

Megoldás. A (2) képlet szerint at

2. példa megtalálja trigonometrikus függvény integrálja

Megoldás. A (3) képlet szerint at

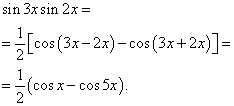
3. példa megtalálja trigonometrikus függvény integrálja

Megoldás. A (4) képlet szerint at az integrandus következő transzformációját kapjuk:

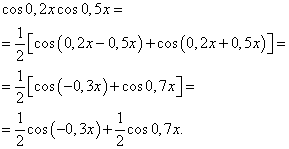
A (6) képlet alkalmazásával kapjuk

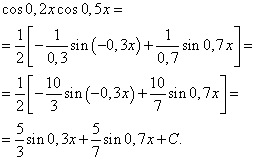
Ugyanazon argumentum szinusz és koszinusz hatványainak szorzatának integrálja

Tekintsük most a függvények integráljait, amelyek ugyanazon argumentum szinusz és koszinusz hatványainak szorzatai, pl.

(7)

Speciális esetekben az egyik indikátor ( m vagy n) lehet nulla.

Az ilyen függvények integrálásakor azt használják, hogy a koszinusz páros hatványa fejezhető ki szinuszon keresztül, és a szinusz differenciálja egyenlő cos-szal x dx(vagy akár a szinusz hatványa is kifejezhető koszinuszban, a koszinusz differenciále pedig egyenlő - sin x dx ) .

Két esetet kell megkülönböztetni: 1) legalább az egyik indikátor mÉs n páratlan; 2) mindkét mutató páros.

Legyen az első eset, mégpedig az indikátor n = 2k+ 1 - páratlan. Akkor, tekintettel arra

Az integrandus úgy kerül bemutatásra, hogy egyik része csak a szinusz függvénye, a másik pedig a szinusz differenciálja. Most változó helyettesítést használunk t= bűn x a megoldás a polinom integrálására redukálódik t. Ha csak a diploma m páratlan, akkor ugyanezt teszik, elkülönítve a sin tényezőt x, amely az integrandus többi részét cos-ban fejezi ki xés hinni t=cos x. Ez a technika akkor is használható, ha a szinusz és a koszinusz hányados hatványainak integrálása , Amikor legalább az egyik mutató páratlan . Az egész lényege az a szinusz és a koszinusz hatványainak hányadosa az különleges eset műveik : Ha egy trigonometrikus függvény egy integrandus nevezőjében van, akkor a foka negatív. De vannak olyan esetek is, amikor a részleges trigonometrikus függvények hatványai csak párosak. Róluk - a következő bekezdésben.

Ha mindkét mutató mÉs n– még akkor is, trigonometrikus képletekkel

csökkentjük a szinusz és a koszinusz kitevőit, ami után a fentivel megegyező típusú integrált kapunk. Ezért az integrációt ugyanazon séma szerint kell folytatni. Ha a páros kitevők egyike negatív, vagyis a szinusz és a koszinusz páros hatványainak hányadosát vesszük figyelembe, akkor ez a séma nem megfelelő . Ekkor a változó változását használjuk attól függően, hogy az integrandus hogyan alakítható át. Egy ilyen esettel foglalkozunk a következő bekezdésben.

4. példa megtalálja trigonometrikus függvény integrálja

Megoldás. A koszinusz kitevő páratlan. Ezért képzeljük el

t= bűn x(Akkor dt=cos x dx ). Akkor kapunk

Visszatérve a régi változóhoz, végre megtaláljuk

5. példa. megtalálja trigonometrikus függvény integrálja

Megoldás. A koszinusz kitevő, mint az előző példában, páratlan, de nagyobb. Képzeljük el

és módosítsa a változót t= bűn x(Akkor dt=cos x dx ). Akkor kapunk

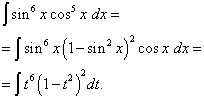
Nyissuk ki a zárójeleket

és megkapjuk

Visszatérve a régi változóhoz, megkapjuk a megoldást

6. példa. megtalálja trigonometrikus függvény integrálja

Megoldás. A szinusz és a koszinusz kitevője páros. Ezért az integrand függvényt a következőképpen alakítjuk át:

Akkor kapunk

A második integrálban megváltoztatjuk a változót, beállítást t= sin2 x. Akkor (1/2)dt= cos2 x dx . Ennélfogva,

Végre megkapjuk

Változócsere módszer használata

Változócsere módszere trigonometrikus függvények integrálásakor olyan esetekben használható, amikor az integrandus csak szinusz vagy csak koszinusz tartalmaz, a szinusz és a koszinusz szorzata, amelyben akár a szinusz, akár a koszinusz az első fokon, érintő vagy kotangens, valamint a szinusz hányadosát tartalmazza. egy és ugyanazon érv szinuszának és koszinuszának akár hatványai is. Ebben az esetben nem csak bűnt lehet permutációt végrehajtani x = tés a bűn x = t, hanem tg x = tés ctg x = t .

8. példa. megtalálja trigonometrikus függvény integrálja

Megoldás. Változtassuk meg a változót: , akkor . Az így kapott integrandus könnyen integrálható az integráltáblázat segítségével:

9. példa. megtalálja trigonometrikus függvény integrálja

Megoldás. Alakítsuk át az érintőt szinusz és koszinusz arányává:

Változtassuk meg a változót: , akkor . A kapott integrandus az táblázat integrál mínusz jellel:

Visszatérve az eredeti változóhoz, végül megkapjuk:

10. példa. megtalálja trigonometrikus függvény integrálja

Megoldás. Változtassuk meg a változót: , akkor .

Alakítsuk át az integrandust a trigonometrikus azonosság alkalmazására :

Megváltoztatjuk a változót, nem felejtve el mínusz jelet tenni az integrál elé (lásd fent, mi egyenlő dt). Ezután beszámítjuk az integrandust és integráljuk a táblázat szerint:

Visszatérve az eredeti változóhoz, végül megkapjuk:

Keresse meg saját maga egy trigonometrikus függvény integrálját, majd nézze meg a megoldást

Univerzális trigonometrikus helyettesítés

Univerzális trigonometrikus helyettesítés használható olyan esetekben, amikor az integrandus nem esik az előző bekezdésekben tárgyalt esetek alá. Alapvetően, amikor a szinusz vagy a koszinusz (vagy mindkettő) egy tört nevezőjében van. Bebizonyosodott, hogy a szinusz és a koszinusz helyettesíthető egy másik kifejezéssel, amely az eredeti szög felének érintőjét tartalmazza a következőképpen:

De ne feledje, hogy az univerzális trigonometrikus helyettesítés gyakran meglehetősen bonyolult algebrai transzformációkkal jár, ezért a legjobb akkor használni, ha más módszer nem működik. Nézzünk olyan példákat, ahol az univerzális trigonometrikus helyettesítéssel együtt a differenciáljel alatti helyettesítést és a határozatlan együtthatók módszerét alkalmazzák.

12. példa. megtalálja trigonometrikus függvény integrálja