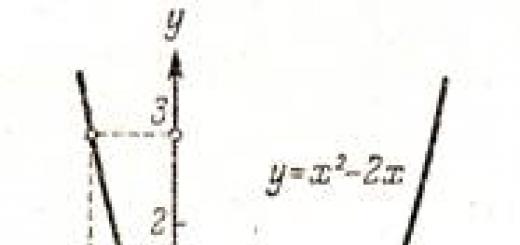A „Funkció y = sinx, ee tulajdonságok és grafikon” című videólecke vizuális anyagokat mutat be erről a témáról, valamint megjegyzéseket tesz hozzá. A demonstráció során megvizsgáljuk a függvény típusát, tulajdonságait, valamint részletesen ismertetjük a különböző szegmenseken való viselkedést. Koordináta sík, a grafikon jellemzői, egy példát ismertetünk grafikus megoldás trigonometrikus egyenletek szinust tartalmazó. A videolecke segítségével a tanár könnyebben megfogalmazhatja a tanuló megértését erről a funkcióról, és megtanítja őket grafikus problémák megoldására.

A videólecke olyan eszközöket használ, amelyek megkönnyítik a memorizálást és a megértést oktatási információk. A grafikonok bemutatásánál és a feladatok megoldásának leírásánál olyan animációs effektusokat alkalmaznak, amelyek segítik a függvény viselkedésének megértését és a megoldás előrehaladásának szekvenciális bemutatását. Ezenkívül az anyag hangoztatása fontos megjegyzésekkel egészíti ki, amelyek helyettesítik a tanár magyarázatát. És így, ezt az anyagot Vizuális segédeszközként is használható. És az óra önálló részeként a tanári magyarázat helyett egy új témában.

A bemutató az óra témájának bemutatásával kezdődik. Megjelenik a szinuszfüggvény, melynek leírása egy memorizálásra szolgáló dobozban van kiemelve - s=sint, amelyben a t argumentum tetszőleges valós szám lehet. A függvény tulajdonságainak leírása a definíció tartományával kezdődik. Megjegyezzük, hogy a függvény definíciós tartománya a valós számok teljes numerikus tengelye, azaz D(f)=(- ∞;+∞). A második tulajdonság a szinuszfüggvény páratlansága. Felhívjuk a tanulók figyelmét, hogy ezt az ingatlant a 9. osztályban tanulmányozták, amikor megjegyezték, hogy a páratlan függvény az f(-x)=-f(x) egyenlőség teljesül. A szinusz esetében a függvény páratlanságának megerősítése az egységkörön látható, negyedekre bontva. Tudva, hogy a függvény milyen előjelet vesz fel a koordinátasík különböző negyedeiben, megjegyezzük, hogy ellentétes előjelű argumentumok esetén az L(t) és N(-t) pontok példáján a szinuszra vonatkozó furcsasági feltétel teljesül. Ezért az s=sint páratlan függvény. Ez azt jelenti, hogy a függvény grafikonja szimmetrikus az origóra.

A szinusz harmadik tulajdonsága a növekvő és csökkenő függvények közötti intervallumokat mutatja. Megjegyzi, hogy ez a függvény a szegmensen növekszik, a [π/2;π] szakaszon pedig csökken. A tulajdonságot az ábra szemlélteti, amelyen látható egységkör az A pontból az óramutató járásával ellentétes irányba haladva pedig nő az ordináta, vagyis a függvény értéke π/2-re nő. Amikor B pontból C-be haladunk, vagyis amikor a szög π/2-ről π-re változik, az ordináta értéke csökken. A kör harmadik negyedében a C pontból D pontba haladva az ordináta 0-ról -1-re csökken, azaz csökken a szinusz értéke. Az utolsó negyedben D pontból A pontba haladva az ordináta értéke -1-ről 0-ra nő. Így általános következtetést vonhatunk le a függvény viselkedéséről. A képernyőn megjelenik az a kimenet, amely sint növekszik a [-(π/2)+2πk szegmensen; (π/2)+2πk], a [(π/2)+2πk intervallumon csökken; (3π/2)+2πk] bármely k egész számra.

A szinusz negyedik tulajdonsága a függvény korlátosságát veszi figyelembe. Megjegyzendő, hogy a sint függvény fent és lent is korlátozott. A tanulók eszébe jutnak a 9. osztályos algebra információi, amikor megismerkedtek egy függvény korlátosságának fogalmával. Egy felülről korlátos függvény feltétele jelenik meg a képernyőn, amelyre van egy bizonyos szám, amelyre a függvény bármely pontjában teljesül az f(x)>=M egyenlőtlenség. Felidézzük egy alább korlátos függvény feltételét is, amelyre a függvény minden pontjánál m-rel kisebb szám van. Sint esetében a -1 feltétel teljesül<= sint<=1. То есть данная функция ограничена сверху и снизу. То есть она является ограниченной.

Az ötödik tulajdonság a függvény legkisebb és legnagyobb értékét veszi figyelembe. Minden egyes t=-(π/2)+2πk pontban a legkisebb -1, a t=(π/2)+2πk pontokban a legnagyobb érték elérését jegyezzük fel.

A figyelembe vett tulajdonságok alapján a szegmensen megszerkesztjük a sint függvény grafikonját. A függvény összeállításához a szinusz táblázatos értékeit használják a megfelelő pontokban. A koordinátasíkon a π/6, π/3, π/2, 2π/3, 5π/6, π pontok koordinátáit jelöljük. A függvény táblázati értékeit ezeken a pontokon megjelölve és sima vonallal összekötve grafikont építünk.

A sint függvény grafikonjának ábrázolásához a [-π;π] szakaszon a függvény koordináták origójához viszonyított szimmetriájának tulajdonságát használjuk. Az ábrán látható, hogy az építés eredményeként kapott egyenes a koordináták origójához képest simán, szimmetrikusan kerül át a [-π;0] szakaszra.

A sint függvény sin(x+2π) = sin x redukciós képletben kifejezett tulajdonságát felhasználva megjegyezzük, hogy minden 2π-nél megismétlődik a szinuszgráf. Így a [π; 3π] a grafikon ugyanaz lesz, mint a [-π;π]-n. Így ennek a függvénynek a grafikonja az ismétlődő [-π;π] töredékeket reprezentálja a teljes definíciós tartományban. Külön meg kell jegyezni, hogy egy függvény ilyen grafikonját szinuszosnak nevezzük. Bemutatjuk a szinuszhullám fogalmát is - a [-π;π] szakaszra épített gráf töredékét és a szegmensre épített szinuszos ívet. Ezeket a töredékeket ismét bemutatjuk memorizálás céljából.

Meg kell jegyezni, hogy a sint függvény egy folytonos függvény a teljes definíciós tartományban, és azt is, hogy a függvény értéktartománya a [-1;1] szegmens értékkészletében található.

A videóóra végén a sin x=x+π egyenlet grafikus megoldását vizsgáljuk meg. Nyilvánvalóan az egyenlet grafikus megoldása a bal oldali kifejezés által adott függvény és a jobb oldali kifejezés által adott függvény grafikonjának metszéspontja lesz. A feladat megoldásához megszerkesztünk egy koordinátasíkot, amelyen felvázoljuk a hozzá tartozó y=sin x szinuszost, és megszerkesztjük az y=x+π függvény grafikonjának megfelelő egyenest. A megszerkesztett gráfok egyetlen B(-π;0) pontban metszik egymást. Ezért x=-π lesz az egyenlet megoldása.

Az „Y függvény = sinx, ee tulajdonságok és grafikon” című videóóra segít növelni a hagyományos iskolai matematika óra hatékonyságát. A távoktatás során vizuális anyagot is használhat. A kézikönyv segíthet a téma elsajátításában azoknak a tanulóknak, akiknek további leckékre van szükségük az anyag mélyebb megértéséhez.

SZÖVEGDEKÓDOLÁS:

Leckénk témája „Az y = sin x függvény, tulajdonságai és grafikonja”.

Korábban már megismerkedtünk az s = sin t függvénnyel, ahol tϵR (es egyenlő a te szinuszával, ahol te a valós számok halmazához tartozik). Vizsgáljuk meg ennek a függvénynek a tulajdonságait:

TULAJDONSÁGOK 1. A definíciós tartomány az R (er) valós számok halmaza, azaz D(f) = (- ; +) (ef-ből de a mínusz végtelentől a plusz végtelenig terjedő intervallumot jelöli).

TULAJDONSÁG 2. Az s = sin t függvény páratlan.

A 9. osztályos órákon megtanultuk, hogy az y = f (x), x ϵX függvényt (az y egyenlő x ef-jével, ahol x az x halmazhoz tartozik) páratlannak nevezzük, ha bármely x értékre a halmazból. X az egyenlőség

f (- x) = - f (x) (eff mínusz x-ből egyenlő mínusz ef x-ből).

És mivel az abszcissza tengelyre szimmetrikus L és N pontok ordinátái ellentétesek, akkor sin(- t) = -sint.

Azaz s = sin t páratlan függvény, és az s = sin t függvény grafikonja szimmetrikus a derékszögű koordináta-rendszer origójához képest. tOs(te o es).

Tekintsük a 3. TULAJDONSÁGOT. A [ 0; ] (nulláról pi-re kettővel) az s = sin t függvény növekszik és csökken a [ szakaszon; ] (pi-ről kettővel pi-re).

Ez jól látható az ábrákon: amikor egy pont a számkör mentén nulláról pi-re kettővel mozog (A pontból B-be), az ordináta fokozatosan 0-ról 1-re növekszik, ha pedig pi-ből kettővel pi-be (a pontból) pont B-től C-ig), az ordináta fokozatosan csökken 1-ről 0-ra.

Amikor egy pont a harmadik negyed mentén mozog (C pontból D pontba), a mozgó pont ordinátája nulláról mínusz egyre csökken, a negyedik negyed mentén haladva pedig mínusz egyről nullára nő. Ezért általános következtetést vonhatunk le: az s = sin t függvény az intervallumon növekszik

(mínusz pi-ről kettő plusz kettő pi ka-val pi-re kettő plusz kettő pi ka), és csökken a [; (pi-ről kettő plusz kettő pi ka három pi kettő plusz kettő pi ka), ahol

(ka az egész számok halmazába tartozik).

TULAJDONSÁG 4. Az s = sint függvény alul és felül korlátos.

A 9. osztályos kurzusból idézzük fel a korlátosság definícióját: az y = f (x) függvényt alulról korlátosnak nevezzük, ha a függvény minden értéke nem kisebb egy bizonyos számnál m múgy, hogy a függvény definíciós tartományából származó bármely x értékre az f (x) egyenlőtlenség ≥ m(az x-ből származó ef nagyobb vagy egyenlő, mint em). Egy y = f (x) függvényt fent korlátosnak mondjuk, ha a függvény összes értéke nem nagyobb egy bizonyos számnál M, ez azt jelenti, hogy van egy szám Múgy, hogy a függvény definíciós tartományából származó bármely x értékre az f (x) egyenlőtlenség ≤ M(eff x-ből kisebb vagy egyenlő, mint em) Egy függvényt korlátosnak nevezünk, ha alul és felül is korlátos.

Térjünk vissza a függvényünkhöz: a korlátosság abból adódik, hogy bármely te-re igaz az egyenlőtlenség - 1 ≤ sint≤ 1. (te szinusza nagyobb vagy egyenlő mínusz 1-nél, de kisebb vagy egyenlő eggyel).

TULAJDONSÁG 5. Egy függvény legkisebb értéke mínusz eggyel egyenlő, és ezt az értéket a függvény bármely t = alakú pontban eléri (te egyenlő mínusz pi-vel, két plusz két csúcstal, és legmagasabb érték függvény egyenlő eggyel, és egy t = alakú bármely pontban elérhető függvénnyel érhető el (te egyenlő pi szorzata kettő plusz két csúcs).

A legnagyobb és legkisebb érték függvények s = sin t jelöli s nevét. és s max. .

A kapott tulajdonságok felhasználásával megszerkesztjük az y = sin x függvény grafikonját (az y egyenlő x-szel), mert jobban megszoktuk, hogy y = f (x) írjuk, nem pedig s = f (t).

Kezdésként válasszunk egy skálát: az ordináta tengely mentén vegyünk két cellát egységszegmensnek, az abszcissza tengely mentén pedig két cella pi háromszoros (mivel ≈ 1). Először készítsük el az y = sin x függvény grafikonját a szakaszon. Ennek a szegmensnek a függvényértékeinek táblázatára van szükségünk, a megfelelő koszinusz- és szinuszszögek értéktáblázatát használjuk:

Ezért az argumentum- és függvényértékek táblázatának elkészítéséhez emlékeznie kell erre x(x) ez a szám ennek megfelelően egyenlő a nullától pi-ig terjedő intervallum szögével, és nál nél(görög) ennek a szögnek a szinuszának értéke.

Jelöljük ezeket a pontokat a koordinátasíkon. A szegmens 3. TULAJDONJA szerint

[ 0; ] (nulláról pi-re kettővel) az y = sin x függvény növekszik és csökken a [ szakaszon; ](pi-ből kettővel pi-be) és a kapott pontokat sima vonallal összekötve megkapjuk a grafikon egy részét (1. ábra).

Egy páratlan függvény grafikonjának origóhoz viszonyított szimmetriáját felhasználva megkapjuk az y = sin x függvény grafikonját már a szakaszon

[-π; π ] (mínusz pi-től pi-ig (2. ábra).

Emlékezzünk vissza, hogy sin(x + 2π)= sinx

(x plusz két pi szinusza egyenlő x szinuszával). Ez azt jelenti, hogy az x + 2π pontban az y = sin x függvény ugyanazt az értéket veszi fel, mint az x pontban. És mivel (x + 2π)ϵ [π; 3π ](x plusz két pi a pi-től három pi-ig terjedő szakaszhoz tartozik), ha xϵ[-π; π ], majd a [π; 3π ] a függvény grafikonja pontosan ugyanúgy néz ki, mint a [-π; π]. Hasonlóképpen a , , [-3π; -π ] és így tovább, az y = sin x függvény grafikonja ugyanúgy néz ki, mint a szakaszon

[-π; π].(3. ábra)

Azt az egyenest, amely az y = sin x függvény grafikonja, szinuszhullámnak nevezzük. A szinuszhullám 2. ábrán látható részét szinuszhullámnak, míg az 1. ábrán szinuszhullámnak vagy félhullámnak nevezzük.

A megszerkesztett gráf segítségével felírjuk ennek a függvénynek még néhány tulajdonságát.

TULAJDONSÁG 6. Az y = sin x függvény folytonos függvény. Ez azt jelenti, hogy a függvény grafikonja folytonos, vagyis nincs benne ugrás vagy defekt.

TULAJDONSÁG 7. Az y = sin x függvény értéktartománya a [-1; 1] (mínusz egytől egyig), vagy így írható fel: (ef-ből e egyenlő a mínusz egytől egyig terjedő szegmenssel).

Nézzünk egy PÉLDÁT. Oldja meg grafikusan a sin x = x + π egyenletet (szinusz x egyenlő x plusz pi).

Megoldás. Készítsünk függvénygrafikonokat y = bűn xÉs y = x + π.

Az y = sin x függvény grafikonja szinuszos.

y = x + π egy lineáris függvény, melynek grafikonja a (0; π) és (- π ; 0) koordinátájú pontokon áthaladó egyenes.

A megszerkesztett gráfoknak egy metszéspontja van - B(- π;0) pont (legyen mínusz pi, nulla koordinátákkal). Ez azt jelenti, hogy ennek az egyenletnek csak egy gyöke van - a B pont abszcisszája - -π. Válasz: x = - π.

Ebben a leckében részletesen megvizsgáljuk az y = sin x függvényt, alapvető tulajdonságait és grafikonját. Az óra elején megadjuk az y = sin t trigonometrikus függvény definícióját a koordinátakörön, és figyelembe vesszük a függvény grafikonját a körön és az egyenesen. Mutassuk meg ennek a függvénynek a periodicitását a grafikonon, és vegyük figyelembe a függvény főbb tulajdonságait. Az óra végén néhány egyszerű feladatot oldunk meg egy függvény grafikonjának és tulajdonságainak segítségével.

Téma: Trigonometrikus függvények

Lecke: y=sinx függvény, alapvető tulajdonságai és grafikonja

Egy függvény mérlegelésekor fontos, hogy minden argumentumértéket egyetlen függvényértékhez társítsunk. Ez levelezés törvényeés függvénynek nevezzük.

Határozzuk meg a megfelelési törvényt.

Bármely valós szám megfelel az egységkör egyetlen pontjának. Egy pontnak egyetlen ordinátája van, amelyet a szám szinuszának nevezünk (1. ábra).

Minden argumentumérték egyetlen függvényértékhez van társítva.

A szinusz definíciójából nyilvánvaló tulajdonságok következnek.

Az ábra azt mutatja mert az egységkör egy pontjának ordinátája.

Tekintsük a függvény grafikonját. Emlékezzünk vissza az érv geometriai értelmezésére. Az argumentum a központi szög, radiánban mérve. A tengely mentén valós számokat vagy szögeket ábrázolunk radiánban, a tengely mentén pedig a függvény megfelelő értékeit.

Például az egységkörön lévő szög megfelel a grafikon egy pontjának (2. ábra).

Megkaptuk a függvény grafikonját a területen, de a szinusz periódusának ismeretében a függvény grafikonját a teljes definíciós tartományban ábrázolhatjuk (3. ábra).

A függvény fő periódusa Ez azt jelenti, hogy a grafikon egy szegmensen megkapható, majd az egész definíciós tartományon keresztül folytatható.

Tekintsük a függvény tulajdonságait:

1) A meghatározás hatálya:

2) Értéktartomány:

3) Páratlan függvény:

4) A legkisebb pozitív időszak:

5) A gráf és az abszcissza tengely metszéspontjainak koordinátái:

6) A gráf ordinátatengellyel való metszéspontjának koordinátái:

7) Azok az időközök, amelyeknél a függvény pozitív értékeket vesz fel:

8) Azok az időközök, amelyeknél a függvény negatív értékeket vesz fel:

9) Növekvő időközök:

10) Csökkenő intervallumok:

11) Minimum pont:

12) Minimális funkciók:

13) Maximális pont:

14) Maximális funkciók:

Megnéztük a függvény tulajdonságait és grafikonját. A tulajdonságok többször is felhasználásra kerülnek a problémák megoldása során.

Bibliográfia

1. Algebra és az elemzés kezdete, 10. évfolyam (két részben). Tankönyv általános oktatási intézmények számára (profilszint), szerk. A. G. Mordkovich. -M.: Mnemosyne, 2009.

2. Algebra és az elemzés kezdete, 10. évfolyam (két részben). Problémakönyv oktatási intézmények számára (profilszint), szerk. A. G. Mordkovich. -M.: Mnemosyne, 2007.

3. Vilenkin N.Ya., Ivashev-Musatov O.S., Shvartsburd S.I. Algebra és matematikai elemzés a 10. osztály számára (tankönyv iskolák és osztályok tanulói számára a matematika elmélyült tanulmányozásával - M.: Prosveshchenie, 1996).

4. Galitsky M.L., Moshkovich M.M., Shvartsburd S.I. Az algebra és a matematikai elemzés elmélyült tanulmányozása.-M.: Oktatás, 1997.

5. Matematikai feladatgyűjtemény felsőoktatási intézményekbe jelentkezők számára (szerkesztette: M.I. Skanavi - M.: Higher School, 1992).

6. Merzlyak A.G., Polonsky V.B., Yakir M.S. Algebrai szimulátor.-K.: A.S.K., 1997.

7. Sahakyan S.M., Goldman A.M., Denisov D.V. Algebrai problémák és elemzési elvek (kézikönyv az általános oktatási intézmények 10-11. osztályos tanulói számára - M.: Prosveshchenie, 2003).

8. Karp A.P. Algebrai feladatgyűjtemény és elemzési elvek: tankönyv. pótlék 10-11 évfolyamon. mélységgel tanult Matematika.-M.: Oktatás, 2006.

Házi feladat

Algebra és az elemzés kezdete, 10. évfolyam (két részben). Problémakönyv oktatási intézmények számára (profilszint), szerk.

A. G. Mordkovich. -M.: Mnemosyne, 2007.

№№ 16.4, 16.5, 16.8.

További webes források

3. Vizsgafelkészítő oktatási portál ().

Megállapítottuk, hogy a trigonometrikus függvények viselkedése, és a függvények y = sin x különösen, a teljes számegyenesen (vagy az argumentum összes értékére x) teljes mértékben meghatározza az intervallumban való viselkedése 0 < x < π / 2 .

Ezért először ábrázoljuk a függvényt y = sin x pontosan ebben az intervallumban.

Készítsük el a függvényünk alábbi értéktáblázatát;

A koordinátasíkon a megfelelő pontokat megjelölve és sima vonallal összekötve az ábrán látható görbét kapjuk

A kapott görbe geometriailag is megszerkeszthető anélkül, hogy függvényértékeket tartalmazó táblázatot kellene összeállítani y = sin x .

1. Oszd fel az 1 sugarú kör első negyedét 8 egyenlő részre A kör osztópontjainak ordinátái a megfelelő szögek szinuszai.

2.A kör első negyede 0-tól ig terjedő szögeknek felel meg π / 2 . Ezért a tengelyen x Vegyünk egy szakaszt, és osszuk fel 8 egyenlő részre.

3. Rajzoljunk a tengellyel párhuzamos egyeneseket! x, és az osztási pontokból merőlegeseket építünk, amíg nem metszik egymást vízszintes vonalakkal.

4. Kösse össze a metszéspontokat egy sima vonallal.

Most nézzük az intervallumot π / 2 < x < π .
Minden argumentum értéke x ebből az intervallumból úgy ábrázolható

x = π / 2 + φ

Ahol 0 < φ < π / 2 . A redukciós képletek szerint

bűn ( π / 2 + φ ) = cos φ = sin( π / 2 - φ ).

Tengelypontok x abszcisszákkal π / 2 + φ És π / 2 - φ szimmetrikusan egymásra a tengelypont körül x abszcisszával π / 2 , és ezekben a pontokban a szinuszok megegyeznek. Ez lehetővé teszi, hogy megkapjuk a függvény grafikonját y = sin x intervallumban [ π / 2 , π ] egyszerűen szimmetrikusan megjelenítve ennek a függvénynek a grafikonját az egyeneshez viszonyított intervallumban x = π / 2 .

Most használja az ingatlant páratlan paritásfüggvény y = sin x,

bűn(- x) = - bűn x,

ezt a függvényt könnyű ábrázolni a [- π , 0].

Az y = sin x függvény 2π periódusú periodikus ;. Ezért ennek a függvénynek a teljes grafikonjának elkészítéséhez elegendő az ábrán látható görbét periodikusan egy ponttal balra és jobbra folytatni. 2π .

Az így kapott görbét ún szinuszos . Ez a függvény grafikonja y = sin x.

Az ábra jól szemlélteti a függvény összes tulajdonságát y = sin x , amit korábban már bebizonyítottunk. Emlékezzünk vissza ezekre a tulajdonságokra.

1) Funkció y = sin x minden értékre meghatározva x , tehát a tartománya az összes valós szám halmaza.

2) Funkció y = sin x korlátozott. Minden általa elfogadott érték -1 és 1 között van, beleértve ezt a két számot is. Következésképpen ennek a függvénynek a változási tartományát a -1 egyenlőtlenség határozza meg < nál nél < 1. Mikor x = π / 2 + 2k π a függvény a legnagyobb értékeket 1-gyel veszi fel, és x = - esetén π / 2 + 2k π - a legkisebb értékek egyenlőek -1-gyel.

3) Funkció y = sin x páratlan (a szinuszhullám szimmetrikus az origóra).

4) Funkció y = sin x periodikus a 2. periódussal π .

5) 2n időközönként π < x < π + 2n π (n bármely egész szám) pozitív, és intervallumokban π + 2k π < x < 2π + 2k π (k bármely egész szám) negatív. x = k-nél π a függvény nullára megy. Ezért az x argumentum ezen értékei (0; ± π ; ±2 π ; ...) függvényeket nulláknak nevezzük y = sin x

6) Időközönként - π / 2 + 2n π < x < π / 2 + 2n π funkció y = bűn x monoton és időközönként növekszik π / 2 + 2k π < x < 3π / 2 + 2k π monoton csökken.

Különös figyelmet kell fordítani a függvény viselkedésére y = sin x a pont közelében x = 0 .

Például sin 0,012 ≈ 0,012; sin(-0,05) ≈ -0,05;

sin 2° = sin π 2 / 180 = bűn π / 90 ≈ 0,03 ≈ 0,03.

Ugyanakkor meg kell jegyezni, hogy az x bármely értékéhez

| bűn x| < | x | . (1)

Valóban, legyen az ábrán látható kör sugara 1,
a / AOB = x.

Aztán bűn x= AC. De AC< АВ, а АВ, в свою очередь, меньше длины дуги АВ, на которую опирается угол x. Ennek az ívnek a hossza nyilvánvalóan egyenlő x, mivel a kör sugara 1. Tehát 0-nál< x < π / 2

bűn x< х.

Ezért a függvény páratlansága miatt y = sin x könnyű megmutatni, hogy amikor - π / 2 < x < 0

| bűn x| < | x | .

Végül, mikor x = 0

| sin x | = | x |.

Így a | x | < π / 2 az (1) egyenlőtlenség bebizonyosodott. Valójában ez az egyenlőtlenség a |-re is igaz x | > π / 2 amiatt, hogy | bűn x | < 1, a π / 2 > 1

Feladatok

1.A függvény grafikonja szerint y = sin x határozzuk meg: a) sin 2; b) sin 4; c) bűn (-3).

2.A függvény grafikonja szerint y = sin x határozza meg, melyik szám az intervallumból
[ - π / 2 , π / 2 ] szinusza egyenlő: a) 0,6; b) -0,8.

3. A függvény grafikonja szerint y = sin x határozza meg, hogy mely számoknak van szinusza,
egyenlő 1/2.

4. Határozza meg megközelítőleg (táblázatok nélkül): a) sin 1°; b) sin 0,03;
c) sin (-0,015); d) sin (-2°30").

Hogyan ábrázoljuk az y=sin x függvényt? Először nézzük meg az intervallum szinuszgrafikonját.

Egyetlen 2 cella hosszúságú szegmenst veszünk fel a notebookban. Az Oy tengelyen jelölünk egyet.

A kényelem kedvéért a π/2 számot 1,5-re kerekítjük (és nem 1,6-ra, ahogy azt a kerekítési szabályok előírják). Ebben az esetben egy π/2 hosszúságú szegmens 3 cellának felel meg.

Az Ox tengelyen nem egyedi szegmenseket jelölünk, hanem π/2 hosszúságú szakaszokat (minden 3 cellában). Ennek megfelelően egy π hosszúságú szegmens 6 cellának, egy π/6 hosszúságú szegmens pedig 1 cellának felel meg.

Ezzel az egységszegmens kiválasztásával a notebook lapján egy dobozban ábrázolt grafikon a lehető legnagyobb mértékben megfelel az y=sin x függvény grafikonjának.

Készítsünk egy táblázatot az intervallum szinuszértékeiről:

A kapott pontokat a koordinátasíkon jelöljük:

Mivel y=sin x páratlan függvény, a szinuszgráf szimmetrikus az origóhoz - O(0;0) ponthoz. Ezt a tényt figyelembe véve folytatjuk a grafikon ábrázolását balra, majd a -π pontokat:

Az y=sin x függvény periodikus, T=2π periódussal. Ezért a [-π;π] intervallumon felvett függvény grafikonja végtelen számú alkalommal ismétlődik jobbra és balra.

Óra és előadás a témában: "Y=sin(x) függvény. Definíciók és tulajdonságok"

Kiegészítő anyagok
Kedves felhasználók, ne felejtsék el megírni észrevételeiket, véleményeiket, kívánságaikat! Minden anyagot vírusirtó programmal ellenőriztek.

Kézikönyvek és szimulátorok az Integral online áruházban 10. osztályhoz az 1C-től
Geometriai feladatokat oldunk meg. Interaktív építési feladatok 7-10
Szoftverkörnyezet "1C: Mathematical Constructor 6.1"

Amit tanulmányozni fogunk:

• Az Y=sin(X) függvény tulajdonságai.
• Függvénygrafikon.
• Hogyan készítsünk grafikont és léptékét.
• Példák.

A szinusz tulajdonságai. Y=sin(X)

Srácok, már találkoztunk trigonometrikus függvények numerikus argumentum. Emlékszel rájuk?

Nézzük meg közelebbről az Y=sin(X) függvényt

Írjuk fel ennek a függvénynek néhány tulajdonságát:
1) A definíciós tartomány a valós számok halmaza.
2) A függvény páratlan. Emlékezzünk a páratlan függvény definíciójára. Egy függvényt páratlannak nevezünk, ha az egyenlőség teljesül: y(-x)=-y(x). Ahogy a szellemképletekből emlékszünk: sin(-x)=-sin(x). A definíció teljesül, ami azt jelenti, hogy Y=sin(X) páratlan függvény.
3) Az Y=sin(X) függvény növekszik a szakaszon, és csökken a [π/2; π]. Amikor az első negyedben haladunk (az óramutató járásával ellentétes irányban), az ordináta növekszik, a második negyedben pedig csökken.

4) Az Y=sin(X) függvény alulról és felülről korlátozott. Ez a tulajdonság abból következik, hogy
-1 ≤ sin(X) ≤ 1
5) A függvény legkisebb értéke -1 (x = - π/2+ πk-nél). A függvény legnagyobb értéke 1 (x = π/2+ πk-nál).

Használjuk az 1-5 tulajdonságokat az Y=sin(X) függvény ábrázolására. A gráfunkat szekvenciálisan készítjük el, tulajdonságainkat alkalmazva. Kezdjük a grafikon felépítését a szegmensen.

Különös figyelmet kell fordítani a skálára. Az ordináta tengelyen célszerűbb egy 2 cellával egyenlő egységszegmenst venni, az abszcissza tengelyen pedig egy π/3-mal egyenlő egységszegmenst (két cellát) (lásd az ábrát).

Az x szinuszfüggvény ábrázolása, y=sin(x)

Számítsuk ki a függvény értékeit a szegmensünkön:

Készítsünk grafikont pontjaink felhasználásával, figyelembe véve a harmadik tulajdonságot.

Átalakító táblázat szellemképletekhez

Használjuk a második tulajdonságot, amely szerint a függvényünk páratlan, ami azt jelenti, hogy szimmetrikusan tükrözhető az origóhoz képest:

Tudjuk, hogy sin(x+ 2π) = sin(x). Ez azt jelenti, hogy a [- π; π] a grafikon ugyanúgy néz ki, mint a [π; 3π] vagy vagy [-3π; - π] és így tovább. Nincs más dolgunk, mint gondosan átrajzolni az előző ábrán látható grafikont a teljes x tengely mentén.

Az Y=sin(X) függvény grafikonját szinuszosnak nevezzük.

Írjunk még néhány tulajdonságot a felépített gráf szerint:
6) Az Y=sin(X) függvény bármely alakú szegmensén növekszik: [- π/2+ 2πk; π/2+ 2πk], k egész szám, és a következő alak bármely szegmensén csökken: [π/2+ 2πk; 3π/2+ 2πk], k – egész szám.
7) Az Y=sin(X) függvény folytonos függvény. Nézzük meg a függvény grafikonját, és győződjünk meg arról, hogy a függvényünkben nincs törés, ez folytonosságot jelent.
8) Értéktartomány: szegmens [- 1; 1]. Ez jól látható a függvény grafikonján is.
9) Y=sin(X) függvény - periodikus függvény. Nézzük meg újra a grafikont, és nézzük meg, hogy a függvény bizonyos időközönként ugyanazokat az értékeket veszi fel.

Példák a szinuszos problémákra

1. Oldja meg a sin(x)= x-π egyenletet!

Megoldás: Készítsünk 2 grafikont a függvényből: y=sin(x) és y=x-π (lásd az ábrát).
Grafikonjaink egy A(π;0) pontban metszik egymást, ez a válasz: x = π

2. Ábrázolja az y=sin(π/6+x)-1 függvényt

Megoldás: A kívánt grafikont úgy kapjuk meg, hogy az y=sin(x) függvény grafikonját π/6 egységgel balra és 1 egységgel lefelé mozgatjuk.

Megoldás: Készítsük el a függvény grafikonját, és vegyük figyelembe a [π/2; 5π/4].
A függvény grafikonja azt mutatja, hogy a legnagyobb és a legkisebb értékeket a szegmens végén, a π/2 és 5π/4 pontokban érjük el.
Válasz: sin(π/2) = 1 – a legnagyobb érték, sin(5π/4) = a legkisebb érték.

Szinuszfeladatok a független megoldáshoz

• Oldja meg az egyenletet: sin(x)= x+3π, sin(x)= x-5π
• Ábrázolja az y=sin(π/3+x)-2 függvényt
• Ábrázolja az y=sin(-2π/3+x)+1 függvényt
• Keresse meg az y=sin(x) függvény legnagyobb és legkisebb értékét a szakaszon!
• Határozzuk meg az y=sin(x) függvény legnagyobb és legkisebb értékét a [- π/3 intervallumon; 5π/6]