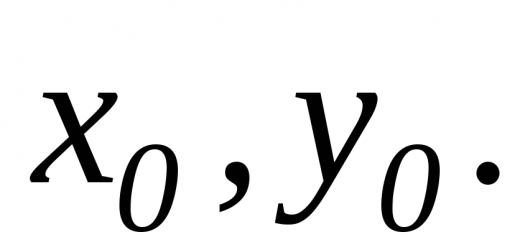A matematikai fizikai feladatok vagy példák megoldása teljesen lehetetlen a derivált és a számítási módszerek ismerete nélkül. A derivált a matematikai elemzés egyik legfontosabb fogalma. Úgy döntöttünk, hogy a mai cikket ennek az alapvető témának szenteljük. Mi a derivált, mi a fizikai és geometriai jelentése, hogyan kell kiszámítani egy függvény deriváltját? Mindezek a kérdések összevonhatók egybe: hogyan lehet megérteni a származékot?

A származék geometriai és fizikai jelentése

Legyen függvény f(x) , meghatározott intervallumban (a, b) . Az x és x0 pont ehhez az intervallumhoz tartozik. Ha x változik, maga a függvény is megváltozik. Az érv megváltoztatása - az értékek különbsége x-x0 . Ez a különbség így van írva delta x és argumentumnövekménynek nevezzük. Egy függvény változása vagy növekménye a függvény értékeinek különbsége két ponton. A származék definíciója:

Egy függvény deriváltja egy pontban a függvény adott pontban való növekménye és az argumentum növekménye arányának határa, amikor az utóbbi nullára hajlik.

Különben így írható:

Mi értelme ilyen határt találni? És íme, mi ez:

egy függvény deriváltja egy pontban egyenlő az OX tengely és a függvény grafikonjának érintője közötti szög érintőjével egy adott pontban.

Fizikai jelentés derivált: az út időbeli deriváltja egyenlő az egyenes vonalú mozgás sebességével.

Valójában az iskolai idők óta mindenki tudja, hogy a sebesség egy adott út x=f(t) és az idő t . átlagsebesség egy bizonyos ideig:

Megtudni a mozgás sebességét egy adott pillanatban t0 ki kell számolni a határértéket:

Első szabály: állítson be egy állandót

A konstans kivehető a derivált előjelből. Ráadásul ezt meg is kell tenni. A matematikai példák megoldása során vegye ezt szabálynak - Ha le tud egyszerűsíteni egy kifejezést, mindenképpen egyszerűsítse .

Példa. Számítsuk ki a deriváltot:

Második szabály: a függvények összegének deriváltja

Két függvény összegének deriváltja egyenlő ezen függvények deriváltjainak összegével. Ugyanez igaz a függvények különbségének deriváltjára is.

Nem bizonyítjuk ezt a tételt, inkább egy gyakorlati példát veszünk figyelembe.

Keresse meg a függvény deriváltját:

Harmadik szabály: a függvények szorzatának deriváltja

Két differenciálható függvény szorzatának deriváltja a következő képlettel számítható ki:

Példa: keresse meg egy függvény deriváltját:

Megoldás:

Itt fontos szót ejteni az összetett függvények deriváltjainak kiszámításáról. Egy komplex függvény deriváltja egyenlő ennek a függvénynek a deriváltjának a szorzatával a köztes argumentumhoz és a köztes argumentum deriváltjának a független változóhoz képest.

A fenti példában a következő kifejezéssel találkozunk:

Ebben az esetben a köztes argumentum az ötödik hatvány nyolcszorosa. Egy ilyen kifejezés deriváltjának kiszámításához először kiszámítjuk a külső függvény deriváltját a köztes argumentumhoz képest, majd megszorozzuk magának a köztes argumentumnak a független változóhoz viszonyított deriváltjával.

Negyedik szabály: két függvény hányadosának deriváltja

Képlet két függvény hányadosának deriváltjának meghatározására:

Megpróbáltunk a nulláról beszélni a próbababák származékairól. Ez a téma nem olyan egyszerű, mint amilyennek látszik, ezért figyelem: a példákban gyakran vannak buktatók, ezért legyen óvatos a származékok kiszámításakor.

Ezzel és más témával kapcsolatos kérdéseivel fordulhat a diákszolgálathoz. Rövid időn belül segítünk megoldani a legnehezebb tesztet és megérteni a feladatokat, még akkor is, ha még soha nem végzett derivált számításokat.

A téma tanulmányozása során a kényelem és az áttekinthetőség érdekében összefoglaló táblázatot mutatunk be.

Állandóy = C Hatványfüggvény y = x p (x p) " = p x p - 1	Exponenciális függvényy = a x (a x) " = a x ln a Főleg mikora = enekünk van y = e x (e x) " = e x
Logaritmikus függvény (log a x) " = 1 x ln a Főleg mikora = enekünk van y = logx (ln x) " = 1 x	Trigonometrikus függvények (sin x) " = cos x (cos x) " = - sin x (t g x) " = 1 cos 2 x (c t g x) " = - 1 sin 2 x
Inverz trigonometrikus függvények (a r c sin x) " = 1 1 - x 2 (a r c cos x) " = - 1 1 - x 2 (a r c t g x) " = 1 1 + x 2 (a r c c t g x) " = - 1 1 + x 2	Hiperbolikus függvények (s h x) " = c h x (c h x) " = s h x (t h x) " = 1 c h 2 x (c t h x) " = - 1 s h 2 x

Vizsgáljuk meg, hogyan kaptuk meg a megadott táblázat képleteit, vagy más szóval, bizonyítsuk be az egyes függvénytípusokhoz tartozó derivált képletek származtatását.

Egy állandó származéka

Bizonyíték 1

A visszavonás érdekében ezt a képletet, vegyük alapul egy függvény deriváltjának meghatározását egy pontban. Használjuk x 0 = x, ahol x bármely valós szám értékét veszi fel, vagy más szóval x tetszőleges szám az f (x) = C függvény tartományából. Írjuk fel egy függvény növekményének és az argumentum növekményének arányának határát ∆ x → 0 értékkel:

lim ∆ x → 0 ∆ f (x) ∆ x = lim ∆ x → 0 C - C ∆ x = lim ∆ x → 0 0 ∆ x = 0

Vegye figyelembe, hogy a 0 ∆ x kifejezés a határjel alá esik. Nem a „nulla osztva nullával” bizonytalanságról van szó, mivel a számláló nem végtelenül kicsi értéket tartalmaz, hanem pontosan nullát. Más szóval, egy állandó függvény növekménye mindig nulla.

Tehát az f (x) = C konstans függvény deriváltja a teljes definíciós tartományban nullával egyenlő.

1. példa

Az állandó függvények a következők:

f 1 (x) = 3, f 2 (x) = a, a ∈ R, f 3 (x) = 4. 13 7 22 , f 4 (x) = 0, f 5 (x) = - 8 7

Megoldás

Ismertesse a megadott feltételeket. Az első függvényben a 3 természetes szám deriváltját látjuk. A következő példában a származékát kell vennie A, Ahol A- bármilyen valós szám. A harmadik példa megadja a 4-es irracionális szám deriváltját. 13 7 22, a negyedik a nulla deriváltja (nulla egész szám). Végül az ötödik esetben megkapjuk a származékot racionális tört - 8 7 .

Válasz: származékai meghatározott funkciókat nulla minden valódi x(a teljes definíciós területen)

f 1 " (x) = (3) " = 0, f 2 " (x) = (a) " = 0, a ∈ R , f 3 " (x) = 4. 13 7 22 " = 0, f 4 " (x) = 0 " = 0 , f 5 " (x) = - 8 7 " = 0

Hatványfüggvény származéka

Menjünk tovább teljesítmény funkcióés származékának képlete, amelynek alakja: (x p) " = p x p - 1, ahol a kitevő p bármilyen valós szám.

Bizonyíték 2

Adjuk meg a képlet bizonyítását, amikor a kitevő az természetes szám: p = 1, 2, 3, …

Ismét a derivált definíciójára hagyatkozunk. Írjuk fel egy hatványfüggvény növekményének és az argumentum növekményének arányának határát:

(x p) " = lim ∆ x → 0 = ∆ (x p) ∆ x = lim ∆ x → 0 (x + ∆ x) p - x p ∆ x

A számlálóban a kifejezés egyszerűsítésére Newton binomiális képletét használjuk:

(x + ∆ x) p - x p = C p 0 + x p + C p 1 · x p - 1 · ∆ x + C p 2 · x p - 2 · (∆ x) 2 + . . . + + C p p - 1 x (∆ x) p - 1 + C p p (∆ x) p - x p = = C p 1 x p - 1 ∆ x + C p 2 x p - 2 (∆ x) 2 + . . . + C p p - 1 x (∆ x) p - 1 + C p p (∆ x) p

És így:

(x p) " = lim ∆ x → 0 ∆ (x p) ∆ x = lim ∆ x → 0 (x + ∆ x) p - x p ∆ x = = lim ∆ x → 0 (C p 1 x p - 1 ∆ x + C p 2 x p - 2 (∆ x) 2 + ... + C p p - 1 x (∆ x) p - 1 + C p p (∆ x) p) ∆ x = = lim ∆ x → 0 (C p 1 x p - 1 + C p 2 x p - 2 ∆ x + .. + C p p - 1 x ( ∆ x) p - 2 + C p p ( ∆ x) p - 1) = = C p 1 · x p - 1 + 0 + 0 + ... + 0 = p ! 1 ! · (p - 1) ! · x p - 1 = p · x p - 1

Így bebizonyítottuk a hatványfüggvény derivált képletét, ha a kitevő természetes szám.

Bizonyíték 3

Bizonyítékot szolgáltatni arra az esetre, amikor p- nullától eltérő valós szám esetén a logaritmikus deriváltot használjuk (itt meg kell értenünk a különbséget a logaritmikus függvény deriváltjától). A teljesebb megértés érdekében tanácsos tanulmányozni a logaritmikus függvény deriváltját, és jobban megérteni egy implicit függvény deriváltját és egy komplex függvény deriváltját.

Vegyünk két esetet: mikor x pozitív és mikor x negatív.

Tehát x > 0. Ekkor: x p > 0 . Logaritáljuk az y = x p egyenlőséget e bázisra, és alkalmazzuk a logaritmus tulajdonságát:

y = x p ln y = ln x p ln y = p · ln x

Ebben a szakaszban egy implicit módon meghatározott függvényt kaptunk. Határozzuk meg a származékát:

(ln y) " = (p · ln x) 1 y · y " = p · 1 x ⇒ y " = p · y x = p · x p x = p · x p - 1

Most azt az esetet vesszük figyelembe, amikor x - negatív szám.

Ha a jelző p Van páros szám, akkor a hatványfüggvény definiálva van x-re< 0 , причем является четной: y (x) = - y ((- x) p) " = - p · (- x) p - 1 · (- x) " = = p · (- x) p - 1 = p · x p - 1

Aztán x p< 0 и возможно составить доказательство, используя логарифмическую производную.

Ha p páratlan szám, akkor a hatványfüggvény x-re van definiálva< 0 , причем является нечетной: y (x) = - y (- x) = - (- x) p . Тогда x p < 0 , а значит логарифмическую производную задействовать нельзя. В такой ситуации возможно взять за основу доказательства правила дифференцирования и правило нахождения производной сложной функции:

y " (x) = (- (- x) p) " = - ((- x) p) " = - p · (- x) p - 1 · (- x) " = = p · (- x) p - 1 = p x p - 1

Az utolsó átmenet annak köszönhető, hogy ha p akkor páratlan szám p - 1 vagy páros szám vagy nulla (p = 1 esetén), tehát negatív esetén x a (- x) p - 1 = x p - 1 egyenlőség igaz.

Tehát bebizonyítottuk a hatványfüggvény derivált képletét bármely valós p-re.

2. példa

Adott funkciók:

f 1 (x) = 1 x 2 3, f 2 (x) = x 2 - 1 4, f 3 (x) = 1 x log 7 12

Határozza meg származékaikat!

Megoldás

A megadott függvények egy részét a fok tulajdonságai alapján y = x p táblázatos alakra alakítjuk, majd a képletet használjuk:

f 1 (x) = 1 x 2 3 = x - 2 3 ⇒ f 1 " (x) = - 2 3 x - 2 3 - 1 = - 2 3 x - 5 3 f 2 " (x) = x 2 - 1 4 = 2 - 1 4 x 2 - 1 4 - 1 = 2 - 1 4 x 2 - 5 4 f 3 (x) = 1 x log 7 12 = x - log 7 12 ⇒ f 3" ( x) = - log 7 12 x - log 7 12 - 1 = - log 7 12 x - log 7 12 - log 7 7 = - log 7 12 x - log 7 84

Exponenciális függvény deriváltja

4. bizonyítás

Vezessük le a derivált képletet a definíció alapján:

(a x) " = lim ∆ x → 0 a x + ∆ x - a x ∆ x = lim ∆ x → 0 a x (a ∆ x - 1) ∆ x = a x lim ∆ x → 0 a ∆ x - 1 ∆ x = 0 0

Elbizonytalanodtunk. Kibontásához írjunk fel egy új z = a ∆ x - 1 változót (z → 0 mint ∆ x → 0). Ebben az esetben a ∆ x = z + 1 ⇒ ∆ x = log a (z + 1) = ln (z + 1) ln a . Az utolsó átmenethez az új logaritmusbázisra való áttérés képletét használták.

Helyettesítsük be az eredeti határt:

(a x) " = a x · lim ∆ x → 0 a ∆ x - 1 ∆ x = a x · ln a · lim ∆ x → 0 1 1 z · ln (z + 1) = = a x · ln a · lim ∆ x → 0 1 ln (z + 1) 1 z = a x · ln a · 1 ln lim ∆ x → 0 (z + 1) 1 z

Emlékezzünk a második figyelemre méltó határra, majd megkapjuk a derivált képletét exponenciális függvény:

(a x) " = a x · ln a · 1 ln lim z → 0 (z + 1) 1 z = a x · ln a · 1 ln e = a x · ln a

3. példa

Az exponenciális függvények a következők:

f 1 (x) = 2 3 x , f 2 (x) = 5 3 x , f 3 (x) = 1 (e) x

Meg kell találni a származékaikat.

Megoldás

Az exponenciális függvény és a logaritmus tulajdonságainak deriválására a képletet használjuk:

f 1 "(x) = 2 3 x " = 2 3 x ln 2 3 = 2 3 x (ln 2 - ln 3) f 2 " (x) = 5 3 x " = 5 3 x ln 5 1 3 = 1 3 5 3 x ln 5 f 3 " (x) = 1 (e) x " = 1 e x " = 1 e x ln 1 e = 1 e x ln e - 1 = - 1 e x

Logaritmikus függvény deriváltja

Bizonyíték 5

Bizonyítsuk be a logaritmikus függvény deriváltjának képletét bármelyikre x a definíció területén és bármely elfogadható értékeket a logaritmus a alapja. A derivált definíciója alapján a következőket kapjuk:

(log a x) " = lim ∆ x → 0 log a (x + ∆ x) - log a x ∆ x = lim ∆ x → 0 log a x + ∆ x x ∆ x = = lim ∆ x → 0 1 ∆ x log a 1 + ∆ x x = lim ∆ x → 0 log a 1 + ∆ x x 1 ∆ x = = lim ∆ x → 0 log a 1 + ∆ x x 1 ∆ x · x x = lim ∆ x → 0 1 x · log a 1 + ∆ x x x ∆ x = = 1 x · log a lim ∆ x → 0 1 + ∆ x x x ∆ x = 1 x · log a e = 1 x · ln e ln a = 1 x · ln a

A jelzett egyenlőségláncból jól látható, hogy a transzformációk a logaritmus tulajdonságain alapultak. A lim ∆ x → 0 1 + ∆ x x x ∆ x = e egyenlőség a második figyelemre méltó határnak megfelelően igaz.

4. példa

A logaritmikus függvények adottak:

f 1 (x) = log ln 3 x, f 2 (x) = ln x

Ki kell számítani a származékaikat.

Megoldás

Alkalmazzuk a származtatott képletet:

f 1 " (x) = (log ln 3 x) " = 1 x · ln (ln 3) ; f 2 " (x) = (ln x) " = 1 x ln e = 1 x

Tehát a természetes logaritmus deriváltja eggyel osztva x.

Trigonometrikus függvények származékai

6. bizonyítás

Használjunk néhányat trigonometrikus képletekés az első figyelemre méltó határérték a trigonometrikus függvény deriváltjának levezetéséhez.

A szinuszfüggvény deriváltjának definíciója szerint a következőt kapjuk:

(sin x) " = lim ∆ x → 0 sin (x + ∆ x) - sin x ∆ x

A szinuszok különbségének képlete lehetővé teszi a következő műveletek végrehajtását:

(sin x) " = lim ∆ x → 0 sin (x + ∆ x) - sin x ∆ x = = lim ∆ x → 0 2 sin x + ∆ x - x 2 cos x + ∆ x + x 2 ∆ x = = lim ∆ x → 0 sin ∆ x 2 · cos x + ∆ x 2 ∆ x 2 = = cos x + 0 2 · lim ∆ x → 0 sin ∆ x 2 ∆ x 2

Végül az első csodálatos határt használjuk:

sin " x = cos x + 0 2 · lim ∆ x → 0 sin ∆ x 2 ∆ x 2 = cos x

Tehát a függvény deriváltja bűn x akarat cos x.

Bebizonyítjuk a koszinusz deriváltjának képletét is:

cos " x = lim ∆ x → 0 cos (x + ∆ x) - cos x ∆ x = = lim ∆ x → 0 - 2 sin x + ∆ x - x 2 sin x + ∆ x + x 2 ∆ x = = - lim ∆ x → 0 sin ∆ x 2 sin x + ∆ x 2 ∆ x 2 = = - sin x + 0 2 lim ∆ x → 0 sin ∆ x 2 ∆ x 2 = - sin x

Azok. derivált cos funkciókat x lesz – sin x.

Levezetjük az érintő és a kotangens deriváltjainak képleteit a differenciálás szabályai alapján:

t g " x = sin x cos x " = sin " x · cos x - sin x · cos " x cos 2 x = = cos x · cos x - sin x · (- sin x) cos 2 x = sin 2 x + cos 2 x cos 2 x = 1 cos 2 x c t g " x = cos x sin x " = cos " x · sin x - cos x · sin " x sin 2 x = = - sin x · sin x - cos x · cos x sin 2 x = - sin 2 x + cos 2 x sin 2 x = - 1 sin 2 x

Inverz trigonometrikus függvények deriváltjai

Az inverz függvények deriváltjairól szóló rész átfogó tájékoztatást ad az arcszinusz, arkoszinusz, arctangens és arckotangens deriváltjainak bizonyításáról, ezért itt nem fogjuk megkettőzni az anyagot.

Hiperbolikus függvények származékai

Bizonyíték 7

A hiperbolikus szinusz, koszinusz, tangens és kotangens deriváltjainak képleteit a differenciálási szabály és az exponenciális függvény deriváltjának formulája segítségével levezethetjük:

s h " x = e x - e - x 2 " = 1 2 e x " - e - x " = = 1 2 e x - - e - x = e x + e - x 2 = c h x c h " x = e x + e - x 2 " = 1 2 e x " + e - x " = = 1 2 e x + - e - x = e x - e - x 2 = s h x t h " x = s h x c h x " = s h " x · c h x - s h x · c h " x c h 2 x = c h 2 x - s h 2 x c h 2 x = 1 c h 2 x c t h " x = c h x s h x " = c h " x · s h x - c h x · s h " x s h 2 x = s h 2 x - c h 2 x s h 2 x = - 1 s h 2 x

Ha hibát észlel a szövegben, jelölje ki, és nyomja meg a Ctrl+Enter billentyűkombinációt

A matematikai fizikai feladatok vagy példák megoldása teljesen lehetetlen a derivált és a számítási módszerek ismerete nélkül. A derivált a matematikai elemzés egyik legfontosabb fogalma. Úgy döntöttünk, hogy a mai cikket ennek az alapvető témának szenteljük. Mi a derivált, mi a fizikai és geometriai jelentése, hogyan kell kiszámítani egy függvény deriváltját? Mindezek a kérdések összevonhatók egybe: hogyan lehet megérteni a származékot?

A származék geometriai és fizikai jelentése

Legyen függvény f(x) , meghatározott intervallumban (a, b) . Az x és x0 pont ehhez az intervallumhoz tartozik. Ha x változik, maga a függvény is megváltozik. Az érv megváltoztatása - az értékek különbsége x-x0 . Ez a különbség így van írva delta x és argumentumnövekménynek nevezzük. Egy függvény változása vagy növekménye a függvény értékeinek különbsége két ponton. A származék definíciója:

Egy függvény deriváltja egy pontban a függvény adott pontban való növekménye és az argumentum növekménye arányának határa, amikor az utóbbi nullára hajlik.

Különben így írható:

Mi értelme ilyen határt találni? És íme, mi ez:

egy függvény deriváltja egy pontban egyenlő az OX tengely és a függvény grafikonjának érintője közötti szög érintőjével egy adott pontban.

A származék fizikai jelentése: az út időbeli deriváltja egyenlő az egyenes vonalú mozgás sebességével.

Valójában az iskolai idők óta mindenki tudja, hogy a sebesség egy adott út x=f(t) és az idő t . Átlagsebesség egy bizonyos időszak alatt:

Megtudni a mozgás sebességét egy adott pillanatban t0 ki kell számolni a határértéket:

Első szabály: állítson be egy állandót

A konstans kivehető a derivált előjelből. Ráadásul ezt meg is kell tenni. A matematikai példák megoldása során vegye ezt szabálynak - Ha le tud egyszerűsíteni egy kifejezést, mindenképpen egyszerűsítse .

Példa. Számítsuk ki a deriváltot:

Második szabály: a függvények összegének deriváltja

Két függvény összegének deriváltja egyenlő ezen függvények deriváltjainak összegével. Ugyanez igaz a függvények különbségének deriváltjára is.

Nem bizonyítjuk ezt a tételt, inkább egy gyakorlati példát veszünk figyelembe.

Keresse meg a függvény deriváltját:

Harmadik szabály: a függvények szorzatának deriváltja

Két differenciálható függvény szorzatának deriváltja a következő képlettel számítható ki:

Példa: keresse meg egy függvény deriváltját:

Megoldás:

Itt fontos szót ejteni az összetett függvények deriváltjainak kiszámításáról. Egy komplex függvény deriváltja egyenlő ennek a függvénynek a deriváltjának a szorzatával a köztes argumentumhoz és a köztes argumentum deriváltjának a független változóhoz képest.

A fenti példában a következő kifejezéssel találkozunk:

Ebben az esetben a köztes argumentum az ötödik hatvány nyolcszorosa. Egy ilyen kifejezés deriváltjának kiszámításához először kiszámítjuk a külső függvény deriváltját a köztes argumentumhoz képest, majd megszorozzuk magának a köztes argumentumnak a független változóhoz viszonyított deriváltjával.

Negyedik szabály: két függvény hányadosának deriváltja

Képlet két függvény hányadosának deriváltjának meghatározására:

Megpróbáltunk a nulláról beszélni a próbababák származékairól. Ez a téma nem olyan egyszerű, mint amilyennek látszik, ezért figyelem: a példákban gyakran vannak buktatók, ezért legyen óvatos a származékok kiszámításakor.

Ezzel és más témával kapcsolatos kérdéseivel fordulhat a diákszolgálathoz. Rövid időn belül segítünk megoldani a legnehezebb tesztet és megérteni a feladatokat, még akkor is, ha még soha nem végzett derivált számításokat.

Nagyon könnyű megjegyezni.

Nos, ne menjünk messzire, nézzük meg azonnal inverz függvény. Melyik függvény az exponenciális függvény inverze? Logaritmus:

Esetünkben az alap a szám:

Egy ilyen logaritmust (vagyis egy bázissal rendelkező logaritmust) „természetesnek” nevezünk, és erre egy speciális jelölést használunk: írunk helyette.

Mivel egyenlő? Természetesen, .

A természetes logaritmus deriváltja is nagyon egyszerű:

Példák:

1. Keresse meg a függvény deriváltját!
2. Mi a függvény deriváltja?

Válaszok: Kiállító és természetes logaritmus- a függvények deriváltjaik szempontjából egyedülállóan egyszerűek. Az exponenciális és logaritmikus függvények bármely más bázissal eltérő deriválttal rendelkeznek, amit később, a differenciálás szabályainak áttekintése után elemezünk.

A megkülönböztetés szabályai

Mi szabályai? Megint egy új kifejezés, megint?!...

Különbségtétel a származék megtalálásának folyamata.

Ez minden. Mi másnak nevezhetjük ezt a folyamatot egy szóval? Nem derivált... A matematikusok a differenciált a függvény azonos növekményének nevezik. Ez a kifejezés a latin differentia - differencia szóból származik. Itt.

Mindezen szabályok származtatása során két függvényt fogunk használni, például, és. Szükségünk lesz képletekre is a növekedésükhöz:

Összesen 5 szabály van.

Az állandót kivesszük a derivált előjelből.

Ha - néhány állandó szám(állandó), akkor.

Nyilvánvalóan a különbségre is érvényes ez a szabály: .

Bizonyítsuk be. Legyen, vagy egyszerűbben.

Példák.

Keresse meg a függvények származékait:

1. egy ponton;
2. egy ponton;
3. egy ponton;
4. azon a ponton.

Megoldások:

1. (a derivált minden pontban ugyanaz, mivel ez lineáris függvény, emlékezik?);

A termék származéka

Itt minden hasonló: vezessünk be egy új függvényt, és keressük meg a növekményét:

Derivált:

Példák:

1. Keresse meg az és függvények deriváltjait;
2. Keresse meg a függvény deriváltját egy pontban.

Megoldások:

Exponenciális függvény deriváltja

Most már elegendő tudása ahhoz, hogy megtanulja, hogyan kell megtalálni bármely exponenciális függvény deriváltját, és nem csak a kitevőket (elfelejtette már, mi az?).

Szóval, hol van néhány szám.

A függvény deriváltját már ismerjük, ezért próbáljuk meg a függvényünket egy új bázisra redukálni:

Erre fogjuk használni egyszerű szabály: . Akkor:

Nos, sikerült. Most próbálja meg megtalálni a származékot, és ne felejtse el, hogy ez a függvény összetett.

Megtörtént?

Itt ellenőrizd magad:

A képlet nagyon hasonlított egy kitevő deriváltjához: úgy ahogy volt, ugyanaz marad, csak egy tényező jelent meg, ami csak egy szám, de nem változó.

Példák:
Keresse meg a függvények származékait:

Válaszok:

Ez csak egy szám, amit számológép nélkül nem lehet kiszámolni, vagyis nem lehet egyszerűbb formában leírni. Ezért ebben a formában hagyjuk a válaszban.

Vegye figyelembe, hogy itt két függvény hányadosa van, ezért alkalmazzuk a megfelelő differenciálási szabályt:

Ebben a példában két függvény szorzata:

Logaritmikus függvény deriváltja

Itt is hasonló a helyzet: már ismeri a természetes logaritmus deriváltját:

Ezért egy tetszőleges logaritmus más bázisú kereséséhez, például:

Ezt a logaritmust az alapra kell redukálnunk. Hogyan lehet megváltoztatni a logaritmus alapját? Remélem emlékszel erre a képletre:

Csak most írjuk helyette:

A nevező egyszerűen egy állandó (állandó szám, változó nélkül). A származékot nagyon egyszerűen kapjuk meg:

Származékai exponenciális és logaritmikus függvények szinte soha nem jelennek meg az egységes államvizsgán, de nem ártana ismerni őket.

Komplex függvény származéka.

Mi történt " összetett funkció"? Nem, ez nem logaritmus és nem arctangens. Ezeket a függvényeket nehéz lehet megérteni (bár ha nehéznek találja a logaritmust, olvassa el a „Logaritmusok” témakört, és minden rendben lesz), de matematikai szempontból a „komplex” szó nem azt jelenti, hogy „nehéz”.

Képzeljen el egy kis futószalagot: két ember ül, és valamilyen tárggyal valamilyen műveletet végez. Például az első egy csokoládét csomagol egy csomagolóanyagba, a második pedig egy szalaggal köti össze. Az eredmény egy összetett tárgy: egy szalaggal becsomagolt és átkötött csokoládé. Egy csokoládé szelet elfogyasztásához fordított sorrendben kell végrehajtania a fordított lépéseket.

Készítsünk egy hasonló matematikai csővezetéket: először megkeressük egy szám koszinuszát, majd négyzetre emeljük a kapott számot. Tehát kapunk egy számot (csokoládé), megkeresem a koszinuszát (csomagolóanyag), majd négyzetre teszed, amit kaptam (szalaggal megkötöd). Mi történt? Funkció. Ez egy példa egy összetett függvényre: amikor az érték meghatározásához az első műveletet közvetlenül a változóval hajtjuk végre, majd egy második műveletet az elsőből eredővel.

Más szavakkal, a komplex függvény olyan függvény, amelynek argumentuma egy másik függvény: .

Példánkra .

Könnyen megtehetjük ugyanezeket a lépéseket fordított sorrendben: először négyzetre tesszük, majd megkeresem a kapott szám koszinuszát: . Könnyű kitalálni, hogy az eredmény szinte mindig más lesz. Az összetett függvények fontos jellemzője: ha megváltozik a műveletek sorrendje, akkor a funkció megváltozik.

Második példa: (ugyanaz). .

Az a művelet, amelyet utoljára hajtunk végre, el lesz nevezve "külső" funkció, és az elsőként végrehajtott művelet - ennek megfelelően "belső" funkció(ezek informális elnevezések, csak az anyag egyszerű nyelvezetű magyarázatára használom).

Próbáld meg eldönteni, hogy melyik funkció külső és melyik belső:

Válaszok: A belső és külső függvények szétválasztása nagyon hasonló a változók megváltoztatásához: például egy függvényben

1. Milyen műveletet hajtunk végre először? Először számoljuk ki a szinust, és csak azután kockázzuk fel. Ez azt jelenti, hogy ez egy belső funkció, de külső.
   Az eredeti funkció pedig az összetételük: .
2. Belső: ; külső: .
   Vizsga: .
3. Belső: ; külső: .
   Vizsga: .
4. Belső: ; külső: .
   Vizsga: .
5. Belső: ; külső: .
   Vizsga: .

Változókat változtatunk és függvényt kapunk.

Nos, most kibontjuk a csokoládét, és megkeressük a származékát. Az eljárás mindig fordított: először megkeressük a külső függvény deriváltját, majd az eredményt megszorozzuk a belső függvény deriváltjával. Az eredeti példához képest így néz ki:

Egy másik példa:

Tehát végül fogalmazzuk meg a hivatalos szabályt:

Algoritmus egy komplex függvény deriváltjának megtalálására:

Egyszerűnek tűnik, igaz?

Vizsgáljuk meg példákkal:

Megoldások:

1) Belső: ;

Külső: ;

2) Belső: ;

(Csak most ne próbáld megvágni! Semmi sem jön ki a koszinusz alól, emlékszel?)

3) Belső: ;

Külső: ;

Azonnal világos, hogy ez egy háromszintű komplex függvény: elvégre ez már önmagában is komplex funkció, és a gyökeret is kivonjuk belőle, vagyis végrehajtjuk a harmadik műveletet (csomagolóba tesszük a csokoládét és szalaggal az aktatáskában). De nincs okunk félni: ezt a funkciót továbbra is a megszokott sorrendben „pakoljuk ki”: a végétől.

Vagyis először megkülönböztetjük a gyökér, majd a koszinusz, és csak azután a zárójelben lévő kifejezést. És akkor az egészet megszorozzuk.

Ilyen esetekben célszerű a műveleteket számozni. Vagyis képzeljük el, mit tudunk. Milyen sorrendben hajtjuk végre a műveleteket a kifejezés értékének kiszámításához? Nézzünk egy példát:

Minél később hajtják végre a műveletet, annál „külsőbb” lesz a megfelelő funkció. A műveletek sorrendje ugyanaz, mint korábban:

Itt a fészekrakás általában 4 szintű. Határozzuk meg a cselekvés menetét.

1. Radikális kifejezés. .

2. Gyökér. .

3. Szinusz. .

4. Négyzet. .

5. Az egészet összerakva:

DERIVÁLT. RÖVIDEN A FŐ DOLOGOKRÓL

Függvény származéka- a függvény növekményének és az argumentum növekményének aránya az argumentum végtelenül kicsiny növekedéséhez:

Alapvető származékok:

A megkülönböztetés szabályai:

Az állandót kivesszük a derivált előjelből:

Az összeg származéka:

A termék származéka:

A hányados származéka:

Egy összetett függvény származéka:

Algoritmus egy komplex függvény deriváltjának megtalálására:

1. Meghatározzuk a „belső” függvényt, és megkeressük a származékát.
2. Meghatározzuk a „külső” függvényt, és megkeressük a származékát.
3. Az első és a második pont eredményét megszorozzuk.

ELSŐ SZÁRMAZÉK

ELSŐ SZÁRMAZÉK

(első származék) Az a sebesség, amellyel egy függvény értéke növekszik, ha argumentuma bármely ponton nő, ha maga a függvény definiálva van ezen a ponton. A grafikonon egy függvény első deriváltja a meredekségét mutatja. Ha y=f(x), pontban az első származéka x0 az a határ, amelyre hajlik f(x0+а)–f(x0)/а mint A végtelenül hajlamos kis méret. Az első származékot jelölhetjük dy/dx vagy y´(x). Funkció y(x) Megvan állandó érték azon a ponton x0, Ha dy/dx azon a ponton x0 egyenlő nullával. A nullával egyenlő első derivált szükséges, de nem elégséges feltétele annak, hogy a függvény egy adott pontban elérje maximumát vagy minimumát.

Gazdaság. Szótár. - M.: "INFRA-M", "Ves Mir" Kiadó. J. Black. Főszerkesztő: a közgazdaságtudomány doktora Osadchaya I.M.. 2000 .

Közgazdasági szótár. 2000 .

Nézze meg, mi az "ELSŐ SZÁRMAZÉK" más szótárakban:

- (derivált) Az a sebesség, amellyel egy függvény értéke növekszik, ha argumentumát bármely ponton növeljük, ha magát a függvényt ezen a ponton definiáljuk. A grafikonon egy függvény első deriváltja a meredekségét mutatja. Ha y=f(x), akkor az első deriváltja a pontban... ... Közgazdasági szótár

Ennek a kifejezésnek más jelentése is van, lásd Származék. A származékos származék fogalmának illusztrációja ... Wikipédia

A derivált a differenciálszámítás alapfogalma, egy függvény változási sebességét jellemzi. Egy függvény növekményének és argumentuma növekményének arányának határaként definiálható, mivel az argumentum növekménye nullára hajlik, ha egy ilyen határérték... ... Wikipédia

Határérték probléma speciális típus; abban áll, hogy megoldást keresünk a Dváltozók x=(x1,..., x n) tartományában. differenciálegyenlet(1) akár 2 m-t is rendelhet adott értékeket minden m-nél nem magasabb rendű derivált a D régió S határán (vagy annak egy részén) ... Matematikai Enciklopédia

- (második derivált) A függvény első deriváltjának első deriváltja. Az első derivált a függvény meredekségét méri; a második derivált azt méri, hogyan változik a meredekség az argumentum növekedésével. y második deriváltja = f(x)… … Közgazdasági szótár

Ez a cikk vagy szakasz felülvizsgálatra szorul. Kérjük, javítsa a cikket a cikkírás szabályai szerint. Törtszám a ... Wikipédiáról

- (kereszt parciális derivált) Egy függvény egyik argumentumának két vagy több változóból történő megváltoztatásának hatása egy adott függvény deriváltjára egy másik argumentumhoz képest. Ha y=f(x,z), akkor annak deriváltja, vagy az y függvény első deriváltja az x argumentumhoz képest egyenlő... ... Közgazdasági szótár

pontsebesség analógja- Egy pont mozgásának első deriváltja a mechanizmus általánosított koordinátája mentén...

a kapcsolat szögsebességének analógja- A láncszem forgásszögének első deriváltja a mechanizmus általánosított koordinátájához képest... Politechnikai terminológiai magyarázó szótár

a mechanizmus általános sebessége- A mechanizmus általánosított koordinátájának első deriváltja az idő függvényében... Politechnikai terminológiai magyarázó szótár

Könyvek

• Differenciálgeometria és topológia feladatgyűjteménye, Mishchenko A.S. Ez a feladatgyűjtemény célja, hogy a lehető legjobban tükrözze a differenciálgeometria és topológia kurzusokkal szemben támasztott meglévő követelményeit, mind az új programokból, mind pedig más kurzusokból...
• Tudományos cikkeim. 3. könyv. A sűrűségmátrixok módszere a lézer, egy tetszőleges atom kvantumelméletében, Bondarev Borisz Vladimirovics. Ez a könyv olyan megjelent tudományos cikkeket vizsgál, amelyekben a sűrűségmátrixok módszerével új kvantumelméletek lézer, tetszőleges atom és kvantumoszcillátor csillapítással...