Tanulság a témában „Végtelenül csökkenő geometriai progresszió”

Az óra célja: a tanulók megismertetése egy új típusú sorozattal - egy végtelenül csökkenő geometriai progresszióval.

Feladatok:

egy numerikus sorozat határának kezdeti elképzelésének megfogalmazása; megismerkedni a végtelen periodikus törtek közönségessé alakításának egy másik módszerével a végtelenül csökkenő geometriai haladás összegének képletével;

az iskolások személyiségének olyan intellektuális tulajdonságainak fejlesztése, mint a logikus gondolkodás, az értékelő cselekvések képessége és az általánosítás;

tevékenység, kölcsönös segítségnyújtás, kollektivizmus és a téma iránti érdeklődés előmozdítása.

Felszerelés: számítógép osztály, projektor, vetítővászon.

Az óra típusa: lecke - tanulás új téma.

Az órák alatt

én . Org. pillanat. Mondja el az óra témáját és célját!

II . A tanulók tudásának frissítése.1. Házi feladat ellenőrzése.

1) Az aritmetikai és geometriai folyamatokkal kapcsolatos alapképletek ellenőrzése. Két diák jegyzeteket készít képletekről a táblánál.

2) A többi diák igen matematikai diktálás az „Összegképletek” témában.

Feladatok:

№1. Keresse meg az első öt tag összegét! aritmetikai progresszió, ha annak első tagja 6 (1. opció), -20 (2. opció), az ötödik tag pedig -6 (1. opció), 20 (2. opció).

№2. Határozza meg egy aritmetikai sorozat első öt tagjának összegét, ha az első tagja -20 (1. lehetőség), 6 (2. lehetőség), és a különbség 10 (1. lehetőség), -3 (2. lehetőség).

№3. Határozza meg egy geometriai progresszió első öt tagjának összegét, ha az első tagja egyenlő 1-gyel (1. lehetőség), -1-gyel (2. lehetőség), és a nevező -2 (1. lehetőség), 2 (2. lehetőség).

A diktálás végén két tanuló munkáját szelektíven ellenőrzik értékelésre, a többiek önellenőrzést végeznek a tábla lapjaira írt kész megoldások segítségével.

Megoldások:

Feladatok

1. Az aritmetikai progressziót a képlet adja meg a n = 7 – 4 n. megtalálja a 10 . (-33)

2. Számtani haladásban a 3 = 7 És a 5 = 1 . megtalálja a 4 . (4)

3. Számtani haladásban a 3 = 7 És a 5 = 1 . megtalálja a 17 . (-35)

4. Számtani haladásban a 3 = 7 És a 5 = 1 . megtalálja S 17 . (-187)

5. A geometriai progresszióhoz
keresse meg az ötödik kifejezést.

6. Geometriai progresszióhoz
megtalálja n th tagja.

7. Exponenciálisan b 3 = 8 És b 5 = 2 . megtalálja b 4 . (4)

8. Exponenciálisan b 3 = 8 És b 5 = 2 . megtalálja b 1 És q .

9. Exponenciálisan b 3 = 8 És b 5 = 2 . megtalálja S 5 . (62)

III . Új téma tanulása(bemutató bemutató).

Vegyünk egy négyzetet, amelynek oldala egyenlő 1-gyel. Rajzoljunk egy másik négyzetet, amelynek oldala fele akkora, mint az első négyzet, majd egy másikat, amelynek oldala a második fele, majd a következőt stb. Minden alkalommal az új négyzet oldala egyenlő az előző felével.

Ennek eredményeként négyzetek oldalainak sorozatát kaptuk nevezővel geometriai progressziót képezve .

És ami nagyon fontos, minél több ilyen teret építünk, annál kisebb lesz a tér oldala. Például,

Azok. Ahogy az n szám növekszik, a progresszió tagjai közelítenek a nullához.

Ezzel az ábrával egy másik sorozatot is figyelembe vehet.

Például a négyzetek területeinek sorrendje:

. És még egyszer, ha n korlátlanul növekszik, akkor a terület olyan közel közelít a nullához, amennyire csak akarja.

Nézzünk egy másik példát. Egyenlő oldalú háromszög, amelynek oldalai egyenlők 1 cm. Szerkesszük meg a következő háromszöget az 1. háromszög oldalainak felezőpontjaival, a háromszög középvonalára vonatkozó tétel szerint - a 2. oldala egyenlő az első oldalának felével, a 3. oldala egyenlő a 2. oldal felével stb. Ismét megkapjuk a háromszögek oldalainak hosszsorozatát.

nál nél
.

Ha egy negatív nevezővel rendelkező geometriai progressziót tekintünk.

Aztán ismét növekvő számokkal n a progresszió feltételei közelítenek a nullához.

Figyeljünk ezeknek a sorozatoknak a nevezőire. A nevezők abszolút értékben mindenhol kisebbek voltak, mint 1.

Megállapíthatjuk: egy geometriai progresszió végtelenül csökkenő lesz, ha nevezőjének modulusa kisebb, mint 1.

Frontális munka.

Meghatározás:

Egy geometriai haladásról azt mondjuk, hogy végtelenül csökkenő, ha nevezőjének modulusa kisebb egynél.
.

A definíció segítségével eldöntheti, hogy egy geometriai progresszió végtelenül csökkenő-e vagy sem.

Feladat

Végtelenül csökkenő geometriai progresszió-e a sorozat, ha a következő képlettel adjuk meg:

;
.

Megoldás:

. meg fogjuk találni q .

;
;
;
.

ez a geometriai progresszió végtelenül csökken.

b) ez a sorozat nem egy végtelenül csökkenő geometriai progresszió.

Tekintsünk egy négyzetet, amelynek oldala egyenlő 1-gyel. Oszd ketté, az egyik felét félbe, stb. Az összes eredményül kapott téglalap területe végtelenül csökkenő geometriai progressziót alkot:

Az így kapott összes téglalap területének összege egyenlő lesz az 1. négyzet területével és egyenlő 1-gyel.

De ennek az egyenlőségnek a bal oldalán végtelen számú tag összege található.

Tekintsük az első n tag összegét.

Egy geometriai haladás első n tagjának összegére vonatkozó képlet szerint egyenlő .

Ha n akkor korlátlanul növekszik

vagy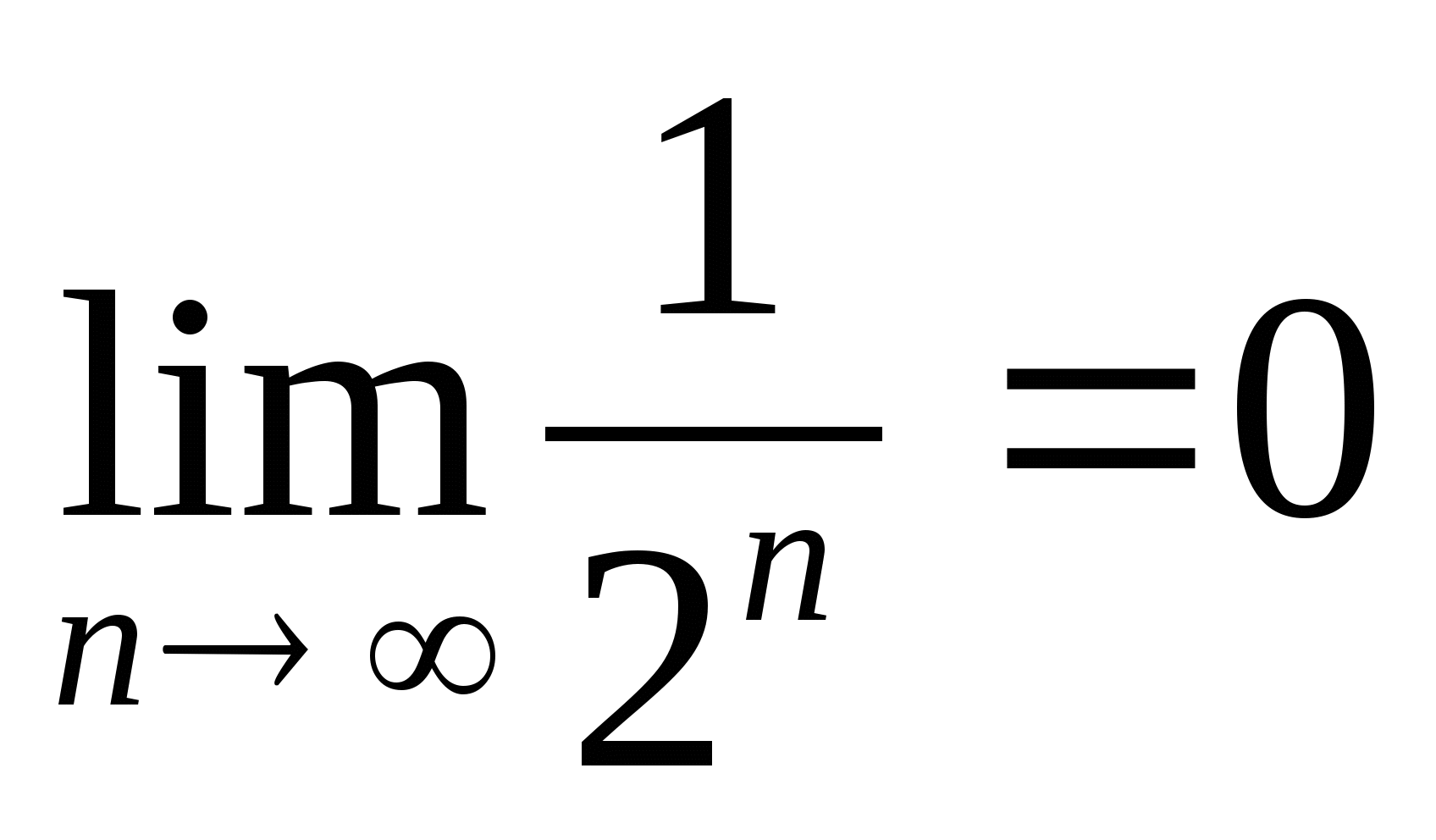
. Ezért
, azaz
.

Egy végtelenül csökkenő geometriai progresszió összege sorozatkorlát van S 1 , S 2 , S 3 , …, S n , … .

Például a továbblépéshez
,

Mert

Egy végtelenül csökkenő geometriai progresszió összege képlet segítségével találhatjuk meg
.

III . Megértés és konszolidáció(feladatok elvégzése).

2. feladat. Határozzuk meg egy végtelenül csökkenő geometriai progresszió összegét, ahol az első tag 3, a második tag pedig 0,3.

Megoldás:

3. feladat. tankönyv, 160. o., 433. sz. (1)

Keresse meg egy végtelenül csökkenő geometriai progresszió összegét:

Megoldás:

4. feladat. Írjuk fel a 0,(5) végtelen periodikus tizedes törtet köztörtként!

1. módszer. Legyen x=0,(5)= 0,555... / 10 2. módszer. 0,(5)=0,555…=

5. feladat. tankönyv, 162. o., 445. szám (3) (önálló megoldás)

Írjuk fel a 0,(12) végtelen periodikus tizedes törtet köztörtként!

Válasz: 0,(12)= 4/33.

IV . Összegzés.

Milyen sorozattal ismerkedtél meg ma?

Határozzon meg egy végtelenül csökkenő geometriai progressziót.

Hogyan bizonyítható, hogy a geometriai haladás végtelenül csökken?

Adja meg a végtelenül csökkenő geometriai progresszió összegének képletét!

V . Házi feladat.

SZÁMSZORZAT VI

l48. §. Egy végtelenül csökkenő geometriai progresszió összege

Eddig, amikor összegekről beszéltünk, mindig azt feltételeztük, hogy ezekben az összegekben a tagok száma véges (például 2, 15, 1000 stb.). De bizonyos problémák (különösen a felsőbb matematika) megoldása során végtelen számú tag összegével kell számolni.

S= a 1 + a 2 + ... + a n + ... . (1)

Mik ezek az összegek? A-priory végtelen számú tag összege a 1 , a 2 , ..., a n , ... az S összeg határának nevezzük n első P számok mikor P -> ∞ :

S=S n = (a 1 + a 2 + ... + a n ). (2)

Limit (2) természetesen létezhet vagy nem. Ennek megfelelően azt mondják, hogy az (1) összeg létezik vagy nem létezik.

Hogyan tudhatjuk meg, hogy minden konkrét esetben létezik-e az (1) összeg? Közös döntés Ez a kérdés messze túlmutat programunk keretein. Van azonban egy fontos különleges eset, amelyet most figyelembe kell vennünk. Egy végtelenül csökkenő geometriai progresszió tagjainak összegzéséről lesz szó.

Hadd a 1 , a 1 q , a 1 q 2, ... egy végtelenül csökkenő geometriai progresszió. Ez azt jelenti, hogy | q |< 1. Сумма первых P ennek a progressziónak a feltételei egyenlőek

A változók határaira vonatkozó alaptételekből (lásd 136. §) a következőket kapjuk:

De 1 = 1, a qn = 0. Ezért

Tehát egy végtelenül csökkenő geometriai haladás összege egyenlő ennek a haladásnak az első tagjával, osztva eggyel, mínusz ennek a progressziónak a nevezője.

1) Az 1, 1/3, 1/9, 1/27, ... geometriai haladás összege egyenlő

és a geometriai progresszió összege 12; -6; 3; - 3/2, ... egyenlő

2) Alakítson át egy 0,454545 ... egyszerű periodikus törtet közönségessé.

A probléma megoldásához képzeljük el ezt a törtet végtelen összegként:

Ennek az egyenlőségnek a jobb oldala egy végtelenül csökkenő geometriai progresszió összege, amelynek első tagja 45/100, nevezője pedig 1/100. Ezért

A leírt módszerrel azt is be lehet szerezni Általános szabály egyszerű periodikus törtek átalakítása közönséges törtekké (lásd II. fejezet, 38. §):

Egy egyszerű periódusos tört közönséges törté konvertálásához a következőket kell tennie: tegye a pontot a számlálóba decimális, és a nevező egy olyan kilencből álló szám, amelyet annyiszor vesznek fel, ahány számjegy van a tizedes tört periódusában.

3) Alakítsa át a 0,58333 .... vegyes periodikus törtet közönséges törtté.

Képzeljük el ezt a törtet végtelen összegként:

Ennek az egyenlőségnek a jobb oldalán minden tag, 3/1000-től kezdve, végtelenül csökkenő geometriai progressziót alkot, amelynek első tagja 3/1000, nevezője pedig 1/10. Ezért

A leírt módszerrel a vegyes periodikus törtek közönséges törtekké való átalakításának általános szabálya érhető el (lásd II. fejezet, 38. §). Szándékosan nem mutatjuk be itt. Nem kell emlékezni erre a nehézkes szabályra. Sokkal hasznosabb tudni, hogy bármely kevert periodikus tört ábrázolható egy végtelenül csökkenő geometriai progresszió és egy bizonyos szám összegeként. És a képlet

egy végtelenül csökkenő geometriai progresszió összegéhez természetesen emlékezned kell.

Gyakorlatként azt javasoljuk, hogy az alább közölt 995-1000. számú feladatokon kívül még egyszer forduljon a 301. számú feladat 38. §-ához.

Feladatok

995. Mit nevezünk egy végtelenül csökkenő geometriai progresszió összegének?

996. Határozza meg a végtelenül csökkenő geometriai progressziók összegét:

997. Milyen értékeken x progresszió

végtelenül csökken? Keresse meg egy ilyen haladás összegét.

998.V egyenlő oldalú háromszög az oldalával A egy új háromszöget írunk fel oldalai felezőpontjainak összekapcsolásával; ebbe a háromszögbe ugyanúgy új háromszöget írunk, és így tovább a végtelenségig.

a) ezen háromszögek kerületeinek összege;

b) területeik összege.

999. Négyzet oldallal A új négyzetet írunk fel oldalai felezőpontjainak összekapcsolásával; ebbe a négyzetbe ugyanúgy négyzetet írnak, és így tovább a végtelenségig. Határozzuk meg ezen négyzetek kerületének összegét és területük összegét!

1000. Állítsunk össze egy végtelenül csökkenő geometriai progressziót úgy, hogy összege 25/4, tagjai négyzetösszege pedig 625/24 legyen.

Tekintsük most egy végtelen geometriai progresszió összegzésének kérdését. Nevezzük egy adott végtelen haladás részösszegét az első tagok összegének. Jelöljük a részösszeget szimbólummal

Minden végtelen fejlődéshez

részösszegeiből összeállíthatunk egy (szintén végtelen) sorozatot

A korlátlan növekedésű sorozatnak legyen határa

Ebben az esetben az S számot, azaz egy progresszió részösszegeinek határát végtelen progresszió összegének nevezzük. Bebizonyítjuk, hogy a végtelenül csökkenő geometriai haladásnak mindig van összege, és ennek az összegnek egy képletét fogjuk levezetni (azt is megmutathatjuk, hogy ha egy végtelen haladásnak nincs összege, akkor nem létezik).

Írjuk fel a részösszeg kifejezését a (91.1) képlet segítségével a progresszió tagjainak összegeként, és tekintsük a részösszeg határát

A 89. tételből ismert, hogy csökkenő progresszió esetén; ezért a különbséghatártételt alkalmazva azt találjuk

(itt is érvényes a szabály: a konstans tényezőt a határjelen túlra vesszük). A létezés bizonyítást nyer, és egyúttal megkapjuk a végtelenül csökkenő geometriai progresszió összegének képletét:

Az egyenlőség (92,1) a formába is írható

Itt paradoxnak tűnhet, hogy az összeg végtelen szám a kifejezésekhez nagyon határozott végső értéket rendelnek.

Világos szemléltetéssel magyarázható ez a helyzet. Vegyünk egy négyzetet oldallal egyenlő eggyel(72. ábra). Osszuk ezt a négyzetet vízszintes vonallal két egyenlő részre és felső rész Vigye fel az alsóra úgy, hogy egy téglalap képződjön a 2 és a oldalú oldalakkal. Ezután ennek a téglalapnak a jobb felét ismét kettéosztjuk egy vízszintes vonallal, és a felső részt az alsóhoz rögzítjük (a 72. ábra szerint). Folytatva ezt a folyamatot, az eredeti, 1-es területű négyzetet folyamatosan egyforma méretű figurákká alakítjuk (egy ritkító lépcsős lépcső formáját öltve).

Ennek a folyamatnak a végtelen folytatásával a négyzet teljes területe végtelen számú tagra bomlik - az 1-es alappal és magassággal rendelkező téglalapok területére. A téglalapok területei pontosan végtelenül csökkenő progressziót alkotnak, ennek összege

azaz, ahogy az várható is, megegyezik a tér területével.

Példa. Határozzuk meg a következő végtelen folyamatok összegét:

Megoldás, a) Észrevesszük, hogy ez a progresszió Ezért a (92.2) képlet segítségével azt találjuk

b) Itt azt jelenti, hogy ugyanazt a (92.2) képletet használjuk

c) Azt találjuk, hogy ennek a progressziónak nincs összege.

Az 5. bekezdésben egy végtelenül csökkenő progresszió tagok összegére vonatkozó képlet alkalmazását mutattuk be egy periodikus tizedes tört közönséges törtté való átalakítására.

Feladatok

1. Egy végtelenül csökkenő geometriai progresszió összege 3/5, első négy tagjának összege 13/27. Keresse meg a progresszió első tagját és nevezőjét!

2. Keressen négy olyan számot, amelyek egy váltakozó geometriai sorozatot alkotnak, amelyekben a második tag 35-tel kisebb, mint az első, a harmadik pedig 560-al nagyobb, mint a negyedik.

3. Mutassuk meg, hogy ha a sorozat

végtelenül csökkenő geometriai progressziót alkot, majd a sorozat

bármelyiknél végtelenül csökkenő geometriai progressziót alkot. Vajon igaz lesz-e ez az állítás, amikor

Vezess le egy képletet a geometriai progresszió tagjainak szorzatára!

A geometriai progresszió az az újfajta numerikus sorozat, amellyel hamarosan megismerkedünk. A sikeres randevúzáshoz nem árt legalább ismerni és megérteni. Akkor nem lesz probléma a geometriai haladással.)

Mi a geometriai progresszió? A geometriai progresszió fogalma.

A túrát szokás szerint az alapokkal kezdjük. Írok egy befejezetlen számsort:

1, 10, 100, 1000, 10000, …

Meg tudod találni a mintát, és meg tudod mondani, hogy mely számok jönnek ezután? A paprika tiszta, ezután következnek a 100 000, 1 000 000 és így tovább a számok. Még sok szellemi erőfeszítés nélkül is minden világos, igaz?)

RENDBEN. Egy másik példa. Ezt a sorrendet írom le:

1, 2, 4, 8, 16, …

Meg tudja mondani, hogy melyik szám következik a 16-os szám és a név után? nyolcadik sorozat tagja? Ha kitaláltad, hogy ez a 128-as szám, akkor nagyon jó. Tehát a csata fele a megértésben van érzékÉs Főbb pontok A geometriai progresszió már megtörtént. tovább nőhetsz.)

És most ismét áttérünk a szenzációkról a szigorú matematikára.

A geometriai progresszió kulcspontjai.

Kulcspont #1

A geometriai progresszió az számsor.Így a progresszió is. Semmi csicsás. Csak ez a sorrend van elrendezve eltérően. Ezért természetesen más a neve, igen...

Kulcspont #2

A második kulcsponttal a kérdés bonyolultabb lesz. Menjünk vissza egy kicsit, és emlékezzünk az aritmetikai progresszió legfontosabb tulajdonságára. Itt van: minden tag különbözik az előzőtől ugyanennyivel.

Lehetséges-e hasonló kulcstulajdonságot megfogalmazni egy geometriai progresszióhoz? Gondolkozz egy kicsit... Nézze meg közelebbről a megadott példákat. Kitaláltad? Igen! Geometriai progresszióban (bármilyen!) minden tagja eltér az előzőtől ugyanannyiszor. Mindig!

Az első példában ez a szám tíz. Bármelyik tagot is választja a sorozatnak, az nagyobb, mint az előző tízszer.

A második példában ez egy kettő: mindegyik tag nagyobb, mint az előző kétszer.

Ez a kulcsfontosságú pont, hogy a geometriai progresszió különbözik az aritmetikai progressziótól. A számtani sorozatban minden következő tagot kapunk hozzáadásával ugyanaz az érték, mint az előző tag. És itt - szorzás az előző futamidőt ugyanennyivel. Ez az egész különbség.)

Kulcspont #3

Ez a kulcspont teljesen azonos az aritmetikai progresszióéval. Ugyanis: A geometriai progresszió minden tagja a helyén áll. Minden pontosan ugyanaz, mint a számtani sorozatban, és a megjegyzések szerintem feleslegesek. Van az első tag, van a százelső stb. Cseréljünk fel legalább két tagot – a minta (és vele együtt a geometriai progresszió) eltűnik. Ami megmarad, az csak egy számsor, minden logika nélkül.

Ez minden. Ez a geometriai progresszió lényege.

Kifejezések és megnevezések.

De most, miután megértettük a geometriai progresszió jelentését és kulcspontjait, továbbléphetünk az elméletre. Egyébként mi az elmélet a jelentés megértése nélkül, igaz?

Hogyan jelöljük a geometriai progressziót?

Hogyan írják le a geometriai progressziót? Általános nézet? Nincs mit! A progresszió minden tagja betűként is meg van írva. Csak az aritmetikai progresszióhoz, általában a betűt használják "A", geometrikusnak – betű "b". Tag szám, mint általában, jelzi index a jobb alsó sarokban. Egyszerűen felsoroljuk magukat a progresszió tagjait, vesszővel vagy pontosvesszővel elválasztva.

Mint ez:

b 1,b 2 , b 3 , b 4 , b 5 , b 6 , …

Röviden ezt a folyamatot a következőképpen írjuk: (b n) .

Vagy így, véges előrehaladáshoz:

b 1, b 2, b 3, b 4, b 5, b 6.

b 1, b 2, …, b 29, b 30.

Vagy röviden:

(b n), n=30 .

Valójában ez az összes megjelölés. Minden ugyanaz, csak a betű más, igen.) És most közvetlenül a definícióra térünk át.

A geometriai progresszió definíciója.

A geometriai progresszió olyan számsorozat, amelyben az első tag nem nulla, és minden további tag egyenlő az előző taggal, megszorozva ugyanazzal a nullától eltérő számmal.

Ez az egész definíció. A legtöbb szó és kifejezés világos és ismerős az Ön számára. Ha természetesen megérti a geometriai progresszió jelentését „az ujjain” és általában. De van néhány új mondat is, amelyekre külön figyelmet szeretnék fordítani.

Először is a szavak: "amelynek az első tagja nem nulla".

Ezt a korlátozást az első ciklusban nem véletlenül vezették be. Mit gondolsz, mi fog történni, ha az első tag b 1 egyenlő lesz a nullával? Mivel lesz egyenlő a második tag, ha mindegyik tag nagyobb, mint az előző? ugyanannyiszor? Mondjuk háromszor? Nézzük... Szorozzuk meg az első tagot (azaz 0-t) 3-mal, és kapjunk... nullát! Mi a helyzet a harmadik taggal? Szintén nulla! És a negyedik tag is nulla! Stb…

Csak kapunk egy zacskó bagelt, nullák sorozatát:

0, 0, 0, 0, …

Természetesen egy ilyen sorozatnak joga van az élethez, de gyakorlati érdeke nincs. Minden tiszta. Bármely tagja nulla. Tetszőleges számú tag összege is nulla... Milyen érdekességeket lehet vele kezdeni? Semmi…

A következő kulcsszavak: "ugyanazzal a nullától eltérő számmal szorozva."

Ennek a számnak külön neve is van - a geometriai progresszió nevezője. Kezdjük az ismerkedést.)

Geometriai progresszió nevezője.

Minden olyan egyszerű, mint a körte pucolása.

A geometriai progresszió nevezője egy nem nulla szám (vagy mennyiség), amely azt jelzi hányszora progresszió minden tagját több, mint az előző.

Ismét a számtani progresszió analógiájára, kulcsszó Ebben a meghatározásban a szóra kell figyelni "több". Ez azt jelenti, hogy a geometriai progresszió minden tagját megkapjuk szorzás pont erre a nevezőre előző tag.

Hadd magyarázzam.

A számításhoz mondjuk második fasz, venni kell első tagja és szaporodnak azt a nevezőre. Számításhoz tizedik fasz, venni kell kilencedik tagja és szaporodnak azt a nevezőre.

Maga a geometriai progresszió nevezője bármi lehet. Teljesen bárki! Egész, töredékes, pozitív, negatív, irracionális – minden. Kivéve a nullát. Ezt mondja nekünk a definícióban szereplő „nem nulla” szó. Miért van szükség erre a szóra - erről később.

A geometriai progresszió nevezője leggyakrabban a levél jelzi q.

Hogyan lehet megtalálni q? Nincs mit! A progresszió bármely tagját fel kell vennünk és osztjuk az előző taggal. Az osztály az töredék. Innen a név - „progressziós nevező”. A nevező, általában törtben ül, igen...) Bár logikusan az érték q hívni kell magán geometriai progresszió, hasonló különbség számtani progresszióhoz. De megegyeztünk, hogy felhívjuk névadó. És a kereket sem fogjuk újra feltalálni.)

Határozzuk meg például a mennyiséget q ehhez a geometriai haladáshoz:

2, 6, 18, 54, …

Minden elemi. Vegyük Bármi sorszám. Azt veszünk, amit akarunk. Kivéve a legelsőt. Például 18. És oszd el előző szám. Vagyis 6-kor.

Kapunk:

q = 18/6 = 3

Ez minden. Ez a helyes válasz. Ennél a geometriai progressziónál a nevező három.

Most keressük meg a nevezőt q egy másik geometriai progresszióhoz. Például ez:

1, -2, 4, -8, 16, …

Minden a régi. Nem számít, milyen jelei vannak maguknak a tagoknak, mi továbbra is elfogadjuk Bármi a sorozat számát (például 16), és oszd el vele előző szám(azaz -8).

Kapunk:

d = 16/(-8) = -2

És ennyi.) A progresszió nevezője ezúttal negatívnak bizonyult. Mínusz kettő. Megtörténik.)

Vegyük most ezt a folyamatot:

1, 1/3, 1/9, 1/27, …

És ismét, függetlenül a sorozatban szereplő számok típusától (egész számok, páros törtek, akár negatív, akár irracionális), tetszőleges számot veszünk (például 1/9), és elosztjuk az előző számmal (1/3). Természetesen a törtekkel való munka szabályai szerint.

Kapunk:

Ennyi.) Itt a nevező törtnek bizonyult: q = 1/3.

Mi a véleményed erről a "fejlődésről"?

3, 3, 3, 3, 3, …

Nyilvánvalóan itt q = 1 . Formailag ez is geometriai progresszió, csak azzal azonos tagok.) De az ilyen progresszió a tanulmányozás és praktikus alkalmazás nem érdekes. Ugyanaz, mint a folyamatos nullákkal végzett progresszió. Ezért nem vesszük figyelembe őket.

Mint látható, a progresszió nevezője bármi lehet - egész, tört, pozitív, negatív - bármi! Nem lehet csak nulla. Nem tudod kitalálni, miért?

Nos, menjünk néhányhoz konkrét példa Lássuk, mi történik, ha nevezőt vesszük q nulla.) Legyen például nekünk b 1 = 2 , A q = 0 . Akkor mivel lesz egyenlő a második tag?

Számítunk:

b 2 = b 1 · q= 2 0 = 0

Mi a helyzet a harmadik taggal?

b 3 = b 2 · q= 0 0 = 0

A geometriai folyamatok típusai és viselkedése.

Minden többé-kevésbé világos volt: ha a progresszió különbség d pozitív, akkor a progresszió növekszik. Ha a különbség negatív, akkor a progresszió csökken. Csak két lehetőség van. Nincs harmadik.)

De a geometriai progresszió viselkedésével minden sokkal érdekesebb és változatosabb lesz!)

Nem számít, hogyan viselkednek itt a kifejezések: növekednek, csökkennek, és végtelenül közelítenek a nullához, sőt előjeleket is váltanak, felváltva „pluszba”, majd „mínuszba” vetve magukat! És ebben a sokféleségben jól kell tudni érteni, igen...

Találjuk ki?) Kezdjük a legegyszerűbb esettel.

A nevező pozitív ( q >0)

Pozitív nevező esetén először is a geometriai progresszió tagjai léphetnek be plusz a végtelen(vagyis korlátlanul növelhető) és mehet bele mínusz végtelen(vagyis korlátlanul csökkenteni). Már megszoktuk a progressziónak ezt a viselkedését.

Például:

(b n): 1, 2, 4, 8, 16, …

Itt minden egyszerű. A progresszió minden tagját megkapjuk több, mint az előző. Sőt, minden kifejezés kiderül szorzás előző tag bekapcsolva pozitív szám +2 (pl. q = 2 ). Egy ilyen progresszió viselkedése nyilvánvaló: a progresszió minden tagja korlátlanul nő, az űrbe kerülve. Plusz a végtelen...

És most íme a fejlemény:

(b n): -1, -2, -4, -8, -16, …

Itt is megkapjuk a progresszió minden tagját szorzás előző tag bekapcsolva pozitív szám +2. De egy ilyen progresszió viselkedése pontosan az ellenkezője: a progresszió minden tagját megkapjuk kevesebb, mint az előző, és minden tagja korlátlanul csökken, mínusz végtelenig.

Most pedig gondoljuk át: mi a közös ebben a két folyamatban? Így van, nevező! Itt-ott q = +2 . Pozitív szám. Kettő. És itt viselkedés Ez a két folyamat alapvetően különbözik egymástól! Nem tudod kitalálni, miért? Igen! Minden arról szól első tag!Ő szólítja a dallamot, ahogy mondani szokták.) Nézze meg maga.

Az első esetben a progresszió első tagja pozitív(+1), és ezért az összes további kifejezés, amelyet a -val szorozva kapunk pozitív névadó q = +2 , is lesz pozitív.

De a második esetben az első kifejezés negatív(-1). Ezért a progresszió minden további tagját úgy kapjuk meg, hogy megszorozzuk pozitív q = +2 , is meg lesz szerezve negatív. Mert a „mínusz” a „plusz” közé mindig „mínuszt” ad, igen.)

Amint láthatja, az aritmetikai sorozattól eltérően a geometriai sorozat nem csak attól függően viselkedhet, a nevezőtőlq, hanem attól is függ az első tagtól, Igen.)

Ne feledje: a geometriai progresszió viselkedését egyedileg meghatározza az első tag b 1 és nevezőq .

És most elkezdjük elemezni a kevésbé ismert, de sokkal érdekesebb eseteket!

Vegyük például ezt a sorozatot:

(b n): 1, 1/2, 1/4, 1/8, 1/16, …

Ez a sorozat is egy geometriai progresszió! Ennek a progressziónak minden tagja ki is derül szorzás az előző tag, ugyanazzal a számmal. Ez csak egy szám... tört: q = +1/2 . Vagy +0,5 . Sőt (fontos!) a szám egynél kevesebb:q = 1/2<1.

Miért érdekes ez a geometriai progresszió? Merre tartanak a tagjai? Nézzük meg:

1/2 = 0,5;

1/4 = 0,25;

1/8 = 0,125;

1/16 = 0,0625;

…….

Milyen érdekességeket lehet itt észrevenni? Először is azonnal észrevehető a progresszió csökkenése: minden tagja Kevésbé pontosan az előzőt 2 alkalommal. Vagy a geometriai progresszió definíciója szerint minden tag több előző 1/2 alkalommal, mert progresszió nevezője q = 1/2 . És ha megszorozzuk egynél kisebb pozitív számmal, az eredmény általában csökken, igen...

Mit több látható ennek a progressziónak a viselkedésén? Csökkennek a tagjai? korlátlan, mínusz végtelenbe megy? Nem! Különleges módon tűnnek el. Eleinte elég gyorsan csökkennek, majd egyre lassabban. És miközben állandóan megmaradt pozitív. Bár nagyon-nagyon kicsi. És ők maguk mire törekednek? Nem tippelted? Igen! A nulla felé törekednek!) Sőt, figyelj, a mi progressziónk tagjai nulláról származnak soha ne érd el! Csak végtelenül közel közeledik hozzá. Ez nagyon fontos.)

Hasonló helyzet fordul elő a következő folyamatban:

(b n): -1, -1/2, -1/4, -1/8, -1/16, …

Itt b 1 = -1 , A q = 1/2 . Minden a régi, csak most a másik oldalról, alulról közelítenek a feltételek a nullához. Állandóan maradni negatív.)

Olyan geometriai progresszió, amelynek feltételei korlátlanul közeledik a nullához(nem számít pozitív vagy negatív oldalról), a matematikában különleges neve van - végtelenül csökkenő geometriai progresszió. Ez a folyamat annyira érdekes és szokatlan, hogy még szóba is kerül külön leckét .)

Tehát mindent megfontoltunk, ami lehetséges pozitív a nevezők nagyok és kisebbek is. Magát az egységet nem tekintjük nevezőnek a fentebb említett okok miatt (emlékezzünk a hármassoros példára...)

Összefoglaljuk:

pozitívÉs több mint egy (q>1), akkor a progresszió feltételei:

a) korlátlanul növeli (hab 1 >0);

b) korlátlanul csökkenteni (hab 1 <0).

Ha a geometriai progresszió nevezője pozitív És egynél kevesebb (0< q<1), то члены прогрессии:

a) végtelenül közel nullához felett(Hab 1 >0);

b) végtelenül közelít a nullához alulról(Hab 1 <0).

Most az esetet kell megvizsgálni negatív nevező.

A nevező negatív ( q <0)

Nem megyünk messzire a példával. Miért pont bozontos nagymama?!) Legyen például a progresszió első tagja b 1 = 1 , és vegyük a nevezőt q = -2.

A következő sorrendet kapjuk:

(b n): 1, -2, 4, -8, 16, …

És így tovább.) A progresszió minden tagját megkapjuk szorzás előző tag bekapcsolva negatív szám-2. Ebben az esetben minden páratlan helyen álló tag (első, harmadik, ötödik stb.) az lesz pozitív, és páros helyeken (második, negyedik stb.) – negatív. A jelek szigorúan váltakoznak. Plusz-mínusz-plusz-mínusz... Ezt a geometriai progressziót - növekvő jel váltakozó.

Merre tartanak a tagjai? De sehol.) Igen, abszolút értékben (azaz modulo) progressziónk tagjai korlátlanul növekednek (innen ered a „növekedés” elnevezés). De ugyanakkor a progresszió minden tagja felváltva dob a melegbe, majd a hidegbe. Vagy „plusz” vagy „mínusz”. Ingadozó a fejlődésünk... Ráadásul az ingadozások köre minden lépéssel rohamosan növekszik, igen.) Ezért a progresszió tagjainak törekvései valahova eljutnak kimondottan Itt Nem. Sem plusz végtelenhez, sem mínusz végtelenhez, sem nullához - sehol.

Nézzünk most valami tört nevezőt nulla és mínusz egy között.

Például legyen b 1 = 1 , A q = -1/2.

Ezután megkapjuk a progressziót:

(b n): 1, -1/2, 1/4, -1/8, 1/16, …

És megint van egy váltakozó jelünk! Ám az előző példával ellentétben itt már egyértelmű tendencia, hogy a tagok a nullához közelednek.) Csak ezúttal nem szigorúan felülről vagy alulról közelítünk a nullához, hanem megint habozó. Váltakozva pozitív és negatív értékeket vesz fel. De ugyanakkor ők modulok egyre közelebb kerülnek a dédelgetett nullához.)

Ezt a geometriai progressziót ún végtelenül csökkenő jel, váltakozó.

Miért érdekes ez a két példa? És az a tény, hogy mindkét esetben megtörténik jelek váltakozása! Ez a trükk csak a negatív nevezővel rendelkező progressziókra jellemző, igen.) Ezért ha valamelyik feladatban geometriai progresziót látunk váltakozó tagokkal, akkor már biztosan tudni fogja, hogy annak nevezője 100%-ban negatív, és nem fog hibázni. a jelben.)

Egyébként negatív nevező esetén az első tag előjele egyáltalán nem befolyásolja magának a progressziónak a viselkedését. A progresszió első tagjának előjelétől függetlenül a tagok előjele minden esetben betartandó. A kérdés csak az, milyen helyeken(páros vagy páratlan) lesznek bizonyos előjelű tagok.

Emlékezik:

Ha a geometriai progresszió nevezője negatív , akkor a progresszió feltételeinek előjelei mindig váltakozó.

Ugyanakkor maguk a tagok:

a) korlátlanul növelnimodulo, Haq<-1;

b) végtelenül közelít a nullához, ha -1< q<0 (прогрессия бесконечно убывающая).

Ez minden. Minden tipikus esetet elemeztünk.)

A geometriai folyamatok különféle példáinak elemzése során rendszeresen használtam a következő szavakat: "nullára hajlamos", "hajlamos a végtelenségig", "hajlamos mínusz végtelenre"... Rendben van.) Ezek a beszédfigurák (és konkrét példák) csak a kezdeti bevezetés viselkedés sokféle számsorozat. A geometriai progresszió példájával.

Miért kell egyáltalán ismernünk a progresszió viselkedését? Mi a különbség, hogy hova megy? A nulla felé, a plusz végtelenbe, a mínusz végtelenbe... Mit tesz ez velünk?

A helyzet az, hogy már az egyetemen, a felsőbb matematika szakon szüksége lesz arra, hogy a legkülönfélébb numerikus sorozatokkal (bármilyen, nem csak progresszióval!) tudjon dolgozni, és hogy pontosan el tudja képzelni, hogy ez vagy az a sorozat. viselkedik - akár növekszik, akár korlátlanul csökken, akár egy adott számra (és nem feltétlenül nullára) hajlik-e, vagy egyáltalán nem hajlik semmire... A matematika során egy egész részt szentelnek ennek a témának elemzés - határok elmélete.És egy kicsit konkrétabban - a koncepció a számsorozat határa. Nagyon érdekes téma! Érdemes egyetemre menni és rájönni.)

Néhány példa ebből a szakaszból (korlátozott sorozatok), és különösen, végtelenül csökkenő geometriai progresszió Az iskolában kezdik megszokni. Kezdjük megszokni.)

Ezenkívül a sorozatok viselkedésének jól tanulmányozása nagy hasznot hoz a jövőben, és nagyon hasznos lesz funkciókutatás. A legváltozatosabb. De az a képesség, hogy kompetens módon dolgozzon a függvényekkel (származékok kiszámítása, teljes tanulmányozása, grafikonjaik felépítése), már drámaian megnöveli matematikai szintjét! Vannak kétségei? Nincs szükség. Emlékezz a szavaimra is.)

Nézzük a geometriai progressziót az életben?

A körülöttünk lévő életben nagyon-nagyon gyakran találkozunk geometriai progresszióval. Még anélkül is, hogy tudnánk.)

Például a különféle mikroorganizmusok, amelyek mindenhol hatalmas mennyiségben vesznek körül minket, és amelyeket mikroszkóp nélkül sem láthatunk, pontosan geometriai progresszióban szaporodnak.

Tegyük fel, hogy egy baktérium felére osztva szaporodik, így 2 baktériumra hoz utódokat. Viszont mindegyikük, amikor szaporodnak, szintén felére oszlik, így 4 baktérium közös utódját adják. A következő generáció 8 baktériumot fog termelni, majd 16 baktériumot, 32, 64 és így tovább. Minden következő generációval a baktériumok száma megduplázódik. Tipikus példa a geometriai progresszióra.)

Ezenkívül egyes rovarok – levéltetvek és legyek – exponenciálisan szaporodnak. És néha a nyulak is, egyébként.)

A geometriai progresszió másik, a mindennapi élethez közelebb álló példája az ún kamatos kamat. Ez az érdekes jelenség gyakran megtalálható a bankbetéteknél, és ún kamat tőkésítése. Ami?

Maga persze még fiatal. Iskolában tanulsz, bankba nem jársz. De a szüleid már felnőttek és független emberek. Elmennek dolgozni, pénzt keresnek a mindennapi kenyerükre, és a pénz egy részét beteszik a bankba, így spórolnak.)

Tegyük fel, hogy édesapja szeretne egy bizonyos összeget megtakarítani egy családi nyaralásra Törökországban, és 50 000 rubelt helyez el a bankban évi 10%-os áron három évre. éves kamatkapitalizációval. Ráadásul ezalatt az egész időszak alatt semmit nem lehet tenni a letéttel. A számláról sem pótolni, sem pénzt nem lehet felvenni. Mennyi haszna lesz ez után a három év után?

Nos, először is ki kell találnunk, hogy mennyi az évi 10%. Ez azt jelenti egy évben A bank 10%-ot ad hozzá a kezdeti betét összegéhez. Honnan? Természetesen attól kezdeti befizetés összege.

A számla méretét egy év után számítjuk ki. Ha a kezdeti betét összege 50 000 rubel (azaz 100%) volt, akkor egy év múlva mennyi kamata lesz a számlán? Így van, 110%! 50 000 rubeltől.

Tehát 50 000 rubel 110%-át számítjuk ki:

50000·1,1 = 55000 rubel.

Remélem megérted, hogy egy érték 110%-ának megtalálása azt jelenti, hogy ezt az értéket meg kell szorozni 1,1-gyel? Ha nem érti, miért van ez így, emlékezzen az ötödik és hatodik osztályra. Ugyanis – kapcsolat a százalékok és a törtek és részek között.)

Így a növekedés az első évben 5000 rubel lesz.

Mennyi pénz lesz a számlán két év múlva? 60 000 rubel? Sajnos (vagy inkább szerencsére) nem minden ilyen egyszerű. A kamattőkésítés teljes trükkje az, hogy minden újabb kamatfelhalmozáskor ugyanazokat a kamatokat már figyelembe veszik az új összegből! Attól, aki már a számlán van Pillanatnyilag. Az előző időszakra felhalmozott kamat pedig hozzáadódik az eredeti betét összegéhez, és így maga is részt vesz az új kamat számításában! Vagyis a teljes számla teljes részévé válnak. Vagy általános főváros. Innen ered a neve - kamat tőkésítése.

Ez a közgazdaságtanban van. A matematikában pedig az ilyen százalékokat nevezik kamatos kamat. Vagy százalékos kamat.) A trükkjük az, hogy szekvenciális számításnál minden alkalommal a százalékokat számítják ki az új értéktől.És nem az eredetiből...

Ezért az összeg kiszámításához keresztül két év, a számlán lévő összeg 110%-át kell kiszámítanunk egy évben. Vagyis már 55 000 rubeltől.

55 000 rubel 110%-át számoljuk:

55000·1,1 = 60500 rubel.

Ez azt jelenti, hogy a százalékos növekedés a második évben 5500 rubel, két évre pedig 10 500 rubel lesz.

Most már sejtheti, hogy három év után a számlán lévő összeg 60 500 rubel 110% -a lesz. Ez megint 110% az előzőtől (tavaly)összegeket.

Itt gondoljuk:

60500·1,1 = 66550 rubel.

Most a pénzösszegeket évenkénti sorrendbe rendezzük:

50000;

55000 = 50000 1,1;

60500 = 55000·1,1 = (50000·1,1)·1,1;

66550 = 60500 1,1 = ((50000 1,1) 1,1) 1,1

Szóval hogy is van ez? Miért nem geometriai progresszió? Első tag b 1 = 50000 , és a nevező q = 1,1 . Mindegyik kifejezés szigorúan 1,1-szer nagyobb, mint az előző. Minden szigorúan összhangban van a definícióval.)

És hány további kamatbónuszt „halmoz fel” apád, miközben 50 000 rubele három éve a bankszámláján hever?

Számítunk:

66550 – 50000 = 16550 rubel

Persze nem sokat. De ez akkor van, ha a kezdeti befizetés összege kicsi. Mi van, ha több van? Mondjuk nem 50, hanem 200 ezer rubelt? Ezután a növekedés három év alatt 66 200 rubel lesz (ha számolsz). Ami már nagyon jó.) Mi van, ha a hozzájárulás még nagyobb? Ez az...

Következtetés: minél magasabb az induló betét, annál jövedelmezőbb a kamatkapitalizáció. Ezért a bankok hosszú távra biztosítják a kamattőkésített betéteket. Mondjuk öt évig.

Emellett mindenféle rossz betegség, mint az influenza, a kanyaró és a még szörnyűbb betegségek (ugyanaz a SARS a 2000-es évek elején vagy a pestis a középkorban) szeretnek exponenciálisan terjedni. Innen a járványok léptéke, igen...) És mindez annak köszönhető, hogy a geometriai progresszió -val egész pozitív nevező (q>1) – olyan dolog, ami nagyon gyorsan növekszik! Emlékezzen a baktériumok szaporodására: egy baktériumból kettő, kettőből négy, négyből nyolc és így tovább... Ugyanez vonatkozik minden fertőzés terjedésére.)

A geometriai progresszió legegyszerűbb feladatai.

Kezdjük, mint mindig, egy egyszerű problémával. Pusztán a jelentés megértéséhez.

1. Ismeretes, hogy a geometriai progresszió második tagja 6, a nevező pedig -0,5. Keresse meg az első, harmadik és negyedik kifejezést.

Tehát megadatott nekünk végtelen geometriai progresszió, de ismert második időszak ez a fejlődés:

b 2 = 6

Ezen kívül azt is tudjuk progresszió nevezője:

q = -0,5

És meg kell találni első, harmadikÉs negyedik ennek a fejlődésnek a tagjai.

Tehát cselekszünk. Felírjuk a sorrendet a feladat feltételei szerint. Közvetlenül általános formában, ahol a második tag hat:

b 1, 6,b 3 , b 4 , …

Most kezdjük el a keresést. Kezdjük, mint mindig, a legegyszerűbbel. Kiszámolhatja például a harmadik tagot b 3? Tud! Te és én már tudjuk (közvetlenül a geometriai progresszió értelmében), hogy a harmadik tag (b 3) több mint a második (b 2 ) V "q" egyszer!

Tehát ezt írjuk:

b 3 =b 2 · q

E kifejezés helyett hatot helyettesítünk b 2és helyette -0,5 qés számolunk. És persze a mínuszokat sem hagyjuk figyelmen kívül...

b3 = 6·(-0,5) = -3

Mint ez. A harmadik kifejezés negatívnak bizonyult. Nem csoda: a mi nevezőnk q– negatív. És a pluszt mínuszral megszorozva természetesen mínusz lesz.)

Most számoljuk a progresszió következő, negyedik tagját:

b 4 =b 3 · q

b 4 = -3·(-0,5) = 1,5

A negyedik tag ismét pluszban van. Az ötödik tag ismét mínusz, a hatodik plusz, és így tovább. A jelek váltakoznak!

Tehát a harmadik és a negyedik kifejezést megtaláltuk. Az eredmény a következő sorrend:

b 1; 6; -3; 1,5; ...

Most már csak az első kifejezést kell megtalálni b 1 a jól ismert második szerint. Ehhez a másik irányba, balra lépünk. Ez azt jelenti, hogy ebben az esetben nem kell a progresszió második tagját megszoroznunk a nevezővel, hanem feloszt.

Osztjuk és megkapjuk:

Ez minden.) A probléma válasza a következő lesz:

-12; 6; -3; 1,5; …

Mint látható, a megoldási elv ugyanaz, mint a -ban. Tudjuk Bármi tagja és névadó geometriai progresszió - bármely más tagját megtalálhatjuk. Megtaláljuk a kívántat.) Az egyetlen különbség az, hogy az összeadást/kivonást felváltja a szorzás/osztás.

Ne feledje: ha ismerjük egy geometriai sorozat legalább egy tagját és nevezőjét, akkor mindig megtaláljuk ennek a progressziónak bármely másik tagját.

A következő probléma a hagyomány szerint az OGE valódi verziójából származik:

2.

...; 150; X; 6; 1,2; ...

Szóval hogy is van ez? Ezúttal nincs első tag, nincs nevező q, csak egy számsor van megadva... Valami már ismerős, igaz? Igen! Hasonló feladatot már megoldottak a számtani haladásban!

Tehát nem félünk. Minden a régi. Fordítsuk meg a fejünket, és emlékezzünk a geometriai progresszió elemi jelentésére. Figyelmesen megnézzük a sorozatunkat, és kitaláljuk, hogy a három fő (első tag, nevező, tagszám) geometriai progressziójának mely paraméterei rejtőznek benne.

Tagszámok? Nincs taglétszám, igen... De van négy egymást követő számok. Nem látom értelmét elmagyarázni, mit jelent ez a szó ebben a szakaszban.) Van-e kettő szomszédos ismert számok? Eszik! Ezek a 6 és 1.2. Tehát megtalálhatjuk progresszió nevezője. Tehát vesszük az 1,2 számot és elosztjuk az előző számra. Hatig.

Kapunk:

Kapunk:

x= 150 · 0,2 = 30

Válasz: x = 30 .

Mint látható, minden nagyon egyszerű. A fő nehézség csak a számításokban van. Különösen nehéz a negatív és a tört nevezők esetében. Tehát akinek problémái vannak, ismételje meg a számolást! Hogyan dolgozzunk törtekkel, hogyan dolgozzunk negatív számokkal, és így tovább... Különben itt kíméletlenül lelassul.

Most módosítsunk egy kicsit a problémán. Ez most érdekes lesz! Távolítsuk el belőle az utolsó 1.2-es számot. Most oldjuk meg ezt a problémát:

3. A geometriai progresszió több egymást követő tagja van kiírva:

...; 150; X; 6; ...

Keresse meg az x betűvel jelzett progresszió tagját!

Minden ugyanaz, csak két szomszédos híres Most nincsenek tagjaink a progressziónak. Ez a fő probléma. Mert a nagyságrend q két szomszédos kifejezésen keresztül könnyen meghatározhatjuk nem tehetjük. Van esélyünk megbirkózni a feladattal? Biztosan!

Írjuk fel az ismeretlen kifejezést" x"közvetlenül a geometriai progresszió értelmében! Általánosságban.

Igen igen! Pontosan ismeretlen nevezővel!

Egyrészt X-re a következő arányt írhatjuk fel:

x= 150·q

Másrészt jogunk van ugyanazt az X-et végig leírni következő tag, a hatoson keresztül! Osszuk el a hatot a nevezővel.

Mint ez:

x = 6/ q

Nyilvánvaló, hogy most egyenlőségjelet tehetünk mindkét arány között. Mivel kifejezzük ugyanaz(x), hanem kettő különböző utak.

Kapjuk az egyenletet:

Mindent megszorozva ezzel q, egyszerűsítve és lerövidítve a következő egyenletet kapjuk:

q2 = 1/25

Megoldjuk és megkapjuk:

q = ±1/5 = ±0,2

Hoppá! A nevező dupla lett! +0,2 és -0,2. És melyiket érdemes választani? Zsákutca?

Nyugodt! Igen, a probléma valóban fennáll két megoldás! Nincs ezzel semmi baj. Előfordul.) Nem csodálkozik, ha például a szokásos probléma megoldása során két gyökeret kap? Itt is ugyanaz a történet.)

Mert q = +0,2 kapunk:

X = 150 0,2 = 30

És azért q = -0,2 akarat:

X = 150·(-0,2) = -30

Kettős választ kapunk: x = 30; x = -30.

Mit jelent ez az érdekes tény? És ami létezik két progresszió, megfelel a probléma feltételeinek!

Mint ezek:

…; 150; 30; 6; …

…; 150; -30; 6; …

Mindkettő megfelelő.) Szerinted miért oszlottak meg a válaszaink? Már csak a progresszió egy meghatározott tagjának kiesése miatt (1,2), hat után jön. A geometriai haladás előző (n-1)-edik és azt követő (n+1)-edik tagjának ismeretében pedig már semmit sem mondhatunk egyértelműen a közöttük álló n-edik tagról. Két lehetőség van: plusz és mínusz.

De nem baj. Általános szabály, hogy a geometriai haladással kapcsolatos feladatokban további információk találhatók, amelyek egyértelmű választ adnak. Mondjuk a szavakat: "váltakozó progresszió" vagy "előrehaladás pozitív nevezővel"és így tovább... Ezek a szavak szolgáljanak támpontként arra vonatkozóan, hogy a végső válasz elkészítésekor melyik plusz vagy mínusz jelet válasszuk. Ha nincs ilyen információ, akkor igen, a feladatnak meglesz két megoldás.)

Most mi magunk döntünk.

4. Határozza meg, hogy a 20-as szám tagja-e egy geometriai sorozatnak:

4 ; 6; 9; …

5. Adott egy váltakozó geometriai progresszió jele:

…; 5; x ; 45; …

Keresse meg a betű által jelzett progresszió tagját! x .

6. Keresse meg a geometriai progresszió negyedik pozitív tagját:

625; -250; 100; …

7. A geometriai progresszió második tagja -360, az ötödik tagja pedig 23,04. Keresse meg ennek a folyamatnak az első tagját.

Válaszok (rendellenesen): -15; 900; Nem; 2.56.

Gratulálok, ha minden sikerült!

Valami nem stimmel? Volt valahol kettős válasz? Olvassa el figyelmesen a feladat feltételeit!

Az utolsó probléma nem oldódik meg? Nincs ott semmi bonyolult.) Közvetlenül a geometriai progresszió jelentése szerint dolgozunk. Nos, rajzolhatsz egy képet. Segít.)

Amint látja, minden elemi. Ha a progresszió rövid. mi van ha hosszú? Vagy nagyon nagy a szükséges tagok száma? Szeretnék az aritmetikai progresszió analógiájával valahogy egy kényelmes képletet kapni, amely megkönnyíti a megtalálást Bármi bármely geometriai progresszió tagja száma szerint. Anélkül, hogy sokszorosára megszoroznánk q. És van egy ilyen képlet!) Részletek a következő leckében.

Óra és előadás a témában: "Számsorozatok. Geometriai progresszió"

Kiegészítő anyagok
Kedves felhasználók, ne felejtsék el megírni észrevételeiket, véleményeiket, kívánságaikat! Az összes anyagot egy vírusirtó program ellenőrizte.

Oktatási segédanyagok és szimulátorok az Integral webáruházban 9. osztályosoknak
Hatványok és gyökök Függvények és gráfok

Srácok, ma egy másik típusú progresszióval fogunk megismerkedni.
A mai óra témája a geometriai progresszió.

Geometriai progresszió

Meghatározás. Geometriai sorozatnak nevezzük azt a numerikus sorozatot, amelyben minden tag a másodiktól kezdve egyenlő az előző és valamilyen rögzített szám szorzatával.
Definiáljuk rekurzívan a sorozatunkat: $b_(1)=b$, $b_(n)=b_(n-1)*q$,
ahol b és q bizonyos megadott számok. A q számot a progresszió nevezőjének nevezzük.

Példa. 1,2,4,8,16... Olyan geometriai sorozat, amelyben az első tag egyenlő eggyel, és $q=2$.

Példa. 8,8,8,8... Egy geometriai sorozat, amelyben az első tag egyenlő nyolcval,
és $q=1$.

Példa. 3,-3,3,-3,3... Geometriai progresszió, amelyben az első tag egyenlő hárommal,
és $q=-1$.

A geometriai progresszió monoton tulajdonságokkal rendelkezik.
Ha $b_(1)>0$, $q>1$,
akkor a sorrend növekszik.
Ha $b_(1)>0$, akkor $0 A sorozatot általában a következő formában jelöljük: $b_(1), b_(2), b_(3), ..., b_(n), ...$.

Csakúgy, mint egy aritmetikai sorozatnál, ha egy geometriai sorozatban az elemek száma véges, akkor a haladást véges geometriai sorozatnak nevezzük.

$b_(1), b_(2), b_(3), ..., b_(n-2), b_(n-1), b_(n)$.
Vegye figyelembe, hogy ha egy sorozat geometriai sorozat, akkor a tagok négyzeteinek sorozata is geometriai folyamat. A második sorozatban az első tag egyenlő: $b_(1)^2$, a nevező pedig egyenlő: $q^2$.

Egy geometriai progresszió n-edik tagjának képlete

A geometriai progresszió analitikus formában is megadható. Lássuk, hogyan kell ezt csinálni:
$b_(1)=b_(1)$.
$b_(2)=b_(1)*q$.
$b_(3)=b_(2)*q=b_(1)*q*q=b_(1)*q^2$.
$b_(4)=b_(3)*q=b_(1)*q^3$.
$b_(5)=b_(4)*q=b_(1)*q^4$.
Könnyen észrevehetjük a mintát: $b_(n)=b_(1)*q^(n-1)$.
Képletünket "egy geometriai progresszió n-edik tagjának képletének" nevezik.

Térjünk vissza példáinkhoz.

Példa. 1,2,4,8,16... Geometriai progresszió, amelyben az első tag egyenlő eggyel,
és $q=2$.
$b_(n)=1*2^(n)=2^(n-1)$.

Példa. 16,8,4,2,1,1/2… Egy geometriai sorozat, amelyben az első tag tizenhat, és $q=\frac(1)(2)$.
$b_(n)=16*(\frac(1)(2))^(n-1)$.

Példa. 8,8,8,8... Olyan geometriai sorozat, amelyben az első tag egyenlő nyolczal, és $q=1$.
$b_(n)=8*1^(n-1)=8$.

Példa. 3,-3,3,-3,3... Olyan geometriai sorozat, amelyben az első tag egyenlő hárommal, és $q=-1$.
$b_(n)=3*(-1)^(n-1)$.

Példa. Adott egy $b_(1), b_(2), …, b_(n), … $ geometriai progresszió.
a) Ismeretes, hogy $b_(1)=6, q=3$. Keresse meg $b_(5)$.
b) Ismeretes, hogy $b_(1)=6, q=2, b_(n)=768$. Keresse meg n.
c) Ismeretes, hogy $q=-2, b_(6)=96$. Keresse meg $b_(1)$.
d) Ismeretes, hogy $b_(1)=-2, b_(12)=4096$. Keresse meg a q-t.

Megoldás.
a) $b_(5)=b_(1)*q^4=6*3^4=486$.
b) $b_n=b_1*q^(n-1)=6*2^(n-1)=768$.
$2^(n-1)=\frac(768)(6)=128$, mivel $2^7=128 => n-1=7; n=8$.
c) $b_(6)=b_(1)*q^5=b_(1)*(-2)^5=-32*b_(1)=96 => b_(1)=-3$.
d) $b_(12)=b_(1)*q^(11)=-2*q^(11)=4096 => q^(11)=-2048 => q=-2$.

Példa. A geometriai progresszió hetedik és ötödik tagjának különbsége 192, a progresszió ötödik és hatodik tagjának összege 192. Határozzuk meg ennek a progressziónak a tizedik tagját.

Megoldás.
Tudjuk, hogy: $b_(7)-b_(5)=192$ és $b_(5)+b_(6)=192$.
Tudjuk még: $b_(5)=b_(1)*q^4$; $b_(6)=b_(1)*q^5$; $b_(7)=b_(1)*q^6$.
Akkor:
$b_(1)*q^6-b_(1)*q^4=192$.
$b_(1)*q^4+b_(1)*q^5=192$.
Kaptunk egy egyenletrendszert:
$\begin(esetek)b_(1)*q^4(q^2-1)=192\\b_(1)*q^4(1+q)=192\end(esetek)$.
Az egyenleteinket egyenlítve a következőket kapjuk:
$b_(1)*q^4(q^2-1)=b_(1)*q^4(1+q)$.
$q^2-1=q+1$.
$q^2-q-2=0$.
Két q megoldást kaptunk: $q_(1)=2, q_(2)=-1$.
Helyettesítse be egymás után a második egyenletet:
$b_(1)*2^4*3=192 => b_(1)=4$.
$b_(1)*(-1)^4*0=192 =>$ nincs megoldás.
Ezt kaptuk: $b_(1)=4, q=2$.
Keressük a tizedik tagot: $b_(10)=b_(1)*q^9=4*2^9=2048$.

Véges geometriai progresszió összege

Legyen véges geometriai progressziónk. Csakúgy, mint egy aritmetikai sorozatnál, számítsuk ki a tagok összegét.

Legyen adott egy véges geometriai progresszió: $b_(1),b_(2),…,b_(n-1),b_(n)$.
Vezessük be a tagok összegének elnevezését: $S_(n)=b_(1)+b_(2)+⋯+b_(n-1)+b_(n)$.
Abban az esetben, ha $q=1$. A geometriai progresszió minden tagja egyenlő az első taggal, ekkor nyilvánvaló, hogy $S_(n)=n*b_(1)$.
Tekintsük most a $q≠1$ esetet.
A fenti összeget szorozzuk meg q-val.
$S_(n)*q=(b_(1)+b_(2)+⋯+b_(n-1)+b_(n))*q=b_(1)*q+b_(2)*q+⋯ +b_(n-1)*q+b_(n)*q=b_(2)+b_(3)+⋯+b_(n)+b_(n)*q$.
Jegyzet:
$S_(n)=b_(1)+(b_(2)+⋯+b_(n-1)+b_(n))$.
$S_(n)*q=(b_(2)+⋯+b_(n-1)+b_(n))+b_(n)*q$.

$S_(n)*q-S_(n)=(b_(2)+⋯+b_(n-1)+b_(n))+b_(n)*q-b_(1)-(b_(2) )+⋯+b_(n-1)+b_(n))=b_(n)*q-b_(1)$.

$S_(n)(q-1)=b_(n)*q-b_(1)$.

$S_(n)=\frac(b_(n)*q-b_(1))(q-1)=\frac(b_(1)*q^(n-1)*q-b_(1)) (q-1)=\frac(b_(1)(q^(n)-1))(q-1)$.

$S_(n)=\frac(b_(1)(q^(n)-1))(q-1)$.

Megkaptuk a véges geometriai haladás összegének képletét.

Példa.
Határozzuk meg egy olyan geometriai folyamat első hét tagjának összegét, amelynek első tagja 4, nevezője pedig 3.

Megoldás.
$S_(7)=\frac(4*(3^(7)-1))(3-1)=2*(3^(7)-1)=4372$.

Példa.
Keresse meg a geometriai progresszió ismert ötödik tagját: $b_(1)=-3$; $b_(n)=-3072 $; $S_(n)=-4095 $.

Megoldás.
$b_(n)=(-3)*q^(n-1)=-3072$.
$q^(n-1)=1024$.
$q^(n)=1024q$.

$S_(n)=\frac(-3*(q^(n)-1))(q-1)=-4095$.
-4095 $(q-1)=-3*(q^(n)-1)$.
-4095 $(q-1)=-3*(1024q-1)$.
$1365q-1365=1024q-1$.
$341q = $1364.
$q=4$.
$b_5=b_1*q^4=-3*4^4=-3*256=-768$.

A geometriai progresszió jellemző tulajdonsága

Srácok, egy geometriai progresszió adott. Nézzük meg ennek három egymást követő tagját: $b_(n-1),b_(n),b_(n+1)$.
Tudjuk:
$\frac(b_(n))(q)=b_(n-1)$.
$b_(n)*q=b_(n+1)$.
Akkor:
$\frac(b_(n))(q)*b_(n)*q=b_(n)^(2)=b_(n-1)*b_(n+1)$.
$b_(n)^(2)=b_(n-1)*b_(n+1)$.
Ha a progresszió véges, akkor ez az egyenlőség az első és az utolsó kivételével minden tagra érvényes.
Ha nem ismert előre, hogy a sorozat milyen formában van, de ismert, hogy: $b_(n)^(2)=b_(n-1)*b_(n+1)$.
Akkor nyugodtan kijelenthetjük, hogy ez egy geometriai progresszió.

Egy számsorozat csak akkor geometriai haladás, ha az egyes tagok négyzete egyenlő a haladás két szomszédos tagjának szorzatával. Ne felejtsük el, hogy véges haladás esetén ez a feltétel nem teljesül az első és az utolsó tagra.

Nézzük ezt az azonosságot: $\sqrt(b_(n)^(2))=\sqrt(b_(n-1)*b_(n+1))$.
$|b_(n)|=\sqrt(b_(n-1)*b_(n+1))$.
$\sqrt(a*b)$ az átlag geometriai számok a és b.

Egy geometriai progresszió bármely tagjának modulusa megegyezik két szomszédos tagjának geometriai átlagával.

Példa.
Keresse meg x-et úgy, hogy $x+2; 2x+2; A 3x+3$ egy geometriai progresszió három egymást követő tagja volt.

Megoldás.
Használjuk a jellemző tulajdonságot:
$(2x+2)^2=(x+2)(3x+3)$.
$4x^2+8x+4=3x^2+3x+6x+6$.
$x^2-x-2=0$.
$x_(1)=2$ és $x_(2)=-1$.
Helyettesítsük be szekvenciálisan megoldásainkat az eredeti kifejezésbe:
$x=2$ esetén a következő sorozatot kaptuk: 4;6;9 – egy geometriai progresszió, ahol $q=1.5$.
$x=-1$ esetén a következő sorrendet kapjuk: 1;0;0.
Válasz: $x=2.$

Önállóan megoldandó problémák

1. Határozza meg a 16;-8;4;-2… geometriai haladás nyolcadik első tagját.
2. Határozza meg a 11,22,44… geometriai haladás tizedik tagját.
3. Ismeretes, hogy $b_(1)=5, q=3$. Keresse meg $b_(7)$.
4. Ismeretes, hogy $b_(1)=8, q=-2, b_(n)=512$. Keresse meg n.
5. Határozza meg a 3;12;48… geometriai haladás első 11 tagjának összegét!
6. Keress x-et úgy, hogy $3x+4; 2x+4; x+5$ egy geometriai progresszió három egymást követő tagja.