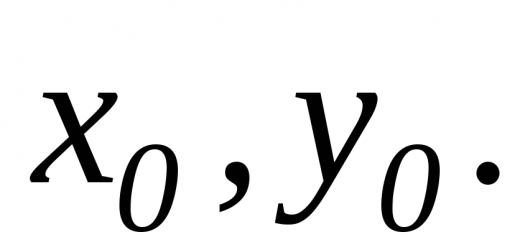Teorem o promjeni količine gibanja točke

Budući da je masa točke konstantna, a njezino ubrzanje, jednadžba koja izražava osnovni zakon dinamike može se prikazati u obliku

Jednadžba istovremeno izražava teorem o promjeni količine gibanja točke u diferencijalnom obliku: vremenski derivat momenta količine gibanja točke jednaka je geometrijskom zbroju sila koje djeluju na točku.

Integrirajmo ovu jednadžbu. Neka masa bude točka m, krećući se pod utjecajem sile (slika 15), ima u trenutku t=0 brzina, a trenutno t 1-brzinski.

sl.15

Pomnožimo onda obje strane jednakosti s i uzmimo od njih određene integrale. U ovom slučaju, s desne strane, gdje se integracija odvija tijekom vremena, granice integrala će biti 0 i t 1, a lijevo, gdje je integrirana brzina, granice integrala će biti odgovarajuće vrijednosti brzine i . Budući da je integral od jednaki , tada kao rezultat dobivamo:

.

Desni integrali predstavljaju impulse sila koje djeluju. Dakle, konačno ćemo imati:

.

Jednadžba izražava teorem o promjeni količine gibanja točke u konačnom obliku: promjena količine gibanja točke u određenom vremenskom razdoblju jednaka je geometrijskom zbroju impulsa svih sila koje djeluju na točku u istom vremenskom razdoblju ( riža. 15).

Pri rješavanju zadataka često se umjesto vektorskih jednadžbi koriste jednadžbe u projekcijama.

Kada pravocrtno kretanje, koji se javlja duž osi Oh teorem je izražen prvom od ovih jednadžbi.

Primjer 9. Pronađite zakon gibanja materijalna točka mase m, krećući se duž osi x pod utjecajem sile konstantne u modulu F(Sl. 16) pri početnim uvjetima: , pri .

sl.16

Riješenje. Napravimo diferencijalnu jednadžbu gibanja točke u projekciji na os x: . Integrirajući ovu jednadžbu, nalazimo: . Konstanta je određena iz početnog uvjeta za brzinu i jednaka je . Konačno

.

Nadalje, uzimajući u obzir da je v = dx/dt, dolazimo do diferencijalne jednadžbe: , čijim integriranjem dobivamo

Konstanta se određuje iz početnog uvjeta za koordinatu točke. Jednako je. Prema tome, zakon gibanja točke ima oblik

Primjer 10. Težinsko opterećenje R(Sl. 17) počinje se kretati iz mirovanja duž glatke horizontalne ravnine pod utjecajem sile F = kt. Pronađite zakon gibanja tereta.

Sl.17

Riješenje. Izaberimo ishodište koordinatnog sustava OKO u početni položaj tereta i usmjerite os x u smjeru kretanja (slika 17). Tada početni uvjeti imaju oblik: x(t = 0) = 0,v( t = 0) = 0. Na teret djeluju sile F,P i ravninska sila reakcije N. Projekcije tih sila na os x imaju značenja Fx = F = kt, Rx = 0, Nx= 0 pa se odgovarajuća jednadžba gibanja može napisati na sljedeći način: . Odvajanjem varijabli u ovoj diferencijalnoj jednadžbi i zatim integriranjem, dobivamo: v = gkt 2 /2P + C 1 . Zamjena početnih podataka ( v(0) = 0), nalazimo da C 1 = 0, i dobivamo zakon promjene brzine .

Posljednji izraz je, pak, diferencijalna jednadžba, čijom integracijom nalazimo zakon gibanja materijalne točke: . Ovdje uključena konstanta određena je iz drugog početnog uvjeta x(0) = 0. Lako je provjeriti da je . Konačno

Primjer 11. Na teretu koji miruje na vodoravnoj glatkoj ravnini (vidi sl. 17) na udaljenosti a od ishodišta, počinje djelovati u pozitivnom smjeru osi x sila F = k 2 (P/g)x, Gdje R - težina tereta. Pronađite zakon gibanja tereta.

Riješenje. Jednadžba gibanja razmatranog tereta (materijalne točke) u projekciji na os x

Početni uvjeti jednadžbe (1) imaju oblik: x(t = 0) = a, v( t = 0) = 0.

Predstavimo vremensku derivaciju brzine uključenu u jednadžbu (1) na sljedeći način:

.

Zamjenom ovog izraza u jednadžbu (1) i smanjenjem za ( P/g), dobivamo

Odvajanjem varijabli u posljednjoj jednadžbi nalazimo da je . Integrirajući potonje, imamo: . Korištenje početnih uvjeta , dobivamo , i, prema tome,

, . (2)

Budući da sila djeluje na teret u pozitivnom smjeru osi x, onda je jasno da bi se trebao kretati u istom smjeru. Stoga u rješenju (2) treba izabrati znak plus. Zamjenom dalje u drugom izrazu (2) s , dobivamo diferencijalnu jednadžbu za određivanje zakona gibanja tereta. Odakle, odvajanjem varijabli, imamo

.

Integrirajući potonje, nalazimo: . Nakon pronalaženja konstante koju konačno dobivamo

Primjer 12. Lopta M mase m(slika 18) pada bez početne brzine pod utjecajem sile teže. Dok lopta pada, doživljava otpor, gdje – konstantan koeficijent otpora. Pronađite zakon gibanja lopte.

Sl.18

Riješenje. Uvedimo koordinatni sustav s ishodištem u točki u kojoj se lopta nalazi t = 0, usmjeravanje osi na okomito prema dolje (slika 18). Diferencijalna jednadžba gibanja lopte u projekciji na os na tada ima oblik

Početni uvjeti za loptu zapisani su na sljedeći način: g(t = 0) = 0, v( t = 0) = 0.

Odvajanje varijabli u jednadžbi (1)

i integrirajući, nalazimo: , gdje je . Ili nakon pronalaženja konstante

ili . (2)

Iz toga slijedi da je najveća brzina, tj. brzina pri , jednaka je .

Da biste pronašli zakon gibanja, zamijenite v u jednadžbi (2) s dy/dt. Zatim, integrirajući dobivenu jednadžbu uzimajući u obzir početni uvjet, konačno nalazimo

.

Primjer 13. Istraživačka podmornica sferičnog oblika i mase m= = 1,5×10 5 kg počinje ponirati s ugašenim motorima, imajući horizontalnu brzinu v x 0 = 30 m/s i negativni uzgon R 1 = 0.01mg, Gdje – vektorski zbroj Arhimedove sile uzgona Q i gravitacije mg, djelujući na čamac (slika 20). Sila otpora vode , kg/s. Odredite jednadžbe gibanja čamca i njegove putanje.

Sustav o kojem se govori u teoremu može biti bilo koji mehanički sustav koji se sastoji od bilo kojeg tijela.

Izjava teorema

Količina gibanja (impulsa) mehaničkog sustava je veličina jednaka zbroju količina gibanja (impulsa) svih tijela uključenih u sustav. Impuls vanjskih sila koje djeluju na tijela sustava je zbroj impulsa svih vanjske sile, djelujući na tijela sustava.

( kg m/s)

Teorem o promjeni količine gibanja stanja sustava

Promjena količine gibanja sustava u određenom vremenskom razdoblju jednaka je impulsu vanjskih sila koje djeluju na sustav u istom vremenskom razdoblju.

Zakon očuvanja količine gibanja sustava

Ako je zbroj svih vanjskih sila koje djeluju na sustav jednak nuli, tada je količina gibanja (zamah) sustava konstantna veličina.

, dobivamo izraz teorema o promjeni količine gibanja sustava u diferencijalnom obliku:

Integrirajući obje strane rezultirajuće jednakosti tijekom proizvoljno uzetog vremenskog razdoblja između nekih i , dobivamo izraz teorema o promjeni količine gibanja sustava u integralnom obliku:

Zakon očuvanja količine gibanja (Zakon očuvanja količine gibanja) kaže da je vektorski zbroj impulsa svih tijela sustava konstantna vrijednost ako je vektorski zbroj vanjskih sila koje djeluju na sustav jednak nuli.

(moment količine gibanja m 2 kg s −1)

Teorem o promjeni kutne količine gibanja u odnosu na središte

vremenska derivacija momenta količine gibanja (kinetičkog momenta) materijalne točke u odnosu na bilo koje fiksno središte jednaka je momentu sile koja djeluje na točku u odnosu na isto središte.

dk 0 /dt = M 0 (F ) .

Teorem o promjeni kutne količine gibanja u odnosu na os

vremenska derivacija momenta količine gibanja (kinetičkog momenta) materijalne točke u odnosu na bilo koju fiksnu os jednaka je momentu sile koja djeluje na tu točku u odnosu na istu os.

dk x /dt = M x (F ); dk g /dt = M g (F ); dk z /dt = M z (F ) .

Razmotrimo materijalnu točku M masa m , krećući se pod utjecajem sile F (Slika 3.1). Zapišimo i konstruirajmo vektor kutne količine gibanja (kinetičke količine gibanja) M 0 materijalna točka u odnosu na središte O :

Razlikujmo izraz za kutni moment (kinetički moment k 0) po vremenu:

Jer dr /dt = V , To vektorski proizvod V ⊗ m ⋅ V (kolinearni vektori V I m ⋅ V ) jednaka je nuli. U isto vrijeme d(m ⋅ V) /dt = F prema teoremu o momentu količine gibanja materijalne točke. Stoga to dobivamo

dk 0 /dt = r ⊗F , (3.3)

Gdje r ⊗F = M 0 (F ) – vektor-moment sile F u odnosu na fiksni centar O . Vektor k 0 ⊥ ravnina ( r , m ⊗V ), i vektor M 0 (F ) ⊥ avion ( r ,F ), konačno imamo

dk 0 /dt = M 0 (F ) . (3.4)

Jednadžba (3.4) izražava teorem o promjeni kutne količine gibanja (kutne količine gibanja) materijalne točke u odnosu na središte: vremenska derivacija momenta količine gibanja (kinetičkog momenta) materijalne točke u odnosu na bilo koje fiksno središte jednaka je momentu sile koja djeluje na točku u odnosu na isto središte.

Projiciranjem jednakosti (3.4) na osi Kartezijevih koordinata dobivamo

dk x /dt = M x (F ); dk g /dt = M g (F ); dk z /dt = M z (F ) . (3.5)

Jednadžbe (3.5) izražavaju teorem o promjeni kutne količine gibanja (kinetičke količine gibanja) materijalne točke u odnosu na os: vremenska derivacija momenta količine gibanja (kinetičkog momenta) materijalne točke u odnosu na bilo koju fiksnu os jednaka je momentu sile koja djeluje na tu točku u odnosu na istu os.

Razmotrimo posljedice koje slijede iz teorema (3.4) i (3.5).

Korolar 1. Razmotrimo slučaj kada sila F tijekom cijelog kretanja točka prolazi kroz stacionarno središte O (slučaj centralne sile), tj. Kada M 0 (F ) = 0. Tada iz teorema (3.4) slijedi da k 0 = konst ,

oni. u slučaju središnje sile, kutni moment (kinetički moment) materijalne točke u odnosu na središte te sile ostaje konstantan po veličini i smjeru (slika 3.2).

Slika 3.2

Od stanja k 0 = konst slijedi da je putanja pokretne točke ravna krivulja, čija ravnina prolazi kroz središte te sile.

Korolar 2. Neka M z (F ) = 0, tj. sila prelazi os z ili paralelno s njim. U ovom slučaju, kao što se može vidjeti iz treće jednadžbe (3.5), k z = konst ,

oni. ako je moment sile koji djeluje na točku u odnosu na bilo koju fiksnu os uvijek jednak nuli, tada kutni moment (kinetički moment) točke u odnosu na tu os ostaje konstantan.

Dokaz teorema o promjeni količine gibanja

Neka se sustav sastoji od materijalnih točaka s masama i akceleracijama. Sve sile koje djeluju na tijela sustava dijelimo u dvije vrste:

Vanjske sile su sile koje djeluju iz tijela koja nisu uključena u razmatrani sustav. Rezultanta vanjskih sila koje djeluju na materijalnu točku s brojem ja označimo

Unutarnje sile su sile kojima tijela samog sustava međusobno djeluju. Sila kojom na točku s brojem ja vrijedi točka s brojem k, označit ćemo , a snagu utjecaja ja th točka na k th točka - . Očito, kada , tada

Koristeći uvedenu notaciju, zapisujemo drugi Newtonov zakon za svaku od razmatranih materijalnih točaka u obliku

S obzirom na to i zbrajajući sve jednadžbe drugog Newtonovog zakona, dobivamo:

Izraz predstavlja zbroj svih unutarnjih sila koje djeluju u sustavu. Prema Newtonovom trećem zakonu, u ovom zbroju, svaka sila odgovara sili tako da, prema tome, vrijedi Budući da se cijeli zbroj sastoji od takvih parova, sam zbroj je nula. Dakle, možemo pisati

Koristeći oznaku količine gibanja sustava dobivamo

Uvođenjem u razmatranje promjene količine gibanja vanjskih sila , dobivamo izraz teorema o promjeni količine gibanja sustava u diferencijalnom obliku:

Dakle, svaka od posljednjih dobivenih jednadžbi dopušta nam da kažemo: promjena momenta količine gibanja sustava događa se samo kao rezultat djelovanja vanjskih sila, a unutarnje sile ne mogu utjecati na tu vrijednost.

Integrirajući obje strane dobivene jednakosti u proizvoljno uzetom vremenskom intervalu između nekih i , dobivamo izraz teorema o promjeni momenta količine gibanja sustava u integralnom obliku:

gdje su i vrijednosti količine gibanja sustava u trenucima vremena i, odnosno, i je impuls vanjskih sila u određenom vremenskom razdoblju. Sukladno prethodno rečenom i uvedenim oznakama,

Diferencijalna jednadžba gibanja materijalne točke pod utjecajem sile F može se prikazati u sljedećem vektorskom obliku:

Budući da masa točke m prihvaća kao konstanta, tada se može unijeti pod znakom izvedenice. Zatim

Formula (1) izražava teorem o promjeni količine gibanja točke u diferencijalnom obliku: prva derivacija po vremenu količine gibanja točke jednaka je sili koja djeluje na točku.

U projekcijama na koordinatne osi (1) može se prikazati kao

Ako se obje strane (1) pomnože s dt, tada dobivamo drugi oblik istog teorema - teorem o momentu u diferencijalnom obliku:

oni. diferencijal količine gibanja točke jednak je elementarnom impulsu sile koja djeluje na točku.

Projiciranjem oba dijela (2) na koordinatne osi dobivamo

Integrirajući oba dijela (2) od nule do t (slika 1), imamo

gdje je brzina točke u trenutku t; - brzina pri t = 0;

S- impuls sile tijekom vremena t.

Izraz u obliku (3) često se naziva teorem o količini gibanja u konačnom (ili integralnom) obliku: promjena količine gibanja točke u bilo kojem vremenskom razdoblju jednaka je impulsu sile u istom vremenskom razdoblju.

U projekcijama na koordinatne osi ovaj se teorem može prikazati u sljedećem obliku:

Za materijalnu točku, teorem o promjeni količine gibanja u bilo kojem od oblika u biti se ne razlikuje od diferencijalnih jednadžbi gibanja točke.

Teorem o promjeni količine gibanja sustava

Količinu gibanja sustava nazvat ćemo vektorskom veličinom Q, jednaka geometrijskom zbroju (glavnom vektoru) količina gibanja svih točaka sustava.

Razmotrimo sustav koji se sastoji od n materijalne bodove. Skladajmo za ovaj sustav diferencijalne jednadžbe kretanja i zbrajati ih pojam po pojam. Tada dobivamo:

Posljednji zbroj, zbog svojstva unutarnjih sila, jednak je nuli. Osim,

Konačno nalazimo:

Jednadžba (4) izražava teorem o promjeni količine gibanja sustava u diferencijalnom obliku: vremenska derivacija količine gibanja sustava jednaka je geometrijskom zbroju svih vanjskih sila koje djeluju na sustav.

Pronađimo drugi izraz za teorem. Prepustite se trenutku t= 0 količina gibanja sustava je Q 0, iu trenutku vremena t 1 postaje jednaka P 1. Zatim, množenje obje strane jednakosti (4) sa dt i integrirajući, dobivamo:

Ili gdje:

(S- impuls sile)

budući da integrali s desne strane daju impulse vanjskih sila,

jednadžba (5) izražava teorem o promjeni količine gibanja sustava u integralnom obliku: promjena količine gibanja sustava u određenom vremenskom razdoblju jednaka je zbroju impulsa vanjskih sila koje djeluju na sustav u istom vremenskom razdoblju.

U projekcijama na koordinatne osi imat ćemo:

Zakon očuvanja količine gibanja

Iz teorema o promjeni količine gibanja sustava mogu se dobiti sljedeći važni korolari:

1. Neka je zbroj svih vanjskih sila koje djeluju na sustav jednak nuli:

Tada iz jednadžbe (4) slijedi da u ovom slučaju Q = konst.

Tako, ako je zbroj svih vanjskih sila koje djeluju na sustav jednak nuli, tada će vektor količine gibanja sustava biti konstantan po veličini i smjeru.

2. 01Neka su vanjske sile koje djeluju na sustav takve da je zbroj njihovih projekcija na neku os (na primjer Ox) jednak nuli:

Tada iz jednadžbi (4`) slijedi da u ovom slučaju Q = konst.

Tako, ako je zbroj projekcija svih vanjskih sila koje djeluju na bilo koju os jednak nuli, tada je projekcija količine gibanja sustava na tu os konstantna vrijednost.

Ovi rezultati izražavaju zakon očuvanja količine gibanja sustava. Iz njih slijedi da unutarnje sile ne mogu promijeniti ukupnu količinu gibanja sustava.

Pogledajmo neke primjere:

· Fenomen vraćanja rolne. Ako pušku i metak smatramo jednim sustavom, tada će pritisak barutnih plinova tijekom hica biti unutarnja sila. Ta sila ne može promijeniti ukupni zamah sustava. Ali budući da barutni plinovi, djelujući na metak, pridaju mu određenu količinu gibanja usmjerenu prema naprijed, oni moraju istovremeno priopćiti pušci istu količinu gibanja u suprotnom smjeru. To će uzrokovati pomicanje puške unatrag, tj. povratak tzv. Slična pojava događa se prilikom pucanja iz pištolja (povratak).

· Rad propelera (elise). Propeler daje kretanje određenoj masi zraka (ili vode) duž osi propelera, odbacujući tu masu natrag. Ako bačenu masu i zrakoplov (ili brod) promatramo kao jedan sustav, tada sile međudjelovanja između propelera i okoline, kao unutarnje, ne mogu promijeniti ukupnu količinu gibanja tog sustava. Stoga, kada se masa zraka (vode) baci natrag, zrakoplov (ili brod) dobiva odgovarajuću brzinu prema naprijed tako da ukupna količina gibanja sustava koji se razmatra ostaje jednaka nuli, jer je bila nula prije početka kretanja .

Sličan učinak postiže se djelovanjem vesala ili kotača s lopaticama.

· Povratni pogon.U raketi (raketa) plinoviti produkti izgaranja goriva velikom brzinom izbacuju se iz otvora na repu rakete (iz mlaznice mlaznog motora). Sile pritiska koje djeluju u ovom slučaju bit će unutarnje sile i ne mogu promijeniti ukupni moment raketno-barutnog plinskog sustava. Ali budući da plinovi koji izlaze imaju određenu količinu gibanja usmjerenu unatrag, raketa dobiva odgovarajuću brzinu prema naprijed.

Teorem o momentima oko osi.

Razmotrimo materijalnu točku mase m, krećući se pod utjecajem sile F. Nađimo za to odnos između momenta vektora mV I F u odnosu na neku fiksnu os Z.

m z (F) = xF - yF (7)

Slično za vrijednost m(mV), ako se izvadi m bit će izvan zagrada

m z (mV) = m(xV - yV)(7`)

Uzimajući derivacije u odnosu na vrijeme s obje strane ove jednakosti, nalazimo

Na desnoj strani rezultirajućeg izraza, prva zagrada je jednaka 0, jer dx/dt=V i du/dt = V, druga zagrada prema formuli (7) jednaka je

mz(F), jer prema osnovnom zakonu dinamike:

Konačno ćemo imati (8)

Rezultirajuća jednadžba izražava teorem momenata oko osi: vremenska derivacija momenta količine gibanja točke u odnosu na bilo koju os jednaka je momentu djelujuća sila oko iste osi. Sličan teorem vrijedi za trenutke oko bilo kojeg središta O.

(Fragmenti matematičke simfonije)

Veza između impulsa sile i osnovne jednadžbe Newtonove dinamike izražena je teoremom o promjeni količine gibanja materijalne točke.

Teorema. Promjena količine gibanja materijalne točke u određenom vremenskom razdoblju jednaka je impulsu sile () koja djeluje na materijalnu točku u istom vremenskom razdoblju. Matematički dokaz ovog teorema može se nazvati fragmentom matematičke simfonije. Evo ga.

Diferencijalna količina gibanja materijalne točke jednaka je elementarnom impulsu sile koja djeluje na materijalnu točku. Integrirajući izraz (128) za diferencijalnu količinu gibanja materijalne točke, imamo

(129)

Teorem je dokazan i matematičari svoju misiju smatraju završenom, ali inženjeri, čija je sudbina da sveto vjeruju matematičarima, imaju pitanja kada koriste dokazanu jednadžbu (129). Ali oni su čvrsto blokirani slijedom i ljepotom matematičkih operacija (128 i 129), koje nas fasciniraju i potiču da ih nazovemo fragmentom matematičke simfonije. Koliko se generacija inženjera slagalo s matematičarima i bilo zadivljeno njihovom misterijom? matematički simboli! Ali tu je bio jedan inženjer koji se nije slagao s matematičarima i postavljao im je pitanja.

Dragi matematičari! Zašto ni u jednom od vaših udžbenika na teorijska mehanika ne uzima li se u obzir postupak primjene vašeg simfonijskog rezultata (129) u praksi, na primjer, kada se opisuje proces ubrzavanja automobila? Lijeva strana jednadžbe (129) vrlo je jasna. Automobil počinje ubrzavanje od brzine i završava ga, na primjer, pri brzini. Sasvim je prirodno da jednadžba (129) postaje

I odmah se postavlja prvo pitanje: kako iz jednadžbe (130) odrediti silu pod čijim se utjecajem automobil ubrzava do brzine od 10 m/s? Odgovor na ovo pitanje ne nalazimo ni u jednom od bezbrojnih udžbenika teorijske mehanike. Idemo dalje. Nakon ubrzanja automobil se počinje gibati jednoliko brzinom 10 m/s. Koja sila pokreće automobil?????????? Ne preostaje mi ništa drugo nego crvenjeti zajedno s matematičarima. Prvi zakon Newtonove dinamike kaže da kada se automobil kreće jednoliko, na njega ne djeluju nikakve sile, a automobil, slikovito rečeno, kiha na taj zakon, troši benzin i obavlja rad, prevalivši, primjerice, put od 100 km. Gdje je sila koja je izvršila rad da se automobil pomakne 100 km? Simfonijski Matematička jednadžba(130) šuti, ali život ide dalje i traži odgovor. Počinjemo ga tražiti.

Budući da se automobil giba pravocrtno i jednoliko, sila koja ga pokreće je konstantna po veličini i smjeru i jednadžba (130) postaje

(131)

Dakle, jednadžba (131) u ovom slučaju opisuje ubrzano gibanje tijela. Čemu je jednaka sila? Kako izraziti njegovu promjenu kroz vrijeme? Matematičari radije zaobilaze ovo pitanje i prepuštaju ga inženjerima, smatrajući da oni moraju tražiti odgovor na to pitanje. Inženjerima preostaje još jedna opcija - uzeti u obzir da ako nakon završetka ubrzanog kretanja tijela počinje faza jednolikog kretanja koju prati radnja stalna sila predstaviti jednadžbu (131) za trenutak prijelaza iz ubrzanog u ravnomjerno kretanje u ovom obliku

(132)

Strelica u ovoj jednadžbi ne označava rezultat integriranja ove jednadžbe, već proces prijelaza iz njenog integralnog oblika u pojednostavljeni oblik. Sila u ovoj jednadžbi je ekvivalentna prosječnoj sili koja je promijenila količinu gibanja tijela od nule do konačne vrijednosti. Dakle, dragi matematičari i teorijski fizičari, nepostojanje vaše metode za određivanje veličine vašeg impulsa tjera nas da pojednostavimo proceduru za određivanje sile, a nepostojanje metode za određivanje vremena djelovanja ove sile općenito nas stavlja u bezizlazan položaj te smo prisiljeni upotrijebiti izraz za analizu procesa promjene količine gibanja tijela . Rezultat je da što dulje sila djeluje, to je njen impuls veći. To jasno proturječi dugo uvriježenoj ideji da što je kraće trajanje njegovog djelovanja, to je veći impuls sile.

Obratimo pozornost na činjenicu da se promjena količine gibanja materijalne točke (impuls sile) tijekom njezinog ubrzanog gibanja događa pod djelovanjem Newtonove sile i sila otpora gibanju, u obliku sila koje stvaraju mehanički otpori i sila inercije. Ali Newtonova dinamika u velikoj većini problema zanemaruje silu tromosti, a Mehanodinamika tvrdi da do promjene količine gibanja tijela tijekom njegovog ubrzanog gibanja dolazi zbog viška Newtonove sile nad silama otpora gibanju, uključujući sila inercije.

Kad se tijelo giba usporeno, npr. automobil s isključenim mjenjačem, nema Newtonove sile, a do promjene količine gibanja automobila dolazi zbog viška sila otpora gibanju nad silom inercija, koja pokreće automobil kada se kreće sporo.

Kako sada možemo vratiti rezultate spomenutih "simfonijskih" matematičkih radnji (128) u glavni tok uzročno-posljedičnih odnosa? Postoji samo jedan izlaz - pronaći novu definiciju pojmova "impuls sile" i "sila udara". Da biste to učinili, podijelite obje strane jednadžbe (132) s vremenom t. Kao rezultat ćemo imati

. (133)

Napomenimo da je izraz mV/t brzina promjene momenta (mV/t) materijalne točke ili tijela. Ako uzmemo u obzir da je V/t akceleracija, onda je mV/t sila koja mijenja moment količine gibanja tijela. Ista dimenzija lijevo i desno od znaka jednakosti daje nam pravo da silu F nazovemo udarnom silom i označimo simbolom, a impuls S - udarnim impulsom i označimo simbolom. To dovodi do nove definicije udarne sile. Sila udara koja djeluje na materijalnu točku ili tijelo jednaka je omjeru promjene količine gibanja materijalne točke ili tijela i vremena te promjene.

Obratimo posebnu pozornost na činjenicu da u formiranju udarnog impulsa (134) sudjeluje samo Newtonova sila koja je promijenila brzinu automobila od nule do maksimalne - , stoga jednadžba (134) u potpunosti pripada Newtonskoj dinamici. Budući da je eksperimentalno mnogo lakše odrediti veličinu brzine nego ubrzanje, formula (134) je vrlo prikladna za proračune.

Ovaj neobičan rezultat proizlazi iz jednadžbe (134).

Obratimo pozornost na činjenicu da je prema novim zakonima mehanodinamike generator impulsa sile pri ubrzanom gibanju materijalne točke ili tijela Newtonova sila. Ona tvori ubrzanje gibanja točke ili tijela, pri čemu automatski nastaje inercijalna sila, usmjerena suprotno od Newtonove sile, a udarna Newtonova sila mora nadvladati djelovanje inercijske sile, stoga se inercijalna sila mora prikazati u ravnoteža sila na lijevoj strani jednadžbe (134). Budući da je inercijalna sila jednaka masi točke ili tijela pomnoženoj s usporenjem koje stvara, tada jednadžba (134) postaje

(136)

Dragi matematičari! Pogledajte u kakvom je obliku matematički model, koji opisuje udarni impuls, koji ubrzava kretanje udarenog tijela od nulte brzine do maksimalne V (11). Provjerimo sada njegov rad u određivanju udarnog impulsa, koji je jednak udarnoj sili koja je aktivirala 2. agregat SShG (Sl. 120), i ostavit ćemo vas s vašom beskorisnom jednadžbom (132). Kako ne bismo komplicirali prikaz, za sada ćemo ostaviti formulu (134) i koristiti formule koje daju prosječne vrijednosti sila. Vidite u kakvu ste poziciju stavili inženjera koji pokušava riješiti određeni problem.

Počnimo s Newtonovom dinamikom. Stručnjaci su otkrili da se 2. agregat podigao na visinu od 14 m. Budući da se podigao u polju gravitacije, na visini od h = 14 m pokazalo se da je njegova potencijalna energija jednaka

a prosječna kinetička energija bila je jednaka

Riža. 120. Fotografija turbinske sobe prije katastrofe

Iz jednakosti kinetičke (138) i potencijalne (137) energije slijedi Prosječna brzina podizanje agregata (sl. 121, 122)

Riža. 121. Foton turbinske sobe nakon katastrofe

Prema novim zakonima mehanodinamike, uspon agregata sastojao se od dvije faze (slika 123): prva faza OA - ubrzani uspon i druga faza AB - spori uspon , , .

Vrijeme i udaljenost njihovog djelovanja približno su jednaki (). Tada će se kinematička jednadžba ubrzane faze podizanja agregata napisati na sljedeći način:

. (140)

Riža. 122. Pogled na bunar agregata i sam agregat nakon havarije

Zakon promjene brzine porasta agregata u prvoj fazi ima oblik

. (141)

Riža. 123. Pravilnost promjena brzine leta V pogonske jedinice

Zamjenom vremena iz jednadžbe (140) u jednadžbu (141), imamo

. (142)

Vrijeme podizanja bloka u prvoj fazi određuje se iz formule (140)

. (143)

Tada će ukupno vrijeme podizanja agregata na visinu od 14 m biti jednako . Masa agregata i poklopca je 2580 tona. Prema Newtonovoj dinamici, sila koja je podigla agregat jednaka je

Dragi matematičari! Slijedimo vaše simfonijske matematičke rezultate i zapisujemo vašu formulu (129), slijedeći Newtonovu dinamiku, kako bismo odredili udarni puls koji je pokrenuo 2. jedinicu snage

i postaviti osnovno pitanje: kako odrediti trajanje udarnog impulsa koji je pokrenuo 2. agregat????????????????

poštovani!!! Sjetite se koliko su generacije vaših kolega kredom ispisivale po pločama, nespretno učeći studente kako odrediti udarni impuls, a nitko nije objasnio kako se u svakom konkretnom slučaju može odrediti trajanje udarnog impulsa. Reći ćete da je trajanje udarnog impulsa jednako vremenskom intervalu promjene brzine agregata od nule do, pretpostavit ćemo, maksimalne vrijednosti od 16,75 m/s (139). Ona je u formuli (143) i jednaka je 0,84 s. Za sada se slažemo s vama i određujemo prosječnu vrijednost udarnog impulsa

Odmah se postavlja pitanje: zašto je veličina udarnog impulsa (146) manja od Newtonove sile od 50600 tona? Vi, dragi matematičari, nemate odgovor. Idemo dalje.

Prema Newtonskoj dinamici, glavna sila koja se odupirala porastu pogonske jedinice bila je gravitacija. Budući da je ta sila usmjerena protiv kretanja agregata, ona stvara usporavanje, koje je jednako ubrzanju slobodan pad. Tada je gravitacijska sila koja djeluje na pogonsku jedinicu koja leti prema gore jednaka

Newtonova dinamika ne uzima u obzir druge sile koje su spriječile djelovanje Newtonove sile od 50 600 tona (144), a mehanodinamika tvrdi da se usponu agregata opirala i inercijalna sila jednaka

Odmah se postavlja pitanje: kako pronaći količinu usporavanja u kretanju agregata? Newtonova dinamika šuti, ali mehanodinamika odgovara: u trenutku djelovanja Newtonove sile, koja je podigla pogonski agregat, njemu su se oduprli: sila gravitacije i sila tromosti, stoga je jednadžba sila koje djeluju na pogon jedinica u tom trenutku zapisuje se na sljedeći način.

Promotrimo sustav koji se sastoji od materijalnih točaka. Sastavimo diferencijalne jednadžbe gibanja (13) za ovaj sustav i zbrajamo ih član po član. Onda dobivamo

Posljednji zbroj, zbog svojstva unutarnjih sila, jednak je nuli. Osim,

Napokon nalazimo

Jednadžba (20) izražava teorem o promjeni količine gibanja sustava u diferencijalnom obliku: vremenska derivacija količine gibanja sustava jednaka je geometrijskom zbroju svih vanjskih sila koje djeluju na sustav. U projekcijama na koordinatne osi bit će:

Pronađimo drugi izraz za teorem. Neka je u trenutku vremena količina gibanja sustava jednaka i u trenutku postaje jednaka . Zatim, množenjem obje strane jednakosti (20) i integracijom, dobivamo

budući da integrali s desne strane daju impulse vanjskih sila.

Jednadžba (21) izražava teorem o promjeni količine gibanja sustava u integralnom obliku: promjena količine gibanja sustava u određenom vremenskom razdoblju jednaka je zbroju impulsa koji djeluju na sustav vanjskih sila tijekom isto vremensko razdoblje.

U projekcijama na koordinatne osi bit će:

Istaknimo vezu između dokazanog teorema i teorema o gibanju središta mase. Budući da , dakle, supstituirajući tu vrijednost u jednakost (20) i uzimajući u obzir da dobivamo , tj. jednadžbu (16).

Prema tome, teorem o gibanju središta mase i teorem o promjeni količine gibanja sustava su u biti dvije različite oblike isti teorem. U slučajevima kada se proučava kretanje čvrsta(ili sustava tijela), jednako možete koristiti bilo koji od ovih oblika, a jednadžba (16) je obično praktičnija za korištenje. Za kontinuirani medij (tekućina, plin) pri rješavanju zadataka obično koriste teorem o promjeni količine gibanja sustava. Ovaj teorem također ima važne primjene u teoriji udara (vidi Poglavlje XXXI) iu proučavanju mlaznog gibanja (vidi § 114).