Protozoa trigonometrijske jednadžbe obično se rješavaju pomoću formula. Podsjećam vas da su najjednostavnije trigonometrijske jednadžbe:

sinx = a

cosx = a

tgx = a

ctgx = a

x je kut koji treba pronaći,
a je bilo koji broj.

A evo i formula s kojima možete odmah zapisati rješenja ovih najjednostavnijih jednadžbi.

Za sinus:

Za kosinus:

x = ± arccos a + 2π n, n ∈ Z

Za tangentu:

x = arctan a + π n, n ∈ Z

Za kotangens:

x = arcctg a + π n, n ∈ Z

Zapravo, to je to teorijski dio rješavanje jednostavnih trigonometrijskih jednadžbi. Štoviše, sve!) Baš ništa. Međutim, broj pogrešaka na ovu temu jednostavno je izvan tablica. Pogotovo ako primjer malo odstupa od predloška. Zašto?

Da, jer puno ljudi piše ova pisma, a da uopće ne razumije njihovo značenje! Oprezno zapisuje, da se ne dogodi nešto...) Ovo treba srediti. Trigonometrija za ljude, ili ipak ljudi za trigonometriju!?)

Idemo to shvatiti?

Jedan kut će biti jednak arccos a, drugi: -arccos a.

I uvijek će tako ispasti. Za bilo koje A.

Ako mi ne vjerujete, prijeđite mišem preko slike ili dodirnite sliku na tabletu.) Promijenio sam broj A na nešto negativno. U svakom slučaju, imamo jedan kut arccos a, drugi: -arccos a.

Stoga se odgovor uvijek može napisati kao dva niza korijena:

x 1 = arccos a + 2π n, n ∈ Z

x 2 = - arccos a + 2π n, n ∈ Z

Spojimo ove dvije serije u jednu:

x= ± arccos a + 2π n, n ∈ Z

I to je sve. dobio opća formula riješiti najjednostavniju trigonometrijsku jednadžbu s kosinusom.

Ako shvatite da to nije nekakva nadznanstvena mudrost, ali samo skraćena verzija dva niza odgovora, Također ćete moći rješavati zadatke "C". S nejednakostima, s odabiranjem korijena iz zadanog intervala... Tu odgovor s plus/minusom ne funkcionira. Ali ako se prema odgovoru odnosite poslovno i podijelite ga na dva odvojena odgovora, sve će biti riješeno.) Zapravo, to je razlog zašto to istražujemo. Što, kako i gdje.

U najjednostavnijoj trigonometrijskoj jednadžbi

sinx = a

također dobivamo dva niza korijena. Stalno. A mogu se i ove dvije serije snimiti u jednom redu. Samo će ovaj redak biti složeniji:

x = (-1) n arcsin a + π n, n ∈ Z

Ali suština ostaje ista. Matematičari su jednostavno osmislili formulu kako bi napravili jedan umjesto dva unosa za niz korijena. To je sve!

Provjerimo matematičare? I nikad se ne zna...)

U prethodnoj lekciji detaljno je obrađeno rješenje (bez ikakvih formula) trigonometrijske jednadžbe sa sinusom:

Odgovor je rezultirao s dva niza korijena:

x 1 = π /6 + 2π n, n ∈ Z

x 2 = 5π /6 + 2π n, n ∈ Z

Ako riješimo istu jednadžbu pomoću formule, dobit ćemo odgovor:

x = (-1) n arcsin 0,5 + π n, n ∈ Z

Zapravo, ovo je nedovršen odgovor.) Učenik to mora znati arcsin 0,5 = π /6. Kompletan odgovor bi bio:

x = (-1) n π /6+ π n, n ∈ Z

Ovo postavlja zanimljivo pitanje. Odgovorite putem x 1; x 2 (ovo je točan odgovor!) i kroz lonely x (i ovo je točan odgovor!) - jesu li to ista stvar ili ne? Sada ćemo saznati.)

Zamjenjujemo u odgovoru sa x 1 vrijednosti n =0; 1; 2; itd., brojimo, dobivamo niz korijena:

x 1 = π/6; 13π/6; 25π/6 i tako dalje.

S istom zamjenom u odgovoru sa x 2 , dobivamo:

x 2 = 5π/6; 17π/6; 29π/6 i tako dalje.

Sada zamijenimo vrijednosti n (0; 1; 2; 3; 4...) u opću formulu za jednostruku x . Odnosno, dižemo minus jedan na nultu potenciju, zatim na prvu, drugu itd. Pa, naravno, zamijenit ćemo 0 u drugi član; 1; 2 3; 4, itd. I brojimo. Dobijamo seriju:

x = π/6; 5π/6; 13π/6; 17π/6; 25π/6 i tako dalje.

To je sve što možete vidjeti.) Opća formula nam daje potpuno iste rezultate kao što su dva odgovora zasebno. Samo sve odjednom, po redu. Matematičari se nisu prevarili.)

Također se mogu provjeriti formule za rješavanje trigonometrijskih jednadžbi s tangensom i kotangensom. Ali nećemo.) Već su jednostavni.

Posebno sam napisao sve ove zamjene i provjere. Ovdje je važno shvatiti jednu stvar jednostavna stvar: postoje formule za rješavanje elementarnih trigonometrijskih jednadžbi, samo kratak sažetak odgovora. Radi ove sažetosti, morali smo umetnuti plus/minus u rješenje kosinusa i (-1) n u rješenje sinusa.

Ovi umeci ni na koji način ne smetaju u zadacima u kojima samo trebate napisati odgovor na elementarnu jednadžbu. Ali ako trebate riješiti nejednadžbu ili trebate učiniti nešto s odgovorom: odabrati korijene na intervalu, provjeriti ODZ itd., ova umetanja mogu lako uznemiriti osobu.

Što bih trebao napraviti? Da, ili napiši odgovor u dvije serije, ili riješi jednadžbu/nejednadžbu pomoću trigonometrijske kružnice. Tada ti umetci nestaju i život postaje lakši.)

Možemo sažeti.

Za rješavanje najjednostavnijih trigonometrijskih jednadžbi postoje gotove formule odgovora. Četiri komada. Dobri su za trenutno zapisivanje rješenja jednadžbe. Na primjer, trebate riješiti jednadžbe:

sinx = 0,3

Lako: x = (-1) n arcsin 0,3 + π n, n ∈ Z

cosx = 0,2

Nema problema: x = ± arccos 0,2 + 2π n, n ∈ Z

tgx = 1,2

Lako: x = arctan 1,2 + π n, n ∈ Z

ctgx = 3,7

Jedan ostao: x= arcctg3,7 + π n, n ∈ Z

cos x = 1,8

Ako ti, sjajeći znanjem, odmah napišeš odgovor:

x= ± arccos 1.8 + 2π n, n ∈ Z

onda već blistaš, ovo... ono... iz lokve.) Točan odgovor: nema rješenja. Ne razumijem zašto? Pročitajte što je ark kosinus. Osim toga, ako na desnoj strani izvorne jednadžbe postoje tablične vrijednosti sinusa, kosinusa, tangensa, kotangensa, - 1; 0; √3; 1/2; √3/2 i tako dalje. - odgovor će kroz lukove nedorečen. Lukovi se moraju pretvoriti u radijane.

A ako naiđete na nejednakost, npr

onda je odgovor:

x πn, n ∈ Z

postoje rijetke gluposti, da ...) Ovdje morate trigonometrijski krug odlučiti. Što ćemo učiniti u odgovarajućoj temi.

Za one koji herojski čitaju ove retke. Jednostavno ne mogu ne cijeniti vaš ogromni trud. Bonus za vas.)

Bonus:

Kada zapisuju formule u alarmantnoj borbenoj situaciji, čak i iskusni štreberi često se zbune gdje πn, I gdje 2π n. Evo jednostavnog trika za vas. U svatko formule vrijedan πn. Osim jedine formule s ark kosinusom. Stoji tamo 2πn. Dva peen. Ključna riječ - dva. U ovoj istoj formuli postoje dva znak na početku. Plus i minus. Tu i tamo - dva.

Pa ako si napisao dva znak ispred ark kosinusa, lakše je zapamtiti što će se dogoditi na kraju dva peen. A događa se i obrnuto. Osoba će propustiti znak ± , dolazi do kraja, piše ispravno dva Pien, i doći će k sebi. Nešto je naprijed dva znak! Osoba će se vratiti na početak i ispraviti grešku! Kao ovo.)

Ako vam se sviđa ova stranica...

Usput, imam još nekoliko zanimljivih stranica za vas.)

Možete vježbati rješavanje primjera i saznati svoju razinu. Testiranje uz trenutnu provjeru. Učimo - sa zanimanjem!)

Možete se upoznati s funkcijama i derivacijama.

cos jednadžbax = A

Svaki korijen jednadžbe

cos x = A (1)

može se smatrati apscisom neke sjecišne točke sinusoide y = cosx s ravnom linijom y =A , i obrnuto, apscisa svake takve sjecišne točke jedan je od korijena jednadžbe (1). Dakle, skup svih korijena jednadžbe (1) podudara se sa skupom apscisa svih sjecišnih točaka kosinusnog vala y = cosx s ravnom linijom y = A .

Ako | A| >1 , zatim kosinus y = cosx ne siječe s linijom y = A .

U ovom slučaju jednadžba (1) nema korijena.

Na |A| < 1 postoji beskonačno mnogo točaka sjecišta.

za a > 0

za< 0.

Sve te sjecišne točke podijelit ćemo u dvije skupine:

A -2 , A - 1 , A 1 , A 2 , ... ,

B -2 , B - 1 , B 1 , B 2 , ... ,

Točka A ima apscisu arccos A , a sve ostale točke prve skupine odvojene su od nje na udaljenostima umnošcima 2 π

arccos a+ 2k π . (2)

Točka U, kao što se lako može razumjeti iz slika, ima apscisu - arccosA , a sve ostale točke druge skupine udaljene su od nje na udaljenostima koje su višekratnike 2 π . Stoga su njihove apscise izražene kao

arccos A+ 2nπ . (3)

Dakle, jednadžba (1) ima dvije skupine korijena definirane formulama (2) i (3). Ali ove dvije formule očito se mogu napisati kao jedna formula

x = ± arccos a+ 2m π , (4)

Gdje m prolazi kroz sve cijele brojeve (m = 0, ±1, ±2, ±3, ...).

Rezoniranje koje smo proveli pri izvođenju ove formule ispravno je samo ako
| a| =/= 1. Međutim, formalno relacija (4) određuje sve korijene jednadžbe cosx=a i na | A| =1. (Dokaži!) Stoga možemo reći da formula (4) daje sve korijene jednadžbe (1) za bilo koje vrijednosti A , Samo ako |A| < 1 .

Ali ipak u tri posebna slučaja ( A = 0, A = -1, A= +1) preporučamo da ne koristite formulu (4) , ali koristite druge relacije. Korisno je zapamtiti da su korijeni jednadžbe cos x = 0 dati su formulom

x = π / 2 +n π ; (5)

korijeni jednadžbe cos x = -1 dati su formulom

x = π + 2m π ; (6)

i konačno, korijeni jednadžbe cos x = 1 dati su formulom

x = 2m π ; (7)

Zaključno napominjemo da formule (4) , (5), (6) i (7) točni su samo pod pretpostavkom da je željeni kut x izraženo u radijanima. Ako je izraženo u stupnjevima, tada je potrebno te formule prirodno promijeniti. Dakle, formula (4) treba zamijeniti formulom

x = ± arccos a+ 360° n,

formula (5) formula

x = 90° + 180° n itd.

Centrirano u točki A.
α - kut izražen u radijanima.

Definicija
Sinus (sin α) je trigonometrijska funkcija koja ovisi o kutu α između hipotenuze i kraka pravokutni trokut, jednaka omjeru duljina suprotne stranice |BC| na duljinu hipotenuze |AC|.

Kosinus (cos α) je trigonometrijska funkcija koja ovisi o kutu α između hipotenuze i kraka pravokutnog trokuta, jednaka omjeru duljine susjednog kraka |AB| na duljinu hipotenuze |AC|.

Prihvaćene oznake

;
;
.

;
;
.

Graf funkcije sinusa, y = sin x

Graf kosinusne funkcije, y = cos x

Svojstva sinusa i kosinusa

Periodičnost

Funkcije y = grijeh x i y = cos x periodic s periodom 2π.

Paritet

Funkcija sinusa je neparna. Funkcija kosinus je paran.

Područje definiranja i vrijednosti, ekstremi, porast, pad

Funkcije sinus i kosinus su kontinuirane u svojoj domeni definicije, to jest za sve x (vidi dokaz kontinuiteta). Njihova glavna svojstva prikazana su u tablici (n - cijeli broj).

	y = grijeh x	y = cos x
Opseg i kontinuitet	- ∞ < x < + ∞	- ∞ < x < + ∞
Raspon vrijednosti	-1 ≤ y ≤ 1	-1 ≤ y ≤ 1
Povećavajući se
Silazni
Maksimalno, y = 1
Minimalni, y = - 1
Nule, y = 0
Točke presjeka s osi ordinata, x = 0	y = 0	y = 1

Osnovne formule

Zbroj kvadrata sinusa i kosinusa

Formule za sinus i kosinus iz zbroja i razlike

;
;

Formule za umnožak sinusa i kosinusa

Formule zbroja i razlike

Izražavanje sinusa kroz kosinus

;
;
;
.

Izražavanje kosinusa kroz sinus

;
;
;
.

Izražavanje kroz tangentu

; .

Kada, imamo:
; .

u:
; .

Tablica sinusa i kosinusa, tangensa i kotangensa

Ova tablica prikazuje vrijednosti sinusa i kosinusa za određene vrijednosti argumenta.

Izrazi kroz kompleksne varijable

;

Eulerova formula

Izrazi preko hiperboličkih funkcija

;
;

Derivati

; . Izvođenje formula >>>

Derivacije n-tog reda:
{ -∞ < x < +∞ }

Sekans, kosekans

Inverzne funkcije

Inverzne funkcije na sinus i kosinus su arksinus i arkosinus.

Arksinus, arcsin

Arkosinus, arkos

Reference:
U. Bronstein, K.A. Semendjajev, Priručnik iz matematike za inženjere i studente, “Lan”, 2009.

Najjednostavnije trigonometrijske jednadžbe su jednadžbe

Cos (x) = a, sin (x) = a, tg (x) = a, ctg (x) = a

Jednadžba cos(x) = a

Obrazloženje i obrazloženje

1. Korijenje cosx jednadžbe= a. Kada | a | > 1 jednadžba nema korijena, jer | cosx |< 1 для любого x (прямая y = а при а >1 ili na a< -1 не пересекает график функцииy = cosx).

Neka | a |< 1. Тогда прямая у = а пересекает график функции

y = cos x. Na intervalu funkcija y = cos x opada od 1 do -1. Ali opadajuća funkcija uzima svaku od svojih vrijednosti samo u jednoj točki svoje domene definicije, stoga jednadžba cos x = a ima samo jedan korijen na ovom intervalu, koji je, prema definiciji arkosinusa, jednak: x 1 = arccos a (i za ovaj korijen cos x = A).

Kosinus - ravnomjerna funkcija, dakle, na intervalu [-n; 0] jednadžba cos x = i također ima samo jedan korijen - broj nasuprot x 1, tj

x 2 = -arccos a.

Dakle, na intervalu [-n; p] (duljina 2p) jednadžba cos x = a s | a |< 1 имеет только корни x = ±arccos а.

Funkcija y = cos x je periodična s periodom 2n, stoga se svi ostali korijeni razlikuju od onih koji se nalaze s 2n (n € Z). Dobivamo sljedeću formulu za korijene jednadžbe cos x = a kada

x = ±arccos a + 2pp, n £ Z.

1. Posebni slučajevi rješavanja jednadžbe cosx = a.

Korisno je zapamtiti posebne oznake za korijene jednadžbe cos x = a kada

a = 0, a = -1, a = 1, što se lako može dobiti korištenjem jedinične kružnice kao reference.

Budući da je kosinus jednak apscisi odgovarajuće točke jedinični krug, dobivamo da je cos x = 0 ako i samo ako je odgovarajuća točka jedinične kružnice točka A ili točka B.

Slično, cos x = 1 ako i samo ako je odgovarajuća točka jedinične kružnice točka C, dakle,

x = 2πp, k € Z.

Također cos x = -1 ako i samo ako je odgovarajuća točka jedinične kružnice točka D, dakle x = n + 2n,

Jednadžba sin(x) = a

Obrazloženje i obrazloženje

1. Korijenje sinx jednadžbe= a. Kada | a | > 1 jednadžba nema korijena, jer | sinx |< 1 для любого x (прямая y = а на рисунке при а >1 ili na a< -1 не пересекает график функции y = sinx).

Zakharova Lyudmila Vladimirovna
MBOU "Srednje" sveobuhvatna škola br. 59" Barnaul
profesorica matematike [e-mail zaštićen]

№1 Najjednostavnije trigonometrijske jednadžbe

Cilj: 1. Izvesti formule za rješenja najjednostavnijih trigonometrijskih jednadžbi oblika sinx =a, cosx=a, tgx=a, ctgx=a;

2. Naučiti rješavati jednostavne trigonometrijske jednadžbe pomoću formula.

Oprema: 1) Tablice s grafikonima trigonometrijske funkcije y= sinx, y=cosx, y=tgx, y=ctgx; 2) Tablica vrijednosti inverznih trigonometrijskih funkcija; 3) Zbirna tablica formula za rješavanje jednostavnih trigonometrijskih jednadžbi.

Plan predavanja:

1 .Izvođenje formula za korijene jednadžbe

a) sinx =a,

b) cosx= a,

c) tgx= a,

d) ctgx= A.

2 . Usmeni frontalni rad na učvršćivanju dobivenih formula.

3 . Papirologija učvrstiti naučeno gradivo

Tijekom nastave.

U algebri, geometriji, fizici i drugim predmetima susrećemo se s raznim problemima čije rješavanje uključuje rješavanje jednadžbi. Proučavali smo svojstva trigonometrijskih funkcija, pa je prirodno obratiti se na jednadžbe u kojima je nepoznanica sadržana pod predznakom funkcije

Definicija: Jednadžbe oblika sinx = a , cosx= a , tgx= a , ctgx= A nazivaju se najjednostavnije trigonometrijske jednadžbe.

Vrlo je važno naučiti rješavati najjednostavnije trigonometrijske jednadžbe, budući da se sve metode i tehnike rješavanja bilo koje trigonometrijske jednadžbe sastoje u njihovom reduciranju na najjednostavnije.

Počnimo s izvođenjem formula koje “aktivno” rade pri rješavanju trigonometrijskih jednadžbi.

1.Jednadžbe oblika sinx = a.

Riješimo jednadžbu sinx = a grafički. Da bismo to učinili, u jednom koordinatnom sustavu ćemo konstruirati grafove funkcija y=sinx i y= A.

1) Ako A> 1 i A grijeh x= A nema rješenja, budući da pravac i sinusni val nemaju zajedničkih točaka.

2) Ako -1a a prelazi sinusni val beskonačno mnogo puta. To znači da jednadžba sinx= a ima beskonačno mnogo rješenja.

Budući da je period sinusa 2 , zatim riješiti jednadžbu sinx= a dovoljno je pronaći sva rješenja na bilo kojem segmentu duljine 2.

Rješavanje jednadžbe na [-/2; /2] po definiciji arkusina x= arcsin a, a na x=-arcsin a. Uzimajući u obzir periodičnost funkcije u=sinx, dobivamo sljedeće izraze

x = -arcsin a+2n, n Z.

Obje serije rješenja mogu se kombinirati

X = (-1) n arcsin a+n, nZ.

U sljedeća tri slučaja radije koriste jednostavnije relacije nego opću formulu:

Ako A=-1, tada sin x =-1, x=-/2+2n

Ako A=1, tada sin x =1, x =/2+2n

Ako a= 0, tada je sin x =0. x = n,

Primjer: Riješite jednadžbu sinx =1/2.

Kreirajmo formule za rješenja x=arcsin 1/2+ 2n

X= - arcsin a+2n

Izračunajmo vrijednost arcsin1/2. Zamijenimo pronađenu vrijednost u formule rješenja

x=5/6+2n

ili prema općoj formuli

X= (-1) n arcsin 1/2+n,

X= (-1) n /6+n,

2. Jednadžbe oblika cosx= a.

Riješimo jednadžbu cosx= a također grafički, iscrtavanjem funkcija y= cosx i y= A.

1) Ako je 1, onda je jednadžba cosx= a nema rješenja jer grafovi nemaju zajedničkih točaka.

2) Ako je -1 a cosx= a Ima beskonačan skup odluke.

Naći ćemo sva rješenja cosx= a na intervalu duljine 2 jer je period kosinusa 2.

Prema definiciji ark kosinusa, rješenje jednadžbe bit će x= arcos a. S obzirom na paritet kosinusne funkcije, rješenje jednadžbe na [-;0] bit će x=-arcos a.

Dakle, rješavanje jednadžbe cosx= a x= + arcos a+ 2 n,

U tri slučaja nećemo koristiti opću formulu, već jednostavnije relacije:

Ako A=-1, tada cosx =-1, x =-/2+2n

Ako A=1, tada je cosx =1, x = 2n,

Ako je a=0, tada je cosx=0. x =/2+n

Primjer: Riješite jednadžbu cos x =1/2,

Kreirajmo formule za rješenja x=arccos 1/2+ 2n

Izračunajmo vrijednost arccos1/2.

Zamijenimo pronađenu vrijednost u formule rješenja

X= + /3+ 2n, nZ.

Jednadžbe oblika tgx= a.

Budući da je period tangente jednak, tada da bismo pronašli sva rješenja jednadžbe tgx= a, dovoljno je pronaći sva rješenja na bilo kojem intervalu duljine . Prema definiciji arktangensa, rješenje jednadžbe na (-/2; /2) je arktan a. Uzimajući u obzir period funkcije, sva rješenja jednadžbe mogu se napisati u obliku

x= arktan a+ n, nZ.

Primjer: Riješite jednadžbu tan x = 3/3

Kreirajmo formulu za rješavanje x= arktan 3/3 +n, nZ.

Izračunajmo vrijednost arktangensa arctan 3/3= /6, dakle

X=/6+ n, nZ.

Izvođenje formule za rješavanje jednadžbe S tgx= a mogu se pružiti studentima.

Primjer.

Riješite jednadžbu ctg x = 1.

x = arcctg 1 + n, nZ,

X = /4 + n, nZ.

Kao rezultat proučavanog materijala, studenti mogu ispuniti tablicu:

"Rješavanje trigonometrijskih jednadžbi."

jednadžba

Vježbe za učvršćivanje naučenog gradiva.

(usmeno) Koja se od napisanih jednadžbi može riješiti pomoću formula:

a) x= (-1) n arcsin a+n, nZ;

b) x= + arcos a+ 2n?

cos x = 2/2, tan x = 1, sin x = 1/3, cos x = 3/3, sin x = -1/2, cos x = 2/3, sin x = 3, cos x = 2 .

Koja od sljedećih jednadžbi nema rješenja?

Riješite jednadžbe:

a) sin x = 0; e) sin x = 2/2; h) sin x = 2;

b) cos x = 2/2; e) cos x = -1/2; i) cos x = 1;

d) tan x = 3; g) krevetić x = -1; j) tan x = 1/3.

3. Riješite jednadžbe:

a) sin 3x = 0; e) 2cos x = 1;

b) cos x/2 =1/2; e) 3 tg 3x =1;

d) sin x/4 = 1; g) 2cos(2x+ /5) = 3.

Pri rješavanju ovih jednadžbi korisno je zapisati pravila za rješavanje jednadžbi oblika grijeh V x = a, I S grijeh V x = a, | a|1.

Grijeh V x = a, |a|1.

V x = (-1) n arcsin a+n, nZ,

x= (-1) n 1/ V arcsin a+n/ V, nZ.

Sažimanje lekcije:

Danas smo na satu izvodili formule za rješavanje jednostavnih trigonometrijskih jednadžbi.

Pogledali smo primjere rješavanja jednostavnih trigonometrijskih jednadžbi.

Ispunili smo tablicu koju ćemo koristiti za rješavanje jednadžbi.

Domaća zadaća.

№2 Rješavanje trigonometrijskih jednadžbi

Cilj: Metode proučavanja rješavanja trigonometrijskih jednadžbi: 1) svodljive na kvadratne, 2) svodljive na homogene trigonometrijske jednadžbe.

Razvijati sposobnosti zapažanja kod učenika pri korištenju na razne načine rješavanje trigonometrijskih jednadžbi.

Frontalni rad s učenicima.

Koje su formule za korijene trigonometrijskih jednadžbi? cos x= a, sin x= a, tgx = a, ctg x = a.

Riješite jednadžbe (usmeno):

cos x=-1, sin x=0, tgx =0, cos x=1, cos x=1,5, sin x=0.

Pronađite pogreške i razmislite o razlozima za pogreške.

cos x=1/2, x= + /6+2k,k Z.

sin x= 3/2, x= /3+k, kZ.

tgx = /4, x=1+ k, kZ.

2. Učenje novog gradiva.

Ova lekcija će pokriti neke od najčešćih metoda za rješavanje trigonometrijskih jednadžbi.

Trigonometrijske jednadžbe svedene na kvadratne.

Ova klasa može uključivati ​​jednadžbe koje uključuju jednu funkciju (sinus ili kosinus) ili dvije funkcije istog argumenta, ali je jedna od njih reducirana na drugu pomoću osnovnih trigonometrijskih identiteta.

Na primjer, ako cosh ulazi u jednadžbu u parnim potencijama, tada ga zamijenimo s 1-sin 2 x, ako je sin 2 x, tada ga zamijenimo s 1-cos 2 x.

Primjer.

Riješite jednadžbu: 8 sin 2 x - 6sin x -5 =0.

Rješenje: Označimo sin x=t, tada je 8t 2 - 6t – 5=0,

D = 196,

T1 = -1/2, t2 = -5/4.

Izvršimo obrnutu zamjenu i riješimo sljedeće jednadžbe.

X=(-1) k+1 /6+ k, kZ.

Budući da je -5/4>1, jednadžba nema korijena.

Odgovor: x=(-1) k+1 /6+ k, kZ.

Rješavanje vježbi konsolidacije.

Riješite jednadžbu:

1) 2sin 2 x+ 3cos x = 0;

2) 5sin 2 x+ 6cos x -6 = 0;

3) 2sin 2 x+ 3cos 2 x = -2sin x;

4) 3 tg 2 x +2 tgx-1=0.

Homogene trigonometrijske jednadžbe.

Definicija: 1) Jednadžba oblikaa sinx + b cosx=0, (a=0, b=0) naziva se homogena jednadžba prvog stupnja s obzirom na sin x i cos x.

Odlučuje se dana jednadžba dijeljenjem oba dijela po cosx 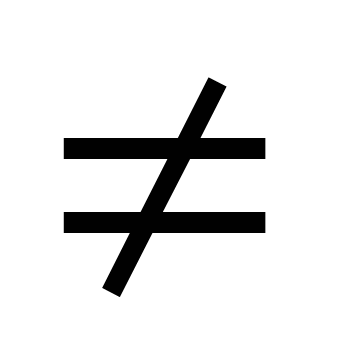0. Rezultat je jednadžba atgx+ b=0.

2) Jednadžba oblikaa grijeh 2 x + b sinx cosx + c cos 2 x =0 naziva se homogena jednadžba drugog stupnja, gdje su a, b, c bilo koji brojevi.

Ako je a = 0, tada jednadžbu rješavamo dijeljenjem obje strane s cos 2 x 0. Kao rezultat toga dobivamo jednadžbu atg 2 x+ btgx+s =0.

Komentar: Jednadžba oblikaa grijeh mx + b cos mx=0 ili

a grijeh 2 mx + b grijeh mx cos mx + c cos 2 mx =0 također su homogeni. Da bismo ih riješili, obje strane jednadžbe podijelimo s cos mx=0 ili cos 2 mx=0

3) Razne jednadžbe koje u početku nisu homogene mogu se svesti na homogene jednadžbe. Na primjer,grijeh 2 mx + b grijeh mx cos mx + c cos 2 mx = d, I a sinx + b cosx= d. Da biste riješili ove jednadžbe, morate desnu stranu pomnožiti s "trigonometrijska jedinica" oni. na grijeh 2 x + cos 2 x i izvoditi matematičke transformacije.

Vježbe za konsolidaciju proučenog materijala:

1) 2sin x- 3cos x = 0; 5) 4 sin 2 x – sin2x =3;

2) sin 2x+ cos2x = 0; 6) 3 sin 2 x + sinx cosx =2 cos 2 x ;

3) sin x+ 3cos x = 0; 7) 3 sin 2 x- sinx cosx =2;

4) sin 2 x -3 sinx cosx +2 cos 2 x =0

3. Sažimanje lekcije. Domaća zadaća.

U ovoj lekciji, ovisno o pripremljenosti grupe, možete razmotriti rješavanje jednadžbi oblika a sin mx +b cos mx=c, gdje a, b, c nisu istovremeno jednaki nuli.

Vježbe jačanja:

1. 3sin x + cos x=2;

2. 3sin 2x + cos 2x= 2;

3. sin x/3 + cos x/3=1;

4. 12 sin x +5 cos x+13=0.

№ 3 Rješavanje trigonometrijskih jednadžbi

Cilj: 1) Proučiti metodu rješavanja trigonometrijskih jednadžbi faktorizacijom; naučiti rješavati trigonometrijske jednadžbe pomoću raznih trigonometrijske formule;

2) Provjera: znanja učenika o formulama za rješavanje jednostavnih trigonometrijskih jednadžbi; sposobnost rješavanja jednostavnih trigonometrijskih jednadžbi.

Plan učenja:

Provjera domaće zadaće.

Matematički diktat.

Učenje novog gradiva.

Samostalni rad.

Sažimanje lekcije. Domaća zadaća.

Napredak lekcije:

Provjera domaće zadaće (rješenja trigonometrijskih jednadžbi ukratko su ispisana na ploči).

Matematički diktat.

U 1

1. Koje se jednadžbe nazivaju najjednostavnijim trigonometrijskim jednadžbama?

2. Kako se zove jednadžba oblikaa sinx + b cosx=0? Navedite način rješavanja.

3. Zapišite formulu za korijene jednadžbe tgx = a(ctg x= a).

4. Napiši formule za korijene jednadžbi oblika cosx= a, Gdje A=1, A=0, A=-1.

5. Zapišite opću formulu za korijene jednadžbe grijeh x= a, | a|

6. Kako se rješavaju jednadžbe oblikaa cosx= b, | b|

U 2

1. Napiši formule za korijene jednadžbi cosx= a,| a|

2. Zapišite opću formulu za korijene jednadžbe

= a, | a|

3. Kako se nazivaju jednadžbe oblika? grijeh x= a, tgx = a, grijeh x= a?

4. Zapišite formule za korijene jednadžbe grijeh x= a, Ako A=1, A=0, A=-1.

5. Kako se rješavaju jednadžbe oblika grijeh a x= b, | b|

6. Koje se jednadžbe nazivaju homogenim jednadžbama drugog stupnja? Kako se rješavaju?

Učenje novog gradiva.

Metoda faktorizacije.

Jedna od najčešće korištenih metoda za rješavanje trigonometrijskih jednadžbi je metoda faktorizacije.

Ako se jednadžba f(x) =0 može prikazati kao f 1 (x) f 2 (x) =0, tada se problem svodi na rješavanje dvije jednadžbe f 1 (x) = 0, f 2 (x) = 0 .

(S učenicima je korisno zapamtiti pravilo “ Umnožak faktora jednak je nuli ako je barem jedan od faktora jednak nuli, a ostali imaju smisla»)

Učvršćivanje naučenog gradiva kroz rješavanje jednadžbi različite složenosti.

(sin x-1/2)(sin x+1)=0; 2) (cosx- 2/2)(sin x+ 2/2)=0;(sam)

3) sin 2 x+ sin x cosx=0; 4) sin 2 x- sin x =0;

5) sin 2x – cosx=0; 6) 4 cos 2 x -1 =0; (2 načina)

7) cosx+ cos3x=0; 8) grijeh 3x= grijeh 17x;

9) sin x+ sin 2x+ sin 3x=0; 10) cos3x cos5x

11) sin x cos5x = sin 9x cos3x sin 2x sin 2x

12) 3 cosx sin x+ cos 2 x=0(sam)

13) 2 cos 2 x - sin (x- /2)+ tanx tan (x+/2)=0.

Samostalni rad.

Opcija-1 Opcija-2

1) 6 sin 2 x+ 5sin x -1=0; 1) 3 cos 2 x+2 cosx -5=0;

2) sin 2x – cos2x=0; 2) 3 cos x/2 - sin x/2=0;

3) 5 sin 2 x+ sin x cosx -2 cos 2 x=2; 3) 4sin 2 x- sin x cosx +7cos 2 x=5;

4) sin x+sin5x=sin3x+sin7x; 4) grijeh x-grijeh 2x +sin 3x-sin 4x=0;

5) sin x+cosx=1. 5) sin x+cosx=2.

8. Sažimanje lekcije. Domaća zadaća.