– izračunavanje težišta ravnog omeđenog lika. Mnogi čitatelji intuitivno razumiju što je težište, ali ipak preporučujem ponavljanje gradiva iz jedne od lekcija analitička geometrija, gdje sam se ljubio problem o težištu trokuta i dešifrirao ga u pristupačnom obliku fizičko značenje ovaj pojam.
U samostalnom i testni zadaci za rješenje se u pravilu predlaže najjednostavniji slučaj - ravan omeđen homogena brojka, odnosno stalna brojka fizička gustoća– igračke od stakla, drveta, lima, lijevanog željeza, teško djetinjstvo itd. Nadalje, prema zadanim postavkama, govorit ćemo samo o takvim brojkama =)
Prvo pravilo i najjednostavniji primjer : ako ravna figura ima centar simetrije, onda je to težište ove figure. Na primjer, središte okrugle homogene ploče. To je logično i razumljivo u svakodnevnom životu - masa takve figure je "prilično raspoređena u svim smjerovima" u odnosu na središte. Ne želim to okrenuti.
Međutim, u surovoj stvarnosti, malo je vjerojatno da će vam baciti slatkiš eliptična čokoladica, pa ćete se morati naoružati nekim ozbiljnim kuhinjskim alatom:
Koordinate težišta ravnog homogenog ograničenog lika izračunavaju se pomoću sljedeće formule :
, ili:
, gdje je područje regije (slika); ili vrlo kratko:
, Gdje
Integral ćemo konvencionalno zvati “X” integral, a integral “Y” integral.
Napomena za pomoć
: za stan ograničeno heterogena figure, čija je gustoća određena funkcijom, formule su složenije:
, Gdje 
– masa figure;u slučaju jednolike gustoće, one se pojednostavljuju na gornje formule.
Zapravo, sve novosti završavaju na formulama, ostalo je vaše umijeće rješavati dvostruke integrale Usput, sada je izvrsna prilika da vježbate i poboljšate svoju tehniku. I, kao što znate, nema granica savršenstvu =)
Dodajmo okrepljujuću porciju parabola:
Primjer 1
Odredite koordinate težišta homogenog ravnog lika omeđenog crtama.
Riješenje: linije su ovdje elementarne: definiraju x-os, a jednadžba – parabola, koja se lako i brzo može konstruirati pomoću geometrijske transformacije grafova:
– parabola, pomaknut 2 jedinice ulijevo i 1 jedinicu dolje.
Dovršit ću cijeli crtež odjednom s gotovom točkom težišta figure: 
Drugo pravilo: ako figura ima osi simetrije, tada težište ove figure nužno leži na ovoj osi.
U našem slučaju, lik je simetričan u odnosu na ravno, odnosno zapravo već znamo “x” koordinatu točke “em”.
Također imajte na umu da je okomito središte gravitacije pomaknuto bliže x-osi, budući da je lik tamo masivniji.
Da, možda još nisu svi u potpunosti razumjeli što je težište: podignite kažiprst prema gore i mentalno postavite osjenčani "potplat" s točkom na njega. Teoretski, brojka ne bi trebala pasti.
Pomoću formula nalazimo koordinate težišta figure 
, Gdje .
Ovdje je očigledan redoslijed obilaska područja (slika): 
Pažnja! Odlučivanje o najpovoljnijem redoslijedu obilaska jednom- i iskoristiti ga za sve integrali!
1) Prvo izračunajte površinu figure. Zbog relativne jednostavnosti integrala, rješenje se može napisati kompaktno; glavna stvar je da se ne zbunite u izračunima:
Gledamo crtež i procjenjujemo površinu po ćelijama. Ispostavilo se da je riječ o slučaju.
2) X koordinata težišta je već pronađena “ grafička metoda", tako da se možete pozvati na simetriju i prijeći na sljedeću točku. Međutim, još uvijek ne preporučujem da to radite - postoji velika vjerojatnost da će rješenje biti odbijeno s formulacijom "upotrijebite formulu".
Imajte na umu da ovdje možete proći samo mentalnim izračunima - ponekad uopće nije potrebno smanjiti razlomke na zajednički nazivnik ili mučiti kalkulator.
Tako: 
, što je i bilo potrebno dobiti.
3) Odredite ordinatu težišta. Izračunajmo integral “igre”:
Ali ovdje bi bilo teško bez kalkulatora. Za svaki slučaj, komentirat ću da se kao rezultat množenja polinoma dobije 9 članova, a neki od njih su slični. Usmeno sam dao slične uvjete (kao što se obično radi u sličnim slučajevima) i odmah zapisao ukupan iznos.
Kao rezultat: 
, što je vrlo, vrlo slično istini.
Na završna faza označite točku na crtežu. Prema uvjetu nije bilo potrebno crtati bilo što, ali u većini zadataka prisiljeni smo, htjeli-ne htjeli, nacrtati figuru. Ali postoji apsolutni plus - vizualna i prilično učinkovita provjera rezultata.
Odgovor: 
Sljedeća dva primjera trebate sami riješiti.
Primjer 2
Odredite koordinate težišta homogenog ravnog lika omeđenog crtama 
Usput, ako zamislite kako se parabola nalazi i vidite točke u kojima siječe os, onda ovdje zapravo možete bez crteža.
I još kompliciranije:
Primjer 3
Odredite težište homogenog ravnog lika omeđenog crtama
Ako imate poteškoća s konstruiranjem grafikona, proučite (ponovite) lekcija o parabolama i/ili Primjer br. 11. članka Dvostruki integrali za lutke.
Primjeri rješenja na kraju lekcije.
Osim toga, desetak-dva sličnih primjera može se pronaći u pripadajućoj arhivi na stranici Gotova rješenja za višu matematiku.
Pa, ne mogu a da ne obradujem ljubitelje više matematike, koji me često traže da analiziram teške probleme:
Primjer 4
Odredite težište homogenog ravnog lika omeđenog crtama. Nacrtajte lik i njegovo težište na crtežu.
Riješenje: uvjet ovog zadatka već kategorički zahtijeva završetak crteža. Ali zahtjev nije tako formalan! – čak i osoba s prosječnom razinom obuke može zamisliti ovu brojku u svom umu: 
Ravna linija siječe krug na 2 dijela i dodatnu klauzulu (cm. linearne nejednakosti)
ukazuje da je riječ o malom zasjenjenom komadu.
Slika je simetrična u odnosu na ravnu liniju (prikazana isprekidanom linijom), tako da težište treba ležati na ovoj liniji. I, očito, njegove koordinate su jednake modulo. Izvrsna smjernica koja praktički eliminira mogućnost pogrešnog odgovora!
Sada loše vijesti =) Na horizontu se nazire neugodan integral korijena, koji smo detaljno ispitali u primjeru br. 4 lekcije Učinkovite metode rješavanja integrala. I tko zna što će se tamo još nacrtati. Čini se da zbog prisutnosti krug isplativo, ali nije sve tako jednostavno. Jednadžba pravca se transformira u oblik 
a integrali također neće ispasti šećer (iako obožavatelji trigonometrijski integrali cijenit će). S tim u vezi, pažljivije je zadržati se Kartezijeve koordinate Oh.
Redoslijed obilaska figure: 
1) Izračunajte površinu figure:
Racionalnije je uzeti prvi integral subsumirajući diferencijalni predznak:
A u drugom integralu vršimo standardnu zamjenu:
Izračunajmo nove granice integracije: 
2) Pronađimo.
Ovdje je u 2. integralu opet korišten metoda podvođenja funkcije pod diferencijalni predznak. Vježbajte i usvojite ove optimalne (po mom mišljenju) tehnike rješavanja standardnih integrala.
Nakon teških i dugotrajnih proračuna, ponovno usmjeravamo pažnju na crtež (zapamtite da bodova još ne znamo! ) i dobivamo duboko moralno zadovoljstvo od pronađene vrijednosti.
3) Na temelju ranije provedene analize, ostaje da se uvjerimo da .
Sjajno: 
Povucimo točku 
na crtežu. Sukladno tekstu uvjeta, isti ispisujemo kao konačan odgovor: 
Sličan zadatak koji možete riješiti sami:
Primjer 5
Odredite težište homogenog ravnog lika omeđenog crtama. Izvršite crtež.
Ovaj problem je zanimljiv jer sadrži figuru prilično male veličine, a ako negdje pogriješite, postoji velika vjerojatnost da uopće "ne uđete" u to područje. Što je svakako dobro sa stajališta kontrole odlučivanja.
Ogledni dizajn na kraju lekcije.
Ponekad ima smisla prijelaz na polarne koordinate u dvostrukim integralima. Ovisi o figuri. Tražio sam i tražio uspješan primjer, ali ga nisam mogao pronaći, pa ću demonstrirati rješenje u 1. demo problemu gornje lekcije: 
Podsjetit ću vas da smo u tom primjeru išli polarne koordinate, saznali redoslijed obilaženja područja 
i izračunao njegovu površinu
Nađimo težište ove figure. Shema je ista: 
. Vrijednost se gleda izravno s crteža, a koordinatu "x" treba pomaknuti malo bliže osi ordinata, jer se tamo nalazi masivniji dio polukruga.
U integralima koristimo standardne formule prijelaza:
Vjerojatno, najvjerojatnije, nisu pogriješili.
Predavanje 4. Težište.
Ovo predavanje pokriva sljedeća pitanja
1. Težište čvrsta.
2. Koordinate težišta nehomogenih tijela.
3. Koordinate težišta homogenih tijela.
4. Metode određivanja koordinata težišta.
5. Težišta nekih homogenih tijela.
Proučavanje ovih pitanja nužno je u budućnosti za proučavanje dinamike gibanja tijela uzimajući u obzir trenje klizanja i kotrljanja, dinamiku gibanja središta mase mehaničkog sustava, kinetičke momente, za rješavanje problema u disciplina “Čvrstoća materijala”.
Dovođenje paralelnih sila.
Nakon što smo razmotrili dovođenje ravnog sustava i proizvoljnog prostornog sustava sila u središte, ponovno se vraćamo na razmatranje posebnog slučaja sustava paralelnih sila.
Dovođenje dviju paralelnih sila.
U tijeku razmatranja takvog sustava sila moguća su sljedeća tri slučaja redukcije.
1. Sustav dviju kolinearnih sila. Promotrimo sustav dviju paralelnih sila usmjerenih u jednom smjeru P I Q, primijenjen u točkama A I U. Pretpostavit ćemo da su sile okomite na ovaj segment (sl. 1, A).
S, koji pripada segmentu AB i zadovoljavaju uvjet:
AC/NE = Q/P.(1)
Glavni vektor sustava R C = P + Q jednak je po modulu zbroju ovih sila: R C = P + Q.
S uzimajući u obzir (1) jednaka je nuli:MC = P ∙ AC- Q∙ CB = 0.
Dakle, kao rezultat lijevanja dobili smo: R C ≠ 0, MC= 0. To znači da je glavni vektor ekvivalentan rezultanti koja prolazi kroz centar redukcije, to jest:
Rezultanta kolinearnih sila jednaka je po modulu njihovom zbroju, a njezina linija djelovanja dijeli segment koji povezuje točke njihove primjene, obrnuto proporcionalno modulima tih sila na unutarnji način.
Imajte na umu da položaj točke S neće promijeniti ako sile R I Q okrenuti kutα. Točka S, koji ima ovo svojstvo se zove centar paralelnih sila.
2. Sustav dvojke antikolinearni a sile koje nisu jednake po veličini. Neka snaga P I Q, primijenjen u točkama A I U, paralelne, usmjerene u suprotnim smjerovima i nejednake veličine (Sl. 1, b).
Odaberimo točku kao redukcijsko središte S, koji još uvijek zadovoljava relaciju (1) i leži na istom pravcu, ali izvan segmenta AB.
Glavni vektor ovog sustava R C = P + Q modul će sada biti jednak razlici između modula vektora: R C = Q - P.
Glavna točka u vezi centra S još uvijek je nula:MC = P ∙ AC- Q∙ NE= 0, dakle
Rezultat antikolinearni a sile koje nisu jednake po veličini jednake su njihovoj razlici, usmjerene prema većoj sili, a njezina linija djelovanja dijeli segment koji povezuje točke njihova djelovanja, obrnuto proporcionalno vanjskim modulima tih sila.
Sl. 1
3. Sustav dvojke antikolinearni a sile jednake po veličini. Uzmimo prethodni slučaj redukcije kao početni. Popravimo silu R, i snagu Q usmjerimo modul na silu R.
Zatim na Q → R u formuli (1) odnos AC/NE → 1. Ovo znači da AC → NE, odnosno udaljenost AC →∞ .
U ovom slučaju, modul glavnog vektora R C → 0, a modul glavnog momenta ne ovisi o položaju središta redukcije i ostaje jednak izvornoj vrijednosti:
MC = P ∙ AC- Q∙ NE = P ∙ ( AC- NE) =P ∙ AB.
Dakle, u granici smo dobili sustav sila za koji R C = 0, MC≠ 0, a središte redukcije je uklonjeno u beskonačnost, što se ne može zamijeniti rezultantom. Nije teško prepoznati par sila u ovom sustavu, dakle par sila nema rezultantu.
Središte sustava paralelnih sila.
Razmotrite sustav n snaga P i, primijenjen u točkamaA i (x i , y i , z i) i paralelna s osiOv s ort l(slika 2).
Ako unaprijed isključimo slučaj sustava ekvivalentnog paru sila, nije teško na temelju prethodnog paragrafa dokazati postojanje njegove rezultanteR.
Odredimo koordinate središtaC(x c, g c, z c) paralelne sile, odnosno koordinate točke primjene rezultante ovog sustava.
U tu svrhu koristimo Varignonov teorem na temelju kojeg:
M0 (R) = Σ M0(P i).
sl.2
Vektor-moment sile može se prikazati kao vektorski produkt, dakle:
M 0 (R) = r c× R = Σ M0i(P i) = Σ ( r i× P i ).
S obzirom na to R = Rv ∙ l, A P i = Pvi ∙ l i koristeći svojstva vektorski proizvod, dobivamo:
r c × Rv ∙ l = Σ ( r i × Pvi ∙ l),
r c ∙ R v× l = Σ ( r i ∙ Pvi × l) = Σ ( r i ∙ Pvi ) × l,
ili:
[ r c R v - Σ ( r i Pvi )] × l= 0.
Posljednji izraz vrijedi samo ako je izraz u uglatim zagradama jednak nuli. Stoga, izostavljanje indeksava uzimajući u obzir da rezultantaR = Σ P i , odavde dobivamo:
r c = (Σ P i r i )/(Σ P i ).
Projiciranjem posljednje vektorske jednakosti na koordinatnu os dobivamo traženu izraz za koordinate središta paralelnih sila:
x c = (Σ P i x i)/(Σ P i );
y c = (Σ P i y i )/(Σ P i );(2)
z c = (Σ P i z i )/(Σ P i ).
Težište tijela.
Koordinate težišta homogenog tijela.
Razmotrimo vaganje krutog tijela P i volumen V u koordinatnom sustavu Oxyz, gdje su sjekire x I g spojen na površinu zemlje, i os z usmjeren u zenit.
Razbijemo li tijelo na elementarne dijelove s volumenom∆ V ja , tada će sila privlačenja djelovati na svaki njegov dio∆ P i, usmjeren prema središtu Zemlje. Pretpostavimo da su dimenzije tijela znatno manje od dimenzija Zemlje, tada se sustav sila koji djeluje na elementarne dijelove tijela može smatrati ne konvergentnim, već paralelnim (slika 3), a svi zaključci prethodnog poglavlja primjenjivi su na njega.
sl.3
Definicija . Težište čvrstog tijela je središte paralelnih sila gravitacije elementarnih dijelova tog tijela.
Prisjetimo se toga specifična gravitacija elementarnog dijela tijela naziva se odnos njegove težine∆ P i na volumen ∆ V ja : γ ja = ∆ P i/ ∆ V ja . Za homogeno tijelo ova vrijednost je konstantna:γ ja = γ = P/ V.
Zamjenom ∆ u (2) P i = γ ja ∙∆ V ja umjesto P i, uzimajući u obzir posljednju napomenu i smanjujući brojnik i nazivnik zag, dobivamo izrazi za koordinate težišta homogenog tijela:
x c = (Σ ∆ V i∙ x i)/(Σ ∆ V i);
y c = (Σ ∆ V i∙ y i )/(Σ ∆ V i);(3)
z c = (Σ ∆ V i∙ z i )/(Σ ∆ V i).
Nekoliko je teorema korisno za određivanje težišta.
1) Ako homogeno tijelo ima ravninu simetrije, tada je njegovo težište u toj ravnini.
Ako sjekire x I na koja se nalazi u ovoj ravnini simetrije, zatim za svaku točku s koordinatama. I koordinata prema (3), bit će jednaka nuli, jer ukupno svi članovi suprotnih predznaka uništavaju se u parovima. To znači da se težište nalazi u ravnini simetrije.
2) Ako homogeno tijelo ima os simetrije, tada je težište tijela na toj osi.
Doista, u ovom slučaju, ako je osznacrtati duž osi simetrije, za svaku točku s koordinatamamožete pronaći točku s koordinatama i koordinate i , izračunat pomoću formule (3), bit će jednak nuli.
Treći teorem dokazuje se na sličan način.
3) Ako homogeno tijelo ima centar simetrije, tada je težište tijela u ovoj točki.
I još nekoliko komentara.
Prvi. Ako se tijelo može podijeliti na dijelove za koje je poznata težina i položaj težišta, tada nema potrebe razmatrati svaku točku, au formulama (3) P i – određena kao težina odgovarajućeg dijela i– kao koordinate njegovog težišta.
Drugi. Ako je tijelo homogeno, tada je težina pojedinog njegovog dijela, Gdje - specifična težina materijala od kojeg je tijelo izrađeno, i V i - volumen ovog dijela tijela. I formule (3) će imati prikladniji oblik. Na primjer,
I slično, gdje - volumen cijelog tijela.
Treća bilješka. Neka tijelo ima oblik tanke ploče s površinom F i debljine t, ležeći u avionu Oxy. Zamjena u (3)∆ V ja =t ∙ ∆F ja , dobivamo koordinate težišta homogene ploče:
x c = (Σ ∆ F i∙ x i) / (Σ ∆ F i);
y c = (Σ ∆ F i∙ y i ) / (Σ ∆ F i).
z c = (Σ ∆ F i∙ z ja ) / (Σ ∆ F i).
Gdje – koordinate težišta pojedinih ploča;– ukupna površina tijela.
Četvrta bilješka. Za tijelo u obliku tanke zakrivljene šipke dužine L s površinom presjeka a elementarni volumen∆ V ja = a ∙∆ L ja , Zato koordinate težišta tankog zakrivljenog štapa bit će jednako:
x c = (Σ ∆ L i∙ x i)/(Σ ∆ L i);
y c = (Σ ∆ L i∙ y i )/(Σ ∆ L i);(4)
z c = (Σ ∆ L i∙ z i )/(Σ ∆ L i).
Gdje – koordinate težištaja-th odjeljak; .
Imajte na umu da je, prema definiciji, težište geometrijska točka; može ležati i izvan granica danog tijela (npr. za prsten).
Bilješka.
U ovom dijelu tečaja ne pravimo razliku između gravitacije, gravitacije i tjelesne težine. U stvarnosti, gravitacija je razlika između gravitacijske sile Zemlje i centrifugalne sile uzrokovane njezinom rotacijom.
Koordinate težišta nehomogenih tijela.
Koordinate težišta nehomogena čvrsta tvar(Sl.4) u odabranom referentnom sustavu određuju se na sljedeći način:
sl.4
Gdje - težina po jedinici volumena tijela (specifična težina)
- težina cijelog tijela.
nejednolika površina(Sl. 5), tada se koordinate težišta u odabranom referentnom sustavu određuju na sljedeći način:
sl.5
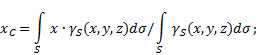
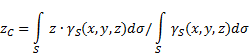
Gdje - težina po jedinici površine tijela,
- težina cijelog tijela.
Ako je krutina nejednolika linija(Sl. 6), tada se koordinate težišta u odabranom referentnom sustavu određuju na sljedeći način:
sl.6
Gdje - težina po dužini tijela,
Težina cijelog tijela.
Metode određivanja koordinata težišta.
Na temelju gore dobivenih općih formula moguće je naznačiti specifične metode određivanje koordinata težišta tijela.
1. Simetrija. Ako homogeno tijelo ima ravninu, os ili centar simetrije (sl. 7), tada njegovo težište leži u ravnini simetrije, osi simetrije ili u centru simetrije.
sl.7
2. Cijepanje. Tijelo se probija konačni broj dijelova (slika 8), za svaki od njih su poznati položaj težišta i površina.
sl.8
S = S 1 + S 2.
3.Metoda negativne površine. Poseban slučaj metode particioniranja (slika 9). Za tijela koja imaju izreze vrijedi ako su poznata težišta tijela bez izreza i izrezanog dijela. Tijelo u obliku ploče s izrezom predstavljeno je kombinacijom pune ploče (bez izreza) s površinom S 1 i područje odsječenog dijela S2.
Sl.9
S = S 1 - S 2.
4.Metoda grupiranja. Dobra je nadopuna zadnje dvije metode. Nakon podjele figure na sastavne elemente, zgodno je neke od njih ponovno kombinirati kako bi se zatim pojednostavilo rješenje uzimajući u obzir simetriju ove skupine.
Težišta nekih homogenih tijela.
1) Težište kružnog luka. Razmotrite luk AB radiusR sa središnjim kutom. Zbog simetrije, težište ovog luka leži na osiVol(slika 10).
Sl.10
Nađimo koordinatu prema formuli . Da biste to učinili, odaberite na luku AB element MM ’ duljina, čiji je položaj određen kutom. Koordinirati x element MM' htjeti. Zamjenom ovih vrijednosti x I d l i imajući na umu da se integral mora proširiti preko cijele duljine luka, dobivamo:
gdje je L duljina luka AB, jednaka .
Odavde konačno nalazimo da težište kružnog luka leži na njegovoj osi simetrije na udaljenosti od središta O jednako
gdje je kut mjereno u radijanima.
2) Težište površine trokuta. Promotrimo trokut koji leži u ravnini Oxy, čije su koordinate vrhova poznate: A i (x i,y i ), (ja= 1,2,3). Razbijanje trokuta u uske trake paralelne sa strane A 1 A 2, dolazimo do zaključka da težište trokuta mora pripadati središnjici A 3 M 3 (slika 11).
Sl.11
Razbijanje trokuta na trake paralelne sa stranicom A 2 A 3, možemo potvrditi da mora ležati na medijani A 1 M 1 . Tako, težište trokuta nalazi se u sjecištu njegovih središnjica, koji, kao što je poznato, od svake sredine odvaja treći dio, računajući od odgovarajuće strane.
Konkretno, za medijan A 1 M 1 dobivamo, uzimajući u obzir da su koordinate točke M 1 - ovo je aritmetička sredina koordinata vrhova A 2 i A 3 :
x c = x 1 + (2/3) ∙ (xM 1 - x 1 ) = x 1 + (2/3) ∙ [(x 2 + x 3 )/2 - x 1 ] = (x 1 + x 2 + x 3 )/3.
Dakle, koordinate težišta trokuta su aritmetička sredina koordinata njegovih vrhova:
x c =(1/3) Σ x i ; g c =(1/3) Σ y i .
3) Težište područja kružnog sektora. Razmotrimo sektor kruga s radijusom R sa središnjim kutom 2α , smješten simetrično oko osi Vol (Sl. 12) .
Očito je da g c = 0, a udaljenost od središta kružnice iz koje je taj sektor odsječen do njezina težišta može se odrediti formulom:
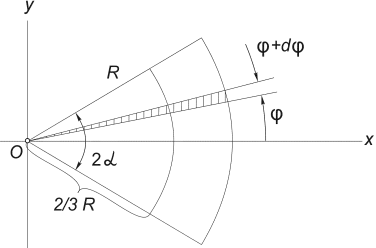
sl.12
Najlakši način za izračunavanje ovog integrala je dijeljenje domene integracije na elementarne sektore s kutom dφ . Točno do infinitezimala prvog reda, takav se sektor može zamijeniti trokutom s bazom jednakom R × dφ i visine R. Površina takvog trokuta dF =(1/2)R 2 ∙ dφ , a težište mu je na udaljenosti 2/3 R od vrha, stoga u (5) stavljamo x = (2/3)R∙ cosφ. Zamjena u (5) F= α R 2, dobivamo:
Koristeći posljednju formulu, izračunavamo, posebno, udaljenost do težišta polukrug.
Zamjenom α = π /2 u (2) dobivamo: x c = (4 R)/(3π) ≅ 0,4 R .
Primjer 1.Odredimo težište homogenog tijela prikazanog na sl. 13.
sl.13
Riješenje.Tijelo je homogeno, sastoji se od dva dijela simetričnog oblika. Koordinate njihovih težišta:
Njihov volumen:
Prema tome, koordinate težišta tijela
Primjer 2. Nađimo težište ploče savijene pod pravim kutom. Dimenzije su na crtežu (slika 14).
sl.14
Riješenje. Koordinate centara gravitacije:
0.
područja:
Zato:
Primjer 3.
Na kvadratnom listu
cm kvadratna rupa izrezana
cm (slika 15). Nađimo težište lista. Primjer 4. Odredite položaj težišta ploče prikazane na sl. 16. Dimenzije su dane u centimetrima.
sl.16
Riješenje. Podijelimo ploču na figure (slika 17), središtačija je težina poznata.
Površine ovih figura i koordinate njihovih težišta:
1) pravokutnik sa stranicama 30 i 40 cm,S 1 =30 ∙ 40=1200 cm 2 ; x 1=15 cm; na 1 =20 cm.
2) pravokutni trokut s bazom od 50 cm i visinom od 40 cm;S 2 =0,5 ∙ 50 ∙ 40= 1000 cm 2 ; x 2 =30+50/3=46,7 cm; y 2 =40/3 =13,3 cm;
3) polukrug radijus krug r = 20 cm;S 3 =0,5 ∙π∙ 20 2 =628 cm 2 ; x 3 =4 R /3 π =8,5 cm; na
Riješenje. Prisjetimo se da je u fizici gustoća tijelaρ i njegovu specifičnu težinugpovezani su relacijom:γ = ρ g , Gdjeg - ubrzanje slobodan pad. Da biste pronašli masu takvog homogenog tijela, morate pomnožiti gustoću s njegovim volumenom.
sl.19
Izraz "linearna" ili "linearna" gustoća znači da se za određivanje mase rešetkaste šipke linearna gustoća mora pomnožiti s duljinom ove šipke.
Da biste riješili problem, možete koristiti metodu particioniranja. Predstavljajući danu rešetku kao zbroj 6 pojedinačnih šipki, dobivamo:
GdjeL i duljinaja th rešetkasta šipka, ix i , y i - koordinate svog težišta.
Rješenje ovog problema može se pojednostaviti grupiranjem zadnjih 5 šipki rešetke. Lako je vidjeti da oni tvore lik sa središtem simetrije smještenim u sredini četvrtog štapa, gdje se nalazi i težište ove grupe štapova.
Dakle, dana rešetka može biti predstavljena kombinacijom samo dvije skupine šipki.
Prvu skupinu čini prvi štap, za njemL 1 = 4 m,x 1 = 0 m,g 1 = 2 m. Drugu skupinu šipki čini pet šipki, za njuL 2 = 20 m,x 2 = 3 m,g 2 = 2 m.
Koordinate težišta rešetke nalaze se pomoću formule:
x c = (L 1 ∙ x 1 + L 2 ∙ x 2 )/(L 1 + L 2 ) = (4∙0 + 20∙3)/24 = 5/2 m;
g c = (L 1 ∙ g 1 + L 2 ∙ g 2 )/(L 1 + L 2 ) = (4∙2 + 20∙2)/24 = 2 m.
Imajte na umu da centar S leži na ravnoj crti koja spaja S 1 i S 2 i dijeli segment S 1 S 2 u vezi: S 1 S/SS 2 = (x c - x 1 )/(x 2 - x c ) = L 2 / L 1 = 2,5/0,5.
Pitanja za samotestiranje
- Što se naziva središtem paralelnih sila?
- Kako se određuju koordinate središta paralelnih sila?
- Kako odrediti središte paralelnih sila čija je rezultanta nula?
- Koja svojstva ima centar paralelnih sila?
- Koje formule se koriste za izračunavanje koordinata središta paralelnih sila?
- Kako se zove težište tijela?
- Zašto se gravitacijske sile Zemlje koje djeluju na točku na tijelu mogu uzeti kao sustav paralelnih sila?
- Napiši formulu za određivanje položaja težišta nehomogenih i homogenih tijela, formulu za određivanje položaja težišta ravnih presjeka?
- Zapišite formulu za određivanje položaja težišta jednostavnog geometrijski oblici: pravokutnik, trokut, trapez i polukrug?
- Što se zove statički moment površine?
- Navedite primjer tijela čije se težište nalazi izvan tijela.
- Kako se svojstva simetrije koriste za određivanje težišta tijela?
- Što je bit metode negativnih pondera?
- Gdje se nalazi težište kružnog luka?
- Kojom se grafičkom konstrukcijom može pronaći težište trokuta?
- Zapišite formulu koja određuje težište kružnog isječka.
- Koristeći formule za određivanje težišta trokuta i kružnog isječka, izvedite sličnu formulu za kružni isječak.
- Koje formule se koriste za izračunavanje koordinata težišta homogenih tijela, ravnih likova i pravaca?
- Kako se naziva statički moment površine ravne figure u odnosu na os, kako se izračunava i koju dimenziju ima?
- Kako odrediti položaj težišta nekog područja ako je poznat položaj težišta pojedinih njegovih dijelova?
- Koji se pomoćni teoremi koriste za određivanje položaja težišta?
Cilj rada – analitički i eksperimentalno odrediti težište složene figure.
Teorijska pozadina. Materijalna tijela se sastoje od elementarne čestice, čiji je položaj u prostoru određen njihovim koordinatama. Sile privlačenja svake čestice prema Zemlji mogu se smatrati sustavom paralelnih sila, rezultanta tih sila naziva se sila teže tijela ili težina tijela. Težište tijela je točka primjene sile teže.
Težište je geometrijska točka, koji se mogu nalaziti izvan tijela (na primjer, disk s rupom, šuplja lopta itd.). Velik praktični značaj ima definiciju težišta tankih ravnih homogenih ploča. Njihovu debljinu obično možemo zanemariti i pretpostaviti da se težište nalazi u ravnini. Ako koordinatna ravnina xOy je poravnat s ravninom figure, tada je položaj težišta određen s dvije koordinate:
gdje je površina dijela figure, ();
– koordinate težišta dijelova figure, mm (cm).
| Presjek figure | A, mm 2 | X c ,mm | Yc, mm |
 | bh | b/2 | h/2 |
 | bh/2 | b/3 | h/3 |
 | R 2a | ||
| Na 2α = π πR 2 /2 |
Postupak rada.
Nacrtajte lik složenog oblika koji se sastoji od 3-4 jednostavne figure (pravokutnik, trokut, krug itd.) U mjerilu 1:1 i označite njegove dimenzije.
Nacrtajte koordinatne osi tako da pokrivaju cijeli lik, rastavite složeni lik na jednostavne dijelove, odredite površinu i koordinate težišta svakog jednostavnog lika u odnosu na odabrani koordinatni sustav.
Analitički izračunajte koordinate težišta cijelog lika. Izrežite ovu figuru od tankog kartona ili šperploče. Izbušite dvije rupe, rubovi rupa trebaju biti glatki, a promjer rupa neka bude nešto veći od promjera igle za vješanje figure.
Prvo objesite figuru na jednu točku (rupu), olovkom povucite crtu koja se podudara s viskom. Ponovite isto kad figuru objesite na neko drugo mjesto. Središte gravitacije figure, pronađeno eksperimentalno, mora se podudarati.
Odredite analitički koordinate težišta tanke homogene ploče. Provjerite eksperimentalno
Algoritam rješenja
1. Analitička metoda.
a) Nacrtaj crtež u mjerilu 1:1.
b) Rastaviti složenu figuru na jednostavnu
c) Odaberite i nacrtajte koordinatne osi (ako je lik simetričan, onda po osi simetrije, inače po konturi lika)
d) Izračunaj površinu prostih likova i cijelog lika
e) Označite položaj težišta svakog jednostavnog lika na crtežu
f) Izračunajte koordinate težišta svake figure
(x i y os)
g) Izračunajte koordinate težišta cijelog lika pomoću formule
h) Označite položaj težišta na crtežu C (
2. Eksperimentalno određivanje.
Točnost rješenja zadatka može se provjeriti eksperimentalno. Izrežite ovu figuru od tankog kartona ili šperploče. Izbušite tri rupe, rubovi rupa trebaju biti glatki, a promjer rupa neka bude nešto veći od promjera igle za vješanje figure.
Prvo objesite figuru na jednu točku (rupu), olovkom povucite crtu koja se podudara s viskom. Ponovite isto kad vješate figuru na drugim točkama. Vrijednost koordinata težišta figure, koja se nalazi pri vješanju figure na dvije točke: . Središte gravitacije figure, pronađeno eksperimentalno, mora se podudarati.
3. Zaključak o položaju težišta tijekom analitičkog i eksperimentalnog određivanja.
Vježbajte
Analitički i eksperimentalno odrediti težište ravnog presjeka.
 |  |  |
 |  |  |
 |  |  |
 |  |  |
 |  |  |
 |  |  |
 |  |  |
 |  |  |
 |  |  |
 |  |  |
Primjer izvedbe
Zadatak
Odredite koordinate težišta tanke homogene ploče.
I Analitička metoda
1. Crtež je nacrtan u mjerilu (dimenzije se obično daju u mm)
2. Složenu figuru rastavljamo na jednostavne.
1- Pravokutnik
2- Trokut (pravokutnik)
3- Površina polukruga (ne postoji, znak minus).
Nalazimo položaj težišta jednostavnih figura točaka, i
3. Nacrtajte koordinatne osi kako vam odgovara i označite ishodište koordinata.
4. Izračunajte površine jednostavnih likova i površinu cijelog lika. [veličina u cm]
(3. ne, znak -).
Područje cijele figure
5. Nađi koordinatu središnje točke. , i na crtežu.
6. Izračunajte koordinate točaka C 1, C 2 i C 3
7. Izračunajte koordinate točke C
8. Označite točku na crtežu
II Iskusan
Koordinate težišta eksperimentalno.
Kontrolna pitanja.
1. Može li se sila teže nekog tijela promatrati kao rezultanta sustava paralelnih sila?
2. Može li se locirati težište cijelog tijela?
3. U čemu je bit eksperimentalnog određivanja težišta ravnog lika?
4. Kako se određuje težište složene figure koja se sastoji od više jednostavnih likova?
5. Kako treba lik složenog oblika racionalno podijeliti na jednostavne likove pri određivanju težišta cijelog lika?
6. Koji znak ima površina rupa u formuli za određivanje težišta?
7. U sjecištu kojih linija trokuta se nalazi njegovo težište?
8. Ako je figuru teško rastaviti na mali broj jednostavnih figura, koja metoda određivanja težišta može dati najbrži odgovor?
“Rješavanje složenih problema”
Cilj rada: moći rješavati složene probleme (kinematika, dinamika)
Teorijska pozadina: Brzina je kinematička mjera kretanja točke, koja karakterizira brzinu promjene njezina položaja. Brzina točke je vektor koji karakterizira brzinu i smjer kretanja točke ovaj trenutak vrijeme. Kada se gibanje točke zadaje jednadžbama, projekcije brzine na kartezijeve koordinatne osi jednake su:
Modul brzine točke određuje se formulom
Smjer brzine određen je kosinusima smjera:
Obilježje brzine promjene brzine je ubrzanje a. Ubrzanje točke jednako je vremenskoj derivaciji vektora brzine:
Pri zadavanju gibanja točke jednadžbe za projekciju ubrzanja na koordinatne osi jednake su:
Modul ubrzanja:
Modul punog ubrzanja
Modul tangencijalnog ubrzanja određuje se formulom
Normalni modul ubrzanja određuje se formulom
gdje je polumjer zakrivljenosti putanje u datoj točki.
Smjer ubrzanja određen je kosinusima smjera
Jednadžba rotacijskog gibanja krutog tijela oko nepomične osi ima oblik
Kutna brzina tijela:
Ponekad se kutna brzina karakterizira brojem okretaja u minuti i označava se slovom . Ovisnost između i ima oblik
Kutno ubrzanje tijela:
Sila jednaka umnošku mase dane točke s njezinom akceleracijom i smjerom u smjeru koji je izravno suprotan akceleraciji točke naziva se sila tromosti.
Snaga je rad koji sila izvrši u jedinici vremena.
Osnovna dinamička jednadžba za rotacijsko gibanje
– moment tromosti tijela u odnosu na os rotacije je zbroj umnožaka masa materijalnih točaka s kvadratom njihovih udaljenosti od ove osi
Vježbajte
Tijelo mase m se uz pomoć sajle namotane na bubanj promjera d giba gore ili dolje po kosoj ravnini s kutom nagiba α. Jednadžba gibanja tijela S=f(t), jednadžba rotacije bubnja, gdje je S u metrima; φ - u radijanima; t – u sekundama. P i ω su redom snaga i kutna brzina na osovini bubnja u trenutku završetka ubrzavanja odnosno početka kočenja. Vrijeme t 1 – vrijeme ubrzanja (od mirovanja do zadane brzine) ili kočenja (od zadane brzine do zaustavljanja). Koeficijent trenja klizanja između tijela i ravnine je –f. Zanemariti gubitke trenja na bubnju, kao i masu bubnja. Kod rješavanja zadataka uzeti g=10 m/s 2
| br. var | α, stupanj | Zakon gibanja | Na primjer, kretanje | m, kg | t 1 , s | d, m | P, kW | , rad/s | f | Def. količinama |
| S=0,8t 2 | dolje | - | - | 0,20 | 4,0 | 0,20 | m,t 1 | |||
| φ=4t 2 | dolje | 1,0 | 0,30 | - | - | 0,16 | P,ω | |||
| S=1,5t-t 2 | gore | - | - | - | 4,5 | 0,20 | m, d | |||
| ω=15t-15t 2 | gore | - | - | 0,20 | 3,0 | - | 0,14 | m,ω | ||
| S=0,5t 2 | dolje | - | - | 1,76 | 0,20 | d,t 1 | ||||
| S=1,5t 2 | dolje | - | 0,6 | 0,24 | 9,9 | - | 0,10 | m,ω | ||
| S=0,9t 2 | dolje | - | 0,18 | - | 0,20 | P, t 1 | ||||
| φ=10t 2 | dolje | - | 0,20 | 1,92 | - | 0,20 | P, t 1 | |||
| S=t-1,25t 2 | gore | - | - | - | 0,25 | P,d | ||||
| φ=8t-20t 2 | gore | - | 0,20 | - | - | 0,14 | P, ω |
Primjer izvedbe
Problem 1(slika 1).
Rješenje 1. Pravocrtno kretanje (slika 1, a). Točka koja se jednoliko giba u nekom trenutku primila je novi zakon gibanja i nakon određenog vremena stala. Odrediti sve kinematičke karakteristike kretanja točke za dva slučaja; a) kretanje po ravnoj stazi; b) kretanje po zakrivljenoj stazi konstantnog polumjera zakrivljenosti r=100cm
Slika 1(a).
Zakon promjene brzine točke
Početnu brzinu točke nalazimo iz uvjeta:
Vrijeme kočenja do zaustavljanja nalazimo iz uvjeta:
u , odavde .
Zakon gibanja točke u periodi jednolikog gibanja
Udaljenost koju točka prijeđe duž putanje tijekom perioda kočenja je
Zakon promjene tangencijalne akceleracije točke
iz čega slijedi da se točka tijekom perioda kočenja kretala jednako sporo, budući da je tangencijalna akceleracija negativna i konstantne vrijednosti.
Normalno ubrzanje točaka na pravocrtnoj putanji gibanja jednaka nuli, tj. .
Rješenje 2. Krivuljasto kretanje (slika 1, b).
Slika 1(b)
U ovom slučaju, u usporedbi sa slučajem pravocrtno kretanje Sve kinematičke karakteristike ostaju nepromijenjene, osim normalnog ubrzanja.
Zakon promjene normalne akceleracije točke
Normalno ubrzanje točke u početnom trenutku kočenja
Numeriranje pozicija točaka na trajektoriji prihvaćeno na crtežu: 1 – Trenutna pozicija točke u ravnomjernom gibanju prije početka kočenja; 2 – položaj točke u trenutku kočenja; 3 – trenutni položaj točke tijekom perioda kočenja; 4 – konačni položaj točke.
Zadatak 2.
Teret (slika 2, a) podiže se pomoću bubnjastog vitla. Promjer bubnja je d=0,3m, a zakon njegove rotacije je .
Ubrzanje bubnja trajalo je do kutne brzine. Odrediti sve kinematičke karakteristike kretanja bubnja i tereta.
Riješenje. Zakon promjene kutne brzine bubnja. Početnu kutnu brzinu nalazimo iz uvjeta: ; dakle, ubrzanje je počelo iz stanja mirovanja. Vrijeme ubrzanja ćemo naći iz uvjeta: . Kut rotacije bubnja tijekom perioda ubrzanja.
Iz zakona promjene kutne akceleracije bubnja slijedi da se tijekom perioda akceleracije bubanj vrtio jednoliko ubrzano.
Kinematičke karakteristike opterećenja jednake su odgovarajućim karakteristikama bilo koje točke vučnog užeta, a time i točke A koja leži na rubu bubnja (slika 2, b). Kao što je poznato, linearne karakteristike točke rotacijskog tijela određene su njezinim kutnim karakteristikama.
Put koji prijeđe teret tijekom perioda ubrzanja, . Brzina tereta na kraju ubrzanja.
Ubrzanje tereta.
Zakon kretanja tereta.
Udaljenost, brzina i ubrzanje tereta mogu se odrediti i drugačije, preko pronađenog zakona gibanja tereta:
Zadatak 3. Teret, koji se jednoliko kreće prema gore duž nagnute potporne ravnine, u nekom je trenutku doživio kočenje u skladu s novim zakonom gibanja 
, gdje je s u metrima, a t u sekundama. Masa tereta m = 100 kg, koeficijent trenja klizanja između tereta i ravnine f = 0,25. Odredite silu F i snagu na vučnom užetu za dva vremenska trenutka: a) jednoliko kretanje prije početka kočenja;
b) početni moment kočenja. Pri proračunu uzeti g=10 m/.
Riješenje. Određujemo kinematičke karakteristike gibanja tereta.
Zakon promjene brzine tereta
Početna brzina tereta (pri t=0)
Ubrzanje tereta
Budući da je akceleracija negativna, kretanje je sporo.
1. Jednoliko kretanje tereta.
Za određivanje pogonske sile F razmatramo ravnotežu tereta na koju djeluje sustav konvergentnih sila: sila na sajli F, gravitacijska sila tereta G=mg, normalna reakcija oslonac ploha N i sila trenja usmjerena prema gibanju tijela. Prema zakonu trenja, . Odabiremo smjer koordinatnih osi, kao što je prikazano na crtežu, i sastavljamo dvije jednadžbe ravnoteže za opterećenje:
Snaga na kabelu prije početka kočenja određena je dobro poznatom formulom
Gdje je m/s.
2. Sporo kretanje tereta.
Kao što je poznato, s neravnim kretanje naprijed tijela, sustav sila koje na njega djeluju u smjeru gibanja nije uravnotežen. Prema d'Alembertovom principu (kinetostatička metoda), tijelo se u ovom slučaju može smatrati uvjetnom ravnotežom ako svim silama koje na njega djeluju dodamo silu inercije, čiji je vektor usmjeren suprotno od vektora ubrzanja. Vektor ubrzanja je u našem slučaju usmjeren suprotno od vektora brzine, jer se teret kreće sporo. Izrađujemo dvije jednadžbe ravnoteže za opterećenje:
Uključite kabel na početku kočenja
Kontrolna pitanja.
1. Kako odrediti brojčana vrijednost i smjer brzine točke u trenutku?
2. Što karakterizira normalnu i tangencijalnu komponentu ukupnog ubrzanja?
3. Kako prijeći s izražavanja kutne brzine u min -1 na izražavanje u rad/s?
4. Kako se zove tjelesna težina? Navedite jedinicu mjerenja mase
5. Na koji pokret materijalna točka nastaje inercijalna sila? Koja mu je brojčana vrijednost i koji mu je smjer?
6. State d'Alembertov princip
7. Nastaje li sila tromosti pri jednolikom krivuljastom gibanju materijalne točke?
8. Što je okretni moment?
9. Kako se izražava odnos između zakretnog momenta i kutne brzine za danu prenesenu snagu?
10. Osnovna dinamička jednadžba za rotacijsko gibanje.
Praktični rad br.7
"Proračun konstrukcija za čvrstoću"
Cilj rada: odrediti čvrstoću, dimenzije presjeka i dopušteno opterećenje
Teorijska pozadina.
Poznavajući faktore sile i geometrijske karakteristike presjeka tijekom vlačne (tlačne) deformacije, pomoću formula možemo odrediti naprezanje. I razumjeti hoće li naš dio (osovina, zupčanik itd.) izdržati vanjsko opterećenje. Potrebno je usporediti ovu vrijednost s dopuštenim naponom.
Dakle, jednadžba statičke čvrstoće
Na temelju njega rješavaju se 3 vrste problema:
1) ispitivanje čvrstoće
2) određivanje dimenzija presjeka
3) određivanje dopuštenog opterećenja
Dakle, jednadžba statičke krutosti
Na temelju njega se također rješavaju 3 vrste problema
Jednadžba statičke vlačne (tlačne) čvrstoće
1) Prvi tip - ispitivanje čvrstoće
,
tj. rješavamo lijevu stranu i uspoređujemo je s dopuštenim naprezanjem.
2) Drugi tip - određivanje dimenzija presjeka
s desne strane površina presjeka
Krug presjeka
dakle promjer d
Pravokutni presjek
Presjek kvadrat
A = a² (mm²)
Polukružni dio
Sekcije: kanal, I-greda, kut itd.
Vrijednosti područja - iz tablice, prihvaćene prema GOST-u
3) Treća vrsta je određivanje dopuštenog opterećenja;
uzeti na manju stranu, cijeli broj
VJEŽBA
Zadatak
A) Provjera čvrstoće (izračun testa)
Za zadanu gredu konstruirajte dijagram uzdužnih sila i provjerite čvrstoću u oba presjeka. Za drveni materijal (čelik St3) prihvatiti 
| Opcija br. | ||||||
| 12,5 | 5,3 | - | - | |||
| 2,3 | - | - | ||||
| 4,2 | - | - |
B) Odabir presjeka (dizajnirani proračun)
Za zadanu gredu konstruirajte dijagram uzdužnih sila i odredite dimenzije presjeka u oba presjeka. Za drveni materijal (čelik St3) prihvatiti
| Opcija br. | ||
| 1,9 | 2,5 | |
| 2,8 | 1,9 | |
| 3,2 |
B) Određivanje dopuštene uzdužne sile
Za određenu gredu odredite dopuštene vrijednosti opterećenja i ,
konstruirati dijagram uzdužnih sila. Za drveni materijal (čelik St3) prihvatiti. Pri rješavanju zadatka pretpostaviti da je vrsta opterećenja ista na oba dijela grede.
| Opcija br. | ||||
| - | - | |||
| - | - | |||
| - | - |
Primjer ispunjavanja zadatka
Problem 1(slika 1).
Provjerite čvrstoću stupa izrađenog od I-profila zadane veličine. Za materijal stupa (čelik St3) prihvatite dopuštena vlačna naprezanja 
i tijekom kompresije . U slučaju preopterećenja ili znatnog podopterećenja, odaberite veličine I-grede koje osiguravaju optimalnu čvrstoću stupa.
Riješenje.
Zadana greda ima dva presjeka 1, 2. Granice presjeka su presjeci u kojima se vanjske sile. Budući da se sile koje opterećuju gredu nalaze duž njene središnje uzdužne osi, u poprečnim presjecima nastaje samo jedan unutarnji faktor sile - uzdužna sila, tj. dolazi do napetosti (sabijanja) grede.
Za određivanje uzdužne sile koristimo se metodom presjeka. Mentalno crtajući dio unutar svakog odjeljka, odbacit ćemo donji fiksni dio grede i ostaviti ga za razmatranje gornji dio. U presjeku 1 uzdužna sila je konstantna i jednaka
Znak minus označava da je greda komprimirana u oba dijela.
Gradimo dijagram uzdužnih sila. Nakon što smo nacrtali osnovnu (nultu) liniju dijagrama paralelnu s osi grede, dobivene vrijednosti crtamo okomito na nju u proizvoljnom mjerilu. Kao što vidite, pokazalo se da je dijagram ocrtan ravnim linijama paralelnim s osnovnom.
Provjeravamo čvrstoću drveta, tj. Određujemo projektirano naprezanje (za svaki odjeljak posebno) i uspoređujemo ga s dopuštenim. Da bismo to učinili, koristimo uvjet tlačne čvrstoće
gdje je površina geometrijska karakteristika čvrstoće poprečnog presjeka. Iz tablice valjanog čelika uzimamo:
za I-gredu
za I-gredu
Ispitivanje čvrstoće:
Vrijednosti uzdužnih sila uzimaju se u apsolutnoj vrijednosti.
Čvrstoća grede je osigurana, međutim, postoji značajno (više od 25%) podopterećenje, što je neprihvatljivo zbog prekomjerne potrošnje materijala.
Iz uvjeta čvrstoće određujemo nove dimenzije I-grede za svaki dio grede:
Stoga potrebna površina
Prema tablici GOST odabiremo I-gredu br. 16, za koju;
Stoga potrebna površina
Prema tablici GOST odabiremo I-gredu br. 24, za koju;
Kod odabranih veličina I-grede također dolazi do podopterećenja, ali je beznačajno (manje od 5%)
Zadatak br. 2.
Za gredu zadanih dimenzija poprečnog presjeka odredite dopuštene vrijednosti opterećenja i . Za drveni materijal (čelik St3), prihvatite dopuštena vlačna naprezanja 
i tijekom kompresije 
.
Riješenje.
Zadana greda ima dva presjeka 1, 2. Dolazi do napetosti (sabijanja) grede.
Metodom presjeka određujemo uzdužnu silu izražavajući je kroz tražene sile i. Izvodeći dio unutar svakog odjeljka, odbacit ćemo lijevi dio grede i ostaviti ga za razmatranje desna strana. U presjeku 1 uzdužna sila je konstantna i jednaka
U presjeku 2 uzdužna sila je također konstantna i jednaka
Znak plus označava da je greda rastegnuta u oba dijela.
Gradimo dijagram uzdužnih sila. Dijagram je ocrtan ravnim linijama paralelnim s osnovnom.
Iz uvjeta vlačne čvrstoće određujemo dopuštene vrijednosti opterećenja i prethodno izračunavši površine zadanih presjeka:
Kontrolna pitanja.
1. Koji čimbenici unutarnje sile nastaju u presjeku grede tijekom napetosti i tlačenja?
2. Zapišite uvjete vlačne i tlačne čvrstoće.
3. Kako se dodjeljuju predznaci uzdužne sile i normalnog naprezanja?
4. Kako će se promijeniti napon ako se površina presjeka poveća za 4 puta?
5. Razlikuju li se uvjeti čvrstoće za vlačne i tlačne proračune?
6. U kojim jedinicama se mjeri napon?
7. Koji mehaničke karakteristike odabran kao krajnje naprezanje za duktilne i lomljive materijale?
8. Koja je razlika između graničnog i dopuštenog naprezanja?
Praktični rad br.8
“Rješavanje zadataka određivanja glavnih središnjih momenata tromosti ravnih geometrijskih figura”
Cilj rada: analitički odrediti momente tromosti ravnih tijela složenog oblika
Teorijska pozadina. Koordinate težišta presjeka mogu se izraziti kroz statički moment:
gdje je u odnosu na os Ox
u odnosu na os Oy
Statički moment površine figure u odnosu na os koja leži u istoj ravnini jednak je umnošku površine figure i udaljenosti njezina težišta do ove osi. Statički moment ima dimenziju. Statički moment može biti pozitivan, negativan ili jednak nuli (u odnosu na bilo koju središnju os).
Aksijalni moment tromosti presjeka je zbroj umnožaka ili integrala elementarnih površina uzetih preko cijelog presjeka s kvadratima njihovih udaljenosti do određene osi koja leži u ravnini presjeka koji se razmatra.
Aksijalni moment tromost se izražava u jedinicama - . Aksijalni moment tromosti je veličina koja je uvijek pozitivna i nije jednaka nuli.
Osi koje prolaze kroz težište figure nazivaju se središnje. Moment tromosti oko središnje osi naziva se centralni moment tromosti.
Moment tromosti oko bilo koje osi jednak je središtu
Nacrtajte shemu sustava i na njoj označite težište. Ako je pronađeno težište izvan sustava objekata, dobili ste netočan odgovor. Možda ste izmjerili udaljenosti od različitih referentnih točaka. Ponovite mjerenja.
- Na primjer, ako djeca sjede na ljuljački, težište će biti negdje između djece, a ne desno ili lijevo od ljuljačke. Također, težište se nikada neće poklopiti s točkom u kojoj dijete sjedi.
- Ovi argumenti vrijede u dvodimenzionalnom prostoru. Nacrtajte kvadrat koji će sadržavati sve objekte sustava. Središte gravitacije treba biti unutar ovog kvadrata.
Provjerite svoju matematiku ako dobijete mali rezultat. Ako je referentna točka na jednom kraju sustava, mali rezultat postavlja težište blizu kraja sustava. Ovo može biti točan odgovor, ali u velikoj većini slučajeva ovaj rezultat ukazuje na pogrešku. Kada ste izračunali momente, jeste li pomnožili odgovarajuće težine i udaljenosti? Kad biste umjesto množenja dodali težine i udaljenosti, dobili biste puno manji rezultat.
Ispravite pogrešku ako ste pronašli više težišta. Svaki sustav ima samo jedno težište. Ako ste pronašli više centara gravitacije, najvjerojatnije niste zbrojili sve trenutke. Centar gravitacije jednaka omjeru“ukupni” trenutak do “ukupne” težine. Nema potrebe dijeliti "svaki" trenutak sa "svakom" težinom: na ovaj način ćete pronaći položaj svakog predmeta.
Provjerite referentnu točku ako se odgovor razlikuje za neku cjelobrojnu vrijednost. U našem primjeru, odgovor je 3,4 m. Recimo da ste dobili odgovor 0,4 m ili 1,4 m, ili neki drugi broj koji završava na ".4". To je zato što niste odabrali lijevi kraj ploče kao svoju početnu točku, već točku koja se nalazi cijelo vrijeme udesno. Zapravo, vaš je odgovor točan bez obzira koju referentnu točku odaberete! Samo zapamtite: referentna točka je uvijek na poziciji x = 0. Evo primjera:
- U našem primjeru, referentna točka bila je na lijevom kraju ploče i otkrili smo da je težište 3,4 m od te referentne točke.
- Ako kao referentnu točku odaberete točku koja se nalazi 1 m desno od lijevog kraja ploče, dobit ćete odgovor 2,4 m. Odnosno, težište je 2,4 m od nove referentne točke, što , pak, nalazi se 1 m od lijevog kraja ploče. Dakle, težište je na udaljenosti 2,4 + 1 = 3,4 m od lijevog kraja ploče. Ispostavilo se da je to stari odgovor!
- Napomena: kada mjerite udaljenosti, zapamtite da su udaljenosti do "lijeve" referentne točke negativne, a do "desne" referentne točke pozitivne.
Mjerite udaljenosti ravnim linijama. Pretpostavimo da je dvoje djece na ljuljački, ali je jedno dijete puno više od drugog ili jedno dijete visi ispod daske umjesto da sjedi na njoj. Zanemarite ovu razliku i izmjerite udaljenosti duž ravne linije ploče. Mjerenje udaljenosti pod kutovima dat će bliske, ali ne posve točne rezultate.
- Za problem daske s klackalicom, zapamtite da je težište između desnog i lijevog kraja daske. Kasnije ćete naučiti izračunati težište složenijih dvodimenzionalnih sustava.
Autor: Uzmimo tijelo proizvoljnog oblika. Da li ga je moguće objesiti na konac tako da nakon vješanja zadrži svoj položaj (tj. da se ne počne okretati) kada bilo koji početna orijentacija (sl. 27.1)?
Drugim riječima, postoji li točka u odnosu na koju bi zbroj momenata gravitacije koji djeluju na različite dijelove tijela bio jednak nuli na bilo koji orijentacija tijela u prostoru?
Čitač: Da, mislim da jesam. Ova točka se zove težište tijela.
Dokaz. Radi jednostavnosti, razmotrimo tijelo u obliku ravne ploče proizvoljnog oblika, proizvoljno orijentirane u prostoru (slika 27.2). Uzmimo koordinatni sustav x 0na s početkom u središtu mase – točka S, Zatim x C = 0, kod C = 0.
Zamislimo ovo tijelo kao zbirku veliki broj točkaste mase m i, od kojih je položaj svakog određen radijus vektorom.
Po definiciji, centar mase je , a koordinata x C = .
Budući da u koordinatnom sustavu koji smo usvojili x C= 0, tada . Pomnožimo ovu jednakost sa g i dobivamo
Kao što se može vidjeti sa Sl. 27.2, | x i| - ovo je rame moći. I ako x i> 0, tada moment sile M i> 0, a ako x j < 0, то Mj < 0, поэтому с учетом знака можно утверждать, что для любого x i moment sile će biti jednak M i = m i gx i. Tada je jednakost (1) ekvivalentna jednakosti , gdje je M i– moment sile teže. To znači da će pri proizvoljnoj orijentaciji tijela zbroj momenata gravitacije koji djeluju na tijelo biti jednak nuli u odnosu na njegovo središte mase.
Da bi tijelo koje razmatramo bilo u ravnoteži, potrebno je na njega primijeniti točku S sila T = mg, usmjeren okomito prema gore. Moment te sile u odnosu na točku S jednaka nuli.
Budući da naše razmišljanje ni na koji način nije ovisilo o tome kako je točno tijelo orijentirano u prostoru, dokazali smo da se težište poklapa sa središtem mase, što smo i trebali dokazati.
Problem 27.1. Nađite težište bestežinskog štapa duljine l, na čijim su krajevima učvršćene dvije točkaste mase T 1 i T 2 .
| T 1 T 2 l | Riješenje. Nećemo tražiti centar gravitacije, već centar mase (jer je to isto). Predstavimo os x(Slika 27.3).  Riža. 27.3 |
| x C =? | |
Odgovor: na udaljenosti od mase T 1 .
STOP! Odlučite sami: B1–B3.
Izjava 1 . Ako homogeno ravno tijelo ima os simetrije, težište je na toj osi.
Doista, za bilo koju masu točke m i, koja se nalazi desno od osi simetrije, postoji ista masa točke koja se nalazi simetrično u odnosu na prvu (sl. 27.4). U ovom slučaju zbroj momenata sila .
Budući da se cijelo tijelo može prikazati podijeljeno na slične parove točaka, ukupni moment gravitacije u odnosu na bilo koju točku koja leži na osi simetrije jednak je nuli, što znači da se težište tijela nalazi na ovoj osi . Ovo dovodi do važnog zaključka: ako tijelo ima više osi simetrije, tada se težište nalazi u sjecištu tih osi(Slika 27.5).
Riža. 27.5 
Izjava 2. Ako dva tijela imaju mase T 1 i T 2 spojeni u jedno, tada će težište takvog tijela ležati na ravnoj liniji koja povezuje težišta prvog i drugog tijela (sl. 27.6).
Riža. 27.6 
Riža. 27.7
Dokaz. Postavimo složeno tijelo tako da segment koji povezuje težišta tijela bude okomit. Zatim zbroj momenata gravitacije prvog tijela u odnosu na točku S 1 jednak nuli, a zbroj momenata gravitacije drugog tijela u odnosu na točku S 2 jednaka je nuli (sl. 27.7).
primijeti da rame gravitacija bilo koje točkaste mase t i isti u odnosu na bilo koju točku koja leži na segmentu S 1 S 2, a time i moment gravitacije u odnosu na bilo koju točku koja leži na segmentu S 1 S 2, isto. Posljedično, gravitacijska sila cijelog tijela je nula u odnosu na bilo koju točku na segmentu S 1 S 2. Dakle, težište kompozitnog tijela leži na segmentu S 1 S 2 .
Važan praktični zaključak proizlazi iz tvrdnje 2, koja je jasno formulirana u obliku uputa.
upute,
kako pronaći težište čvrstog tijela ako se može slomiti
na dijelove od kojih su poznati položaji težišta svakog od njih
1. Svaki dio treba zamijeniti masom koja se nalazi u težištu tog dijela.
2. Pronađite centar mase(a to je isto što i težište) rezultirajućeg sustava točkastih masa, odabirom prikladnog koordinatnog sustava x 0na, prema formulama:
Zapravo, uredimo kompozitno tijelo tako da segment S 1 S 2 bio vodoravan i objesite ga na niti na točkama S 1 i S 2 (Sl. 27.8, A). Jasno je da će tijelo biti u ravnoteži. A ta se ravnoteža neće poremetiti ako svako tijelo zamijenimo točkastim masama T 1 i T 2 (Sl. 27.8, b).
Riža. 27.8
STOP! Odlučite sami: C3.
Problem 27.2. Na dva vrha jednakostraničan trokut postavljaju se kuglice mase T svaki. Kuglica mase 2 postavljena je u treći vrh T(Sl. 27.9, A). Strana trokuta A. Odredite težište ovog sustava.
| T 2T A |  Riža. 27.9 |
| x C = ? kod C = ? | |
Riješenje. Uvedimo koordinatni sustav x 0na(Sl. 27.9, b). Zatim
,
.
Odgovor: x C = A/2; ; težište leži na pola visine OGLAS.
