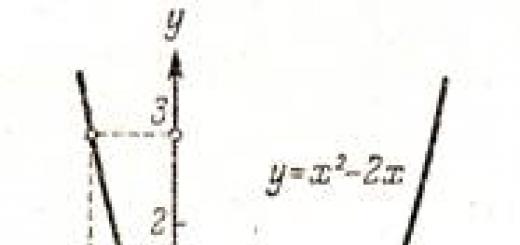Ekscentrična kompresija. Izrada jezgre presjeka. Savijanje s uvijanjem. Proračuni čvrstoće pri složenim stanjima naprezanja.
Ekscentrična kompresija- ovo je vrsta deformacije kod koje uzdužna sila u presjeku štapa ne djeluje u težištu. Kod ekscentrične kompresije, osim uzdužne sile (N), nastaju dva momenta savijanja (M x i M y).
Pretpostavlja se da štap ima visoku krutost na savijanje kako bi se zanemario progib štapa pod ekscentričnom kompresijom.
Pretvorimo formulu za momente pod ekscentričnom kompresijom, zamjenjujući vrijednosti momenata savijanja:
Označimo koordinate određene točke neutralne (nulte) linije pri ekscentričnoj kompresiji xN, yN i zamijenimo ih u formulu za normalna naprezanja pri ekscentričnoj kompresiji. S obzirom da su naprezanja u točkama neutralne linije jednaka nuli, nakon kontrakcije za P/F dobivamo jednadžbu neutralne linije pri ekscentričnom pritisku:
 (35)
(35)
Nulta linija za ekscentričnu kompresiju i točka primjene opterećenja uvijek se nalaze duž različite strane od težišta presjeka.

Riža. 43. Ekscentrična kompresija
Segmenti odsječeni nul-linijom od koordinatnih osi, označeni kao ax i ay, mogu se lako pronaći iz jednadžbe nul-linije pod ekscentričnom kompresijom. Ako prvo uzmemo xN = 0, yN = ay, a zatim uzmemo yN = 0, xN = ax, tada nalazimo sjecišta nulte linije za ekscentričnu kompresiju s glavnim središnjim osima:


Riža. 44. Neutralna linija pri ekscentričnom naprezanju - kompresiji
Neutralna linija pod ekscentričnom kompresijom podijelit će presjek na dva dijela. U jednom dijelu naprezanja će biti tlačna, u drugom - vlačna. Proračuni čvrstoće, kao u slučaju kosog savijanja, provode se korištenjem normalnih naprezanja koja nastaju u opasnoj točki poprečnog presjeka (najdalje od nulte linije).
(36)
Jezgra presjeka je malo područje oko težišta poprečnog presjeka, karakterizirano činjenicom da svaka tlačna uzdužna sila primijenjena unutar jezgre uzrokuje tlačna naprezanja u svim točkama poprečnog presjeka.
Primjeri jezgri presjeka za pravokutni i kružni presjek štapa.

Riža. 45. Oblik jezgre presjeka za pravokutnik i krug
Savijanje s torzijom. Osovine strojeva i mehanizama često su podvrgnute takvom opterećenju (istodobno djelovanje momenata torzije i savijanja). Za izračunavanje drva potrebno je prije svega utvrditi opasne dijelove. U tu svrhu konstruiraju se dijagrami momenata savijanja i momenta.
Koristeći načelo neovisnosti o djelovanju sila, odredit ćemo naprezanja koja nastaju u gredi odvojeno za torziju i savijanje.
Tijekom torzije nastaju tangencijalni naponi u presjecima grede koji dosežu najveća vrijednost na točkama konture presjeka. Pri savijanju u poprečnim presjecima grede nastaju normalna naprezanja koja svoju najveću vrijednost postižu u krajnjim vanjskim vlaknima grede.
Promotrimo ravni štap opterećen na kraju silama usmjerenim paralelno s osi Oh. Rezultanta ovih sila F primijenjen u točki S. U lokalnom desnom koordinatnom sustavu yOz, podudarajući se s glavnim središnjim osima presjeka, koordinate točke S jednak A I b(Slika 5.18).
Zamijenimo primijenjeno opterećenje statički ekvivalentnim sustavom sila i momenata. Da bismo to učinili, prenosimo rezultantnu silu F na težište presjeka OKO i opteretiti štap s dva momenta savijanja jednaka umnošku sile T^ njegovih krakova u odnosu na koordinatne osi: Mff = Fa I M z = Fb.
Imajte na umu da će prema pravilu desnog koordinatnog sustava za točku C koja leži u prvoj četvrtini momenti savijanja formalno biti sljedeći:
Riža. 5.18.Ravni štap opterećen na kraju silama usmjerenim paralelno s osiOh
znakovi puhanja: M y = Fa i M 7 = -Fb. U ovom slučaju, u elementarnom području koje leži u prvoj četvrtini, oba momenta uzrokuju vlačno naprezanje.
Koristeći načelo neovisnosti o djelovanju sila, određujemo naprezanja u trenutnoj točki presjeka s koordinatama na I z od svakog faktora snage posebno. Ukupni napon dobiva se zbrajanjem sve tri komponente napona:
Odredimo položaj neutralne osi. Da bismo to učinili, u skladu s formulom (5.69), izjednačavamo vrijednost normalnog napona u trenutnoj točki s nulom:

Kao rezultat jednostavnih transformacija dobivamo jednadžbu neutralne linije
Gdje ja y I i z - glavni polumjeri tromosti, određeno formulama (3.14).
Dakle, u slučaju ekscentrična napetost-sabijanje neutralna linija ne prolazi kroz težište presjeka (slika 5.19), kao što je naznačeno prisutnošću u jednadžbi (5.70) slobodnog člana različitog od nule.
Najveća naprezanja javljaju se u točkama presjeka A I U, najdalje od neutralne linije. Utvrdimo vezu između koordinata točke djelovanja sile i položaja neutralne crte. Da bismo to učinili, odredimo točke sjecišta ove linije koordinatnih osi:

Riža. 5.19.
Dobivene formule pokazuju da koordinata točke primjene sile A a koordinata točke u kojoj neutralna linija siječe koordinatnu os Oz(točka g 0) imaju suprotne predznake. Isto se može reći i za količine b I y 0 . Dakle, točka primjene rezultantne sile i neutralna linija su na suprotnim stranama u odnosu na ishodište.
Prema dobivenim formulama, kako se točka primjene sile približava težištu presjeka, neutralna linija se udaljava od središnje zone. U graničnom slučaju (a = b = 0) dolazimo do slučaja centralne napetosti-sabijanja.
Zanimljivo je odrediti zonu djelovanja sile u kojoj će naponi u presjeku imati isti predznak. Konkretno, za materijale koji imaju slabu vlačnu čvrstoću, racionalno je djelovati tlačnu silu upravo u ovoj zoni, tako da u presjeku djeluju samo tlačna naprezanja. Ova zona oko težišta presjeka naziva se sekcijska jezgra.
Ako se sila primjenjuje u središtu presjeka, tada neutralna linija ne siječe presjek. Ako se sila primjenjuje duž granice jezgre presjeka, neutralna linija dodiruje konturu presjeka. Za određivanje jezgre poprečnog presjeka možete koristiti formulu (5.71).
Ako se neutralna crta prikaže kao tangenta na konturu presjeka i uzmu u obzir svi mogući položaji tangente i točke primjene sile koje odgovaraju tim položajima, tada će točke primjene sile ocrtavati jezgru presjeka. .

Riža. 5.20.
A - elipsa; 6 - pravokutnik
Ekscentrično rastezanje Ova vrsta opterećenja grede naziva se u kojoj vanjske sile djeluju duž uzdužne osi grede, ali se ne podudaraju s njom (slika 8.4). Naprezanja se određuju pomoću načela neovisnosti sila. Ekscentrično rastezanje je kombinacija aksijalnog istezanja i kosog (u nekim slučajevima ravnog) savijanja. Formula za normalna naprezanja može se dobiti kao algebarski zbroj normalna naprezanja koja proizlaze iz svake vrste opterećenja:Gdje  ;
;  ;
;
y F, z F– koordinate točke primjene sile F.
Za određivanje opasnih točaka presjeka potrebno je pronaći položaj neutralne crte (NL) kao geometrijsko mjesto točaka u kojima su naprezanja nula.
 .
.
Jednadžba n.l. može se napisati kao jednadžba ravne linije u segmentima:
 ,
,
Gdje  I
I  – segmenti odsječeni n.l. na koordinatnim osama,
– segmenti odsječeni n.l. na koordinatnim osama,
 ,
,  su glavni polumjeri tromosti presjeka.
su glavni polumjeri tromosti presjeka.
Neutralna linija dijeli presjek na zone s vlačnim i tlačnim naprezanjem. Dijagram normalnog naprezanja prikazan je na sl. 8.4.
Ako je presjek simetričan u odnosu na glavne osi, tada se uvjet čvrstoće piše za plastične materijale za koje [ s c] = [s str] = [s], kao
 . (8.5)
. (8.5)
Za lomljive materijale koji [ s c]¹[ s str], uvjet čvrstoće treba zapisati posebno za opasnu točku presjeka u vlačnoj zoni:

a za opasnu točku dionice u komprimiranoj zoni:
 ,
,
Gdje z 1, y 1 I z 2, y 2– koordinate točaka presjeka najudaljenijih od neutralne crte u vlačnoj 1 i stlačenoj zoni 2 presjeka (sl. 8.4).
Svojstva nulte linije
1. Nulta linija dijeli cijeli odjeljak u dvije zone - napetost i kompresiju.
2. Nulta crta je ravna jer su koordinate x i y na prvoj potenciji.
3. Nulta linija ne prolazi kroz ishodište (sl. 8.4).
4. Ako točka primjene sile leži na glavnoj središnjoj tromosti presjeka, tada je odgovarajuća nul linija okomita na ovu os i prolazi s druge strane ishodišta (slika 8.5).
5. Ako se točka primjene sile pomiče duž zrake koja izlazi iz ishodišta, tada se odgovarajuća nulta linija pomiče iza nje (sl. 8.6):
n.l.Riža. 8.5 Sl. 8.6
a) kada se točka primjene sile pomiče duž zrake koja izlazi iz ishodišta od nule do beskonačnosti (y F ®∞, z F ®∞), A y®0; A z ®0. Granično stanje ovog slučaja: nulta linija će prolaziti kroz ishodište (zavoj);
b) kada se točka primjene sile (t. K) pomiče duž zrake koja izlazi iz ishodišta koordinata od beskonačnosti do nule (y F ® 0 i z F ® 0), A y®∞; A z ®∞. Granično stanje u ovom slučaju: nulta linija se pomiče u beskonačnost, a tijelo će doživjeti jednostavnu napetost (kompresiju).
6. Ako se točka primjene sile (točka K) kreće duž ravne crte koja siječe koordinatne osi, tada će se nulta linija okretati oko određenog središta koje se nalazi u kvadrantu nasuprot točke K.
8.2.3. Jezgra odjeljka
Neki materijali (beton, zidanje) mogu izdržati vrlo mala vlačna naprezanja, dok drugi (primjerice tlo) uopće ne mogu izdržati napetost. Takvi se materijali koriste za izradu konstrukcijskih elemenata u kojima se ne pojavljuju vlačna naprezanja, a ne koriste se za izradu nastavnih elemenata koji su podložni savijanju, uvijanju, središnjem i ekscentričnom naprezanju.
Od ovih materijala moguće je izraditi samo središnje stisnute elemente, kod kojih ne nastaju vlačna naprezanja, kao i ekscentrično stisnute elemente, ako u njima ne nastaju vlačna naprezanja. To se događa kada se točka primjene tlačne sile nalazi unutar ili na granici nekog središnjeg područja poprečnog presjeka, koje se naziva jezgra presjeka.
Jezgra odjeljka grede naziva se njezino određeno središnje područje, koje ima svojstvo da sila primijenjena u bilo kojoj točki uzrokuje naprezanja istog predznaka u svim točkama poprečnog presjeka grede, tj. nulta linija ne prolazi kroz presjek grede.
Ako se točka primjene tlačne sile nalazi izvan jezgre presjeka, tada u presjeku nastaju tlačna i vlačna naprezanja. U tom slučaju nulta linija siječe presjek grede.
Ako se sila primjenjuje na granici jezgre presjeka, tada nulta linija dodiruje konturu presjeka (u točki ili duž linije); na mjestu dodira normalna naprezanja su nula.
Pri proračunu ekscentrično komprimiranih šipki izrađenih od materijala koji teško podnosi vlačna naprezanja, važno je znati oblik i dimenzije jezgre presjeka. To omogućuje, bez izračunavanja naprezanja, da se utvrdi da li na presjeku grede nastaju vlačna naprezanja (slika 8.7).
Iz definicije proizlazi da je jezgra sekcije određeno područje koje se nalazi unutar same sekcije.

Za lomljive materijale treba primijeniti tlačno opterećenje u jezgri presjeka kako bi se isključile vlačne zone u presjeku (slika 8.7).
Za konstrukciju jezgre presjeka potrebno je uzastopno kombinirati nultu liniju s konturom poprečnog presjeka tako da nulta linija ne siječe presjek, a istovremeno izračunati odgovarajuću točku
primjena tlačne sile K s kor-
Riža. 8,7 dinara y F I z F prema formulama:
 ; .
; .
Rezultirajuće točke primjene sile s koordinatama y F, z F moraju biti povezani ravnim segmentima. Područje omeđeno dobivenom isprekidanom linijom bit će jezgra presjeka.
Redoslijed izrade jezgre presjeka
1. Odredite položaj težišta poprečnog presjeka i glavne središnje osi tromosti y i z, kao i vrijednosti kvadrata polumjera tromosti ja y , i z .
2. Prikaži sve moguće položaje n.l. u odnosu na konturu presjeka.
3. Za svaku poziciju n.l. definirati segmente a y I a z, odsječen njime od glavnih središnjih osi tromosti y i z.
4. Za svaku poziciju n.l. postaviti koordinate centra pritiska y F, I z F .
5. Spojite rezultirajuće centre pritiska ravnim segmentima, unutar kojih će se nalaziti jezgra presjeka.
Torzija sa savijanjem
Vrsta opterećenja pri kojoj je greda istodobno izložena torzijskim momentima i momentima savijanja naziva se savijanje s uvijanjem.
Pri proračunu ćemo se koristiti načelom neovisnosti djelovanja sila. Odredimo odvojeno naprezanja tijekom savijanja i torzije (slika 8.8) .
Prilikom savijanja u poprečnom presjeku nastaju normalna naprezanja koja postižu najveću vrijednost u krajnjim vanjskim vlaknima
 .
.
Kada se u poprečnom presjeku pojavi torzija, nastaju tangencijalni naponi koji postižu svoje najveće vrijednosti u točkama poprečnog presjeka blizu površine osovine
 .
.
| s |
| t |
| C |
| B |
| x |
| g |
| z |
| Riža. 8.9 |
| s |
| s |
| t |
| t |
| Riža. 8.10 |
| C |
| x |
| z |
| g |
| M |
| T |
| Riža. 8.8 |
Normalni i tangencijalni naponi istodobno postižu svoje najveće vrijednosti u točkama S I U presjek osovine (sl. 8.9). Razmotrimo stanje naprezanja u točki S(Slika 8.10). Vidi se da je elementarni paralelopiped odabran oko točke S, nalazi se u ravnom napetom stanju.
Stoga ćemo za ispitivanje čvrstoće koristiti jednu od hipoteza čvrstoće.
Uvjet čvrstoće prema trećoj hipotezi čvrstoće (hipoteza najvećih tangencijalnih naprezanja)
 .
.
S obzirom na to  ,
,  , dobivamo uvjet čvrstoće osovine
, dobivamo uvjet čvrstoće osovine
 . (8.6)
. (8.6)
Ako se osovina savija u dvije ravnine, tada će stanje čvrstoće biti
 .
.
Korištenje četvrte hipoteze (energetske) snage
 ,
,
nakon zamjene s I t dobivamo
 . (8.7)
. (8.7)
Pitanja za samotestiranje
1. Kakav se zavoj naziva kosim?
2. Koje vrste savijanja je kombinacija kosog savijanja?
3. Koje formule se koriste za određivanje normalnih naprezanja u presjecima grede pri kosom savijanju?
4. Kakav je položaj neutralne osi pri kosom savijanju?
5. Kako se određuju opasne točke u presjeku pri kosom savijanju?
6. Kako se određuju pomaci točaka osi grede pri kosom savijanju?
7. Koju vrstu složenog otpora nazivamo ekscentričnom napetosti (ili kompresijom)?
8. Koje formule se koriste za određivanje normalnih naprezanja u presjecima štapa pri ekscentričnom naprezanju i pritisku? Kako izgleda dijagram tih naprezanja?
9. Kako se određuje položaj neutralne osi pri ekscentričnom naprezanju i sabijanju? Zapiši odgovarajuće formule.
10. Koja naprezanja nastaju u presjeku grede pri savijanju uz torziju?
11. Koji su opasni presjeci okrugle grede pri savijanju uz torziju?
12. Koje su točke kružnog presjeka opasne pri torzijskom savijanju?
13. Kakvo se stanje naprezanja javlja u tim točkama?
Mnogi elementi građevinskih konstrukcija (stupovi, nosači, nosači) pod utjecajem su tlačnih sila koje se ne primjenjuju u težištu presjeka. Na sl. Na slici 12.9 prikazan je stup na koji se oslanja podna greda. Kao što se vidi, sila djeluje u odnosu na os stupa s ekscentričnosti e, i tako, u proizvoljnom dijelu Ah ah stupova zajedno s uzdužnom silom N = -R javlja se moment savijanja čija je veličina jednaka Ponovno. Ekscentrična napetost (sabijanje) štapa predstavlja vrstu deformacije kod koje rezultante vanjske sile djeluju po ravnoj liniji paralelnoj s osi štapa. U nastavku ćemo uglavnom razmatrati probleme ekscentrične kompresije. Kod ekscentrične napetosti u svim zadanim proračunskim formulama treba promijeniti predznak ispred sile R na suprotnost.
Neka je šipka proizvoljnog presjeka (sl. 12.10) na kraju opterećena ekscentrično primijenjenom tlačnom silom R, paralelno s osi Oh. Prihvatimo pozitivno

pravci glavnih osi tromosti presjeka OU I Oz tako da mjesto primjene sile R bio u prvoj četvrtini koordinatnih osi. Označimo koordinate točke djelovanja sile R kroz y r I z P -
Unutarnje sile u proizvoljnom presjeku štapa su jednake
Predznaci minus za momente savijanja su zbog činjenice da u prvoj četvrtini koordinatnih osi ti momenti uzrokuju kompresiju. Veličine unutarnjih sila u ovom primjeru ne mijenjaju se duž duljine štapa, pa će raspodjela naprezanja u presjecima dovoljno udaljenim od mjesta primjene opterećenja biti ista.
Zamjenom (12.11) u (12.1) dobivamo formulu za normalna naprezanja pri ekscentričnoj kompresiji:

Ova se formula može pretvoriti u obrazac

Gdje ja, ja- glavni polumjeri tromosti presjeka. pri čemu
Stavljajući o = 0 u (12.12), dobivamo jednadžbu nulta linija:
Ovdje je y 0 i z 0 - koordinate točaka nulte linije (sl. 12.11). Jednadžba (12.14) je jednadžba pravca koji ne prolazi kroz težište presjeka. Da bismo nacrtali nultu liniju, nalazimo točke njezina sjecišta s koordinatnim osima. Pretpostavljajući u (12.14) sekvencijalno y 0 = 0 i z 0= 0, prema tome nalazimo
Gdje a z I i y- segmenti odsječeni nultom linijom na koordinatnim osima (sl. 12.11).


Utvrdimo značajke položaja nulte linije tijekom ekscentrične kompresije.
- 1. Iz formula (12.15) slijedi da i y I a z imaju znakove suprotne znakovima odnosno y r I z P - Dakle, nulta linija prolazi kroz one četvrtine koordinatnih osi koje ne sadrže točku primjene sile (sl. 12.12).
- 2. Kako se točka primjene sile približava R u ravnoj liniji na središte gravitacije koordinate presjeka ove točke y r I zP se smanjuju. Iz (12.15) slijedi da su apsolutne vrijednosti duljina segmenata i y I a z porast, odnosno nulta linija se udaljava od težišta, ostajući paralelna sama sa sobom (sl. 12.13). U granici kod Z P = y P = 0 (sila primijenjena u težištu) nulta linija se pomiče u beskonačnost. U tom će slučaju naprezanja u presjeku biti konstantna i jednaka o = -P/F.
- 3. Ako je mjesto primjene sile R nalazi se na jednoj od glavnih osi, nulta linija je paralelna s drugom osi. Doista, stavljajući u (12.15), na primjer, y r= 0, dobivamo to i y= to jest, nulta linija ne siječe os OU(Slika 12.14).
- 4. Ako se točka primjene sile giba po ravnoj liniji koja ne prolazi kroz težište, tada se nulta crta rotira oko određene točke. Dokažimo ovo svojstvo. Točke primjene sile R x I R 2, koji se nalaze na koordinatnim osima odgovaraju nultim linijama 1 - 1 i 2-2, paralelnim s osi (sl. 12.15), koje se sijeku u točki D. Budući da ova točka pripada dvjema nul linijama, naprezanja u ovoj točki od istovremeno primijenjenih sila R x I R 2 bit će jednaka nuli. Budući da svaka sila R 3,čija se točka primjene nalazi na ravnoj liniji R ( R 2 , Limenka



rastaviti na dvije paralelne komponente nanesene u točkama Pj i R 2, onda slijedi da je stres u točki D od djelovanja sile R 3 također su jednaki nuli. Dakle, nulta linija je 3-3, što odgovara sili R 3, prolazi kroz točku D.
Drugim riječima, na mnoge točke R, smješten na ravnoj liniji R ( R 2 , odgovara snopu pravaca koji prolaze kroz točku D. Vrijedi i obrnuto: kada se nulta crta okreće oko određene točke, točka primjene sile pomiče se po ravnoj liniji koja ne prolazi kroz težište.
Ako nulta linija siječe presjek, onda ga dijeli na zone kompresije i napetosti. Kao i kod kosog savijanja, iz hipoteze ravnih presjeka proizlazi da naprezanja postižu svoje najveće vrijednosti u točkama koje su najudaljenije od nulte linije. Priroda dijagrama naprezanja u ovom slučaju prikazana je na sl. 12.16, A.
Ako se nulta linija nalazi izvan presjeka, tada će na svim točkama presjeka naprezanja biti istog znaka (sl. 12.16, b).
Primjer 12.3. Konstruirajmo dijagram normalnih naprezanja u proizvoljnom presjeku ekscentrično stisnutog stupa pravokutni presjek s dimenzijama b x h(Slika 12.17). Kvadrati polumjera tromosti presjeka prema (12.22) su jednaki 

Segmenti odsječeni nultom linijom na koordinatnim osima određuju se formulama (12.15):

Zamjenjujući sekvencijalno u (12.12) koordinate točaka C i najudaljenijih od nulte crte U(Sl. 12.18)
pronaći ćemo 


Dijagram o je prikazan na sl. 12.18. Najveća tlačna naprezanja prema apsolutna vrijednostčetiri puta veća od vrijednosti naprezanja koja bi bila u slučaju središnje primjene sile. Osim toga, u presjeku su se pojavila značajna vlačna naprezanja. Primijetimo da iz (12.12) slijedi da u težištu (y = z= 0) naponi su jednaki o = -P/F.
Primjer 12.4. Izrezana traka je opterećena vlačnom silom R(Sl. 12.19, A). Usporedimo naprezanja u presjeku LV, dovoljno udaljen od kraja i mjesta izreza, s naprezanjima u presjeku CD na mjestu izreza.
U presjeku AB(Sl. 12.19, b) sila R uzrokuje centralnu napetost i naprezanja su jednaka a = P/F = P/bh.

U presjeku CD(Sl. 12.19, V) linija sile R ne prolazi kroz težište presjeka, pa dolazi do ekscentrične napetosti. Promjenom predznaka u formuli (12.12) u suprotan i prihvaćanjem y r= 0, dobivamo za ovaj odjeljak
Uzimanje 

Nulta linija u odjeljku CD paralelno s osi OU i siječe os Oz na daljinu a =-i 2 y /z P- b/ 12. U točkama presjeka koje su najudaljenije od nulte crte C(z - -b/ 4) i D(z - b/ 4) naponi prema (12.16) su jednaki

Dijagrami normalnog naprezanja za presjeke LW I CD prikazano na sl. 12.19, b, c.
Dakle, unatoč činjenici da je odjeljak CD ima površinu dvostruko manju od presjeka AB, Zbog ekscentrične primjene sile, vlačna naprezanja u oslabljenom presjeku povećavaju se ne dva, već osam puta. Osim toga, u ovom presjeku pojavljuju se značajna tlačna naprezanja.
Treba napomenuti da gornji izračun ne uzima u obzir dodatna lokalna naprezanja koja nastaju u blizini točke C zbog prisutnosti udubljenja. Ta naprezanja ovise o polumjeru utora (kako se radijus smanjuje, povećavaju se) i mogu značajno premašiti pronađenu vrijednost i sa = 8P/bh. U ovom slučaju, priroda dijagrama naprezanja u blizini točke C značajno će se razlikovati od linearne. Određivanje lokalnih naprezanja (koncentracije naprezanja) raspravlja se u 18. poglavlju.
Mnogi građevinski materijali (beton, cigla itd.) imaju slabu vlačnu čvrstoću. Njihova vlačna čvrstoća višestruko je manja od tlačne čvrstoće. Stoga je pojava vlačnih naprezanja u konstrukcijskim elementima izrađenim od takvih materijala nepoželjna. Da bi ovaj uvjet bio ispunjen, nulta linija mora biti izvan sekcije. U protivnom će nulta linija presijecati presjek i u njemu će se pojaviti vlačna naprezanja. Ako je nulta linija tangenta na konturu presjeka, tada je odgovarajući položaj točke primjene sile granični. U skladu sa svojstvom 2 nulte linije, ako se točka primjene sile približi težištu presjeka, nulta linija će se udaljiti od nje. Geometrijsko mjesto graničnih točaka koje odgovaraju različitim tangentama na konturu presjeka je granica sekcijske jezgre. Jezgra presjeka je konveksno područje oko težišta, koje ima sljedeće svojstvo: ako se točka primjene sile nalazi unutar ili na granici ovog područja, tada na svim točkama presjeka naprezanja imaju isti znak. Jezgra presjeka je konveksna figura, budući da nulte linije moraju dodirivati ovojnicu konture presjeka, a ne ju presijecati.
Kroz točku A(Sl. 12.20) možete povući bezbrojne tangente (nulte linije); u ovom slučaju samo tangenta AC je tangenta na ovojnicu i mora joj odgovarati određena točka na konturi jezgre presjeka. U isto vrijeme, na primjer, nemoguće je nacrtati tangentu na područje AB kontura presjeka jer siječe presjek.
Konstruirajmo jezgru presjeka za pravokutnik (slika 12.21). Za tangentu 1 - 1 a 7 - b/ 2; A= . Iz (12.15) nalazimo za točku 1 koja odgovara ovoj tangenti, z P = -i 2 y / a 7 = -b/6; g r - 0. Za tangentu 2-2 a y - k/ 2; a 7 =°°, a koordinate točke 2 bit će jednake naR- -h/6; z P - 0. Prema svojstvu 4 nulte linije, točke primjene sile koje odgovaraju različitim tangentama na donju desnu kutnu točku presjeka nalaze se na ravnoj liniji 1-2. Položaj točaka 3 i 4 određen je iz uvjeta simetrije. Dakle, jezgra presjeka za pravokutnik je romb s dijagonalama b/3 i IZ.


Za konstrukciju jezgre presjeka kružnice dovoljno je nacrtati jednu tangentu (slika 12.22). pri čemu a = R; A= °o.
"U U ^ ^
S obzirom da za krug ja y - J y /F - R / 4, iz (12.15) dobivamo 
Dakle, jezgra presjeka kruga je krug s radijusom R/4.
Na sl. 12.23, a, 6 prikazane su jezgre presjeka za I-gredu i kanal. Dostupnost četiri kutne točke Glavni dio u svakom od ovih primjera nastao je zbog činjenice da je kontura omotača i I-grede i kanala pravokutnik.


Ekscentrična kompresija. Izgradnja sekcijske jezgre. Savijanje s uvijanjem. Proračuni čvrstoće pri složenim stanjima naprezanja.
Ekscentrična kompresija je vrsta deformacije kod koje uzdužna sila u presjeku štapa ne djeluje u težištu. Na ekscentrična kompresija, osim uzdužne sile (N) nastaju dva momenta savijanja ( i ).
Pretpostavlja se da štap ima visoku krutost na savijanje kako bi se zanemario progib štapa pod ekscentričnom kompresijom.
Pretvorimo formulu za momente pod ekscentričnom kompresijom zamjenom vrijednosti momenata savijanja: .
Označimo koordinate određene točke nulte linije pri ekscentričnoj kompresiji i zamijenimo ih u formulu za normalna naprezanja pri ekscentričnoj kompresiji. Uzimajući u obzir da su naprezanja u točkama nulte crte jednaka nuli, nakon smanjenja za , dobivamo jednadžbu nulte crte za ekscentričnu kompresiju: ![]() .
.
Nulta linija za ekscentričnu kompresiju i točka primjene opterećenja uvijek se nalaze na suprotnim stranama težišta presjeka.

Segmenti odsječeni nul-linijom od koordinatnih osi, označeni i, mogu se lako pronaći iz jednadžbe nul-linije pod ekscentričnom kompresijom. Ako prvo uzmete ![]() a zatim prihvatiti
a zatim prihvatiti ![]() , tada nalazimo točke sjecišta nulte linije tijekom ekscentrične kompresije s glavnim središnjim osima:
, tada nalazimo točke sjecišta nulte linije tijekom ekscentrične kompresije s glavnim središnjim osima:

Nulta linija tijekom ekscentrične kompresije podijelit će presjek na dva dijela. U jednom dijelu naprezanja će biti tlačna, u drugom - vlačna. Proračuni čvrstoće, kao u slučaju kosog savijanja, provode se korištenjem normalnih naprezanja koja nastaju u opasnoj točki poprečnog presjeka (najdalje od nulte linije). 
Jezgra presjeka je malo područje oko težišta poprečnog presjeka, karakterizirano činjenicom da svaka tlačna uzdužna sila primijenjena unutar jezgre uzrokuje tlačna naprezanja u svim točkama poprečnog presjeka.
Primjeri jezgri presjeka za pravokutni i kružni presjek štapa.

Savijanje s uvijanjem. Osovine strojeva i mehanizama često su podvrgnute takvom opterećenju (istodobno djelovanje momenata torzije i savijanja). Za izračunavanje drva potrebno je prije svega utvrditi opasne dijelove. U tu svrhu konstruiraju se dijagrami momenata savijanja i momenta.
Koristeći načelo neovisnosti o djelovanju sila, odredit ćemo naprezanja koja nastaju u gredi odvojeno za torziju i savijanje.
Tijekom torzije nastaju tangencijalni naponi u poprečnim presjecima grede, koji postižu svoje najveće vrijednosti u točkama konture presjeka  Kod savijanja nastaju normalni naprezanja u poprečnim presjecima grede, koji postižu najveću vrijednost u vanjskim vlaknima grede.
Kod savijanja nastaju normalni naprezanja u poprečnim presjecima grede, koji postižu najveću vrijednost u vanjskim vlaknima grede.  .
.