1. Pravilo za zbrajanje razlomaka s istim nazivnicima:
Primjer 1:
Primjer 2:
Pravilo za zbrajanje razlomaka s različitim nazivnicima:
Primjer 1:
Primjer 2:
Ovdje se nazivnici nisu množili, već je uzet najmanji zajednički faktor a2.
(Imenitelj ima najveću snagu 2.)
Dodatni faktor za prvi razlomak je 1, za drugi je a.
2. Pravilo za oduzimanje razlomaka s istim nazivnicima:
Pravilo za oduzimanje razlomaka s različitim nazivnicima:
3. Pravilo množenja običnih razlomaka:
4. Pravilo za dijeljenje razlomaka:
Primjer:
Obični (prosti) razlomak. Brojnik i nazivnik razlomka.
Ispravan i Ne pravilan razlomak. Mješoviti broj.
Nepotpuni kvocijent. Cijeli i razlomački dijelovi. Obrnuti razlomci. Dio jedinice ili nekoliko njezinih dijelova nazivamo običnim ili prostim razlomkom. Količina jednake dijelove, na koji je jedinica podijeljena naziva se nazivnik, a broj uzetih dijelova naziva se brojnik. Razlomak se piše kao:

Ovdje je 3 brojnik, 7 je nazivnik.
Ako je brojnik manji od nazivnika, tada je razlomak manji od 1 i zove se pravilan razlomak. Ako je brojnik jednak nazivniku, tada je razlomak jednak 1. Ako je brojnik veći od nazivnika, tada je razlomak veći od 1. U oba potonja slučaja razlomak se naziva nepravim. Ako se brojnik podijeli s nazivnikom, tada je ovaj razlomak jednak kvocijentu dijeljenja: 63 / 7 = 9. Ako se dijeljenje izvodi s ostatkom, tada se ovaj nepravi razlomak može prikazati mješoviti broj:
Ovdje 9- nepotpuni kvocijent(cijeli dio mješovitog broja), 2 – ostatak (brojnik razlomka), 7 – nazivnik.
Često je potrebno riješiti obrnuti problem - obrnuti mješoviti broj u razlomak. Da biste to učinili, pomnožite cijeli dio mješovitog broja s nazivnikom i dodajte brojnik razlomka. Ovo će biti brojnik običnog razlomka, ali nazivnik ostaje isti. 
Recipročni razlomci su dva razlomka čiji je umnožak jednak 1. Na primjer, 3 / 7 i 7 / 3; 15/1 i 1/15 itd.
Proširenje razlomaka. Smanjenje razlomka. Uspoređivanje razlomaka.
Dovodi do zajednički nazivnik. Zbrajanje i oduzimanje razlomci.
Množenje razlomaka. Dijeljenje razlomaka
Proširenje razlomaka.Vrijednost razlomka se ne mijenja ako se njegov brojnik i nazivnik pomnože istim brojem koji nije nula proširenjem razlomka. Na primjer,
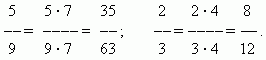
Smanjenje razlomka. Vrijednost razlomka se ne mijenja ako njegov brojnik i nazivnik podijelite s istim brojem koji nije nula.. Ova transformacija se zovesmanjivanje razlomka. Na primjer, 
Uspoređivanje razlomaka.Od dva razlomka s istim brojnicima veći je onaj čiji je nazivnik manji:

Od dva razlomka s istim nazivnikom veći je onaj čiji je brojnik veći:

Da biste usporedili razlomke koji imaju različite brojnike i nazivnike, morate ih proširiti kako biste ih doveli do zajedničkog nazivnika.
PRIMJER Usporedite dva razlomka:
Transformacija koja se ovdje koristi zove se dovođenje razlomaka na zajednički nazivnik.
Zbrajanje i oduzimanje razlomaka.Ako su nazivnici razlomaka isti, tada da bi razlomke zbrajali, treba im zbrojiti brojnike, a da bi razlomke oduzeli, treba im oduzeti brojnike (istim redoslijedom). Rezultirajući zbroj ili razlika bit će brojnik rezultata; nazivnik će ostati isti. Ako su nazivnici razlomaka različiti, prvo morate razlomke svesti na zajednički nazivnik. Prilikom dodavanja mješoviti brojevi posebno se zbrajaju njihovi cijeli i razlomački dijelovi. Kada oduzimate mješovite brojeve, preporučamo da ih prvo pretvorite u nepravilne razlomke, zatim oduzmete jedan od drugog, a zatim rezultat ponovno pretvorite, ako je potrebno, u oblik mješovitog broja.
PRIMJER
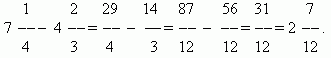
Množenje razlomaka.Pomnožiti broj razlomkom znači pomnožiti ga s brojnikom i umnožak podijeliti s nazivnikom. Stoga imamo opće pravilo množenje razlomaka:da biste pomnožili razlomke, morate odvojeno pomnožiti njihove brojnike i nazivnike i prvi umnožak podijeliti s drugim.
PRIMJER 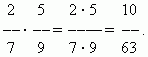
Dijeljenje razlomaka. Da bi se određeni broj podijelio s razlomkom, potrebno je taj broj pomnožiti s recipročnim razlomkom.Ovo pravilo proizlazi iz definicije dijeljenja (vidi odjeljak “Aritmetičke operacije”).
PRIMJER 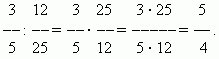
Decimal. Cijeli dio. Decimalna točka.
Decimalna mjesta. Svojstva decimalnih razlomaka.
Periodni decimalni razlomak. Razdoblje
Decimalrezultat je dijeljenja jedan s deset, sto, tisuću itd. dijelovi. Ovi su razlomci vrlo prikladni za izračune jer se temelje na istom sustavu položaja na kojem se temelji brojanje i pisanje cijelih brojeva. Zahvaljujući tome, zapis i pravila za rad s decimalnim razlomcima u biti su isti kao i za cijele brojeve. Pri pisanju decimalnih razlomaka nema potrebe označavati nazivnik, to je određeno mjestom koje zauzima odgovarajuća znamenka. Prvo je napisano cijeli dio brojeve, a zatim stavite desnodecimalna točka. Prva znamenka iza decimalne točke označava broj desetinki, druga – broj stotinki, treća – broj tisućinki itd. Pozivaju se brojevi koji se nalaze iza decimalne točkedecimale.
PRIMJER 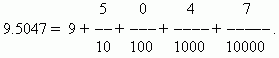
Jedna od prednosti decimalnih razlomaka je ta što se lako svode na obične razlomke: broj iza decimalne točke (u našem slučaju 5047) je brojnik; nazivnik je jednak n -tu potenciju od 10, gdje n - broj decimalnih mjesta (u našem slučaju n = 4): 
Ako decimalni razlomak ne sadrži cijeli broj, ispred decimalne točke stavlja se nula:
Svojstva decimalnih razlomaka.
1. Decimala se ne mijenja ako dodate nule s desne strane:
2.
Decimalni se razlomak ne mijenja ako uklonite nule koje se nalaze
na kraju decimale:
0.00123000 = 0.00123 .
Pažnja! Ne možete ukloniti nule koje se ne nalaze na kraju decimalno!br />
Ova svojstva vam omogućuju brzo množenje i dijeljenje decimala s 10, 100, 1000 itd.
Periodička decimala sadrži beskonačno ponavljajuću skupinu brojeva koja se naziva točka. Razdoblje je napisano u zagradi. Na primjer, 0,12345123451234512345… = 0.(12345).
PRIMJER Ako 47 podijelimo s 11, dobit ćemo 4,27272727... = 4.(27).
Množenje decimala.
Dijeljenje decimala.
Zbrajanje i oduzimanje decimala. Ove se operacije izvode na isti način kao zbrajanje i oduzimanje cijelih brojeva. Samo trebate zapisati odgovarajuća decimalna mjesta jedno ispod drugog.
PRIMJER
Množenje decimala. U prvoj fazi množimo decimalne razlomke kao cijele brojeve, ne uzimajući u obzir decimalni zarez. Tada vrijedi sljedeće pravilo: broj decimalnih mjesta u umnošku jednak je zbroju decimalnih mjesta u svim faktorima.
Bilješka: prije stavljanja decimalne točkeproizvod se ne može odbaciti s nulama na kraju!
PRIMJER
Zbroj brojeva decimalnih mjesta u faktorima jednak je: 3 + 4 = 7. Zbroj brojeva u umnošku je 6. Dakle, trebate dodati jednu nulu lijevo: 0197056 i staviti decimalnu točku ispred: 0,0197056.
Decimalno dijeljenje
Dijeljenje decimale cijelim brojem
Ako dividenda je manja od djelitelja, u cijelobrojni dio kvocijenta upišite nulu i iza nje stavite decimalnu točku. Zatim, ne uzimajući u obzir decimalnu točku dividende, dodamo sljedeću znamenku razlomka njegovom cijelom dijelu i ponovno usporedimo dobiveni cijeli dio dividende s djeliteljem. Ako je novi broj opet manji od djelitelja, iza decimalne točke u količniku stavljamo još jednu nulu i cijelom dijelu djelitelja pribrajamo sljedeću znamenku njegovog razlomačkog dijela. Ponavljamo ovaj postupak sve dok rezultirajuća dividenda ne postane veća od djelitelja. Nakon toga slijedi dijeljenje kao kod cijelih brojeva. Ako dividenda je veća ili jednaka djelitelju, prvo podijelimo njegov cijeli dio, rezultat dijeljenja upišemo u kvocijent i stavimo decimalnu točku. Nakon toga nastavlja se dijeljenje kao i kod cijelih brojeva.
PRIMJER Podijelite 1,328 sa 64.
Riješenje: 
Dijeljenje jednog decimalnog razlomka drugim.
Najprije decimalne točke u djelitelju i djelitelju prenesemo na broj decimalnih mjesta u djelitelju, odnosno djelitelj učinimo cijelim brojem. Sada vršimo dijeljenje kao u prethodnom slučaju.
PRIMJER Podijelite 0,04569 s 0,0006.
Rješenje: Pomaknite decimalne točke za 4 mjesta udesno i podijelite 456,9 sa 6:
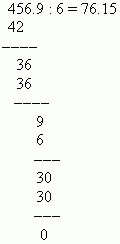
Kako bi rikverc decimal u običnom, trebate uzeti broj iza decimalne točke kao brojnik, a uzeti n-tu potenciju desetice kao nazivnik (ovdje je n broj decimalnih mjesta). Cijeli dio koji nije nula pohranjuje se u običnom razlomku; nulti cijeli dio je izostavljen. Na primjer: 
Da biste razlomak pretvorili u decimalu, morate brojnik podijeliti nazivnikom u skladu s pravilima dijeljenja.
PRIMJER Pretvorite 5/8 u decimalu.
Rješenje: dijeljenje 5 s 8 daje 0,625. (Racun molim!).
U većini slučajeva ovaj proces može trajati neograničeno dugo. Tada je nemoguće točno pretvoriti razlomak u decimalu. Ali u praksi to nikada nije potrebno. Dijeljenje se prekida ako su decimalna mjesta već dobivena.
PRIMJER Pretvorite 1/3 u decimalu.
Rješenje: Dijeljenje 1 sa 3 bit će beskonačno: 1:3 = 0,3333… .
Provjerite molim vas!
Množenje i dijeljenje razlomaka.
Pažnja!
Postoje dodatni
materijali u posebnom odjeljku 555.
Za one koji su jako "ne baš..."
I za one koji "jako...")
Ova operacija je puno ljepša od zbrajanja-oduzimanja! Jer je lakše. Podsjećamo, da biste razlomak pomnožili s razlomkom, morate pomnožiti brojnike (to će biti brojnik rezultata) i nazivnike (ovo će biti nazivnik). To je:
Na primjer:

Sve je krajnje jednostavno. I nemojte, molim vas, tražiti zajednički nazivnik! Nema potrebe za njim ovdje...
Da biste podijelili razlomak s razlomkom, morate obrnuti drugi(ovo je važno!) razlomak i pomnožite ih, tj.:

Na primjer:

Ako naiđete na množenje ili dijeljenje s cijelim brojevima i razlomcima, u redu je. Kao i kod zbrajanja, pravimo razlomak od cijelog broja s jedinicom u nazivniku - i samo naprijed! Na primjer:

U srednjoj školi često se morate baviti trokatnim (ili čak četverokatnim!) razlomcima. Na primjer:
Kako mogu učiniti da ovaj razlomak izgleda pristojno? Da, vrlo jednostavno! Koristite podjelu u dvije točke:

Ali ne zaboravite na redoslijed podjele! Za razliku od množenja, ovo je ovdje vrlo važno! Naravno, nećemo brkati 4:2 ili 2:4. Ali lako je pogriješiti u trokatnici. Imajte na umu na primjer:
U prvom slučaju (izraz lijevo):

U drugom (izraz desno):

Osjećate li razliku? 4 i 1/9!
Što određuje redoslijed podjele? Ili sa zagradama, ili (kao ovdje) s duljinom vodoravnih linija. Razvijte svoje oko. A ako nema zagrada ili crtica, na primjer:
zatim podijeli i pomnoži redom, s lijeva na desno!
I još jedna vrlo jednostavna i važna tehnika. U akcijama sa stupnjevima, bit će vam tako korisno! Podijelimo jedan s bilo kojim razlomkom, na primjer s 13/15:

Snimak se preokrenuo! A ovo se uvijek događa. Kada dijelite 1 bilo kojim razlomkom, rezultat je isti razlomak, samo naopako.
To je to za operacije s razlomcima. Stvar je prilično jednostavna, ali daje više nego dovoljno grešaka. Uzmite u obzir praktične savjete, i bit će ih manje (pogrešaka)!
Praktični savjeti:
1. Najvažnija stvar pri radu s frakcijskim izrazima je točnost i pažljivost! Nije uobičajene riječi, nisu dobre želje! Ovo je krajnja potreba! Izvršite sve izračune na Jedinstvenom državnom ispitu kao punopravni zadatak, fokusiran i jasan. Bolje je napisati dva dodatna retka u nacrtu nego zabrljati dok radite mentalne izračune.
2. U primjerima sa različiti tipovi razlomci - idite na obične razlomke.
3. Smanjujemo sve razlomke dok ne stanu.
4. Višerazinske frakcijske izraze reduciramo na obične dijeljenjem kroz dvije točke (vodimo redoslijed dijeljenja!).
5. Podijelite jedinicu s razlomkom u glavi, jednostavno okrećući razlomak.
Evo zadataka koje svakako morate izvršiti. Nakon svih zadataka daju se odgovori. Koristite materijale o ovoj temi i praktične savjete. Procijenite koliko ste primjera uspjeli točno riješiti. Prvi put! Bez kalkulatora! I izvući prave zaključke...
Upamtite - točan odgovor je primljeno iz drugog (pogotovo trećeg) puta se ne računa! Takav je surov život.
Tako, riješiti u ispitnom načinu ! Usput, ovo je već priprema za Jedinstveni državni ispit. Rješavamo primjer, provjeravamo, rješavamo sljedeći. Sve smo odlučili - ponovno provjerili od prvog do zadnjeg. Ali samo Zatim pogledajte odgovore.
Izračunati:


Jesi li odlučio?
Tražimo odgovore koji odgovaraju vašima. Namjerno sam ih zapisao u neredu, daleko od iskušenja, da tako kažem... Evo ih, odgovora, ispisanih točkom i zarezom.
0; 17/22; 3/4; 2/5; 1; 25.
Sada donosimo zaključke. Ako je sve uspjelo, sretan sam zbog tebe! Osnovni izračuni s razlomcima nisu vaš problem! Možete raditi ozbiljnije stvari. Ako ne...
Dakle, imate jedan od dva problema. Ili oboje odjednom.) Nedostatak znanja i (ili) nepažnja. Ali ovo rješiv Problemi.
Ako vam se sviđa ova stranica...
Usput, imam još nekoliko zanimljivih stranica za vas.)
Možete vježbati rješavanje primjera i saznati svoju razinu. Testiranje uz trenutnu provjeru. Učimo - sa zanimanjem!)
Možete se upoznati s funkcijama i derivacijama.
496. Pronaći x, ako:
497. 1) Ako dodate 10 1/2 na 3/10 nepoznatog broja, dobit ćete 13 1/2. Pronađite nepoznati broj.
2) Ako oduzmete 10 1/2 od 7/10 nepoznatog broja, dobit ćete 15 2/5. Pronađite nepoznati broj.
498 *. Ako od 3/4 nepoznatog broja oduzmete 10 i dobivenu razliku pomnožite s 5, dobit ćete 100. Odredite broj.
499 *. Ako nepoznati broj povećate za 2/3, dobit ćete 60. Koji je to broj?
500 *. Dodate li nepoznatom broju isti iznos i još 20 1/3, dobit ćete 105 2/5. Pronađite nepoznati broj.
501. 1) Prinos krumpira kod sadnje u četvrtasti grozd prosječno je 150 centnera po hektaru, a kod konvencionalne sadnje 3/5 ove količine. Koliko se više krumpira može ubrati s površine od 15 ha ako se krumpir sadi metodom kvadrata?
2) Iskusni radnik izradio je 18 dijelova za 1 sat, a neiskusni radnik 2/3 te količine. Koliko još dijelova može proizvesti iskusan radnik u 7-satnom radnom vremenu?
502. 1) Pioniri okupljeni unutar tri dana 56 kg raznog sjemena. Prvog dana prikupljeno je 3/14 ukupne količine, drugog puta više, a trećeg dana ostatak žita. Koliko su kilograma sjemena pioniri sakupili treći dan?
2) Kod mljevenja pšenice rezultat je bio: brašno 4/5 od ukupne količine pšenice, griz - 40 puta manje od brašna, a ostalo su mekinje. Koliko je brašna, griza i posija zasebno nastalo pri mljevenju 3 tone pšenice?
503. 1) Tri garaže mogu primiti 460 automobila. Broj automobila koji stanu u prvu garažu je 3/4 od broja automobila koji stanu u drugu, a treća garaža ima 1 1/2 puta više automobila od prve. Koliko automobila stane u svaku garažu?
2) Tvornica s tri radionice zapošljava 6000 radnika. U drugoj radionici ima 1 1/2 puta manje radnika nego u prvoj, a broj radnika u trećoj radionici je 5/6 od broja radnika u drugoj radionici. Koliko je radnika u svakoj radionici?
504. 1) Iz cisterne s kerozinom izliveno je prvo 2/5, zatim 1/3 ukupnog kerozina, a nakon toga je u cisterni ostalo 8 tona kerozina. Koliko je kerozina bilo u spremniku na početku?
2) Biciklisti su se utrkivali tri dana. Prvog dana prešli su 4/15 cijelog puta, drugog 2/5, a trećeg dana preostalih 100 km. Koliki su put biciklisti prevalili u tri dana?
505. 1) Ledolomac se tri dana probijao kroz ledeno polje. Prvi dan je prešao 1/2 cijele udaljenosti, drugi dan 3/5 preostale udaljenosti i treći dan preostalih 24 km. Odredi duljinu puta koji je ledolomac prevalio u tri dana.
2) Tri grupe školaraca sadile su drveće da ozelene selo. Prva desetina posadila je 7/20 svih stabala, druga 5/8 preostalih stabala, a treća preostalih 195 stabala. Koliko su stabala ukupno zasadila tri tima?
506. 1) Kombajn je s jedne parcele požnjeo pšenicu za tri dana. Prvog dana ubrao je sa 5/18 ukupne površine parcele, drugog dana sa 7/13 preostale površine, a trećeg dana sa preostale površine od 30 1/2. hektara. U prosjeku je sa svakog hektara požnjeveno 20 centnera pšenice. Koliko je pšenice požnjeveno na cijelom području?
2) Prvog dana sudionici relija prevalili su 3/11 cijele rute, drugog dana 7/20 preostale rute, trećeg dana 5/13 novog ostatka, a četvrtog dana preostalu trasu. 320 km. Koliko je duga trasa relija?
507. 1) Prvog dana auto je prešao 3/8 cijele udaljenosti, drugog dana 15/17 onoga što je prešao prvog, a trećeg dana preostalih 200 km. Koliko je benzina potrošeno ako automobil za 10 km potroši 1 3/5 kg benzina?
2) Grad se sastoji od četiri četvrti. I 4/13 svih stanovnika grada živi u prvom okrugu, 5/6 stanovnika prvog kvarta živi u drugom, 4/11 stanovnika prvog živi u trećem; dva okruga zajedno, a 18 tisuća ljudi živi u četvrtom okrugu. Koliko kruha treba cijelom stanovništvu grada za 3 dana, ako ga prosječno jedna osoba dnevno pojede 500 g?
508. 1) Turist je prvi dan propješačio 10/31 cijelog puta, drugi 9/10 onoga što je propješačio prvog dana, treći ostatak puta, a treći dan je išao 12 km više nego drugog dana. Koliko je kilometara turist prešao svakog od tri dana?
2) Automobil je prešao cijeli put od grada A do grada B za tri dana. Prvog dana automobil je prešao 7/20 cijele udaljenosti, drugog 8/13 preostale udaljenosti, a trećeg dana je automobil prešao 72 km manje nego prvog dana. Kolika je udaljenost između gradova A i B?
509. 1) Izvršni odbor dodijelio je zemljište radnicima triju tvornica za okućnice. Prvoj biljci dodijeljeno je 9/25 od ukupnog broja parcela, drugoj biljci 5/9 od broja parcela dodijeljenih prvoj, a trećoj - preostale parcele. Koliko je ukupno parcela dodijeljeno radnicima triju tvornica, ako je prvoj tvornici dodijeljeno 50 parcela manje od treće?
2) Avion je za tri dana dopremio smjenu zimskih radnika na polarnu postaju iz Moskve. Prvog dana je preletio 2/5 cijele udaljenosti, drugog - 5/6 udaljenosti koju je prešao prvog dana, a trećeg dana je preletio 500 km manje nego drugog dana. Koliko je avion preletio u tri dana?
510. 1) Pogon je imao tri radionice. Broj radnika u prvoj radionici je 2/5 svih radnika u pogonu; u drugoj radionici ima 1 1/2 puta manje radnika nego u prvoj, a u trećoj radionici ima 100 radnika više nego u drugoj. Koliko radnika ima u tvornici?
2) Kolhoz uključuje stanovnike tri susjedna sela. Broj obitelji u prvom selu je 3/10 svih obitelji na kolektivnoj farmi; u drugom je selu broj obitelji 1 1/2 puta veći nego u prvom, a u trećem je selu broj obitelji 420 manji nego u drugom. Koliko obitelji ima na kolektivnoj farmi?
511. 1) Artel je u prvom tjednu potrošio 1/3 svojih zaliha sirovina, au drugom 1/3 ostatka. Koliko je sirovina ostalo u artelu ako je u prvom tjednu potrošnja sirovina bila 3/5 tona veća nego u drugom tjednu?
2) Od uvezenog ugljena utrošeno je 1/6 za grijanje kuće u prvom mjesecu, a 3/8 ostatka u drugom mjesecu. Koliko je ugljena ostalo za grijanje kuće ako je u drugom mjesecu potrošeno 1 3/4 više nego u prvom mjesecu?
512. 3/5 ukupnog zemljišta kolektivne farme namijenjeno je za sjetvu žitarica, 13/36 ostatka zauzimaju povrtnjaci i livade, ostalo zemljište je šuma, a sjetvena površina kolektivne farme je 217 hektara veće od šumske površine, 1/3 zemlje namijenjene za sjetvu žitarica zasijana je raži, a ostalo je pšenica. Koliko je hektara zemlje zadruga zasijala pšenicom, a koliko raži?
513. 1) Trasa tramvaja duga je 14 3/8 km. Na ovoj ruti tramvaj napravi 18 stanica, trošeći u prosjeku do 1 1/6 minute po stanici. Prosječna brzina tramvaja na cijeloj trasi je 12 1/2 km na sat. Koliko tramvaju treba da završi jednu vožnju?
2) Autobusna linija 16 km. Na ovoj ruti autobus ima 36 stanica po 3/4 minute. u prosjeku svaki. Prosječna brzina autobusa je 30 km na sat. Koliko autobusu treba jedna ruta?
514*. 1) Sada je 6 sati. večeri. Koji dio dana je preostali dio dana iz prošlosti, a koji je ostao?
2) Parobrod prijeđe udaljenost između dva grada strujom za 3 dana. a natrag istu udaljenost za 4 dana. Koliko će dana splavi ploviti nizvodno od jednog grada do drugog?
515. 1) Koliko će se dasaka upotrijebiti za postavljanje poda u prostoriji čija je duljina 6 2/3 m, širina 5 1/4 m, ako je duljina svake daske 6 2/3 m, a širina 3/ 80 duljine?
2) Pravokutna platforma ima duljinu 45 1/2 m, a širina joj je 5/13 njezine duljine. Ovo područje je omeđeno stazom širine 4/5 m. Pronađite površinu staze.
516. Pronađite prosjek aritmetički brojevi:

517. 1) Aritmetička sredina dvaju brojeva je 6 1/6. Jedan od brojeva je 3 3/4. Pronađite drugi broj.
2) Aritmetička sredina dvaju brojeva je 14 1/4. Jedan od ovih brojeva je 15 5/6. Pronađite drugi broj.
518. 1) Teretni je vlak bio na putu tri sata. U prvom satu prešao je 36 1/2 km, u drugom 40 km i u trećem 39 3/4 km. Odredi prosječnu brzinu vlaka.
2) Auto je u prva dva sata prešao 81 1/2 km, au sljedeća 2 1/2 sata 95 km. Koliko je kilometara prosječno prešao po satu?
519. 1) Traktorist je obavio zadatak oranja zemlje za tri dana. Prvog dana obrao je 12 1/2 hektara, drugog dana 15 3/4 hektara i trećeg dana 14 1/2 hektara. Koliko je prosječno hektara zemlje dnevno preorao vozač traktora?
2) Grupa školaraca koja je bila na trodnevnom turističkom izletu bila je prvi dan na putu 6 1/3 sati, a drugi 7 sati. a treći dan – 4 2/3 sata. Koliko sati u prosjeku školarci putuju svaki dan?
520. 1) U kući žive tri obitelji. Prva obitelj ima 3 žarulje za osvjetljavanje stana, druga 4, a treća 5 žarulja. Koliko bi svaka obitelj trebala platiti za struju ako su sve lampe iste, a ukupni račun za struju (za cijelu kuću) iznosi 7 1/5 rubalja?
2) Lastir je glancao podove u stanu u kojem su živjele tri obitelji. Prva obitelj imala je stambeni prostor od 36 1/2 četvornih metara. m, drugi je 24 1/2 sq. m, a treći - 43 m2. m. Za sav rad plaćeno je 2 rublja. 08 kop. Koliko je svaka obitelj platila?
521. 1) Na okućnici krumpir je sakupljen iz 50 grmova po 1 1/10 kg po grmu, iz 70 grmova po 4/5 kg po grmu, iz 80 grmova po 9/10 kg po grmu. Koliko se kilograma krumpira prosječno ubere sa svakog grma?
2) Terenska posada na površini od 300 hektara dobila je žetvu od 20 1/2 kvintala ozime pšenice po 1 hektaru, od 80 hektara do 24 kvintala po 1 ha, a od 20 hektara - 28 1/2 kvintala po 1 ha. Koliki je prosječni prinos u brigadi s 1 hektarom?
522. 1) Zbroj dvaju brojeva je 7 1/2. Jedan broj je 4 4/5 veći od drugog. Pronađite ove brojeve.
2) Zbrojimo li brojeve koji izražavaju širinu Tatarskog i Kerčkog tjesnaca, dobit ćemo 11 7/10 km. Tatarski tjesnac je 3 1/10 km širi od Kerčkog tjesnaca. Kolika je širina svakog tjesnaca?
523. 1) Zbroj tri broja je 35 2 / 3. Prvi broj je veći od drugog za 5 1/3 i veći od trećeg za 3 5/6. Pronađite ove brojeve.
2) Otoci Nova Zemlja, Sahalin i Severnaya Zemlya zajedno zauzimaju površinu od 196 7/10 tisuća četvornih metara. km. Površina Novaya Zemlya je 44 1/10 tisuća četvornih metara. km više površine Severnaya Zemlya i 5 1/5 tisuća četvornih. km veće od područja Sahalina. Kolika je površina svakog od navedenih otoka?
524. 1) Stan se sastoji od tri sobe. Površina prve sobe je 24 3/8 kvadratnih metara. m i iznosi 13/36 ukupne površine stana. Površina druge sobe je 8 1/8 kvadratnih metara. m više od površine trećeg. Kolika je površina druge sobe?
2) Biciklist je tijekom trodnevnog natjecanja prvog dana bio na cesti 3 1/4 sata, što je bilo 13/43 ukupnog vremena putovanja. Drugi dan je jahao 1 1/2 sat više nego treći dan. Koliko je sati biciklist putovao drugog dana natjecanja?
525. Tri komada željeza zajedno teže 17 1/4 kg. Ako se težina prvog komada smanji za 1 1/2 kg, a težina drugog za 2 1/4 kg, tada će sva tri komada imati istu težinu. Koliko je težio svaki komad željeza?
526. 1) Zbroj dva broja je 15 1/5. Ako se prvi broj smanji za 3 1/10, a drugi poveća za 3 1/10, tada će ti brojevi biti jednaki. Čemu je svaki broj jednak?
2) U dvije kutije bilo je 38 1/4 kg žitarica. Ako sipate 4 3/4 kg žitarica iz jedne kutije u drugu, tada će u obje kutije biti jednake količine žitarica. Koliko je žitarica u svakoj kutiji?
527 . 1) Zbroj dva broja je 17 17 / 30. Ako od prvog broja oduzmete 5 1/2 i dodate ga drugom, tada će prvi i dalje biti veći od drugog za 2 17/30. Pronađite oba broja.
2) U dva sanduka ima 24 1/4 kg jabuka. Ako 3 1/2 kg prebacite iz prve kutije u drugu, tada će u prvoj još uvijek biti 3/5 kg više jabuka nego u drugoj. Koliko je kilograma jabuka u svakoj kutiji?
528 *. 1) Zbroj dva broja je 8 11/14, a njihova razlika je 2 3/7. Pronađite ove brojeve.
2) Čamac se kretao uz rijeku brzinom 15 1/2 km na sat, a protiv struje 8 1/4 km na sat. Kolika je brzina toka rijeke?
529. 1) U dvije garaže ima 110 automobila, au jednoj od njih 1 1/5 puta više nego u drugoj. Koliko je automobila u svakoj garaži?
2) Stambena površina stana koji se sastoji od dvije sobe je 47 1/2 m2. m. Površina jedne sobe je 8/11 površine druge. Pronađite površinu svake sobe.
530. 1) Legura koja se sastoji od bakra i srebra teška je 330 g. Masa bakra u ovoj leguri je 5/28 mase srebra. Koliko srebra, a koliko bakra ima u leguri?
2) Zbroj dva broja je 6 3/4, a količnik je 3 1/2. Pronađite ove brojeve.
531. Zbroj tri broja je 22 1/2. Drugi broj je 3 1/2 puta, a treći je 2 1/4 puta prvi. Pronađite ove brojeve.
532. 1) Razlika dvaju brojeva je 7; kvocijent dijeljenja više za manje od 5 2/3. Pronađite ove brojeve.
2) Razlika između dva broja je 29 3/8, a njihov višestruki omjer je 8 5/6. Pronađite ove brojeve.
533. U razredu broj odsutnih učenika je 3/13 od broja prisutnih učenika. Koliko je učenika u razredu prema popisu ako je nazočnih 20 više nego odsutnih?
534. 1) Razlika između dva broja je 3 1/5. Jedan broj je 5/7 drugog. Pronađite ove brojeve.
2) Otac stariji od mog sina za 24 godine. Broj sinovljevih godina jednak je 5/13 očevih godina. Koliko godina ima otac, a koliko sin?
535. Nazivnik razlomka je 11 jedinica veći od njegovog brojnika. Kolika je vrijednost razlomka ako je njegov nazivnik 3 3/4 puta veći od brojnika?
br. 536 - 537 usmeno.
536. 1) Prvi broj je 1/2 drugog. Koliko je puta drugi broj veći od prvog?
2) Prvi broj je 3/2 drugog. Koji je dio prvog broja drugi broj?
537. 1) 1/2 prvog broja jednaka je 1/3 drugog broja. Koji je dio prvog broja drugi broj?
2) 2/3 prvog broja jednako je 3/4 drugog broja. Koji je dio prvog broja drugi broj? Koji je dio drugog broja prvi?
538. 1) Zbroj dva broja je 16. Odredi te brojeve ako je 1/3 drugog broja jednaka 1/5 prvog.
2) Zbroj dva broja je 38. Odredi te brojeve ako je 2/3 prvog broja jednako 3/5 drugog.
539 *. 1) Dva dječaka zajedno su skupila 100 gljiva. 3/8 broja gljiva koje je sakupio prvi dječak brojčano je jednako 1/4 broja gljiva koje je sakupio drugi dječak. Koliko je svaki dječak skupio gljiva?
2) Ustanova zapošljava 27 osoba. Koliko muškaraca radi, a koliko žena ako je 2/5 svih muškaraca jednako 3/5 svih žena?
540 *. Tri dječaka kupila su odbojkašku loptu. Odredite doprinos svakog dječaka, znajući da je 1/2 doprinosa prvog dječaka jednaka 1/3 doprinosa drugog, odnosno 1/4 doprinosa trećeg, a da je doprinos trećeg dječak je 64 kopecks više od doprinosa prvog.
541 *. 1) Jedan broj je veći od drugog za 6. Odredi te brojeve ako su 2/5 jednog broja jednake 2/3 drugog.
2) Razlika dva broja je 35. Odredi te brojeve ako je 1/3 prvog broja jednaka 3/4 drugog broja.
542. 1) Prvi tim može završiti neki posao za 36 dana, a drugi za 45 dana. Za koliko će dana oba tima, radeći zajedno, završiti ovaj posao?
2) Putnički vlak prijeđe udaljenost između dva grada za 10 sati, a teretni vlak tu udaljenost prijeđe za 15 sati. Oba su vlaka napustila ove gradove u isto vrijeme jedan prema drugome. Za koliko sati će se sresti?
543. 1) Brzi vlak prijeđe udaljenost između dva grada za 6 1/4 sati, a putnički vlak za 7 1/2 sati. Koliko sati kasnije će se ti vlakovi sresti ako krenu iz oba grada u isto vrijeme jedan prema drugom? (Odgovor zaokružite na najbliži 1 sat.)
2) Dva motociklista krenula su istovremeno iz dva grada jedan prema drugom. Jedan motociklist može prijeći cijelu udaljenost između ovih gradova za 6 sati, a drugi za 5 sati. Koliko će se sati nakon polaska motociklisti sresti? (Odgovor zaokružite na najbliži 1 sat.)
544. 1) Tri vozila različite nosivosti mogu prevesti neki teret radeći odvojeno: prvo za 10 sati, drugo za 12 sati. a treći za 15 sati.Za koliko sati mogu zajednički prevesti isti teret?
2) Dva vlaka kreću istovremeno iz dvije stanice jedan prema drugome: prvi vlak prijeđe udaljenost između tih stanica za 12 1/2 sati, a drugi za 18 3/4 sati. Koliko će se sati nakon polaska vlakovi susresti?
545. 1) Dvije slavine spojene su na kadu. Kroz jedan od njih kupka se može napuniti za 12 minuta, kroz drugi 1 1/2 puta brže. Za koliko minuta ćete napuniti 5/6 cijele kade ako otvorite obje slavine odjednom?
2) Dva daktilografa moraju prekucati rukopis. Prvi vozač može obaviti ovaj posao za 3 1/3 dana, a drugi 1 1/2 puta brže. Koliko će dana trebati obojici daktilografa da obave posao ako rade istovremeno?
546. 1) Bazen se prvom cijevi napuni za 5 sati, a kroz drugu cijev se može isprazniti za 6 sati.Nakon koliko sati će se cijeli bazen napuniti ako se obje cijevi otvore istovremeno?
Bilješka. Za sat vremena bazen se napuni do (1/5 - 1/6 kapaciteta).
2) Dva traktora su obradila njivu za 6 sati. Prvi traktor, koji radi sam, mogao bi ovu njivu obrati za 15 sati.Koliko sati bi trebalo drugom traktoru, koji radi sam, da ore ovu njivu?
547 *. Dva vlaka napuštaju dvije stanice istovremeno jedan prema drugom i susreću se nakon 18 sati. nakon njegova oslobađanja. Koliko je vremena potrebno drugom vlaku da prijeđe udaljenost između stanica ako prvi vlak prijeđe tu udaljenost za 1 dan 21 sat?
548 *. Bazen se puni s dvije cijevi. Prvo su otvorili prvu cijev, a zatim nakon 3 3/4 sata, kada je pola bazena bilo ispunjeno, otvorili su drugu cijev. Nakon 2 i pol sata zajedničkog rada, bazen je bio pun. Odredite kapacitet bazena ako kroz drugu cijev protječe 200 kanti vode na sat.
549. 1) Kurirski vlak krenuo je iz Lenjingrada za Moskvu i putuje 1 km za 3/4 minute. 1/2 sata nakon što je ovaj vlak krenuo iz Moskve, iz Moskve je za Lenjingrad krenuo brzi vlak čija je brzina bila jednaka 3/4 brzine brzog vlaka. Na kojoj će udaljenosti vlakovi biti jedan od drugog 2 1/2 sata nakon polaska kurirskog vlaka, ako je udaljenost između Moskve i Lenjingrada 650 km?
2) Od kolhoza do grada 24 km. Kamion napušta kolektivnu farmu i prijeđe 1 km za 2 1/2 minute. Nakon 15 min. Nakon što je ovaj automobil napustio grad, biciklist se odvezao do kolektivne farme, brzinom upola manjom od brzine kamiona. Koliko će vremena nakon polaska biciklist sresti kamion?
550. 1) Iz jednog sela izašao je pješak. 4 1/2 sata nakon što je pješak otišao, u istom smjeru vozio je biciklist čija je brzina bila 2 1/2 puta veća od brzine pješaka. Koliko sati nakon izlaska pješaka će ga preteći biciklist?
2) Brzi vlak prijeđe 187 1/2 km za 3 sata, a teretni vlak prijeđe 288 km za 6 sati. 7 1/4 sata nakon polaska teretnog vlaka, vozilo hitne pomoći kreće u istom smjeru. Koliko će trebati brzom vlaku da sustigne teretni vlak?
551. 1) Iz dvije zadruge kroz koje prolazi put do regionalnog centra, dva zadruga su izjahala u okrug u isto vrijeme na konjima. Prvi od njih je putovao 8 3/4 km na sat, a drugi 1 1/7 puta više od prvog. Drugi kolhoznik je sustigao prvog nakon 3 4/5 sata. Odredite udaljenost između kolektivnih farmi.
2) 26 1/3 sati nakon polaska vlaka Moskva-Vladivostok, čija je prosječna brzina bila 60 km na sat, avion TU-104 poletio je u istom smjeru, brzinom 14 1/6 puta od brzine vlaka. Koliko će sati nakon polijetanja avion sustići vlak?
552. 1) Udaljenost između gradova duž rijeke je 264 km. Parobrod je ovu udaljenost prešao nizvodno za 18 sati, trošeći 1/12 ovog vremena na zaustavljanje. Brzina rijeke je 1 1/2 km na sat. Koliko bi brodu trebalo da prijeđe 87 km bez zaustavljanja? stoječa voda?
2) Motorni čamac je prešao 207 km rijekom za 13 1/2 sati, pri čemu je 1/9 tog vremena proveo na zaustavljanjima. Brzina rijeke je 1 3/4 km na sat. Koliko kilometara ovaj čamac može prijeći u mirnoj vodi za 2 1/2 sata?
553. Brod je prevalio udaljenost od 52 km preko akumulacije bez zaustavljanja za 3 sata i 15 minuta. Dalje, idući rijekom protiv struje, čija je brzina 1 3/4 km na sat, ovaj je čamac prešao 28 1/2 km za 2 1/4 sata, napravivši 3 zaustavljanja u jednakom trajanju. Koliko je minuta brod čekao na svakom stajalištu?
554. Iz Lenjingrada u Kronstadt u 12 sati. Parobrod je krenuo poslijepodne i prevalio cijelu udaljenost između ovih gradova za 1 i 2 sata. Na putu je susreo još jedan brod koji je krenuo iz Kronstadta za Lenjingrad u 12.18 sati. i hodanje brzinom 1 1/4 puta većom od prve. U koje vrijeme su se dva broda susrela?
555. Vlak je trebao prijeći udaljenost od 630 km za 14 sati. Nakon što je prešao 2/3 ove udaljenosti, zadržan je 1 sat i 10 minuta. Kojom brzinom treba nastaviti putovanje da bi bez kašnjenja stigao na odredište?
556. U 4:20 ujutro ujutro je teretni vlak krenuo iz Kijeva za Odesu sa Prosječna brzina 31 1/5 km na sat. Nakon nekog vremena iz Odese mu je u susret izašao poštanski vlak čija je brzina bila 1 17/39 puta veća od brzine teretnog vlaka i susreo se s teretnim vlakom 6 1/2 sati nakon njegova polaska. U koliko sati je poštanski vlak krenuo iz Odese, ako je udaljenost između Kijeva i Odese 663 km?
557*. Sat pokazuje podne. Koliko će vremena trebati da se poklope kazaljke sata i minute?
558. 1) Pogon ima tri radionice. Broj radnika u prvoj radionici je 9/20 svih radnika tvornice, u drugoj radionici ima 1 1/2 puta manje radnika nego u prvoj, a u trećoj radionici ima 300 radnika manje nego u drugi. Koliko radnika ima u tvornici?
2) U gradu postoje tri srednje škole. Broj učenika u prvoj školi je 3/10 svih učenika u ove tri škole; u drugoj školi ima 1 1/2 puta više učenika nego u prvoj, a u trećoj je školi 420 učenika manje nego u drugoj. Koliko učenika ima u tri škole?
559. 1) Dva kombajnera su radila na istom području. Nakon što je jedan kombajner požnjeo 9/16 cijele parcele, a drugi 3/8 iste parcele, pokazalo se da je prvi kombajner požnjeo 97 1/2 hektara više od drugog. Prosječno je sa svakog hektara ovršeno 32 1/2 kvintala žita. Koliko je centnera žita ovršio svaki kombajner?
2) Dva brata su kupila fotoaparat. Jedan je imao 5/8, a drugi 4/7 cijene kamere, a prvi je imao 2 rublje. 25 kopejki više od drugog. Svatko je platio pola cijene uređaja. Koliko je svima ostalo novca?
560. 1) Osobni automobil kreće iz grada A prema gradu B, udaljenost između njih je 215 km, brzinom 50 km na sat. U isto vrijeme kamion je krenuo iz grada B prema gradu A. Koliko je kilometara prešao osobni automobil prije susreta s kamionom, ako je brzina kamiona na sat bila 18/25 brzine osobnog automobila?
2) Između gradova A i B 210 km. Osobni automobil krenuo je iz grada A prema gradu B. U isto vrijeme kamion je krenuo iz grada B prema gradu A. Koliko je kilometara prešao kamion prije susreta s osobnim automobilom, ako se osobni automobil kretao brzinom od 48 km na sat, a brzina kamiona na sat bila je 3/4 brzine osobnog automobila?
561. Kolhoz je požnjeo pšenicu i raž. Pšenicom je zasijano 20 hektara više nego raži. Ukupna žetva raži iznosila je 5/6 ukupne žetve pšenice uz prinos od 20 c po 1 ha i za pšenicu i za raž. Zadruga je državi prodala 7/11 cjelokupnog uroda pšenice i raži, a ostatak žitarica ostavila za svoje potrebe. Koliko su kamioni od dvije tone trebali prijeći da odvezu kruh koji se prodaje državi?
562. U pekaru se nosilo raženo i pšenično brašno. Težina pšeničnog brašna iznosila je 3/5 težine raženog brašna, a dovezeno je 4 tone više raženog brašna nego pšeničnog. Koliko će pšeničnog, a koliko raženog kruha ispeći pekara od ovog brašna ako peciva čine 2/5 ukupnog brašna?
563. U roku od tri dana tim radnika završio je 3/4 cjelokupnog posla na popravci autoputa između dva kolektivna gospodarstva. Prvog dana popravljeno je 2 2/5 km ove magistrale, drugog dana 1 1/2 puta više nego prvog, a trećeg dana 5/8 onoga što je popravljeno u prva dva dana zajedno. Pronađite duljinu autoceste između kolektivnih farmi.
564. Popunite prazna mjesta u tablici, gdje je S površina pravokutnika, A- osnovica pravokutnika, a h-visina (širina) pravokutnika.

565. 1) Duljina čestice pravokutnog oblika je 120 m, a širina parcele je 2/5 njezine dužine. Pronađite opseg i područje mjesta.
2) Širina pravokutnog odsječka je 250 m, a duljina je 1 1/2 puta veća od širine. Pronađite opseg i područje mjesta.
566. 1) Opseg pravokutnika je 6 1/2 inča, njegova baza je 1/4 inča veća od njegove visine. Pronađite površinu ovog pravokutnika.
2) Opseg pravokutnika je 18 cm, njegova visina je 2 1/2 cm manja od osnovice. Pronađite površinu pravokutnika.
567. Izračunajte površine likova prikazanih na slici 30. tako da ih podijelite na pravokutnike i mjerenjem odredite dimenzije pravokutnika.

568. 1) Koliko će ploča suhe žbuke biti potrebno za oblaganje stropa prostorije duljine 4 1/2 m i širine 4 m, ako su dimenzije ploče gipsa 2 m x l 1/2 m?
2) Koliko je dasaka dužine 4 1/2 m i širine 1/4 m potrebno da se postavi pod dug 4 1/2 m i širok 3 1/2 m?
569. 1) Grahom je zasijana pravokutna parcela duljine 560 m i širine 3/4 njezine duljine. Koliko je sjemena bilo potrebno za sjetvu parcele ako je posijan 1 center po 1 hektaru?
2) Žetva pšenice od 25 kvintala po hektaru prikupljena je s pravokutnog polja. Koliko je pšenice požnjeveno s cijele njive ako je duljina njive 800 m, a širina 3/8 njezine duljine?
570 . 1) Zemljište pravokutnog oblika, dužine 78 3/4 m i širine 56 4/5 m, izgrađeno je tako da 4/5 njegove površine zauzimaju zgrade. Odredite površinu zemljišta ispod zgrada.
2) Na zemljištu pravokutnog oblika, čija je dužina 9/20 km, a širina 4/9 njegove dužine, kolektivna farma planira urediti vrt. Koliko će stabala biti posađeno u ovom vrtu ako je za svako stablo potrebna prosječna površina od 36 m2?
571. 1) Za normalno dnevno osvjetljenje prostorije potrebno je da površina svih prozora bude najmanje 1/5 površine poda. Odredi ima li dovoljno svjetla prostorija čija je duljina 5 1/2 m, a širina 4 m. Ima li soba jedan prozor dimenzija 1 1/2 m x 2 m?
2) Pomoću uvjeta prethodnog zadatka utvrdite ima li dovoljno svjetla u vašoj učionici.
572. 1) Staja ima dimenzije 5 1/2 m x 4 1/2 m x 2 1/2 m. Koliko će sijena (po težini) stati u ovu staju ako je ispunjena do 3/4 svoje visine i ako je 1 kub. . m sijena teži 82 kg?
2) Hrpa drva ima oblik pravokutnog paralelopipeda čije su dimenzije 2 1/2 m x 3 1/2 m x 1 1/2 m. Kolika je težina hrpe drva ako je 1 kub. m drva za ogrjev teži 600 kg?
573. 1) Pravokutni akvarij napuni se vodom do 3/5 njegove visine. Duljina akvarija je 1 1/2 m, širina 4/5 m, visina 3/4 m. Koliko se litara vode ulije u akvarij?
2) Bazen u obliku pravokutnog paralelopipeda ima duljinu 6 1/2 m, širinu 4 m i visinu 2 m. Bazen je napunjen vodom do 3/4 svoje visine. Izračunajte količinu vode ulivene u bazen.
574. Oko parcele pravokutnog oblika, dužine 75 m i širine 45 m potrebno je izgraditi ogradu. Koliko kubnih metara dasaka treba ući u njegovu konstrukciju ako je debljina daske 2 1/2 cm, a visina ograde 2 1/4 m?
575. 1) Koliki je kut minuta i satna kazaljka u 13 sati? u 15 sati? u 17 sati? u 21 sat? u 23:30?
2) Za koliko će se stupnjeva satna kazaljka okrenuti za 2 sata? 5 sati? 8 sati? 30 min.?
3) Koliko stupnjeva ima luk jednak polovini kružnice? 1/4 kruga? 1/24 kruga? 5/24 krugova?
576. 1) Kutomjerom nacrtaj: a) pravi kut; b) kut od 30°; c) kut od 60°; d) kut od 150°; e) kut od 55°.
2) Kutomjerom izmjeri kutove lika i pronađi zbroj svih kutova pojedinog lika (slika 31).

577. Prati ove korake:

578. 1) Polukrug je podijeljen na dva luka od kojih je jedan za 100° veći od drugog. Pronađite veličinu svakog luka.
2) Polukrug je podijeljen na dva luka od kojih je jedan za 15° manji od drugog. Pronađite veličinu svakog luka.
3) Polukrug je podijeljen na dva luka od kojih je jedan dvostruko veći od drugog. Pronađite veličinu svakog luka.
4) Polukrug je podijeljen na dva luka od kojih je jedan 5 puta manji od drugog. Pronađite veličinu svakog luka.
579. 1) Dijagram "Pismenost stanovništva u SSSR-u" (slika 32) prikazuje broj pismenih ljudi na sto ljudi stanovništva. Na temelju podataka u dijagramu i njegovom mjerilu odredite broj pismenih muškaraca i žena za svaku od navedenih godina.

Rezultate upiši u tablicu:

2) Koristeći podatke iz dijagrama "Sovjetski izaslanici u svemir" (slika 33), izradite zadatke.

580. 1) Prema kružnom dijagramu „Dnevna rutina za učenika petog razreda” (slika 34), ispunite tablicu i odgovorite na pitanja: koji dio dana je namijenjen spavanju? za domaću zadaću? u školu?

2) Napravite tortni dijagram o svojoj dnevnoj rutini.

Zbrajanje razlomaka s jednakim nazivnicima
Postoje dvije vrste zbrajanja razlomaka:
- Zbrajanje razlomaka s jednakim nazivnicima
- Zbrajanje razlomaka s različitim nazivnicima
Prvo, naučimo zbrajanje razlomaka s istim nazivnicima. Ovdje je sve jednostavno. Da biste zbrojili razlomke s istim nazivnicima, morate zbrojiti njihove brojnike, a nazivnik ostaviti nepromijenjen. Na primjer, zbrojimo razlomke i . Zbrojite brojnike i ostavite nazivnik nepromijenjen:

Ovaj primjer lako je razumjeti ako se sjetimo pizze koja je podijeljena na četiri dijela. Dodate li pizzu na pizzu, dobit ćete pizzu:

Primjer 2. Zbrojite razlomke i .

Pokazalo se da je odgovor nepravi razlomak. Kada dođe kraj zadatka, uobičajeno je riješiti se nepravih razlomaka. Da biste se riješili nepravilnog razlomka, morate odabrati cijeli njegov dio. U našem slučaju, cijeli dio se lako izolira - dva podijeljeno s dva jednako je jedan:

Ovaj primjer lako je razumjeti ako se sjetimo pizze koja je podijeljena na dva dijela. Dodate li još pizze na pizzu, dobit ćete jednu cijelu pizzu:

Primjer 3. Zbrojite razlomke i .
Opet zbrajamo brojnike, a nazivnik ostavljamo nepromijenjenim:
![]()
Ovaj primjer lako je razumjeti ako se sjetimo pizze koja je podijeljena na tri dijela. Ako na pizzu dodate još pizze, dobit ćete pizzu:

Primjer 4. Pronađite vrijednost izraza 
Ovaj primjer je riješen na potpuno isti način kao i prethodni. Brojnike je potrebno zbrojiti, a nazivnik ostaviti nepromijenjenim:
Pokušajmo naše rješenje prikazati pomoću crteža. Ako dodate pizze na pizzu i dodate još pizza, dobit ćete 1 cijelu pizzu i više pizza.

Kao što vidite, nema ništa komplicirano u zbrajanju razlomaka s istim nazivnicima. Dovoljno je razumjeti sljedeća pravila:
- Da biste zbrojili razlomke s istim nazivnikom, morate zbrojiti njihove brojnike i ostaviti nazivnik nepromijenjen;
Zbrajanje razlomaka s različitim nazivnicima
Naučimo sada kako zbrajati razlomke s različitim nazivnicima. Kod zbrajanja razlomaka, nazivnici razlomaka moraju biti isti. Ali nisu uvijek isti.
Na primjer, razlomci se mogu zbrajati jer imaju iste nazivnike.
Ali razlomci se ne mogu odmah zbrajati jer ti razlomci imaju različite nazivnike. U takvim slučajevima razlomke je potrebno svesti na isti (zajednički) nazivnik.
Postoji nekoliko načina svođenja razlomaka na isti nazivnik. Danas ćemo pogledati samo jednu od njih, budući da se druge metode početniku mogu činiti kompliciranima.
Bit ove metode je da se prvo pretražuje LCM nazivnika obaju razlomaka. LCM se zatim dijeli s nazivnikom prvog razlomka kako bi se dobio prvi dodatni faktor. Isto čine s drugim razlomkom - LCM se podijeli s nazivnikom drugog razlomka i dobije se drugi dodatni faktor.
Brojnici i nazivnici razlomaka zatim se množe svojim dodatnim faktorima. Kao rezultat ovih radnji, razlomci koji su imali različite nazivnike pretvaraju se u razlomke koji imaju iste nazivnike. A takve razlomke već znamo zbrajati.
Primjer 1. Zbrojimo razlomke i
Prije svega, nalazimo najmanji zajednički višekratnik nazivnika obaju razlomaka. Nazivnik prvog razlomka je broj 3, a nazivnik drugog razlomka je broj 2. Najmanji zajednički višekratnik ovih brojeva je 6
LCM (2 i 3) = 6
Sada se vratimo razlomcima i . Prvo podijelite LCM s nazivnikom prvog razlomka i dobijete prvi dodatni faktor. LCM je broj 6, a nazivnik prvog razlomka je broj 3. Podijelimo 6 sa 3, dobivamo 2.
Dobiveni broj 2 je prvi dodatni množitelj. Zapisujemo ga do prvog razlomka. Da biste to učinili, napravite malu kosu crtu preko razlomka i zapišite dodatni faktor koji se nalazi iznad:
Isto radimo s drugim razlomkom. LCM podijelimo s nazivnikom drugog razlomka i dobijemo drugi dodatni faktor. LCM je broj 6, a nazivnik drugog razlomka je broj 2. Podijelimo 6 sa 2, dobivamo 3.
Dobiveni broj 3 je drugi dodatni množitelj. Zapisujemo ga do drugog razlomka. Opet, napravimo malu kosu liniju preko drugog razlomka i zapišemo dodatni faktor koji se nalazi iznad njega:
Sada imamo sve spremno za dodavanje. Ostaje pomnožiti brojnike i nazivnike razlomaka njihovim dodatnim faktorima:

Pažljivo pogledajte do čega smo došli. Došli smo do zaključka da su se razlomci koji su imali različite nazivnike pretvorili u razlomke koji su imali iste nazivnike. A takve razlomke već znamo zbrajati. Uzmimo ovaj primjer do kraja:

Ovo dovršava primjer. Ispada dodati .
Pokušajmo naše rješenje prikazati pomoću crteža. Ako dodate pizzu na pizzu, dobit ćete jednu cijelu pizzu i još jednu šestinu pizze:

Svođenje razlomaka na isti (zajednički) nazivnik također se može prikazati pomoću slike. Svođenjem razlomaka i na zajednički nazivnik dobili smo razlomke i . Ove dvije frakcije bit će predstavljene istim komadima pizze. Jedina razlika bit će što će ovaj put biti podijeljeni na jednake dijelove (svedeni na isti nazivnik).

Prvi crtež predstavlja razlomak (četiri komada od šest), a drugi crtež predstavlja razlomak (tri komada od šest). Zbrajanjem ovih komada dobivamo (sedam komada od šest). Ovaj razlomak je nepravilan, pa smo istaknuli cijeli njegov dio. Kao rezultat, dobili smo (jednu cijelu pizzu i još jednu šestu pizzu).
Imajte na umu da smo ovaj primjer opisali previše detaljno. U obrazovne ustanove Nije uobičajeno pisati tako detaljno. Morate biti u mogućnosti brzo pronaći LCM oba nazivnika i dodatnih faktora uz njih, kao i brzo pomnožiti pronađene dodatne faktore sa svojim brojnicima i nazivnicima. Da smo u školi, morali bismo napisati ovaj primjer na sljedeći način:

Ali postoji i druga strana medalje. Ako u prvim fazama učenja matematike ne vodite detaljne bilješke, tada se počinju javljati takva pitanja. “Odakle dolazi taj broj?”, “Zašto se razlomci odjednom pretvaraju u sasvim druge razlomke? «.
Kako biste olakšali zbrajanje razlomaka s različitim nazivnicima, možete upotrijebiti sljedeće upute korak po korak:
- Odredite LCM nazivnika razlomaka;
- Podijelite LCM s nazivnikom svakog razlomka i dobijete dodatni faktor za svaki razlomak;
- Pomnožite brojnike i nazivnike razlomaka s njihovim dodatnim faktorima;
- Zbrojite razlomke koji imaju iste nazivnike;
- Ako se ispostavi da je odgovor nepravilan razlomak, odaberite cijeli njegov dio;
Primjer 2. Pronađite vrijednost izraza  .
.
Poslužimo se gore navedenim uputama.
Korak 1. Pronađite LCM nazivnika razlomaka
Odredite LCM nazivnika obaju razlomaka. Nazivnici razlomaka su brojevi 2, 3 i 4

Korak 2. Podijelite LCM s nazivnikom svakog razlomka i dobijete dodatni faktor za svaki razlomak
Podijelite LCM s nazivnikom prvog razlomka. LCM je broj 12, a nazivnik prvog razlomka je broj 2. Podijelimo 12 sa 2, dobijemo 6. Dobili smo prvi dodatni faktor 6. Zapisujemo ga iznad prvog razlomka:
Sada dijelimo LCM s nazivnikom drugog razlomka. LCM je broj 12, a nazivnik drugog razlomka je broj 3. Podijelimo 12 sa 3, dobivamo 4. Dobivamo drugi dodatni faktor 4. Zapisujemo ga iznad drugog razlomka:
Sada dijelimo LCM s nazivnikom trećeg razlomka. LCM je broj 12, a nazivnik trećeg razlomka je broj 4. Podijelimo 12 sa 4, dobijemo 3. Dobijemo treći dodatni faktor 3. Zapišemo ga iznad trećeg razlomka:
Korak 3. Pomnožite brojnike i nazivnike razlomaka s njihovim dodatnim faktorima
Množimo brojnike i nazivnike njihovim dodatnim faktorima:
Korak 4. Zbrojite razlomke s istim nazivnicima
Došli smo do zaključka da su se razlomci koji su imali različite nazivnike pretvorili u razlomke koji su imali iste (zajedničke) nazivnike. Ostaje samo zbrojiti ove razlomke. Zbrojite:

Dodavanje nije stalo u jedan redak, pa smo preostali izraz premjestili u sljedeći redak. To je dozvoljeno u matematici. Kada izraz ne stane u jedan red, premješta se u sljedeći red, a potrebno je staviti znak jednakosti (=) na kraju prvog i na početku novog retka. Znak jednakosti u drugom retku označava da se radi o nastavku izraza koji je bio u prvom retku.
Korak 5. Ako se ispostavi da je odgovor netočan razlomak, odaberite cijeli njegov dio
Pokazalo se da je naš odgovor netočan razlomak. Moramo istaknuti cijeli dio toga. Ističemo:

Dobili smo odgovor
Oduzimanje razlomaka s jednakim nazivnicima
Postoje dvije vrste oduzimanja razlomaka:
- Oduzimanje razlomaka s jednakim nazivnicima
- Oduzimanje razlomaka s različitim nazivnicima
Prvo, naučimo kako oduzimati razlomke s istim nazivnicima. Ovdje je sve jednostavno. Da biste od jednog razlomka oduzeli drugi, morate od brojnika prvog razlomka oduzeti brojnik drugog razlomka, ali nazivnik ostaviti isti.
Na primjer, pronađimo vrijednost izraza. Da biste riješili ovaj primjer, morate brojnik drugog razlomka oduzeti od brojnika prvog razlomka, a nazivnik ostaviti nepromijenjen. Napravimo to:

Ovaj primjer lako je razumjeti ako se sjetimo pizze koja je podijeljena na četiri dijela. Ako od pizze režete pizze, dobit ćete pizze:

Primjer 2. Pronađite vrijednost izraza.
Opet, od brojnika prvog razlomka oduzmite brojnik drugog razlomka i ostavite nazivnik nepromijenjen:

Ovaj primjer lako je razumjeti ako se sjetimo pizze koja je podijeljena na tri dijela. Ako od pizze režete pizze, dobit ćete pizze:

Primjer 3. Pronađite vrijednost izraza 
Ovaj primjer je riješen na potpuno isti način kao i prethodni. Od brojnika prvog razlomka potrebno je oduzeti brojnike preostalih razlomaka:

Kao što vidite, nema ništa komplicirano u oduzimanju razlomaka s istim nazivnicima. Dovoljno je razumjeti sljedeća pravila:
- Da biste od jednog razlomka oduzeli drugi, trebate od brojnika prvog razlomka oduzeti brojnik drugog razlomka, a nazivnik ostaviti nepromijenjen;
- Ako se ispostavi da je odgovor netočan razlomak, tada morate istaknuti cijeli njegov dio.
Oduzimanje razlomaka s različitim nazivnicima
Na primjer, razlomak možete oduzeti od razlomka jer razlomci imaju iste nazivnike. Ali ne možete oduzeti razlomak od razlomka, jer ti razlomci imaju različite nazivnike. U takvim slučajevima razlomke je potrebno svesti na isti (zajednički) nazivnik.
Zajednički nazivnik nalazimo koristeći isti princip koji smo koristili pri zbrajanju razlomaka s različitim nazivnicima. Prije svega, pronađite LCM nazivnika obaju razlomaka. Zatim se LCM podijeli s nazivnikom prvog razlomka i dobije se prvi dodatni faktor koji je zapisan iznad prvog razlomka. Slično, LCM se podijeli s nazivnikom drugog razlomka i dobije se drugi dodatni faktor koji je napisan iznad drugog razlomka.
Razlomci se zatim množe svojim dodatnim faktorima. Kao rezultat ovih operacija, razlomci koji su imali različite nazivnike pretvaraju se u razlomke koji imaju iste nazivnike. A takve razlomke već znamo oduzimati.
Primjer 1. Pronađite značenje izraza:
Ovi razlomci imaju različite nazivnike, pa ih trebate svesti na isti (zajednički) nazivnik.
Prvo nalazimo LCM nazivnika obaju razlomaka. Nazivnik prvog razlomka je broj 3, a nazivnik drugog razlomka je broj 4. Najmanji zajednički višekratnik ovih brojeva je 12
LCM (3 i 4) = 12
Sada se vratimo razlomcima i
Nađimo dodatni faktor za prvi razlomak. Da biste to učinili, podijelite LCM s nazivnikom prvog razlomka. LCM je broj 12, a nazivnik prvog razlomka je broj 3. Podijelimo 12 sa 3, dobijemo 4. Napiši četvorku iznad prvog razlomka:
Isto radimo s drugim razlomkom. Podijelite LCM s nazivnikom drugog razlomka. LCM je broj 12, a nazivnik drugog razlomka je broj 4. Podijelimo 12 sa 4, dobivamo 3. Napiši trojku preko drugog razlomka:
Sada smo spremni za oduzimanje. Ostaje pomnožiti razlomke njihovim dodatnim faktorima:

Došli smo do zaključka da su se razlomci koji su imali različite nazivnike pretvorili u razlomke koji su imali iste nazivnike. A takve razlomke već znamo oduzimati. Uzmimo ovaj primjer do kraja:

Dobili smo odgovor
Pokušajmo naše rješenje prikazati pomoću crteža. Ako izrežete pizzu od pizze, dobit ćete pizzu

Ovo je detaljna verzija rješenja. Da smo u školi, morali bismo kraće rješavati ovaj primjer. Takvo bi rješenje izgledalo ovako:

Svođenje razlomaka na zajednički nazivnik također se može prikazati pomoću slike. Svodeći ove razlomke na zajednički nazivnik, dobili smo razlomke i . Ovi će razlomci biti predstavljeni istim kriškama pizze, ali ovaj put će biti podijeljeni na jednake dijelove (svedeni na isti nazivnik):

Prva slika prikazuje razlomak (osam komada od dvanaest), a druga slika razlomak (tri komada od dvanaest). Rezanjem tri komada od osam komada, dobivamo pet komada od dvanaest. Razlomak opisuje ovih pet dijelova.
Primjer 2. Pronađite vrijednost izraza 
Ti razlomci imaju različite nazivnike, pa ih prvo treba svesti na isti (zajednički) nazivnik.
Nađimo LCM nazivnika ovih razlomaka.
Nazivnici razlomaka su brojevi 10, 3 i 5. Najmanji zajednički višekratnik ovih brojeva je 30
LCM(10, 3, 5) = 30
Sada nalazimo dodatne faktore za svaki razlomak. Da biste to učinili, podijelite LCM s nazivnikom svakog razlomka.
Nađimo dodatni faktor za prvi razlomak. LCM je broj 30, a nazivnik prvog razlomka je broj 10. Podijelimo 30 sa 10, dobivamo prvi dodatni faktor 3. Zapisujemo ga iznad prvog razlomka:
Sada nalazimo dodatni faktor za drugi razlomak. Podijelite LCM s nazivnikom drugog razlomka. LCM je broj 30, a nazivnik drugog razlomka je broj 3. Podijelimo 30 sa 3, dobivamo drugi dodatni faktor 10. Zapisujemo ga iznad drugog razlomka:
Sada nalazimo dodatni faktor za treći razlomak. Podijelite LCM s nazivnikom trećeg razlomka. LCM je broj 30, a nazivnik trećeg razlomka je broj 5. Podijelimo 30 sa 5, dobivamo treći dodatni faktor 6. Zapisujemo ga iznad trećeg razlomka:
Sada je sve spremno za oduzimanje. Ostaje pomnožiti razlomke njihovim dodatnim faktorima:
Došli smo do zaključka da su se razlomci koji su imali različite nazivnike pretvorili u razlomke koji su imali iste (zajedničke) nazivnike. A takve razlomke već znamo oduzimati. Završimo ovaj primjer.
Nastavak primjera neće stati u jedan redak, pa nastavak premještamo u sljedeći redak. Ne zaboravite na znak jednakosti (=) u novom retku:

Ispostavilo se da je odgovor obični razlomak i čini se da nam sve odgovara, ali je preglomazan i ružan. Trebali bismo to učiniti jednostavnijim. Što može biti učinjeno? Možete skratiti ovaj razlomak.
Da biste smanjili razlomak, trebate podijeliti njegov brojnik i nazivnik s (NOT) brojeva 20 i 30.
Dakle, nalazimo gcd brojeva 20 i 30:

Sada se vraćamo našem primjeru i dijelimo brojnik i nazivnik razlomka s pronađenim gcd, odnosno s 10

Dobili smo odgovor
Množenje razlomka brojem
Da biste pomnožili razlomak s brojem, morate brojnik razlomka pomnožiti s tim brojem, a nazivnik ostaviti nepromijenjen.
Primjer 1. Pomnožite razlomak s brojem 1.
Pomnožite brojnik razlomka s brojem 1
![]()
Snimanje se može shvatiti kao da traje pola puta. Na primjer, ako jednom uzmete pizzu, dobit ćete pizzu

Iz zakona množenja znamo da ako se množenik i faktor zamijene, umnožak se neće promijeniti. Ako je izraz napisan kao , tada će umnožak i dalje biti jednak . Opet, pravilo za množenje cijelog broja i razlomka funkcionira:
![]()
Ovaj zapis se može shvatiti kao uzimanje polovice jednog. Na primjer, ako postoji 1 cijela pizza i mi uzmemo pola, tada ćemo imati pizzu:

Primjer 2. Pronađite vrijednost izraza
Pomnožite brojnik razlomka s 4
![]()
Odgovor je bio nepravilan razlomak. Istaknimo cijeli dio:
![]()
Izraz se može shvatiti kao uzimanje dvije četvrtine 4 puta. Na primjer, ako uzmete 4 pizze, dobit ćete dvije cijele pizze

A ako zamijenimo množenik i množitelj, dobit ćemo izraz . Također će biti jednako 2. Ovaj izraz se može shvatiti kao uzimanje dvije pizze od četiri cijele pizze:

Broj koji se množi razlomkom i nazivnik razlomka rastavljaju se ako imaju zajednički faktor veći od jedan.
Na primjer, izraz se može izračunati na dva načina.
Prvi način. Pomnožite broj 4 s brojnikom razlomka, a nazivnik razlomka ostavite nepromijenjenim:
![]()
Drugi način. Četvorka koja se množi i četiri u nazivniku razlomka mogu se smanjiti. Ove četvorke se mogu smanjiti za 4, budući da je najveći zajednički djelitelj za dvije četvorke sama četvorka:

Dobili smo isti rezultat 3. Nakon smanjivanja četvorki umjesto njih nastaju novi brojevi: dvije jedinice. Ali množenje jedan s tri, a zatim dijeljenje s jedan ne mijenja ništa. Stoga se rješenje može ukratko napisati:
Smanjenje se može izvesti čak i kada smo se odlučili za prvu metodu, ali u fazi množenja broja 4 i brojnika 3 odlučili smo se za smanjenje:

Ali, na primjer, izraz se može izračunati samo na prvi način - pomnožite 7 s nazivnikom razlomka, a nazivnik ostavite nepromijenjenim:
![]()
To je zbog činjenice da broj 7 i nazivnik razlomka nemaju zajednički djelitelj veći od jedan, te se prema tome ne poništavaju.
Neki učenici pogrešno skraćuju broj koji se množi i brojnik razlomka. Ne možeš to učiniti. Na primjer, sljedeći unos nije točan:
Smanjenje razlomka znači da i brojnik i nazivnik podijelit će se istim brojem. U situaciji s izrazom, dijeljenje se vrši samo u brojniku, jer je to pisanje isto što i pisanje . Vidimo da se dijeljenje vrši samo u brojniku, a u nazivniku nema dijeljenja.
Množenje razlomaka
Da biste pomnožili razlomke, morate pomnožiti njihove brojnike i nazivnike. Ako se odgovor pokaže kao netočan razlomak, morate istaknuti cijeli njegov dio.
Primjer 1. Pronađite vrijednost izraza.
![]()
Dobili smo odgovor. Preporučljivo je smanjiti ovaj udio. Razlomak se može smanjiti za 2. Tada će konačno rješenje imati sljedeći oblik:

Izraz se može shvatiti kao uzimanje pizze od pola pizze. Recimo da imamo pola pizze:
Kako od ove polovice uzeti dvije trećine? Prvo morate ovu polovicu podijeliti na tri jednaka dijela:

I uzmi dva od ova tri komada:

Napravit ćemo pizzu. Prisjetite se kako pizza izgleda podijeljena na tri dijela:

Jedan komad ove pizze i dva komada koje smo uzeli imat će iste dimenzije:

Drugim riječima, govorimo o otprilike iste veličine pizze. Stoga je vrijednost izraza

Primjer 2. Pronađite vrijednost izraza
Pomnožimo brojnik prvog razlomka s brojnikom drugog razlomka i nazivnik prvog razlomka s nazivnikom drugog razlomka:

Odgovor je bio nepravilan razlomak. Istaknimo cijeli dio:
![]()
Primjer 3. Pronađite vrijednost izraza
Pomnožimo brojnik prvog razlomka s brojnikom drugog razlomka i nazivnik prvog razlomka s nazivnikom drugog razlomka:
![]()
Pokazalo se da je odgovor obični razlomak, ali bilo bi dobro da se skrati. Da biste smanjili ovaj razlomak, morate brojnik i nazivnik ovog razlomka podijeliti s najvećim zajedničkim djeliteljem (NZD) brojeva 105 i 450.
Dakle, pronađimo gcd brojeva 105 i 450:

Sada dijelimo brojnik i nazivnik našeg odgovora s gcd-om koji smo sada pronašli, to jest s 15
Predstavljanje cijelog broja kao razlomka
Bilo koji cijeli broj može se predstaviti kao razlomak. Na primjer, broj 5 može se predstaviti kao . Ovo neće promijeniti značenje pet, budući da izraz znači "broj pet podijeljen s jedan", a to je, kao što znamo, jednako pet:
Recipročni brojevi
Sada ćemo se upoznati s vrlo zanimljiva tema u matematici. To se zove "obrnuti brojevi".
Definicija. Obrnuto prema brojua je broj koji, kada se pomnoži saa daje jedan.
Zamijenimo u ovoj definiciji umjesto varijable a broj 5 i pokušajte pročitati definiciju:
Obrnuto prema broju 5 je broj koji, kada se pomnoži sa 5 daje jedan.
Je li moguće pronaći broj koji pomnožen s 5 daje jedan? Ispostavilo se da je moguće. Zamislimo pet kao razlomak:
Zatim pomnožite ovaj razlomak samim sobom, samo zamijenite brojnik i nazivnik. Drugim riječima, pomnožimo razlomak samim sobom, samo naopako:
Što će se dogoditi kao rezultat toga? Ako nastavimo rješavati ovaj primjer, dobit ćemo jedan:
![]()
To znači da je obrnuto od broja 5 broj , jer kad pomnožite 5 s dobit ćete jedan.
Recipročna vrijednost broja može se pronaći i za bilo koji drugi cijeli broj.
Pronaći recipročni broj Moguće je i za bilo koji drugi razlomak. Da biste to učinili, samo ga okrenite.
Dijeljenje razlomka brojem
Recimo da imamo pola pizze:
Podijelimo ga jednako na dvoje. Koliko će pizze dobiti svaka osoba?

Vidljivo je da su se nakon dijeljenja pizze na pola dobila dva jednaka komada od kojih svaki čini pizzu. Tako da svi dobiju pizzu.
Ovaj članak ispituje operacije nad razlomcima. Oblikovat će se i obrazložiti pravila za zbrajanje, oduzimanje, množenje, dijeljenje ili stepenovanje razlomaka oblika A B, pri čemu A i B mogu biti brojevi, brojčani izrazi ili izrazi s varijablama. U zaključku će se razmotriti primjeri rješenja s detaljnim opisima.
Yandex.RTB R-A-339285-1
Pravila za izvođenje operacija s općim brojčanim razlomcima
Brojčani razlomci opći pogled imaju brojnik i nazivnik u kojima se nalaze cijeli brojevi ili numeričke izraze. Ako uzmemo u obzir razlomke kao što su 3 5, 2, 8 4, 1 + 2 3 4 (5 - 2), 3 4 + 7 8 2, 3 - 0, 8, 1 2 2, π 1 - 2 3 + π, 2 0, 5 ln 3, onda je jasno da brojnik i nazivnik mogu imati ne samo brojeve, već i izraze raznih vrsta.
Definicija 1
Postoje pravila prema kojima se radnje izvode obični razlomci. Također je prikladan za opće razlomke:
- Pri oduzimanju razlomaka sa sličnim nazivnicima dodaju se samo brojnici, a nazivnik ostaje isti, i to: a d ± c d = a ± c d, vrijednosti a, c i d ≠ 0 su neki brojevi ili numerički izrazi.
- Pri zbrajanju ili oduzimanju razlomka s različitim nazivnicima potrebno ga je svesti na zajednički nazivnik, a zatim dobivene razlomke s istim eksponentima zbrajati ili oduzimati. Doslovno to izgleda ovako: a b ± c d = a · p ± c · r s, gdje su vrijednosti a, b ≠ 0, c, d ≠ 0, p ≠ 0, r ≠ 0, s ≠ 0 realni brojevi, i b · p = d · r = s. Kada je p = d i r = b, tada je a b ± c d = a · d ± c · d b · d.
- Kod množenja razlomaka radnja se izvodi s brojnicima, a nakon toga s nazivnicima, tada dobivamo a b · c d = a · c b · d, gdje a, b ≠ 0, c, d ≠ 0 djeluju kao realni brojevi.
- Pri dijeljenju razlomka s razlomkom prvi množimo s drugim inverzom, odnosno mijenjamo brojnik i nazivnik: a b: c d = a b · d c.
Obrazloženje za pravila
Definicija 2Postoje sljedeće matematičke točke na koje se trebate osloniti prilikom izračuna:
- kosa crta označava znak dijeljenja;
- dijeljenje brojem tretira se kao množenje njegovom recipročnom vrijednošću;
- primjena svojstva operacija s realnim brojevima;
- primjena osnovnog svojstva razlomaka i brojevnih nejednakosti.
Uz njihovu pomoć možete izvršiti transformacije obrasca:
a d ± c d = a · d - 1 ± c · d - 1 = a ± c · d - 1 = a ± c d ; a b ± c d = a · p b · p ± c · r d · r = a · p s ± c · e s = a · p ± c · r s ; a b · c d = a · d b · d · b · c b · d = a · d · a · d - 1 · b · c · b · d - 1 = = a · d · b · c · b · d - 1 · b · d - 1 = a · d · b · c b · d · b · d - 1 = = (a · c) · (b · d) - 1 = a · c b · d
Primjeri
U prethodnom paragrafu je rečeno o operacijama s razlomcima. Nakon toga razlomak treba pojednostaviti. Ova je tema detaljno obrađena u odlomku o pretvaranju razlomaka.
Prvo, pogledajmo primjer zbrajanja i oduzimanja razlomaka s istim nazivnikom.
Primjer 1
S obzirom na razlomke 8 2, 7 i 1 2, 7, tada je prema pravilu potrebno dodati brojnik i prepisati nazivnik.
Riješenje
Tada dobivamo razlomak oblika 8 + 1 2, 7. Nakon izvršenog zbrajanja dobivamo razlomak oblika 8 + 1 2, 7 = 9 2, 7 = 90 27 = 3 1 3. Dakle, 8 2, 7 + 1 2, 7 = 8 + 1 2, 7 = 9 2, 7 = 90 27 = 3 1 3.
Odgovor: 8 2 , 7 + 1 2 , 7 = 3 1 3
Postoji još jedno rješenje. Za početak prelazimo na oblik običnog razlomka, nakon čega provodimo pojednostavljenje. Ovako izgleda:
8 2 , 7 + 1 2 , 7 = 80 27 + 10 27 = 90 27 = 3 1 3
Primjer 2
Oduzmimo od 1 - 2 3 · log 2 3 · log 2 5 + 1 razlomak oblika 2 3 3 · log 2 3 · log 2 5 + 1 .
Budući da su zadani jednaki nazivnici, to znači da računamo razlomak s istim nazivnikom. Shvaćamo to
1 - 2 3 log 2 3 log 2 5 + 1 - 2 3 3 log 2 3 log 2 5 + 1 = 1 - 2 - 2 3 3 log 2 3 log 2 5 + 1
Postoje primjeri izračunavanja razlomaka s različitim nazivnicima. Važna točka je svođenje na zajednički nazivnik. Bez toga nećemo moći izvoditi daljnje operacije s razlomcima.
Proces nejasno podsjeća na svođenje na zajednički nazivnik. Odnosno, traži se najmanji zajednički djelitelj u nazivniku, nakon čega se razlomcima dodaju faktori koji nedostaju.
Ako razlomci koji se zbrajaju nemaju zajedničke faktore, tada njihov umnožak može postati jedan.
Primjer 3
Pogledajmo primjer zbrajanja razlomaka 2 3 5 + 1 i 1 2.
Riješenje
U ovom slučaju, zajednički nazivnik je umnožak nazivnika. Tada dobivamo da je 2 · 3 5 + 1. Tada pri postavljanju dodatnih faktora imamo da je za prvi razlomak jednak 2, a za drugi 3 5 + 1. Nakon množenja razlomci se svode na oblik 4 2 · 3 5 + 1. Opće smanjenje od 1 2 bit će 3 5 + 1 2 · 3 5 + 1. Zbrojimo dobivene razlomke i dobijemo to
2 3 5 + 1 + 1 2 = 2 2 2 3 5 + 1 + 1 3 5 + 1 2 3 5 + 1 = = 4 2 3 5 + 1 + 3 5 + 1 2 3 5 + 1 = 4 + 3 5 + 1 2 3 5 + 1 = 5 + 3 5 2 3 5 + 1
Odgovor: 2 3 5 + 1 + 1 2 = 5 + 3 5 2 3 5 + 1
Kada se radi o općim razlomcima, tada se obično ne govori o najmanjem zajedničkom nazivniku. Neisplativo je uzeti umnožak brojnika kao nazivnik. Prvo morate provjeriti postoji li broj koji ima manju vrijednost od njihovog proizvoda.
Primjer 4
Razmotrimo primjer 1 6 · 2 1 5 i 1 4 · 2 3 5, kada je njihov umnožak jednak 6 · 2 1 5 · 4 · 2 3 5 = 24 · 2 4 5. Zatim uzimamo 12 · 2 3 5 kao zajednički nazivnik.
Pogledajmo primjere množenja općih razlomaka.
Primjer 5
Da biste to učinili, trebate pomnožiti 2 + 1 6 i 2 · 5 3 · 2 + 1.
Riješenje
Slijedeći pravilo, potrebno je prepisati i umnožak brojnika napisati kao nazivnik. Dobivamo da je 2 + 1 6 2 5 3 2 + 1 2 + 1 2 5 6 3 2 + 1. Nakon što se razlomak pomnoži, možete ga smanjiti kako biste ga pojednostavili. Tada je 5 · 3 3 2 + 1: 10 9 3 = 5 · 3 3 2 + 1 · 9 3 10.
Koristeći pravilo prijelaza s dijeljenja na množenje recipročnim razlomkom, dobivamo razlomak koji je recipročan zadanom. Da biste to učinili, brojnik i nazivnik su zamijenjeni. Pogledajmo primjer:
5 3 3 2 + 1: 10 9 3 = 5 3 3 2 + 1 9 3 10
Zatim moraju pomnožiti i pojednostaviti dobiveni razlomak. Ako je potrebno, riješite se iracionalnosti u nazivniku. Shvaćamo to
5 3 3 2 + 1: 10 9 3 = 5 3 3 9 3 10 2 + 1 = 5 2 10 2 + 1 = 3 2 2 + 1 = 3 2 - 1 2 2 + 1 2 - 1 = 3 2 - 1 2 2 2 - 1 2 = 3 2 - 1 2
Odgovor: 5 3 3 2 + 1: 10 9 3 = 3 2 - 1 2
Ovaj stavak je primjenjiv kada je broj ili brojčani izraz može se prikazati kao razlomak s nazivnikom jednakim 1, tada se radnja s takvim razlomkom smatra zasebnim odlomkom. Na primjer, izraz 1 6 · 7 4 - 1 · 3 pokazuje da se korijen od 3 može zamijeniti drugim 3 1 izrazom. Tada će ovaj unos izgledati kao množenje dvaju razlomaka oblika 1 6 · 7 4 - 1 · 3 = 1 6 · 7 4 - 1 · 3 1.
Izvođenje operacija nad razlomcima koji sadrže varijable
Pravila o kojima se govori u prvom članku primjenjiva su na operacije s razlomcima koji sadrže varijable. Razmotrite pravilo oduzimanja kada su nazivnici isti.
Potrebno je dokazati da A, C i D (D nije jednak nuli) mogu biti bilo koji izrazi, a jednakost A D ± C D = A ± C D je ekvivalentna svom području dopuštenih vrijednosti.
Potrebno je uzeti skup ODZ varijabli. Tada A, C, D moraju uzeti odgovarajuće vrijednosti a 0 , c 0 i d 0. Zamjenom oblika A D ± C D dobiva se razlika oblika a 0 d 0 ± c 0 d 0 , gdje korištenjem pravila zbrajanja dobivamo formulu oblika a 0 ± c 0 d 0 . Ako zamijenimo izraz A ± C D, tada ćemo dobiti isti razlomak oblika a 0 ± c 0 d 0. Odavde zaključujemo da se odabrana vrijednost koja zadovoljava ODZ, A ± C D i A D ± C D smatraju jednakima.
Za bilo koju vrijednost varijabli ovi će izrazi biti jednaki, odnosno nazivaju se identično jednakima. To znači da se ovaj izraz smatra dokazivom jednakošću oblika A D ± C D = A ± C D .
Primjeri zbrajanja i oduzimanja razlomaka s varijablama
Kada imate iste nazivnike, trebate samo zbrajati ili oduzimati brojnike. Ovaj se razlomak može pojednostaviti. Ponekad morate raditi s razlomcima koji su identički jednaki, ali to se na prvi pogled ne vidi jer se moraju izvršiti neke transformacije. Na primjer, x 2 3 x 1 3 + 1 i x 1 3 + 1 2 ili 1 2 sin 2 α i sin a cos a. Najčešće je potrebno pojednostavljenje izvornog izraza kako bi se vidjeli isti nazivnici.
Primjer 6
Izračunajte: 1) x 2 + 1 x + x - 2 - 5 - x x + x - 2, 2) l g 2 x + 4 x · (l g x + 2) + 4 · l g x x · (l g x + 2) , x - 1 x - 1 + x x + 1 .
Riješenje
- Za izračun morate oduzeti razlomke koji imaju isti nazivnik. Tada dobivamo da je x 2 + 1 x + x - 2 - 5 - x x + x - 2 = x 2 + 1 - 5 - x x + x - 2 . Nakon toga možete proširiti zagrade i dodati slične pojmove. Dobivamo da je x 2 + 1 - 5 - x x + x - 2 = x 2 + 1 - 5 + x x + x - 2 = x 2 + x - 4 x + x - 2
- Budući da su nazivnici isti, preostaje samo zbrojiti brojnike, ostavljajući nazivnik: l g 2 x + 4 x (l g x + 2) + 4 l g x x (l g x + 2) = l g 2 x + 4 + 4 x (l g x + 2)
Dodavanje je dovršeno. Vidi se da je moguće smanjiti razlomak. Njegov brojnik se može presavijati pomoću formule za kvadrat zbroja, tada dobivamo (l g x + 2) 2 iz skraćenih formula množenja. Onda to shvaćamo
l g 2 x + 4 + 2 l g x x (l g x + 2) = (l g x + 2) 2 x (l g x + 2) = l g x + 2 x - Zadani su razlomci oblika x - 1 x - 1 + x x + 1 s različitim nazivnicima. Nakon transformacije možete prijeći na zbrajanje.
Razmotrimo dvostruko rješenje.
Prva metoda je da se nazivnik prvog razlomka faktorizira korištenjem kvadrata, uz njegovu kasniju redukciju. Dobivamo djelić forme
x - 1 x - 1 = x - 1 (x - 1) x + 1 = 1 x + 1
Dakle, x - 1 x - 1 + x x + 1 = 1 x + 1 + x x + 1 = 1 + x x + 1 .
U ovom slučaju potrebno je osloboditi se iracionalnosti u nazivniku.
1 + x x + 1 = 1 + x x - 1 x + 1 x - 1 = x - 1 + x x - x x - 1
Druga metoda je množenje brojnika i nazivnika drugog razlomka s izrazom x - 1. Time se oslobađamo iracionalnosti i prelazimo na zbrajanje razlomaka s istim nazivnikom. Zatim
x - 1 x - 1 + x x + 1 = x - 1 x - 1 + x x - 1 x + 1 x - 1 = = x - 1 x - 1 + x x - x x - 1 = x - 1 + x · x - x x - 1
Odgovor: 1) x 2 + 1 x + x - 2 - 5 - x x + x - 2 = x 2 + x - 4 x + x - 2, 2) l g 2 x + 4 x · (l g x + 2) + 4 · l g x x · (l g x + 2) = l g x + 2 x, 3) x - 1 x - 1 + x x + 1 = x - 1 + x · x - x x - 1 .
U posljednjem smo primjeru otkrili da je svođenje na zajednički nazivnik neizbježno. Da biste to učinili, morate pojednostaviti razlomke. Pri zbrajanju ili oduzimanju uvijek treba tražiti zajednički nazivnik, koji izgleda kao umnožak nazivnika s dodatnim faktorima dodanim brojnicima.
Primjer 7
Izračunajte vrijednosti razlomaka: 1) x 3 + 1 x 7 + 2 2, 2) x + 1 x ln 2 (x + 1) (2 x - 4) - sin x x 5 ln (x + 1) (2 x - 4) , 3) 1 cos 2 x - x + 1 cos 2 x + 2 cos x x + x
Riješenje
- Nijedan složene kalkulacije nazivnik nije potreban, pa trebate odabrati njihov umnožak oblika 3 x 7 + 2 · 2, zatim odabrati x 7 + 2 · 2 za prvi razlomak kao dodatni faktor, a 3 za drugi. Množenjem dobivamo razlomak oblika x 3 + 1 x 7 + 2 2 = x x 7 + 2 2 3 x 7 + 2 2 + 3 1 3 x 7 + 2 2 = = x x 7 + 2 2 + 3 3 x 7 + 2 2 = x x 7 + 2 2 x + 3 3 x 7 + 2 2
- Vidljivo je da su nazivnici prikazani u obliku umnoška, što znači da su dodatne transformacije nepotrebne. Zajednički nazivnik će se smatrati umnoškom oblika x 5 · ln 2 x + 1 · 2 x - 4 . Dakle x 4
je dodatni faktor prvom razlomku, a ln(x + 1)
na drugu. Zatim oduzimamo i dobivamo:
x + 1 x · ln 2 (x + 1) · 2 x - 4 - sin x x 5 · ln (x + 1) · 2 x - 4 = = x + 1 · x 4 x 5 · ln 2 (x + 1 ) · 2 x - 4 - sin x · ln x + 1 x 5 · ln 2 (x + 1) · (2 x - 4) = = x + 1 · x 4 - sin x · ln (x + 1) ) x 5 · ln 2 (x + 1) · (2 x - 4) = x · x 4 + x 4 - sin x · ln (x + 1) x 5 · ln 2 (x + 1) · ( 2 x - 4 ) - Ovaj primjer ima smisla kada radite s nazivnicima razlomaka. Potrebno je primijeniti formule za razliku kvadrata i kvadrat zbroja jer će one omogućiti prijelaz na izraz oblika 1 cos x - x · cos x + x + 1 (cos x + x) 2. Vidi se da su razlomci svedeni na zajednički nazivnik. Dobivamo da je cos x - x · cos x + x 2 .
Onda to shvaćamo
1 cos 2 x - x + 1 cos 2 x + 2 cos x x + x = = 1 cos x - x cos x + x + 1 cos x + x 2 = = cos x + x cos x - x cos x + x 2 + cos x - x cos x - x cos x + x 2 = = cos x + x + cos x - x cos x - x cos x + x 2 = 2 cos x cos x - x cos x + x 2
Odgovor:
1) x 3 + 1 x 7 + 2 2 = x x 7 + 2 2 x + 3 3 x 7 + 2 2, 2) x + 1 x ln 2 (x + 1) 2 x - 4 - sin x x 5 · ln (x + 1) · 2 x - 4 = = x · x 4 + x 4 - sin x · ln (x + 1) x 5 · ln 2 (x + 1) · ( 2 x - 4) , 3) 1 cos 2 x - x + 1 cos 2 x + 2 · cos x · x + x = 2 · cos x cos x - x · cos x + x 2 .
Primjeri množenja razlomaka s varijablama
Pri množenju razlomaka brojnik se množi brojnikom, a nazivnik nazivnikom. Tada možete primijeniti svojstvo redukcije.
Primjer 8
Pomnožite razlomke x + 2 · x x 2 · ln x 2 · ln x + 1 i 3 · x 2 1 3 · x + 1 - 2 sin 2 · x - x.
Riješenje
Množenje treba obaviti. Shvaćamo to
x + 2 x x 2 ln x 2 ln x + 1 3 x 2 1 3 x + 1 - 2 sin (2 x - x) = = x - 2 x 3 x 2 1 3 x + 1 - 2 x 2 ln x 2 ln x + 1 sin (2 x - x)
Broj 3 pomaknut je na prvo mjesto radi praktičnosti izračuna, a razlomak možete smanjiti za x 2, tada dobivamo izraz oblika
3 x - 2 x x 1 3 x + 1 - 2 ln x 2 ln x + 1 sin (2 x - x)
Odgovor: x + 2 x x 2 ln x 2 ln x + 1 3 x 2 1 3 x + 1 - 2 sin (2 x - x) = 3 x - 2 x x 1 3 x + 1 - 2 ln x 2 · ln x + 1 · grijeh (2 · x - x) .
Podjela
Dijeljenje razlomaka je slično množenju, budući da se prvi razlomak množi drugim recipročnim. Ako uzmemo na primjer razlomak x + 2 x x 2 ln x 2 ln x + 1 i podijelimo ga s 3 x 2 1 3 x + 1 - 2 sin 2 x - x, tada se može napisati kao
x + 2 · x x 2 · ln x 2 · ln x + 1: 3 · x 2 1 3 · x + 1 - 2 sin (2 · x - x) , zatim zamijenite umnoškom oblika x + 2 · x x 2 · ln x 2 ln x + 1 3 x 2 1 3 x + 1 - 2 sin (2 x - x)
Potenciranje
Prijeđimo na razmatranje operacija s općim razlomcima s potenciranjem. Ako postoji potencija s prirodnim eksponentom, tada se radnja smatra množenjem jednakih razlomaka. Ali preporuča se koristiti opći pristup koji se temelji na svojstvima stupnjeva. Svaki izraz A i C, gdje C nije identički jednak nuli, i bilo koji realni r na ODZ za izraz oblika A C r vrijedi jednakost A C r = A r C r. Rezultat je razlomak podignut na potenciju. Na primjer, razmotrite:
x 0, 7 - π · ln 3 x - 2 - 5 x + 1 2, 5 = = x 0, 7 - π · ln 3 x - 2 - 5 2, 5 x + 1 2, 5
Postupak izvođenja operacija s razlomcima
Operacije s razlomcima izvode se prema određenim pravilima. U praksi primjećujemo da izraz može sadržavati više razlomaka ili razlomaka. Zatim je potrebno izvršiti sve radnje u strogom redoslijedu: podići na potenciju, pomnožiti, podijeliti, zatim dodati i oduzeti. Ako postoje zagrade, prva radnja se izvodi u njima.
Primjer 9
Izračunajte 1 - x cos x - 1 c o s x · 1 + 1 x .
Riješenje
Budući da imamo isti nazivnik, zatim 1 - x cos x i 1 c o s x , ali oduzimanja se ne mogu izvoditi po pravilu, prvo se izvode operacije u zagradama, zatim množenje, pa zbrajanje. Onda kada izračunamo to dobijemo
1 + 1 x = 1 1 + 1 x = x x + 1 x = x + 1 x
Zamjenom izraza u izvorni dobivamo da je 1 - x cos x - 1 cos x · x + 1 x. Pri množenju razlomaka imamo: 1 cos x · x + 1 x = x + 1 cos x · x. Nakon što smo izvršili sve zamjene, dobivamo 1 - x cos x - x + 1 cos x · x. Sada morate raditi s razlomcima koji imaju različite nazivnike. Dobivamo:
x · 1 - x cos x · x - x + 1 cos x · x = x · 1 - x - 1 + x cos x · x = = x - x - x - 1 cos x · x = - x + 1 cos x x
Odgovor: 1 - x cos x - 1 c o s x · 1 + 1 x = - x + 1 cos x · x .
Ako primijetite grešku u tekstu, označite je i pritisnite Ctrl+Enter










