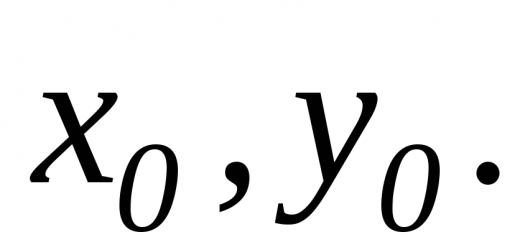Ograničenja svim studentima matematike zadaju mnogo problema. Da biste riješili ograničenje, ponekad morate upotrijebiti mnogo trikova i odabrati iz niza metoda rješenja upravo onu koja je prikladna za određeni primjer.

U ovom članku nećemo vam pomoći da shvatite granice svojih mogućnosti ili shvatite granice kontrole, već ćemo pokušati odgovoriti na pitanje: kako razumjeti granice u višoj matematici? Razumijevanje dolazi s iskustvom, pa ćemo u isto vrijeme dati nekoliko detaljni primjeri rješenja granica s objašnjenjima.

Pojam limita u matematici

Prvo pitanje je: koja je to granica i granica čega? Možemo govoriti o granicama numeričkih nizova i funkcija. Zanima nas pojam limesa funkcije jer se s njim učenici najčešće susreću. Ali prvo, najopćenitija definicija ograničenja:

Recimo da postoji neka promjenjiva vrijednost. Ako se ta vrijednost u procesu promjene neograničeno približava određenom broju a , To a – granica ove vrijednosti.

Za funkciju definiranu u određenom intervalu f(x)=y takav se broj naziva limitom A , kojoj funkcija teži kada x , težeći određenoj točki A . Točka A pripada intervalu na kojem je funkcija definirana.

Zvuči glomazno, ali je napisano vrlo jednostavno:

Lim- s engleskog ograničiti- granica.

Postoji i geometrijsko objašnjenje za određivanje granice, ali ovdje nećemo ulaziti u teoriju, jer nas više zanima praktična nego teorijska strana problema. Kad to kažemo x teži nekoj vrijednosti, to znači da varijabla ne poprima vrijednost broja, već mu se približava beskonačno blizu.

Dajmo konkretan primjer. Zadatak je pronaći granicu.

Da bismo riješili ovaj primjer, zamijenit ćemo vrijednost x=3 u funkciju. Dobivamo:

Usput, ako vas zanimaju osnovne operacije na matricama, pročitajte poseban članak o ovoj temi.

U primjerima x može težiti bilo kojoj vrijednosti. To može biti bilo koji broj ili beskonačnost. Evo primjera kada x teži beskonačnosti:

Intuitivno je jasno što je što veći broj u nazivniku, to će manju vrijednost poprimiti funkcija. Dakle, s neograničenim rastom x značenje 1/x smanjit će se i približiti nuli.

Kao što vidite, da biste riješili granicu, samo trebate zamijeniti vrijednost kojoj želite težiti u funkciju x . Međutim, ovo je najjednostavniji slučaj. Pronalaženje granice često nije tako očito. Unutar granica postoje neizvjesnosti tipa 0/0 ili beskonačnosti/beskonačnosti . Što učiniti u takvim slučajevima? Pribjegavajte trikovima!

Neizvjesnosti unutar

Neodređenost oblika beskonačnost/beskonačnost

Neka postoji granica:

Pokušamo li u funkciju zamijeniti beskonačnost, dobit ćemo beskonačnost i u brojniku i u nazivniku. Općenito, vrijedi reći da postoji određeni element umjetnosti u rješavanju takvih nesigurnosti: morate primijetiti kako možete transformirati funkciju na takav način da nesigurnost nestane. U našem slučaju, brojnik i nazivnik dijelimo s x u višem stupnju. Što će se dogoditi?

Iz primjera o kojem smo već raspravljali, znamo da će članovi koji sadrže x u nazivniku težiti nuli. Tada je rješenje granice:

Za rješavanje nesigurnosti tipa beskonačnosti/beskonačnosti podijeliti brojnik i nazivnik sa x do najvišeg stupnja.

Usput! Za naše čitatelje sada postoji popust od 10% na bilo koju vrstu posla

Druga vrsta nesigurnosti: 0/0

Kao i uvijek, zamjena vrijednosti u funkciju x=-1 daje 0 u brojniku i nazivniku. Pogledajte malo bolje i to ćete primijetiti u našem brojniku kvadratna jednadžba. Pronađimo korijene i napišimo:

Smanjimo i dobijemo:

Dakle, ako ste suočeni s nesigurnošću tipa 0/0 – rastavljaju brojnik i nazivnik.

Kako bismo vam olakšali rješavanje primjera, donosimo tablicu s ograničenjima nekih funkcija:

L'Hopitalova vladavina unutar

Još jedan moćan način za uklanjanje obje vrste neizvjesnosti. Što je bit metode?

Ako postoji nesigurnost u granici, uzimajte derivaciju brojnika i nazivnika dok nesigurnost ne nestane.

L'Hopitalovo pravilo izgleda ovako:

Važna točka : granica u kojoj umjesto brojnika i nazivnika moraju postojati izvedenice brojnika i nazivnika.

A sada - pravi primjer:

Postoji tipična neizvjesnost 0/0 . Uzmimo izvodnice brojnika i nazivnika:

Voila, neizvjesnost se rješava brzo i elegantno.

Nadamo se da ćete ove informacije moći korisno primijeniti u praksi i pronaći odgovor na pitanje “kako riješiti granice u višoj matematici”. Ukoliko trebate izračunati limes niza ili limes funkcije u točki, a nemate baš vremena za taj posao, obratite se stručnoj studentskoj službi za brzo i detaljno rješenje.

Definicija je dana konačna granica sekvence. Raspravljaju se srodna svojstva i ekvivalentna definicija. Dana je definicija da točka a nije granica niza. Razmatraju se primjeri u kojima se pomoću definicije dokazuje postojanje limita.

Sadržaj

Vidi također: Limit niza – osnovni teoremi i svojstva
Glavne vrste nejednakosti i njihova svojstva

Ovdje ćemo pogledati definiciju konačnog limita niza. Slučaj niza koji konvergira u beskonačnost razmatran je na stranici “Definicija beskonačno velikog niza”.

Limit niza je broj a if, za bilo koji pozitivan broj ε > 0 postoji takva stvar prirodni broj N ε ovisno o ε tako da za sve prirodne n > N ε vrijedi nejednakost
| x n - a|< ε .
Ovdje je x n element niza s brojem n. Ograničenje niza označeno na sljedeći način:
.
Ili u .

Transformirajmo nejednakost:
;
;
.

ε - okolina točke a - je otvoreni interval (a - ε, a + ε). Konvergentni niz je niz koji ima limit. Također se kaže da slijed konvergira do a. Divergentni niz je niz koji nema ograničenja.

Iz definicije slijedi da ako niz ima limit a, tada bez obzira koju ε-okolicu točke a odaberemo, samo konačni broj elementi slijeda ili nijedan ( prazan skup). A svaka ε-susjednost sadrži beskonačan broj elemenata. Zapravo, dajući određeni broj ε, time imamo broj . Dakle, svi elementi niza s brojevima , po definiciji, nalaze se u ε - okolici točke a . Prvi elementi mogu se nalaziti bilo gdje. To jest, izvan ε-susjedstva ne može biti više od elemenata - to jest, konačan broj.

Također napominjemo da razlika ne mora cijelo vrijeme monotono težiti nuli, odnosno opadati. Može težiti nuli nemonotono: može se povećavati ili smanjivati, imajući lokalne maksimume. Međutim, ti bi maksimumi, kako n raste, trebali težiti nuli (možda također ne monotono).

Koristeći logičke simbole postojanja i univerzalnosti, definicija granice može se napisati na sljedeći način:
(1) .

Određivanje da a nije granica

Sada razmotrimo obrnutu tvrdnju da broj a nije granica niza.

Broj a nije granica niza, ako postoji takav da za svaki prirodni broj n postoji takav prirodni m > n, Što
.

Napišimo ovu tvrdnju logičkim simbolima.
(2) .

Izjava koja broj a nije granica niza, znači da
možete odabrati takvu ε - okolinu točke a, izvan koje će biti beskonačan broj elemenata niza.

Pogledajmo primjer. Neka je dan niz sa zajedničkim elementom
(3)
Svaka okolina točke sadrži beskonačan broj elemenata. Međutim, ova točka nije granica niza, budući da svaka okolina točke također sadrži beskonačan broj elemenata. Uzmimo ε - okolinu točke s ε = 1 . Ovo će biti interval (-1, +1) . Svi elementi osim prvog s parnim n pripadaju ovom intervalu. Ali svi elementi s neparnim n su izvan ovog intervala, jer zadovoljavaju nejednakost x n > 2 . Budući da je broj neparnih elemenata beskonačan, bit će beskonačan broj elemenata izvan odabranog susjedstva. Dakle, točka nije granica niza.

Sada ćemo to pokazati, striktno se pridržavajući tvrdnje (2). Točka nije granica niza (3), jer postoji takva da za svaki prirodni n postoji neparan niz za koji vrijedi nejednakost
.

Također se može pokazati da nijedna točka a ne može biti limit ovog niza. Uvijek možemo odabrati ε - okolinu točke a koja ne sadrži ni točku 0 ni točku 2. I tada će izvan odabrane okoline biti beskonačan broj elemenata niza.

Ekvivalentna definicija granice niza

Ekvivalentnu definiciju limita niza možemo dati ako proširimo pojam ε - susjedstva. Ekvivalentnu definiciju ćemo dobiti ako umjesto ε-okoline sadrži bilo koju okolinu točke a. Okolica točke je svaki otvoreni interval koji sadrži tu točku. Matematički okolina točke definira se na sljedeći način: , gdje je ε 1 i ε 2 - proizvoljni pozitivni brojevi.

Tada je ekvivalentna definicija granice sljedeća.

Limit niza je broj a ako za bilo koju njegovu okolinu postoji prirodan broj N takav da svi elementi niza s brojevima pripadaju toj okolini.

Ova se definicija također može prikazati u proširenom obliku.

Granica niza je broj a ako za bilo koje pozitivne brojeve i postoji prirodan broj N koji ovisi o i takav da nejednakosti vrijede za sve prirodne brojeve
.

Dokaz ekvivalentnosti definicija

Dokažimo da su dvije gore prikazane definicije limita niza ekvivalentne.

Neka je broj a limit niza prema prvoj definiciji. To znači da postoji funkcija, tako da su za bilo koji pozitivan broj ε zadovoljene sljedeće nejednakosti:
(4) u .

Pokažimo da je broj a limit niza prema drugoj definiciji. To jest, trebamo pokazati da postoji takva funkcija da za sve pozitivne brojeve ε 1 i ε 2 zadovoljene su sljedeće nejednakosti:
(5) u .

Neka su nam dva pozitivna broja: ε 1 i ε 2 . I neka je ε najmanji od njih: . Zatim ; ; . Iskoristimo ovo u (5):
.
Ali nejednakosti su zadovoljene za . Tada su nejednakosti (5) također zadovoljene za .

To jest, pronašli smo funkciju za koju su nejednakosti (5) zadovoljene za sve pozitivne brojeve ε 1 i ε 2 .
Prvi dio je dokazan.

Neka je sada broj a granica niza prema drugoj definiciji. To znači da postoji funkcija takva da za bilo koje pozitivne brojeve ε 1 i ε 2 zadovoljene su sljedeće nejednakosti:
(5) u .

Pokažimo da je broj a limit niza prema prvoj definiciji. Da biste to učinili, morate staviti . Tada kada vrijede sljedeće nejednakosti:
.
Ovo odgovara prvoj definiciji s .
Ekvivalentnost definicija je dokazana.

Primjeri

Primjer 1

Dokaži to .

(1) .
U našem slučaju;
.

.
Iskoristimo svojstva nejednakosti. Onda ako i , Onda
.

.
Zatim
u .
To znači da je broj granica zadanog niza:
.

Primjer 2

Koristeći se definicijom limita niza dokažite to
.

Zapišimo definiciju limita niza:
(1) .
U našem slučaju, ;
.

Unesite pozitivne brojeve i:
.
Iskoristimo svojstva nejednakosti. Onda ako i , Onda
.

To jest, za bilo koji pozitivan, možemo uzeti bilo koji prirodni broj veći ili jednak:
.
Zatim
u .
.

Primjer 3

.

Uvodimo oznaku , .
Preobrazimo razliku:
.
Za prirodne n = 1, 2, 3, ... imamo:
.

Zapišimo definiciju limita niza:
(1) .
Unesite pozitivne brojeve i:
.
Onda ako i , Onda
.

To jest, za bilo koji pozitivan, možemo uzeti bilo koji prirodni broj veći ili jednak:
.
pri čemu
u .
To znači da je broj granica niza:
.

Primjer 4

Koristeći se definicijom limita niza dokažite to
.

Zapišimo definiciju limita niza:
(1) .
U našem slučaju, ;
.

Unesite pozitivne brojeve i:
.
Onda ako i , Onda
.

To jest, za bilo koji pozitivan, možemo uzeti bilo koji prirodni broj veći ili jednak:
.
Zatim
u .
To znači da je broj granica niza:
.

Reference:
L.D. Kudrjavcev. Tečaj matematičke analize. Svezak 1. Moskva, 2003.
CM. Nikolskog. Tečaj matematičke analize. Svezak 1. Moskva, 1983.

Vidi također:

Dane su definicije limesa funkcije prema Heineu (kroz nizove) i po Cauchyju (kroz epsilon i delta susjedstva). Definicije su dane u univerzalnom obliku, primjenjive i na dvostrane i na jednostrane granice na konačnim i beskonačno udaljenim točkama. Razmatra se definicija da točka a nije limit funkcije. Dokaz istovjetnosti Heineovih i Cauchyjevih definicija.

Sadržaj

Vidi također: Okolica točke
Određivanje limita funkcije u krajnjoj točki
Određivanje limita funkcije u beskonačnosti

Prva definicija limita funkcije (prema Heineu)

(x) u točki x 0 :
,
Ako
1) postoji takva punktirana okolina točke x 0
2) za bilo koji niz (xn), konvergirajući prema x 0 :
, čiji elementi pripadaju susjedstvu,
podslijed (f(xn)) konvergira u:
.

Ovdje x 0 a a mogu biti ili konačni brojevi ili točke u beskonačnosti. Susjedstvo može biti dvostrano ili jednostrano.

.

Druga definicija limita funkcije (prema Cauchyju)

Broj a nazivamo limesom funkcije f (x) u točki x 0 :
,
Ako
1) postoji takva punktirana okolina točke x 0 , na kojem je definirana funkcija;
2) za svaki pozitivan broj ε > 0 postoji takav broj δ ε > 0 , ovisno o ε, da za sve x koji pripadaju punktiranoj δ ε - okolini točke x 0 :
,
vrijednosti funkcije f (x) pripadaju ε-okolici točke a:
.

Bodovi x 0 a a mogu biti ili konačni brojevi ili točke u beskonačnosti. Susjedstvo također može biti dvostrano ili jednostrano.

Zapišimo ovu definiciju koristeći se logičkim simbolima postojanja i univerzalnosti:
.

Ova definicija koristi susjedstva s jednako udaljenim krajevima. Ekvivalentna definicija može se dati korištenjem proizvoljnih susjedstava točaka.

Definicija korištenjem proizvoljnih susjedstava
Broj a nazivamo limesom funkcije f (x) u točki x 0 :
,
Ako
1) postoji takva punktirana okolina točke x 0 , na kojem je definirana funkcija;
2) za bilo koju okolinu U (a) točke a postoji takva punktirana okolina točke x 0 da za sve x koji pripadaju punktiranoj okolini točke x 0 :
,
vrijednosti funkcije f (x) pripadaju četvrti U (a) točke a:
.

Koristeći se logičkim simbolima postojanja i univerzalnosti, ova se definicija može napisati na sljedeći način:
.

Jednostrane i dvostrane granice

Gore navedene definicije su univerzalne u smislu da se mogu koristiti za bilo koju vrstu susjedstva. Ako koristimo kao lijevo probušeno susjedstvo krajnje točke, dobivamo definiciju lijeve granice. Ako koristimo okolinu beskonačne točke kao okolinu, dobivamo definiciju limita u beskonačnosti.

Da bi se odredila Heineova granica, to se svodi na činjenicu da se nameće dodatno ograničenje proizvoljnom nizu koji konvergira u : njegovi elementi moraju pripadati odgovarajućoj probušenoj okolini točke .

Da bi se odredila Cauchyjeva granica, u svakom slučaju potrebno je transformirati izraze i u nejednadžbe, koristeći odgovarajuće definicije okoline točke.
Vidi "Susjedstvo točke".

Određivanje te točke a nije limit funkcije

Često postaje potrebno koristiti uvjet da točka a nije granica funkcije na . Konstruirajmo negacije gornjih definicija. U njima pretpostavljamo da funkcija f (x) je definirana na nekoj punktiranoj okolini točke x 0 . Točke a i x 0 mogu biti ili konačni brojevi ili beskonačno udaljeni. Sve dolje navedeno odnosi se i na bilateralna i na jednostrana ograničenja.

Prema Heineu.
Broj a nije granica funkcije f (x) u točki x 0 : ,
ako takav niz postoji (xn), konvergirajući prema x 0 :
,
čiji elementi pripadaju susjedstvu,
koji je redoslijed (f(xn)) ne konvergira u:
.
.

Prema Cauchyju.
Broj a nije granica funkcije f (x) u točki x 0 :
,
ako postoji takav pozitivan broj ε > 0 , pa za svaki pozitivan broj δ > 0 , postoji x koji pripada probušenoj δ-okolici točke x 0 :
,
da je vrijednost funkcije f (x) ne pripada ε-okolici točke a:
.
.

Naravno, ako točka a nije limit funkcije na , to ne znači da ne može imati limit. Može postojati granica, ali ona nije jednaka a. Također je moguće da je funkcija definirana u probušenoj okolini točke , ali nema ograničenje na .

Funkcija f(x) = sin(1/x) nema ograničenja pri x → 0.

Na primjer, funkcija je definirana na , ali nema ograničenja. Da bismo to dokazali, uzmimo niz . Konvergira u točku 0 : . Jer dakle .
Uzmimo slijed. Također konvergira do točke 0 : . Ali pošto , dakle .
Tada granica ne može biti jednaka niti jednom broju a. Doista, za , Postoji niz s kojim . Stoga svaki broj različit od nule nije ograničenje. Ali to također nije ograničenje, budući da postoji niz s kojim .

Ekvivalencija Heineove i Cauchyjeve definicije limesa

Teorema
Heineova i Cauchyjeva definicija limita funkcije su ekvivalentne.

Dokaz

U dokazu pretpostavljamo da je funkcija definirana u nekoj punktiranoj okolini točke (konačnoj ili u beskonačnosti). Točka a također može biti konačna ili u beskonačnosti.

Heineov dokaz ⇒ Cauchyjev

Neka funkcija ima limit a u točki prema prvoj definiciji (prema Heineu). To jest, za bilo koji niz koji pripada probušenoj okolini točke i ima granicu
(1) ,
granica niza je:
(2) .

Pokažimo da funkcija ima Cauchyjev limit u točki. Odnosno, za svakoga postoji nešto što je za svakoga.

Pretpostavimo suprotno. Neka su zadovoljeni uvjeti (1) i (2), ali funkcija nema Cauchyjev limit. Odnosno, postoji nešto što postoji za bilo koga, dakle
.

Uzmimo , gdje je n prirodan broj. Tada postoji , i
.
Tako smo konstruirali niz koji konvergira prema , ali granica niza nije jednaka . To je u suprotnosti s uvjetima teorema.

Prvi dio je dokazan.

Cauchyjev dokaz ⇒ Heineov

Neka funkcija ima limit a u točki prema drugoj definiciji (po Cauchyju). Odnosno, za bilo koga to postoji
(3) za sve .

Pokažimo da funkcija ima limit a u točki prema Heineu.
Uzmimo proizvoljan broj. Prema Cauchyjevoj definiciji broj postoji, pa vrijedi (3).

Uzmimo proizvoljan niz koji pripada probušenoj okolini i konvergira . Po definiciji konvergentnog niza, za bilo koji postoji taj
u .
Tada iz (3) slijedi da
u .
Budući da ovo vrijedi za svakoga, onda
.

Teorem je dokazan.

Reference:
L.D. Kudrjavcev. Tečaj matematičke analize. Svezak 1. Moskva, 2003.

Vidi također:

Danas ćemo u razredu pogledati strogi redoslijed I stroga definicija limita funkcije, te naučiti rješavati relevantne probleme teorijske prirode. Članak je prvenstveno namijenjen studentima prve godine prirodnih znanosti i tehničkih specijalnosti koji su počeli proučavati teoriju matematičke analize i naišli su na poteškoće u razumijevanju ovog dijela više matematike. Osim toga, materijal je prilično dostupan srednjoškolcima.

Tijekom godina postojanja stranice dobio sam desetak pisama otprilike sljedećeg sadržaja: “Ne razumijem se dobro u matematičku analizu, što da radim?”, “Uopće se ne razumijem u matematiku, ja sam razmišljam o prekidu studija” itd. I doista, matan je taj koji često prorijedi studentsku grupu nakon prve sesije. Zašto je to tako? Zato što je predmet nezamislivo složen? Nikako! Teorija matematičke analize nije toliko teška koliko je osebujna. I trebate je prihvatiti i voljeti takvu kakva jest =)

Počnimo s najtežim slučajem. Prva i najvažnija stvar je da ne morate odustati od studija. Shvatite dobro, uvijek možete odustati;-) Naravno, ako vam nakon godinu ili dvije bude muka od odabrane specijalnosti, onda da, trebali biste razmisliti o tome (i nemoj se ljutiti!) o promjeni djelatnosti. Ali za sada vrijedi nastaviti. I molim vas, zaboravite rečenicu "Ništa ne razumijem" - ne događa se da UOPĆE ništa ne razumijete.

Što učiniti ako je teorija loša? Ovo se, usput, ne odnosi samo na matematičku analizu. Ako je teorija loša, onda se prvo treba OZBILJNO posvetiti praksi. U ovom slučaju rješavaju se dva strateška zadatka odjednom:

– Prvo, značajan udio teorijsko znanje nastala kroz praksu. I zato mnogi ljudi razumiju teoriju kroz... – tako je! Ne, ne, ne razmišljaš o tome =)

– I, drugo, praktične vještine će vas vrlo vjerojatno “izvući” kroz ispit, čak i ako... ali nemojmo se toliko uzbuđivati! Sve je pravo i sve se može "podići" u prilično kratkom vremenu. Matematička analiza je moj omiljeni dio više matematike i stoga jednostavno nisam mogao a da vam ne pružim ruku pomoći:

Na početku 1. semestra obično se obrađuju granice slijeda i funkcije. Ne razumijete što je to i ne znate kako ih riješiti? Počnite s člankom Ograničenja funkcija, u kojem se “na prste” ispituje sam pojam i analiziraju najjednostavniji primjeri. Zatim, obradite druge lekcije na tu temu, uključujući lekciju o unutar sekvenci, o čemu sam zapravo već formulirao strogu definiciju.

Koje simbole osim znakova nejednakosti i modula poznajete?

– duga okomita palica glasi ovako: “takvo to”, “takvo to”, “takvo to” ili “takvo to”, u našem slučaju, očito, govorimo o broju - dakle “takvom”;

– za sve “en” veće od ;

– znak modula znači udaljenost, tj. ovaj unos nam govori da je udaljenost između vrijednosti manja od epsilon.

Pa, je li smrtno teško? =)

Nakon savladavanja prakse, veselim se što ću vas vidjeti u sljedećem odlomku:

I zapravo, razmislimo malo – kako formulirati strogu definiciju niza? ...Prvo što mi pada na pamet na svijetu praktična nastava: “granica niza je broj kojem se članovi niza beskonačno približavaju.”

U redu, zapišimo podslijed :

Nije to teško razumjeti podslijed približavaju se beskonačno blizu broju –1 i parnim članovima – na “jedan”.

Ili možda postoje dvije granice? Ali zašto ih onda nijedan niz ne može imati deset ili dvadeset? Ovako možete daleko dogurati. S tim u vezi logično je pretpostaviti da ako niz ima granicu, onda je jedinstven.

Bilješka : niz nema ograničenja, ali se iz njega mogu razlikovati dva podniza (vidi gore), od kojih svaki ima svoj limit.

Stoga se gornja definicija pokazuje neodrživom. Da, radi za slučajeve poput (što nisam sasvim ispravno upotrijebio u pojednostavljenim objašnjenjima praktičnih primjera), ali sada moramo pronaći strogu definiciju.

Pokušaj drugi: “granica niza je broj kojem se približavaju SVI članovi niza, osim možda njihovih konačni količine." Ovo je bliže istini, ali ipak nije sasvim točno. Tako, na primjer, niz polovica članova uopće se ne približava nuli - jednostavno su joj jednaki =) Usput, "trepereće svjetlo" općenito ima dvije fiksne vrijednosti.

Formulaciju nije teško razjasniti, ali onda se postavlja još jedno pitanje: kako napisati definiciju matematički znakovi? Znanstveni svijet Dugo sam se borio s tim problemom dok nisam riješio situaciju slavni maestro, koji je, u biti, formalizirao klasičnu matematičku analizu u svoj njezinoj strogosti. Cauchy je predložio operaciju okruženje , koji je značajno unaprijedio teoriju.

Razmotrite neku točku i njezinu proizvoljan-okruženje:

Vrijednost "epsilon" je uvijek pozitivna, i, štoviše, imamo ga pravo sami izabrati. Pretpostavimo da u ovom susjedstvu ima mnogo članova (ne nužno sve) neki slijed. Kako zapisati činjenicu da je, primjerice, deseti termin u susjedstvu? Neka bude s njegove desne strane. Tada bi udaljenost između točaka i trebala biti manja od “epsilon”: . Međutim, ako se "x desetina" nalazi lijevo od točke "a", tada će razlika biti negativna, pa joj se mora dodati znak modul: .

Definicija: broj se naziva limitom niza ako za bilo koji njegovu okolinu (unaprijed odabrano) postoji prirodan broj TAKAV da SVIčlanovi niza s većim brojevima bit će unutar susjedstva:

Ili ukratko: ako

Drugim riječima, koliko god malu "epsilon" vrijednost koju uzmemo, prije ili kasnije "beskonačni rep" niza će POTPUNO biti u ovom susjedstvu.

Na primjer, "beskonačni rep" niza će POTPUNO ući u bilo koju proizvoljno malu okolinu točke. Dakle, ova vrijednost je granica niza po definiciji. Dopustite mi da vas podsjetim da se niz čija je granica nula naziva infinitezimalnog.

Treba napomenuti da za niz više nije moguće reći "beskrajni rep" će ući“- članovi s neparnim brojevima zapravo su jednaki nuli i “nikamo ne idu” =) Zato je u definiciji korišten glagol “pojaviti se”. I, naravno, članovi ovakvog niza također "nigdje ne idu". Usput, provjerite je li broj njegova granica.

Sada ćemo pokazati da niz nema ograničenja. Razmotrimo, na primjer, susjedstvo točke . Potpuno je jasno da ne postoji taj broj nakon kojeg će SVI pojmovi završiti u datom susjedstvu - neparni pojmovi će uvijek “iskočiti” na “minus jedan”. Iz sličnog razloga, u točki nema ograničenja.

Učvrstimo gradivo vježbom:

Primjer 1

Dokažite da je limit niza nula. Specificirajte broj nakon kojeg će svi članovi niza zajamčeno biti unutar proizvoljno male okoline točke.

Bilješka : Za mnoge nizove, traženi prirodni broj ovisi o vrijednosti - otuda zapis .

Riješenje: smatrati proizvoljan ima li ikakvih broj – tako da će SVI članovi s višim brojevima biti unutar ovog susjedstva:

Da bismo pokazali postojanje traženog broja, izražavamo ga kroz .

Budući da se za bilo koju vrijednost "en", znak modula može ukloniti:

Koristimo „školske“ radnje s nejednakostima koje sam ponavljao u razredu Linearne nejednadžbe I Funkcijska domena. U ovom slučaju, važna okolnost je da su "epsilon" i "en" pozitivni:

Budući da je s lijeve strane riječ o prirodnim brojevima, i desni dio V opći slučaj je razlomak, tada ga treba zaokružiti:

Bilješka : ponekad se jedinica doda s desne strane radi sigurnosti, ali u stvarnosti je to pretjerano. Relativno govoreći, ako rezultat oslabimo zaokruživanjem prema dolje, tada će najbliži odgovarajući broj (“tri”) i dalje zadovoljavati izvornu nejednakost.

Sada gledamo nejednakost i prisjećamo se što smo u početku razmatrali proizvoljan- susjedstvo, tj. "epsilon" može biti jednako bilo tko pozitivan broj.

Zaključak: za bilo koju proizvoljno malu -okolicu točke, vrijednost je pronađena . Dakle, broj je granica niza po definiciji. Q.E.D.

Usput, iz dobivenog rezultata prirodni obrazac je jasno vidljiv: što je susjedstvo manje, to je broj veći, nakon čega će SVI članovi niza biti u ovom susjedstvu. Ali bez obzira na to koliko malen bio "epsilon", uvijek će postojati "beskonačni rep" unutra, a izvana - čak i ako je velik, međutim konačni broj članova.

Kakvi su vaši dojmovi? =) Slažem se da je malo čudno. Ali strogo! Molim vas ponovno pročitajte i razmislite o svemu.

Pogledajmo sličan primjer i upoznajmo druge tehničke metode:

Primjer 2

Riješenje: po definiciji niza potrebno je dokazati da (reci na glas!!!).

Razmotrimo proizvoljan- susjedstvo točke i čeka, postoji li prirodni broj – takav da za sve veće brojeve vrijedi nejednakost:

Da biste pokazali postojanje takvog, trebate izraziti "en" kroz "epsilon". Izraz pojednostavljujemo pod znakom modula:

Modul uništava znak minus:

Nazivnik je pozitivan za svaki "en", stoga se štapići mogu ukloniti:

Nasumično:

Sada moramo ekstrahirati Korijen, ali caka je u tome što će za neki "epsilon" desna strana biti negativna. Da bi izbjegli ovu nevolju ojačajmo nejednakost po modulu:

Zašto se to može učiniti? Ako se, relativno gledano, pokaže da , tada će i uvjet biti zadovoljen. Modul može samo povećaj traženi broj, a to će i nama odgovarati! Grubo rečeno, ako odgovara stoti, onda odgovara i dvjestoti! Prema definiciji, trebate pokazati sama činjenica postojanja broja(barem neki), nakon čega će svi članovi niza biti u -susjedstvu. Usput, zato se ne bojimo konačnog zaokruživanja desne strane prema gore.

Vađenje korijena:

I zaokružite rezultat:

Zaključak: jer vrijednost "epsilon" odabrana je proizvoljno, tada je vrijednost pronađena za bilo koju proizvoljno malu okolinu točke , tako da za sve veće brojeve vrijedi nejednakost . Tako, a-priorat. Q.E.D.

Savjetujem posebno razumijevanje jačanja i slabljenja nejednakosti tipična je i vrlo uobičajena tehnika u matematičkoj analizi. Jedino što trebate pratiti je ispravnost ove ili one akcije. Tako, na primjer, nejednakost ni pod kojim uvjetima nije moguće popustiti, oduzimajući, recimo, jedan:

Opet, uvjetno: ako broj točno odgovara, onda prethodni možda više ne odgovara.

Sljedeći primjer za neovisno rješenje:

Primjer 3

Dokažite to pomoću definicije niza

Kratko rješenje i odgovor na kraju lekcije.

Ako slijed beskrajno velik, tada se definicija granice formulira na sličan način: točka se naziva granica niza ako za bilo koji, velik koliko hoćeš broj, postoji broj takav da će za sve veće brojeve nejednakost biti zadovoljena. Broj je pozvan blizina točke “plus beskonačnost”:

Drugim riječima, kako god veliki značaj Bez obzira na sve, "beskonačni rep" niza definitivno će ići u -blizinu točke, ostavljajući samo konačan broj članova s ​​lijeve strane.

Standardni primjer:

I skraćeni zapis: , ako

Za slučaj sami zapišite definiciju. Točna verzija je na kraju lekcije.

Nakon što ste shvatili praktične primjere i shvatili definiciju limita niza, možete se obratiti literaturi o računici i/ili svojoj bilježnici za predavanja. Preporučujem preuzimanje prvog sveska Bohana (jednostavniji - za dopisne studente) i Fichtenholtz (opširnije i detaljnije). Među ostalim autorima preporučujem Piskunova, čiji je tečaj namijenjen tehničkim sveučilištima.

Pokušajte savjesno proučavati teoreme koji se tiču ​​limita niza, njihove dokaze, posljedice. U početku se teorija može činiti "mutnom", ali to je normalno - samo se trebate naviknuti. A mnogi će ga i kušati!

Stroga definicija limita funkcije

Počnimo s istom stvari - kako formulirati ovaj koncept? Verbalna definicija limita funkcije formulirana je puno jednostavnije: “broj je limit funkcije ako s “x” teži (i lijevo i desno), odgovarajuće vrijednosti funkcije teže » (vidi crtež). Čini se da je sve normalno, ali riječi su riječi, značenje je značenje, ikona je ikona, a strogih matematičkih zapisa nema dovoljno. A u drugom odlomku ćemo se upoznati s dva pristupa rješavanju ovog pitanja.

Neka je funkcija definirana na nekom intervalu, uz moguću iznimku točke. U obrazovna literatura opće je prihvaćeno da je funkcija tu Ne definirano:

Ovaj izbor naglašava bit limita funkcije: "x" beskrajno blizu približava , a odgovarajuće vrijednosti funkcije su beskrajno blizu Za . Drugim riječima, pojam limita ne podrazumijeva “točan pristup” točkama, već naime beskonačno bliska aproksimacija, nije bitno je li funkcija definirana u točki ili ne.

Prva definicija limita funkcije, ne iznenađuje, formulirana je pomoću dva niza. Prvo, pojmovi su povezani, a drugo, granice funkcija se obično proučavaju nakon granica nizova.

Razmotrite slijed bodova (nije na crtežu), koji pripadaju intervalu I različito od, koji konvergira Za . Tada odgovarajuće vrijednosti funkcije također tvore numerički niz, čiji se članovi nalaze na ordinatnoj osi.

Limit funkcije prema Heineu za bilo koji nizovi točaka (pripada i razlikuje se od), koji konvergira u točku, odgovarajući niz vrijednosti funkcije konvergira u .

Eduard Heine je njemački matematičar. ...I nema potrebe tako nešto misliti, postoji samo jedan gay u Europi - Gay-Lussac =)

Nastala je druga definicija granice... da, da, u pravu ste. Ali prvo, shvatimo njegov dizajn. Promotrimo proizvoljnu -okolicu točke (“crnački” kvart). Na temelju prethodnog stavka natuknica znači da neku vrijednost funkcija se nalazi unutar "epsilon" susjedstva.

Sada nalazimo -susjedstvo koje odgovara zadanom -susjedstvu (mentalno nacrtajte crne točkaste linije s lijeva na desno, a zatim odozgo prema dolje). Imajte na umu da je odabrana vrijednost duž duljine manjeg segmenta, u ovom slučaju - duž duljine kraćeg lijevog segmenta. Štoviše, "malina" -susjedstvo točke može se čak i reducirati, jer u sljedećoj definiciji važna je sama činjenica postojanja ovo susjedstvo. I, slično, notacija znači da je neka vrijednost unutar "delta" susjedstva.

Granica Cauchyjeve funkcije: broj se naziva limitom funkcije u točki if za bilo koji unaprijed odabrani susjedstvo (malo koliko želite), postoji-okolica točke, TAKVA, to: KAO SAMO vrijednosti (pripada) uključeno u ovo područje: (crvene strelice)– DAKLE ODMAH je zajamčeno da će odgovarajuće vrijednosti funkcije ući u -susjedstvo: (plave strelice).

Moram vas upozoriti da sam radi jasnoće malo improvizirao, pa nemojte pretjerivati ​​=)

Kratki unos: , ako

Što je bit definicije? Slikovito govoreći, beskonačnim smanjivanjem -susjedstva, "pratimo" vrijednosti funkcije do njihove granice, ne ostavljajući im alternativu pristupu negdje drugdje. Dosta neobično, ali opet strogo! Da biste u potpunosti razumjeli ideju, ponovno pročitajte tekst.

! Pažnja: ako trebate samo formulirati Heineova definicija ili samo Cauchyjeva definicija molim te ne zaboravi na značajan preliminarni komentari: "Razmotrite funkciju koja je definirana na određenom intervalu, uz moguću iznimku točke". Ovo sam jednom rekao na samom početku i nisam svaki put ponavljao.

Prema odgovarajućem teoremu matematičke analize, Heineova i Cauchyjeva definicija su ekvivalentne, ali je druga opcija najpoznatija (ipak bih!), koja se također naziva "jezično ograničenje":

Primjer 4

Dokažite to pomoću definicije limita

Riješenje: funkcija je definirana na cijelom brojevnom pravcu osim točke. Pomoću definicije dokazujemo postojanje limita u danoj točki.

Bilješka : vrijednost susjedstva "delta" ovisi o "epsilon", otuda oznaka

Razmotrimo proizvoljan-okruženje. Zadatak je pomoću te vrijednosti provjeriti je li postoji li-okruženje, TAKVA, što iz nejednakosti slijedi nejednakost .

Pretpostavljajući da , transformiramo posljednju nejednadžbu:
(proširio kvadratni trinom)

Definicija 1. Neka E- beskonačan broj. Ako neka okolina sadrži točke skupa E, drugačije od točke A, To A nazvao ultimativno točka skupa E.

Definicija 2. (Heinrich Heine (1821.-1881.)). Neka funkcija
definirana na setu x I A nazvao ograničiti funkcije
u točki (ili kada
, ako za bilo koji niz vrijednosti argumenata
, približavajući se , odgovarajući niz vrijednosti funkcije konvergira u broj A. Pišu:
.

Primjeri. 1) Funkcija
ima granicu jednaku S, u bilo kojoj točki brojevne crte.

Dapače, za bilo koju točku i bilo koji niz vrijednosti argumenata
, približavajući se i koji se sastoji od brojeva osim , odgovarajući niz vrijednosti funkcije ima oblik
, a znamo da ovaj niz konvergira u S. Zato
.

2) Za funkciju

.

Ovo je očito, jer ako
, onda
.

3) Dirichletova funkcija
nema ograničenja ni u jednom trenutku.

Doista, neka
I
, i sve - racionalni brojevi. Zatim
za sve n, Zato
. Ako
i to je sve su dakle iracionalni brojevi
za sve n, Zato
. Vidimo da uvjeti definicije 2 nisu zadovoljeni, dakle
ne postoji.

4)
.

Doista, uzmimo proizvoljan niz
, približavajući se

broj 2. Zatim . Q.E.D.

Definicija 3. (Cauchy (1789-1857)). Neka funkcija
definirana na setu x I je granična točka ovog skupa. Broj A nazvao ograničiti funkcije
u točki (ili kada
, ako postoji
biti će
, tako da za sve vrijednosti argumenta x, zadovoljavajući nejednakost

,

nejednakost je istinita

.

Pišu:
.

Cauchyjeva definicija također se može dati korištenjem susjedstva, ako primijetimo da , a:

neka funkcionira
definirana na setu x I je granična točka ovog skupa. Broj A nazvan limit funkcije
u točki , ako postoji -okolica točke A
postoji probušena - okolina točke
,tako da
.

Korisno je ovu definiciju ilustrirati crtežom.

Primjer 5.
.

Doista, uzmimo
nasumično i pronaći
, takav da za svakoga x, zadovoljavajući nejednakost
nejednakost vrijedi
. Posljednja nejednadžba je ekvivalentna nejednadžbi
, pa vidimo da je dovoljno uzeti
. Izjava je dokazana.

Pravedan

Teorema 1. Definicije limita funkcije prema Heineu i prema Cauchyju su ekvivalentne.

Dokaz. 1) Neka
prema Cauchyju. Dokažimo da je isti broj i limit prema Heineu.

Idemo uzeti
proizvoljno. Prema definiciji 3 postoji
, takav da za svakoga
nejednakost vrijedi
. Neka
– proizvoljan niz takav da
na
. Zatim postoji broj N takav da za svakoga
nejednakost vrijedi
, Zato
za sve
, tj.

prema Heineu.

2) Neka sada
prema Heineu. Dokažimo to
a prema Cauchyju.

Pretpostavimo suprotno, tj. Što
prema Cauchyju. Onda postoji
takav da za bilo koga
biti će
,
I
. Razmotrite slijed
. Za navedeno
i bilo koji n postoji

I
. To znači da
, Iako
, tj. broj A nije granica
u točki prema Heineu. Dobili smo kontradikciju, koja dokazuje tvrdnju. Teorem je dokazan.

Teorema 2 (o jedinstvenosti limita). Ako u točki postoji limit funkcije , onda je on jedini.

Dokaz. Ako je limit definiran prema Heineu, tada njegova jedinstvenost slijedi iz jedinstvenosti limita niza. Ako je limit definiran prema Cauchyju, tada njegova jedinstvenost proizlazi iz istovjetnosti definicija limita prema Cauchyju i prema Heineu. Teorem je dokazan.

Slično Cauchyjevom kriteriju za nizove, vrijedi i Cauchyjev kriterij postojanja limita funkcije. Prije nego što ga formuliramo, dajmo

Definicija 4. Kažu da funkcija
zadovoljava Cauchyjev uvjet u točki , ako postoji
postoji

, tako da
I
, nejednakost vrijedi
.

Teorema 3 (Cauchyjev kriterij postojanja limita). Kako bi funkcija
imao u točki konačne granice, potrebno je i dovoljno da u ovoj točki funkcija zadovoljava Cauchyjev uvjet.

Dokaz.Nužnost. Neka
. To moramo dokazati
zadovoljava u točki Cauchyjevo stanje.

Idemo uzeti
proizvoljno i staviti
. Po definiciji granice za postoji
, tako da za bilo koje vrijednosti
, zadovoljavajući nejednakosti
I
, nejednakosti su zadovoljene
I
. Zatim

Potreba je dokazana.

Adekvatnost. Neka funkcija
zadovoljava u točki Cauchyjevo stanje. Moramo dokazati da je u pitanju konačna granica.

Idemo uzeti
proizvoljno. Po definiciji postoji 4
, tako da iz nejednakosti
,
slijedi to
- ovo je dano.

Pokažimo to prvo za bilo koji niz
, približavajući se , podslijed
vrijednosti funkcije konvergiraju. Doista, ako
, tada, na temelju definicije limita niza, za dano
postoji broj N, takav da za bilo koji

I
. Jer
u točki zadovoljava Cauchyjev uvjet, imamo
. Zatim, prema Cauchyjevom kriteriju za nizove, niz
konvergira. Pokažimo da sve takve sekvence
konvergiraju do iste granice. Pretpostavimo suprotno, tj. što su sekvence
I
,
,
, tako da. Razmotrimo slijed. Jasno je da konvergira u , dakle, ovim što je gore dokazano, niz konvergira, što je nemoguće, budući da podnizovi
I
imaju različite granice I . Rezultirajuća kontradikcija pokazuje da =. Stoga, prema Heineovoj definiciji, funkcija ima u točki konačna granica. Dostatnost, a time i teorem, je dokazana.