Lekcija na temu “Beskonačno padajuća geometrijska progresija”

Svrha lekcije: upoznavanje učenika s novom vrstom niza – beskonačno padajućom geometrijskom progresijom.

Zadaci:

formuliranje početne ideje o granici numeričkog niza; upoznavanje s drugim načinom pretvaranja beskonačnih periodičnih razlomaka u obične pomoću formule za zbroj beskonačno padajuće geometrijske progresije;

razvoj intelektualnih kvaliteta osobnosti učenika kao što su logičko razmišljanje, sposobnost procjenjivanja i generalizacije;

poticanje aktivnosti, međusobnog pomaganja, kolektivizma i interesa za predmet.

Oprema: informatički razred, projektor, platno.

Vrsta lekcije: lekcija – učenje nova tema.

Tijekom nastave

ja . Org. trenutak. Navedite temu i svrhu lekcije.

II . Obnavljanje znanja učenika.1. Provjera domaće zadaće.

1) Provjera osnovnih formula vezanih uz aritmetičke i geometrijske progresije. Dva učenika pripremaju bilješke o formulama na ploči.

2) Ostali učenici rade matematički diktat na temu “Formule zbroja”.

Zadaci:

№1. Pronađite zbroj prvih pet članova aritmetička progresija, ako je njegov prvi član jednak 6 (1. opcija), -20 (2. opcija), a peti član je -6 (1. opcija), 20 (2. opcija).

№2. Nađite zbroj prvih pet članova aritmetičke progresije ako je njegov prvi član -20 (1. opcija), 6 (2. opcija), a razlika je 10 (1. opcija), -3 (2. opcija).

№3. Nađite zbroj prvih pet članova geometrijske progresije ako je njegov prvi član jednak 1 (1. opcija), -1 (2. opcija), a nazivnik je -2 (1. opcija), 2 (2. opcija).

Na kraju diktata rad dva učenika selektivno se provjerava za ocjenjivanje, ostali rade samoprovjeru pomoću gotovih rješenja ispisanih na preklopima ploče.

rješenja:

Zadaci

1. Aritmetička progresija dana je formulom a n = 7 – 4 n. Pronaći a 10 . (-33)

2. U aritmetičkoj progresiji a 3 = 7 I a 5 = 1 . Pronaći a 4 . (4)

3. U aritmetičkoj progresiji a 3 = 7 I a 5 = 1 . Pronaći a 17 . (-35)

4. U aritmetičkoj progresiji a 3 = 7 I a 5 = 1 . Pronaći S 17 . (-187)

5. Za geometrijsku progresiju
pronađite peti član.

6. Za geometrijsku progresiju
pronaći n th član.

7. Eksponencijalno b 3 = 8 I b 5 = 2 . Pronaći b 4 . (4)

8. Eksponencijalno b 3 = 8 I b 5 = 2 . Pronaći b 1 I q .

9. Eksponencijalno b 3 = 8 I b 5 = 2 . Pronaći S 5 . (62)

III . Učenje nove teme(demonstracija prezentacije).

Razmotrimo kvadrat sa stranicom jednakom 1. Nacrtajmo još jedan kvadrat čija je stranica polovica veličine prvog kvadrata, zatim još jedan čija je stranica polovica drugog, zatim sljedeći, itd. Svaki put je stranica novog kvadrata jednaka polovici prethodnog.

Kao rezultat, dobili smo niz stranica kvadrata tvoreći geometrijsku progresiju s nazivnikom .

I što je vrlo važno, što više budemo gradili takvih kvadrata, stranica će kvadrata biti manja. Na primjer,

Oni. Kako se broj n povećava, članovi progresije se približavaju nuli.

Koristeći ovu sliku, možete razmotriti drugi niz.

Na primjer, niz površina kvadrata:

. I opet, ako n raste neograničeno, tada se područje približava nuli koliko god želite.

Pogledajmo još jedan primjer. Jednakostranični trokut sa stranicama jednakim 1 cm. Konstruirajmo sljedeći trokut s vrhovima u središtima stranica 1. trokuta, prema teoremu o središnjici trokuta - stranica 2. jednaka je polovici stranice prvog, stranica 3. jednaka je polovici stranice 2. itd. Opet dobivamo niz duljina stranica trokuta.

na
.

Ako uzmemo u obzir geometrijsku progresiju s negativnim nazivnikom.

Zatim, opet, sa sve većim brojevima n uvjeti progresije približavaju se nuli.

Obratimo pozornost na nazivnike ovih nizova. Svugdje su nazivnici bili manji od 1 u apsolutnoj vrijednosti.

Možemo zaključiti: geometrijska progresija će biti beskonačno padajuća ako je modul njezina nazivnika manji od 1.

Frontalni rad.

Definicija:

Kaže se da je geometrijska progresija beskonačno opadajuća ako je modul njezina nazivnika manji od jedan.
.

Pomoću definicije možete odlučiti je li geometrijska progresija beskonačno padajuća ili ne.

Zadatak

Je li niz beskonačno padajuća geometrijska progresija ako je dan formulom:

;
.

Riješenje:

. Naći ćemo q .

;
;
;
.

ova geometrijska progresija je beskonačno opadajuća.

b) ovaj niz nije beskonačno padajuća geometrijska progresija.

Razmotrite kvadrat sa stranicom jednakom 1. Podijelite ga na pola, jednu od polovica na pola, itd. Površine svih rezultirajućih pravokutnika čine beskonačno padajuću geometrijsku progresiju:

Zbroj površina svih pravokutnika dobivenih na ovaj način bit će jednak površini 1. kvadrata i jednak 1.

Ali na lijevoj strani ove jednakosti nalazi se zbroj beskonačnog broja članova.

Razmotrimo zbroj prvih n članova.

Prema formuli za zbroj prvih n članova geometrijske progresije, on je jednak .

Ako n povećava se bez ograničenja, dakle

ili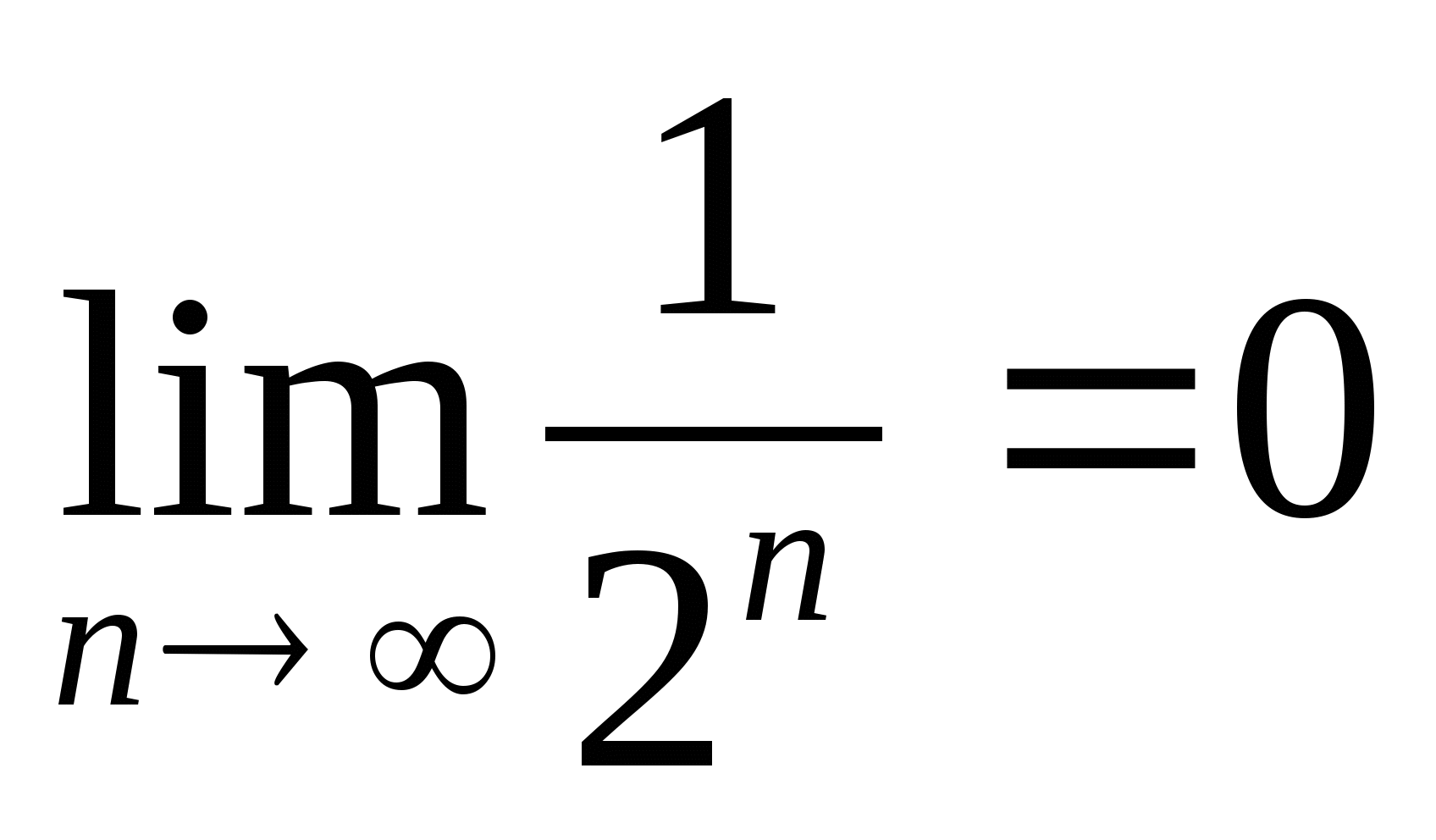
. Zato
, tj.
.

Zbroj beskonačno opadajuće geometrijske progresije postoji ograničenje niza S 1 , S 2 , S 3 , …, S n , … .

Na primjer, za napredovanje
,

Jer

Zbroj beskonačno opadajuće geometrijske progresije može se pronaći pomoću formule
.

III . Razumijevanje i konsolidacija(izvršavanje zadataka).

Zadatak br. 2. Nađite zbroj beskonačno padajuće geometrijske progresije s prvim članom 3, a drugim 0,3.

Riješenje:

Zadatak br. 3. udžbenik, str.160, br.433(1)

Nađi zbroj beskonačno padajuće geometrijske progresije:

Riješenje:

Zadatak br. 4. Zapiši beskonačni periodični decimalni razlomak 0,(5) kao obični razlomak.

1. metoda. Neka je x=0,(5)= 0,555... / 10 2. metoda. 0,(5)=0,555…=

Zadatak br. 5. udžbenik, str.162, br.445(3) (samostalno rješenje)

Zapišite beskonačni periodični decimalni razlomak 0,(12) kao obični razlomak.

Odgovor: 0,(12)= 4/33.

IV . Sažimajući.

S kojim slijedom ste se danas upoznali?

Definirajte beskonačno padajuću geometrijsku progresiju.

Kako dokazati da je geometrijska progresija beskonačno opadajuća?

Navedite formulu za zbroj beskonačno padajuće geometrijske progresije.

V . Domaća zadaća.

NUMERIČKI NIZOVI VI

§ l48. Zbroj beskonačno opadajuće geometrijske progresije

Do sada, kada govorimo o zbrojevima, uvijek smo pretpostavljali da je broj članova u tim zbrojevima konačan (npr. 2, 15, 1000 itd.). Ali kada se rješavaju neki problemi (osobito više matematike) mora se raditi sa zbrojevima beskonačnog broja članova

S= a 1 + a 2 + ... + a n + ... . (1)

Koji su to iznosi? A-priorat zbroj beskonačnog broja članova a 1 , a 2 , ..., a n , ... zove se limit sume S n prvi P brojevi kada P -> ∞ :

S=S n = (a 1 + a 2 + ... + a n ). (2)

Granica (2), naravno, može, ali i ne mora postojati. Prema tome, kažu da zbroj (1) postoji ili ne postoji.

Kako možemo saznati postoji li zbroj (1) u svakom konkretnom slučaju? Zajednička odluka Ovo pitanje daleko nadilazi opseg našeg programa. Međutim, postoji jedan važan poseban slučaj, što sada moramo razmotriti. Govorit ćemo o zbrajanju članova beskonačno opadajuće geometrijske progresije.

Neka a 1 , a 1 q , a 1 q 2, ... je beskonačno padajuća geometrijska progresija. To znači da | q |< 1. Сумма первых P uvjeti ove progresije su jednaki

Iz osnovnih teorema o granicama varijabli (vidi § 136) dobivamo:

Ali 1 = 1, a qn = 0. Prema tome

Dakle, zbroj beskonačno opadajuće geometrijske progresije jednak je prvom članu ove progresije podijeljen s jedan minus nazivnik ove progresije.

1) Zbroj geometrijske progresije 1, 1/3, 1/9, 1/27, ... jednak je

a zbroj geometrijske progresije je 12; -6; 3; - 3/2 , ... jednako

2) Pretvorite jednostavni periodični razlomak 0,454545 ... u obični.

Da biste riješili ovaj problem, zamislite ovaj razlomak kao beskonačnu sumu:

Desna strana ove jednakosti je zbroj beskonačno opadajuće geometrijske progresije, čiji je prvi član jednak 45/100, a nazivnik je 1/100. Zato

Koristeći opisanu metodu, također se može dobiti opće pravilo pretvorba jednostavnih periodičnih razlomaka u obične (vidi II. poglavlje, § 38):

Da biste jednostavni periodični razlomak pretvorili u obični, potrebno je učiniti sljedeće: stavite točku u brojnik decimal, a nazivnik je broj koji se sastoji od devetki uzetih onoliko puta koliko ima znamenki u periodi decimalnog razlomka.

3) Pretvorite mješoviti periodički razlomak 0,58333 .... u obični razlomak.

Zamislimo ovaj razlomak kao beskonačnu sumu:

Na desnoj strani te jednakosti svi članovi, počevši od 3/1000, tvore beskonačno padajuću geometrijsku progresiju, čiji je prvi član jednak 3/1000, a nazivnik 1/10. Zato

Korištenjem opisane metode može se dobiti opće pravilo za pretvaranje mješovitih periodičnih razlomaka u obične razlomke (vidi II. poglavlje, § 38). Namjerno ga ovdje ne predstavljamo. Nema potrebe zapamtiti ovo glomazno pravilo. Mnogo je korisnije znati da se svaki mješoviti periodički razlomak može prikazati kao zbroj beskonačno padajuće geometrijske progresije i određenog broja. I formula

za zbroj beskonačno opadajuće geometrijske progresije, morate se, naravno, sjetiti.

Kao vježbu predlažemo da, uz dolje navedene zadatke br. 995-1000, još jednom pogledate zadatak br. 301 § 38.

Vježbe

995. Kako se zove zbroj beskonačno padajuće geometrijske progresije?

996. Odredi zbrojeve beskonačno opadajućih geometrijskih progresija:

997. Kod kojih vrijednosti x napredovanje

da li beskonačno opada? Nađite zbroj takve progresije.

998.V jednakostraničan trokut sa strane A upisuje se novi trokut spajanjem središta njegovih stranica; u taj se trokut na isti način upisuje novi trokut i tako u nedogled.

a) zbroj opsega svih tih trokuta;

b) zbroj njihovih površina.

999. Kvadrat sa stranicom A upisuje se novi kvadrat spajanjem središta njegovih stranica; kvadrat je upisan u ovaj kvadrat na isti način, i tako dalje ad infinitum. Odredite zbroj opsega svih tih kvadrata i zbroj njihovih površina.

1000. Sastavite beskonačno padajuću geometrijsku progresiju tako da je njezin zbroj jednak 25/4, a zbroj kvadrata njegovih članova jednak 625/24.

Razmotrimo sada pitanje zbrajanja beskonačne geometrijske progresije. Nazovimo djelomični zbroj dane beskonačne progresije zbrojem njegovih prvih članova. Označimo parcijalni zbroj simbolom

Za svaki beskonačni napredak

može se sastaviti (također beskonačan) niz njegovih parcijalnih suma

Neka niz s neograničenim porastom ima limit

U tom slučaju broj S, tj. limit parcijalnih zbrojeva neke progresije, nazivamo sumom beskonačne progresije. Dokazat ćemo da beskonačna padajuća geometrijska progresija uvijek ima zbroj, te ćemo izvesti formulu za taj zbroj (također možemo pokazati da ako beskonačni progres nema zbroj, ne postoji).

Napišimo izraz za parcijalni zbroj kao zbroj članova progresije pomoću formule (91.1) i razmotrimo granicu parcijalnog zbroja na

Iz teorema 89 poznato je da za padajuću progresiju; dakle, primjenom teorema granice razlike, nalazimo

(ovdje se također koristi pravilo: konstantni faktor se uzima iza znaka granice). Postojanje je dokazano, a ujedno je dobivena formula za zbroj beskonačno padajuće geometrijske progresije:

Jednakost (92.1) se također može napisati u obliku

Ovdje se može činiti paradoksalnim da iznos beskonačan broj pojmovima se dodjeljuje vrlo određena konačna vrijednost.

Za objašnjenje ove situacije može se dati jasna ilustracija. Razmotrimo kvadrat sa stranom jednako jedan(Slika 72). Ovaj kvadrat podijelite vodoravnom crtom na dva jednaka dijela i gornji dio Nanesite ga na donji tako da dobijete pravokutnik sa stranicama 2 i . Nakon toga, desnu polovicu ovog pravokutnika ponovno ćemo podijeliti na pola vodoravnom crtom i pričvrstiti gornji dio na donji (kao što je prikazano na slici 72). Nastavljajući ovaj proces, kontinuirano transformiramo izvorni kvadrat s površinom jednakom 1 u figure jednake veličine (poprimajući oblik stubišta sa tanjim stepenicama).

Beskonačnim nastavkom ovog procesa cjelokupna površina kvadrata se rastavlja na beskonačan broj članova - površine pravokutnika s bazama jednakim 1 i visinama. Površine pravokutnika upravo tvore beskonačnu opadajuću progresiju, njen zbroj

tj., kao što se i očekivalo, jednaka površini kvadrata.

Primjer. Pronađite zbrojeve sljedećih beskonačnih progresija:

Rješenje, a) Primjećujemo da je ova progresija Stoga, pomoću formule (92.2) nalazimo

b) Ovdje to znači da korištenjem iste formule (92.2) imamo

c) Nalazimo da ova progresija stoga nema zbroj.

U paragrafu 5. prikazana je primjena formule za zbroj članova beskonačno padajuće progresije na pretvorbu periodičkog decimalnog razlomka u obični razlomak.

Vježbe

1. Zbroj beskonačno padajuće geometrijske progresije je 3/5, a zbroj njezina prva četiri člana je 13/27. Pronađite prvi član i nazivnik progresije.

2. Nađite četiri broja koji čine izmjeničnu geometrijsku progresiju, u kojoj je drugi član manji od prvog za 35, a treći veći od četvrtog za 560.

3. Pokažite da ako niz

tvori beskonačno padajuću geometrijsku progresiju, zatim niz

za bilo koju, tvori beskonačno padajuću geometrijsku progresiju. Hoće li ova izjava vrijediti kada

Izvedite formulu za umnožak članova geometrijske progresije.

Geometrijska progresija je nova vrsta numerički niz s kojim ćemo se upoznati. Za uspješan spoj ne škodi barem znati i razumjeti. Tada neće biti problema s geometrijskom progresijom.)

Što je geometrijska progresija? Pojam geometrijske progresije.

Turu, kao i obično, započinjemo s osnovama. Zapisujem nedovršeni niz brojeva:

1, 10, 100, 1000, 10000, …

Možete li uočiti obrazac i reći koji će brojevi biti sljedeći? Papar je jasan, pa slijede brojke 100.000, 1.000.000 i tako dalje. Čak i bez puno mentalnog napora, sve je jasno, zar ne?)

U REDU. Još jedan primjer. Pišem ovaj niz:

1, 2, 4, 8, 16, …

Možete li reći koji će brojevi doći sljedeći nakon broja 16 i imena osmičlan niza? Ako ste shvatili da će to biti broj 128, onda vrlo dobro. Dakle, pola bitke je u razumijevanju osjećaj I ključne točke već je učinjena geometrijska progresija. Možete dalje rasti.)

A sada opet prelazimo sa senzacija na strogu matematiku.

Ključne točke geometrijske progresije.

Ključna točka #1

Geometrijska progresija je niz brojeva. Tako je i s progresijom. Ništa otmjeno. Samo ovaj niz je uređen različito. Stoga, naravno, ima drugačije ime, da...

Ključna točka #2

S drugom ključnom točkom, pitanje će biti kompliciranije. Vratimo se malo unatrag i prisjetimo se ključnog svojstva aritmetičke progresije. Evo ga: svaki član je drugačiji od prethodnog u istom iznosu.

Je li moguće formulirati slično ključno svojstvo za geometrijsku progresiju? Razmislite malo... Pažljivije pogledajte navedene primjere. Jeste li pogodili? Da! U geometrijskoj progresiji (bilo kojoj!) svaki njen član razlikuje se od prethodnog isto toliko puta. Stalno!

U prvom primjeru, ovaj broj je deset. Koji god član niza uzmete, veći je od prethodnog deset puta.

U drugom primjeru to je dvojka: svaki član je veći od prethodnog dvaput.

To je ključna točka po kojoj se geometrijska progresija razlikuje od aritmetičke progresije. U aritmetičkoj progresiji dobiva se svaki sljedeći član dodavanjem istu vrijednost u odnosu na prethodni izraz. I ovdje - množenje prethodnog roka za isti iznos. To je sva razlika.)

Ključna točka #3

Ova ključna točka potpuno je identična onoj za aritmetičku progresiju. Naime: Svaki član geometrijske progresije stoji na svom mjestu. Sve je potpuno isto kao u aritmetičkoj progresiji i komentari su, mislim, nepotrebni. Postoji prvi pojam, postoji sto prvi, itd. Zamijenimo barem dva pojma – uzorak (a s njim i geometrijska progresija) će nestati. Ono što će ostati je samo niz brojeva bez ikakve logike.

To je sve. To je cijela poanta geometrijske progresije.

Termini i oznake.

Ali sada, nakon što smo razumjeli značenje i ključne točke geometrijske progresije, možemo prijeći na teoriju. Inače, što je teorija bez razumijevanja značenja, zar ne?

Kako označiti geometrijsku progresiju?

Kako se piše geometrijska progresija opći pogled? Nema problema! Svaki član progresije također je napisan kao slovo. Samo za aritmetičku progresiju, obično se koristi slovo "A", za geometrijske – slov "b". Članski broj, kao i obično, naznačeno je indeks dolje desno. Jednostavno navodimo članove same progresije, odvojene zarezom ili točkom i zarezom.

Kao ovo:

b 1,b 2 , b 3 , b 4 , b 5 , b 6 , …

Ukratko, ova progresija se piše ovako: (b n) .

Ili ovako, za konačne progresije:

b 1, b 2, b 3, b 4, b 5, b 6.

b 1, b 2, …, b 29, b 30.

Ili, ukratko:

(b n), n=30 .

To je, zapravo, sva oznaka. Sve je isto, samo je slovo drugačije, da.) A sada prelazimo izravno na definiciju.

Definicija geometrijske progresije.

Geometrijska progresija je niz brojeva u kojem je prvi član različit od nule, a svaki sljedeći član jednak je prethodnom članu pomnoženom s istim brojem koji nije nula.

To je cijela definicija. Većina riječi i fraza vam je jasna i poznata. Ako, naravno, razumijete značenje geometrijske progresije "na prstima" i općenito. Ali postoji i nekoliko novih izraza na koje bih želio obratiti posebnu pozornost.

Prvo, riječi: „čiji je prvi član različit od nule".

Ovo ograničenje na prvi termin nije uvedeno slučajno. Što mislite da će se dogoditi ako prvi član b 1 će biti jednaka nuli? Čemu će biti jednak drugi član ako je svaki član veći od prethodnog? isti broj puta? Recimo tri puta? Da vidimo... Pomnožite prvi član (tj. 0) s 3 i dobit ćete... nulu! Što je s trećim članom? Također nula! I četvrti član je također nula! I tako dalje…

Dobivamo samo vrećicu peciva, niz nula:

0, 0, 0, 0, …

Naravno, takav niz ima pravo na život, ali nije od praktičnog interesa. Sve je jasno. Bilo koji njegov član je nula. Zbroj bilo kojeg broja članova također je nula... Što zanimljivo možete učiniti s njim? Ništa…

Sljedeće ključne riječi: "pomnoženo s istim brojem koji nije nula."

Ovaj isti broj ima i svoje posebno ime - nazivnik geometrijske progresije. Počnimo se upoznavati.)

Nazivnik geometrijske progresije.

Sve je jednostavno kao guljenje krušaka.

Nazivnik geometrijske progresije je broj različit od nule (ili količina) koji označava koliko putasvaki termin progresije više od prethodnog.

Opet, po analogiji s aritmetičkom progresijom, ključna riječ Ono na što treba obratiti pozornost u ovoj definiciji je riječ "više". To znači da je svaki član geometrijske progresije dobiven množenje upravo ovom nazivniku prethodni član.

Dopustite da objasnim.

Za izračunavanje, recimo drugi kurac, treba uzeti prvičlan i pomnožiti to na nazivnik. Za izračun deseti kurac, treba uzeti devetičlan i pomnožiti to na nazivnik.

Nazivnik same geometrijske progresije može biti bilo što. Apsolutno bilo tko! Cjelina, razlomak, pozitivno, negativno, iracionalno - sve. Osim nula. To je ono što nam govori riječ "ne-nula" u definiciji. Zašto je ova riječ potrebna ovdje - više o tome kasnije.

Nazivnik geometrijske progresije najčešće označen slovom q.

Kako ga pronaći q? Nema problema! Moramo uzeti bilo koji termin progresije i podijelite s prethodnim članom. Podjela je frakcija. Otuda naziv - "nazivnik progresije". Nazivnik, obično sjedi u razlomku, da...) Iako, logično, vrijednost q treba pozvati privatna geometrijska progresija, slično razlika za aritmetičku progresiju. Ali dogovorili smo se za poziv nazivnik. A nećemo ni izmišljati kotač.)

Definirajmo, na primjer, količinu q za ovu geometrijsku progresiju:

2, 6, 18, 54, …

Sve je elementarno. Uzmimo ga bilo koji redni broj. Uzimamo što god želimo. Osim onog prvog. Na primjer, 18. I podijelite sa prethodni broj. Naime, u 6.

Dobivamo:

q = 18/6 = 3

To je sve. Ovo je točan odgovor. Za ovu geometrijsku progresiju, nazivnik je tri.

Nađimo sada nazivnik q za drugu geometrijsku progresiju. Na primjer, ovaj:

1, -2, 4, -8, 16, …

Sve isto. Bez obzira kakve znakove imaju sami članovi, mi i dalje preuzimamo bilo koji broj niza (na primjer, 16) i podijelite s prethodni broj(tj. -8).

Dobivamo:

d = 16/(-8) = -2

I to je to.) Ovaj put je nazivnik progresije ispao negativan. Minus dva. Događa se.)

Uzmimo sada ovu progresiju:

1, 1/3, 1/9, 1/27, …

I opet, bez obzira na vrstu brojeva u nizu (jesu li cijeli brojevi, čak i razlomci, čak i negativni, čak i iracionalni), uzmemo bilo koji broj (npr. 1/9) i podijelimo s prethodnim brojem (1/3). Prema pravilima za rad s razlomcima, naravno.

Dobivamo:

To je sve.) Ovdje se pokazalo da je nazivnik razlomak: q = 1/3.

Što mislite o ovom "napretku"?

3, 3, 3, 3, 3, …

Očito ovdje q = 1 . Formalno, ovo je također geometrijska progresija, samo sa identični članovi.) Ali takve progresije su za proučavanje i praktična aplikacija Ne zainteresiran. Isto kao progresije s čvrstim nulama. Stoga ih nećemo razmatrati.

Kao što vidite, nazivnik progresije može biti bilo što - cijeli broj, razlomak, pozitivan, negativan - bilo što! Ne može biti samo nula. Ne možete pogoditi zašto?

Pa, idemo na neke konkretan primjer Pogledajmo što će se dogoditi ako ga uzmemo kao nazivnik q nula.) Neka nam je npr b 1 = 2 , A q = 0 . Čemu će onda biti jednak drugi član?

Mi računamo:

b 2 = b 1 · q= 2 0 = 0

Što je s trećim članom?

b 3 = b 2 · q= 0 0 = 0

Vrste i ponašanje geometrijskih progresija.

Sve je bilo više-manje jasno: ako je progresija razlika d je pozitivan, tada se progresija povećava. Ako je razlika negativna, progresija se smanjuje. Postoje samo dvije mogućnosti. Trećeg nema.)

Ali s ponašanjem geometrijske progresije, sve će biti mnogo zanimljivije i raznovrsnije!)

Bez obzira na to kako se članovi ovdje ponašaju: oni rastu, i opadaju, i neograničeno se približavaju nuli, pa čak i mijenjaju predznake, naizmjenično se bacajući u “plus” pa u “minus”! I u svoj toj raznolikosti treba znati dobro razumjeti, da...

Hajde da to shvatimo?) Počnimo s najjednostavnijim slučajem.

Nazivnik je pozitivan ( q >0)

S pozitivnim nazivnikom, prvo, mogu ići članovi geometrijske progresije plus beskonačnost(tj. povećati bez ograničenja) i može ići u minus beskonačnost(tj. smanjivati ​​bez ograničenja). Već smo navikli na ovakvo ponašanje progresija.

Na primjer:

(b n): 1, 2, 4, 8, 16, …

Ovdje je sve jednostavno. Dobiven je svaki član progresije više od prethodnog. Štoviše, svaki izraz ispada množenje prethodni član na pozitivan broj +2 (tj. q = 2 ). Ponašanje takve progresije je očito: svi članovi progresije rastu neograničeno, odlazeći u svemir. Plus beskonačnost...

A sada evo napredovanja:

(b n): -1, -2, -4, -8, -16, …

Ovdje se također dobiva svaki član progresije množenje prethodni član na pozitivan broj +2. Ali ponašanje takve progresije je upravo suprotno: svaki član progresije je dobiven manje od prethodnog, a svi njegovi članovi opadaju bez ograničenja, idući do minus beskonačnosti.

Sada razmislimo: što ove dvije progresije imaju zajedničko? Tako je, nazivnik! Tu i tamo q = +2 . Pozitivan broj. Dva. I ovdje ponašanje Ove dvije progresije su bitno različite! Ne možete pogoditi zašto? Da! Sve je o prvi član! On je, kako kažu, taj koji zove melodiju.) Pogledajte sami.

U prvom slučaju, prvi član progresije pozitivan(+1) i, prema tome, svi sljedeći članovi dobiveni množenjem sa pozitivan nazivnik q = +2 , također će biti pozitivan.

Ali u drugom slučaju, prvi mandat negativan(-1). Stoga, svi sljedeći članovi progresije, dobiveni množenjem sa pozitivan q = +2 , također će se dobiti negativan. Jer "minus" na "plus" uvijek daje "minus", da.)

Kao što vidite, za razliku od aritmetičke progresije, geometrijska progresija može se ponašati potpuno drugačije ne samo ovisno o od nazivnikaq, ali i ovisno od prvog člana, da.)

Zapamtite: ponašanje geometrijske progresije jedinstveno je određeno njezinim prvim članom b 1 i nazivnikq .

A sada počinjemo analizirati manje poznate, ali mnogo zanimljivije slučajeve!

Uzmimo, na primjer, ovaj niz:

(b n): 1, 1/2, 1/4, 1/8, 1/16, …

Ovaj niz je također geometrijska progresija! Svaki član ove progresije također ispada množenje prethodni član, istim brojem. To je samo broj - razlomak: q = +1/2 . Ili +0,5 . Štoviše (važno!) broj manje od jednog:q = 1/2<1.

Zašto je ova geometrijska progresija zanimljiva? Kamo se kreću njegovi članovi? Pogledajmo:

1/2 = 0,5;

1/4 = 0,25;

1/8 = 0,125;

1/16 = 0,0625;

…….

Što zanimljivosti možete primijetiti ovdje? Prvo, odmah se uočava pad u progresiji: svaki njen član manje prethodni točno 2 puta. Ili, prema definiciji geometrijske progresije, svaki član više prethodni 1/2 puta, jer nazivnik progresije q = 1/2 . A kada se pomnoži s pozitivnim brojem manjim od jedan, rezultat se obično smanjuje, da...

Što više može se vidjeti u ponašanju ove progresije? Je li njezinih članova sve manje? neograničen, ide u minus beskonačno? Ne! Nestaju na poseban način. U početku se smanjuju prilično brzo, a zatim sve sporije. I dok ostaje cijelo vrijeme pozitivan. Iako vrlo, vrlo mali. A čemu oni sami teže? Niste pogodili? Da! Oni teže ka nuli!) Štoviše, obratite pažnju, članovi naše progresije su od nule nikad dosegnuti! Samo prilazeći mu beskrajno blizu. Vrlo je važno.)

Slična situacija dogodit će se u sljedećoj progresiji:

(b n): -1, -1/2, -1/4, -1/8, -1/16, …

Ovdje b 1 = -1 , A q = 1/2 . Sve je isto, samo će se sada termini približiti nuli s druge strane, odozdo. Ostati cijelo vrijeme negativan.)

Takva geometrijska progresija, čiji uvjeti pristup nuli bez ograničenja(bez obzira s pozitivne ili negativne strane), u matematici ima poseban naziv - beskonačno padajuća geometrijska progresija. Ova progresija je toliko zanimljiva i neobična da će se o njoj čak i raspravljati zasebna lekcija .)

Dakle, razmotrili smo sve moguće pozitivan nazivnici su i veliki i manji. Samu jedinicu ne smatramo nazivnikom iz gore navedenih razloga (sjetite se primjera s nizom trojki...)

Ukratko:

pozitivanI više od jednog (q>1), tada su uvjeti progresije:

a) povećavati bez ograničenja (akob 1 >0);

b) smanjivati ​​bez ograničenja (akob 1 <0).

Ako je nazivnik geometrijske progresije pozitivan I manje od jednog (0< q<1), то члены прогрессии:

a) beskonačno blizu nule iznad(Akob 1 >0);

b) približavajući se beskonačno blizu nuli Od ispod(Akob 1 <0).

Sada ostaje razmotriti slučaj negativni nazivnik.

Nazivnik je negativan ( q <0)

Nećemo ići daleko za primjerom. Zašto baš čupava baba?!) Neka je, na primjer, prvi član progresije b 1 = 1 , i uzmimo nazivnik q = -2.

Dobivamo sljedeći niz:

(b n): 1, -2, 4, -8, 16, …

I tako dalje.) Dobiva se svaki član progresije množenje prethodni član na negativan broj-2. U tom slučaju bit će svi članovi koji stoje na neparnim mjestima (prvi, treći, peti itd.). pozitivan, a na parnim mjestima (drugo, četvrto itd.) – negativan. Znakovi se strogo izmjenjuju. Plus-minus-plus-minus... Ova geometrijska progresija se zove - rastući predznak izmjenični.

Kamo se kreću njegovi članovi? Ali nigdje.) Da, u apsolutnoj vrijednosti (tj. modulo)članovi naše progresije povećavaju se bez ograničenja (otuda naziv "povećanje"). Ali istovremeno vas svaki član progresije naizmjenično baca u toplinu, pa u hladnoću. Ili "plus" ili "minus". Naša progresija se koleba... Štoviše, opseg fluktuacija brzo raste sa svakim korakom, da.) Dakle, težnje članova progresije nekamo idu posebno Ovdje Ne. Ni do plus beskonačno, ni do minus beskonačno, ni do nule – nigdje.

Razmotrimo sada neki razlomački nazivnik između nula i minus jedan.

Na primjer, neka bude b 1 = 1 , A q = -1/2.

Tada dobivamo progresiju:

(b n): 1, -1/2, 1/4, -1/8, 1/16, …

I opet imamo izmjenu znakova! Ali, za razliku od prethodnog primjera, ovdje već postoji jasna tendencija da se članovi približavaju nuli.) Samo što se ovaj put naši članovi približavaju nuli ne striktno odozgo ili odozdo, već opet oklijevajući. Naizmjenično uzimanje pozitivnih i negativnih vrijednosti. Ali u isto vrijeme oni moduli sve bliže i bliže željenoj nuli.)

Ova geometrijska progresija se zove beskonačno opadajući znak, izmjenični.

Zašto su ova dva primjera zanimljiva? I činjenica da se u oba slučaja odvija izmjena znakova! Ovaj trik je tipičan samo za progresije s negativnim nazivnikom, da.) Dakle, ako u nekom zadatku vidite geometrijsku progresiju s izmjeničnim članovima, već ćete sigurno znati da je njen nazivnik 100% negativan i nećete pogriješiti u znaku.)

Usput, u slučaju negativnog nazivnika, predznak prvog člana uopće ne utječe na ponašanje same progresije. Bez obzira na predznak prvog člana progresije, u svakom slučaju će se poštovati predznak članova. Jedino pitanje je, na kojim mjestima(parni ili neparni) postojat će članovi s određenim predznacima.

Zapamtiti:

Ako je nazivnik geometrijske progresije negativan , tada su znakovi uvjeta progresije uvijek naizmjenično.

Ujedno, sami članovi:

a) povećavati bez ograničenjamodulo, Akoq<-1;

b) beskonačno se približavati nuli ako je -1< q<0 (прогрессия бесконечно убывающая).

To je sve. Analizirani su svi tipični slučajevi.)

U procesu analize raznih primjera geometrijskih progresija, povremeno sam koristio riječi: "teži nuli", "teži plus beskonačno", "teži minus beskonačno"... U redu je.) Ove figure govora (i konkretni primjeri) samo su početni uvod u ponašanje niz nizova brojeva. Na primjeru geometrijske progresije.

Zašto uopće moramo znati ponašanje progresije? Kakve veze ima kamo ide? Prema nuli, do plus beskonačno, do minus beskonačno... Što nam to radi?

Stvar je u tome što će vam već na sveučilištu, na tečaju više matematike, trebati sposobnost rada s širokim spektrom numeričkih nizova (s bilo kojim, ne samo progresijama!) i sposobnost da točno zamislite kako ovaj ili onaj niz ponaša - raste li neograničeno opada, teži li određenom broju (a ne nužno nuli) ili čak ne teži baš ničemu... Ovoj je temi posvećen cijeli jedan dio u kolegiju matematike. analiza - teorija granica. I malo konkretnije – koncept granica niza brojeva. Jako zanimljiva tema! Ima smisla otići na fakultet i shvatiti to.)

Neki primjeri iz ovog odjeljka (nizovi koji imaju ograničenje), a posebno, beskonačno padajuća geometrijska progresija Počinju se navikavati u školi. Navikavamo se na to.)

Štoviše, sposobnost dobrog proučavanja ponašanja nizova uvelike će vam koristiti u budućnosti i bit će vrlo korisna u istraživanje funkcije. Najraznolikiji. Ali sposobnost kompetentnog rada s funkcijama (izračunavanje izvedenica, njihovo potpuno proučavanje, izrada njihovih grafikona) već dramatično povećava vašu matematičku razinu! Imate li kakvih nedoumica? Nema potrebe. Zapamtite i moje riječi.)

Pogledajmo geometrijsku progresiju u životu?

U životu koji nas okružuje vrlo često se susrećemo s geometrijskom progresijom. Čak ni ne znajući.)

Primjerice, razni mikroorganizmi koji nas posvuda okružuju u golemim količinama i koje ne možemo niti vidjeti bez mikroskopa razmnožavaju se upravo geometrijskom progresijom.

Recimo da se jedna bakterija razmnožava dijeljenjem na pola, dajući potomstvo u 2 bakterije. Zauzvrat, svaki od njih, kada se umnožava, također se dijeli na pola, dajući zajedničko potomstvo od 4 bakterije. Sljedeća generacija će proizvesti 8 bakterija, zatim 16 bakterija, 32, 64 i tako dalje. Sa svakom sljedećom generacijom broj bakterija se udvostručuje. Tipičan primjer geometrijske progresije.)

Također, neki insekti – lisne uši i muhe – množe se eksponencijalno. A ponekad i zečevi, usput.)

Drugi primjer geometrijske progresije, bliži svakodnevnom životu, je tzv zajednički interes. Ova zanimljiva pojava često se nalazi u bankovnim depozitima i tzv kapitalizacija kamata.Što je?

I sami ste, naravno, još mladi. Učiš u školi, ne ideš u banke. Ali vaši su roditelji već odrasli i samostalni ljudi. Idu na posao, zarađuju za kruh, a dio novca stavljaju u banku, štede.)

Recimo da vaš tata želi uštedjeti određenu količinu novca za obiteljski odmor u Turskoj i stavlja 50 000 rubalja u banku uz 10% godišnje na razdoblje od tri godine uz godišnju kapitalizaciju kamata.Štoviše, tijekom cijelog tog razdoblja ništa se ne može učiniti s depozitom. Ne možete nadopuniti depozit niti podići novac s računa. Koliko će dobiti nakon te tri godine?

Pa, prije svega, moramo shvatiti koliko je 10% godišnje. To znači da u godini Banka će dodati 10% na početni iznos depozita. Iz čega? Naravno, od početni iznos depozita.

Veličinu računa izračunavamo nakon godinu dana. Ako je početni iznos depozita bio 50 000 rubalja (tj. 100%), koliko će nakon godinu dana biti kamata na računu? Tako je, 110%! Od 50.000 rubalja.

Dakle, izračunavamo 110% od 50.000 rubalja:

50000·1,1 = 55000 rubalja.

Nadam se da razumijete da pronalaženje 110% vrijednosti znači množenje te vrijednosti s brojem 1,1? Ako vam nije jasno zašto je to tako, sjetite se petog i šestog razreda. Naime – povezanost između postotaka i razlomaka i dijelova.)

Dakle, povećanje za prvu godinu bit će 5000 rubalja.

Koliko će novca biti na računu za dvije godine? 60.000 rubalja? Nažalost (ili bolje rečeno, na sreću), sve nije tako jednostavno. Cijeli trik kapitalizacije kamata je u tome što će se sa svakim novim obračunavanjem kamata te iste kamate već uzeti u obzir od novog iznosa! Od onoga koji već je na računu Trenutno. A obračunate kamate za prethodno razdoblje zbrajaju se s prvobitnim iznosom depozita i tako sudjeluju u obračunu novih kamata! Odnosno, oni postaju puni dio ukupnog računa. Ili općenito glavni. Otuda naziv - kapitalizacija kamata.

To je u ekonomiji. A u matematici se takvi postoci nazivaju zajednički interes. Ili postotak kamata.) Njihov trik je da se kod uzastopnog računanja postoci izračunavaju svaki put od nove vrijednosti. I to ne iz originala...

Stoga, za izračun iznosa kroz dvije godine, moramo izračunati 110% iznosa koji će biti na računu u godini. Odnosno, već od 55.000 rubalja.

Računamo 110% od 55.000 rubalja:

55000·1,1 = 60500 rubalja.

To znači da će postotak povećanja za drugu godinu biti 5.500 rubalja, a za dvije godine - 10.500 rubalja.

Sada već možete pretpostaviti da će nakon tri godine iznos na računu biti 110% od 60 500 rubalja. To je opet 110% od prethodne (prošle godine) iznose.

Ovdje mislimo:

60500·1,1 = 66550 rubalja.

Sada raspoređujemo naše novčane iznose po godinama redom:

50000;

55000 = 50000 1,1;

60500 = 55000·1,1 = (50000·1,1)·1,1;

66550 = 60500 1,1 = ((50000 1,1) 1,1) 1,1

Pa kako je? Zašto ne geometrijska progresija? Prvi član b 1 = 50000 , i nazivnik q = 1,1 . Svaki član je striktno 1,1 puta veći od prethodnog. Sve je u strogom skladu s definicijom.)

I koliko će dodatnih bonusa na kamate "akumulirati" vaš tata dok njegovih 50.000 rubalja leži na bankovnom računu tri godine?

Mi računamo:

66550 – 50000 = 16550 rubalja

Ne puno, naravno. Ali to je ako je početni iznos depozita mali. Što ako ima više? Recimo, ne 50, nego 200 tisuća rubalja? Tada će povećanje tijekom tri godine biti 66 200 rubalja (ako izračunate). Što je već jako dobro.) Što ako je doprinos još veći? To je to...

Zaključak: što je veći početni depozit, kapitalizacija kamata postaje isplativija. Zato depozite s kapitalizacijom kamata banke daju na duge rokove. Recimo pet godina.

Također, sve vrste loših bolesti poput gripe, ospica i još strašnijih bolesti (isti SARS početkom 2000-ih ili kuga u srednjem vijeku) vole se širiti eksponencijalno. Otuda i razmjeri epidemija, da...) A sve zbog činjenice da geometrijska progresija s cijeli pozitivni nazivnik (q>1) – stvar koja jako brzo raste! Sjetite se razmnožavanja bakterija: od jedne bakterije dobiju se dvije, od dvije četiri, od četiri osam i tako dalje... Isto je i sa širenjem bilo koje infekcije.)

Najjednostavniji zadaci geometrijske progresije.

Počnimo, kao i uvijek, s jednostavnim problemom. Čisto da shvatim smisao.

1. Poznato je da je drugi član geometrijske progresije 6, a nazivnik -0,5. Pronađite prvi, treći i četvrti član.

Tako nam je dano beskrajan geometrijska progresija, ali poznata drugi termin ovaj napredak:

b 2 = 6

Osim toga, također znamo nazivnik progresije:

q = -0,5

I trebate pronaći prvi, treći I Četvrtačlanovi ove progresije.

Pa djelujemo. Zapisujemo niz prema uvjetima zadatka. Izravno u općem obliku, gdje je drugi član šest:

b 1, 6,b 3 , b 4 , …

Sada počnimo tražiti. Počinjemo, kao i uvijek, s najjednostavnijim. Možete izračunati, na primjer, treći član b 3? Limenka! Vi i ja već znamo (izravno u smislu geometrijske progresije) da treći član (b 3) više od drugog (b 2 ) V "q" jednom!

Pa pišemo:

b 3 =b 2 · q

Zamjenjujemo šest u ovaj izraz umjesto b 2 i -0,5 umjesto toga q i brojimo. A ne ignoriramo ni minus, naravno...

b 3 = 6·(-0,5) = -3

Kao ovo. Treći član ispao je negativan. Nije ni čudo: naš nazivnik q– negativno. A množenje plusa s minusom bit će, naravno, minus.)

Sada računamo sljedeći, četvrti član progresije:

b 4 =b 3 · q

b 4 = -3·(-0,5) = 1,5

Četvrti mandat opet je s plusom. Peti član će opet biti minus, šesti će biti plus, i tako dalje. Znakovi se izmjenjuju!

Dakle, pronađeni su treći i četvrti član. Rezultat je sljedeći niz:

b 1; 6; -3; 1,5; ...

Sada preostaje samo pronaći prvi član b 1 prema poznatoj drugoj. Da bismo to učinili, zakoračimo u drugom smjeru, ulijevo. To znači da u ovom slučaju ne trebamo pomnožiti drugi član progresije s nazivnikom, već podijeliti.

Podijelimo i dobijemo:

To je sve.) Odgovor na problem će biti ovakav:

-12; 6; -3; 1,5; …

Kao što vidite, princip rješenja je isti kao u . Znamo bilo kojičlan i nazivnik geometrijska progresija - možemo pronaći bilo koji drugi njezin član. Naći ćemo onu koju želimo.) Jedina razlika je u tome što je zbrajanje/oduzimanje zamijenjeno množenjem/dijeljenjem.

Zapamtite: ako znamo barem jedan član i nazivnik geometrijske progresije, tada uvijek možemo pronaći bilo koji drugi član ove progresije.

Sljedeći problem, prema tradiciji, dolazi iz prave verzije OGE-a:

2.

...; 150; X; 6; 1.2; ...

Pa kako je? Ovaj put nema prvog člana, nema nazivnika q, dan je samo niz brojeva... Nešto već poznato, zar ne? Da! Sličan problem već je riješen u aritmetičkoj progresiji!

Dakle, ne bojimo se. Sve isto. Obratimo se glavi i sjetimo se elementarnog značenja geometrijske progresije. Pažljivo gledamo naš niz i otkrivamo koji su parametri geometrijske progresije od tri glavna (prvi član, nazivnik, broj člana) skriveni u njemu.

Članski brojevi? Nema članskog broja, da... Ali ima ih četiri uzastopni brojevima. Ne vidim smisla objašnjavati što ova riječ znači u ovoj fazi.) Postoje li dva susjedni poznati brojevi? Jesti! To su 6 i 1.2. Tako da možemo pronaći nazivnik progresije. Dakle, uzimamo broj 1,2 i dijelimo na prethodni broj. Do šest.

Dobivamo:

Dobivamo:

x= 150·0,2 = 30

Odgovor: x = 30 .

Kao što vidite, sve je vrlo jednostavno. Glavna poteškoća je samo u izračunima. Posebno je teško u slučaju negativnih i razlomaka. Pa tko ima problema neka ponovi aritmetiku! Kako raditi s razlomcima, kako raditi s negativnim brojevima, i tako dalje... Inače ćete ovdje nemilosrdno usporiti.

Sada malo modificirajmo problem. Sada će postati zanimljivo! Uklonimo zadnji broj 1.2 iz njega. Sada riješimo ovaj problem:

3. Ispisano je nekoliko uzastopnih članova geometrijske progresije:

...; 150; X; 6; ...

Pronađite član progresije označen slovom x.

Sve je isto, samo dva susjedna poznati Sada nemamo članova progresije. To je glavni problem. Budući da veličina q kroz dva susjedna pojma možemo lako odrediti ne možemo. Imamo li šanse nositi se sa zadatkom? Sigurno!

Zapišimo nepoznati pojam " x"izravno u smislu geometrijske progresije! Općenito.

Da da! Pravo s nepoznatim nazivnikom!

S jedne strane, za X možemo napisati sljedeći omjer:

x= 150 ·q

S druge strane, imamo sva prava taj isti X opisati kroz Sljedećičlan, kroz šest! Podijelite šest s nazivnikom.

Kao ovo:

x = 6/ q

Očito, sada možemo izjednačiti oba ova omjera. Budući da izražavamo isto veličina (x), ali dva različiti putevi.

Dobivamo jednadžbu:

Množeći sve sa q, pojednostavljujući i skraćujući, dobivamo jednadžbu:

q2 = 1/25

Rješavamo i dobivamo:

q = ±1/5 = ±0,2

Ups! Nazivnik se pokazao dvostrukim! +0,2 i -0,2. A koji biste trebali odabrati? Slijepa ulica?

Smiriti! Da, problema stvarno ima dva rješenja! Ništa loše u tome. Događa se.) Niste iznenađeni kada, na primjer, dobijete dva korijena pri rješavanju uobičajenog problema? Ovdje je ista priča.)

Za q = +0,2 dobit ćemo:

X = 150 0,2 = 30

I za q = -0,2 htjeti:

X = 150·(-0,2) = -30

Dobivamo dvostruki odgovor: x = 30; x = -30.

Što znači ova zanimljiva činjenica? I što postoji dvije progresije, zadovoljavajući uvjete problema!

Kao ove:

…; 150; 30; 6; …

…; 150; -30; 6; …

Obje su prikladne.) Što mislite zašto smo imali podijeljene odgovore? Samo zbog eliminacije određenog člana progresije (1,2), koji dolazi nakon šest. A znajući samo prethodni (n-1)-ti i sljedeći (n+1)-ti član geometrijske progresije, ne možemo više ništa jednoznačno reći o n-tom članu koji stoji između njih. Postoje dvije opcije - s plusom i s minusom.

Ali nema problema. U pravilu, u zadacima geometrijske progresije postoje dodatne informacije koje daju nedvosmislen odgovor. Recimo riječi: "izmjenično napredovanje" ili "progresija s pozitivnim nazivnikom" i tako dalje... Upravo bi te riječi trebale poslužiti kao nagovještaj koji znak, plus ili minus, treba odabrati prilikom pripreme konačnog odgovora. Ako takvih informacija nema, onda da, zadatak će imati dva rješenja.)

Sada odlučujemo sami.

4. Utvrditi da li je broj 20 član geometrijske progresije:

4 ; 6; 9; …

5. Predznak izmjenične geometrijske progresije dan je:

…; 5; x ; 45; …

Pronađite termin progresije označen slovom x .

6. Nađite četvrti pozitivni član geometrijske progresije:

625; -250; 100; …

7. Drugi član geometrijske progresije jednak je -360, a njegov peti član jednak je 23,04. Pronađite prvi član ove progresije.

Odgovori (u neredu): -15; 900; Ne; 2.56.

Čestitamo ako je sve uspjelo!

Nešto ne štima? Negdje je postojao dvostruki odgovor? Pažljivo pročitajte uvjete zadatka!

Zadnji problem ne rješava? Tu nema ništa komplicirano.) Radimo izravno prema značenju geometrijske progresije. Pa, možete nacrtati sliku. Pomaže.)

Kao što vidite, sve je elementarno. Ako je progresija kratka. Što ako je dugo? Ili je broj potrebnih članova jako velik? Želio bih, po analogiji s aritmetičkom progresijom, nekako dobiti prikladnu formulu koja olakšava pronalaženje bilo kojičlan bilo koje geometrijske progresije po njegovom broju. Bez množenja mnogo, mnogo puta sa q. I postoji takva formula!) Detalji su u sljedećoj lekciji.

Lekcija i prezentacija na temu: "Brojevni nizovi. Geometrijska progresija"

Dodatni materijali
Dragi korisnici, ne zaboravite ostaviti svoje komentare, recenzije, želje! Svi materijali su provjereni antivirusnim programom.

Obrazovna pomagala i simulatori u Internet trgovini Integral za 9. razred
Potence i korijeni Funkcije i grafovi

Dečki, danas ćemo se upoznati s drugom vrstom progresije.
Tema današnje lekcije je geometrijska progresija.

Geometrijska progresija

Definicija. Brojčani niz u kojem je svaki član, počevši od drugog, jednak umnošku prethodnog i nekog fiksnog broja naziva se geometrijska progresija.
Definirajmo naš niz rekurzivno: $b_(1)=b$, $b_(n)=b_(n-1)*q$,
gdje su b i q određeni zadani brojevi. Broj q naziva se nazivnik progresije.

Primjer. 1,2,4,8,16... Geometrijska progresija u kojoj je prvi član jednak jedan, a $q=2$.

Primjer. 8,8,8,8... Geometrijska progresija u kojoj je prvi član jednak osam,
i $q=1$.

Primjer. 3,-3,3,-3,3... Geometrijska progresija u kojoj je prvi član jednak tri,
i $q=-1$.

Geometrijska progresija ima svojstva monotonije.
Ako $b_(1)>0$, $q>1$,
tada se niz povećava.
Ako $b_(1)>0$, $0 Niz se obično označava u obliku: $b_(1), b_(2), b_(3), ..., b_(n), ...$.

Kao i u aritmetičkoj progresiji, ako je u geometrijskoj progresiji broj elemenata konačan, tada se progresija naziva konačnom geometrijskom progresijom.

$b_(1), b_(2), b_(3), ..., b_(n-2), b_(n-1), b_(n)$.
Imajte na umu da ako je niz geometrijska progresija, onda je niz kvadrata članova također geometrijska progresija. U drugom nizu, prvi član je jednak $b_(1)^2$, a nazivnik je jednak $q^2$.

Formula za n-ti član geometrijske progresije

Geometrijska progresija također se može specificirati u analitičkom obliku. Pogledajmo kako to učiniti:
$b_(1)=b_(1)$.
$b_(2)=b_(1)*q$.
$b_(3)=b_(2)*q=b_(1)*q*q=b_(1)*q^2$.
$b_(4)=b_(3)*q=b_(1)*q^3$.
$b_(5)=b_(4)*q=b_(1)*q^4$.
Lako uočavamo obrazac: $b_(n)=b_(1)*q^(n-1)$.
Naša formula se zove "formula n-tog člana geometrijske progresije".

Vratimo se našim primjerima.

Primjer. 1,2,4,8,16... Geometrijska progresija u kojoj je prvi član jednak jedan,
i $q=2$.
$b_(n)=1*2^(n)=2^(n-1)$.

Primjer. 16,8,4,2,1,1/2… Geometrijska progresija u kojoj je prvi član jednak šesnaest, a $q=\frac(1)(2)$.
$b_(n)=16*(\frac(1)(2))^(n-1)$.

Primjer. 8,8,8,8... Geometrijska progresija u kojoj je prvi član jednak osam, a $q=1$.
$b_(n)=8*1^(n-1)=8$.

Primjer. 3,-3,3,-3,3... Geometrijska progresija u kojoj je prvi član jednak tri, a $q=-1$.
$b_(n)=3*(-1)^(n-1)$.

Primjer. Dana je geometrijska progresija $b_(1), b_(2), …, b_(n), … $.
a) Poznato je da je $b_(1)=6, q=3$. Pronađite $b_(5)$.
b) Poznato je da je $b_(1)=6, q=2, b_(n)=768$. Pronađite n.
c) Poznato je da je $q=-2, b_(6)=96$. Pronađite $b_(1)$.
d) Poznato je da je $b_(1)=-2, b_(12)=4096$. Nađi q.

Riješenje.
a) $b_(5)=b_(1)*q^4=6*3^4=486$.
b) $b_n=b_1*q^(n-1)=6*2^(n-1)=768$.
$2^(n-1)=\frac(768)(6)=128$, budući da je $2^7=128 => n-1=7; n=8$.
c) $b_(6)=b_(1)*q^5=b_(1)*(-2)^5=-32*b_(1)=96 => b_(1)=-3$.
d) $b_(12)=b_(1)*q^(11)=-2*q^(11)=4096 => q^(11)=-2048 => q=-2$.

Primjer. Razlika između sedmog i petog člana geometrijske progresije je 192, a zbroj petog i šestog člana progresije je 192. Nađite deseti član ove progresije.

Riješenje.
Znamo da je: $b_(7)-b_(5)=192$ i $b_(5)+b_(6)=192$.
Također znamo: $b_(5)=b_(1)*q^4$; $b_(6)=b_(1)*q^5$; $b_(7)=b_(1)*q^6$.
Zatim:
$b_(1)*q^6-b_(1)*q^4=192$.
$b_(1)*q^4+b_(1)*q^5=192$.
Dobili smo sustav jednadžbi:
$\begin(cases)b_(1)*q^4(q^2-1)=192\\b_(1)*q^4(1+q)=192\end(cases)$.
Izjednačavanjem naših jednadžbi dobivamo:
$b_(1)*q^4(q^2-1)=b_(1)*q^4(1+q)$.
$q^2-1=q+1$.
$q^2-q-2=0$.
Dobili smo dva rješenja q: $q_(1)=2, q_(2)=-1$.
Zamijenite redom u drugu jednadžbu:
$b_(1)*2^4*3=192 => b_(1)=4$.
$b_(1)*(-1)^4*0=192 =>$ nema rješenja.
Dobili smo da je: $b_(1)=4, q=2$.
Nađimo deseti član: $b_(10)=b_(1)*q^9=4*2^9=2048$.

Zbroj konačne geometrijske progresije

Neka imamo konačnu geometrijsku progresiju. Izračunajmo, baš kao i za aritmetičku progresiju, zbroj njenih članova.

Neka je dana konačna geometrijska progresija: $b_(1),b_(2),…,b_(n-1),b_(n)$.
Uvedimo oznaku za zbroj njegovih članova: $S_(n)=b_(1)+b_(2)+⋯+b_(n-1)+b_(n)$.
U slučaju kada je $q=1$. Svi članovi geometrijske progresije jednaki su prvom članu, onda je očito $S_(n)=n*b_(1)$.
Razmotrimo sada slučaj $q≠1$.
Pomnožimo gornji iznos s q.
$S_(n)*q=(b_(1)+b_(2)+⋯+b_(n-1)+b_(n))*q=b_(1)*q+b_(2)*q+⋯ +b_(n-1)*q+b_(n)*q=b_(2)+b_(3)+⋯+b_(n)+b_(n)*q$.
Bilješka:
$S_(n)=b_(1)+(b_(2)+⋯+b_(n-1)+b_(n))$.
$S_(n)*q=(b_(2)+⋯+b_(n-1)+b_(n))+b_(n)*q$.

$S_(n)*q-S_(n)=(b_(2)+⋯+b_(n-1)+b_(n))+b_(n)*q-b_(1)-(b_(2 )+⋯+b_(n-1)+b_(n))=b_(n)*q-b_(1)$.

$S_(n)(q-1)=b_(n)*q-b_(1)$.

$S_(n)=\frac(b_(n)*q-b_(1))(q-1)=\frac(b_(1)*q^(n-1)*q-b_(1)) (q-1)=\frac(b_(1)(q^(n)-1))(q-1)$.

$S_(n)=\frac(b_(1)(q^(n)-1))(q-1)$.

Dobili smo formulu za zbroj konačne geometrijske progresije.

Primjer.
Pronađite zbroj prvih sedam članova geometrijske progresije čiji je prvi član 4, a nazivnik 3.

Riješenje.
$S_(7)=\frac(4*(3^(7)-1))(3-1)=2*(3^(7)-1)=4372$.

Primjer.
Pronađite peti član geometrijske progresije koji je poznat: $b_(1)=-3$; $b_(n)=-3072$; $S_(n)=-4095$.

Riješenje.
$b_(n)=(-3)*q^(n-1)=-3072$.
$q^(n-1)=1024$.
$q^(n)=1024q$.

$S_(n)=\frac(-3*(q^(n)-1))(q-1)=-4095$.
$-4095(q-1)=-3*(q^(n)-1)$.
$-4095(q-1)=-3*(1024q-1)$.
$1365q-1365=1024q-1$.
$341q=$1364.
$q=4$.
$b_5=b_1*q^4=-3*4^4=-3*256=-768$.

Karakteristično svojstvo geometrijske progresije

Ljudi, data je geometrijska progresija. Pogledajmo njegova tri uzastopna člana: $b_(n-1),b_(n),b_(n+1)$.
Mi to znamo:
$\frac(b_(n))(q)=b_(n-1)$.
$b_(n)*q=b_(n+1)$.
Zatim:
$\frac(b_(n))(q)*b_(n)*q=b_(n)^(2)=b_(n-1)*b_(n+1)$.
$b_(n)^(2)=b_(n-1)*b_(n+1)$.
Ako je progresija konačna, tada ova jednakost vrijedi za sve članove osim za prvi i posljednji.
Ako se unaprijed ne zna kakav oblik niz ima, ali se zna da je: $b_(n)^(2)=b_(n-1)*b_(n+1)$.
Tada možemo sa sigurnošću reći da je ovo geometrijska progresija.

Brojevni niz je geometrijska progresija samo kada je kvadrat svakog člana jednak umnošku dvaju susjednih članova progresije. Ne zaboravite da za konačnu progresiju ovaj uvjet nije zadovoljen za prvi i zadnji član.

Pogledajmo ovaj identitet: $\sqrt(b_(n)^(2))=\sqrt(b_(n-1)*b_(n+1))$.
$|b_(n)|=\sqrt(b_(n-1)*b_(n+1))$.
$\sqrt(a*b)$ naziva se prosjek geometrijski brojevi a i b.

Modul bilo kojeg člana geometrijske progresije jednak je geometrijskoj sredini njegova dva susjedna člana.

Primjer.
Nađite x tako da je $x+2; 2x+2; 3x+3$ bila su tri uzastopna člana geometrijske progresije.

Riješenje.
Iskoristimo karakteristično svojstvo:
$(2x+2)^2=(x+2)(3x+3)$.
$4x^2+8x+4=3x^2+3x+6x+6$.
$x^2-x-2=0$.
$x_(1)=2$ i $x_(2)=-1$.
Zamijenimo naša rješenja redom u izvorni izraz:
Uz $x=2$ dobili smo niz: 4;6;9 – geometrijska progresija uz $q=1,5$.
Za $x=-1$, dobivamo niz: 1;0;0.
Odgovor: $x=2.$

Problemi koje treba samostalno riješiti

1. Pronađite osmi prvi član geometrijske progresije 16;-8;4;-2….
2. Pronađite deseti član geometrijske progresije 11,22,44….
3. Poznato je da je $b_(1)=5, q=3$. Pronađite $b_(7)$.
4. Poznato je da je $b_(1)=8, q=-2, b_(n)=512$. Pronađite n.
5. Nađi zbroj prvih 11 članova geometrijske progresije 3;12;48….
6. Nađite x tako da je $3x+4; 2x+4; x+5$ su tri uzastopna člana geometrijske progresije.