Protozoaires équations trigonométriques sont généralement résolus à l’aide de formules. Permettez-moi de vous rappeler que les équations trigonométriques les plus simples sont :

sinx = un

cosx = un

tgx = un

ctgx = un

x est l'angle à trouver,
a est n’importe quel nombre.

Et voici les formules avec lesquelles vous pouvez immédiatement écrire les solutions de ces équations les plus simples.

Pour le sinus :

Pour le cosinus :

x = ± arccos a + 2π n, n ∈ Z

Pour la tangente :

x = arctan a + π n, n ∈ Z

Pour la cotangente :

x = arcctg a + π n, n ∈ Z

En fait, c'est ça partie théorique résoudre des équations trigonométriques simples. D'ailleurs, tout !) Rien du tout. Cependant, le nombre d’erreurs sur ce sujet est tout simplement hors du commun. Surtout si l'exemple s'écarte légèrement du modèle. Pourquoi?

Oui, parce que beaucoup de gens écrivent ces lettres, sans en comprendre du tout le sens ! Il écrit avec prudence, de peur que quelque chose n'arrive...) Il faut régler ce problème. Trigonométrie pour les gens, ou gens pour la trigonométrie, après tout !?)

Voyons ça ?

Un angle sera égal à arccos un, deuxième: -arccos a.

Et cela fonctionnera toujours ainsi. Pour toute UN.

Si vous ne me croyez pas, passez votre souris sur l'image ou touchez l'image sur votre tablette.) J'ai changé le numéro UN à quelque chose de négatif. Quoi qu'il en soit, nous avons un coin arccos un, deuxième: -arccos a.

Par conséquent, la réponse peut toujours s’écrire sous la forme de deux séries de racines :

x 1 = arccos a + 2π n, n ∈ Z

x 2 = - arccos a + 2π n, n ∈ Z

Combinons ces deux séries en une seule :

x= ± arccos a + 2π n, n ∈ Z

Et c'est tout. A obtenu formule générale pour résoudre l'équation trigonométrique la plus simple avec cosinus.

Si vous comprenez qu'il ne s'agit pas d'une sorte de sagesse superscientifique, mais juste une version abrégée de deux séries de réponses, Vous serez également capable de gérer les tâches « C ». Avec des inégalités, avec une sélection de racines dans un intervalle donné... Là, la réponse avec un plus/moins ne fonctionne pas. Mais si vous traitez la réponse de manière pragmatique et la divisez en deux réponses distinctes, tout sera résolu.) En fait, c’est pourquoi nous l’examinons. Quoi, comment et où.

Dans l'équation trigonométrique la plus simple

sinx = un

on obtient également deux séries de racines. Toujours. Et ces deux séries peuvent aussi être enregistrées en une seule ligne. Seule cette ligne sera plus délicate :

x = (-1) n arcsin a + π n, n ∈ Z

Mais l’essence reste la même. Les mathématiciens ont simplement conçu une formule pour créer une entrée au lieu de deux pour une série de racines. C'est tout!

Vérifions les mathématiciens ? Et on ne sait jamais...)

Dans la leçon précédente, la solution (sans aucune formule) d'une équation trigonométrique avec sinus a été discutée en détail :

La réponse a abouti à deux séries de racines :

x 1 = π /6 + 2π n, n ∈ Z

x 2 = 5π /6 + 2π n, n ∈ Z

Si nous résolvons la même équation en utilisant la formule, nous obtenons la réponse :

x = (-1) n arcsin 0,5 + π n, n ∈ Z

En fait, c'est une réponse inachevée.) L'étudiant doit savoir que arcsin 0,5 = π /6. La réponse complète serait :

x = (-1)n π /6+ π n, n ∈ Z

Cela soulève une question intéressante. Répondre via x1 ; x2 (c'est la bonne réponse !) et par la solitude X (et c'est la bonne réponse !) - est-ce la même chose ou pas ? Nous le découvrirons maintenant.)

Nous remplaçons la réponse par x1 valeurs n =0; 1; 2 ; etc., on compte, on obtient une série de racines :

x 1 = π/6 ; 13π/6 ; 25π/6 et ainsi de suite.

Avec la même substitution en réponse avec x2 , on a:

x2 = 5π/6 ; 17π/6 ; 29π/6 et ainsi de suite.

Maintenant, remplaçons les valeurs n (0 ; 1 ; 2 ; 3 ; 4...) dans la formule générale pour un seul X . C'est-à-dire que nous élevons moins un à la puissance zéro, puis à la première, à la seconde, etc. Eh bien, bien sûr, nous remplaçons 0 dans le deuxième terme ; 1; 2 3 ; 4, etc Et nous comptons. On obtient la série :

X = π/6 ; 5π/6 ; 13π/6 ; 17π/6 ; 25π/6 et ainsi de suite.

C'est tout ce que vous pouvez voir.) La formule générale nous donne exactement les mêmes résultats tout comme les deux réponses séparément. Juste tout à la fois, dans l'ordre. Les mathématiciens n'étaient pas dupes.)

Les formules de résolution d'équations trigonométriques avec tangente et cotangente peuvent également être vérifiées. Mais nous ne le ferons pas.) Ils sont déjà simples.

J'ai écrit toutes ces substitutions et vérifications spécifiquement. Il est important de comprendre une chose ici Chose simple: il existe des formules pour résoudre des équations trigonométriques élémentaires, juste un bref résumé des réponses. Pour cette brièveté, nous avons dû insérer plus/moins dans la solution cosinus et (-1) n dans la solution sinus.

Ces inserts ne gênent en rien les tâches où il suffit d'écrire la réponse à une équation élémentaire. Mais si vous avez besoin de résoudre une inégalité, ou si vous devez faire quelque chose avec la réponse : sélectionner des racines sur un intervalle, vérifier l'ODZ, etc., ces insertions peuvent facilement déstabiliser une personne.

Donc qu'est ce que je devrais faire? Oui, soit écrivez la réponse en deux séries, soit résolvez l'équation/inégalité à l'aide du cercle trigonométrique. Ensuite ces insertions disparaissent et la vie devient plus facile.)

Nous pouvons résumer.

Pour résoudre les équations trigonométriques les plus simples, il existe des formules de réponse toutes faites. Quatre pièces. Ils sont parfaits pour écrire instantanément la solution d’une équation. Par exemple, vous devez résoudre les équations :

sinx = 0,3

Facilement: x = (-1) n arcsin 0,3 + π n, n ∈ Z

cosx = 0,2

Aucun problème: x = ± arccos 0,2 + 2π n, n ∈ Z

tgx = 1,2

Facilement: x = arctan 1,2 + π n, n ∈ Z

ctgx = 3,7

Un dernier: x= arcctg3,7 + π n, n ∈ Z

cosx = 1,8

Si vous, brillant de connaissances, écrivez instantanément la réponse :

x= ± arccos 1,8 + 2π n, n ∈ Z

alors tu brilles déjà, ceci... cela... d'une flaque d'eau.) Bonne réponse : il n'y a pas de solutions. Vous ne comprenez pas pourquoi ? Lisez ce qu'est l'arc cosinus. De plus, si sur le côté droit de l'équation d'origine se trouvent les valeurs tabulaires du sinus, du cosinus, de la tangente, de la cotangente, - 1; 0; √3; 1/2; √3/2 et ainsi de suite. - la réponse à travers les arches sera inachevée. Les arches doivent être converties en radians.

Et si vous rencontrez des inégalités, comme

alors la réponse est :

x πn, n ∈ Z

il y a des bêtises rares, oui...) Ici, vous devez cercle trigonométrique décider. Ce que nous ferons dans le sujet correspondant.

Pour ceux qui lisent héroïquement ces lignes. Je ne peux tout simplement pas m’empêcher d’apprécier vos efforts titanesques. Bonus pour vous.)

Prime:

Lorsqu'ils écrivent des formules dans une situation de combat alarmante, même les nerds chevronnés ne savent souvent pas où πn, Et où 2πn. Voici une astuce simple pour vous. Dans tout le monde des formules qui valent πn. Sauf pour la seule formule avec arc cosinus. Il est là 2πn. Deux panne. Mot-clé - deux. Dans cette même formule il y a deux signe au début. Plus et moins. Ici et là - deux.

Alors si tu écris deux signe avant l'arc cosinus, c'est plus facile de se rappeler ce qui va se passer à la fin deux panne. Et cela se produit aussi dans l'autre sens. La personne manquera le signe ± , arrive à la fin, écrit correctement deux Pien, et il reprendra ses esprits. Il y a quelque chose à venir deux signe! La personne reviendra au début et corrigera l’erreur ! Comme ça.)

Si vous aimez ce site...

Au fait, j'ai quelques autres sites intéressants pour vous.)

Vous pouvez vous entraîner à résoudre des exemples et découvrir votre niveau. Test avec vérification instantanée. Apprenons - avec intérêt !)

Vous pouvez vous familiariser avec les fonctions et les dérivées.

équation du cosX = UN

Chaque racine de l'équation

parce que X = UN (1)

peut être considéré comme l'abscisse d'un point d'intersection de la sinusoïde y = cosX avec une ligne droite y =UN , et, à l'inverse, l'abscisse de chacun de ces points d'intersection est l'une des racines de l'équation (1). Ainsi, l'ensemble de toutes les racines de l'équation (1) coïncide avec l'ensemble des abscisses de tous les points d'intersection de l'onde cosinusoïdale y = cosX avec une ligne droite y = UN .

Si | UN| >1 , alors le cosinus y = cosX ne coupe pas une ligne y = UN .

Dans ce cas, l’équation (1) n’a pas de racines.

À |UN| < 1 il existe une infinité de points d'intersection.

pour un > 0

pour un< 0.

Nous diviserons tous ces points d’intersection en deux groupes :

A -2 , A - 1 , A 1 , A 2 , ... ,

B -2 , B - 1 , B 1 , B 2 , ... ,

Point UN a une abscisse arccos UN , et tous les autres points du premier groupe en sont séparés par des distances multiples de 2 π

arccos un+ 2k π . (2)

Point DANS, comme on peut facilement le comprendre à partir des figures, a pour abscisse - arccosUN , et tous les autres points du deuxième groupe en sont supprimés à des distances multiples de 2 π . Leurs abscisses sont donc exprimées par

arccos UN+ 2nπ . (3)

Ainsi, l'équation (1) comporte deux groupes de racines définis par les formules (2) et (3). Mais ces deux formules peuvent évidemment s’écrire comme une seule formule

X = ± arccos un+ 2m π , (4)

Où m parcourt tous les entiers (m = 0, ±1, ±2, ±3, ...).

Le raisonnement que nous avons effectué pour dériver cette formule n’est correct que si
| un| =/= 1. Cependant, formellement la relation (4) détermine toutes les racines de l'équation parce quex=une et à | UN| =1. (Prouvez-le !) Nous pouvons donc dire que la formule (4) donne toutes les racines de l'équation (1) pour toutes les valeurs UN , Si seulement |UN| < 1 .

Mais toujours dans trois cas particuliers ( UN = 0, UN = -1, UN= +1) nous recommandons de ne pas utiliser la formule (4) , mais utilisez d'autres relations. Il est utile de rappeler que les racines de l’équation parce que X = 0 sont donnés par la formule

X = π / 2 +n π ; (5)

racines de l'équation parce que X = -1 sont donnés par la formule

X = π + 2m π ; (6)

et enfin, les racines de l'équation parce que X = 1 sont donnés par la formule

X = 2m π ; (7)

En conclusion, notons que les formules (4) , (5), (6) et (7) ne sont corrects que dans l'hypothèse où l'angle souhaité X exprimé en radians. Si cela est exprimé en degrés, alors ces formules doivent naturellement être modifiées. Donc la formule (4) devrait être remplacé par la formule

X = ± arccos un+ 360°n,

formule (5) formule

X = 90° + 180°n etc.

Centré en un point UN.
α - angle exprimé en radians.

Définition
Sinus (sin α) est une fonction trigonométrique dépendant de l'angle α entre l'hypoténuse et la jambe triangle rectangle, égal au rapport longueur du côté opposé |BC| à la longueur de l'hypoténuse |AC|.

Cosinus (cos α) est une fonction trigonométrique dépendant de l'angle α entre l'hypoténuse et la branche d'un triangle rectangle, égal au rapport de la longueur de la branche adjacente |AB| à la longueur de l'hypoténuse |AC|.

Notations acceptées

;
;
.

;
;
.

Graphique de la fonction sinus, y = sin x

Graphique de la fonction cosinus, y = cos x

Propriétés du sinus et du cosinus

Périodicité

Fonctions y = péché x et y = parce que x périodique avec période 2π.

Parité

La fonction sinusoïdale est étrange. La fonction cosinus est paire.

Domaine de définition et valeurs, extrema, augmentation, diminution

Les fonctions sinus et cosinus sont continues dans leur domaine de définition, c'est-à-dire pour tout x (voir preuve de continuité). Leurs principales propriétés sont présentées dans le tableau (n - entier).

	y = péché x	y = parce que x
Portée et continuité	- ∞ < x < + ∞	- ∞ < x < + ∞
Plage de valeurs	-1 ≤ y ≤ 1	-1 ≤ y ≤ 1
En augmentant
Descendant
Maxima, y ​​​​= 1
Minima, y ​​​​= - 1
Des zéros, y = 0
Intercepter les points avec l'axe des ordonnées, x = 0	y = 0	y = 1

Formules de base

Somme des carrés du sinus et du cosinus

Formules pour le sinus et le cosinus à partir de la somme et de la différence

;
;

Formules pour le produit des sinus et des cosinus

Formules de somme et de différence

Exprimer le sinus par le cosinus

;
;
;
.

Exprimer le cosinus par le sinus

;
;
;
.

Expression par tangente

; .

Quand nous avons:
; .

À :
; .

Tableau des sinus et cosinus, tangentes et cotangentes

Ce tableau montre les valeurs des sinus et des cosinus pour certaines valeurs de l'argument.

Expressions via des variables complexes

;

La formule d'Euler

Expressions via des fonctions hyperboliques

;
;

Dérivés

; . Formules dérivées > > >

Dérivées du nième ordre :
{ -∞ < x < +∞ }

Sécant, cosécant

Fonctions inverses

Fonctions inverses au sinus et au cosinus sont respectivement l'arc sinus et l'arc cosinus.

Arc sinus, arc sinus

Arccosinus, arccos

Les références:
DANS. Bronstein, KA (2004). Semendyaev, Manuel de mathématiques pour ingénieurs et étudiants, « Lan », 2009.

Les équations trigonométriques les plus simples sont les équations

Cos (x) = a, sin (x) = a, tg (x) = a, ctg (x) = a

Équation cos(x) = a

Explication et justification

1. Racines équations cosx= une. Quand | un | > 1 l'équation n'a pas de racines, puisque | cosx |< 1 для любого x (прямая y = а при а >1 ou à un< -1 не пересекает график функцииy = cosx).

Laissez | un |< 1. Тогда прямая у = а пересекает график функции

y = cosx. Sur l'intervalle, la fonction y = cos x décroît de 1 à -1. Mais une fonction décroissante ne prend chacune de ses valeurs qu'en un point de son domaine de définition, donc l'équation cos x = a n'a qu'une seule racine sur cet intervalle, qui, par définition d'arccosinus, est égale à : x 1 = arccos a (et pour cette racine cos x = A).

Cosinus - même fonction, donc sur l'intervalle [-n; 0] l'équation cos x = et n'a également qu'une seule racine - le nombre opposé x 1, c'est-à-dire

x 2 = -arccos a.

Ainsi, sur l'intervalle [-n; p] (longueur 2p) équation cos x = a avec | un |< 1 имеет только корни x = ±arccos а.

La fonction y = cos x est périodique de période 2n, donc toutes les autres racines diffèrent de celles trouvées par 2n (n € Z). On obtient la formule suivante pour les racines de l'équation cos x = a lorsque

x = ±arccos a + 2pp, n £ Z.

1. Cas particuliers de résolution de l'équation cosx = a.

Il est utile de se rappeler des notations spéciales pour les racines de l'équation cos x = a lorsque

a = 0, a = -1, a = 1, qui peut être facilement obtenu en utilisant le cercle unité comme référence.

Puisque le cosinus est égal à l'abscisse du point correspondant cercle unitaire, on obtient que cos x = 0 si et seulement si le point correspondant du cercle unité est le point A ou le point B.

De même, cos x = 1 si et seulement si le point correspondant du cercle unité est le point C, donc,

x = 2πп, k € Z.

Aussi cos x = -1 si et seulement si le point correspondant du cercle unité est le point D, donc x = n + 2n,

Équation sin(x) = a

Explication et justification

1. Racines équations sinx= une. Quand | un | > 1 l'équation n'a pas de racines, puisque | péché |< 1 для любого x (прямая y = а на рисунке при а >1 ou à un< -1 не пересекает график функции y = sinx).

Zakharova Lyudmila Vladimirovna
MBOU "Secondaire" école polyvalente N° 59" Barnaoul
professeur de mathématiques [email protégé]

№1 Les équations trigonométriques les plus simples

Cible: 1. Dériver des formules pour les solutions des équations trigonométriques les plus simples de la forme sinx = une, cosx = une, tgx = une, ctgx = une;

2. Apprenez à résoudre des équations trigonométriques simples à l'aide de formules.

Équipement: 1) Tableaux avec graphiques fonctions trigonométriques y= sinx, y=cosx, y=tgx, y=ctgx; 2) Tableau des valeurs des fonctions trigonométriques inverses ; 3) Tableau récapitulatif des formules pour résoudre des équations trigonométriques simples.

Plan de cours:

1 .Dérivation de formules pour les racines de l'équation

une) sinx = une,

b) cosx= un,

c) tgx= un,

d) ctgx= UN.

2 . Travail frontal oral pour consolider les formules reçues.

3 . Formalités administratives consolider le matériel étudié

Pendant les cours.

En algèbre, en géométrie, en physique et dans d'autres matières, nous sommes confrontés à une variété de problèmes dont la solution implique la résolution d'équations. Nous avons étudié les propriétés des fonctions trigonométriques, il est donc naturel de se tourner vers des équations dans lesquelles l'inconnue est contenue sous le signe de la fonction

Définition: Équations de la forme péché = un , cosx= un , tgx= un , ctgx= UN sont appelées les équations trigonométriques les plus simples.

Il est très important d'apprendre à résoudre les équations trigonométriques les plus simples, car toutes les méthodes et techniques de résolution de toute équation trigonométrique consistent à les réduire au plus simple.

Commençons par dériver des formules qui fonctionnent « activement » lors de la résolution d'équations trigonométriques.

1.Équations de la forme sinx = un.

Résolvons l'équation sinx = un graphiquement. Pour ce faire, dans un système de coordonnées nous construirons des graphiques des fonctions y=sinx et y= UN.

1) Si UN> 1 et UN péché x= UN n'a pas de solutions, puisque la droite et la sinusoïde n'ont pas de points communs.

2) Si -1a a traverse l'onde sinusoïdale une infinité de fois. Cela signifie que l'équation péchéx= un a une infinité de solutions.

Puisque la période du sinus est de 2 , puis résoudre l'équation péchéx= un il suffit de trouver toutes les solutions sur n'importe quel segment de longueur 2.

Résoudre l'équation sur [-/2; /2] par définition de l'arc sinus x= arcsin un, et sur x=-arcsin un. Compte tenu de la périodicité de la fonction у=sinx, on obtient les expressions suivantes

x = -arcsin un+2n, nZ.

Les deux séries de solutions peuvent être combinées

X = (-1) n arc sinus un+n, nZ.

Dans les trois cas suivants, ils préfèrent utiliser des relations plus simples plutôt qu’une formule générale :

Si UN=-1, alors sin x =-1, x=-/2+2n

Si UN=1, alors sin x =1, x =/2+2n

Si une = 0, alors péché x =0. x = n,

Exemple : Résoudre une équation péchéx =1/2.

Créons des formules de solutions x=arcsin 1/2+ 2n

X= - arcsin a+2n

Calculons la valeur arcsin1/2. Remplaçons la valeur trouvée dans les formules de solution

x=5/6+2n

ou selon la formule générale

X= (-1) n arcsin 1/2+n,

X= (-1)n/6+n,

2. Équations de la forme cosx= un.

Résolvons l'équation cosx= unégalement graphiquement, en traçant les fonctions y= cosx et y= UN.

1) Si un 1, alors l'équation cosx= un n'a pas de solutions, puisque les graphiques n'ont pas de points communs.

2) Si -1 un cosx= un Il a ensemble infini les décisions.

Nous trouverons toutes les solutions cosx= un sur un intervalle de longueur 2 puisque la période du cosinus est 2.

Par la définition de l'arc cosinus, la solution de l'équation sera x= arcos a. Compte tenu de la parité de la fonction cosinus, la solution de l'équation sur [-;0] sera x=-arcos un.

Ainsi, en résolvant l’équation cosx= un x= + arcos un+ 2n,

Dans trois cas, nous n'utiliserons pas la formule générale, mais des relations plus simples :

Si UN=-1, alors cosx =-1, x =-/2+2n

Si UN=1, alors cosx =1, x = 2n,

Si a=0, alors cosx=0. x =/2+n

Exemple : Résoudre une équation cos x = 1/2,

Créons des formules de solutions x=arccos 1/2+ 2n

Calculons la valeur arccos1/2.

Remplaçons la valeur trouvée dans les formules de solution

X= + /3+ 2n, nZ.

Équations de la forme tgx= un.

Puisque la période de la tangente est égale, alors pour trouver toutes les solutions de l'équation tgx= un, il suffit de trouver toutes les solutions sur n'importe quel intervalle de longueur . Par définition de l'arctangente, la solution de l'équation sur (-/2; /2) est arctan un. Compte tenu de la période de la fonction, toutes les solutions de l'équation peuvent s'écrire sous la forme

x= arctan un+ n, nZ.

Exemple: Résous l'équation bronzage x = 3/3

Créons une formule pour résoudre x= arctan 3/3 +n, nZ.

Calculons la valeur de l'arctangente arctan 3/3= /6, alors

X=/6+ n, nZ.

Dérivation de la formule pour résoudre l'équation Avec tgx= un peuvent être proposés aux étudiants.

Exemple.

Résous l'équation ctg x = 1.

x = arcсtg 1 + n, nZ,

X = /4 + n, nZ.

Grâce à la matière étudiée, les étudiants peuvent remplir le tableau :

"Résoudre des équations trigonométriques."

l'équation

Exercices pour consolider la matière étudiée.

(Oral) Laquelle des équations écrites peut être résolue à l'aide des formules :

a) x= (-1) n arcsin un+n, nZ;

b)x= + arcos un+ 2h ?

cos x = 2/2, tan x= 1, péché x = 1/3, cos x = 3/3, péché x = -1/2, cos x= 2/3, péché x = 3, cos x = 2 .

Laquelle des équations suivantes n’a pas de solution ?

Résolvez les équations :

a) péché x = 0 ; e) péché x = 2/2 ; h) péché x = 2 ;

b) cosx = 2/2 ; e) cos x = -1/2 ; je) cosx = 1 ;

d) bronzage x = 3 ; g) lit bébé x = -1 ; j) bronzage x = 1/ 3.

3. Résolvez les équations :

a) péché 3x = 0 ; e) 2cosx = 1 ;

b) cosx/2 =1/2 ; e) 3 tg 3x =1 ;

d) péché x/4 = 1 ; g) 2cos(2x+ /5) = 3.

Lors de la résolution de ces équations, il est utile d'écrire les règles de résolution des équations de la forme péché V X = un, Et Avec péché V X = un, | un|1.

Péché V X = une, |une|1.

V x = (-1) n arc sinus un+n, nZ,

x= (-1)n1/ V arcsin un+n/ V, nZ.

Résumer la leçon :

Aujourd'hui, en classe, nous avons dérivé des formules pour résoudre des équations trigonométriques simples.

Nous avons examiné des exemples de résolution d'équations trigonométriques simples.

Nous avons rempli le tableau que nous utiliserons pour résoudre les équations.

Devoirs.

№2 Résolution d'équations trigonométriques

Cible: Méthodes d'étude pour résoudre des équations trigonométriques : 1) réductibles à des équations quadratiques ; 2) réductibles à des équations trigonométriques homogènes.

Développer les capacités d'observation des élèves lors de l'utilisation de diverses façons résoudre des équations trigonométriques.

Travail frontal avec les étudiants.

Quelles sont les formules des racines des équations trigonométriques ? parce que x= un, péché x= un, tgx = un, ctg x = un.

Résoudre les équations (oralement) :

cos x=-1, sin x=0, tgx =0, cos x=1, cos x=1,5, sin x=0.

Trouvez les erreurs et réfléchissez aux raisons de ces erreurs.

cosx=1/2, x= + /6+2k,k Z.

péché X= 3/2, X= /3+k, kZ.

tgx = /4, x=1+ k, kZ.

2. Étudier du nouveau matériel.

Cette leçon couvrira certaines des méthodes les plus courantes pour résoudre des équations trigonométriques.

Équations trigonométriques réduites à quadratiques.

Cette classe peut inclure des équations qui incluent une fonction (sinus ou cosinus) ou deux fonctions du même argument, mais l'une d'elles est réduite à la seconde en utilisant des identités trigonométriques de base.

Par exemple, si cosх entre dans l'équation en puissances paires, alors nous le remplaçons par 1-sin 2 x, si sin 2 x, alors nous le remplaçons par 1-cos 2 x.

Exemple.

Résoudre l'équation : 8 péché 2 x - 6 péché x -5 =0.

Solution : Notons péché x=t, alors 8t 2 - 6t – 5=0,

ré = 196,

T 1 = -1/2, t 2 = -5/4.

Effectuons la substitution inverse et résolvons les équations suivantes.

X=(-1) k+1 /6+ k, kZ.

Puisque -5/4>1, l’équation n’a pas de racine.

Réponse : x=(-1) k+1 /6+ k, kZ.

Résoudre des exercices de consolidation.

Résous l'équation:

1) 2péché 2 x+ 3cos x = 0 ;

2) 5sin 2 x+ 6cos x -6 = 0 ;

3) 2sin 2 x+ 3cos 2 x = -2sin x ;

4) 3 tg 2 x +2 tgx-1=0.

Équations trigonométriques homogènes.

Définition: 1) Équation de la formeun péché + b cosx=0, (a=0, b=0) est appelée une équation homogène du premier degré par rapport à sin x et cos x.

Est en train d'être décidé équation donnée en divisant les deux parties par cosx 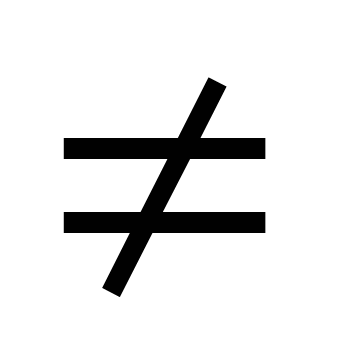0. Le résultat est l'équation atgx+b=0.

2) Équation de la formeun péché 2 X + b péché cosx + c parce que 2 X =0 est appelée une équation homogène du deuxième degré, où a, b, c sont des nombres quelconques.

Si a = 0, alors nous résolvons l'équation en divisant les deux côtés par parce que 2 x 0. En conséquence, nous obtenons l'équation atg 2 x+ btgx+с =0.

Commentaire:Équation de la formeun péché MX + b parce que MX=0 ou

un péché 2 MX + b péché MX parce que MX + c parce que 2 MX =0 sont également homogènes. Pour les résoudre, les deux côtés de l'équation sont divisés par cos MX=0 ou parce que 2 MX=0

3) Diverses équations qui ne sont pas à l'origine des équations homogènes peuvent être réduites à des équations homogènes. Par exemple,péché 2 MX + b péché MX parce que MX + c parce que 2 MX = d, Et un péché + b cosx= d. Pour résoudre ces équations, il faut multiplier le membre de droite par "unité trigonométrique" ceux. sur péché 2 X + parce que 2 X et effectuer des transformations mathématiques.

Exercices pour consolider la matière étudiée :

1) 2 péché x- 3cos x = 0 ; 5) 4 péché 2 x – sin2x =3 ;

2) péché 2x+ cos2x = 0 ; 6) 3 sin 2 x + sinx cosx =2 cos 2 x ;

3) péché x+ 3cos x = 0 ; 7) 3 péché 2 x- sinx cosx =2 ;

4) sin 2 x -3 sinx cosx +2 cos 2 x =0

3. Résumer la leçon. Devoirs.

Dans cette leçon, selon le niveau de préparation du groupe, vous pouvez envisager de résoudre des équations de la forme a sin mx +b cos mx=c, où a, b, c ne sont pas égaux à zéro en même temps.

Exercices de renforcement :

1. 3 péché x + cos x=2 ;

2. 3péché 2x + cos 2x= 2 ;

3. péché x/3 + cos x/3=1 ;

4. 12 péché x +5 cos x+13=0.

№ 3 Résolution d'équations trigonométriques

Cible: 1) Étudier la méthode de résolution d'équations trigonométriques par factorisation ; apprendre à résoudre des équations trigonométriques en utilisant diverses formules trigonométriques;

2) Vérifier : la connaissance des élèves des formules de résolution d'équations trigonométriques simples ; capacité à résoudre des équations trigonométriques simples.

Plan de cours:

Vérification des devoirs.

Dictée mathématique.

Apprendre du nouveau matériel.

Travail indépendant.

Résumer la leçon. Devoirs.

Déroulement de la leçon :

Vérification des devoirs (les solutions des équations trigonométriques sont brièvement écrites au tableau).

Dictée mathématique.

EN 1

1. Quelles équations sont appelées les équations trigonométriques les plus simples ?

2. Quel est le nom de l'équation de la formeun péché + b cosx=0 ? Indiquez un moyen de le résoudre.

3.Écrivez la formule des racines de l'équation tgx = un(ctg x= un).

4. Écrivez les formules des racines des équations de la forme cosx= un, Où UN=1, UN=0, UN=-1.

5. Écrivez la formule générale des racines de l'équation péché x= un, | un|

6. Comment les équations de la forme sont résoluesun cosx= b, | b|

À 2 HEURES

1. Notez les formules des racines des équations cosx= un,| un|

2. Écrivez la formule générale des racines de l'équation

= un, | un|

3. Comment s’appellent les équations de la forme ? péché x= un, tgx = un, péché x= un?

4.Écrivez les formules des racines de l'équation péché x= un, Si UN=1, UN=0, UN=-1.

5. Comment les équations de la forme sont résolues péché un x= b, | b|

6. Quelles équations sont appelées équations homogènes du deuxième degré ? Comment sont-ils résolus ?

Apprendre du nouveau matériel.

Méthode de factorisation.

L'une des méthodes les plus couramment utilisées pour résoudre des équations trigonométriques est la méthode de factorisation.

Si l'équation f(x) =0 peut être représentée par f 1 (x) f 2 (x) =0, alors le problème se réduit à résoudre deux équations f 1 (x) = 0, f 2 (x) = 0 .

(Avec les élèves il est utile de rappeler la règle « Le produit des facteurs est égal à zéro si au moins un des facteurs est égal à zéro et que les autres ont un sens»)

Consolidation du matériel étudié par la résolution d'équations de complexité variable.

(péché x-1/2)(péché x+1)=0; 2) (cosx- 2/2)(sin x+ 2/2)=0;(soi)

3) péché 2 x+ péché x cosx=0; 4) péché 2 x- péché x =0 ;

5) péché 2x – cosx=0 ; 6) 4 cos 2 x -1 =0 ; (2 façons)

7) cosx+ cos3x=0; 8) péché 3x= péché 17x ;

9) péché x+ péché 2x+ péché 3x=0; 10) cos3x cos5x

11) péché x cos5x = péché 9x cos3x péché 2x péché 2x

12) 3 cosx sin x+ cos 2 x=0(soi)

13) 2 cos 2 x - sin (x- /2)+ tanx tan (x+/2)=0.

Travail indépendant.

Option-1 Option-2

1) 6 péché 2 x+ 5 péché x -1=0; 1) 3 cos 2 x+2 cosx -5=0 ;

2) péché 2x – cos2x=0 ; 2) 3 cos x/2 - péché x/2=0 ;

3) 5 péché 2 x+ péché x cosx -2 cos 2 x=2; 3) 4sin 2 x- sin x cosx +7cos 2 x=5 ;

4) péchéx+sin5x=sin3x+sin7x; 4) péché x-péché 2x + péché 3x-péché 4x=0 ;

5) péchéx+cosx=1. 5) péchéx+cosx=2.

8. Résumer la leçon. Devoirs.