Signes suffisants d’un extremum d’une fonction. Signes d'augmentation et de diminution locales d'une fonction. Conditions nécessaires et suffisantes pour l'existence d'un extremum d'une fonction en un point. Un signe suffisant de l'existence d'un extremum

La fonction y = f(x) est appelée en augmentant (décroissant) dans un certain intervalle, si pour x 1< x 2 выполняется неравенство (f(x 1) < f (x 2) (f(x 1) >f(x2)).

Si la fonction différentiable y = f(x) augmente (diminue) sur un intervalle, alors sa dérivée sur cet intervalle f " (x) > 0

(f" (x)< 0).

Point xo appelé point maximum local (le minimum) fonction f(x), s'il existe un voisinage du point xo, pour tous les points dont l'inégalité f(x) ≤ f(x о) (f(x) ≥ f(x о)) est vraie.

Les points maximum et minimum sont appelés points extrêmes, et les valeurs de la fonction en ces points sont ses extrêmes.

Conditions nécessaires pour un extremum. Si le point xo est un point extremum de la fonction f(x), alors soit f " (x o) = 0, soit f (x o) n'existe pas. De tels points sont appelés critique, et la fonction elle-même est définie au point critique. Parmi ses points critiques, il faut chercher les extrema d’une fonction.

La première condition suffisante. Laisser xo- point critique. Si f "(x) lors du passage par un point xo change le signe plus en moins, puis au point xo la fonction a un maximum, sinon elle a un minimum. Si, en passant par le point critique, la dérivée ne change pas de signe, alors au point xo il n'y a pas d'extrême.

Deuxième condition suffisante. Soit la fonction f(x) avoir une dérivée
f "(x) à proximité du point xo et la dérivée seconde au point lui-même xo. Si f"(x o) = 0, >0 (<0), то точка xo est le point minimum (maximum) local de la fonction f(x). Si =0, alors vous devez soit utiliser la première condition suffisante, soit utiliser des dérivées supérieures.

Sur un segment, la fonction y = f(x) peut atteindre sa valeur minimale ou maximale soit aux points critiques, soit aux extrémités du segment.

Étudier les conditions et tracer des graphiques.

Trouver le domaine d'une fonction

Trouver les points d'intersection du graphique avec les axes de coordonnées

Trouver les intervalles du signe de constance

Examiner l'uniformité, l'étrangeté

Trouver les asymptotes du graphique d'une fonction

Trouver les intervalles de monotonie d'une fonction

Trouver les extrema de la fonction

Trouver des intervalles de convexité et des points d'inflexion

Asymptotes des graphiques de fonctions. Schéma général d'étude et de tracé de graphiques de fonctions. Exemples.

Verticale

Asymptote verticale - une ligne droite, soumise à l'existence d'une limite .

En règle générale, lors de la détermination de l'asymptote verticale, ils recherchent non pas une limite, mais deux limites unilatérales (gauche et droite). Ceci est fait afin de déterminer comment la fonction se comporte lorsqu'elle s'approche de l'asymptote verticale depuis différentes directions. Par exemple:

Remarque : faites attention aux signes de l'infini dans ces égalités.

[modifier]Horizontal

Asymptote horizontale - une ligne droite, sous réserve de l'existence d'une limite

[modifier] Oblique

Asymptote oblique - une ligne droite, soumise à l'existence de limites

Exemple d'asymptote oblique

Remarque : une fonction ne peut pas avoir plus de deux asymptotes obliques (horizontales) !

Remarque : Si au moins une des deux limites mentionnées ci-dessus n'existe pas (ou est égale à ), alors l'asymptote oblique en (ou ) n'existe pas !

Relation entre les asymptotes obliques et horizontales

Si lors du calcul de la limite , alors il est évident que l'asymptote oblique coïncide avec l'asymptote horizontale. Quel est le lien entre ces deux types d’asymptotes ?

La chose est, que l'asymptote horizontale est un cas particulier de l'obliqueà , et des commentaires ci-dessus, il s'ensuit que

1. La fonction a soit une seule asymptote oblique, soit une asymptote verticale, soit une oblique et une verticale, soit deux obliques, soit deux verticales, ou n'a aucune asymptote du tout.

2. L'existence des asymptotes indiquées au paragraphe 1.) est directement liée à l'existence des limites correspondantes.

Graphique d'une fonction avec deux asymptotes horizontales

]Trouver des asymptotes

L'ordre de recherche des asymptotes

1. Trouver des asymptotes verticales.

2. Trouver deux limites

3. Trouver deux limites :

si au point 2.), alors , et la limite est recherchée à l'aide de la formule de l'asymptote horizontale, .

Le point extremum d'une fonction est le point dans le domaine de définition de la fonction auquel la valeur de la fonction prend une valeur minimale ou maximale. Les valeurs de la fonction en ces points sont appelées extrema (minimum et maximum) de la fonction.

Définition. Point X1 domaine de fonction F(X) est appelé point maximum de la fonction , si la valeur de la fonction en ce point est supérieure aux valeurs de la fonction en des points suffisamment proches, situés à droite et à gauche de celle-ci (c'est-à-dire que l'inégalité est vraie F(X0 ) > F(X 0 + Δ X) X1 maximum.

Définition. Point X2 domaine de fonction F(X) est appelé point minimum de la fonction, si la valeur de la fonction en ce point est inférieure aux valeurs de la fonction en des points suffisamment proches, situés à droite et à gauche de celle-ci (c'est-à-dire que l'inégalité est vraie F(X0 ) < F(X 0 + Δ X) ). Dans ce cas on dit que la fonction a au point X2 le minimum.

Disons un point X1 - point maximum de la fonction F(X) . Puis dans l'intervalle jusqu'à X1 la fonction augmente, donc la dérivée de la fonction est supérieure à zéro ( F "(X) > 0 ), et dans l'intervalle après X1 la fonction diminue donc, dérivée d'une fonction moins que zéro ( F "(X) < 0 ). Тогда в точке X1

Supposons également que le point X2 - point minimum de la fonction F(X) . Puis dans l'intervalle jusqu'à X2 la fonction est décroissante et la dérivée de la fonction est inférieure à zéro ( F "(X) < 0 ), а в интервале после X2 la fonction est croissante et la dérivée de la fonction est supérieure à zéro ( F "(X) > 0 ). Dans ce cas également au point X2 la dérivée de la fonction est nulle ou n'existe pas.

Théorème de Fermat (signe nécessaire de l'existence d'un extremum d'une fonction). Si le point X0 - point extrême de la fonction F(X) alors à ce stade la dérivée de la fonction est égale à zéro ( F "(X) = 0 ) ou n'existe pas.

Définition. Les points auxquels la dérivée d'une fonction est nulle ou n'existe pas sont appelés points critiques .

Exemple 1. Considérons la fonction.

À ce point X= 0 la dérivée de la fonction est nulle, donc le point X= 0 est le point critique. Cependant, comme on peut le voir sur le graphique de la fonction, elle augmente dans tout le domaine de définition, donc le point X= 0 n'est pas le point extrême de cette fonction.

Ainsi, les conditions selon lesquelles la dérivée d'une fonction en un point est égale à zéro ou n'existe pas sont des conditions nécessaires pour un extremum, mais pas suffisantes, puisque d'autres exemples de fonctions peuvent être donnés pour lesquelles ces conditions sont remplies, mais la fonction n'a pas d'extremum au point correspondant. C'est pourquoi il doit y avoir des preuves suffisantes, permettant de juger s'il y a un extremum à un point critique particulier et de quel type d'extremum il s'agit - maximum ou minimum.

Théorème (le premier signe suffisant de l'existence d'un extremum d'une fonction). Point critique X0 F(X) si, en passant par ce point, la dérivée de la fonction change de signe, et si le signe passe de « plus » à « moins », alors c'est un point maximum, et si de « moins » à « plus », alors c'est un point minimum.

Si près du point X0 , à gauche et à droite de celui-ci, la dérivée conserve son signe, cela signifie que la fonction soit ne fait que diminuer, soit n'augmente que dans un certain voisinage du point X0 . Dans ce cas, au moment X0 il n'y a pas d'extrême.

Donc, pour déterminer les points extrêmes de la fonction, vous devez procéder comme suit :

Trouvez la dérivée de la fonction.
Égalisez la dérivée à zéro et déterminez les points critiques.
Mentalement ou sur papier, marquez les points critiques sur la droite numérique et déterminez les signes de la dérivée de la fonction dans les intervalles résultants. Si le signe de la dérivée passe de « plus » à « moins », alors le point critique est le point maximum, et s'il passe de « moins » à « plus », alors le point minimum.
Calculez la valeur de la fonction aux points extrêmes.

Exemple 2. Trouver les extrema de la fonction .

Solution. Trouvons la dérivée de la fonction :

Égalons la dérivée à zéro pour trouver les points critiques :

Puisque pour toute valeur de « x », le dénominateur n'est pas égal à zéro, nous assimilons le numérateur à zéro :

J'ai un point critique X= 3 . Déterminons le signe de la dérivée dans les intervalles délimités par ce point :

dans la plage de moins l'infini à 3 - un signe moins, c'est-à-dire que la fonction diminue,

dans l'intervalle de 3 à plus l'infini, il y a un signe plus, c'est-à-dire que la fonction augmente.

C'est-à-dire la période X= 3 est le point minimum.

Trouvons la valeur de la fonction au point minimum :

Ainsi, on trouve le point extremum de la fonction : (3 ; 0), et c'est le point minimum.

Théorème (le deuxième signe suffisant de l'existence d'un extremum d'une fonction). Point critique X0 est le point extrême de la fonction F(X) si la dérivée seconde de la fonction à ce stade n'est pas égale à zéro ( F ""(X) ≠ 0 ), et si la dérivée seconde est supérieure à zéro ( F ""(X) > 0 ), alors le point maximum, et si la dérivée seconde est inférieure à zéro ( F ""(X) < 0 ), то точкой минимума.

Remarque 1. Si au moment X0 Si les dérivées première et seconde disparaissent, alors à ce stade, il est impossible de juger de la présence d’un extremum sur la base du deuxième critère suffisant. Dans ce cas, il faut utiliser le premier critère suffisant pour l’extremum d’une fonction.

Remarque 2. Le deuxième critère suffisant pour l'extremum d'une fonction n'est pas applicable même lorsque la dérivée première n'existe pas en un point stationnaire (alors la dérivée seconde n'existe pas non plus). Dans ce cas, vous devez également utiliser le premier signe suffisant d’un extremum d’une fonction.

Caractère local des extrema de la fonction

Des définitions ci-dessus, il s'ensuit que l'extremum d'une fonction est de nature locale - il s'agit de la valeur la plus grande et la plus petite de la fonction par rapport aux valeurs proches.

Disons que vous examinez vos revenus sur une période d'un an. Si en mai vous avez gagné 45 000 roubles, en avril 42 000 roubles et en juin 39 000 roubles, alors les gains de mai sont le maximum de la fonction de gains par rapport aux valeurs proches. Mais en octobre, vous avez gagné 71 000 roubles, en septembre 75 000 roubles et en novembre 74 000 roubles, donc les gains d'octobre sont le minimum de la fonction de gains par rapport aux valeurs proches. Et vous pouvez facilement constater que le maximum parmi les valeurs d'avril-mai-juin est inférieur au minimum de septembre-octobre-novembre.

D'une manière générale, sur un intervalle, une fonction peut avoir plusieurs extrema, et il peut s'avérer qu'un minimum de la fonction soit supérieur à n'importe quel maximum. Ainsi, pour la fonction illustrée dans la figure ci-dessus, .

Autrement dit, il ne faut pas penser que le maximum et le minimum d'une fonction sont respectivement ses valeurs les plus grandes et les plus petites sur l'ensemble du segment considéré. Au point maximum, la fonction a la plus grande valeur uniquement par rapport aux valeurs qu'elle a en tous points suffisamment proches du point maximum, et au point minimum, elle a la plus petite valeur uniquement par rapport à ces valeurs qu'il soit en tous points suffisamment proche du point minimum.

Par conséquent, nous pouvons clarifier le concept ci-dessus de points extremum d'une fonction et appeler points minimum points minimum locaux et points maximum points maximum locaux.

Nous recherchons ensemble les extrema de la fonction

Exemple 3.

Solution : La fonction est définie et continue sur toute la droite numérique. Son dérivé existe également sur toute la droite numérique. Par conséquent, dans ce cas, les points critiques sont uniquement ceux où, c'est-à-dire , d'où et . Points critiques et diviser tout le domaine de définition de la fonction en trois intervalles de monotonie : . Sélectionnons un point de contrôle dans chacun d'eux et trouvons le signe de la dérivée à ce point.

Pour l'intervalle, le point de contrôle peut être : find. En prenant un point dans l'intervalle, nous obtenons, et en prenant un point dans l'intervalle, nous avons. Donc, dans les intervalles et , et dans l'intervalle . D'après le premier critère suffisant pour un extremum, il n'y a pas d'extremum au point (puisque la dérivée conserve son signe dans l'intervalle), et au point la fonction a un minimum (puisque la dérivée change de signe de moins à plus en passant à travers ce point). Trouvons les valeurs correspondantes de la fonction : , a . Dans l'intervalle la fonction diminue, puisque dans cet intervalle , et dans l'intervalle elle augmente, puisque dans cet intervalle .

Pour clarifier la construction du graphe, on retrouve les points d'intersection de celui-ci avec les axes de coordonnées. Lorsque l'on obtient une équation dont les racines sont et , c'est-à-dire que l'on trouve deux points (0 ; 0) et (4 ; 0) du graphique de la fonction. En utilisant toutes les informations reçues, nous construisons un graphique (voir le début de l'exemple).

Pour l'auto-vérification lors des calculs, vous pouvez utiliser calculateur de dérivée en ligne .

Exemple 4. Trouvez les extrema de la fonction et construisez son graphique.

Le domaine de définition d'une fonction est la droite numérique entière, à l'exception du point, c'est-à-dire .

Pour raccourcir l'étude, on peut utiliser le fait que cette fonction est paire, puisque . Son graphique est donc symétrique par rapport à l’axe Oy et l'étude ne peut être réalisée que pour l'intervalle.

Trouver la dérivée et points critiques de la fonction :

1) ;

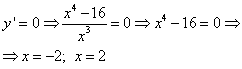2) ,

mais la fonction souffre d'une discontinuité en ce point, elle ne peut donc pas être un point extremum.

Ainsi, la fonction donnée présente deux points critiques : et . Compte tenu de la parité de la fonction, nous vérifierons uniquement le point en utilisant le deuxième critère suffisant pour un extremum. Pour ce faire, on trouve la dérivée seconde et déterminons son signe en : on obtient . Puisque et , c'est le point minimum de la fonction, et .

Pour avoir une image plus complète du graphe d’une fonction, découvrons son comportement aux limites du domaine de définition :

(ici le symbole indique le désir Xà zéro en partant de la droite, et X reste positif; signifie de la même manière aspiration Xà zéro en partant de la gauche, et X reste négatif). Ainsi, si , alors . Ensuite, nous trouvons

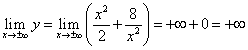ceux. si donc .

Le graphique d'une fonction n'a pas de points d'intersection avec les axes. L'image est au début de l'exemple.

Pour l'auto-vérification lors des calculs, vous pouvez utiliser calculateur de dérivée en ligne .

Nous continuons à rechercher ensemble les extrema de la fonction

Exemple 8. Trouvez les extrema de la fonction.

Solution. Trouvons le domaine de définition de la fonction. Puisque l’inégalité doit être satisfaite, on obtient de .

Trouvons la dérivée première de la fonction.

Pour trouver les maxima et les minima d’une fonction, vous pouvez utiliser l’un des trois signes suffisants d’un extremum. Bien que le plus courant et le plus pratique soit le premier.

Première condition suffisante pour un extremum.

Laissez la fonction y = f(x) est différentiable dans un -voisinage du point, et est continue au point lui-même. Alors

Autrement dit:

Algorithme.

On retrouve le domaine de définition de la fonction.

On retrouve la dérivée de la fonction sur le domaine de définition.

On détermine les zéros du numérateur, les zéros du dénominateur de la dérivée et les points du domaine de définition auxquels la dérivée n'existe pas (ces points sont appelés points d'extremum possibles, en passant par ces points, la dérivée peut simplement changer de signe).

Ces points divisent le domaine de définition de la fonction en intervalles dans lesquels la dérivée conserve son signe. On détermine les signes de la dérivée sur chacun des intervalles (par exemple, en calculant la valeur de la dérivée d'une fonction en tout point d'un intervalle particulier).

On sélectionne les points auxquels la fonction est continue et, par lesquels la dérivée change de signe.

Exemple. Trouvez les extrema de la fonction.
Solution.
Le domaine d’une fonction est l’ensemble des nombres réels sauf x = 2.
Trouver la dérivée :

Les zéros du numérateur sont des points x = -1 Et x = 5, le dénominateur tend vers zéro à x = 2. Marquez ces points sur l’axe des nombres

Nous déterminons les signes de la dérivée à chaque intervalle ; pour ce faire, nous calculons la valeur de la dérivée en l'un des points de chaque intervalle, par exemple aux points x = -2, x = 0, x = 3 Et x=6.

Par conséquent, sur l'intervalle la dérivée est positive (sur la figure nous mettons un signe plus sur cet intervalle). De même

Par conséquent, nous mettons un moins au-dessus du deuxième intervalle, un moins au-dessus du troisième et un plus au-dessus du quatrième.

Il reste à sélectionner les points auxquels la fonction est continue et sa dérivée change de signe. Ce sont les points extrêmes.
À ce point x = -1 la fonction est continue et la dérivée change de signe du plus au moins donc, selon le premier signe d'un extremum, x = -1 est le point maximum ; le maximum de la fonction lui correspond.
À ce point x = 5 la fonction est continue et la dérivée change de signe de moins à plus, donc, x = -1 est le point minimum ; le minimum de la fonction lui correspond.
Illustration graphique.

Répondre: .

Le deuxième signe suffisant d'un extremum d'une fonction.
Laisser ,

si , alors est le point minimum ;

si , alors est le point maximum.

Comme vous pouvez le constater, ce critère nécessite l'existence d'une dérivée au moins jusqu'au second ordre au point .
Exemple. Trouvez les extrema de la fonction.
Solution.
Commençons par le domaine de définition :

Différencions la fonction d'origine :

La dérivée tend vers zéro à x = 1, c’est-à-dire qu’il s’agit d’un point d’extremum possible.
Nous trouvons la dérivée seconde de la fonction et calculons sa valeur à x = 1:

Par conséquent, par la deuxième condition suffisante pour un extremum, x = 1- point maximum. Ensuite - le maximum de la fonction.
Illustration graphique.

Répondre: .
Le troisième signe suffisant d'un extremum d'une fonction.
Laissez la fonction y = f(x) a des dérivés jusqu'à n-ème ordre dans le -voisinage du point et dérivées jusqu'à n+1-ième ordre au point lui-même. Qu'il en soit ainsi.
Alors,

Fin du travail -

Ce sujet appartient à la section :

Algèbre et géométrie analytique. Le concept de matrice, les opérations sur les matrices et leurs propriétés

Le concept de matrice concerne les opérations sur les matrices et leurs propriétés.. une matrice est un tableau rectangulaire composé de nombres qui ne peuvent pas l'être.. et l'addition matricielle est une opération par élément..

Si vous avez besoin de matériel supplémentaire sur ce sujet, ou si vous n'avez pas trouvé ce que vous cherchiez, nous vous recommandons d'utiliser la recherche dans notre base de données d'œuvres :

Que ferons-nous du matériel reçu :

Si ce matériel vous a été utile, vous pouvez l'enregistrer sur votre page sur les réseaux sociaux :

Tous les sujets de cette section :

Définition de la différentiabilité
L'opération consistant à trouver la dérivée est appelée différenciation d'une fonction. Une fonction est dite dérivable en un certain point si elle a une dérivée finie en ce point, et

Règle de différenciation
Corollaire 1. Le facteur constant peut être soustrait du signe de la dérivée :

Signification géométrique de la dérivée. Équation tangente
L'angle d'inclinaison d'une droite y = kx+b est l'angle mesuré à partir de la position

Signification géométrique de la dérivée d'une fonction en un point
Considérons la sécante AB du graphe de la fonction y = f(x) telle que les points A et B ont respectivement des coordonnées

Solution
La fonction est définie pour tous les nombres réels. Puisque (-1; -3) est un point de tangence, alors

Conditions nécessaires pour un extremum et conditions suffisantes pour un extremum
Définition d'une fonction croissante. La fonction y = f(x) augmente sur l'intervalle X si pour tout

Conditions de monotonie et de constance d'une fonction
Condition de monotonie (non stricte) d'une fonction sur un intervalle. Laissez la fonction avoir une dérivée dans chaque

Définition de la primitive
Une primitive d'une fonction f(x) sur l'intervalle (a; b) est une fonction F(x) telle que l'égalité

Examen
Pour vérifier le résultat, on différencie l'expression résultante : En conséquence, on obtient

La primitive du produit d'une constante et d'une fonction est égale au produit d'une constante et de la primitive d'une fonction
Une condition suffisante pour l’existence d’une primitive d’une fonction donnée sur un intervalle est

Définition
Qu'il soit défini sur

Signification géométrique
L'intégrale définie est numériquement égale à l'aire de la figure délimitée par l'axe des abscisses et les droites

Propriétés d'une intégrale définie
Propriétés de base d'une intégrale définie. Propriété 1. La dérivée d'une intégrale définie par rapport à la limite supérieure est égale à l'intégrande dans laquelle au lieu d'une variable est intégrée

Formule de Newton-Leibniz (avec preuve)
Formule de Newton-Leibniz. Soit la fonction y = f(x) continue sur un intervalle et F(x) une des primitives de la fonction sur cet intervalle, alors l'équation

Théorème (la première condition suffisante pour un extremum). Soit la fonction continue en un point et la dérivée change de signe lorsqu'elle passe par le point. Vient ensuite le point d'extremum : maximum si le signe passe de « + » à « – », et minimum si de « – » à « + ».

Preuve. Laissez à et à .

D'après le théorème de Lagrange , où .Alors si , alors ; Voilà pourquoi , ainsi, , ou . Si donc; Voilà pourquoi , ainsi, ou .

Ainsi, il est prouvé qu'en tout point proche de , c'est-à-dire – le point maximum de la fonction.

La preuve du théorème pour le point minimum s'effectue de la même manière. Le théorème est prouvé.

Si, en passant par un point, la dérivée ne change pas de signe, alors il n'y a pas d'extremum au point.

Théorème (deuxième condition suffisante pour extremum). Soit la dérivée d'une fonction deux fois différentiable en un point égale à 0 (), et sa dérivée seconde en ce point soit différente de zéro () et continue dans un certain voisinage du point. C’est alors le point extrême ; c'est le point minimum et c'est le point maximum.

Un algorithme pour trouver les extrema d'une fonction en utilisant la première condition suffisante pour un extremum.

1. Trouvez la dérivée.

2. Trouvez les points critiques de la fonction.

3. Recherchez le signe de la dérivée à gauche et à droite de chaque point critique et tirez une conclusion sur la présence d'extrema.

4. Trouvez les valeurs extrêmes de la fonction.

Un algorithme pour trouver les extrema d'une fonction en utilisant la deuxième condition suffisante pour un extremum.

1. Trouvez la dérivée.

2. Trouvez la dérivée seconde.

3. Trouvez les points auxquels .

4. Déterminez le signe à ces points.

5. Tirer une conclusion sur l'existence et la nature des extrema.

6. Trouvez les valeurs extrêmes de la fonction.

Exemple. Considérons . Nous trouverons . Ensuite, à et à . Etudions les points critiques en utilisant la première condition suffisante pour l'extremum. Nous avons cela pour et pour, et pour. Aux points et la dérivée change de signe : at de « + » à « – » et at at de « – » à « + ». Cela signifie qu'en un point la fonction a un maximum, et en un point elle a un minimum ; . A titre de comparaison, nous étudions les points critiques en utilisant la deuxième condition suffisante pour l'extremum. Trouvons la dérivée seconde. Nous avons : , ce qui signifie qu'à un moment donné la fonction a un maximum et à un moment donné elle a un minimum.

Le concept d'asymptote d'un graphe de fonctions. Asymptotes horizontales, obliques et verticales. Exemples.

Définition. Une asymptote du graphique d'une fonction est une ligne droite qui a la propriété que la distance d'un point à cette ligne droite tend vers zéro lorsque le point du graphique s'éloigne indéfiniment de l'origine.

Il existe des asymptotes verticales (Fig. 6.6 a), horizontales (Fig. 6.6 b) et inclinées (Fig. 6.6 c).

En figue. 6.6a est montré asymptote verticale.

Sur la figure 6.6b - asymptote horizontale.

En figue. 6,6 V – asymptote oblique.

Théorème 1. Aux points d'asymptotes verticales (par exemple, ) la fonction subit une discontinuité, sa limite à gauche et à droite du point est égale à :

Théorème 2. Laissez la fonction être définie pour suffisamment grande et il y a des limites finies

ET .

Alors la droite est l’asymptote oblique du graphique de la fonction.

Théorème 3. Laissez la fonction être définie pour suffisamment grande et il y a une limite de la fonction. Alors la droite est l’asymptote horizontale du graphique de la fonction.

L'asymptote horizontale est un cas particulier de l'asymptote oblique, lorsque . Par conséquent, si dans une direction une courbe a une asymptote horizontale, alors dans cette direction il n'y en a pas d'inclinée, et vice versa.

Exemple. Trouvez les asymptotes du graphique de la fonction.

Solution. Au point où la fonction n’est pas définie, trouvons les limites de la fonction à gauche et à droite du point :

; .

C’est donc une asymptote verticale.

Schéma général d'étude des fonctions et de construction de leurs graphiques. Exemple.

Schéma général de recherche fonctionnelle et le tracer.

1. Trouvez le domaine de définition.

2. Étudiez la fonction de régularité - impair.

3. Recherchez les asymptotes verticales et les points de discontinuité (le cas échéant).

4. Étudier le comportement d'une fonction à l'infini ; trouver les asymptotes horizontales et obliques (le cas échéant).

5. Trouver les extrema et les intervalles de monotonie de la fonction.

6. Trouvez les points d'intersection du graphique avec les axes de coordonnées et, si nécessaire pour la construction schématique du graphique, trouvez des points supplémentaires.

7. Dessinez schématiquement un graphique.

Schéma détaillé de l'étude de fonction et tracer .

1. Trouver le domaine de définition .

un. Si y a un dénominateur, il ne doit pas atteindre 0.

b. L'expression radicale d'une racine de degré pair doit être non négative (supérieure ou égale à zéro).

c. L'expression du sous-log doit être positive.

2. Étudiez la fonction de parité - bizarrerie.

un. Si , alors la fonction est paire.

b. Si , alors la fonction est impaire.

c. Si ni , ni , alors est une fonction de forme générale.

3. Recherchez les asymptotes verticales et les points de discontinuité (le cas échéant).

un. Une asymptote verticale ne peut survenir qu'à la limite du domaine de définition de la fonction.

b. Si ( ou ), alors est l'asymptote verticale du graphique.

4. Étudier le comportement d'une fonction à l'infini ; trouver les asymptotes horizontales et obliques (le cas échéant).

un. Si , alors est l’asymptote horizontale du graphique.

b. Si , alors la ligne droite est l'asymptote inclinée du graphique.

c. Si les limites indiquées aux paragraphes a, b n'existent que lorsque unilatéral tend vers l'infini ( ou ), alors les asymptotes résultantes seront unilatérales : gaucher à et droitier quand .

5. Trouver les extrema et les intervalles de monotonie de la fonction.

un. Trouvez la dérivée.

b. Trouver les points critiques (ces points où ou où n'existe pas).

c. Sur l'axe des nombres, marquez le domaine de définition et ses points critiques.

d. Sur chacun des intervalles numériques résultants, déterminez le signe de la dérivée.

e. Sur la base des signes de la dérivée, tirez une conclusion sur la présence d'extrema dans y et leur type.

F. Trouvez des valeurs extrêmes.

g. Sur la base des signes de la dérivée, tirez des conclusions sur l'augmentation et la diminution.

6. Trouvez les points d'intersection du graphique avec les axes de coordonnées et, si nécessaire pour le tracé schématique du graphique, trouvez des points supplémentaires.

un. Afin de trouver les points d'intersection du graphique avec l'axe, il est nécessaire de résoudre l'équation. Les points où se trouvent des zéros seront les points d'intersection du graphique avec l'axe.

b. Le point d'intersection du graphique avec l'axe ressemble à . Il n'existe que si le point est dans le domaine de la fonction.

8. Dessinez schématiquement un graphique.

un. Construire un système de coordonnées et des asymptotes.

b. Marquez les points extrêmes.

c. Marquez les points d'intersection du graphique avec les axes de coordonnées.

d. Construire schématiquement un graphe pour qu'il passe par les points marqués et se rapproche des asymptotes.

Exemple. Explorez la fonction et construisez schématiquement son graphique.

2. – fonction de forme générale.

3. Puisque et , alors les droites et sont des asymptotes verticales ; les points sont des points d'arrêt. , quand n'est pas inclus dans le domaine de définition de la fonction

Billet n°1

fonction primitiveThéorèmePreuve intégrale indéfinie

Le point (X 0 ;Y 0) est appelé point maximum point minimum fonctions : pour tout point (x;y) différent de (X 0 ;Y 0), du δ-voisinage du point (X 0 ;Y 0) l'inégalité f(x;y)>f(X 0 ;Y 0) est satisfait.

Preuve:

Billet n°2

PreuveSignification géométrique

incrément privé dérivée partielle Signification géométrique

Billet n°3

19. Détermination des points maximum et minimum de la fonction z=f(x,y). Le point (X 0 ;Y 0) est appelé point maximum fonction z=f(x;y), s'il existe un δ-voisinage du point (X 0 ;Y 0) tel que l'inégalité f(x;y) est vraie point minimum fonctions : pour tout point (x;y) différent de (X 0 ;Y 0), du δ-voisinage du point (X 0 ;Y 0) l'inégalité f(x;y)>f(X 0 ;Y 0) est satisfait. Soit en un point stationnaire (X 0 ;Y 0) et une partie de son voisinage la fonction f(x;y) avoir des dérivées partielles continues jusqu'au second ordre inclus. Calculons au point (X 0 ;Y 0) les valeurs A=f"" xx (X 0 ;Y 0), B=f"" xy (X 0 ;Y 0), C=f"" aa (X 0 ;Y 0). Notons Δ=|AB ; BC|=AC-B^2. Alors : 1) si Δ><0; минимум, если A>0 ; 2) si Δ<0, то функция f(x;y) в точке (X 0 ;Y 0) экстремума не имеет. В случае Δ=0 экстремум в точке (X 0 ;Y 0) может быть, а может не быть. Необходимы дополнительные исследования.

Billet n°4 Par une intégrale définie Propriétés Preuve. en un point de coordonnées (x;y;z).Δu/Δl=LimΔl→0(Δ l u/Δl)=(δu/δx)*cosα+(δu/δy)*cosβ+(δu/δz)*cosγ . Supposons que la fonction u(x;y;z) soit continue et ait des dérivées continues par rapport à ses arguments dans le domaine D : Δu=(δu/δx)Δx+(δu/δy)Δy+(δu/δz)Δz+ E 1 Δx+E 2 Δy + E 3 Δz, où E 1, E 2, E 3 tendent vers zéro lorsque Δl→0. Divisons l'égalité entière par Δl. Δu/Δl=(δu/δx)(Δx/Δl)+(δu/δy)(Δy/Δl)+(δu/δz)(Δz/Δl)+E 1 (Δx/Δl)+E 2 (Δy/ Δl) + E 3 (Δz/Δl). Δx/Δl = cosα ; Δy/Δl = cosβ ; Δz/Δl = cosγ. L'égalité peut être représentée comme suit : Δu/Δl=(δu/δx)cosα+(δu/δy)cosβ+(δu/δz)cosγ+E 1 cosα+E 2 cosβ+E 3 cosγ. En passant à la limite, on obtient Δu/Δl=LimΔl→0(Δ l u/Δl)=(δu/δx)*cosα+(δu/δy)*cosβ+(δu/δz)*cosγ.

Billet n°5

1. Fonction primitive. Théorème sur la différence entre deux primitives (avec preuve). Intégrale indéfinie : définition La fonction F(x) est appelée fonction primitive f(x) sur l'intervalle (a;b), si pour tout x∈(a;b) l'égalité F"(x)=f(x) est vraie. Théorème. Si la fonction F(x) est une primitive de la fonction f(x) sur (a;b), alors l'ensemble de toutes les primitives de f(x) est donné par la formule F(x)+C, où C= const. Preuve. La fonction F(x)+C est une primitive de f(x). En effet, (F(x)+C)"=F"(x)=f(x). Soit Ф(x) une autre fonction primitive f(x), différente de F(x), c'est-à-dire Ф"(x)=f(x). Alors pour tout x∈(a;b) nous avons (Ф(х)-F(x))"=Ф"(x)-F"(x)=f( x )-f(x)=0. Et cela signifie que Ф(x)-F(x)=C, C=const. Par conséquent, Ф(x)=F(x)+C. L’ensemble de toutes les fonctions primitives F(x)+C pour f(x) est appelé intégrale indéfinie de la fonction f(x) et est désigné par le symbole ∫f(x)dx.

19. Détermination des points maximum et minimum de la fonction z=f(x,y). Le point (X 0 ;Y 0) est appelé point maximum fonction z=f(x;y), s'il existe un δ-voisinage du point (X 0 ;Y 0) tel que l'inégalité f(x;y) est vraie point minimum fonctions : pour tout point (x;y) différent de (X 0 ;Y 0), du δ-voisinage du point (X 0 ;Y 0) l'inégalité f(x;y)>f(X 0 ;Y 0) est satisfait. 20. Un signe suffisant de l'existence d'un extremum de la fonction z=f(x;y). (formulation). Soit en un point stationnaire (X 0 ;Y 0) et une partie de son voisinage la fonction f(x;y) avoir des dérivées partielles continues jusqu'au second ordre inclus. Calculons au point (X 0 ;Y 0) les valeurs A=f"" xx (X 0 ;Y 0), B=f"" xy (X 0 ;Y 0), C=f"" aa (X 0 ;Y 0). Notons Δ=|AB ; BC|=AC-B^2. Alors : 1) si Δ>0, alors la fonction f(x;y) au point (X 0 ;Y 0) a un extremum : maximum si A<0; минимум, если A>0 ; 2) si Δ<0, то функция f(x;y) в точке (X 0 ;Y 0) экстремума не имеет. В случае Δ=0 экстремум в точке (X 0 ;Y 0) может быть, а может не быть. Необходимы дополнительные исследования.

Billet n°6

3. Calcul d'une intégrale définie sur un segment. Formule de Newton-Leibniz (dérivation). Si la fonction y=f(x) est continue sur un intervalle et F(x) est l'une de ses primitives sur (F"(x)=f(x)), alors la formule ∫(de a à b) f( x) contient )dx=F(b)-F(a). Cette formule est la formule de Newton-Leibniz. Considérons l'identité : F(b)-F(a)=F(x n)-F(x 0)= (F(x n) -F(x n -1))+(f(x n -1)-F(x n -2))+…(F(x 2)-F(x 1))+(F(x 1 )-F(x 0)). Transformons chaque différence entre parenthèses en utilisant la formule de Lagrange : f(b)-f(a)=f'(c)*(b-a). On obtient F(b)-F(a )=F'(c n)( x n -x n -1)+F'(c n -1)(x n -1 -x n -2)+F'(c 2)(x 2 -x 1)+F'(c 1)(x 1 -x 0 )= ΣF'(Ci)ΔXi=Σf(Ci)ΔXi, c'est-à-dire F(b)-F(a)= Σf(Ci)ΔXi, où Ci est un point de l'intervalle (X i -1 ,X i). Donc puisque la fonction y=f(x) est continue sur , alors elle est intégrable sur . Il existe donc une limite de la somme intégrale égale à l'intégrale définie de f(x) en passant à la limite à λ=maxΔXi→0, on obtient F(b)-F( a)=lim Σf(Ci)ΔXi, soit ∫(de a à b) f(x)dx=F( b)-F(a).

La fonction z=f(x;y) est appelée différenciable

11. Propriété d'une fonction différentiable : lien entre la différentiabilité de la fonction z=f(x;y) et la continuité de la fonction z=f(x;y) en un point (formulation, preuve). Si la fonction z=f(x;y) est dérivable au point M(x;y), alors elle est continue en ce point et a des dérivées partielles en ce point. Preuve. Soit la fonction y=f(x) dérivable au point x 0 . À ce stade, nous donnons à l’argument un incrément Δx. La fonction recevra un incrément Δу. Trouvons limΔx→0(Δy). limΔx→0(Δy)= limΔx→0((Δy*Δx)/Δx))= limΔx→0(Δy/Δx)* limΔx→0(Δx)=f"(x0)*0=0. Par conséquent, y =f(x) est continue au point x 0.

Billet n°7

Un signe nécessaire d’un extremum.

Si une fonction continue z=z(x,y) a un extremum au point P0(x0,y0), alors toutes ses dérivées partielles du premier ordre en ce point sont soit égales à zéro, soit n'existent pas

Preuve: La dérivée partielle de la fonction z=f(x,y) par rapport à x au point P0(x0,y0) est la dérivée de la fonction d'une variable φ(x)=f(x,y0) au point x-x0. Mais à ce stade, la fonction φ(x) a évidemment un extremum. Par conséquent, φ'(x0) = 0. Puisque φ'(x0)=f'x(x0,y0), alors f'x(x0,y0)=0 De même, on peut montrer que f'y(x0, y0 )=0 . Le théorème a été prouvé.

Billet n°8

6. Le théorème de la valeur moyenne (formulation, preuve, signification géométrique). Si la fonction f(x) est continue sur le segment , alors il existe un point C∈ tel que ∫(from a to b) f(x)dx=f(c)*(b-a). Preuve. D'après la formule de Newton-Leibniz, on a ∫(de a à b) f(x)dx=F(x)|(de a à b)=F(b)-F(a), où F"(x )=f( x). En appliquant le théorème de Lagrange (le théorème sur l'incrément fini d'une fonction) à la différence F(b)-F(a), on obtient F(b)-F(a)=F"(c )*(ba)=f(c) *(ba). Signification géométrique. Le théorème pour f(x)≥0 a une signification géométrique simple : la valeur de l'intégrale définie est égale, pour certains C∈ (a;b), à l'aire d'un rectangle de hauteur f(c) et de base b-a. Le nombre f(c)=1/(b-a)∫(de a à b) f(x)dx est appelé valeur moyenne de la fonction f(x) sur le segment.

8. Incréments partiels de la fonction z=f(x;y). Dérivées partielles : définition et leur signification géométrique. Soit la fonction z=f(x;y). Puisque x et y sont des variables indépendantes, l’une d’elles peut changer tandis que l’autre reste constante. Donnons à la variable x un incrément ∆x, en gardant la valeur de la variable y inchangée. Alors la fonction z recevra un incrément, que nous appellerons incrément privé z dans x et désignent ∆ x z. Donc, ∆ x z=f(x+∆x;y)–f(x;y). De même, on obtient l'incrément partiel de z par rapport à y : ∆ y z=f(x;у+∆y)–f(x;y). S'il existe une limite lim∆x→0(∆ x z/∆x )=lim∆x→0( (f(x+∆x;y)-f(x;y))/∆x), alors on l'appelle dérivée partielle fonction z=f(x;y) au point M(x;y) dans la variable x et est désignée par l'un des symboles : z" x, δz/δx ; f" x, δf/δx. Signification géométrique. Le graphique de la fonction z=f(x;y) est une certaine surface. Le graphique de la fonction z=f(x 0 ;y 0) est la ligne d'intersection de cette surface avec le plan y=y 0. Sur la base de la signification géométrique de la dérivée pour une fonction d'une variable, nous concluons que f" x (x 0 ;y 0)=tgα, où α est l'angle entre l'axe Ox et la tangente tracée à la courbe z=f (x 0 ;y 0) au point M 0 (x 0 ;y 0 ;f(x 0 ;y 0)). Similaire à f" y (x 0 ;y 0)=tgβ.

Billet n°9

Preuve Signification géométrique

Plan tangent Normal à la surface

Billet n°10

10. Définition d'une fonction différentiable z=f(x;y) en un point. Définition du différentiel total dz et sa forme. La fonction z=f(x;y) est appelée différenciable au point M(x;y), si son incrément total en ce point peut être représenté par : ∆z=A*∆x+B*∆y+α*∆x+β*∆y, où α=α(∆ x;∆y)→0 et β=β(∆x;∆y)→0 pour ∆x→0 et ∆y→0. La partie principale de l'incrément de la fonction z=f(x;y), linéaire par rapport à ∆x et ∆y, est appelée différentiel complet cette fonction et est désignée par le symbole dz : dz=A*∆x+B*∆y. dz = (δz/δx)dx+(δz/δy)dy.

Billet n°11

4. Définition d'une intégrale définie sur un segment. Propriétés de base d'une intégrale définie sur un segment (avec preuve de l'une d'elles). Par une intégrale définie sur un segment d'une fonction f(x), la limite de la somme intégrale Σf(c i)Δx i est appelée si cette limite existe et ne dépend ni de la division du segment en parties, ni du choix des points t à l'intérieur de chacune des parties, à condition que la longueur des plus grands segments partiels (∆xi) tende vers zéro, soit ∫(de a à b) f(x)dx=lim Δx i →0 Σf(c i)Δx i . Propriétés: 1) Si c est un nombre constant et que la fonction f(x) est intégrable sur , alors ∫(de a à b) c*f(x)dx=c*∫(de a à b) f(x)dx .2) Si les fonctions f 1 (x) b f 2 (x) sont intégrables sur , alors leur somme est également intégrable ∫(de a à b) (f 1 (x)+f 2 (x))dx=∫( de a à b) f 1 (x)dx+∫(de a à b) f 2 (x)dx. 3)∫(de a à b) f(x)dx= -∫(de b à a) f(x)dx. 4)Si la fonction f(x) est intégrable sur et un

10. Définition d'une fonction différentiable z=f(x;y) en un point. La fonction z=f(x;y) est appelée différenciable au point M(x;y), si son incrément total en ce point peut être représenté par : ∆z=A*∆x+B*∆y+α*∆x+β*∆y, où α=α(∆ x;∆y)→0 et β=β(∆x;∆y)→0 pour ∆x→0 et ∆y→0.

12. Propriété d'une fonction différentiable : lien entre la différentiabilité de la fonction z=f(x,y) et l'existence de dérivées partielles en un point (formulation, preuve). Théorème : Si une fonction est dérivable en un point, alors en ce point il existe des dérivées partielles finies, A et B sont numériquement égaux. Soit : Δz=AΔx+BΔy+0(ρ) Prouver : Ǝ(δz/δx(x 0 ; y 0)=A Preuve : Donnons x 0 →Δx, y=y 0 =>Δ x z=(A*Δx+0(│x│). ρ=√(Δx 2 +Δy 2)=│Δx│. Δ x z/Δx=A +0(│x│)/Δx. LimΔx→0 (Δ x z/Δx)=lim=A. δz/Δx(x 0 ;y 0)=A. De même : Y 0 →Δy, x=x 0 => Δ y Z. δz/Δy(x 0 ;y 0)=B.

Billet n°12

Preuve

Billet n°13

2. Le problème de l'aire d'un trapèze curviligne, conduisant à la notion d'intégrale définie sur un segment. Définition d'une intégrale définie sur un segment. Soit la fonction y=f(x)≥0 sur le segment. Une figure délimitée en haut par le graphique de la fonction y=f(x), en bas par l'axe Ox, et sur le côté par les droites x=a et x=b est appelée un trapèze curviligne. Trouvons l'aire de ce trapèze. f(c 1)Δx 1 +f(c 2)Δx 2 +..+f(c n)Δx n =Σf(c i)Δx i =Sn. Avec une diminution de toutes les valeurs de Δx i, la précision de l'approximation d'un trapèze curviligne avec une figure en escalier et la précision de la formule résultante augmentent. Par conséquent, pour la valeur exacte de l'aire S d'un trapèze curviligne, on prend la limite S vers laquelle tend l'aire de la figure en escalier Sn lorsque n augmente sans limite de sorte que λ=maxΔx i →0 : S=lim n →∞ Sn=lim n→∞(λ→0 ) Σf(c i)Δx i , c'est-à-dire S=∫(de a à b) f(x)dx. Ainsi, l'intégrale définie d'une fonction indéfinie est numériquement égale à l'aire d'un trapèze curviligne. Si la somme intégrale Sn a une limite I, qui ne dépend ni de la méthode de division du segment en segments numériques ni de la choix des points en eux, alors le nombre I est appelé l'intégrale définie de la fonction y=f(x) sur le segment et est noté ∫(de a à b) f(x)dx. Ainsi, ∫(de a à b) f(x)dx=lim n→∞(λ→0) Σf(c i)Δx i .

17. Plan tangent et normal à la surface (définition).Plan tangentà une surface en un point M, un plan passant par ce point de la surface est appelé si l'angle entre ce plan et la sécante passant par le point M et tout autre point M 1 de la surface tend vers zéro lorsque M tend vers M 1. Normal à la surface en un point M est une droite passant par ce point perpendiculaire au plan tangent.

Billet n°14

5. Théorème d'estimation d'une intégrale définie sur un segment (formulation, preuve, signification géométrique). Estimation de l'intégrale. Si m et M sont respectivement les plus petites et les plus grandes valeurs de la fonction y=f(x) sur le segment , (a Preuve. Puisque pour tout x∈ nous avons m≤f(x)≤M, alors ∫(de a à b) mdx≤ ∫(de a à b) f(x)dx≤∫(de a à b) Mdx. On obtient : m(b-a)≤∫(de a à b) f(x)dx≤M(b-a). Signification géométrique. L'aire d'un trapèze curviligne est comprise entre les aires de rectangles dont la base est , et dont les hauteurs sont m et M.

Billet n°15

Billet n°16

21. Dérivée de la fonction u=u(x;y;z) dans la direction l (définition). La limite LimΔl→0(Δu/Δl) est appelée dérivée de la fonction u(x;y;z) dans la direction du vecteur l en un point de coordonnées (x; y; z).

22. Dégradé de la fonction u=u(x;y;z) en un point (définition). Un vecteur de coordonnées (δu/δx ; δu/δy ; δu/δz) est appelé

Billet n°17

7. Intégrale avec une limite supérieure variable. Théorème sur la dérivée d'une intégrale à limite supérieure variable (formulation, preuve). La dérivée d'une intégrale définie par rapport à une limite supérieure de variable est égale à l'intégrande dans laquelle la variable d'intégration est remplacée par cette limite, c'est-à-dire (∫(de a à x) f(t)dt)" x = f (X). Preuve. D'après la formule de Newton-Leibniz, on a : ∫(de a à x) f(t)dt=F(t)|(de a à x)=F(x)-F(a). Par conséquent, (∫(from a to x) f(t)dt)" x =(F(x)-F(a))" x =F"(x)-0=f(x). Cela signifie que a l'intégrale définie avec une limite supérieure variable est l'une des primitives de l'intégrande.

incrément complet continu continu

Billet n°18

1. Fonction primitive. Théorème sur la différence entre deux primitives (avec preuve). Intégrale indéfinie : définition, propriétés les plus simples de l'intégrale indéfinie (avec preuve de l'une d'elles). La fonction F(x) est appelée fonction primitive f(x) sur l'intervalle (a;b), si pour tout x∈(a;b) l'égalité F"(x)=f(x) est vraie. Théorème. Si la fonction F(x) est une primitive de la fonction f(x) sur (a;b), alors l'ensemble de toutes les primitives de f(x) est donné par la formule F(x)+C, où C= const. Preuve. La fonction F(x)+C est une primitive de f(x). En effet, (F(x)+C)"=F"(x)=f(x). Soit Ф(x) une autre fonction primitive f(x), différente de F(x), c'est-à-dire Ф"(x)=f(x). Alors pour tout x∈(a;b) nous avons (Ф(х)-F(x))"=Ф"(x)-F"(x)=f( x )-f(x)=0. Et cela signifie que Ф(x)-F(x)=C, C=const. Par conséquent, Ф(x)=F(x)+C. L’ensemble de toutes les fonctions primitives F(x)+C pour f(x) est appelé intégrale indéfinie de la fonction f(x) et est désigné par le symbole ∫f(x)dx. Propriétés: 1) La différentielle de l'intégrale indéfinie est égale à l'intégrande, et la dérivée de l'intégrale indéfinie est égale à l'intégrande d(∫f(x)dx)=f(x)dx, (∫f(x)dx )"=f(x).d (∫f(x)dx)=d(F(x)+C)=dF(x)+dC=F"(x)dx=f(x)dx. et (∫f(x)dx)"=(F(x)+C)"=F"(x)+0=f(x).2) L'intégrale indéfinie de la différentielle d'une fonction est égale à la somme de cette fonction et une constante arbitraire : ∫dF(x)=F(x)+C.∫dF(x)=F"(x)dx=∫f(x)dx=F(x)+C.3) Le facteur constant peut être soustrait du signe intégral : ∫af(x)dx=a∫f(x)dx.4) L'intégrale indéfinie de la somme algébrique d'un nombre fini de fonctions continues est égale à la somme algébrique de les intégrales des sommes des fonctions : ∫(f(x)±g(x))dx=∫f (x)dx±∫g(x)dx.5) (Invariance de la formule d'intégration). Si ∫f(x)dx=F(x)+C, alors ∫f(u)du=F(u)+C, où u=φ(x) est une fonction arbitraire avec une dérivée continue.

22. Dégradé de la fonction u=u(x;y;z) en un point (définition, propriétés). Relation entre la dérivée directionnelle et le gradient d'une fonction (justification). Un vecteur de coordonnées (δu/δx ; δu/δy ; δu/δz) est appelé gradient de la fonction u=f(x;y;z) et est noté gradU = (δu/δx ; δu/δy ; δu/δz). gradU=(δu/δx)*i+(δu/δy)*j+(δu/δz)*k. Propriétés: 1)gradC=0; 2)grad(c*u)=c*gradU; 3)grad(u+v)=gradU+gradV; 4)grad(u*v)=u*gradV+v*gradU, où u*v sont des produits scalaires des vecteurs u et v. Connexion. Soit la fonction u=u(x;y;z) et le champ de gradient gradU=(δu/δx)*i+(δu/δy)*j+(δu/δz)*k. Alors la dérivée Δu/Δl dans la direction d'un vecteur l est égale à la projection du vecteur GradU sur le vecteur l.

Billet n°19

4. Définition d'une intégrale définie sur un segment. Propriétés de base d'une intégrale définie sur un segment (avec preuve de l'une d'elles). Par une intégrale définie sur un segment d'une fonction f(x), la limite de la somme intégrale Σf(c i)Δx i est appelée si cette limite existe et ne dépend ni de la division du segment en parties, ni du choix des points t à l'intérieur de chacune des parties, à condition que la longueur des plus grands segments partiels (∆xi) tende vers zéro, soit ∫(de a à b) f(x)dx=lim Δx i →0 Σf(c i)Δx i . Propriétés: 1) Si c est un nombre constant et que la fonction f(x) est intégrable sur , alors ∫(de a à b) c*f(x)dx=c*∫(de a à b) f(x)dx . Preuve. Composons la somme intégrale de la fonction c*f(x). Nous avons Σс*f(c i)Δx i =с*Σf(c i)Δx i . Alors lim n→∞ Σс*f(c i)Δx i =c*lim n→∞ f(c i)=с*∫(de a à b) f(x)dx. Il s'ensuit que la fonction с*f(x) est intégrable sur et la formule ∫(de a à b) с*f(x)dx= с*∫(de a à b) f(x)dx.2) Si les fonctions f 1 (x) b f 2 (x) sont intégrables sur , alors leur somme est intégrable et ∫(de a à b) (f 1 (x)+f 2 (x))dx=∫(de a à b ) f 1 (x)dx+∫(de a à b) f 2 (x)dx. 3)∫(de a à b) f(x)dx= -∫(de b à a) f(x)dx. 4)Si la fonction f(x) est intégrable sur et un

17. Plan tangent et normal à la surface (définition). Théorème sur l'existence d'un plan tangent (formulation, preuve). Plan tangentà une surface en un point M, un plan passant par ce point de la surface est appelé si l'angle entre ce plan et la sécante passant par le point M et tout autre point M 1 de la surface tend vers zéro lorsque M tend vers M 1. Normal à la surface en un point M est une droite passant par ce point perpendiculaire au plan tangent. Théorème. Si δF/δx ; δF/δy ; δF/δz sont définis au voisinage du point Mo et sont continus au point M 0 lui-même et en même temps ne s'annulent pas, alors toutes les lignes tangentes aux lignes sur la surface se trouvent dans le même plan. Preuve. L : système (x=x(t); y=y(t); z=z(t)). Ligne tangente (M 0 ;P) y=(x"(t 0); y"(t o); z"(t 0)). L∈Q (surface). F(x(t), y(t) , z(t))=0 est une fonction complexe de la variable t. On utilise la règle de différentiabilité d'une fonction complexe : (δF/δx)*(dx/dt)+(δF/δy)*(dy/dt )+(δF/δz)*( dz/dt)=0 ; (δF(M 0)/δx)*x"(t 0)+(δF(M 0)/δy)*y"(t 0)+ (δF(M 0)/δz) *z"(t 0)=0; g=(x"(t 0),y"(t 0),z"(t 0)); désigne n=(δF(M 0)/δx; δF(M 0)/δy; δF(M 0) /δz); n⊥g. Puisqu’un nombre infini de lignes situées sur la surface peuvent être tracées à travers un point donné, et un nombre infini de lignes tangentes à celles-ci, donc toutes les lignes tangentes se trouvent dans le même plan.

Billet n°20

9. Incrément complet de la fonction z=f(x;y). Continuité de la fonction z=f(x;y) en un point (deux définitions). Soit la fonction z=f(x;y). Donnons à la variable indépendante x un incrément ∆x, et à la variable y un incrément ∆y. Alors incrément complet∆z de la fonction est déterminé par l'égalité : ∆z=f(x+∆x;y+∆y)-f(x;y). 1)La fonction z=f(x;y) est appelée continu au point M 0 (x 0 ;y 0)∈ D(z), si sa limite en ce point coïncide avec la valeur de la fonction en ce point, c'est-à-dire limX→X 0 \Y→Y 0 (f(x;y))= f(x 0;y 0). 2) Fonction z=f(x;y) continu sur un ensemble s'il est continu en tout point de cet ensemble

Billet n°21

21. Dérivée de la fonction u=u(x;y;z) dans la direction l (définition, formule de calcul, dérivation de la formule de calcul). La limite LimΔl→0(Δu/Δl) est appelée dérivée de la fonction u(x;y;z) dans la direction du vecteur l en un point de coordonnées (x;y;z).Δu/Δl=LimΔl→0(Δ l u/Δl)=(δu/δx)*cosα+(δu/δy)*cosβ+(δu/δz)*cosγ . Supposons que la fonction u(x;y;z) soit continue et ait des dérivées continues par rapport à ses arguments dans le domaine D : Δu=(δu/δx)Δx+(δu/δy)Δy+(δu/δz)Δz+ E 1 Δx+E 2 Δy + E 3 Δz, où E 1, E 2, E 3 tendent vers zéro lorsque Δl→0. Divisons l'égalité entière par Δl. Δu/Δl=(δu/δx)(Δx/Δl)+(δu/δy)(Δy/Δl)+(δu/δz)(Δz/Δl)+E 1 (Δx/Δl)+E 2 (Δy/ Δl) + E 3 (Δz/Δl). Δx/Δl = cosα ; Δy/Δl = cosβ ; Δz/Δl = cosγ. L'égalité peut être représentée comme suit : Δu/Δl=(δu/δx)cosα+(δu/δy)cosβ+(δu/δz)cosγ+E 1 cosα+E 2 cosβ+E 3 cosγ. En passant à la limite, on obtient Δu/Δl=LimΔl→0(Δ l u/Δl)=(δu/δx)*cosα+(δu/δy)*cosβ+(δu/δz)*cosγ.

Billet n°22

20. Un signe suffisant de l'existence d'un extremum de la fonction z=f(x;y). (formulation). Soit en un point stationnaire (X 0 ;Y 0) et une partie de son voisinage la fonction f(x;y) avoir des dérivées partielles continues jusqu'au second ordre inclus. Calculons au point (X 0 ;Y 0) les valeurs A=f"" xx (X 0 ;Y 0), B=f"" xy (X 0 ;Y 0), C=f"" aa (X 0 ;Y 0). Notons Δ=|AB ; BC|=AC-B^2. Alors : 1) si Δ>0, alors la fonction f(x;y) au point (X 0 ;Y 0) a un extremum : maximum si A<0; минимум, если A>0 ; 2) si Δ<0, то функция f(x;y) в точке (X 0 ;Y 0) экстремума не имеет. В случае Δ=0 экстремум в точке (X 0 ;Y 0) может быть, а может не быть. Необходимы дополнительные исследования.

Billet n°23

17. Plan tangent à une surface (définition).Plan tangentà une surface en un point M, un plan passant par ce point de la surface est appelé si l'angle entre ce plan et la sécante passant par le point M et tout autre point M 1 de la surface tend vers zéro lorsque M tend vers M 1.

18. Equations d'un plan tangent à une surface spécifiée explicitementÉvidemment. z=f(x;y) au point Mo(Xo;Yo;Zo). K : (δz/δx)|M 0 (X-X 0)+(δz/δy)|M 0 (Y-Y 0)-(Z-Z 0)=0

Billet n°24