Dessinez un schéma du système et marquez dessus le centre de gravité. Si le centre de gravité trouvé se trouve en dehors du système d'objets, vous avez reçu une réponse incorrecte. Vous avez peut-être mesuré des distances à partir de différents points de référence. Répétez les mesures.
- Par exemple, si des enfants sont assis sur une balançoire, le centre de gravité sera quelque part entre les enfants et non à droite ou à gauche de la balançoire. De plus, le centre de gravité ne coïncidera jamais avec le point où l’enfant est assis.
- Ces arguments sont valables dans un espace à deux dimensions. Dessinez un carré qui contiendra tous les objets du système. Le centre de gravité doit être à l’intérieur de ce carré.
Vérifiez vos calculs si vous obtenez un petit résultat. Si le point de référence se trouve à une extrémité du système, un petit résultat place le centre de gravité près de l’extrémité du système. C’est peut-être la bonne réponse, mais dans la grande majorité des cas, ce résultat indique une erreur. Lorsque vous avez calculé les moments, avez-vous multiplié les poids et les distances correspondants ? Si au lieu de multiplier vous ajoutiez les poids et les distances, vous obtiendriez un résultat beaucoup plus petit.
Corrigez l'erreur si vous avez trouvé plusieurs centres de gravité. Chaque système n'a qu'un seul centre de gravité. Si vous avez trouvé plusieurs centres de gravité, vous n’avez probablement pas additionné tous les moments. Le centre de gravité est égal au rapport du moment « total » au poids « total ». Il n'est pas nécessaire de diviser « chaque » instant par « chaque » poids : vous retrouverez ainsi la position de chaque objet.
Vérifiez le point de référence si la réponse diffère d'une valeur entière. Dans notre exemple, la réponse est 3,4 m. Disons que vous avez obtenu la réponse 0,4 m ou 1,4 m, ou un autre nombre se terminant par « .4 ». En effet, vous n'avez pas choisi l'extrémité gauche du plateau comme point de départ, mais un point situé un peu plus à droite. En fait, votre réponse est correcte quel que soit le point de référence que vous choisissez ! N'oubliez pas : le point de référence est toujours à la position x = 0. Voici un exemple :
- Dans notre exemple, le point de référence était à l'extrémité gauche de la planche et nous avons constaté que le centre de gravité était à 3,4 m de ce point de référence.
- Si vous choisissez comme point de référence un point situé à 1 m à droite de l'extrémité gauche du tableau, vous obtiendrez la réponse 2,4 m, c'est-à-dire que le centre de gravité est à 2,4 m du nouveau point de référence, ce qui , quant à lui, est situé à 1 m de l'extrémité gauche du plateau. Ainsi, le centre de gravité est à une distance de 2,4 + 1 = 3,4 m de l'extrémité gauche de la planche. Il s'est avéré que c'était une vieille réponse !
- Remarque : lorsque vous mesurez des distances, n'oubliez pas que les distances jusqu'au point de référence « gauche » sont négatives et celles jusqu'au point de référence « droit » sont positives.
Mesurez les distances en lignes droites. Supposons qu'il y ait deux enfants sur une balançoire, mais qu'un enfant soit beaucoup plus grand que l'autre, ou qu'un enfant soit suspendu sous la planche au lieu de s'asseoir dessus. Ignorez cette différence et mesurez les distances le long de la ligne droite du tableau. Mesurer des distances selon des angles donnera des résultats proches mais pas entièrement précis.
- Pour le problème de la planche à bascule, rappelez-vous que le centre de gravité se situe entre les extrémités droite et gauche de la planche. Plus tard, vous apprendrez à calculer le centre de gravité de systèmes bidimensionnels plus complexes.
Conférence 4. Centre de gravité.
Cette conférence couvre les questions suivantes
1. Centre de gravité d'un corps solide.
2. Coordonnées des centres de gravité des corps inhomogènes.
3. Coordonnées des centres de gravité des corps homogènes.
4. Méthodes de détermination des coordonnées des centres de gravité.
5. Centres de gravité de certains corps homogènes.
L'étude de ces questions est nécessaire à l'avenir pour étudier la dynamique du mouvement des corps prenant en compte les frottements de glissement et de roulement, la dynamique du mouvement du centre de masse d'un système mécanique, les moments cinétiques, pour résoudre des problèmes dans le discipline « Résistance des matériaux ».
Apporter des forces parallèles.
Après avoir envisagé de ramener au centre un système plat et un système spatial arbitraire de forces, revenons à l'examen du cas particulier d'un système de forces parallèles.
Réunir deux forces parallèles.
En considérant un tel système de forces, les trois cas de réduction suivants sont possibles.
1. Système de deux forces colinéaires. Considérons un système de deux forces parallèles dirigées dans une direction P. Et Q, appliqué aux points UN Et DANS. Nous supposerons que les forces sont perpendiculaires à ce segment (Fig. 1, UN).
AVEC, appartenant au segment UN B et satisfaisant la condition :
CA/NE = Q/P..(1)
Vecteur principal du système R.C. = P. + Q est égal en module à la somme de ces forces : R.C. = P. + Q.
AVEC compte tenu de (1) est égal à zéro :MC = P. ∙ CA- Q∙ CB = 0.
Ainsi, à la suite du casting, nous avons obtenu : R.C. ≠ 0, MC= 0. Cela signifie que le vecteur principal est équivalent à la résultante passant par le centre de réduction, soit :
La résultante des forces colinéaires est égale en module à leur somme, et sa ligne d'action divise le segment reliant les points de leur application, en proportion inverse des modules de ces forces de manière interne.
Notez que la position du point AVEC ne changera pas si les forces R. Et Q tourner un angleα. Point AVEC, qui a cette propriété s’appelle centre de forces parallèles.
2. Système de deux anticollinéaire et les forces ne sont pas égales en ampleur. Que la force P. Et Q, appliqué aux points UN Et DANS, parallèles, dirigés dans des directions opposées et de magnitude inégale (Fig. 1, b).
Choisissons un point comme centre de réduction AVEC, qui satisfait toujours la relation (1) et se trouve sur la même ligne, mais en dehors du segment UN B.
Le principal vecteur de ce système R.C. = P. + Q le module sera désormais égal à la différence entre les modules des vecteurs : R.C. = Q - P..
Le point principal concernant le centre AVEC est toujours nul :MC = P. ∙ CA- Q∙ NE= 0, donc
Résultant anticollinéaire et les forces qui ne sont pas égales en grandeur sont égales à leur différence, dirigées vers la plus grande force, et sa ligne d'action divise le segment reliant les points de leur application, en raison inverse des modules extérieurs de ces forces.
Fig. 1
3. Système de deux anticollinéaire et des forces égales en ampleur. Prenons le cas de réduction précédent comme cas initial. Réparons la force R., et la force Q dirigeons le module vers la force R..
Puis à Q → R. dans la formule (1) la relation CA/NE → 1. Cela signifie que CA → NE, c'est-à-dire la distance CA →∞ .
Dans ce cas, le module du vecteur principal R.C. → 0, et le module du moment principal ne dépend pas de la position du centre de réduction et reste égal à la valeur d'origine :
MC = P. ∙ CA- Q∙ NE = P. ∙ ( CA- NE) =P. ∙ UNB.
Donc à la limite on a obtenu un système de forces pour lequel R.C. = 0, MC≠ 0, et le centre de réduction est éloigné à l'infini, qui ne peut être remplacé par la résultante. Il n’est pas difficile de reconnaître quelques forces dans ce système. une paire de forces n'a pas de résultante.
Centre du système de forces parallèles.
Considérez le système n force P je, appliqué aux pointsUn je (x je , et je , z je) et parallèle à l'axeOv avec ortho je(Fig.2).
Si l'on exclut par avance le cas d'un système équivalent à un couple de forces, il n'est pas difficile, à partir du paragraphe précédent, de prouver l'existence de sa résultanteR..
Déterminons les coordonnées du centreC(X c, oui c, z c) forces parallèles, c'est-à-dire les coordonnées du point d'application de la résultante de ce système.
Pour cela, nous utilisons le théorème de Varignon, à partir duquel :
M0 (R.) = Σ M0(P je).

Figure 2
Le moment vectoriel d’une force peut être représenté comme un produit vectoriel, donc :
M 0 (R.) = rc× R. = Σ M0i(P je) = Σ ( r je× P je ).
Étant donné que R. = camping-car ∙ je, UN P je = PVI ∙ je et en utilisant les propriétés du produit vectoriel, on obtient :
rc × camping-car ∙ je = Σ ( r je × PVI ∙ je),
rc ∙ R. v× je = Σ ( r je ∙ PVI × je) = Σ ( r je ∙ PVI ) × je,
ou:
[ r c R v - Σ ( r je PVI )] × je= 0.
La dernière expression n'est valide que si l'expression entre crochets est égale à zéro. Par conséquent, en omettant l’indexvet en tenant compte du fait que la résultanteR. = Σ P je , d'ici on obtient :
rc = (Σ P je r je )/(Σ P je ).
En projetant la dernière égalité vectorielle sur l'axe des coordonnées, on obtient la valeur requise expression des coordonnées du centre des forces parallèles:
xc = (Σ P je x je)/(Σ P je );
oui c = (Σ P je et je )/(Σ P je );(2)
zc = (Σ P je z je )/(Σ P je ).
Centre de gravité des corps.
Coordonnées des centres de gravité d'un corps homogène.
Considérons un corps rigide pesant P. et le volume V dans le système de coordonnées Oxyz, où sont les axes X Et oui relié à la surface de la terre, et l'axe z visant le zénith.
Si l'on décompose le corps en parties élémentaires d'un volume∆ V je , alors la force d'attraction agira sur chaque partie de celui-ci∆ P je, dirigé vers le centre de la Terre. Supposons que les dimensions du corps soient nettement inférieures aux dimensions de la Terre, alors le système de forces appliqué aux parties élémentaires du corps peut être considéré comme non convergent, mais parallèle (Fig. 3), et toutes les conclusions du chapitre précédent lui sont applicables.

Figure 3
Définition . Le centre de gravité d'un corps solide est le centre des forces de gravité parallèles des parties élémentaires de ce corps.
Rappelons que densité spécifique d'une partie élémentaire du corps s'appelle le rapport de son poids∆ P je au volume ∆ V je : γ je = ∆ P je/ ∆ V je . Pour un corps homogène cette valeur est constante :γ je = γ = P./ V.
Remplacer ∆ dans (2) P je = γ je ∙∆ V je au lieu de P je, en tenant compte de la dernière remarque et en réduisant le numérateur et le dénominateur deg, on a expressions pour les coordonnées du centre de gravité d'un corps homogène:
xc = (Σ ∆ VI∙ x je)/(Σ ∆ VI);
oui c = (Σ ∆ VI∙ et je )/(Σ ∆ VI);(3)
zc = (Σ ∆ VI∙ z je )/(Σ ∆ VI).
Plusieurs théorèmes sont utiles pour déterminer le centre de gravité.
1) Si un corps homogène a un plan de symétrie, alors son centre de gravité est dans ce plan.
Si les axes X Et à situé dans ce plan de symétrie, alors pour chaque point de coordonnées. Et la coordonnée d’après (3), sera égal à zéro, car au total Tous les membres de signes opposés sont détruits par paires. Cela signifie que le centre de gravité est situé dans le plan de symétrie.
2) Si un corps homogène a un axe de symétrie, alors le centre de gravité du corps est sur cet axe.
En effet, dans ce cas, si l'axeztracer le long de l'axe de symétrie, pour chaque point avec des coordonnéesvous pouvez trouver un point avec des coordonnées et coordonne et , calculé à l'aide des formules (3), sera égal à zéro.
Le troisième théorème se démontre de la même manière.
3) Si un corps homogène a un centre de symétrie, alors le centre de gravité du corps est en ce point.
Et quelques commentaires supplémentaires.
D'abord. Si le corps peut être divisé en parties pour lesquelles le poids et la position du centre de gravité sont connus, alors il n'est pas nécessaire de considérer chaque point, et dans les formules (3) P je – déterminé comme le poids de la pièce correspondante et– comme les coordonnées de son centre de gravité.
Deuxième. Si le corps est homogène, alors le poids d'une partie individuelle de celui-ci, Où - la densité du matériau à partir duquel le corps est fabriqué, et VI - le volume de cette partie du corps. Et les formules (3) prendront une forme plus pratique. Par exemple,
Et de même, où - le volume de tout le corps.
Troisième remarque. Laissez le corps avoir la forme d'une plaque mince avec une superficie F et épaisseur t, allongé dans l'avion Oxy. Remplacement dans (3)∆ V je =t ∙ ∆F je , on obtient les coordonnées du centre de gravité d'une plaque homogène:
xc = (Σ ∆ Fi∙ x je) / (Σ ∆ Fi);
oui c = (Σ ∆ Fi∙ et je ) / (Σ ∆ Fi).
zc = (Σ ∆ Fi∙ z je ) / (Σ ∆ Fi).
Où – les coordonnées du centre de gravité des plaques individuelles ;– superficie totale du corps.
Quatrième note. Pour un corps en forme de fine tige incurvée de longueur L avec section transversale un volume élémentaire∆ V je = un ∙∆ L je , C'est pourquoi coordonnées du centre de gravité d'une fine tige incurvée sera égal :
xc = (Σ ∆ L je∙ x je)/(Σ ∆ L je);
oui c = (Σ ∆ L je∙ et je )/(Σ ∆ L je);(4)
zc = (Σ ∆ L je∙ z je )/(Σ ∆ L je).
Où – coordonnées du centre de gravitéje-ème section; .
A noter que, selon la définition, le centre de gravité est un point géométrique ; il peut aussi se situer en dehors des limites d'un corps donné (par exemple pour un anneau).
Note.
Dans cette section du cours, nous ne faisons pas de différence entre la gravité, la gravité et le poids corporel. En réalité, la gravité est la différence entre la force gravitationnelle de la Terre et la force centrifuge provoquée par sa rotation.
Coordonnées des centres de gravité des corps inhomogènes.
Coordonnées du centre de gravité solide inhomogène(Fig.4) dans le système de référence sélectionné sont déterminés comme suit :

Figure 4



Où - poids par unité de volume d'un corps (gravité spécifique)
![]() - le poids du corps entier.
- le poids du corps entier.
surface non uniforme(Fig. 5), alors les coordonnées du centre de gravité dans le système de référence sélectionné sont déterminées comme suit :

Figure 5
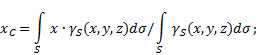

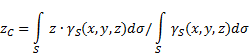
Où - poids par unité de surface corporelle,
![]() - le poids du corps entier.
- le poids du corps entier.
Si le solide est ligne non uniforme(Fig. 6), alors les coordonnées du centre de gravité dans le système de référence sélectionné sont déterminées comme suit :

Figure 6

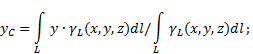

Où - poids par longueur du corps,
Poids du corps entier.
Méthodes de détermination des coordonnées du centre de gravité.
Sur la base des formules générales obtenues ci-dessus, il est possible d'indiquer des méthodes spécifiques déterminer les coordonnées des centres de gravité des corps.
1. Symétrie. Si un corps homogène a un plan, un axe ou un centre de symétrie (Fig. 7), alors son centre de gravité se situe respectivement dans le plan de symétrie, l'axe de symétrie ou au centre de symétrie.

Figure 7
2. Scission. Le corps est divisé en un nombre fini de parties (Fig. 8), pour chacune desquelles la position du centre de gravité et la superficie sont connues.

Figure 8
S = S 1 + S 2.
3.Méthode des zones négatives. Un cas particulier de la méthode de partitionnement (Fig. 9). Elle s'applique aux corps comportant des découpes si les centres de gravité du corps sans découpe et de la partie découpée sont connus. Un corps en forme de plaque avec une découpe est représenté par une combinaison d'une plaque pleine (sans découpe) avec une surface S1 et la surface de la partie coupée S2.

Figure 9
S = S1 - S2.
4.Méthode de regroupement. C'est un bon complément aux deux dernières méthodes. Après avoir divisé une figure en ses éléments constitutifs, il convient d'en combiner à nouveau certains afin de simplifier ensuite la solution en tenant compte de la symétrie de ce groupe.
Centres de gravité de certains corps homogènes.
1) Centre de gravité d'un arc de cercle. Considérez l'arc UN B rayonR. avec angle central. Par symétrie, le centre de gravité de cet arc se situe sur l'axeBœuf(Fig. 10).

Figure 10
Trouvons la coordonnée selon la formule . Pour ce faire, sélectionnez sur l'arc UN Bélément MM ’ longueur, dont la position est déterminée par l'angle. Coordonner Xélément MM' volonté. Remplacer ces valeurs X Et d je et en gardant à l’esprit que l’intégrale doit s’étendre sur toute la longueur de l’arc, on obtient :
![]()
où L est la longueur de l'arc AB, égale à .
De là, nous constatons finalement que le centre de gravité d'un arc de cercle se trouve sur son axe de symétrie à une distance du centreÔ égal
où est l'angle mesuré en radians.
2) Centre de gravité de l'aire du triangle. Considérons un triangle situé dans le plan Oxy, dont les coordonnées des sommets sont connues : Un je (x je,et je ), (je= 1,2,3). Briser le triangle en bandes étroites parallèles au côté UN 1 UN 2, on arrive à la conclusion que le centre de gravité du triangle doit appartenir à la médiane UN 3 M 3 (Fig. 11).

Figure 11
Briser un triangle en bandes parallèles au côté UN 2 UN 3, on peut vérifier qu'il doit se situer sur la médiane UN 1 M 1 . Ainsi, le centre de gravité d'un triangle se situe au point d'intersection de ses médianes, qui, comme on le sait, sépare un tiers de chaque médian, en comptant à partir du côté correspondant.
En particulier, pour la médiane UN 1 M 1 on obtient, en tenant compte du fait que les coordonnées du point M 1 - c'est la moyenne arithmétique des coordonnées des sommets UN 2 et UN 3 :
xc = X 1 + (2/3) ∙ (XM 1 - X 1 ) = X 1 + (2/3) ∙ [(X 2 + X 3 )/2 - X 1 ] = (X 1 + X 2 + X 3 )/3.
Ainsi, les coordonnées du centre de gravité du triangle sont la moyenne arithmétique des coordonnées de ses sommets :
X c =(1/3) Σ x je ; oui c =(1/3) Σ et je .
3) Centre de gravité de l'aire d'un secteur circulaire. Considérons un secteur de cercle de rayon R. avec angle central 2α , situé symétriquement par rapport à l'axe Bœuf (Fig.12) .
Il est évident que oui c = 0, et la distance entre le centre du cercle à partir duquel ce secteur est coupé et son centre de gravité peut être déterminée par la formule :

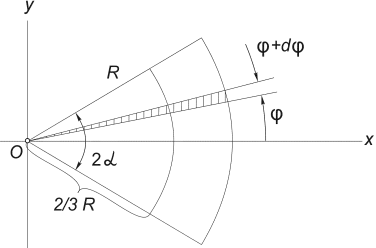
Figure 12
La façon la plus simple de calculer cette intégrale est de diviser le domaine d'intégration en secteurs élémentaires d'un angle dφ . Précis à l'infinitésimal du premier ordre, un tel secteur peut être remplacé par un triangle de base égale à R. × dφ et la hauteur R.. L'aire d'un tel triangle dF =(1/2)R. 2 ∙ dφ , et son centre de gravité est à une distance de 2/3 R. du sommet, donc dans (5) on met X = (2/3)R.∙ cosφ. Remplacement en (5) F= α R. 2, on obtient :

A l'aide de la dernière formule, on calcule notamment la distance au centre de gravité demi-cercle.
En substituant α = π /2 dans (2), on obtient : X c = (4 R.)/(3π) ≅ 0,4 R. .
Exemple 1.Déterminons le centre de gravité du corps homogène représenté sur la Fig. 13.

Figure 13
Solution.Le corps est homogène, composé de deux parties de forme symétrique. Coordonnées de leurs centres de gravité :
Leurs volumes :
Par conséquent, les coordonnées du centre de gravité du corps
Exemple 2. Trouvons le centre de gravité d'une plaque pliée à angle droit. Les dimensions sont indiquées sur le dessin (Fig. 14).

Figure 14
Solution. Coordonnées des centres de gravité :
0.
Domaines :
C'est pourquoi:
Exemple 3.
Sur une feuille carrée
cm trou carré coupé
cm (Fig. 15). Trouvons le centre de gravité de la feuille. Exemple 4. Trouvez la position du centre de gravité de la plaque illustrée à la Fig. 16. Les dimensions sont indiquées en centimètres.

Figure 16
Solution. Divisons la plaque en figures (Fig. 17), centres dont la gravité est connue.
Les aires de ces figures et les coordonnées de leurs centres de gravité :
1) un rectangle de 30 et 40 cm de côté,S 1 =30 ∙ 40=1200cm 2 ; x1=15cm; à 1 =20cm.
2) un triangle rectangle d'une base de 50 cm et d'une hauteur de 40 cm ;S 2 =0,5 ∙ 50 ∙ 40= 1000cm 2 ; X 2 =30+50/3=46,7 cm ; oui 2 =40/3 =13,3cm;
3) cercle de rayon demi-cercle r = 20 cm ;S 3 =0,5 ∙π∙ 20 2 =628 cm 2 ; X 3 =4 R. /3 π =8,5cm; à
Solution. Rappelons qu'en physique la densité d'un corpsρ et sa densitégsont liés par la relation :γ = ρ g , Oùg - Accélération de la gravité. Pour trouver la masse d'un corps aussi homogène, il faut multiplier la densité par son volume.

Figure 19
Le terme « linéaire » ou densité « linéaire » signifie que pour déterminer la masse d'un truss rod, il faut multiplier la densité linéaire par la longueur de cette tige.
Pour résoudre le problème, vous pouvez utiliser la méthode de partitionnement. En représentant une ferme donnée comme une somme de 6 tiges individuelles, on obtient :
OùL je longueurje le truss rod, etx je , et je - coordonnées de son centre de gravité.
La solution à ce problème peut être simplifiée en regroupant les 5 dernières barres de la ferme. Il est facile de voir qu'ils forment une figure avec un centre de symétrie situé au milieu de la quatrième tige, là où se trouve le centre de gravité de ce groupe de tiges.
Ainsi, une ferme donnée peut être représentée par une combinaison de seulement deux groupes de tiges.
Le premier groupe est constitué de la première tige, pour elleL 1 = 4 m,X 1 = 0 m,oui 1 = 2 m Le deuxième groupe de tiges se compose de cinq tiges, pour celaL 2 = 20 m,X 2 = 3 m,oui 2 = 2 m.
Les coordonnées du centre de gravité de la ferme se trouvent à l'aide de la formule :
X c = (L 1 ∙ X 1 + L 2 ∙ X 2 )/(L 1 + L 2 ) = (4∙0 + 20∙3)/24 = 5/2m;
oui c = (L 1 ∙ oui 1 + L 2 ∙ oui 2 )/(L 1 + L 2 ) = (4∙2 + 20∙2)/24 = 2 m.
Notez que le centre AVEC se trouve sur la ligne droite reliant AVEC 1 et AVEC 2 et divise le segment AVEC 1 AVEC 2 concernant : AVEC 1 AVEC/SS 2 = (X c - X 1 )/(X 2 - X c ) = L 2 / L 1 = 2,5/0,5.
Questions d'auto-test
- Qu'est-ce qu'on appelle le centre des forces parallèles ?
- Comment sont déterminées les coordonnées du centre des forces parallèles ?
- Comment déterminer le centre de forces parallèles dont la résultante est nulle ?
- Quelles propriétés possède le centre des forces parallèles ?
- Quelles formules sont utilisées pour calculer les coordonnées du centre des forces parallèles ?
- Comment s'appelle le centre de gravité d'un corps ?
- Pourquoi les forces gravitationnelles de la Terre agissant sur un point d'un corps peuvent-elles être considérées comme un système de forces parallèles ?
- Écrire la formule pour déterminer la position du centre de gravité des corps inhomogènes et homogènes, la formule pour déterminer la position du centre de gravité des sections plates ?
- Écrire la formule pour déterminer la position du centre de gravité de formes géométriques simples : rectangle, triangle, trapèze et demi-cercle ?
- Qu'appelle-t-on le moment statique de l'aire ?
- Donnez un exemple d'un corps dont le centre de gravité est situé à l'extérieur du corps.
- Comment les propriétés de symétrie sont-elles utilisées pour déterminer les centres de gravité des corps ?
- Quelle est l'essence de la méthode des poids négatifs ?
- Où se situe le centre de gravité d'un arc de cercle ?
- Quelle construction graphique peut-on utiliser pour trouver le centre de gravité d'un triangle ?
- Notez la formule qui détermine le centre de gravité d'un secteur circulaire.
- À l'aide de formules qui déterminent les centres de gravité d'un triangle et d'un secteur circulaire, dérivez une formule similaire pour un segment circulaire.
- Quelles formules sont utilisées pour calculer les coordonnées des centres de gravité des corps homogènes, des figures plates et des lignes ?
- Qu'appelle-t-on le moment statique de l'aire d'une figure plane par rapport à l'axe, comment est-il calculé et quelle dimension a-t-il ?
- Comment déterminer la position du centre de gravité d'une zone si la position des centres de gravité de ses différentes parties est connue ?
- Quels théorèmes auxiliaires sont utilisés pour déterminer la position du centre de gravité ?
Auteur: Prenons un corps de forme arbitraire. Est-il possible de l'accrocher à un fil pour qu'une fois suspendu, il conserve sa position (c'est-à-dire qu'il ne commence pas à tourner) lorsque n'importe lequel orientation initiale (Fig. 27.1) ?
En d’autres termes, existe-t-il un point par rapport auquel la somme des moments de gravité agissant sur diverses parties du corps serait égale à zéro à n'importe lequel orientation du corps dans l’espace ?
Lecteur: Oui, je pense. Ce point est appelé centre de gravité du corps.
Preuve. Pour simplifier, considérons un corps sous la forme d'une plaque plane de forme arbitraire, arbitrairement orientée dans l'espace (Fig. 27.2). Prenons le système de coordonnées X 0à avec le début au centre de masse - point AVEC, Alors xC = 0, en C = 0.
 Imaginons ce corps comme un ensemble d'un grand nombre de masses ponctuelles je suis, dont la position de chacun est spécifiée par le rayon vecteur.
Imaginons ce corps comme un ensemble d'un grand nombre de masses ponctuelles je suis, dont la position de chacun est spécifiée par le rayon vecteur.
Par définition, le centre de masse est , et la coordonnée xC = .
Puisque dans le système de coordonnées nous avons adopté xC= 0, alors . Multiplions cette égalité par g et nous obtenons
Comme on peut le voir sur la Fig. 27.2, | x je| - c'est l'épaule du pouvoir. Et si x je> 0, alors le moment de force M je> 0, et si xj < 0, то MJ < 0, поэтому с учетом знака можно утверждать, что для любого x je le moment de force sera égal M je = m je gx je . Alors l'égalité (1) est équivalente à l'égalité , où M je– le moment de gravité. Cela signifie qu'avec une orientation arbitraire du corps, la somme des moments de gravité agissant sur le corps sera égale à zéro par rapport à son centre de masse.
Pour que le corps considéré soit en équilibre, il faut lui appliquer au point AVEC forcer T = mg, dirigé verticalement vers le haut. Le moment de cette force par rapport au point AVECégal à zéro.
Puisque notre raisonnement ne dépendait en aucune façon de la manière dont le corps est orienté exactement dans l'espace, nous avons prouvé que le centre de gravité coïncide avec le centre de masse, ce que nous devions prouver.
Problème 27.1. Trouver le centre de gravité d'une tige en apesanteur de longueur je, aux extrémités duquel sont fixées deux masses ponctuelles T 1 et T 2 .
| T 1 T 2 je | Solution. Nous ne chercherons pas le centre de gravité, mais le centre de masse (puisque c'est la même chose). Introduisons l'axe X(Fig. 27.3). |
| xC =? | |
Répondre: à distance de la masse T 1 .
ARRÊT! Décidez vous-même : B1–B3.
Déclaration 1 . Si un corps plat homogène possède un axe de symétrie, le centre de gravité est sur cet axe.
En effet, pour toute masse ponctuelle je suis, située à droite de l'axe de symétrie, se trouve la même masse ponctuelle située symétriquement par rapport à la première (Fig. 27.4). Dans ce cas, la somme des moments de forces .
Puisque le corps entier peut être représenté comme divisé en paires de points similaires, le moment de gravité total par rapport à tout point situé sur l'axe de symétrie est égal à zéro, ce qui signifie que le centre de gravité du corps est situé sur cet axe. . Cela conduit à une conclusion importante : si un corps a plusieurs axes de symétrie, alors le centre de gravité se situe à l'intersection de ces axes(Fig. 27.5).
Riz. 27,5 
Déclaration 2. Si deux corps ont des masses T 1 et T 2 sont reliés en un seul, alors le centre de gravité d'un tel corps se situera sur un segment de droite reliant les centres de gravité du premier et du deuxième corps (Fig. 27.6).
Riz. 27.6 ![]() Riz. 27,7
Riz. 27,7
Preuve. Positionnons le corps composite de manière à ce que le segment reliant les centres de gravité des corps soit vertical. Alors la somme des moments de gravité du premier corps par rapport au point AVEC 1 est égal à zéro, et la somme des moments de gravité du deuxième corps par rapport au point AVEC 2 est égal à zéro (Fig. 27.7).
remarquerez que épaule gravité de n'importe quelle masse ponctuelle je la même chose par rapport à tout point situé sur le segment AVEC 1 AVEC 2, et donc le moment de gravité par rapport à tout point situé sur le segment AVEC 1 AVEC 2, pareil. Par conséquent, la force gravitationnelle du corps entier est nulle par rapport à n’importe quel point du segment. AVEC 1 AVEC 2. Ainsi, le centre de gravité du corps composite se situe sur le segment AVEC 1 AVEC 2 .
Une conclusion pratique importante découle de l’énoncé 2, qui est clairement formulé sous forme d’instructions.
Instructions,
comment trouver le centre de gravité d'un corps solide s'il peut être brisé
en parties dont les positions des centres de gravité de chacune sont connues
1. Chaque pièce doit être remplacée par une masse située au centre de gravité de cette pièce.
2. Trouver le centre de masse(et c'est la même chose que le centre de gravité) du système de masses ponctuelles résultant, en choisissant un système de coordonnées pratique X 0à, selon les formules :
En fait, disposons le corps composite de manière à ce que le segment AVEC 1 AVEC 2 était horizontal et accrochez-le à des fils à certains endroits AVEC 1 et AVEC 2 (Fig. 27.8, UN). Il est clair que le corps sera en équilibre. Et cet équilibre ne sera pas perturbé si l'on remplace chaque corps par des masses ponctuelles T 1 et T 2 (Fig. 27.8, b).
 Riz. 27,8
Riz. 27,8
ARRÊT! Décidez vous-même : C3.
Problème 27.2. Des boules de masse sont placées à deux sommets d'un triangle équilatéral T chaque. Une boule de masse 2 est placée au troisième sommet T(Fig. 27.9, UN). Côté triangulaire UN. Déterminez le centre de gravité de ce système.
| T 2T UN |  Riz. 27.9 Riz. 27.9 |
| xC = ? en C = ? | |
Solution. Introduisons le système de coordonnées X 0à(Fig. 27.9, b). Alors
![]() ,
,
 .
.
Répondre: xC = UN/2; ; le centre de gravité se trouve à mi-hauteur ANNONCE.
Manuel pour la 7e année
§ 25.3. Comment trouver le centre de gravité d'un corps ?
Rappelons que le centre de gravité est le point où la gravité est appliquée. Voyons comment trouver expérimentalement la position du centre de gravité d'un corps plat - par exemple, une figure de forme arbitraire découpée dans du carton (voir travail de laboratoire n° 12).
Nous accrochons la figurine en carton avec une épingle ou un clou afin qu'elle puisse tourner librement autour d'un axe horizontal passant par le point O (Fig. 25.4, a). Cette figure peut alors être considérée comme un levier avec un point d'appui O.
Riz. 25.4. Comment trouver expérimentalement le centre de gravité d'une figure plate
Lorsqu’une figure est en équilibre, les forces qui agissent sur elle s’équilibrent. Il s'agit de la force gravitationnelle F t appliquée au centre de gravité de la figure T, et de la force élastique F exr appliquée au point O (cette force est appliquée depuis le côté d'une épingle ou d'un clou).
Ces deux forces ne s'équilibrent que si les points d'application de ces forces (points T et O) se situent sur la même verticale (voir Fig. 25.4, a). Sinon, la gravité fera tourner la figure autour du point O (Fig. 25.4, b).
Ainsi, lorsque la figurine est en équilibre, le centre de gravité se trouve sur la même verticale que le point de suspension O. Cela permet de déterminer la position du centre de gravité de la figurine. À l'aide d'un fil à plomb, nous traçons une ligne verticale passant par le point de suspension (ligne bleue sur la Fig. 25.4, c). Le centre de gravité du corps se situe sur la ligne tracée. Répétons cette expérience avec une position différente du point de suspension. En conséquence, nous obtenons une deuxième ligne sur laquelle se trouve le centre de gravité du corps (ligne verte sur la Fig. 25.4, d). Par conséquent, à l'intersection de ces lignes se trouve le centre de gravité souhaité du corps (point rouge G sur la Fig. 25.4, d).
Dans la pratique de l'ingénierie, il arrive qu'il soit nécessaire de calculer les coordonnées du centre de gravité d'une figure plate complexe constituée d'éléments simples pour lesquels l'emplacement du centre de gravité est connu. Cette tâche fait partie de la tâche de détermination...
Caractéristiques géométriques des sections transversales composites de poutres et de tiges. Souvent, les ingénieurs concepteurs de matrices de découpe doivent faire face à des questions similaires lors de la détermination des coordonnées du centre de pression, les développeurs de schémas de chargement pour divers véhicules lors du placement des marchandises, les concepteurs de structures métalliques de construction lors de la sélection des sections transversales des éléments et, bien sûr, étudiants lorsqu'ils étudient les disciplines « Mécanique théorique » et « Résistance des matériaux ».
Bibliothèque de figures élémentaires.

Pour les figures planes symétriques, le centre de gravité coïncide avec le centre de symétrie. Le groupe symétrique d'objets élémentaires comprend : un cercle, un rectangle (y compris un carré), un parallélogramme (y compris un losange), un polygone régulier.
Sur les dix chiffres présentés dans la figure ci-dessus, seuls deux sont basiques. Autrement dit, en utilisant des triangles et des secteurs de cercles, vous pouvez combiner presque toutes les figures présentant un intérêt pratique. Toutes les courbes arbitraires peuvent être divisées en sections et remplacées par des arcs de cercle.
Les huit figures restantes sont les plus courantes, c'est pourquoi elles ont été incluses dans cette bibliothèque unique. Dans notre classification, ces éléments ne sont pas fondamentaux. Un rectangle, un parallélogramme et un trapèze peuvent être formés à partir de deux triangles. Un hexagone est la somme de quatre triangles. Un segment de cercle est la différence entre un secteur de cercle et un triangle. Le secteur annulaire d'un cercle est la différence entre deux secteurs. Un cercle est un secteur de cercle d'angle α=2*π=360˚. Un demi-cercle est donc un secteur de cercle d’angle α=π=180˚.
Calcul sous Excel des coordonnées du centre de gravité d'une figure composée.
Il est toujours plus facile de transmettre et de percevoir une information en considérant un exemple que d'étudier la question à l'aide de calculs purement théoriques. Considérons la solution au problème « Comment trouver le centre de gravité ? » en utilisant l'exemple de la figure composite présentée dans la figure située sous ce texte.

La section composite est un rectangle (de dimensions un1 =80mm, b1 =40 mm), auquel a été ajouté en haut à gauche un triangle isocèle (avec la taille de la base un2 =24 mm et hauteur h2 =42 mm) et dans lequel a été découpé un demi-cercle en haut à droite (avec le centre au point de coordonnées X03 =50mm et oui03 =40 mm, rayon r3 =26mm).
Nous utiliserons un programme pour vous aider à effectuer les calculs MS Excel ou un programme OOo Calc . N’importe lequel d’entre eux s’acquittera facilement de notre tâche !
Dans les cellules avec jaune nous allons le remplir auxiliaire préliminaire calculs .
Nous calculons les résultats dans des cellules avec un remplissage jaune clair.
Bleu la police est donnée initiale .
Noir la police est intermédiaire résultats des calculs .
Rouge la police est final résultats des calculs .
Nous commençons à résoudre le problème - nous commençons la recherche des coordonnées du centre de gravité de la section.
Donnée initiale:
1. Nous écrirons en conséquence les noms des figures élémentaires formant une section composite
à la cellule D3 : Rectangle
à la cellule E3 : Triangle
à la cellule F3 : Demi-cercle
2. A l’aide de la « Bibliothèque de figures élémentaires » présentée dans cet article, nous déterminerons les coordonnées des centres de gravité des éléments de la section composite xci Et yci en mm par rapport aux axes 0x et 0y arbitrairement sélectionnés et écrivez
à la cellule D4 : =80/2 = 40,000
xc 1 = un 1 /2
à la cellule D5 : =40/2 =20,000
yc 1 = b 1 /2
à la cellule E4 : =24/2 =12,000
xc 2 = un 2 /2
à la cellule E5 : =40+42/3 =54,000
yc 2 = b 1 + h 2 /3
à la cellule F4 : =50 =50,000
xc 3 = X03
à la cellule F5 : =40-4*26/3/PI() =28,965
yc 3 = oui 03 -4* r3 /3/ π
3. Calculons les aires des éléments F 1 , F 2 , F3 en mm2, toujours en utilisant les formules de la section « Bibliothèque de figures élémentaires »
dans la cellule D6 : =40*80 =3200
F1 = un 1 * b1
dans la cellule E6 : =24*42/2 =504
F2 = a2 *h2 /2
dans la cellule F6 : =-PI()/2*26^2 =-1062
F3 =-π/2*r3 ^2
L'aire du troisième élément - le demi-cercle - est négative car c'est une découpe - un espace vide !

Calcul des coordonnées du centre de gravité :
4. Déterminer la superficie totale de la figure finale F0 en mm2
dans la cellule fusionnée D8E8F8 : =D6+E6+F6 =2642
F0 = F 1 + F 2 + F3
5. Calculons les moments statiques d'une figure composite Sexe Et Sy en mm3 par rapport aux axes sélectionnés 0x et 0y
dans la cellule fusionnée D9E9F9 : =D5*D6+E5*E6+F5*F6 =60459
Sexe = yc1 * F1 + yc2 *F2 + yc3 *F3
dans la cellule fusionnée D10E10F10 : =D4*D6+E4*E6+F4*F6 =80955
Sy = xc1 * F1 + xc2 *F2 + xc3 *F3
6. Et enfin, calculons les coordonnées du centre de gravité de la section composite Xc Et Oui en mm dans le système de coordonnées sélectionné 0x - 0y
dans la cellule fusionnée D11E11F11 : =D10/D8 =30,640
Xc = Sy / F0
dans la cellule fusionnée D12E12F12 : =D9/D8 =22,883
Yc =Sx /F0
Le problème est résolu, le calcul dans Excel est terminé - les coordonnées du centre de gravité de la section, compilées à l'aide de trois éléments simples, ont été trouvées !
Conclusion.
L'exemple de l'article a été choisi très simple afin de faciliter la compréhension de la méthodologie de calcul du centre de gravité d'une section complexe. La méthode consiste à diviser toute figure complexe en éléments simples avec des emplacements connus des centres de gravité et à effectuer des calculs finaux pour la section entière.
Si la section est constituée de profilés laminés - angles et canaux, il n'est alors pas nécessaire de les diviser en rectangles et carrés avec des secteurs circulaires découpés « π/2 ». Les coordonnées des centres de gravité de ces profils sont données dans les tableaux GOST, c'est-à-dire que l'angle et le canal seront les éléments élémentaires de base dans vos calculs de sections composites (ça ne sert à rien de parler de poutres en I, tuyaux, tiges et hexagones - ce sont des sections à symétrie centrale).
Bien entendu, l’emplacement des axes de coordonnées n’affecte pas la position du centre de gravité de la figurine ! Par conséquent, choisissez un système de coordonnées qui simplifie vos calculs. Si, par exemple, je devais faire pivoter le système de coordonnées de 45˚ dans le sens des aiguilles d'une montre dans notre exemple, alors le calcul des coordonnées des centres de gravité d'un rectangle, d'un triangle et d'un demi-cercle se transformerait en une autre étape de calcul distincte et fastidieuse qui ne peut pas être effectuée " dans la tête".
Le fichier de calcul Excel présenté ci-dessous n'est pas un programme dans ce cas. Il s'agit plutôt d'une esquisse d'une calculatrice, d'un algorithme, d'un modèle qui suit dans chaque cas spécifique créez votre propre séquence de formules pour les cellules avec un remplissage jaune vif.
Ainsi, vous savez maintenant comment trouver le centre de gravité de n’importe quelle section ! Le calcul complet de toutes les caractéristiques géométriques des sections composites complexes arbitraires sera abordé dans l'un des prochains articles de la section « ». Suivez l'actualité sur le blog.
Pour recevoir informations sur la sortie de nouveaux articles et pour téléchargement des fichiers du programme de travail Je vous demande de vous abonner aux annonces dans la fenêtre située en fin d'article ou dans la fenêtre en haut de page.
Après avoir renseigné votre adresse email et cliqué sur le bouton « Recevoir les annonces d'articles » N'OUBLIEZ PAS CONFIRMEZ VOTRE ABONNEMENT en cliquant sur le lien dans une lettre qui vous parviendra immédiatement à l'adresse email indiquée (parfois dans le dossier « Courrier indésirable » )!
Quelques mots sur le verre, la pièce de monnaie et les deux fourchettes, qui sont représentés dans « l'icône d'illustration » au tout début de l'article. Beaucoup d’entre vous connaissent certainement cette « astuce » qui suscite les regards admiratifs des enfants et des adultes non-initiés. Le sujet de cet article est le centre de gravité. C'est lui et le point d'appui, jouant avec notre conscience et notre expérience, qui trompent tout simplement notre esprit !
Le centre de gravité du système « fourchette+pièce » est toujours situé sur fixé distance verticalement vers le bas du bord de la pièce, qui à son tour est le point d’appui. C'est une position d'équilibre stable ! Si vous secouez les fourches, il devient immédiatement évident que le système s'efforce de reprendre sa position stable précédente ! Imaginons un pendule - un point de fixation (= le point d'appui d'une pièce de monnaie sur le bord d'un verre), une tige-axe du pendule (= dans notre cas, l'axe est virtuel, puisque la masse des deux fourchettes est répartis dans différentes directions de l'espace) et une charge en bas de l'axe (= le centre de gravité de l'ensemble du système « fourchette » + pièce de monnaie"). Si vous commencez à dévier le pendule de la verticale dans n'importe quelle direction (avant, arrière, gauche, droite), il reviendra inévitablement à sa position d'origine sous l'influence de la gravité. état d'équilibre stable(la même chose arrive avec nos fourchettes et nos pièces de monnaie) !
Si vous ne comprenez pas, mais que vous voulez comprendre, découvrez-le vous-même. C’est très intéressant d’y « arriver » soi-même ! J'ajouterai que le même principe d'utilisation d'un équilibre stable est également mis en œuvre dans le jouet Vanka-stand-up. Seul le centre de gravité de ce jouet est situé au-dessus du point d'appui, mais en dessous du centre de l'hémisphère de la surface d'appui.
Je suis toujours heureux de voir vos commentaires, chers lecteurs !!!
Demander, RESPECTANT travail de l'auteur, télécharger le fichier APRÈS L'ABONNEMENT pour les annonces d'articles.










