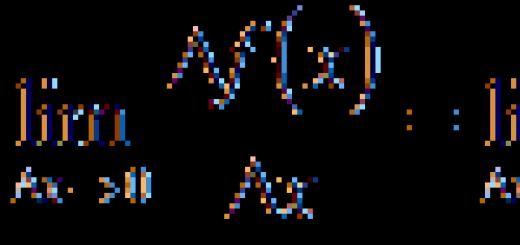Différentiel complet. Signification géométrique du différentiel total. Plan tangent et normal à la surface. Incrément total et différentiel total Exemples de résolution de problèmes

CALCUL DIFFÉRENTIEL DE FONCTIONS DE PLUSIEURS VARIABLES.

Concepts et définitions de base.

Lorsqu'on considère les fonctions de plusieurs variables, nous nous limiterons à Description détaillée fonctions de deux variables, car tous les résultats obtenus seront valables pour des fonctions d'un nombre arbitraire de variables.

Si chaque paire de nombres (x, y), indépendants les uns des autres d'un certain ensemble, selon une règle, est associée à une ou plusieurs valeurs de la variable z, alors la variable z est appelée fonction de deux variables.

Si une paire de nombres (x, y) correspond à une valeur z, alors la fonction est appelée non ambigu, et s’il y en a plus d’un, alors – polysémantique.

Domaine de définition la fonction z est l'ensemble des paires (x, y) pour lesquelles la fonction z existe.

Quartier d'un point M 0 (x 0, y 0) de rayon r est l'ensemble de tous les points (x, y) qui satisfont à la condition.

Le nombre A s'appelle limite fonction f(x, y) lorsque le point M(x, y) tend vers le point M 0 (x 0, y 0), si pour chaque nombre e > 0 il existe un nombre r > 0 tel que pour tout point M (x, y), pour lequel la condition est vraie

la condition est également vraie .

Écrire:

Soit le point M 0 (x 0, y 0) appartenir au domaine de définition de la fonction f(x, y). Alors la fonction z = f(x, y) est appelée continu au point M 0 (x 0, y 0), si

(1)

et le point M(x, y) tend vers le point M 0 (x 0, y 0) de manière arbitraire.

Si à un moment donné la condition (1) n’est pas satisfaite, alors ce point est appelé point de rupture fonctions f(x, y). Cela peut être dans les cas suivants :

1) La fonction z = f(x, y) n'est pas définie au point M 0 (x 0, y 0).

2) Il n'y a pas de limite.

3) Cette limite existe, mais elle n'est pas égale à f(x 0 , y 0).

Propriétés des fonctions de plusieurs variables liées à leur continuité.

Propriété. Si la fonction f(x, y, ...) est définie et continue dans un domaine D fermé et borné, alors il y a au moins un point dans ce domaine

N(x 0 , y 0 , …), tel que pour les points restants l'inégalité est vraie

f(x 0 , y 0 , …) ³ f(x, y, …)

ainsi que le point N 1 (x 01, y 01, ...), tel que pour tous les autres points l'inégalité est vraie

f(x 01 , y 01 , …) £ f(x, y, …)

alors f(X 0 , y 0 , …) = M – valeur la plus élevée fonctions, et f(x 01 , y 01 , ...) = m – plus petite valeur fonctions f(x, y, …) dans le domaine D.

Une fonction continue dans un domaine fermé et borné D atteint au moins une fois valeur la plus élevée et une fois le plus petit.

Propriété. Si la fonction f(x, y, …) est définie et continue dans un domaine borné fermé D, et M et m sont respectivement les plus grandes et les plus petites valeurs de la fonction dans ce domaine, alors pour tout point m О il y a un point

N 0 (x 0 , y 0 , …) tel que f(x 0 , y 0 , …) = m.

En termes simples, une fonction continue englobe tout ce qui se trouve dans le domaine D valeurs intermédiaires entre M et m. Une conséquence de cette propriété peut être la conclusion que si les nombres M et m sont de signes différents, alors dans le domaine D la fonction disparaît au moins une fois.

Propriété. Fonction f(x, y, …), continue dans un domaine fermé et borné D, limité dans cette région, s'il existe un nombre K tel que pour tous les points de la région l'inégalité est vraie .

Propriété. Si une fonction f(x, y, …) est définie et continue dans un domaine fermé et borné D, alors elle uniformément continu dans ce domaine, c'est-à-dire pour tout nombre positif e, il existe un nombre D > 0 tel que pour deux points quelconques (x 1, y 1) et (x 2, y 2) de la région situés à une distance inférieure à D, l'inégalité est vraie

2. Dérivées partielles. Dérivés partiels d'ordres supérieurs.

Soit une fonction z = f(x, y) dans un domaine. Prenons un point arbitraire M(x, y) et définissons l'incrément Dx sur la variable x. Alors la quantité D x z = f(x + Dx, y) – f(x, y) est appelée incrément partiel de la fonction en x.

Vous pouvez écrire

Alors ça s'appelle dérivée partielle fonctions z = f(x, y) dans x.

Désignation:

La dérivée partielle d'une fonction par rapport à y est déterminée de la même manière.

Sens géométrique la dérivée partielle (disons) est la tangente de l'angle d'inclinaison de la tangente tracée au point N 0 (x 0, y 0, z 0) à la section de la surface par le plan y = y 0.

Si une fonction f(x, y) est définie dans un domaine D, alors ses dérivées partielles seront également définies dans le même domaine ou une partie de celui-ci.

Nous appellerons ces dérivées dérivées partielles du premier ordre.

Les dérivées de ces fonctions seront dérivées partielles du second ordre.

En continuant à différencier les égalités résultantes, nous obtenons des dérivées partielles d'ordres supérieurs.

Dérivées partielles de la forme etc. sont appelés dérivés mixtes.

Théorème. Si la fonction f(x, y) et ses dérivées partielles sont définies et continues au point M(x, y) et à son voisinage, alors la relation suivante est vraie :

Ceux. les dérivées partielles d'ordres supérieurs ne dépendent pas de l'ordre de différenciation.

Les différentiels d’ordre supérieur sont définis de la même manière.

…………………

Ici n est la puissance symbolique de la dérivée, qui est remplacée par la puissance réelle après y avoir élevé l'expression entre parenthèses.

Différentiel complet. Signification géométrique du différentiel total. Plan tangent et normal à la surface.

L'expression s'appelle incrément complet fonctions f(x, y) en un certain point (x, y), où a 1 et a 2 sont des fonctions infinitésimales pour Dх ® 0 et Dу ® 0, respectivement.

Différentiel complet la fonction z = f(x, y) est appelée la partie linéaire principale par rapport à Dx et Dу de l'incrément de la fonction Dz au point (x, y).

Pour une fonction d'un nombre arbitraire de variables :

Exemple 3.1. Trouvez le différentiel complet de la fonction.

La signification géométrique de la différentielle totale d'une fonction de deux variables f(x, y) au point (x 0, y 0) est l'incrément de l'application (coordonnées z) du plan tangent à la surface lors du déplacement du point (x 0, y 0) jusqu'au point (x 0 + Dх, у 0 +Dу).

Dérivés partiels d'ordres supérieurs. : Si une fonction f(x, y) est définie dans un domaine D, alors ses dérivées partielles seront également définies dans le même domaine ou une partie de celui-ci. Nous appellerons ces dérivées dérivées partielles du premier ordre.

Les dérivées de ces fonctions seront des dérivées partielles du second ordre.

En continuant à différencier les égalités résultantes, nous obtenons des dérivées partielles d'ordres supérieurs. Définition. Dérivées partielles de la forme etc. sont appelés dérivés mixtes. Théorème de Schwartz:

Si les dérivées partielles d'ordres supérieurs f.m.p. sont continues, alors les dérivées mixtes du même ordre ne diffèrent que par l'ordre de différenciation = les unes des autres.

Ici n est la puissance symbolique de la dérivée, qui est remplacée par la puissance réelle après y avoir élevé l'expression entre parenthèses.

14. Équation du plan tangent et de la normale à la surface !

Soient N et N 0 des points de cette surface. Traçons une ligne droite NN 0. Le plan qui passe par le point N 0 s'appelle plan tangentà la surface si l'angle entre la sécante NN 0 et ce plan tend vers zéro, lorsque la distance NN 0 tend vers zéro.

Définition. Normaleà la surface au point N 0 est une droite passant par le point N 0 perpendiculaire au plan tangent à cette surface.

En tout point, la surface n’a qu’un seul plan tangent ou n’en a pas du tout.

Si la surface est donnée par l'équation z = f(x, y), où f(x, y) est une fonction dérivable au point M 0 (x 0, y 0), plan tangent au point N 0 (x 0 ,y 0, (x 0 ,y 0)) existe et a l'équation :

Équation de la normale à la surface en ce point:

Sens géométrique la différentielle totale d'une fonction de deux variables f(x, y) au point (x 0, y 0) est l'incrément de l'application (coordonnées z) du plan tangent à la surface lors du déplacement du point (x 0 , y 0) jusqu'au point (x 0 + Dx, y 0 +Dу).

Comme vu, signification géométrique La différentielle totale d'une fonction de deux variables est un analogue spatial de la signification géométrique de la différentielle d'une fonction d'une variable.

16. Champ scalaire et ses caractéristiques. Lignes du niveau, dérivées en direction, gradient du champ scalaire.

Si chaque point de l'espace est associé à une grandeur scalaire, alors un champ scalaire apparaît (par exemple, un champ de température, un champ potentiel électrique). Si entré Coordonnées cartésiennes, alors on note aussi ou Le terrain peut être plat s'il est central (sphérique) si cylindrique si

Surfaces et lignes planes : les propriétés des champs scalaires peuvent être étudiées visuellement à l'aide de surfaces planes. Ce sont des surfaces dans l'espace sur lesquelles il prend valeur constante. Leur équation est : . Dans un champ scalaire plat, les lignes de niveau sont des courbes sur lesquelles le champ prend une valeur constante : Dans certains cas, les lignes de niveau peuvent dégénérer en points et les surfaces de niveau en points et courbes.

Dérivée directionnelle et gradient d'un champ scalaire :

Soit le vecteur unitaire avec les coordonnées un champ scalaire. La dérivée directionnelle caractérise l'évolution du champ dans une direction donnée et est calculée à l'aide de la formule La dérivée directionnelle est le produit scalaire d'un vecteur et d'un vecteur de coordonnées , qui est appelé le gradient de la fonction et est noté . Puisque , où l'angle entre et , alors le vecteur indique la direction de l'augmentation la plus rapide du champ et son module est égal à la dérivée dans cette direction. Puisque les composantes du gradient sont des dérivées partielles, il n'est pas difficile d'obtenir les propriétés suivantes du gradient :

17. Extrema de f.m.p. Extremum local de f.m.p., conditions nécessaires et suffisantes à son existence. La plus grande et la plus petite valeur de f.m.p. en quantité limitée zone fermée.

Soit la fonction z = ƒ(x;y) définie dans un domaine D, point N(x0;y0)

Un point (x0;y0) est appelé point maximum de la fonction z=ƒ(x;y) s'il existe un d-voisinage du point (x0;y0) tel que pour tout point (x;y) différent de (xo;yo), de ce voisinage l'inégalité ƒ(x;y) est vraie<ƒ(хо;уо). Аналогично определяется точка минимума функции: для всех точек (х; у), отличных от (х0;у0), из d-окрестности точки (хо;уо) выполняется неравенство: ƒ(х;у)>ƒ(x0;y0). La valeur de la fonction au point maximum (minimum) est appelée le maximum (minimum) de la fonction. Le maximum et le minimum d’une fonction sont appelés ses extrema. Notez que, par définition, le point extremum de la fonction se situe à l’intérieur du domaine de définition de la fonction ; maximum et minimum ont un caractère local (local) : la valeur de la fonction au point (x0 ; y0) est comparée à ses valeurs en des points suffisamment proches de (x0 ; y0). Dans la région D, une fonction peut avoir plusieurs extrema ou aucun.

Conditions nécessaires(1) et suffisantes(2) d’existence :

(1) Si au point N(x0;y0) la fonction différentiable z=ƒ(x;y) a un extremum, alors ses dérivées partielles en ce point sont égales à zéro : ƒ"x(x0;y0)=0, ƒ" y(x0;y0 )=0. Commentaire. Une fonction peut avoir un extremum aux points où au moins une des dérivées partielles n’existe pas. Le point auquel les dérivées partielles du premier ordre de la fonction z ≈ ƒ(x; y) sont égales à zéro, c'est-à-dire f"x=0, f"y=0, est appelé point stationnaire de la fonction z.

Les points stationnaires et les points pour lesquels au moins une dérivée partielle n'existe pas sont appelés points critiques.

(2) Soit la fonction ƒ(x;y) en un point stationnaire (xo; y) et certains de ses environs ont des dérivées partielles continues jusqu'au second ordre inclus. Calculons au point (x0;y0) les valeurs A=f""xx(x0;y0), B=ƒ""xy(x0;y0), C=ƒ""yy(x0;y0) . Notons Alors:

1. si Δ > 0, alors la fonction ƒ(x;y) au point (x0;y0) a un extremum : maximum si A< 0; минимум, если А > 0;

2. si Δ< 0, то функция ƒ(х;у) в точке (х0;у0) экстремума не имеет.

3. Dans le cas de Δ = 0, il peut y avoir ou non un extremum au point (x0; y0). Des recherches supplémentaires sont nécessaires.

Plan tangent et normal à la surface.

plan tangent

Définition. Normaleà la surface au point N 0 est une droite passant par le point N 0 perpendiculaire au plan tangent à cette surface.

En tout point, la surface n’a qu’un seul plan tangent ou n’en a pas du tout.

Si la surface est donnée par l'équation z = f(x, y), où f(x, y) est une fonction dérivable au point M 0 (x 0, y 0), le plan tangent au point N 0 ( x 0,y 0, ( x 0 ,y 0)) existe et a l'équation :

L’équation de la normale à la surface à ce stade est :

Comme vous pouvez le constater, la signification géométrique de la différentielle totale d'une fonction de deux variables est un analogue spatial de la signification géométrique de la différentielle d'une fonction d'une variable.

Exemple. Trouver les équations du plan tangent et normal à la surface

au point M(1, 1, 1).

Équation du plan tangent :

Équation normale :

20.4. Calculs approximatifs utilisant les différentiels totaux.

Soit la fonction f(x, y) dérivable au point (x, y). Trouvons l'incrément total de cette fonction :

Si l'on substitue l'expression dans cette formule

alors on obtient une formule approximative :

Exemple. Calculez approximativement la valeur en fonction de la valeur de la fonction à x = 1, y = 2, z = 1.

À partir de l’expression donnée, nous déterminons x = 1,04 – 1 = 0,04, y = 1,99 – 2 = -0,01,

z = 1,02 – 1 = 0,02.

Trouvons la valeur de la fonction u(x, y, z) =

Trouver des dérivées partielles :

La différentielle totale de la fonction u est égale à :

La valeur exacte de cette expression est 1,049275225687319176.

20.5. Dérivés partiels d'ordres supérieurs.

Si une fonction f(x, y) est définie dans un domaine D, alors ses dérivées partielles seront également définies dans le même domaine ou une partie de celui-ci.

Nous appellerons ces dérivées dérivées partielles du premier ordre.

Les dérivées de ces fonctions seront dérivées partielles du second ordre.

En continuant à différencier les égalités résultantes, nous obtenons des dérivées partielles d'ordres supérieurs.

Définition. Dérivées partielles de la forme etc. sont appelés dérivés mixtes.

Théorème. Si la fonction f(x, y) et ses dérivées partielles sont définies et continues au point M(x, y) et à son voisinage, alors la relation suivante est vraie :

Ceux. les dérivées partielles d'ordres supérieurs ne dépendent pas de l'ordre de différenciation.

Les différentiels d’ordre supérieur sont définis de la même manière.

…………………

Ici n est la puissance symbolique de la dérivée, qui est remplacée par la puissance réelle après y avoir élevé l'expression entre parenthèses.

Pour une fonction d'une variable oui = F(X) à ce point X 0 la signification géométrique de la différentielle désigne l'incrément de l'ordonnée de la tangente tracée au graphique de la fonction au point en abscisse X 0 en se déplaçant vers un point X 0 +  X. Et la différentielle d'une fonction de deux variables à cet égard est un incrément doigtés tangente avion attiré par la surface donnée par l'équation z = F(X, oui) , au point M 0 (X 0 , oui 0 ) en se déplaçant vers un point M(X 0 +  X, oui 0 +  oui). Définissons un plan tangent à une certaine surface :

Df . Avion passant par un point R. 0 surfaces S, appelé plan tangent en un point donné, si l'angle entre ce plan et une sécante passant par deux points R. 0 Et R.(n'importe quel point de la surface S) , tend vers zéro lorsque le point R. tend le long de cette surface jusqu'à un point R. 0 .

Laissez la surface S donné par l'équation z = F(X, oui). On peut alors montrer que cette surface a au point P. 0 (X 0 , oui 0 , z 0 ) plan tangent si et seulement si la fonction z = F(X, oui) est différentiable à ce stade. Dans ce cas, le plan tangent est donné par l’équation :

z – z 0 = +
(6).

§5. Dérivée directionnelle, gradient d'une fonction.

Fonctions dérivées partielles oui= F(X 1 , X 2 .. X n ) par variables X 1 , X 2 . . . X n exprimer le taux de changement d'une fonction dans la direction des axes de coordonnées. Par exemple, est le taux de changement de la fonction par X 1 – c'est-à-dire qu'on suppose qu'un point appartenant au domaine de définition de la fonction se déplace uniquement parallèlement à l'axe OH 1 , et toutes les autres coordonnées restent inchangées. Cependant, on peut supposer que la fonction peut également changer dans une autre direction qui ne coïncide avec la direction d'aucun des axes.

Considérons une fonction de trois variables : toi= F(X, oui, z).

Réparons le problème M 0 (X 0 , oui 0 , z 0 ) et une ligne droite dirigée (axe) je, en passant par ce point. Laisser M(X, oui, z) - point arbitraire de cette ligne et M 0 M- distance de M 0 avant M.

toi = F (X, oui, z) – F(X 0 , oui 0 , z 0 ) – incrément de fonction en un point M 0 .

Trouvons le rapport de l'incrément de la fonction à la longueur du vecteur
:

Df . Dérivée d'une fonction toi = F (X, oui, z) vers je à ce point M 0 est appelée la limite du rapport de l'incrément d'une fonction à la longueur du vecteur M 0 M comme cette dernière tend vers 0 (ou, ce qui revient au même, comme la MÀ M 0 ):

(1)

Cette dérivée caractérise le taux de changement de la fonction au point M 0 dans la direction je.

Laissez l'axe je (vecteur M 0 M) formes avec axes BŒUF, OY, once angles
respectivement.

Notons x-x 0 =
;

oui - oui 0 =
;

z - z 0 =
.

Alors le vecteur M 0 M = (X - X 0 , oui - oui 0 , z - z 0 )=
et ses cosinus directeurs :

;

(4).

(4) – formule de calcul de la dérivée directionnelle.

Considérons un vecteur dont les coordonnées sont les dérivées partielles de la fonction toi= F(X, oui, z) à ce point M 0 :

diplômé toi - fonction dégradé toi= F(X, oui, z) à ce point M(X, oui, z)

Propriétés du dégradé :

Conclusion: longueur du dégradé de fonction toi= F(X, oui, z) – est la valeur la plus possible à ce point M(X, oui, z) , et la direction du vecteur diplômé toi coïncide avec la direction du vecteur quittant le point M, le long duquel la fonction change le plus rapidement. C'est-à-dire la direction du gradient de la fonction diplômé toi - est la direction de l'augmentation la plus rapide de la fonction.

$E \subset \mathbb(R)^(n)$. Ils disent que $f$ a maximum local au point $x_(0) \in E$, s'il existe un voisinage $U$ du point $x_(0)$ tel que pour tout $x \in U$ l'inégalité $f\left(x\right ) \leqslant f est satisfait \left(x_(0)\right)$.

Le maximum local est appelé strict , si le quartier $U$ peut être choisi de telle sorte que pour tout $x \in U$ différent de $x_(0)$ il y ait $f\left(x\right)< f\left(x_{0}\right)$.

Définition
Soit $f$ une fonction réelle sur l'ouvert $E \subset \mathbb(R)^(n)$. Ils disent que $f$ a minimum local au point $x_(0) \in E$, s'il existe un voisinage $U$ du point $x_(0)$ tel que l'inégalité $f\left(x\right) \geqslant f est vraie pour tout $ x \in U$ \left(x_(0)\right)$.

Un minimum local est dit strict si un voisinage $U$ peut être choisi de telle sorte que pour tout $x \in U$ différent de $x_(0)$ il y ait $f\left(x\right) > f\left(x_ ( 0)\droite)$.

L'extremum local combine les notions de minimum local et de maximum local.

Théorème ( condition nécessaire extremum de la fonction différentiable)
Soit $f$ une fonction réelle sur l'ouvert $E \subset \mathbb(R)^(n)$. Si au point $x_(0) \in E$ la fonction $f$ a un extremum local à ce point, alors $$\text(d)f\left(x_(0)\right)=0.$$ Un différentiel égal à zéro équivaut au fait que tous sont égaux à zéro, c'est-à-dire $$\displaystyle\frac(\partial f)(\partial x_(i))\left(x_(0)\right)=0.$$

Dans le cas unidimensionnel, c'est – . Notons $\phi \left(t\right) = f \left(x_(0)+th\right)$, où $h$ est un vecteur arbitraire. La fonction $\phi$ est définie pour des valeurs de $t$ suffisamment petites en valeur absolue. De plus, il est différentiable par rapport à , et $(\phi)’ \left(t\right) = \text(d)f \left(x_(0)+th\right)h$.
Soit $f$ avoir un maximum local au point x $0$. Cela signifie que la fonction $\phi$ à $t = 0$ a un maximum local et, d'après le théorème de Fermat, $(\phi)' \left(0\right)=0$.
Donc, nous avons obtenu que $df \left(x_(0)\right) = 0$, c'est-à-dire la fonction $f$ au point $x_(0)$ est égale à zéro sur n'importe quel vecteur $h$.

Définition
Points auxquels le différentiel est nul, c'est-à-dire ceux dans lesquels toutes les dérivées partielles sont égales à zéro sont appelés stationnaires. Points critiques les fonctions $f$ sont les points auxquels $f$ n'est pas dérivable ou est égal à zéro. Si le point est stationnaire, il ne s'ensuit pas que la fonction ait un extremum en ce point.

Exemple 1.
Soit $f \left(x,y\right)=x^(3)+y^(3)$. Alors $\displaystyle\frac(\partial f)(\partial x) = 3 \cdot x^(2)$,$\displaystyle\frac(\partial f)(\partial y) = 3 \cdot y^(2 )$, donc $\left(0,0\right)$ est un point stationnaire, mais la fonction n'a pas d'extremum à ce stade. En effet, $f \left(0,0\right) = 0$, mais il est facile de voir que dans n'importe quel voisinage du point $\left(0,0\right)$ la fonction prend à la fois des valeurs positives et négatives.

Exemple 2.
La fonction $f \left(x,y\right) = x^(2) − y^(2)$ a un point stationnaire à son origine, mais il est clair qu'il n'y a pas d'extremum en ce point.

Théorème ( condition suffisante extrême).
Soit la fonction $f$ deux fois différenciable de manière continue sur l'ouvert $E \subset \mathbb(R)^(n)$. Soit $x_(0) \in E$ un point stationnaire et $$\displaystyle Q_(x_(0)) \left(h\right) \equiv \sum_(i=1)^n \sum_(j=1 ) ^n \frac(\partial^(2) f)(\partial x_(i) \partial x_(j)) \left(x_(0)\right)h^(i)h^(j).$ $ Alors

si $Q_(x_(0))$ – , alors la fonction $f$ au point $x_(0)$ a un extremum local, à savoir un minimum si la forme est définie positive, et un maximum si la forme est défini négatif;
si la forme quadratique $Q_(x_(0))$ n'est pas définie, alors la fonction $f$ au point $x_(0)$ n'a pas d'extremum.

Utilisons le développement selon la formule de Taylor (12.7 p. 292). Considérant que les dérivées partielles du premier ordre au point $x_(0)$ sont égales à zéro, on obtient $$\displaystyle f \left(x_(0)+h\right)−f \left(x_(0)\ à droite) = \ frac(1)(2) \sum_(i=1)^n \sum_(j=1)^n \frac(\partial^(2) f)(\partial x_(i) \partial x_ (j)) \left(x_(0)+\theta h\right)h^(i)h^(j),$$ où $0<\theta<1$. Обозначим $\displaystyle a_{ij}=\frac{\partial^{2} f}{\partial x_{i} \partial x_{j}} \left(x_{0}\right)$. В силу теоремы Шварца (12.6 стр. 289-290) , $a_{ij}=a_{ji}$. Обозначим $$\displaystyle \alpha_{ij} \left(h\right)=\frac{\partial^{2} f}{\partial x_{i} \partial x_{j}} \left(x_{0}+\theta h\right)−\frac{\partial^{2} f}{\partial x_{i} \partial x_{j}} \left(x_{0}\right).$$ По предположению, все непрерывны и поэтому $$\lim_{h \rightarrow 0} \alpha_{ij} \left(h\right)=0. \left(1\right)$$ Получаем $$\displaystyle f \left(x_{0}+h\right)−f \left(x_{0}\right)=\frac{1}{2}\left.$$ Обозначим $$\displaystyle \epsilon \left(h\right)=\frac{1}{|h|^{2}}\sum_{i=1}^n \sum_{j=1}^n \alpha_{ij} \left(h\right)h_{i}h_{j}.$$ Тогда $$|\epsilon \left(h\right)| \leq \sum_{i=1}^n \sum_{j=1}^n |\alpha_{ij} \left(h\right)|$$ и, в силу соотношения $\left(1\right)$, имеем $\epsilon \left(h\right) \rightarrow 0$ при $h \rightarrow 0$. Окончательно получаем $$\displaystyle f \left(x_{0}+h\right)−f \left(x_{0}\right)=\frac{1}{2}\left. \left(2\right)$$ Предположим, что $Q_{x_{0}}$ – положительноопределенная форма. Согласно лемме о положительноопределённой квадратичной форме (12.8.1 стр. 295, Лемма 1) , существует такое положительное число $\lambda$, что $Q_{x_{0}} \left(h\right) \geqslant \lambda|h|^{2}$ при любом $h$. Поэтому $$\displaystyle f \left(x_{0}+h\right)−f \left(x_{0}\right) \geq \frac{1}{2}|h|^{2} \left(λ+\epsilon \left(h\right)\right).$$ Так как $\lambda>0$, et $\epsilon \left(h\right) \rightarrow 0$ pour $h \rightarrow 0$, alors le côté droit sera positif pour tout vecteur $h$ de longueur suffisamment petite.
Nous sommes donc arrivés à la conclusion que dans un certain voisinage du point $x_(0)$ l'inégalité $f \left(x\right) >f \left(x_(0)\right)$ est vraie si seulement $ x \neq x_ (0)$ (on met $x=x_(0)+h$\right). Cela signifie qu'au point $x_(0)$ la fonction a un minimum local strict, et ainsi la première partie de notre théorème est prouvée.
Supposons maintenant que $Q_(x_(0))$ est une forme indéfinie. Alors il y a des vecteurs $h_(1)$, $h_(2)$ tels que $Q_(x_(0)) \left(h_(1)\right)=\lambda_(1)>0$, $Q_ ( x_(0)) \left(h_(2)\right)= \lambda_(2)<0$. В соотношении $\left(2\right)$ $h=th_{1}$ $t>0 $. On obtient alors $$f \left(x_(0)+th_(1)\right)−f \left(x_(0)\right) = \frac(1)(2) \left[ t^(2) \ lambda_(1) + t^(2) |h_(1)|^(2) \epsilon \left(th_(1)\right) \right] = \frac(1)(2) t^(2) \ left[ \lambda_(1) + |h_(1)|^(2) \epsilon \left(th_(1)\right) \right].$$ Pour $t>0$ suffisamment petit, la main droite le côté est positif. Cela signifie que dans n'importe quel voisinage du point $x_(0)$ la fonction $f$ prend des valeurs $f \left(x\right)$ supérieures à $f \left(x_(0)\right)$.
De même, on constate que dans tout voisinage du point $x_(0)$ la fonction $f$ prend des valeurs inférieures à $f \left(x_(0)\right)$. Ceci, avec le précédent, signifie qu'au point $x_(0)$ la fonction $f$ n'a pas d'extremum.

Considérons cas particulier de ce théorème pour une fonction $f \left(x,y\right)$ de deux variables définies dans un certain voisinage du point $\left(x_(0),y_(0)\right)$ et ayant une partie continue dérivées du premier dans ce voisinage et du second ordre. Supposons que $\left(x_(0),y_(0)\right)$ soit un point stationnaire et dénotons $$\displaystyle a_(11)= \frac(\partial^(2) f)(\partial x ^ (2)) \left(x_(0) ,y_(0)\right), a_(12)=\frac(\partial^(2) f)(\partial x \partial y) \left(x_( 0 ), y_(0)\right), a_(22)=\frac(\partial^(2) f)(\partial y^(2)) \left(x_(0), y_(0)\right ) .$$ Alors le théorème précédent prend la forme suivante.

Théorème
Soit $\Delta=a_(11) \cdot a_(22) − a_(12)^2$. Alors:

si $\Delta>0$, alors la fonction $f$ a un extremum local au point $\left(x_(0),y_(0)\right)$, à savoir un minimum si $a_(11)> 0$ , et maximum si $a_(11)<0$;
si $\Delta<0$, то экстремума в точке $\left(x_{0},y_{0}\right)$ нет. Как и в одномерном случае, при $\Delta=0$ экстремум может быть, а может и не быть.

Exemples de résolution de problèmes

Algorithme pour trouver l'extremum d'une fonction de plusieurs variables :

Trouver des points stationnaires ;
Trouver le différentiel de 2ème ordre en tous les points stationnaires
En utilisant la condition suffisante pour l'extremum d'une fonction de plusieurs variables, nous considérons la différentielle du 2ème ordre en chaque point stationnaire

Examinez la fonction pour extremum $f \left(x,y\right) = x^(3) + 8 \cdot y^(3) + 18 \cdot x — 30 \cdot y$.
Solution
Trouvons les dérivées partielles du 1er ordre : $$\displaystyle \frac(\partial f)(\partial x)=3 \cdot x^(2) - 6 \cdot y;$$ $$\displaystyle \frac(\partial f)(\partial y)=24 \cdot y^(2) — 6 \cdot x.$$ Composons et résolvons le système : $$\displaystyle \begin(cases)\frac(\partial f)(\partial x) = 0\\\frac(\partial f)(\partial y)= 0\end(cases) \Rightarrow \begin(cases)3 \cdot x^(2) - 6 \cdot y= 0\\24 \cdot y^(2) — 6 \cdot x = 0\end(cases) \Rightarrow \begin(cases)x^(2) — 2 \cdot y= 0\\4 \cdot y^(2) — x = 0 \end(cases)$$ À partir de la 2ème équation, nous exprimons $x=4 \cdot y^(2)$ - remplaçons-le dans la 1ère équation : $$\displaystyle \left(4 \cdot y^(2) \right )^(2)-2 \cdot y=0$$ $$16 \cdot y^(4) — 2 \cdot y = 0$$ $$8 \cdot y^(4) — y = 0$$ $ $y \left(8 \cdot y^(3) -1\right)=0$$ En conséquence, 2 points stationnaires sont obtenus :
1) $y=0 \Rightarrow x = 0, M_(1) = \left(0, 0\right)$ ;
2) $\displaystyle 8 \cdot y^(3) -1=0 \Rightarrow y^(3)=\frac(1)(8) \Rightarrow y = \frac(1)(2) \Rightarrow x=1 , M_(2) = \left(\frac(1)(2), 1\right)$
Vérifions si la condition suffisante pour un extremum est satisfaite :
$$\displaystyle \frac(\partial^(2) f)(\partial x^(2))=6 \cdot x; \frac(\partial^(2) f)(\partial x \partial y)=-6; \frac(\partial^(2) f)(\partial y^(2))=48 \cdot y$$
1) Pour le point $M_(1)= \left(0,0\right)$ :
$$\displaystyle A_(1)=\frac(\partial^(2) f)(\partial x^(2)) \left(0,0\right)=0; B_(1)=\frac(\partial^(2) f)(\partial x \partial y) \left(0,0\right)=-6; C_(1)=\frac(\partial^(2) f)(\partial y^(2)) \left(0,0\right)=0;$$
$A_(1) \cdot B_(1) — C_(1)^(2) = -36<0$ , значит, в точке $M_{1}$ нет экстремума.
2) Pour le point $M_(2)$ :
$$\displaystyle A_(2)=\frac(\partial^(2) f)(\partial x^(2)) \left(1,\frac(1)(2)\right)=6; B_(2)=\frac(\partial^(2) f)(\partial x \partial y) \left(1,\frac(1)(2)\right)=-6; C_(2)=\frac(\partial^(2) f)(\partial y^(2)) \left(1,\frac(1)(2)\right)=24;$$
$A_(2) \cdot B_(2) — C_(2)^(2) = 108>0$, ce qui signifie qu'au point $M_(2)$ il y a un extremum, et puisque $A_(2)> 0$, alors c'est le minimum.
Réponse : Le point $\displaystyle M_(2)\left(1,\frac(1)(2)\right)$ est le point minimum de la fonction $f$.
Étudiez la fonction pour l'extremum $f=y^(2) + 2 \cdot x \cdot y - 4 \cdot x - 2 \cdot y - 3$.
Solution
Trouvons des points stationnaires : $$\displaystyle \frac(\partial f)(\partial x)=2 \cdot y - 4;$$ $$\displaystyle \frac(\partial f)(\partial y)=2 \ cdot y + 2 \cdot x — 2.$$
Composons et résolvons le système : $$\displaystyle \begin(cases)\frac(\partial f)(\partial x)= 0\\\frac(\partial f)(\partial y)= 0\end(cases ) \ Rightarrow \begin(cases)2 \cdot y - 4= 0\\2 \cdot y + 2 \cdot x - 2 = 0\end(cases) \Rightarrow \begin(cases) y = 2\\y + x = 1\fin(cas) \Rightarrow x = -1$$
$M_(0) \left(-1, 2\right)$ est un point stationnaire.
Vérifions si la condition suffisante pour l'extremum est remplie : $$\displaystyle A=\frac(\partial^(2) f)(\partial x^(2)) \left(-1,2\right)=0 ; B=\frac(\partial^(2) f)(\partial x \partial y) \left(-1,2\right)=2; C=\frac(\partial^(2) f)(\partial y^(2)) \left(-1,2\right)=2;$$
$A \cdot B — C^(2) = -4<0$ , значит, в точке $M_{0}$ нет экстремума.
Réponse : il n’y a pas d’extrêmes.