La méthode est applicable pour minimiser les fonctions d'algèbre logique d'un nombre quelconque de variables.

Considérons le cas de trois variables. Une fonction booléenne dans DNF peut être représentée sous la forme de toutes sortes de termes conjonctifs pouvant être inclus dans DNF :

où kО(0,1) sont des coefficients. La méthode consiste à sélectionner les coefficients de telle sorte que le DNF résultant soit minimal.

Si nous définissons maintenant toutes les valeurs possibles des variables de 000 à 111, nous obtenons 2 n (2 3 =8) équations pour déterminer les coefficients k:

Considérant les ensembles pour lesquels la fonction prend une valeur nulle, déterminez les coefficients égaux à 0 et rayez-les des équations dont le côté droit contient 1. Parmi les coefficients restants dans chaque équation, un coefficient est égal à un, ce qui détermine la conjonction du rang le plus bas. Les coefficients restants sont égaux à 0. Ainsi, les coefficients unitaires k déterminer la forme minimale appropriée.

Exemple. Réduire une fonction donnée

si les valeurs sont connues :
;
;
;
;
;
;
;
.

Solution.

Après avoir barré les coefficients zéro on obtient :

=1;

=1;

=1;

=1.

Assumons le coefficient à l'unité , correspondant à la conjonction du rang le plus bas et faisant passer les quatre dernières équations à 1, et dans la première équation il convient d'assimiler le coefficient à 1 . Les coefficients restants sont mis à 0.

Répondre: type de fonction minimisée.

Il convient de noter que la méthode des coefficients indéfinis est efficace lorsque le nombre de variables est faible et ne dépasse pas 5-6.

Cube multidimensionnel

Considérons une représentation graphique d'une fonction sous la forme d'un cube multidimensionnel. Chaque sommet n Un cube dimensionnel peut être mis en correspondance avec le constituant de l'unité.

Le sous-ensemble des sommets marqués est un mappage sur n-cube dimensionnel d'une fonction booléenne de n variables dans SDNF.

Pour afficher la fonction de n variables présentées dans tout DNF, il est nécessaire d'établir une correspondance entre ses minitermes et éléments n-cube dimensionnel.

Miniterme du (n-1)ème rang
peut être considéré comme le résultat du collage de deux miniterms n-ème rang, c'est-à-dire

=

Sur n-cube dimensionnel cela correspond au remplacement de deux sommets qui ne diffèrent que par les valeurs de coordonnées X je, reliant ces sommets avec une arête (on dit qu'une arête recouvre les sommets qui lui sont incidents).

Ainsi, les miniterms ( n Le -1)ième ordre correspond aux arêtes d’un cube à n dimensions.

De même, la correspondance des miniterms ( n-2)ème visages d'ordre n-cube dimensionnel, dont chacun couvre quatre sommets (et quatre arêtes).

Éléments n-cube dimensionnel, caractérisé par S les mesures sont appelées S-cubes

Ainsi, les sommets sont des cubes 0, les arêtes sont des cubes 1, les faces sont des cubes 2, etc.

Pour résumer, on peut dire que le miniterme ( n-S) rang en DNF pour la fonction n variables affichées S-un cube chacun S-cube couvre tous les cubes de dimension inférieure qui sont connectés uniquement à ses sommets.

Exemple. En figue. étant donné la cartographie

Voici les miniterms
Et
correspondent à 1 cubes ( S=3-2=1), et miniterme X 3 affiché sur 2 cubes ( S=3-1=2).

Ainsi, tout DNF est mappé à n cube dimensionnel dans sa totalité S-cubes qui couvrent tous les sommets correspondant aux unités constitutives (0-cube).

Constituants. Pour les variables X 1 ,X 2 ,…X n expression
est appelé le constituant de l’unité, et
- constituant de zéro ( signifie soit , ou ).

Ce constituant de un (zéro) se transforme en un (zéro) seulement avec un ensemble correspondant de valeurs de variables, qui est obtenu si toutes les variables sont prises égales à un (zéro) et leurs négations égales à zéro (un).

Par exemple : unité constituante
correspond à l'ensemble (1011), et le constituant est nul
- ensemble (1001).

Puisque SD(K)NF est une disjonction (conjonction) des constituants de un (zéro), on peut affirmer que la fonction booléenne qu'elle représente F(X 1 , X 2 ,…, X n) devient un (zéro) uniquement pour les ensembles de valeurs variables X 1 , X 2 ,…, X n, correspondant à ces copstituées. Sur d'autres postes, cette fonction passe à 0 (un).

L'affirmation inverse est également vraie, sur laquelle elle est basée manière de représenter n'importe quel Fonction booléenne spécifiée par la table.

Pour ce faire, il faut écrire des disjonctions (conjonctions) des constituants de un (zéro), correspondant à des ensembles de valeurs de variables sur lesquelles la fonction prend une valeur égale à un (zéro).

Par exemple, une fonction donnée par une table

correspondre

Les expressions résultantes peuvent être converties sous une autre forme basée sur les propriétés de l’algèbre logique.

L'affirmation inverse est également vraie : si une collection S-cubes couvre l'ensemble de tous les sommets correspondant aux valeurs unitaires de la fonction, puis la disjonction correspondant à celles-ci S-cubes de miniterms est l'expression de cette fonction dans DNF.

On dit qu'une telle collection S-cubes (ou leurs minitermes correspondants) forment une couverture de la fonction. Le désir d'une forme minimale s'entend intuitivement comme la recherche d'un tel revêtement, le nombre S-dont il y aurait moins de cubes, et leurs dimensions S- plus. La couverture correspondant à la forme minimale est appelée couverture minimale.

Par exemple, pour la fonction à=
le revêtement correspond à une forme non minimale :

riz a) à=,

un enrobage sur du riz b) à=
, riz c) à=
minimal.

Riz. Couverture fonctionnelle à=:

a) non minimal ; b), c) minimum.

Afficher une fonction sur n-mesuré clairement et simplement avec n3. Un cube à quatre dimensions peut être représenté comme le montre la Fig., qui montre la fonction de quatre variables et sa couverture minimale correspondant à l'expression à=

Utiliser cette méthode lorsque n>4 nécessite des formations tellement complexes qu'il perd tous ses avantages.

MINISTÈRE DES SCIENCES ET DE L'ÉDUCATION DE LA RÉPUBLIQUE DE BASHKORTO STAN

SAOU SPO Collège Bachkir d'Architecture et de Génie Civil

Khaliullin Askhat Adelzyanovich,

professeur de mathématiques à Bachkirsky

Collège d'architecture et de génie civil

UFA

2014

Introduction _________________________________________________3

Chapitre JE. Aspects théoriques de l'utilisation de la méthode des coefficients incertains_________________________________________________________4

Chapitre II. Recherches de solutions aux problèmes de polynômes par la méthode des coefficients indéfinis_________________________________7

2.1.Facturation d'un polynôme_____________________ 7

2.2. Problèmes avec les paramètres_________________________________ 10

2.3. Résolution d'équations________________________________________________________14

2.4. Équations fonctionnelles______________________________19

Conclusion_________________________________________________23

Liste de la littérature utilisée________________________________________________________24

Application ________________________________________________25

Introduction.

Ce travail est consacré aux aspects théoriques et pratiques de l'introduction de la méthode des coefficients indéfinis dans le cours de mathématiques scolaire. La pertinence de ce sujet est déterminée par les circonstances suivantes.

Personne ne contestera que les mathématiques en tant que science ne se situent pas au même endroit, elles évoluent constamment, de nouvelles tâches d'une complexité accrue apparaissent, ce qui provoque souvent certaines difficultés, car ces tâches sont généralement associées à la recherche. Ces dernières années, de tels problèmes ont été proposés lors des Olympiades mathématiques des écoles, des districts et des républiques, et ils sont également disponibles dans les versions de l'examen d'État unifié. Par conséquent, une méthode spéciale était nécessaire pour permettre de résoudre au moins certains d’entre eux de la manière la plus rapide, la plus efficace et la plus abordable. Cet ouvrage présente clairement le contenu de la méthode des coefficients indéfinis, largement utilisée dans une grande variété de domaines des mathématiques, allant des questions incluses dans le cours de formation générale jusqu'à ses parties les plus avancées. En particulier, les applications de la méthode des coefficients indéfinis dans la résolution de problèmes avec des paramètres, des équations rationnelles et fonctionnelles fractionnaires sont particulièrement intéressantes et efficaces ; ils peuvent facilement intéresser toute personne intéressée par les mathématiques. L'objectif principal du travail proposé et de la sélection des problèmes est de fournir de nombreuses opportunités d'affiner et de développer la capacité à trouver des solutions courtes et non standard.

Ce travail se compose de deux chapitres. La première aborde les aspects théoriques de l’utilisation

méthode des coefficients incertains, et d'autre part, les aspects pratiques et méthodologiques de cette utilisation.

L'annexe à l'ouvrage fournit les conditions pour des tâches spécifiques pour une solution indépendante.

Chapitre je . Aspects théoriques de l'utilisation méthode des coefficients incertains

"L'homme... est né pour être un maître,

souverain, roi de la nature, mais sagesse,

avec lequel il doit gouverner ne lui est pas donné

dès la naissance : cela s'acquiert par l'apprentissage"

N.I.Lobatchevski

Il existe différentes manières et méthodes de résoudre des problèmes, mais l'une des plus pratiques, des plus efficaces, des plus originales, des plus élégantes et en même temps très simple et compréhensible pour tous est la méthode des coefficients indéfinis. La méthode des coefficients indéterminés est une méthode utilisée en mathématiques pour trouver les coefficients d'expressions dont la forme est connue à l'avance.

Avant d’envisager l’application de la méthode des coefficients indéfinis à la résolution de divers types de problèmes, nous présentons un certain nombre d’informations théoriques.

Qu'ils soient donnés

UN n (X) = un 0 X n + un 1 X n-1 + un 2 X n-2 + ··· + un n-1 X + un n

B m (X ) = b 0 X m + b 1 X m -1 + b 2 X m -2 + ··· + b m-1 X + b m ,

polynômes relatifs X avec toutes les chances.

Théorème. Deux polynômes dépendant de un et les mêmes arguments sont identiques si et seulement sin = m et leurs coefficients correspondants sont égauxun 0 = b 0 , un 1 = b 1 , un 2 = b 2 ,··· , un n -1 = b m -1 , un n = b m Et T. d.

Évidemment, les polynômes égaux prennent pour toutes les valeurs X mêmes valeurs. A l'inverse, si les valeurs de deux polynômes sont égales pour toutes les valeurs X, alors les polynômes sont égaux, c'est-à-dire que leurs coefficients sont aux mêmes degrésX correspondre.

Par conséquent, l’idée d’appliquer la méthode des coefficients indéfinis à la résolution de problèmes est la suivante.

Sachons qu'à la suite de certaines transformations, une expression d'un certain type est obtenue et que seuls les coefficients de cette expression sont inconnus. Ensuite ces coefficients sont désignés par des lettres et considérés comme des inconnues. Un système d'équations est ensuite construit pour déterminer ces inconnues.

Par exemple, dans le cas des polynômes, ces équations sont faites à partir de la condition que les coefficients soient égaux pour les mêmes puissances X pour deux polynômes égaux.

Nous allons démontrer ce qui a été dit ci-dessus à l’aide des exemples spécifiques suivants, et commençons par le plus simple.

Ainsi, par exemple, sur la base de considérations théoriques, la fraction

peut être représenté comme une somme

, Où un , b Et c - coefficients à déterminer. Pour les trouver, on assimile la deuxième expression à la première :

=

et se libérer du dénominateur et rassembler les termes avec les mêmes pouvoirs à gauche X, on a:

(un + b + c )X 2 + ( b - c )x - une = 2X 2 – 5 X– 1

Puisque la dernière égalité doit être vraie pour toutes les valeurs X, alors les coefficients aux mêmes puissancesX la droite et la gauche devraient être identiques. Ainsi, trois équations sont obtenues pour déterminer les trois coefficients inconnus :

a+b+c = 2

b - c = - 5

UN= 1, d'où un = 1 , b = - 2 , c = 3

Ainsi,

=
,

la validité de cette égalité est facile à vérifier directement.

Supposons que vous deviez également représenter une fraction

comme un + b
+ c
+ d
, Où un , b , c Et d- coefficients rationnels inconnus. Nous assimilons la deuxième expression à la première :

un + b
+ c
+ d
=
ou, En nous affranchissant du dénominateur, en supprimant, lorsque cela est possible, les facteurs rationnels sous les signes des racines et en ramenant les termes similaires du côté gauche, nous obtenons :

(un- 2 b + 3 c ) + (- a+b +3 d )
+ (a+c - 2 d )
+

+ (avant JC + d )
= 1 +
-
.

Mais une telle égalité n'est possible que dans le cas où les termes rationnels des deux parties et les coefficients des mêmes radicaux sont égaux. Ainsi, quatre équations sont obtenues pour trouver les coefficients inconnus un , b , c Et d :

un- 2b+ 3c = 1

- a+b +3 d = 1

a+c - 2 d = - 1

b - c + d= 0, d'où un = 0 ; b = - ; c = 0 ; d= , c'est
= -
+
.

Chapitre II. Recherches de solutions aux problèmes avec les polynômes méthode des coefficients indéterminés.

« Rien ne contribue mieux à la maîtrise d’un sujet que

la manière d'agir avec lui dans différentes situations"

Académicien B.V. Gnedenko

2. 1. Factorisation d'un polynôme.

Méthodes de factorisation des polynômes :

1) placer le facteur commun entre parenthèses ; 2) méthode de regroupement ; 3) application des formules de multiplication de base ; 4) introduction de termes auxiliaires ; 5) transformation préliminaire d'un polynôme donné à l'aide de certaines formules ; 6) expansion en trouvant les racines d'un polynôme donné ; 7) méthode de saisie du paramètre ; 8)méthode des coefficients indéterminés.

Problème 1. Factoriser le polynôme en facteurs réels X 4 + X 2 + 1 .

Solution. Il n’y a pas de racine parmi les diviseurs du terme libre de ce polynôme. On ne peut pas trouver les racines du polynôme par d'autres moyens élémentaires. Par conséquent, il n’est pas possible d’effectuer le développement requis en trouvant d’abord les racines de ce polynôme. Reste à chercher une solution au problème soit en introduisant des termes auxiliaires, soit par la méthode des coefficients indéterminés. Il est évident que X 4 + X 2 + 1 = X 4 + X 3 + X 2 - X 3 - X 2 - X + X 2 + X + 1 =

= X 2 (X 2 + X + 1) - X (X 2 + X + 1) + X 2 + X + 1 =

= (X 2 + X + 1)(X 2 - X + 1).

Les trinômes quadratiques résultants n'ont pas de racines et sont donc indécomposables en facteurs linéaires réels.

La méthode décrite est techniquement simple, mais difficile en raison de son caractère artificiel. En effet, il est très difficile de trouver les termes auxiliaires requis. Seule une supposition nous a permis de retrouver cette décomposition. Mais

Il existe des moyens plus fiables de résoudre ces problèmes.

On pourrait procéder ainsi : supposer que le polynôme donné se décompose en produit

(X 2 + UN X + b )(X 2 + c X + d )

deux trinômes carrés à coefficients entiers.

Ainsi, nous aurons cela

X 4 + X 2 + 1 = (X 2 + UN X + b )(X 2 + c X + d )

Reste à déterminer les coefficientsun , b , c Et d .

En multipliant les polynômes du côté droit de la dernière égalité, on obtient :X 4 + X 2 + 1 = X 4 +

+ (a + c ) X 3 + (b + UN c + d ) X 2 + (annonce + avant JC ) x + bd .

Mais puisque nous avons besoin que le côté droit de cette égalité se transforme en le même polynôme que celui du côté gauche, nous aurons besoin que les conditions suivantes soient remplies :

a + c = 0

b + UN c + d = 1

annonce + avant JC = 0

bd = 1 .

Le résultat est un système de quatre équations à quatre inconnuesun , b , c Et d . Il est facile de trouver les coefficients de ce systèmeun = 1 , b = 1 , c = -1 Et d = 1.

Le problème est désormais complètement résolu. Nous avons:

X 4 + X 2 + 1 = (X 2 + X + 1)(X 2 - X + 1).

Problème 2. Factoriser le polynôme en facteurs réels X 3 – 6 X 2 + 14 X – 15 .

Solution. Représentons ce polynôme sous la forme

X 3 – 6 X 2 + 14 X – 15 = (X + UN )(X 2 + bx + c) , Où un , b Et Avec - coefficients non encore déterminés. Puisque deux polynômes sont identiquement égaux si et seulement si les coefficients de mêmes puissancesX sont alors égaux, égalisant respectivement les coefficients pourX 2 , X et termes libres, on obtient un système de trois équations à trois inconnues :

a+b= - 6

ab + c = 14

ca = - 15 .

La solution de ce système sera considérablement simplifiée si l'on tient compte du fait que le nombre 3 (diviseur du terme libre) est la racine de cette équation, et, par conséquent,un = - 3 ,

b = - 3 Et Avec = 5 .

Alors X 3 – 6 X 2 + 14 X – 15 = (X – 3)(X 2 – 3 X + 5).

La méthode appliquée des coefficients indéfinis, en comparaison avec la méthode ci-dessus d'introduction de termes auxiliaires, ne contient rien d'artificiel, mais elle nécessite l'application de nombreux principes théoriques et s'accompagne de calculs assez volumineux. Pour les polynômes de degré supérieur, cette méthode des coefficients indéterminés conduit à des systèmes d'équations encombrants.

2.2.Tâches et avec des paramètres.

Ces dernières années, les versions de l'examen d'État unifié ont proposé des tâches paramétrées. Leur solution pose souvent certaines difficultés. Lors de la résolution de problèmes avec des paramètres, ainsi que d'autres méthodes, vous pouvez utiliser très efficacement la méthode des coefficients indéfinis. C'est cette méthode qui permet de simplifier grandement leur solution et d'obtenir rapidement une réponse.

Tâche 3. Déterminer à quelles valeurs du paramètre UNéquation 2 X 3 – 3 X 2 – 36 X + UN – 3 = 0 a exactement deux racines.

Solution. 1 façon. Utiliser un dérivé.

Représentons cette équation sous la forme de deux fonctions

2x3 – 3 X 2 – 36 X – 3 = – UN .

F (X) = 2x 3 – 3 X 2 – 36 X– 3 et φ( X ) = – UN .

Explorons la fonctionF (X) = 2x 3 – 3 X 2 – 36 X – 3 en utilisant la dérivée et construire schématiquement son graphe (Fig. 1.).

F( – X )F (X ) , F (– X ) – F (X ). La fonction n'est ni paire ni impaire.

3. Trouvons les points critiques de la fonction, ses intervalles d'augmentation et de diminution, les extrema. F / (X ) = 6 X 2 – 6 X – 36. D (F / ) = R. , on trouvera donc tous les points critiques de la fonction en résolvant l'équation F / (X ) = 0 .

6(X 2 – X– 6) = 0 ,

X 2 – X– 6 = 0 ,

X 1 = 3 , X 2 = – 2 par le théorème inverse du théorème de Vieta.

F / (X ) = 6(X – 3)(X + 2).

+ maximum - min +

2 3 X

F / (X) > 0 pour tous X< – 2 et X > 3 et la fonction est continue en certains pointsX =– 2 et X = 3, donc, il augmente sur chacun des intervalles (- ; - 2] et [ 3 ; ).

F / (X ) < 0 à - 2 < X< 3, donc, il diminue sur l'intervalle [- 2; 3 ].

X = - 2ème point maximum, car à ce stade, le signe de la dérivée change de"+" à "-".

F (– 2) = 2· (– 8) – 3·4 – 36·(– 2) – 3 = – 16 – 12 + 72 – 3 == 72 – 31 = 41 ,

X = 3 points minimum, car à ce stade le signe de la dérivée change"-" à "+".

F (3) = 2·27 – 3·9 – 36·3 – 3 = 54 – 27 – 108 – 3 = – 138 + +54 = – 84.

Graphique de la fonction φ(X ) = – UN est une droite parallèle à l'axe des x et passant par le point de coordonnées (0; – UN ). Les graphiques ont deux points communs à –UN= 41, soit une =– 41 et – UN= – 84, soit UN = 84 .

à

41φ( X)

2 3 X

3 F ( X ) = 2x3 – 3 X 2 – 36 X – 3

Méthode 2. Méthode des coefficients indéterminés.

Puisque, selon les conditions du problème, cette équation ne doit avoir que deux racines, l'égalité est évidente :

2X 3 – 3 X 2 – 36 X + UN – 3 = (x + b ) 2 (2 X + c ) ,

2X 3 – 3 X 2 – 36 X + UN – 3 = 2 X 3 + (4 b + c ) X 2 + (2 b 2 + +2 avant JC ) X + b 2 c ,

Égalisant maintenant les coefficients aux mêmes degrés X, on obtient un système d'équations

4 b + c = - 3

2b 2 + 2avant JC = - 36

b 2 c = un – 3 .

A partir des deux premières équations du système, on trouveb 2 + b – 6 = 0, d'où b 1 = - 3 ou b 2 = 2 . Valeurs correspondantesAvec 1 et Avec 2 facile à trouver à partir de la première équation du système :Avec 1 = 9 ou Avec 2 = - 11 . Enfin, la valeur souhaitée du paramètre peut être déterminée à partir de la dernière équation du système :

UN = b 2 c + 3 , un 1 = - 41 ou un 2 = 84.

Réponse : cette équation a exactement deux valeurs différentes

racine à UN= - 41 et UN= 84 .

Tâche 4. Trouver la plus grande valeur du paramètreUN , pour lequel l'équationX 3 + 5 X 2 + Oh + b = 0

à coefficients entiers a trois racines différentes dont l’une est égale à – 2.

Solution. 1 façon. Remplacement X= - 2 au côté gauche de l'équation, on obtient

8 + 20 – 2 UN + b= 0, ce qui signifie b = 2 un – 12 .

Puisque le nombre - 2 est une racine, on peut retirer le facteur commun X + 2:

X 3 + 5 X 2 + Oh + b = X 3 + 2 X 2 + 3 X 2 + Oh + (2 un – 12) =

= X 2 (X + 2) + 3 X (X + 2) – 6 X + Oh + (2 un – 12) =

= X 2 (X + 2) + 3 X (X + 2) + (un – 6)(X +2) - 2(un – 6)+ (2 un - 12) =

= (X + 2)(X 2 + 3 X + (un – 6) ) .

Par condition, il existe deux autres racines de l'équation. Cela signifie que le discriminant du deuxième facteur est positif.

D =3 2 - 4 (un – 6) = 33 – 4 un > 0, c'est-à-dire UN < 8,25 .

Il semblerait que la réponse serait une = 8 . Mais lorsque nous substituons le chiffre 8 dans l’équation originale, nous obtenons :

X 3 + 5 X 2 + Oh + b = X 3 + 5 X 2 + 8 X + 4 = (X + 2)(X 2 + 3 X + 2 ) =

= (X + 1) (X + 2) 2 ,

c'est-à-dire que l'équation n'a que deux racines différentes. Mais quand une = 7 produit en fait trois racines différentes.

Méthode 2. Méthode des coefficients indéterminés.

Si l'équation X 3 + 5 X 2 + Oh + b = 0 a une racine X = - 2, alors vous pouvez toujours récupérer les chiffresc Et d pour que devant tout le mondeX l'égalité était vraie

X 3 + 5 X 2 + Oh + b = (X + 2)(X 2 + Avec X + d ).

Pour trouver des numérosc Et d Ouvrons les parenthèses sur le côté droit, ajoutons des termes similaires et obtenons

X 3 + 5 X 2 + Oh + b = X 3 + (2 + Avec ) X 2 +(2 s + d ) X + 2 d

Égalisation des coefficients aux puissances correspondantes X nous avons un système

2 + Avec = 5

2 Avec + d = un

2 d = b , où c = 3 .

Ainsi, X 2 + 3 X + d = 0 , D = 9 – 4 d > 0 ou

d < 2,25, donc d (- ; 2 ].

Les conditions du problème sont satisfaites par la valeur d = 1 . La valeur finale souhaitée du paramètreUN = 7.

RÉPONSE : quand une = 7 cette équation a trois racines différentes.

2.3. Résoudre des équations.

"N'oubliez pas qu'en résolvant de petits problèmes, vous

préparez-vous à affronter des défis importants et difficiles

de nouvelles tâches.

Académicien S.L. Sobolev

Lorsque vous résolvez certaines équations, vous pouvez et devez faire preuve d'ingéniosité et d'esprit et utiliser des techniques spéciales. La maîtrise de diverses techniques de transformation et la capacité d'effectuer un raisonnement logique sont d'une grande importance en mathématiques. L’une de ces astuces consiste à additionner et à soustraire une expression ou un nombre bien choisi. Le fait énoncé lui-même, bien entendu, est bien connu de tous - la principale difficulté est de voir dans une configuration spécifique les transformations d'équations auxquelles il est pratique et opportun de l'appliquer.

À l’aide d’une simple équation algébrique, nous illustrerons une technique non standard de résolution d’équations.

Problème 5. Résoudre l'équation

=
.

Solution. Multiplions les deux côtés de cette équation par 5 et réécrivons-la comme suit

= 0 ; X 0; -
;

= 0 ,

= 0 ,

= 0 ou
= 0

Résolvons les équations résultantes en utilisant la méthode des coefficients indéterminés

X 4 - X 3 –7 X – 3 = (X 2 + ah + b )(X 2 + CX + d ) = 0

X 4 - X 3 –7 X – 3 = X 4 + (a + c ) X 3 + (b + UN c + d ) X 2 + (annonce + avant JC ) x+ + bd

Égaliser les coefficients à X 3 , X 2 , X et conditions gratuites, nous obtenons le système

a + c = -1

b + UN c + d = 0

annonce + avant JC = -7

bd = -3, d'où on trouve :UN = -2 ; b = - 1 ;

Avec = 1 ; d = 3 .

Donc X 4 - X 3 –7X– 3 = (X 2 – 2 X – 1)(X 2 + X + 3) = 0 ,

X 2 – 2 X– 1 = 0 ou X 2 + X + 3 = 0

X 1,2 =
pas de racines.

De même nous avons

X 4 – 12X – 5 = (X 2 – 2 X – 1)(X 2 + 2X + 5) = 0 ,

où X 2 + 2 X + 5 = 0 , D = - 16 < 0 , нет корней.

Répondre: X 1,2 =

Problème 6. Résoudre l'équation

= 10.

Solution. Pour résoudre cette équation, vous devez sélectionner des nombresUN Et b de sorte que les numérateurs des deux fractions sont les mêmes. On a donc le système :

= 0 , X 0; -1 ; -

= - 10

La tâche est donc de trouver les nombresUN Et b , pour lequel l'égalité vaut

(un + 6) X 2 + ah – 5 = X 2 + (5 + 2 b ) X + b

Or, selon le théorème sur l'égalité des polynômes, il faut que le côté droit de cette égalité se transforme en le même polynôme qui se trouve du côté gauche.

En d'autres termes, les relations doivent être satisfaites

un + 6 = 1

UN = 5 + 2 b

– 5 = b , d'où l'on retrouve les valeursUN = - 5 ;

b = - 5 .

A ces valeursUN Et b égalité UN + b = - 10 est également juste.

= 0 , X 0; -1 ; -

= 0 ,

= 0 ,

(X 2 – 5X– 5)(X 2 + 3X + 1) = 0 ,

X 2 – 5X– 5 = 0 ou X 2 + 3X + 1 = 0 ,

X 1,2 =
, X 3,4 =

Répondre: X 1,2 =
, X 3,4 =

Problème 7. Résoudre l'équation

= 4

Solution. Cette équation est plus complexe que les précédentes et nous allons donc la regrouper ainsi : X 0;-1;3;-8;12

0 ,

= - 4.

De la condition d'égalité de deux polynômes

Oh 2 + (un + 6) X + 12 = X 2 + (b + 11) X – 3 b ,

nous obtenons et résolvons un système d'équations pour des coefficients inconnusUN Et b :

UN = 1

un + 6 = b + 11

12 = – 3 b , où une = 1 , b = - 4 .

Polynômes - 3 – 6X + CX 2 + 8 CX Et X 2 + 21 + 12 d – dx sont égaux entre eux à l’identique seulement lorsque

Avec = 1

8 Avec - 6 = - d

3 = 21 + 12 d , Avec = 1 , d = - 2 .

Avec des valeursune = 1 , b = - 4 , Avec = 1 , d = - 2

égalité
= - 4 est correct.

En conséquence, cette équation prend la forme suivante :

= 0 ou
= 0 ou
= 0 ,

= - 4 , = - 3 , = 1 , = -
.

D'après les exemples considérés, il ressort clairement à quel point l'utilisation habile de la méthode des coefficients indéfinis,

aide à simplifier la solution d’une équation plutôt complexe et inhabituelle.

2.4. Équations fonctionnelles.

« Le but le plus élevé des mathématiques... est

est de trouver l'ordre caché dans

le chaos qui nous entoure"

N. Viner

Les équations fonctionnelles sont une classe très générale d'équations dans lesquelles la fonction inconnue est une certaine fonction. Par équation fonctionnelle au sens étroit du terme, on entend des équations dans lesquelles les fonctions souhaitées sont liées à des fonctions connues d'une ou plusieurs variables en utilisant l'opération de formation d'une fonction complexe. Une équation fonctionnelle peut également être considérée comme l'expression d'une propriété caractérisant une classe particulière de fonctions.

[par exemple, équation fonctionnelle F ( X ) = F (- X ) caractérise la classe des fonctions paires, l'équation fonctionnelleF (X + 1) = F (X ) – classe de fonctions ayant la période 1, etc.].

L'une des équations fonctionnelles les plus simples est l'équationF (X + oui ) = F (X ) + F (oui ). Les solutions continues de cette équation fonctionnelle ont la forme

F (X ) = CX . Cependant, dans la classe des fonctions discontinues, cette équation fonctionnelle a d’autres solutions. Associées à l'équation fonctionnelle considérée sont

F (X + oui ) = F (X ) · F (oui ), F (X oui ) = F (X ) + F (oui ), F (X oui ) = F (X )· F (oui ),

solutions continues, qui ont respectivement la forme

e CX , AVECdansX , X α (X > 0).

Ainsi, ces équations fonctionnelles peuvent être utilisées pour définir des fonctions exponentielles, logarithmiques et puissance.

Les équations les plus utilisées sont celles des fonctions complexes dans lesquelles les fonctions requises sont des fonctions externes. Applications théoriques et pratiques

Ce sont précisément ces équations qui ont incité d’éminents mathématiciens à les étudier.

Par exemple, à alignement

F 2 (X) = F (X - oui)· F (X + oui)

N.I.Lobatchevskiutilisé pour déterminer l'angle de parallélisme dans ma géométrie.

Ces dernières années, les problèmes liés à la résolution d'équations fonctionnelles sont assez souvent proposés lors des Olympiades mathématiques. Leur solution ne nécessite pas de connaissances dépassant le cadre du programme de mathématiques des écoles secondaires. Cependant, la résolution d’équations fonctionnelles pose souvent certaines difficultés.

L'un des moyens de trouver des solutions aux équations fonctionnelles est la méthode des coefficients indéfinis. Il peut être utilisé lorsque la forme générale de la fonction souhaitée peut être déterminée par l'apparence de l'équation. Cela s'applique tout d'abord aux cas où des solutions d'équations doivent être recherchées parmi des fonctions rationnelles entières ou fractionnaires.

Décrivons l'essence de cette technique en résolvant les problèmes suivants.

Tâche 8. FonctionF (X ) est défini pour tout réel x et satisfait pour toutX R. condition

3 F(X) - 2 F(1- X) = X 2 .

TrouverF (X ).

Solution. Puisque sur le côté gauche de cette équation sur la variable indépendante x et les valeurs de la fonctionF Seules les opérations linéaires sont effectuées et le côté droit de l'équation est une fonction quadratique, alors il est naturel de supposer que la fonction souhaitée est également quadratique :

F (X) = hache 2 + bx + c , Oùun, b, c – des coefficients à déterminer, c'est-à-dire des coefficients incertains.

En substituant la fonction dans l'équation, on arrive à l'identité :

3(hache 2 + bx+c) – 2(un(1 – X) 2 + b(1 – X) + c) = X 2 .

hache 2 + (5 b + 4 un) X + (c – 2 un – 2 b) = X 2 .

Deux polynômes seront identiquement égaux s'ils sont égaux

coefficients pour les mêmes puissances de la variable :

un = 1

5b + 4un = 0

c– 2 un – 2 b = 0.

De ce système on trouve les coefficients

un = 1 , b = - , c = , Aussisatisfaitégalité

3 F (X ) - 2 F (1- X ) = X 2 sur l'ensemble de tous les nombres réels. En même temps, il y a un telX 0 Tâche 9. Fonctiony =F(X) car tout x est défini, continu et satisfait à la conditionF (F (X)) – F(X) = 1 + 2 X . Trouvez deux de ces fonctions.

Solution. Deux actions sont effectuées sur la fonction souhaitée - l'opération de composition d'une fonction complexe et

soustraction. Considérant que le côté droit de l’équation est une fonction linéaire, il est naturel de supposer que la fonction souhaitée est également linéaire :F(X) = ah +b , OùUN Etb – coefficients incertains. En remplaçant cette fonction parF (F ( (X ) = - X - 1 ;

F 2 (X ) = 2 X+ , qui sont des solutions de l'équation fonctionnelleF (F (X)) – F(X) = 1 + 2 X .

Conclusion.

En conclusion, il convient de noter que ce travail contribuera certainement à l'étude plus approfondie d'une méthode originale et efficace pour résoudre une variété de problèmes mathématiques, qui sont des problèmes de difficulté accrue et nécessitent une connaissance approfondie du cours de mathématiques scolaire et un haut niveau de logique. culture. Quiconque souhaite approfondir de manière indépendante ses connaissances en mathématiques trouvera également Cet ouvrage contient du matériel de réflexion et des tâches intéressantes, dont la solution apportera bénéfice et satisfaction.

L'ouvrage, dans le cadre du programme scolaire existant et sous une forme accessible pour une perception efficace, présente la méthode des coefficients indéfinis, qui permet d'approfondir le cursus scolaire en mathématiques.

Bien entendu, toutes les possibilités de la méthode des coefficients indéfinis ne peuvent être démontrées dans un seul ouvrage. En fait, la méthode nécessite encore des études et des recherches plus approfondies.

Liste de la littérature utilisée.

Glazer G.I..Histoire des mathématiques à l'école.-M. : Education, 1983.

Gomonov S.A. Equations fonctionnelles dans un cours de mathématiques scolaire // Mathématiques à l'école. – 2000. –№10 .

Dorofeev G.V., Potapov M.K., Rozov N.H.. Un manuel de mathématiques. - M. : Nauka, 1972.

Kurosh A.G. Équations algébriques de degrés arbitraires.- M. : Nauka, 1983.

Likhtarnikov L.M.. Introduction élémentaire aux équations fonctionnelles. – Saint-Pétersbourg. : Lan, 1997.

Manturov O.V., Solntsev Yu.K., Sorokin Yu.I., Fedin N.G.. Dictionnaire explicatif des termes mathématiques.-M. : Éducation, 1971

Modenov V.P.. Un manuel de mathématiques. Partie 1.-M. : Université d'État de Moscou, 1977.

Modenov V.P.. Problèmes avec les paramètres.- M. : Examen, 2006.

Potapov M.K., Aleksandrov V.V., Pasichenko P.I.. Algèbre et analyse des fonctions élémentaires. - M. : Nauka, 1980.

Khaliullin A.A.. Vous pouvez le résoudre plus facilement // Mathématiques à l'école. – 2003 . - №8 .

Khalioulline.

4. Développez le polynôme 2X 4 – 5X 3 + 9X 2 – 5X+ 3 pour les multiplicateurs à coefficients entiers.

5. A quelle valeur UN X 3 + 6X 2 + Oh+ 12 par X+ 4 ?

6. A quelle valeur du paramètreUN l'équationX 3 +5 X 2 + + Oh + b = 0 à coefficients entiers a deux racines différentes dont l'une est 1 ?

7. Parmi les racines du polynôme X 4 + X 3 – 18X 2 + Oh + b avec des coefficients entiers, il existe trois entiers égaux. Trouver la valeur b .

8. Trouvez la plus grande valeur entière du paramètre UN,à laquelle l'équation X 3 – 8X 2 + ah +b = 0 à coefficients entiers a trois racines différentes dont l'une est égale à 2.

9. À quelles valeurs UN Et b la division s'effectue sans reste X 4 + 3X 3 – 2X 2 + Oh + b sur X 2 – 3X + 2 ?

10. Factoriser les polynômes :

UN)X 4 + 2 X 2 – X + 2 V)X 4 – 4X 3 +9X 2 –8X + 5 d)X 4 + 12X – 5

b)X 4 + 3X 2 + 2X + 3 G)X 4 – 3X –2 e)X 4 – 7X 2 + 1 .

11. Résolvez les équations :

UN)
= 2 = 2 F (1 – X ) = X 2 .

Trouver F (X) .

13. Fonction à= F (X) Devant tout le monde X défini, continu et satisfait à la condition F ( F (X)) = F (X) + X. Trouvez deux de ces fonctions.

Tout d'abord, examinons la théorie, puis nous résoudrons quelques exemples pour renforcer le matériel sur le développement d'une fonction fractionnaire rationnelle en une somme de fractions simples. Regardons en détail méthode des coefficients indéterminés Et méthode de la valeur partielle, ainsi que leurs combinaisons.

Les fractions les plus simples sont souvent appelées fractions élémentaires.

On distingue : types de fractions simples:

où A, M, N, a, p, q sont des nombres et le discriminant du dénominateur dans les fractions 3) et 4) est inférieur à zéro.

On les appelle respectivement fractions des premier, deuxième, troisième et quatrième types.

Pourquoi même décomposer les fractions dans leur forme la plus simple ?

Donnons une analogie mathématique. Souvent, vous devez simplifier le type d'expression afin de pouvoir effectuer certaines actions avec. Ainsi, la représentation d’une fonction fractionnaire rationnelle comme somme de fractions simples est à peu près la même. Il est utilisé pour étendre les fonctions en séries entières, en séries de Laurent et, bien sûr, pour trouver des intégrales.

Par exemple, cela nécessite de prendre intégrale d'une fonction rationnelle fractionnaire. Après avoir décomposé l'intégrande en fractions simples, tout se résume à des intégrales assez simples

Mais à propos des intégrales dans une autre section.

Exemple.

Décomposez la fraction sous sa forme la plus simple.

Solution.

En général, le rapport des polynômes est décomposé en fractions simples si le degré du polynôme du numérateur est inférieur au degré du polynôme du dénominateur. Sinon, divisez d'abord le polynôme numérateur par le polynôme dénominateur, puis effectuez ensuite le développement de la fonction rationnelle fractionnaire correcte.

Faisons la division avec une colonne (coin) :

La fraction originale prendra donc la forme :

Ainsi, nous développerons en fractions simples

Algorithme pour la méthode des coefficients indéterminés.

Premièrement, on factorise le dénominateur.

Dans notre exemple, tout est simple : nous mettons x entre parenthèses.


Deuxièmement, la fraction à développer est représentée comme une somme de fractions simples avec coefficients incertains.

Ici, il convient de considérer les types d’expressions que vous pouvez avoir dans votre dénominateur.

Assez de théorie, en pratique tout est plus clair.

Il est temps de revenir à l'exemple. La fraction est décomposée en somme de fractions simples des premier et troisième types à coefficients indéterminés A, B et C.


Troisième, nous ramenons la somme résultante de fractions simples à coefficients indéterminés à un dénominateur commun et regroupons les termes au numérateur avec les mêmes puissances de x.



Autrement dit, nous sommes arrivés à l'égalité :


Pour x non nul, cette égalité se réduit à l'égalité de deux polynômes


Et deux polynômes sont égaux si et seulement si les coefficients de mêmes puissances coïncident.

Quatrième, nous égalisons les coefficients pour les mêmes puissances de x.

Dans ce cas, on obtient un système d'équations algébriques linéaires avec des coefficients indéterminés comme inconnues :


Cinquièmement, nous résolvons le système d'équations résultant de la manière qui vous convient (si nécessaire, voir l'article), nous trouvons les coefficients indéterminés.


En sixième, écrivez la réponse.

S'il vous plaît, ne soyez pas paresseux, vérifiez votre réponse en ramenant l'expansion résultante à un dénominateur commun.

Méthode du coefficient incertain est une méthode universelle pour décomposer des fractions en fractions plus simples.

Il est très pratique d'utiliser la méthode des valeurs partielles si le dénominateur est un produit de facteurs linéaires, c'est-à-dire qu'il a une forme similaire à

Regardons un exemple pour montrer les avantages de cette méthode.

Exemple.

Développer une fraction au plus simple.

Solution.

Puisque le degré du polynôme au numérateur est inférieur au degré du polynôme au dénominateur, nous n’avons pas besoin de diviser. Passons à la factorisation du dénominateur.

Tout d’abord, retirons x des parenthèses.

On trouve les racines d’un trinôme quadratique (par exemple, en utilisant le théorème de Vieta) :

Par conséquent, le trinôme quadratique peut s’écrire

Autrement dit, le dénominateur prendra la forme

Avec un dénominateur donné, la fraction originale se décompose en la somme de trois fractions simples du premier type à coefficients indéterminés :

Nous ramenons la somme résultante à un dénominateur commun, mais nous n'ouvrons pas les parenthèses au numérateur et ne donnons pas de parenthèses similaires pour A, B et C (à ce stade c'est précisément la différence avec la méthode des coefficients indéfinis) :

Ainsi, nous sommes arrivés à l'égalité :

Et maintenant, pour trouver les coefficients indéterminés, nous commençons à substituer des « valeurs partielles » dans l’égalité résultante, à laquelle le dénominateur passe à zéro, c’est-à-dire x=0, x=2 et x=3 pour notre exemple.

À x=0 on a :

À x=2 on a :

À x=3 on a :

Répondre:

Comme vous pouvez le constater, la différence entre la méthode des coefficients indéterminés et la méthode des valeurs partielles réside uniquement dans la méthode de recherche des inconnues. Ces méthodes peuvent être combinées pour simplifier les calculs.

Regardons un exemple.

Exemple.

Développer fractionnellement une expression rationnelle aux fractions simples.

Solution.

Puisque le degré du polynôme numérateur est inférieur au degré du polynôme dénominateur et que le dénominateur a déjà été factorisé, l'expression originale sera présentée comme une somme de fractions simples de la forme suivante :

Ramenons-le à un dénominateur commun :

Égalisons les numérateurs.

Évidemment, les zéros du dénominateur sont les valeurs x=1, x=-1 et x=3. Nous utilisons la méthode des valeurs partielles.

À x=1 on a :

À x=-1 on a :

À x=3 on a :

Reste à trouver les inconnues et

Pour ce faire, on substitue les valeurs trouvées à l'égalité des numérateurs :

Après avoir ouvert les parenthèses et ramené des termes similaires avec les mêmes puissances de x, on arrive à l'égalité de deux polynômes :

Nous égalisons les coefficients correspondants aux mêmes degrés, compilant ainsi un système d'équations pour trouver les inconnues restantes et . On obtient un système de cinq équations à deux inconnues :

De la première équation on trouve immédiatement, de la deuxième équation

En conséquence, nous obtenons la décomposition en fractions simples :

Note.

Si l’on décidait immédiatement d’appliquer la méthode des coefficients indéterminés, il faudrait résoudre un système de cinq équations algébriques linéaires à cinq inconnues. L'utilisation de la méthode des valeurs partielles a permis de trouver facilement les valeurs de trois inconnues sur cinq, ce qui a grandement simplifié la solution ultérieure.

Une fonction rationnelle est une fraction de la forme dont le numérateur et le dénominateur sont des polynômes ou des produits de polynômes.

Exemple 1. Étape 2.

.

On multiplie les coefficients indéterminés par des polynômes qui ne sont pas dans cette fraction individuelle, mais qui sont dans d'autres fractions résultantes :

Nous ouvrons les parenthèses et assimilons le numérateur de l'intégrande d'origine à l'expression résultante :

Des deux côtés de l'égalité, nous recherchons des termes avec les mêmes puissances de x et composons à partir d'eux un système d'équations :

.

On annule tous les x et on obtient un système d’équations équivalent :

.

Ainsi, le développement final de l’intégrande en une somme de fractions simples est :

.

Exemple 2. Étape 2. A l'étape 1, nous avons obtenu la décomposition suivante de la fraction originale en somme de fractions simples à coefficients indéterminés aux numérateurs :

.

Nous commençons maintenant à rechercher des coefficients incertains. Pour ce faire, nous assimilons le numérateur de la fraction d'origine dans l'expression de la fonction au numérateur de l'expression obtenue après réduction de la somme des fractions à un dénominateur commun :

Vous devez maintenant créer et résoudre un système d’équations. Pour ce faire, on assimile les coefficients de la variable au degré correspondant au numérateur de l'expression originale de la fonction et aux coefficients similaires dans l'expression obtenue à l'étape précédente :

On résout le système résultant :

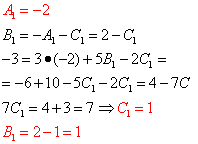
Donc, à partir d'ici

.

Exemple 3. Étape 2. A l'étape 1, nous avons obtenu la décomposition suivante de la fraction originale en somme de fractions simples à coefficients indéterminés aux numérateurs :

Nous commençons à rechercher des coefficients incertains. Pour ce faire, nous assimilons le numérateur de la fraction d'origine dans l'expression de la fonction au numérateur de l'expression obtenue après réduction de la somme des fractions à un dénominateur commun :

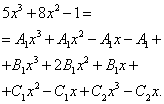
Comme dans les exemples précédents, nous composons un système d'équations :

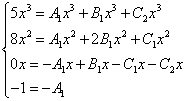
Nous réduisons les x et obtenons un système d'équations équivalent :

En résolvant le système, on obtient les valeurs suivantes des coefficients incertains :

On obtient la décomposition finale de l'intégrande en somme de fractions simples :

.

Exemple 4. Étape 2. A l'étape 1, nous avons obtenu la décomposition suivante de la fraction originale en somme de fractions simples à coefficients indéterminés aux numérateurs :

.

Nous savons déjà grâce aux exemples précédents comment assimiler le numérateur de la fraction originale à l'expression au numérateur obtenue après avoir décomposé la fraction en la somme de fractions simples et ramené cette somme à un dénominateur commun. Par conséquent, juste à des fins de contrôle, nous présentons le système d’équations résultant :

En résolvant le système, on obtient les valeurs suivantes des coefficients incertains :

On obtient la décomposition finale de l'intégrande en somme de fractions simples :

Exemple 5. Étape 2. A l'étape 1, nous avons obtenu la décomposition suivante de la fraction originale en somme de fractions simples à coefficients indéterminés aux numérateurs :

.

Nous réduisons indépendamment cette somme à un dénominateur commun, assimilant le numérateur de cette expression au numérateur de la fraction originale. Le résultat devrait être le système d’équations suivant :

En résolvant le système, on obtient les valeurs suivantes des coefficients incertains :

.

On obtient la décomposition finale de l'intégrande en somme de fractions simples :

.

Exemple 6. Étape 2. A l'étape 1, nous avons obtenu la décomposition suivante de la fraction originale en somme de fractions simples à coefficients indéterminés aux numérateurs :

Nous effectuons les mêmes actions avec ce montant que dans les exemples précédents. Le résultat devrait être le système d’équations suivant :

En résolvant le système, on obtient les valeurs suivantes des coefficients incertains :

.

On obtient la décomposition finale de l'intégrande en somme de fractions simples :

.

Exemple 7. Étape 2. A l'étape 1, nous avons obtenu la décomposition suivante de la fraction originale en somme de fractions simples à coefficients indéterminés aux numérateurs :

.

Après certaines actions avec le montant résultant, le système d'équations suivant doit être obtenu :

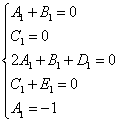
En résolvant le système, on obtient les valeurs suivantes des coefficients incertains :

On obtient la décomposition finale de l'intégrande en somme de fractions simples :

.

Exemple 8. Étape 2. A l'étape 1, nous avons obtenu la décomposition suivante de la fraction originale en somme de fractions simples à coefficients indéterminés aux numérateurs :

.

Apportons quelques modifications aux actions qui ont déjà été amenées à l'automaticité pour obtenir un système d'équations. Il existe une technique artificielle qui, dans certains cas, permet d'éviter des calculs inutiles. En ramenant la somme des fractions à un dénominateur commun, on obtient et en assimilant le numérateur de cette expression au numérateur de la fraction originale, on obtient.