1. La règle pour additionner des fractions avec les mêmes dénominateurs :

Exemple 1:

Exemple 2 :

Règle pour additionner des fractions avec des dénominateurs différents :

Exemple 1:

Exemple 2 :

Ici, les dénominateurs n’ont pas été multipliés, mais le plus petit commun diviseur a2 a été pris.
(Le dénominateur a la puissance la plus élevée de 2.)
Un facteur supplémentaire pour la première fraction est 1, pour la seconde c'est a.

2. Règle pour soustraire des fractions de mêmes dénominateurs :

Règle pour soustraire des fractions avec des dénominateurs différents :

3. Règle de multiplication des fractions ordinaires :

4. Règle de division des fractions :

Exemple:

Fraction ordinaire (simple). Numérateur et dénominateur d'une fraction.
Corriger et Pas fraction propre. Numéro mixte.
Quotient incomplet. Parties entières et fractionnaires. Fractions inversées. Une partie d'une unité ou plusieurs parties de celle-ci sont appelées fraction ordinaire ou simple. Quantité parts égales, dans lequel l'unité est divisée, est appelé le dénominateur, et le nombre de parties prises est appelé le numérateur. La fraction s'écrit :

Ici 3 est le numérateur, 7 est le dénominateur.

Si le numérateur est inférieur au dénominateur, alors la fraction est inférieure à 1 et s'appelle fraction propre. Si le numérateur est égal au dénominateur, alors la fraction est égale à 1. Si le numérateur est supérieur au dénominateur, alors la fraction est supérieure à 1. Dans les deux derniers cas, la fraction est dite impropre. Si le numérateur est divisé par le dénominateur, alors cette fraction est égale au quotient de la division : 63 / 7 = 9. Si la division est effectuée avec un reste, alors cette fraction impropre peut être représentée nombre mixte:

Ici 9 – quotient incomplet(partie entière d'un nombre fractionnaire), 2 – reste (numérateur de la partie fractionnaire), 7 – dénominateur.
Il est souvent nécessaire de résoudre le problème inverse : inverser un nombre mixte en une fraction. Pour ce faire, multipliez la partie entière du nombre fractionnaire par le dénominateur et ajoutez le numérateur de la partie fractionnaire. Ce sera le numérateur de la fraction commune, mais le dénominateur reste le même.

Les fractions réciproques sont deux fractions dont le produit est égal à 1. Par exemple, 3/7 et 7/3 ; 15/1 et 1/15, etc.

Expansion des fractions. Réduire une fraction. Comparer des fractions.
Menant à dénominateur commun. Addition et soustraction fractions.
Multiplier des fractions. Division de fractions
Expansion des fractions.La valeur d'une fraction ne change pas si son numérateur et son dénominateur sont multipliés par le même nombre autre que zéro en développant la fraction. Par exemple :

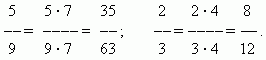
Réduire une fraction. La valeur d'une fraction ne change pas si vous divisez son numérateur et son dénominateur par le même nombre autre que zéro.. Cette transformation est appeléeréduire une fraction. Par exemple,

Comparer des fractions.De deux fractions ayant les mêmes numérateurs, celle dont le dénominateur est le plus petit est la plus grande :

De deux fractions de même dénominateur, celle dont le numérateur est le plus grand est la plus grande :

Pour comparer des fractions ayant des numérateurs et des dénominateurs différents, vous devez les développer pour les amener à un dénominateur commun.
EXEMPLE Comparez deux fractions :

La transformation utilisée ici s'appelle amener les fractions à un dénominateur commun.
Additionner et soustraire des fractions.Si les dénominateurs des fractions sont les mêmes, alors pour additionner les fractions, vous devez ajouter leurs numérateurs, et pour soustraire les fractions, vous devez soustraire leurs numérateurs (dans le même ordre). La somme ou la différence résultante sera le numérateur du résultat ; le dénominateur restera le même. Si les dénominateurs des fractions sont différents, vous devez d'abord réduire les fractions à un dénominateur commun. Lors de l'ajout nombres mixtes leurs parties entières et fractionnaires sont ajoutées séparément. Lors de la soustraction de nombres fractionnaires, nous vous recommandons de les convertir d'abord en fractions impropres, puis de soustraire l'une de l'autre, puis de reconvertir le résultat, si nécessaire, sous forme de nombres fractionnaires.
EXEMPLE

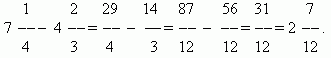
Multiplier des fractions.Multiplier un nombre par une fraction signifie le multiplier par le numérateur et diviser le produit par le dénominateur. Nous avons donc règle générale multiplier des fractions :pour multiplier des fractions, vous devez multiplier leurs numérateurs et dénominateurs séparément et diviser le premier produit par le second.
EXEMPLE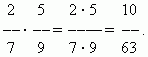
Diviser des fractions. Pour diviser un certain nombre par une fraction, il faut multiplier ce nombre par la fraction réciproque. Cette règle découle de la définition de la division (voir la section « Opérations arithmétiques »).
EXEMPLE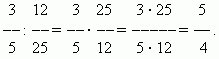

Décimal. La partie entière. Virgule.
Places décimales. Propriétés des fractions décimales.
Fraction décimale périodique. Période
Décimalest le résultat de la division d'un par dix, cent, mille, etc. les pièces. Ces fractions sont très pratiques pour les calculs, car elles sont basées sur le même système de position sur lequel sont basées le comptage et l'écriture des nombres entiers. Grâce à cela, la notation et les règles pour travailler avec des fractions décimales sont essentiellement les mêmes que pour les nombres entiers. Lors de l'écriture de fractions décimales, il n'est pas nécessaire de marquer le dénominateur, celui-ci est déterminé par la place occupée par le chiffre correspondant. D'abord c'est écrit partie entière chiffres, puis mis à droitevirgule. Le premier chiffre après la virgule décimale signifie le nombre de dixièmes, le deuxième – le nombre de centièmes, le troisième – le nombre de millièmes, etc. Les nombres situés après la virgule décimale sont appelésdécimales.
EXEMPLE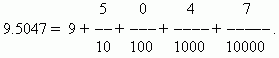
L'un des avantages des fractions décimales est qu'elles se réduisent facilement en fractions ordinaires : le nombre après la virgule (dans notre cas 5047) est le numérateur ; le dénominateur est égal n -ème puissance de 10, où n - nombre de décimales (dans notre cas n = 4):
Si la fraction décimale ne contient pas de partie entière, alors un zéro est placé avant la virgule décimale :

Propriétés des fractions décimales.

1. La décimale ne change pas si vous ajoutez des zéros à droite:

2. La fraction décimale ne change pas si vous supprimez les zéros situés
à la fin de la virgule:

0.00123000 = 0.00123 .

Attention : vous ne pouvez pas supprimer les zéros qui ne se trouvent pas à la fin décimal!br />

Ces propriétés vous permettent de multiplier et de diviser rapidement des décimales par 10, 100, 1000, etc.

Décimal périodique contient un groupe de nombres infiniment répétitifs appelé point. Le point est écrit entre parenthèses. Par exemple, 0,12345123451234512345… = 0.(12345).

EXEMPLE Si nous divisons 47 par 11, nous obtenons 4,27272727... = 4.(27).

Multiplier des décimales.
Diviser des décimales.

Additionner et soustraire des décimales. Ces opérations s'effectuent de la même manière que l'addition et la soustraction d'entiers. Il vous suffit de noter les décimales correspondantes les unes en dessous des autres.
EXEMPLE

Multiplier des décimales. Dans un premier temps, on multiplie les fractions décimales par des nombres entiers, sans tenir compte du point décimal. La règle suivante s'applique alors : le nombre de décimales dans le produit est égal à la somme des décimales de tous les facteurs.
Note: avant de placer le point décimal dansle produit ne peut pas être jeté avec des zéros à droite!
EXEMPLE

La somme des nombres de décimales dans les facteurs est égale à : 3 + 4 = 7. La somme des nombres dans le produit est 6. Il faut donc ajouter un zéro à gauche : 0197056 et mettre une virgule décimale devant lui : 0,0197056.
Division décimale
Diviser un nombre décimal par un nombre entier
Si le dividende est inférieur au diviseur, écrivez un zéro dans la partie entière du quotient et mettez un point décimal après. Ensuite, sans prendre en compte la virgule décimale du dividende, nous ajoutons le chiffre suivant de la partie fractionnaire à sa partie entière et comparons à nouveau la partie entière résultante du dividende avec le diviseur. Si le nouveau nombre est à nouveau inférieur au diviseur, nous mettons un autre zéro après la virgule décimale dans le quotient et ajoutons le chiffre suivant de sa partie fractionnaire à la partie entière du dividende. Nous répétons ce processus jusqu'à ce que le dividende obtenu devienne supérieur au diviseur. Après cela, la division est effectuée comme pour les nombres entiers. Si le dividende est supérieur ou égal au diviseur, nous divisons d'abord toute sa partie, écrivons le résultat de la division dans le quotient et mettons un point décimal. Après cela, la division continue comme dans le cas des nombres entiers.
EXEMPLE Divisez 1,328 par 64.
Solution:
Diviser une fraction décimale par une autre.
Tout d’abord, nous transférons les décimales du dividende et du diviseur au nombre de décimales du diviseur, c’est-à-dire que nous faisons du diviseur un nombre entier. Nous effectuons maintenant la division comme dans le cas précédent.
EXEMPLE Divisez 0,04569 par 0,0006.
Solution : Déplacez les points décimaux de 4 positions vers la droite et divisez 456,9 par 6 :

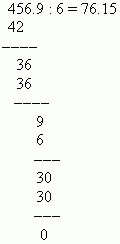
Afin d'inverser décimal dans un nombre ordinaire, vous devez prendre le nombre après la virgule comme numérateur et prendre la nième puissance de dix comme dénominateur (ici n est le nombre de décimales). La partie entière non nulle est stockée dans une fraction ordinaire ; la partie entière nulle est omise. Par exemple:
Afin de convertir une fraction en nombre décimal, vous devez diviser le numérateur par le dénominateur conformément aux règles de division..
EXEMPLE Convertissez 5/8 en décimal.
Solution : Diviser 5 par 8 donne 0,625. (Vérifiez, s'il vous plaît!).
Dans la plupart des cas, ce processus peut se poursuivre indéfiniment. Il est alors impossible de convertir avec précision une fraction en nombre décimal. Mais dans la pratique, cela n’est jamais obligatoire. La division est interrompue si les décimales intéressantes ont déjà été obtenues.
EXEMPLE Convertissez 1/3 en nombre décimal.
Solution : Diviser 1 par 3 sera infini : 1:3 = 0,3333… .
Verifiez le s'il vous plaît!

Multiplier et diviser des fractions.

Attention!
Il y a des supplémentaires
matériaux dans la section spéciale 555.
Pour ceux qui sont très "pas très..."
Et pour ceux qui « beaucoup… »)

Cette opération est bien plus sympa que l’addition-soustraction ! Parce que c'est plus facile. Pour rappel, pour multiplier une fraction par une fraction, il faut multiplier les numérateurs (ce sera le numérateur du résultat) et les dénominateurs (ce sera le dénominateur). C'est-à-dire:

Par exemple:

Tout est extrêmement simple. Et s’il vous plaît, ne cherchez pas de dénominateur commun ! On n'a pas besoin de lui ici...

Pour diviser une fraction par une fraction, il faut inverser deuxième(c'est important !) fraction et multipliez-les, c'est-à-dire :

Par exemple:

Si vous rencontrez une multiplication ou une division avec des nombres entiers et des fractions, ce n'est pas grave. Comme pour l'addition, on fait une fraction à partir d'un nombre entier avec un au dénominateur - et c'est parti ! Par exemple:

Au lycée, on est souvent confronté à des fractions de trois étages (voire quatre étages !). Par exemple:

Comment puis-je rendre cette fraction décente ? Oui, très simple ! Utilisez la division en deux points :

Mais n'oubliez pas l'ordre de division ! Contrairement à la multiplication, c'est très important ici ! Bien entendu, on ne confondra pas 4:2 ou 2:4. Mais il est facile de se tromper sur une fraction de trois étages. A noter par exemple :

Dans le premier cas (expression de gauche) :

Dans la seconde (expression de droite) :

Sentez-vous la différence ? 4 et 1/9 !

Qu’est-ce qui détermine l’ordre de division ? Soit avec des parenthèses, soit (comme ici) avec la longueur des lignes horizontales. Développez votre œil. Et s'il n'y a pas de parenthèses ni de tirets, comme :

puis divise et multiplie dans l'ordre, de gauche à droite!

Et une autre technique très simple et importante. Dans des actions avec diplômes, cela vous sera tellement utile ! Divisons un par n'importe quelle fraction, par exemple par 13/15 :

Le coup s'est retourné ! Et cela arrive toujours. Lorsque l’on divise 1 par n’importe quelle fraction, le résultat est la même fraction, mais à l’envers.

C'est tout pour les opérations avec des fractions. La chose est assez simple, mais elle donne largement assez d'erreurs. Tenez compte des conseils pratiques, et il y en aura moins (erreurs) !

Conseils pratiques :

1. La chose la plus importante lorsque l’on travaille avec des expressions fractionnaires est la précision et l’attention ! N'est pas Mots communs, pas de bons voeux ! C'est une nécessité absolue ! Effectuez tous les calculs de l'examen d'État unifié comme une tâche à part entière, ciblée et claire. Il est préférable d’écrire deux lignes supplémentaires dans votre brouillon plutôt que de faire des erreurs lors de vos calculs mentaux.

2. Dans les exemples avec différents types fractions - allez aux fractions ordinaires.

3. Nous réduisons toutes les fractions jusqu'à ce qu'elles s'arrêtent.

4. Nous réduisons les expressions fractionnaires à plusieurs niveaux aux expressions ordinaires en utilisant la division par deux points (nous suivons l'ordre de division !).

5. Divisez une unité par une fraction dans votre tête, en retournant simplement la fraction.

Voici les tâches que vous devez absolument accomplir. Les réponses sont données après toutes les tâches. Utilisez le matériel sur ce sujet et les conseils pratiques. Estimez combien d’exemples vous avez pu résoudre correctement. La première fois! Sans calculatrice ! Et tirez les bonnes conclusions...

N'oubliez pas : la bonne réponse est reçu dès la deuxième (surtout la troisième) fois ne compte pas ! Telle est la dure vie.

Donc, résoudre en mode examen ! D'ailleurs, il s'agit déjà d'une préparation à l'examen d'État unifié. Nous résolvons l'exemple, le vérifions, résolvons le suivant. Nous avons tout décidé - vérifié à nouveau du début au dernier. Mais, seulement Alors regarde les réponses.

Calculer:

As-tu décidé?

Nous recherchons des réponses qui correspondent aux vôtres. Je les ai volontairement notées dans le désordre, loin de la tentation, pour ainsi dire... Les voici, les réponses, écrites avec des points-virgules.

0; 17/22; 3/4; 2/5; 1; 25.

Maintenant, nous tirons des conclusions. Si tout s'est bien passé, je suis content pour toi ! Les calculs de base avec des fractions ne sont pas votre problème ! Vous pouvez faire des choses plus sérieuses. Sinon...

Vous avez donc l'un des deux problèmes suivants. Ou les deux à la fois.) Manque de connaissances et (ou) inattention. Mais ça soluble Problèmes.

Si vous aimez ce site...

Au fait, j'ai quelques autres sites intéressants pour vous.)

Vous pouvez vous entraîner à résoudre des exemples et découvrir votre niveau. Test avec vérification instantanée. Apprenons - avec intérêt !)

Vous pouvez vous familiariser avec les fonctions et les dérivées.

496. Trouver X, Si:

497. 1) Si vous ajoutez 10 1/2 à 3/10 d’un nombre inconnu, vous obtenez 13 1/2. Trouvez le numéro inconnu.

2) Si vous soustrayez 10 1/2 de 7/10 d'un nombre inconnu, vous obtenez 15 2/5. Trouvez le numéro inconnu.

498 *. Si vous soustrayez 10 des 3/4 d'un nombre inconnu et multipliez la différence obtenue par 5, vous obtenez 100. Trouvez le nombre.

499 *. Si vous augmentez un nombre inconnu des 2/3, vous obtenez 60. De quel nombre s'agit-il ?

500 *. Si vous ajoutez le même montant au nombre inconnu, ainsi que 20 1/3, vous obtenez 105 2/5. Trouvez le numéro inconnu.

501. 1) Le rendement des pommes de terre avec une plantation en grappes carrées est en moyenne de 150 centimes par hectare, et avec une plantation conventionnelle, il représente 3/5 de ce montant. Combien de pommes de terre supplémentaires peuvent être récoltées sur une superficie de 15 hectares si les pommes de terre sont plantées selon la méthode des grappes carrées ?

2) Un ouvrier expérimenté a produit 18 pièces en 1 heure, et un ouvrier inexpérimenté a produit les 2/3 de cette quantité. Combien de pièces supplémentaires un travailleur expérimenté peut-il produire en 7 heures par jour ?

502. 1) Les pionniers rassemblés au sein trois jours 56 kg de graines différentes. Le premier jour, 3/14 du montant total ont été collectés, le deuxième, une fois et demie plus, et le troisième jour, le reste du grain. Combien de kilos de graines les pionniers ont-ils récoltés le troisième jour ?

2) Lors de la mouture du blé, le résultat était : farine 4/5 de la quantité totale de blé, semoule - 40 fois moins que la farine, et le reste était du son. Quelle quantité de farine, de semoule et de son ont été produites séparément lors de la mouture de 3 tonnes de blé ?

503. 1) Trois garages peuvent accueillir 460 voitures. Le nombre de voitures pouvant entrer dans le premier garage est 3/4 du nombre de voitures pouvant entrer dans le deuxième, et le troisième garage contient 1 1/2 fois plus de voitures que le premier. Combien de voitures peuvent contenir chaque garage ?

2) Une usine avec trois ateliers emploie 6 000 ouvriers. Dans le deuxième atelier, il y a 1 1/2 fois moins d'ouvriers que dans le premier, et le nombre d'ouvriers dans le troisième atelier est 5/6 du nombre d'ouvriers dans le deuxième atelier. Combien y a-t-il d’ouvriers dans chaque atelier ?

504. 1) D'abord 2/5, puis 1/3 du kérosène total ont été versés d'un réservoir contenant du kérosène, et après cela, 8 tonnes de kérosène sont restées dans le réservoir. Quelle quantité de kérosène y avait-il initialement dans le réservoir ?

2) Les cyclistes ont couru pendant trois jours. Le premier jour, ils ont parcouru 4/15 de l'ensemble du voyage, le deuxième - 2/5 et le troisième jour les 100 km restants. Quelle distance les cyclistes ont-ils parcourue en trois jours ?

505. 1) Le brise-glace s'est frayé un chemin à travers la banquise pendant trois jours. Le premier jour, il a parcouru la moitié de la distance totale, le deuxième jour les 3/5 de la distance restante et le troisième jour les 24 km restants. Trouvez la longueur du chemin parcouru par le brise-glace en trois jours.

2) Trois groupes d'écoliers ont planté des arbres pour verdir le village. Le premier détachement a planté 7/20 de tous les arbres, le deuxième 5/8 des arbres restants et le troisième les 195 arbres restants. Combien d’arbres les trois équipes ont-elles plantés au total ?

506. 1) Une moissonneuse-batteuse a récolté du blé sur une parcelle en trois jours. Le premier jour, il a récolté sur 5/18 de la superficie totale de la parcelle, le deuxième jour sur 7/13 de la superficie restante, et le troisième jour sur la superficie restante de 30 1/2 hectares. En moyenne, 20 centimes de blé ont été récoltés sur chaque hectare. Quelle quantité de blé a été récoltée dans toute la région ?

2) Le premier jour, les participants au rallye ont parcouru 3/11 de l'ensemble du parcours, le deuxième jour 7/20 du parcours restant, le troisième jour 5/13 du nouveau reste et le quatrième jour le reste 320 km. Quelle est la longueur du parcours du rallye ?

507. 1) Le premier jour, la voiture a parcouru 3/8 de la distance totale, le deuxième jour 15/17 de ce qu'elle a parcouru le premier et le troisième jour les 200 km restants. Quelle quantité d'essence a été consommée si une voiture consomme 1 3/5 kg d'essence pour 10 km ?

2) La ville se compose de quatre quartiers. Et 4/13 de tous les habitants de la ville vivent dans le premier arrondissement, 5/6 des habitants du premier arrondissement vivent dans le deuxième, 4/11 des habitants du premier vivent dans le troisième ; deux districts réunis, et 18 000 personnes vivent dans le quatrième district. De quelle quantité de pain l'ensemble de la population de la ville a-t-elle besoin pendant 3 jours, si en moyenne une personne en consomme 500 g par jour ?

508. 1) Le touriste a marché le premier jour 10/31 de tout le voyage, le deuxième 9/10 de ce qu'il a marché le premier jour, et le troisième le reste du chemin, et le troisième jour il a marché 12 km de plus que le deuxième jour. Combien de kilomètres le touriste a-t-il parcouru au cours de chacun des trois jours ?

2) La voiture a parcouru tout le trajet de la ville A à la ville B en trois jours. Le premier jour, la voiture a parcouru 7/20 de la distance totale, le deuxième 8/13 de la distance restante et le troisième jour, la voiture a parcouru 72 km de moins que le premier jour. Quelle est la distance entre les villes A et B ?

509. 1) Le Comité exécutif a attribué des terrains aux ouvriers de trois usines pour des parcelles de jardin. La première usine s'est vu attribuer 9/25 du nombre total de parcelles, la deuxième usine 5/9 du nombre de parcelles allouées à la première et la troisième - les parcelles restantes. Combien de parcelles au total ont été attribuées aux ouvriers de trois usines, si la première usine se voyait attribuer 50 parcelles de moins que la troisième ?

2) L'avion a livré une équipe de travailleurs d'hiver à la station polaire depuis Moscou en trois jours. Le premier jour, il a parcouru 2/5 de la distance totale, le deuxième - 5/6 de la distance parcourue le premier jour et le troisième jour, il a parcouru 500 km de moins que le deuxième jour. Quelle distance l’avion a-t-il parcouru en trois jours ?

510. 1) L'usine comptait trois ateliers. Le nombre d'ouvriers dans le premier atelier représente les 2/5 de tous les ouvriers de l'usine ; dans le deuxième atelier, il y a 1 1/2 fois moins d'ouvriers que dans le premier, et dans le troisième atelier, il y a 100 ouvriers de plus que dans le deuxième. Combien d’ouvriers y a-t-il dans l’usine ?

2) La ferme collective comprend des habitants de trois villages voisins. Le nombre de familles dans le premier village est de 3/10 de toutes les familles de la ferme collective ; dans le deuxième village, le nombre de familles est 1,5 fois plus grand que dans le premier, et dans le troisième village, le nombre de familles est inférieur de 420 à celui du deuxième. Combien de familles y a-t-il dans la ferme collective ?

511. 1) L'artel a épuisé 1/3 de son stock de matières premières la première semaine, et 1/3 du reste la seconde. Quelle quantité de matières premières reste-t-il dans l'artel si, la première semaine, la consommation de matières premières était de 3/5 tonnes de plus que la deuxième semaine ?

2) Sur le charbon importé, 1/6 a été dépensé pour chauffer la maison le premier mois et 3/8 du reste le deuxième mois. Quelle quantité de charbon reste-t-il pour chauffer la maison si 1 3/4 de plus a été utilisé le deuxième mois que le premier mois ?

512. 3/5 de la superficie totale de la ferme collective sont affectés à l'ensemencement des céréales, 13/36 du reste est occupé par des potagers et des prairies, le reste des terres est constitué de forêt et la superficie ensemencée de la ferme collective est 217 hectares de plus que la superficie forestière, 1/3 des terres allouées aux semis de céréales sont semées de seigle et le reste est du blé. Combien d'hectares de terre la ferme collective a-t-elle semé en blé et combien en seigle ?

513. 1) Le trajet du tramway fait 14 3/8 km. Le long de cet itinéraire, le tramway effectue 18 arrêts, passant en moyenne jusqu'à 1 1/6 minutes par arrêt. La vitesse moyenne du tramway sur tout le parcours est de 12 1/2 km par heure. Combien de temps faut-il à un tramway pour effectuer un trajet ?

2) Ligne d'autobus 16 km. Le long de cet itinéraire, le bus effectue 36 arrêts de 3/4 minutes chacun. en moyenne chacun. La vitesse moyenne des bus est de 30 km/h. Combien de temps prend un bus pour un trajet ?

514*. 1) Il est 6 heures maintenant. soirées. Quelle partie de la journée représente la partie restante de la journée passée et quelle partie de la journée reste-t-elle ?

2) Un bateau à vapeur parcourt la distance entre deux villes avec le courant en 3 jours. et retour sur la même distance en 4 jours. Combien de jours les radeaux flotteront-ils en aval d’une ville à une autre ?

515. 1) Combien de planches seront utilisées pour poser le sol dans une pièce dont la longueur est de 6 2/3 m, la largeur de 5 1/4 m, si la longueur de chaque planche est de 6 2/3 m et sa largeur est de 3/ 80 de la longueur ?

2) Une plate-forme rectangulaire a une longueur de 45 1/2 m et sa largeur est de 5/13 de sa longueur. Cette zone est bordée par un chemin de 4/5 m de large.Retrouvez la zone du chemin.

516. Trouver la moyenne nombres arithmétiques:

517. 1) La moyenne arithmétique de deux nombres est 6 1/6. L'un des nombres est 3 3/4. Trouvez un autre numéro.

2) La moyenne arithmétique de deux nombres est 14 1/4. L'un de ces nombres est 15 5/6. Trouvez un autre numéro.

518. 1) Le train de marchandises a circulé pendant trois heures. Dans la première heure, il a parcouru 36 1/2 km, dans la deuxième 40 km et dans la troisième 39 3/4 km. Trouvez la vitesse moyenne du train.

2) La voiture a parcouru 81 1/2 km au cours des deux premières heures et 95 km au cours des 2 1/2 heures suivantes. Combien de kilomètres parcourait-il en moyenne par heure ?

519. 1) Le conducteur du tracteur a terminé la tâche de labourer la terre en trois jours. Le premier jour, il a labouré 12 1/2 hectares, le deuxième jour 15 3/4 hectares et le troisième jour 14 1/2 hectares. En moyenne, combien d’hectares de terre un conducteur de tracteur laboure-t-il par jour ?

2) Un groupe d'écoliers, effectuant un voyage touristique de trois jours, a parcouru la route pendant 6 heures et demie le premier jour, 7 heures le deuxième. et le troisième jour - 4 2/3 heures. Combien d’heures en moyenne les écoliers voyagent-ils chaque jour ?

520. 1) Trois familles vivent dans la maison. La première famille dispose de 3 ampoules pour éclairer l'appartement, la seconde de 4 et la troisième de 5 ampoules. Combien chaque famille devrait-elle payer pour l'électricité si toutes les lampes étaient identiques et si la facture totale d'électricité (pour toute la maison) était de 7 1/5 roubles ?

2) Un polisseur polissait les sols d'un appartement où vivaient trois familles. La première famille avait une surface habitable de 36 1/2 mètres carrés. m, le second fait 24 1/2 m². m, et le troisième - 43 m². M. Pour tout le travail, 2 roubles ont été payés. 08 kop. Combien chaque famille a-t-elle payé ?

521. 1) Dans la parcelle de jardin, des pommes de terre ont été récoltées sur 50 buissons à 1 1/10 kg par buisson, sur 70 buissons à 4/5 kg par buisson, sur 80 buissons à 9/10 kg par buisson. Combien de kilogrammes de pommes de terre sont récoltés en moyenne dans chaque buisson ?

2) L'équipe de terrain sur une superficie de 300 hectares a reçu une récolte de 20 1/2 quintaux de blé d'hiver par 1 hectare, de 80 hectares à 24 quintaux par 1 ha, et de 20 hectares - 28 1/2 quintaux par 1 ha. Quel est le rendement moyen dans une brigade de 1 hectare ?

522. 1) La somme de deux nombres est 7 1/2. Un nombre est 4 4/5 plus grand que l'autre. Trouvez ces numéros.

2) Si nous additionnons les nombres exprimant la largeur des détroits de Tatar et de Kertch, nous obtenons 11 7/10 km. Le détroit de Tatar est 3 1/10 km plus large que le détroit de Kertch. Quelle est la largeur de chaque détroit ?

523. 1) La somme de trois nombres est 35 2 / 3. Le premier nombre est supérieur au deuxième de 5 1/3 et au troisième de 3 5/6. Trouvez ces numéros.

2) Îles Nouvelle terre, Sakhaline et Severnaya Zemlya occupent ensemble une superficie de 196 7/10 mille mètres carrés. km. La superficie de Novaya Zemlya est de 44 1/10 mille mètres carrés. km de superficie en plus Severnaïa Zemlya et 5 1/5 mille m². km plus grand que la superficie de Sakhaline. Quelle est la superficie de chacune des îles répertoriées ?

524. 1) L'appartement se compose de trois pièces. La superficie de la première pièce est de 24 3/8 m². m et fait 13/36 de la superficie totale de l'appartement. La superficie de la deuxième pièce est de 8 1/8 mètres carrés. m plus que la superficie du troisième. Quelle est la superficie de la deuxième pièce ?

2) Lors d'une compétition de trois jours, le premier jour, un cycliste a passé 3 heures et quart sur la route, soit 13/43 du temps total de trajet. Le deuxième jour, il a roulé 1h30 de plus que le troisième jour. Combien d'heures le cycliste a-t-il parcouru le deuxième jour de la compétition ?

525. Trois morceaux de fer pèsent ensemble 17 1/4 kg. Si le poids de la première pièce est réduit de 1 1/2 kg, celui de la seconde de 2 1/4 kg, alors les trois pièces auront le même poids. Combien pesait chaque morceau de fer ?

526. 1) La somme de deux nombres est 15 1/5. Si le premier nombre est réduit de 3 1/10 et le second est augmenté de 3 1/10, alors ces nombres seront égaux. A quoi est égal chaque nombre ?

2) Il y avait 38 1/4 kg de céréales dans deux boîtes. Si vous versez 4 3/4 kg de céréales d'une boîte dans une autre, il y aura des quantités égales de céréales dans les deux boîtes. Combien de céréales y a-t-il dans chaque boîte ?

527 . 1) La somme de deux nombres est 17 17 / 30. Si vous soustrayez 5 1/2 du premier nombre et l'ajoutez au second, alors le premier sera toujours supérieur au second de 2 17/30. Trouvez les deux nombres.

2) Il y a 24 1/4 kg de pommes dans deux caisses. Si vous transférez 3 1/2 kg de la première boîte à la seconde, alors dans la première il y aura toujours 3/5 kg de pommes de plus que dans la seconde. Combien de kilos de pommes y a-t-il dans chaque boîte ?

528 *. 1) La somme de deux nombres est 8 11/14 et leur différence est 2 3/7. Trouvez ces numéros.

2) Le bateau s'est déplacé le long de la rivière à une vitesse de 15 1/2 km par heure et à contre-courant à 8 1/4 km par heure. Quelle est la vitesse du débit de la rivière ?

529. 1) Il y a 110 voitures dans deux garages, et dans l'un d'eux il y en a 1 1/5 fois plus que dans l'autre. Combien de voitures y a-t-il dans chaque garage ?

2) La surface habitable d'un appartement composé de deux pièces est de 47 1/2 m². m. La superficie d'une pièce est 8/11 de la superficie de l'autre. Trouvez la superficie de chaque pièce.

530. 1) Un alliage composé de cuivre et d'argent pèse 330 g. Le poids du cuivre dans cet alliage est 5/28 du poids de l'argent. Quelle quantité d’argent et de cuivre contient l’alliage ?

2) La somme de deux nombres est 6 3/4 et le quotient est 3 1/2. Trouvez ces numéros.

531. La somme de trois nombres est 22 1/2. Le deuxième nombre est 3 1/2 fois et le troisième est 2 1/4 fois le premier. Trouvez ces numéros.

532. 1) La différence entre deux nombres est 7 ; quotient de division plus pour moins de 5 2/3. Trouvez ces numéros.

2) La différence entre deux nombres est de 29 3/8 et leur rapport multiple est de 8 5/6. Trouvez ces numéros.

533. Dans une classe, le nombre d'élèves absents est de 3/13 du nombre d'élèves présents. Combien d'élèves y a-t-il dans la classe selon la liste s'il y a 20 personnes de plus présentes que absentes ?

534. 1) La différence entre deux nombres est de 3 1/5. Un nombre est 5/7 d’un autre. Trouvez ces numéros.

2) Père plus vieux que mon fils depuis 24 ans. Le nombre des années du fils est égal à 5/13 des années du père. Quel âge a le père et quel âge a le fils ?

535. Le dénominateur d'une fraction est supérieur de 11 unités à son numérateur. Quelle est la valeur d’une fraction si son dénominateur est 3 3/4 fois le numérateur ?

N° 536 - 537 oralement.

536. 1) Le premier nombre est la moitié du deuxième. Combien de fois le deuxième nombre est-il supérieur au premier ?

2) Le premier nombre est 3/2 du second. Quelle partie du premier nombre est le deuxième nombre ?

537. 1) 1/2 du premier nombre est égal à 1/3 du deuxième nombre. Quelle partie du premier nombre est le deuxième nombre ?

2) 2/3 du premier nombre est égal aux 3/4 du deuxième nombre. Quelle partie du premier nombre est le deuxième nombre ? Quelle partie du deuxième nombre est la première ?

538. 1) La somme de deux nombres est 16. Trouvez ces nombres si 1/3 du deuxième nombre est égal à 1/5 du premier.

2) La somme de deux nombres est 38. Trouvez ces nombres si 2/3 du premier nombre est égal à 3/5 du second.

539 *. 1) Deux garçons ont ramassé ensemble 100 champignons. 3/8 du nombre de champignons ramassés par le premier garçon est numériquement égal à 1/4 du nombre de champignons ramassés par le deuxième garçon. Combien de champignons chaque garçon a-t-il ramassé ?

2) L'institution emploie 27 personnes. Combien d’hommes travaillent et combien de femmes travaillent si 2/5 de tous les hommes sont égaux à 3/5 de toutes les femmes ?

540 *. Trois garçons ont acheté un ballon de volley-ball. Déterminer la contribution de chaque garçon, sachant que 1/2 de la contribution du premier garçon est égale à 1/3 de la contribution du deuxième, ou 1/4 de la contribution du troisième, et que la contribution du troisième le garçon coûte 64 kopecks de plus que la contribution du premier.

541 *. 1) Un nombre est 6 de plus que l’autre. Trouvez ces nombres si 2/5 d’un nombre sont égaux aux 2/3 de l’autre.

2) La différence entre deux nombres est 35. Trouvez ces nombres si 1/3 du premier nombre est égal aux 3/4 du deuxième nombre.

542. 1) La première équipe peut réaliser certains travaux en 36 jours et la seconde en 45 jours. En combien de jours les deux équipes, travaillant ensemble, termineront-elles ce travail ?

2) Un train de voyageurs parcourt la distance entre deux villes en 10 heures, et un train de marchandises parcourt cette distance en 15 heures. Les deux trains quittaient ces villes en même temps l'un vers l'autre. Dans combien d’heures vont-ils se retrouver ?

543. 1) Un train rapide parcourt la distance entre deux villes en 6 heures et demie, et un train de voyageurs en 7 heures et demie. Combien d'heures plus tard ces trains se rencontreront-ils s'ils quittent les deux villes en même temps l'une vers l'autre ? (Réponse arrondie à 1 heure près.)

2) Deux motocyclistes sont partis simultanément de deux villes l'une vers l'autre. Un motocycliste peut parcourir toute la distance entre ces villes en 6 heures, et un autre en 5 heures. Combien d'heures après le départ les motocyclistes se retrouveront-ils ? (Réponse arrondie à 1 heure près.)

544. 1) Trois véhicules de capacité de charge différente peuvent transporter une certaine cargaison, en travaillant séparément : le premier en 10 heures, le second en 12 heures. et le troisième en 15 heures. En combien d'heures peuvent-ils transporter la même marchandise, en travaillant ensemble ?

2) Deux trains quittent deux gares simultanément l'une vers l'autre : le premier train parcourt la distance entre ces gares en 12 heures 3/4, et le second en 18 heures 3/4. Combien d'heures après le départ les trains se croiseront-ils ?

545. 1) Deux robinets sont raccordés à la baignoire. Grâce à l'un d'eux, le bain peut être rempli en 12 minutes, grâce à l'autre 1,5 fois plus rapidement. Combien de minutes faudra-t-il pour remplir les 5/6 de toute la baignoire si vous ouvrez les deux robinets en même temps ?

2) Deux dactylographes doivent retaper le manuscrit. Le premier conducteur peut effectuer ce travail en 3 1/3 jours et le second 1 1/2 fois plus rapidement. Combien de jours faudra-t-il aux deux dactylos pour terminer le travail s’ils travaillent simultanément ?

546. 1) La piscine est remplie avec le premier tuyau en 5 heures, et par le deuxième tuyau elle peut être vidée en 6 heures. Au bout de combien d'heures la piscine entière sera-t-elle remplie si les deux tuyaux sont ouverts en même temps ?

Note. En une heure, la piscine est remplie à (1/5 - 1/6 de sa capacité.)

2) Deux tracteurs ont labouré le champ en 6 heures. Le premier tracteur, travaillant seul, pourrait labourer ce champ en 15 heures. Combien d'heures faudrait-il au deuxième tracteur, travaillant seul, pour labourer ce champ ?

547 *. Deux trains quittent deux gares simultanément l'une vers l'autre et se rejoignent au bout de 18 heures. après sa libération. Combien de temps faut-il au deuxième train pour parcourir la distance entre les gares si le premier train parcourt cette distance en 1 jour 21 heures ?

548 *. La piscine est remplie de deux tuyaux. Ils ont d’abord ouvert le premier tuyau, puis après 3 heures 3/4, lorsque la moitié de la piscine était remplie, ils ont ouvert le deuxième tuyau. Après 2h30 de travail ensemble, la piscine était pleine. Déterminez la capacité de la piscine si 200 seaux d'eau par heure sont versés par le deuxième tuyau.

549. 1) Un train de messagerie a quitté Leningrad pour Moscou et parcourt 1 km en 3/4 minutes. Une demi-heure après le départ de ce train de Moscou, un train rapide quittait Moscou pour Léningrad, dont la vitesse était égale aux 3/4 de la vitesse du train express. À quelle distance les trains seront-ils les uns des autres 2 heures et demie après le départ du train de messagerie, si la distance entre Moscou et Léningrad est de 650 km ?

2) De la ferme collective à la ville 24 km. Un camion quitte la ferme collective et parcourt 1 km en 2 minutes et demie. Après 15 minutes. Après que cette voiture ait quitté la ville, un cycliste s'est rendu à la ferme collective, à une vitesse deux fois moins rapide que celle du camion. Combien de temps après le départ le cycliste rencontrera-t-il le camion ?

550. 1) Un piéton est sorti d'un village. 4 heures et demie après le départ du piéton, un cycliste roulait dans la même direction, dont la vitesse était 2 1/2 fois celle du piéton. Combien d'heures après le départ du piéton le cycliste le dépassera-t-il ?

2) Un train rapide parcourt 187 1/2 km en 3 heures et un train de marchandises parcourt 288 km en 6 heures. 7 heures et quart après le départ du train de marchandises, une ambulance part dans la même direction. Combien de temps faudra-t-il au train rapide pour rattraper le train de marchandises ?

551. 1) De deux fermes collectives par lesquelles passe la route menant au centre régional, deux kolkhoziens se sont rendus en même temps à cheval dans le quartier. Le premier d'entre eux parcourait 8 3/4 km par heure et le second était 1 1/7 fois plus que le premier. Le deuxième kolkhozien a rattrapé le premier au bout de 3 heures 4/5. Déterminez la distance entre les fermes collectives.

2) 26 1/3 heures après le départ du train Moscou-Vladivostok, dont la vitesse moyenne était de 60 km/h, un avion TU-104 a décollé dans la même direction, à une vitesse 14 1/6 fois la vitesse du train. Combien d’heures après le départ l’avion rattrapera-t-il le train ?

552. 1) La distance entre les villes situées le long du fleuve est de 264 km. Le bateau à vapeur a parcouru cette distance en aval en 18 heures, passant 1/12 de ce temps à s'arrêter. La vitesse de la rivière est de 1 1/2 km par heure. Combien de temps faudrait-il à un navire pour parcourir 87 km sans s'arrêter ? eau stagnante?

2) Un bateau à moteur a parcouru 207 km le long du fleuve en 13 heures et demie, consacrant 1/9 de ce temps aux escales. La vitesse de la rivière est de 1 3/4 km par heure. Combien de kilomètres ce bateau peut-il parcourir en eau calme en 2 heures et demie ?

553. Le bateau a parcouru une distance de 52 km à travers le réservoir sans s'arrêter en 3 heures 15 minutes. De plus, longeant la rivière à contre-courant dont la vitesse est de 1 3/4 km par heure, ce bateau a parcouru 28 1/2 km en 2 1/4 heures, faisant 3 escales d'égale durée. Combien de minutes le bateau a-t-il attendu à chaque arrêt ?

554. De Leningrad à Kronstadt à 12 heures. Le bateau à vapeur est parti dans l'après-midi et a parcouru toute la distance entre ces villes en 1 heure et demie. En chemin, il rencontra un autre navire qui quittait Cronstadt pour Leningrad à 12h18. et marcher à 1 1/4 fois la vitesse du premier. A quelle heure les deux navires se sont-ils rencontrés ?

555. Le train devait parcourir une distance de 630 km en 14 heures. Après avoir parcouru les 2/3 de cette distance, il a été détenu pendant 1 heure 10 minutes. À quelle vitesse doit-il poursuivre son voyage pour arriver sans tarder à destination ?

556. A 4h20 matin, un train de marchandises a quitté Kiev pour Odessa avec vitesse moyenne 31 1/5 km par heure. Après un certain temps, un train postal est sorti d'Odessa pour le rencontrer, dont la vitesse était 1 17/39 fois supérieure à la vitesse d'un train de marchandises, et a rencontré le train de marchandises 6 1/2 heures après son départ. A quelle heure le train postal a-t-il quitté Odessa, si la distance entre Kiev et Odessa est de 663 km ?

557*. L'horloge indique midi. Combien de temps faudra-t-il pour que les aiguilles des heures et des minutes coïncident ?

558. 1) L'usine dispose de trois ateliers. Le nombre d'ouvriers dans le premier atelier est de 9/20 de tous les ouvriers de l'usine, dans le deuxième atelier il y a 1 1/2 fois moins d'ouvriers que dans le premier, et dans le troisième atelier il y a 300 ouvriers de moins que dans le premier atelier. deuxième. Combien d’ouvriers y a-t-il dans l’usine ?

2) Il y a trois écoles secondaires dans la ville. Le nombre d'élèves de la première école est de 3/10 de l'ensemble des élèves de ces trois écoles ; dans la deuxième école, il y a 1,5 fois plus d'élèves que dans la première, et dans la troisième école, il y a 420 élèves de moins que dans la seconde. Combien d’élèves y a-t-il dans les trois écoles ?

559. 1) Deux opérateurs de moissonneuse-batteuse travaillaient dans la même zone. Après qu'un combineur ait récolté 9/16 de la parcelle entière et le deuxième 3/8 de la même parcelle, il s'est avéré que le premier combineur a récolté 97 1/2 hectares de plus que le second. En moyenne, 32 1/2 quintaux de céréales ont été battus sur chaque hectare. Combien de centièmes de grain chaque opérateur de moissonneuse-batteuse a-t-il battu ?

2) Deux frères ont acheté un appareil photo. L'un avait 5/8, le second 4/7 du prix de l'appareil photo, et le premier avait 2 roubles. 25 kopecks plus que le deuxième. Tout le monde a payé la moitié du prix de l'appareil. Combien d’argent reste-t-il à chacun ?

560. 1) Une voiture particulière quitte la ville A pour la ville B, la distance qui les sépare est de 215 km, à une vitesse de 50 km/h. Au même moment, un camion quitte la ville B pour la ville A. Combien de kilomètres la voiture de tourisme a-t-elle parcourue avant de rencontrer le camion, si la vitesse horaire du camion était 18/25 de la vitesse de la voiture de tourisme ?

2) Entre les villes A et B 210 km. Une voiture de tourisme a quitté la ville A pour la ville B. Au même moment, un camion quitte la ville B pour la ville A. Combien de kilomètres le camion a-t-il parcouru avant de rencontrer la voiture de tourisme, si la voiture de tourisme roulait à une vitesse de 48 km/h et que la vitesse du camion par heure était 3/4 de la vitesse de la voiture de tourisme ?

561. La ferme collective récoltait du blé et du seigle. 20 hectares de plus ont été ensemencés en blé qu'en seigle. La récolte totale de seigle représentait 5/6 de la récolte totale de blé avec un rendement de 20 c par hectare pour le blé et le seigle. La ferme collective vendait à l'État les 7/11 de la récolte totale de blé et de seigle et laissait le reste des céréales pour satisfaire ses besoins. Combien de voyages les camions de deux tonnes ont-ils dû effectuer pour évacuer le pain vendu à l'État ?

562. La farine de seigle et de blé était apportée à la boulangerie. Le poids de la farine de blé était 3/5 du poids de la farine de seigle, et 4 tonnes de farine de seigle de plus que la farine de blé ont été apportées. Quelle quantité de blé et de pain de seigle la boulangerie fera-t-elle avec cette farine si les produits de boulangerie représentent 2/5 de la farine totale ?

563. En trois jours, une équipe d'ouvriers a réalisé les 3/4 de l'ensemble des travaux de réparation de l'autoroute entre les deux fermes collectives. Le premier jour, 2 2/5 km de cette autoroute ont été réparés, le deuxième jour 1 1/2 fois plus que le premier et le troisième jour 5/8 de ce qui a été réparé au cours des deux premiers jours ensemble. Trouvez la longueur de l'autoroute entre les fermes collectives.

564. Remplissez les espaces vides du tableau, où S est l'aire du rectangle, UN- la base du rectangle, un h-hauteur (largeur) du rectangle.

565. 1) La longueur d'un terrain rectangulaire est de 120 m et la largeur du terrain est de 2/5 de sa longueur. Trouvez le périmètre et la superficie du site.

2) La largeur de la section rectangulaire est de 250 m et sa longueur est 1 1/2 fois la largeur. Trouvez le périmètre et la superficie du site.

566. 1) Le périmètre du rectangle est de 6 1/2 pouces, sa base est 1/4 de pouce plus grande que sa hauteur. Trouvez l'aire de ce rectangle.

2) Le périmètre du rectangle est de 18 cm, sa hauteur est inférieure de 2 1/2 cm à la base. Trouvez l'aire du rectangle.

567. Calculez les aires des figures illustrées à la figure 30 en les divisant en rectangles et en trouvant les dimensions du rectangle par mesure.

568. 1) Combien de feuilles de plâtre sec seront nécessaires pour recouvrir le plafond d'une pièce dont la longueur est de 4 1/2 m et la largeur de 4 m, si les dimensions de la feuille de plâtre sont de 2 m x l 1/2 m ?

2) Combien de planches de 4 1/2 m de long et 1/4 m de large faut-il pour poser un plancher de 4 1/2 m de long et 3 1/2 m de large ?

569. 1) Une parcelle rectangulaire de 560 m de long et 3/4 de sa longueur de large a été semée de haricots. Combien de graines fallait-il pour semer la parcelle si 1 centime était semé pour 1 hectare ?

2) Une récolte de blé de 25 quintaux par hectare a été récoltée dans un champ rectangulaire. Quelle quantité de blé a été récoltée sur l'ensemble du champ si la longueur du champ est de 800 m et la largeur est de 3/8 de sa longueur ?

570 . 1) Un terrain rectangulaire de 78 3/4 m de long et 56 4/5 m de large est aménagé de manière à ce que les 4/5 de sa superficie soient occupés par des bâtiments. Déterminez la superficie du terrain sous les bâtiments.

2) Sur un terrain rectangulaire dont la longueur est de 9/20 km et la largeur est de 4/9 de sa longueur, le kolkhoze envisage d'aménager un jardin. Combien d'arbres seront plantés dans ce jardin si une superficie moyenne de 36 m² est requise pour chaque arbre ?

571. 1) Pour un éclairage normal de la pièce à la lumière du jour, il est nécessaire que la superficie de toutes les fenêtres soit d'au moins 1/5 de la surface au sol. Déterminez s'il y a suffisamment de lumière dans une pièce dont la longueur est de 5 1/2 m et la largeur de 4 m. La pièce a-t-elle une fenêtre mesurant 1 1/2 m x 2 m ?

2) En utilisant la condition du problème précédent, découvrez s’il y a suffisamment de lumière dans votre classe.

572. 1) La grange a des dimensions de 5 1/2 m x 4 1/2 m x 2 1/2 m. Quelle quantité de foin (en poids) pourra contenir cette grange si elle est remplie aux 3/4 de sa hauteur et si 1 cu . m de foin pèse 82 kg ?

2) Le tas de bois a la forme d'un parallélépipède rectangle dont les dimensions sont 2 1/2 m x 3 1/2 m x 1 1/2 m. Quel est le poids du tas de bois si 1 cube. m de bois de chauffage pèse 600 kg ?

573. 1) Un aquarium rectangulaire est rempli d’eau jusqu’aux 3/5 de sa hauteur. La longueur de l'aquarium est de 1 1/2 m, la largeur de 4/5 m, la hauteur de 3/4 m. Combien de litres d'eau sont versés dans l'aquarium ?

2) Une piscine en forme de parallélépipède rectangle a une longueur de 6 1/2 m, une largeur de 4 m et une hauteur de 2 m. La piscine est remplie d'eau jusqu'aux 3/4 de sa hauteur. Calculez la quantité d'eau versée dans la piscine.

574. Une clôture doit être construite autour d’un terrain rectangulaire de 75 m de long et 45 m de large. Combien de mètres cubes de planches doivent être nécessaires à sa construction si l'épaisseur de la planche est de 2 1/2 cm et la hauteur de la clôture doit être de 2 1/4 m ?

575. 1) Quel est l'angle de la minute et petite aiguilleà 13 heures ? à 15 heures ? à 17 heures ? à 21 heures ? à 23h30 ?

2) De combien de degrés l’aiguille des heures tournera-t-elle en 2 heures ? 5 heures? 8 heures? 30 minutes.?

3) Combien de degrés contient un arc égal à un demi-cercle ? 1/4 de cercle ? 1/24 de cercle ? 5/24 cercles ?

576. 1) À l’aide d’un rapporteur, tracez : a) un angle droit ; b) un angle de 30° ; c) un angle de 60° ; d) angle de 150° ; e) un angle de 55°.

2) À l'aide d'un rapporteur, mesurez les angles de la figure et trouvez la somme de tous les angles de chaque figure (Fig. 31).

577. Suivez ces étapes:

578. 1) Le demi-cercle est divisé en deux arcs dont l’un est 100° plus grand que l’autre. Trouvez la taille de chaque arc.

2) Le demi-cercle est divisé en deux arcs dont l’un est 15° plus petit que l’autre. Trouvez la taille de chaque arc.

3) Le demi-cercle est divisé en deux arcs dont l’un est deux fois plus grand que l’autre. Trouvez la taille de chaque arc.

4) Le demi-cercle est divisé en deux arcs dont l’un est 5 fois plus petit que l’autre. Trouvez la taille de chaque arc.

579. 1) Le diagramme « Alphabétisation de la population en URSS » (Fig. 32) montre le nombre de personnes alphabétisées pour cent habitants. À partir des données du diagramme et de son échelle, déterminez le nombre d’hommes et de femmes alphabétisés pour chacune des années indiquées.

Écrivez les résultats dans le tableau :

2) À l'aide des données du schéma « Envoyés soviétiques dans l'espace » (Fig. 33), créez des tâches.

580. 1) D'après le diagramme circulaire « Routine quotidienne d'un élève de cinquième » (Fig. 34), remplissez le tableau et répondez aux questions : quelle partie de la journée est réservée au sommeil ? pour les devoirs? à l'école?

2) Construisez un diagramme circulaire sur votre routine quotidienne.

Contenu de la leçon

Additionner des fractions avec des dénominateurs similaires

Il existe deux types d'addition de fractions :

1. Additionner des fractions avec des dénominateurs similaires
2. Additionner des fractions avec différents dénominateurs

Tout d’abord, apprenons l’addition de fractions ayant les mêmes dénominateurs. Tout est simple ici. Pour additionner des fractions avec les mêmes dénominateurs, vous devez additionner leurs numérateurs et laisser le dénominateur inchangé. Par exemple, ajoutons les fractions et . Additionnez les numérateurs et laissez le dénominateur inchangé :

Cet exemple peut être facilement compris si l’on se souvient de la pizza, qui est divisée en quatre parties. Si vous ajoutez une pizza à une pizza, vous obtenez une pizza :

Exemple 2. Ajoutez des fractions et .

La réponse s’est avérée être une fraction impropre. Lorsque la fin de la tâche arrive, il est d'usage de se débarrasser des fractions impropres. Pour vous débarrasser d’une fraction impropre, vous devez en sélectionner la totalité. Dans notre cas, la partie entière est facilement isolée - deux divisé par deux égale un :

Cet exemple peut être facilement compris si l’on pense à une pizza divisée en deux parties. Si vous ajoutez plus de pizza à la pizza, vous obtenez une pizza entière :

Exemple 3. Ajoutez des fractions et .

Encore une fois, nous additionnons les numérateurs et laissons le dénominateur inchangé :

Cet exemple peut être facilement compris si l’on se souvient de la pizza, qui est divisée en trois parties. Si vous ajoutez plus de pizza à la pizza, vous obtenez de la pizza :

Exemple 4. Trouver la valeur d'une expression

Cet exemple se résout exactement de la même manière que les précédents. Les numérateurs doivent être additionnés et le dénominateur laissé inchangé :

Essayons de représenter notre solution à l'aide d'un dessin. Si vous ajoutez des pizzas à une pizza et ajoutez plus de pizzas, vous obtenez 1 pizza entière et plus de pizzas.

Comme vous pouvez le constater, il n’y a rien de compliqué à additionner des fractions ayant les mêmes dénominateurs. Il suffit de comprendre les règles suivantes :

1. Pour additionner des fractions avec le même dénominateur, vous devez additionner leurs numérateurs et laisser le dénominateur inchangé ;

Additionner des fractions avec différents dénominateurs

Apprenons maintenant à additionner des fractions avec des dénominateurs différents. Lors de l'addition de fractions, les dénominateurs des fractions doivent être les mêmes. Mais ils ne sont pas toujours les mêmes.

Par exemple, des fractions peuvent être additionnées car elles ont les mêmes dénominateurs.

Mais les fractions ne peuvent pas être additionnées immédiatement, car ces fractions ont des dénominateurs différents. Dans de tels cas, les fractions doivent être réduites au même dénominateur (commun).

Il existe plusieurs façons de réduire des fractions au même dénominateur. Aujourd'hui, nous n'en examinerons qu'une, car les autres méthodes peuvent sembler compliquées pour un débutant.

L'essence de cette méthode est que l'on recherche d'abord le LCM des dénominateurs des deux fractions. Le LCM est ensuite divisé par le dénominateur de la première fraction pour obtenir le premier facteur supplémentaire. Ils font de même avec la deuxième fraction : le LCM est divisé par le dénominateur de la deuxième fraction et un deuxième facteur supplémentaire est obtenu.

Les numérateurs et dénominateurs des fractions sont ensuite multipliés par leurs facteurs supplémentaires. À la suite de ces actions, des fractions ayant des dénominateurs différents se transforment en fractions ayant les mêmes dénominateurs. Et nous savons déjà comment additionner de telles fractions.

Exemple 1. Additionnons les fractions et

Tout d’abord, on trouve le plus petit commun multiple des dénominateurs des deux fractions. Le dénominateur de la première fraction est le nombre 3 et le dénominateur de la deuxième fraction est le nombre 2. Le plus petit commun multiple de ces nombres est 6.

LCM (2 et 3) = 6

Revenons maintenant aux fractions et . Tout d’abord, divisez le LCM par le dénominateur de la première fraction et obtenez le premier facteur supplémentaire. LCM est le nombre 6 et le dénominateur de la première fraction est le nombre 3. Divisez 6 par 3, nous obtenons 2.

Le nombre 2 résultant est le premier multiplicateur supplémentaire. Nous l'écrivons jusqu'à la première fraction. Pour ce faire, tracez un petit trait oblique sur la fraction et notez le facteur supplémentaire trouvé au-dessus :

On fait de même avec la deuxième fraction. Nous divisons le LCM par le dénominateur de la deuxième fraction et obtenons le deuxième facteur supplémentaire. LCM est le nombre 6 et le dénominateur de la deuxième fraction est le nombre 2. Divisez 6 par 2, nous obtenons 3.

Le nombre 3 résultant est le deuxième multiplicateur supplémentaire. Nous l'écrivons jusqu'à la deuxième fraction. Encore une fois, nous traçons une petite ligne oblique sur la deuxième fraction et notons le facteur supplémentaire trouvé au-dessus :

Maintenant, nous avons tout prêt pour l'ajout. Il reste à multiplier les numérateurs et dénominateurs des fractions par leurs facteurs supplémentaires :

Regardez attentivement où nous en sommes arrivés. Nous sommes arrivés à la conclusion que les fractions ayant des dénominateurs différents se sont transformées en fractions ayant les mêmes dénominateurs. Et nous savons déjà comment additionner de telles fractions. Prenons cet exemple jusqu'au bout :

Ceci complète l’exemple. Il s'avère ajouter .

Essayons de représenter notre solution à l'aide d'un dessin. Si vous ajoutez de la pizza à une pizza, vous obtenez une pizza entière et un autre sixième de pizza :

La réduction de fractions au même dénominateur (commun) peut également être représentée à l’aide d’une image. En réduisant les fractions et à un dénominateur commun, nous obtenons les fractions et . Ces deux fractions seront représentées par les mêmes morceaux de pizza. La seule différence sera que cette fois ils seront répartis en parts égales (réduites au même dénominateur).

Le premier dessin représente une fraction (quatre pièces sur six) et le deuxième dessin représente une fraction (trois pièces sur six). En ajoutant ces pièces, nous obtenons (sept pièces sur six). Cette fraction est impropre, nous en avons donc mis en évidence toute la partie. En conséquence, nous avons obtenu (une pizza entière et une autre sixième pizza).

Veuillez noter que nous avons décrit cet exemple de manière trop détaillée. DANS les établissements d'enseignement Il n’est pas habituel d’écrire avec autant de détails. Vous devez être capable de trouver rapidement le LCM des dénominateurs et des facteurs supplémentaires, ainsi que de multiplier rapidement les facteurs supplémentaires trouvés par vos numérateurs et dénominateurs. Si nous étions à l’école, nous devrions écrire cet exemple comme suit :

Mais il y a aussi un autre revers à la médaille. Si vous ne prenez pas de notes détaillées dès les premières étapes de l’étude des mathématiques, des questions de ce type commencent à apparaître. « D'où vient ce nombre ? », « Pourquoi les fractions se transforment-elles soudainement en fractions complètement différentes ? «.

Pour faciliter l'addition de fractions avec des dénominateurs différents, vous pouvez utiliser les instructions étape par étape suivantes :

1. Trouver le LCM des dénominateurs des fractions ;
2. Divisez le LCM par le dénominateur de chaque fraction et obtenez un facteur supplémentaire pour chaque fraction ;
3. Multiplier les numérateurs et dénominateurs des fractions par leurs facteurs supplémentaires ;
4. Additionnez les fractions qui ont les mêmes dénominateurs ;
5. Si la réponse s'avère être une fraction impropre, sélectionnez sa partie entière ;

Exemple 2. Trouver la valeur d'une expression .

Utilisons les instructions données ci-dessus.

Étape 1. Trouver le LCM des dénominateurs des fractions

Trouvez le LCM des dénominateurs des deux fractions. Les dénominateurs des fractions sont les nombres 2, 3 et 4

Étape 2. Divisez le LCM par le dénominateur de chaque fraction et obtenez un facteur supplémentaire pour chaque fraction

Divisez le LCM par le dénominateur de la première fraction. LCM est le nombre 12, et le dénominateur de la première fraction est le nombre 2. Divisez 12 par 2, nous obtenons 6. Nous avons le premier facteur supplémentaire 6. Nous l'écrivons au-dessus de la première fraction :

Maintenant, nous divisons le LCM par le dénominateur de la deuxième fraction. LCM est le nombre 12, et le dénominateur de la deuxième fraction est le nombre 3. Divisez 12 par 3, nous obtenons 4. Nous obtenons le deuxième facteur supplémentaire 4. Nous l'écrivons au-dessus de la deuxième fraction :

Maintenant, nous divisons le LCM par le dénominateur de la troisième fraction. LCM est le nombre 12, et le dénominateur de la troisième fraction est le nombre 4. Divisez 12 par 4, nous obtenons 3. Nous obtenons le troisième facteur supplémentaire 3. Nous l'écrivons au-dessus de la troisième fraction :

Étape 3. Multipliez les numérateurs et les dénominateurs des fractions par leurs facteurs supplémentaires

On multiplie les numérateurs et les dénominateurs par leurs facteurs supplémentaires :

Étape 4. Additionner des fractions avec les mêmes dénominateurs

Nous sommes arrivés à la conclusion que les fractions ayant des dénominateurs différents se sont transformées en fractions ayant les mêmes dénominateurs (communs). Il ne reste plus qu'à additionner ces fractions. Additionnez-le :

L'ajout ne tenait pas sur une seule ligne, nous avons donc déplacé l'expression restante vers la ligne suivante. Ceci est autorisé en mathématiques. Lorsqu'une expression ne tient pas sur une ligne, elle est déplacée sur la ligne suivante, et il faut mettre un signe égal (=) à la fin de la première ligne et au début de la nouvelle ligne. Le signe égal sur la deuxième ligne indique qu'il s'agit d'une continuation de l'expression qui figurait sur la première ligne.

Étape 5. Si la réponse s'avère être une fraction impropre, sélectionnez-en la partie entière

Notre réponse s’est avérée être une fraction impropre. Il faut en souligner toute une partie. Nous soulignons :

Nous avons reçu une réponse

Soustraire des fractions avec les mêmes dénominateurs

Il existe deux types de soustraction de fractions :

1. Soustraire des fractions avec les mêmes dénominateurs
2. Soustraire des fractions avec des dénominateurs différents

Tout d’abord, apprenons à soustraire des fractions ayant les mêmes dénominateurs. Tout est simple ici. Pour en soustraire un autre à une fraction, vous devez soustraire le numérateur de la deuxième fraction du numérateur de la première fraction, mais laisser le dénominateur inchangé.

Par exemple, trouvons la valeur de l'expression . Pour résoudre cet exemple, vous devez soustraire le numérateur de la deuxième fraction du numérateur de la première fraction et laisser le dénominateur inchangé. Faisons cela:

Cet exemple peut être facilement compris si l’on se souvient de la pizza, qui est divisée en quatre parties. Si vous coupez des pizzas dans une pizza, vous obtenez des pizzas :

Exemple 2. Trouvez la valeur de l'expression.

Encore une fois, du numérateur de la première fraction, soustrayez le numérateur de la deuxième fraction et laissez le dénominateur inchangé :

Cet exemple peut être facilement compris si l’on se souvient de la pizza, qui est divisée en trois parties. Si vous coupez des pizzas dans une pizza, vous obtenez des pizzas :

Exemple 3. Trouver la valeur d'une expression

Cet exemple se résout exactement de la même manière que les précédents. Du numérateur de la première fraction, vous devez soustraire les numérateurs des fractions restantes :

Comme vous pouvez le constater, il n’y a rien de compliqué à soustraire des fractions ayant les mêmes dénominateurs. Il suffit de comprendre les règles suivantes :

1. Pour en soustraire un autre à une fraction, vous devez soustraire le numérateur de la deuxième fraction du numérateur de la première fraction et laisser le dénominateur inchangé ;
2. Si la réponse s'avère être une fraction impropre, vous devez alors en souligner toute la partie.

Soustraire des fractions avec des dénominateurs différents

Par exemple, vous pouvez soustraire une fraction d’une fraction car les fractions ont les mêmes dénominateurs. Mais vous ne pouvez pas soustraire une fraction d'une fraction, car ces fractions ont des dénominateurs différents. Dans de tels cas, les fractions doivent être réduites au même dénominateur (commun).

Le dénominateur commun est trouvé en utilisant le même principe que celui que nous avons utilisé pour additionner des fractions avec des dénominateurs différents. Tout d’abord, trouvez le LCM des dénominateurs des deux fractions. Ensuite, le LCM est divisé par le dénominateur de la première fraction et le premier facteur supplémentaire est obtenu, qui est écrit au-dessus de la première fraction. De même, le LCM est divisé par le dénominateur de la deuxième fraction et un deuxième facteur supplémentaire est obtenu, qui est écrit au-dessus de la deuxième fraction.

Les fractions sont ensuite multipliées par leurs facteurs supplémentaires. À la suite de ces opérations, les fractions ayant des dénominateurs différents sont converties en fractions ayant les mêmes dénominateurs. Et nous savons déjà comment soustraire de telles fractions.

Exemple 1. Trouvez le sens de l'expression :

Ces fractions ont des dénominateurs différents, vous devez donc les réduire au même dénominateur (commun).

Nous trouvons d’abord le LCM des dénominateurs des deux fractions. Le dénominateur de la première fraction est le nombre 3 et le dénominateur de la deuxième fraction est le nombre 4. Le plus petit commun multiple de ces nombres est 12.

LCM (3 et 4) = 12

Revenons maintenant aux fractions et

Trouvons un facteur supplémentaire pour la première fraction. Pour ce faire, divisez le LCM par le dénominateur de la première fraction. LCM est le nombre 12 et le dénominateur de la première fraction est le nombre 3. Divisez 12 par 3, nous obtenons 4. Écrivez un quatre au-dessus de la première fraction :

On fait de même avec la deuxième fraction. Divisez le LCM par le dénominateur de la deuxième fraction. LCM est le nombre 12 et le dénominateur de la deuxième fraction est le nombre 4. Divisez 12 par 4, nous obtenons 3. Écrivez un trois sur la deuxième fraction :

Nous sommes maintenant prêts pour la soustraction. Il reste à multiplier les fractions par leurs facteurs supplémentaires :

Nous sommes arrivés à la conclusion que les fractions ayant des dénominateurs différents se sont transformées en fractions ayant les mêmes dénominateurs. Et nous savons déjà comment soustraire de telles fractions. Prenons cet exemple jusqu'au bout :

Nous avons reçu une réponse

Essayons de représenter notre solution à l'aide d'un dessin. Si vous coupez une pizza dans une pizza, vous obtenez une pizza

Ceci est la version détaillée de la solution. Si nous étions à l’école, nous devrions résoudre cet exemple plus rapidement. Une telle solution ressemblerait à ceci :

La réduction de fractions à un dénominateur commun peut également être représentée à l’aide d’une image. En réduisant ces fractions à un dénominateur commun, nous obtenons les fractions et . Ces fractions seront représentées par les mêmes parts de pizza, mais cette fois elles seront divisées en parts égales (réduites au même dénominateur) :

La première image montre une fraction (huit pièces sur douze) et la deuxième image montre une fraction (trois pièces sur douze). En coupant trois morceaux sur huit morceaux, on obtient cinq morceaux sur douze. La fraction décrit ces cinq pièces.

Exemple 2. Trouver la valeur d'une expression

Ces fractions ont des dénominateurs différents, vous devez donc d'abord les réduire au même dénominateur (commun).

Trouvons le LCM des dénominateurs de ces fractions.

Les dénominateurs des fractions sont les nombres 10, 3 et 5. Le plus petit commun multiple de ces nombres est 30.

LCM(10, 3, 5) = 30

Nous trouvons maintenant des facteurs supplémentaires pour chaque fraction. Pour ce faire, divisez le LCM par le dénominateur de chaque fraction.

Trouvons un facteur supplémentaire pour la première fraction. LCM est le nombre 30, et le dénominateur de la première fraction est le nombre 10. Divisez 30 par 10, nous obtenons le premier facteur supplémentaire 3. Nous l'écrivons au-dessus de la première fraction :

Nous trouvons maintenant un facteur supplémentaire pour la deuxième fraction. Divisez le LCM par le dénominateur de la deuxième fraction. LCM est le nombre 30, et le dénominateur de la deuxième fraction est le nombre 3. Divisez 30 par 3, nous obtenons le deuxième facteur supplémentaire 10. On l'écrit au-dessus de la deuxième fraction :

Nous trouvons maintenant un facteur supplémentaire pour la troisième fraction. Divisez le LCM par le dénominateur de la troisième fraction. LCM est le nombre 30, et le dénominateur de la troisième fraction est le nombre 5. Divisez 30 par 5, nous obtenons le troisième facteur supplémentaire 6. Nous l'écrivons au-dessus de la troisième fraction :

Maintenant, tout est prêt pour la soustraction. Il reste à multiplier les fractions par leurs facteurs supplémentaires :

Nous sommes arrivés à la conclusion que les fractions ayant des dénominateurs différents se sont transformées en fractions ayant les mêmes dénominateurs (communs). Et nous savons déjà comment soustraire de telles fractions. Terminons cet exemple.

La suite de l’exemple ne tiendra pas sur une seule ligne, nous déplaçons donc la suite sur la ligne suivante. N'oubliez pas le signe égal (=) sur la nouvelle ligne :

La réponse s'est avérée être une fraction régulière, et tout semble nous convenir, mais c'est trop encombrant et moche. Nous devrions faire plus simple. Ce qui peut être fait? Vous pouvez raccourcir cette fraction.

Pour réduire une fraction, vous devez diviser son numérateur et son dénominateur par (PGCD) des nombres 20 et 30.

On retrouve donc le pgcd des nombres 20 et 30 :

Revenons maintenant à notre exemple et divisons le numérateur et le dénominateur de la fraction par le pgcd trouvé, c'est-à-dire par 10

Nous avons reçu une réponse

Multiplier une fraction par un nombre

Pour multiplier une fraction par un nombre, vous devez multiplier le numérateur de la fraction par ce nombre et laisser le dénominateur inchangé.

Exemple 1. Multipliez une fraction par le nombre 1.

Multipliez le numérateur de la fraction par le nombre 1

L'enregistrement peut être compris comme prenant la moitié d'une fois. Par exemple, si vous prenez une pizza une fois, vous obtenez une pizza

Grâce aux lois de la multiplication, nous savons que si le multiplicande et le facteur sont inversés, le produit ne changera pas. Si l’expression s’écrit , alors le produit sera toujours égal à . Encore une fois, la règle pour multiplier un nombre entier et une fraction fonctionne :

Cette notation peut être comprise comme prenant la moitié de un. Par exemple, s'il y a 1 pizza entière et qu'on en prend la moitié, alors on aura une pizza :

Exemple 2. Trouver la valeur d'une expression

Multipliez le numérateur de la fraction par 4

La réponse était une fraction impropre. Soulignons toute cette partie :

L'expression peut être comprise comme prenant deux quarts 4 fois. Par exemple, si vous prenez 4 pizzas, vous obtiendrez deux pizzas entières

Et si on échange le multiplicande et le multiplicateur, on obtient l’expression . Elle sera également égale à 2. Cette expression peut être comprise comme prenant deux pizzas sur quatre pizzas entières :

Le nombre multiplié par la fraction et le dénominateur de la fraction sont résolus s'ils ont un facteur commun supérieur à un.

Par exemple, une expression peut être évaluée de deux manières.

Première façon. Multipliez le nombre 4 par le numérateur de la fraction et laissez le dénominateur de la fraction inchangé :

Deuxième façon. Le quatre étant multiplié et le quatre au dénominateur de la fraction peut être réduit. Ces quatre peuvent être réduits de 4, puisque le plus grand diviseur commun à deux quatre est le quatre lui-même :

Nous avons obtenu le même résultat 3. Après avoir réduit les quatre, de nouveaux nombres se forment à leur place : deux uns. Mais multiplier un par trois, puis diviser par un ne change rien. La solution peut donc s’écrire brièvement :

La réduction peut être effectuée même lorsque nous avons décidé d'utiliser la première méthode, mais au stade de la multiplication du nombre 4 et du numérateur 3 nous avons décidé d'utiliser la réduction :

Mais par exemple, l'expression ne peut être calculée que de la première manière - multipliez 7 par le dénominateur de la fraction et laissez le dénominateur inchangé :

Cela est dû au fait que le nombre 7 et le dénominateur de la fraction n'ont pas de diviseur commun supérieur à un et ne s'annulent donc pas.

Certains élèves raccourcissent par erreur le nombre à multiplier et le numérateur de la fraction. Vous ne pouvez pas faire ça. Par exemple, l'entrée suivante n'est pas correcte :

Réduire une fraction signifie que à la fois numérateur et dénominateur sera divisé par le même nombre. Dans le cas de l'expression, la division est effectuée uniquement au numérateur, car l'écrire équivaut à écrire . Nous voyons que la division s'effectue uniquement au numérateur et qu'aucune division ne se produit au dénominateur.

Multiplier des fractions

Pour multiplier des fractions, vous devez multiplier leurs numérateurs et dénominateurs. Si la réponse s’avère être une fraction impropre, vous devez en souligner toute la partie.

Exemple 1. Trouvez la valeur de l'expression.

Nous avons reçu une réponse. Il est conseillé de réduire cette fraction. La fraction peut être réduite de 2. La solution finale prendra alors la forme suivante :

L'expression peut être comprise comme prenant une pizza sur une moitié de pizza. Disons que nous mangeons une demi-pizza :

Comment prélever les deux tiers de cette moitié ? Vous devez d’abord diviser cette moitié en trois parties égales :

Et prenez-en deux parmi ces trois pièces :

Nous ferons des pizzas. Rappelez-vous à quoi ressemble la pizza lorsqu'elle est divisée en trois parties :

Un morceau de cette pizza et les deux morceaux que nous avons pris auront les mêmes dimensions :

Autrement dit, nous parlons de pizza à peu près de la même taille. La valeur de l’expression est donc

Exemple 2. Trouver la valeur d'une expression

Multipliez le numérateur de la première fraction par le numérateur de la deuxième fraction et le dénominateur de la première fraction par le dénominateur de la deuxième fraction :

La réponse était une fraction impropre. Soulignons toute cette partie :

Exemple 3. Trouver la valeur d'une expression

Multipliez le numérateur de la première fraction par le numérateur de la deuxième fraction et le dénominateur de la première fraction par le dénominateur de la deuxième fraction :

La réponse s'est avérée être une fraction régulière, mais ce serait bien si elle était raccourcie. Pour réduire cette fraction, vous devez diviser le numérateur et le dénominateur de cette fraction par le plus grand diviseur commun (PGCD) des nombres 105 et 450.

Trouvons donc le pgcd des nombres 105 et 450 :

Maintenant, nous divisons le numérateur et le dénominateur de notre réponse par le pgcd que nous avons maintenant trouvé, c'est-à-dire par 15

Représenter un nombre entier sous forme de fraction

Tout nombre entier peut être représenté sous forme de fraction. Par exemple, le chiffre 5 peut être représenté par . Cela ne changera pas le sens de cinq, puisque l'expression signifie « le nombre cinq divisé par un », et celui-ci, comme nous le savons, est égal à cinq :

Nombres réciproques

Maintenant, nous allons faire connaissance avec très sujet intéressant en mathématiques. C'est ce qu'on appelle des « numéros inversés ».

Définition. Inverser le numéroun est un nombre qui, multiplié parun en donne un.

Remplaçons dans cette définition la variable un numéro 5 et essayez de lire la définition :

Inverser le numéro 5 est un nombre qui, multiplié par 5 en donne un.

Est-il possible de trouver un nombre qui, multiplié par 5, donne un ? Il s'avère que c'est possible. Imaginons cinq sous forme de fraction :

Multipliez ensuite cette fraction par elle-même, échangez simplement le numérateur et le dénominateur. En d’autres termes, multiplions la fraction par elle-même, uniquement à l’envers :

Que se passera-t-il à la suite de cela ? Si nous continuons à résoudre cet exemple, nous obtenons un :

Cela signifie que l’inverse du nombre 5 est le nombre , puisque lorsque vous multipliez 5 par vous obtenez un.

L’inverse d’un nombre peut également être trouvé pour tout autre nombre entier.

Trouver numéro réciproque C’est également possible pour toute autre fraction. Pour ce faire, retournez-le simplement.

Diviser une fraction par un nombre

Disons que nous mangeons une demi-pizza :

Divisons-le également entre deux. Quelle quantité de pizza chaque personne recevra-t-elle ?

On constate qu'après avoir divisé la moitié de la pizza, on obtient deux morceaux égaux dont chacun constitue une pizza. Donc tout le monde aura une pizza.

Cet article examine les opérations sur les fractions. Des règles d'addition, de soustraction, de multiplication, de division ou d'exponentiation de fractions de la forme A B seront formées et justifiées, où A et B peuvent être des nombres, des expressions numériques ou des expressions avec des variables. En conclusion, des exemples de solutions avec des descriptions détaillées seront considérés.

Yandex.RTB R-A-339285-1

Règles pour effectuer des opérations avec des fractions numériques générales

Fractions numériques vue générale avoir un numérateur et un dénominateur dans lesquels se trouvent entiers ou des expressions numériques. Si l'on considère des fractions telles que 3 5, 2, 8 4, 1 + 2 3 4 (5 - 2), 3 4 + 7 8 2, 3 - 0, 8, 1 2 2, π 1 - 2 3 + π, 2 0, 5 ln 3, alors il est clair que le numérateur et le dénominateur peuvent avoir non seulement des nombres, mais aussi des expressions de différents types.

Définition 1

Il existe des règles selon lesquelles les actions sont effectuées avec fractions ordinaires. Il convient également aux fractions générales :

• Lors de la soustraction de fractions ayant des dénominateurs similaires, seuls les numérateurs sont ajoutés et le dénominateur reste le même, à savoir : a d ± c d = a ± c d, les valeurs a, c et d ≠ 0 sont des nombres ou des expressions numériques.
• Lors de l'ajout ou de la soustraction d'une fraction avec des dénominateurs différents, il est nécessaire de la réduire à un dénominateur commun, puis d'ajouter ou de soustraire les fractions résultantes avec les mêmes exposants. Littéralement, cela ressemble à ceci : a b ± c d = a · p ± c · r s, où les valeurs a, b ≠ 0, c, d ≠ 0, p ≠ 0, r ≠ 0, s ≠ 0 sont des nombres réels, et b · p = d · r = s . Lorsque p = d et r = b, alors a b ± c d = a · d ± c · d b · d.
• Lors de la multiplication de fractions, l'action est effectuée avec des numérateurs, après quoi avec des dénominateurs, nous obtenons alors a b · c d = a · c b · d, où a, b ≠ 0, c, d ≠ 0 agissent comme des nombres réels.
• Lorsqu'on divise une fraction par une fraction, on multiplie le premier par le deuxième inverse, c'est-à-dire qu'on échange le numérateur et le dénominateur : a b : c d = a b · d c.

Justification des règles

Définition 2

Il y a les points mathématiques suivants sur lesquels vous devez vous fier lors du calcul :

• la barre oblique signifie le signe de division ;
• la division par un nombre est assimilée à une multiplication par sa valeur réciproque ;
• application de la propriété des opérations avec des nombres réels ;
• application de la propriété fondamentale des fractions et des inégalités numériques.

Avec leur aide, vous pouvez effectuer des transformations de la forme :

une d ± c d = une · d - 1 ± c · d - 1 = une ± c · d - 1 = une ± c d ; a b ± c d = a · p b · p ± c · r d · r = a · p s ± c · e s = a · p ± c · r s ; a b · c d = a · d b · d · b · c b · d = a · d · a · d - 1 · b · c · b · d - 1 = = a · d · b · c · b · d - 1 · b · d - 1 = a · d · b · c b · d · b · d - 1 = = (a · c) · (b · d) - 1 = a · c b · d

Exemples

Dans le paragraphe précédent, nous avons parlé des opérations avec des fractions. C'est après cela qu'il faut simplifier la fraction. Ce sujet a été abordé en détail dans le paragraphe sur la conversion de fractions.

Tout d'abord, regardons un exemple d'addition et de soustraction de fractions avec le même dénominateur.

Exemple 1

Étant donné les fractions 8 2, 7 et 1 2, 7, alors selon la règle il faut additionner le numérateur et réécrire le dénominateur.

Solution

On obtient alors une fraction de la forme 8 + 1 2, 7. Après avoir effectué l'addition, on obtient une fraction de la forme 8 + 1 2, 7 = 9 2, 7 = 90 27 = 3 1 3. Donc, 8 2, 7 + 1 2, 7 = 8 + 1 2, 7 = 9 2, 7 = 90 27 = 3 1 3.

Répondre: 8 2 , 7 + 1 2 , 7 = 3 1 3

Il existe une autre solution. Pour commencer, on passe à la forme d'une fraction ordinaire, après quoi on effectue une simplification. Cela ressemble à ceci :

8 2 , 7 + 1 2 , 7 = 80 27 + 10 27 = 90 27 = 3 1 3

Exemple 2

Soustrayons de 1 - 2 3 · log 2 3 · log 2 5 + 1 une fraction de la forme 2 3 3 · log 2 3 · log 2 5 + 1 .

Puisque des dénominateurs égaux sont donnés, cela signifie que nous calculons une fraction avec le même dénominateur. Nous obtenons cela

1 - 2 3 log 2 3 log 2 5 + 1 - 2 3 3 log 2 3 log 2 5 + 1 = 1 - 2 - 2 3 3 log 2 3 log 2 5 + 1

Il existe des exemples de calcul de fractions avec différents dénominateurs. Un point important est la réduction à un dénominateur commun. Sans cela, nous ne pourrons pas effectuer d’autres opérations avec des fractions.

Le processus rappelle vaguement une réduction à un dénominateur commun. Autrement dit, le plus petit diviseur commun du dénominateur est recherché, après quoi les facteurs manquants sont ajoutés aux fractions.

Si les fractions ajoutées n’ont pas de facteurs communs, alors leur produit peut en devenir un.

Exemple 3

Regardons l'exemple de l'addition des fractions 2 3 5 + 1 et 1 2.

Solution

Dans ce cas, le dénominateur commun est le produit des dénominateurs. Nous obtenons alors cela 2 · 3 5 + 1. Ensuite, lors de la définition de facteurs supplémentaires, nous obtenons que pour la première fraction, elle est égale à 2 et pour la seconde, elle est égale à 3 5 + 1. Après multiplication, les fractions sont réduites à la forme 4 2 · 3 5 + 1. La réduction générale de 1 2 sera 3 5 + 1 2 · 3 5 + 1. Nous ajoutons les expressions fractionnaires résultantes et obtenons cela

2 3 5 + 1 + 1 2 = 2 2 2 3 5 + 1 + 1 3 5 + 1 2 3 5 + 1 = = 4 2 3 5 + 1 + 3 5 + 1 2 3 5 + 1 = 4 + 3 5 + 1 2 3 5 + 1 = 5 + 3 5 2 3 5 + 1

Répondre: 2 3 5 + 1 + 1 2 = 5 + 3 5 2 3 5 + 1

Lorsque nous parlons de fractions générales, nous ne parlons généralement pas du plus petit dénominateur commun. Il n'est pas rentable de prendre le produit des numérateurs comme dénominateur. Vous devez d’abord vérifier s’il existe un numéro dont la valeur est inférieure à celle de leur produit.

Exemple 4

Prenons l'exemple de 1 6 · 2 1 5 et 1 4 · 2 3 5, lorsque leur produit est égal à 6 · 2 1 5 · 4 · 2 3 5 = 24 · 2 4 5. Ensuite, nous prenons 12 · 2 3 5 comme dénominateur commun.

Regardons des exemples de multiplication de fractions générales.

Exemple 5

Pour ce faire, vous devez multiplier 2 + 1 6 et 2 · 5 3 · 2 + 1.

Solution

En suivant la règle, il faut réécrire et écrire le produit des numérateurs au dénominateur. Nous obtenons cela 2 + 1 6 2 5 3 2 + 1 2 + 1 2 5 6 3 2 + 1. Une fois qu’une fraction a été multipliée, vous pouvez faire des réductions pour la simplifier. Alors 5 · 3 3 2 + 1 : 10 9 3 = 5 · 3 3 2 + 1 · 9 3 10.

En utilisant la règle de passage de la division à la multiplication par une fraction réciproque, on obtient une fraction qui est l'inverse de celle donnée. Pour ce faire, le numérateur et le dénominateur sont inversés. Regardons un exemple :

5 3 3 2 + 1 : 10 9 3 = 5 3 3 2 + 1 9 3 10

Ensuite, ils doivent multiplier et simplifier la fraction obtenue. Si nécessaire, débarrassez-vous de l'irrationalité du dénominateur. Nous obtenons cela

5 3 3 2 + 1 : 10 9 3 = 5 3 3 9 3 10 2 + 1 = 5 2 10 2 + 1 = 3 2 2 + 1 = 3 2 - 1 2 2 + 1 2 - 1 = 3 2 - 1 2 2 2 - 1 2 = 3 2 - 1 2

Répondre: 5 3 3 2 + 1 : 10 9 3 = 3 2 - 1 2

Ce paragraphe est applicable lorsque le nombre ou expression numérique peut être présenté comme une fraction avec un dénominateur égal à 1, alors l'action avec une telle fraction est considérée comme un paragraphe distinct. Par exemple, l'expression 1 6 · 7 4 - 1 · 3 montre que la racine de 3 peut être remplacée par une autre expression 3 1. Ensuite, cette entrée ressemblera à la multiplication de deux fractions de la forme 1 6 · 7 4 - 1 · 3 = 1 6 · 7 4 - 1 · 3 1.

Effectuer des opérations sur des fractions contenant des variables

Les règles discutées dans le premier article sont applicables aux opérations avec des fractions contenant des variables. Considérez la règle de soustraction lorsque les dénominateurs sont les mêmes.

Il est nécessaire de prouver que A, C et D (D non égal à zéro) peuvent être n'importe quelle expression, et l'égalité A D ± C D = A ± C D est équivalente à sa plage de valeurs admissibles.

Il faut prendre un ensemble de variables ODZ. Alors A, C, D doivent prendre les valeurs correspondantes a 0 , c 0 et j 0. La substitution de la forme A D ± C D entraîne une différence de la forme a 0 d 0 ± c 0 d 0 , où, en utilisant la règle d'addition, nous obtenons une formule de la forme a 0 ± c 0 d 0 . Si nous substituons l'expression A ± C D, alors nous obtenons la même fraction de la forme a 0 ± c 0 d 0. De là, nous concluons que la valeur sélectionnée qui satisfait à l'ODZ, A ± C D et A D ± C D est considérée comme égale.

Pour toute valeur des variables, ces expressions seront égales, c'est-à-dire qu'elles sont dites identiquement égales. Cela signifie que cette expression est considérée comme une égalité prouvable de la forme A D ± C D = A ± C D .

Exemples d'ajout et de soustraction de fractions avec des variables

Lorsque vous avez les mêmes dénominateurs, il vous suffit d’ajouter ou de soustraire les numérateurs. Cette fraction peut être simplifiée. Parfois, vous devez travailler avec des fractions identiques, mais à première vue, cela n'est pas perceptible, car certaines transformations doivent être effectuées. Par exemple, x 2 3 x 1 3 + 1 et x 1 3 + 1 2 ou 1 2 sin 2 α et sin a cos a. Le plus souvent, une simplification de l’expression originale est nécessaire afin de retrouver les mêmes dénominateurs.

Exemple 6

Calculer : 1) x 2 + 1 x + x - 2 - 5 - x x + x - 2, 2) l g 2 x + 4 x · (l g x + 2) + 4 · l g x x · (l g x + 2) , x - 1 x - 1 + x x + 1 .

Solution

1. Pour effectuer le calcul, vous devez soustraire les fractions qui ont le même dénominateur. Ensuite, nous obtenons que x 2 + 1 x + x - 2 - 5 - x x + x - 2 = x 2 + 1 - 5 - x x + x - 2 . Après quoi, vous pouvez développer les parenthèses et ajouter des termes similaires. On obtient que x 2 + 1 - 5 - x x + x - 2 = x 2 + 1 - 5 + x x + x - 2 = x 2 + x - 4 x + x - 2
2. Puisque les dénominateurs sont les mêmes, il ne reste plus qu'à additionner les numérateurs en laissant le dénominateur : l g 2 x + 4 x (l g x + 2) + 4 l g x x (l g x + 2) = l g 2 x + 4 + 4 x (l g x + 2)
   L'ajout est terminé. On voit qu'il est possible de réduire la fraction. Son numérateur peut être additionné à l'aide de la formule du carré de la somme, on obtient alors (l g x + 2) 2 à partir de formules de multiplication abrégées. Ensuite, nous obtenons cela
   l g 2 x + 4 + 2 l g x x (l g x + 2) = (l g x + 2) 2 x (l g x + 2) = l g x + 2 x
3. Fractions données de la forme x - 1 x - 1 + x x + 1 avec des dénominateurs différents. Après la transformation, vous pouvez passer à l'ajout.

Considérons une double solution.

La première méthode consiste à factoriser le dénominateur de la première fraction à l'aide de carrés, puis à le réduire. On obtient une fraction de la forme

x - 1 x - 1 = x - 1 (x - 1) x + 1 = 1 x + 1

Donc x - 1 x - 1 + x x + 1 = 1 x + 1 + x x + 1 = 1 + x x + 1 .

Dans ce cas, il est nécessaire de se débarrasser de l'irrationalité du dénominateur.

1 + x x + 1 = 1 + x x - 1 x + 1 x - 1 = x - 1 + x x - x x - 1

La deuxième méthode consiste à multiplier le numérateur et le dénominateur de la deuxième fraction par l'expression x - 1. Ainsi, nous nous débarrassons de l'irrationalité et passons à l'addition de fractions avec le même dénominateur. Alors

x - 1 x - 1 + x x + 1 = x - 1 x - 1 + x x - 1 x + 1 x - 1 = = x - 1 x - 1 + x x - x x - 1 = x - 1 + x · x - xx-1

Répondre: 1) x 2 + 1 x + x - 2 - 5 - x x + x - 2 = x 2 + x - 4 x + x - 2, 2) l g 2 x + 4 x · (l g x + 2) + 4 · l g x x · (l g x + 2) = l g x + 2 x, 3) x - 1 x - 1 + x x + 1 = x - 1 + x · x - x x - 1 .

Dans le dernier exemple, nous avons constaté que la réduction à un dénominateur commun est inévitable. Pour ce faire, vous devez simplifier les fractions. Lors de l'addition ou de la soustraction, vous devez toujours rechercher un dénominateur commun, qui ressemble au produit des dénominateurs avec des facteurs supplémentaires ajoutés aux numérateurs.

Exemple 7

Calculer les valeurs des fractions : 1) x 3 + 1 x 7 + 2 2, 2) x + 1 x ln 2 (x + 1) (2 x - 4) - sin x x 5 ln (x + 1) (2 x - 4) , 3) ​​​​​​1 cos 2 x - x + 1 cos 2 x + 2 cos x x + x

Solution

1. Aucun calculs complexes le dénominateur n'est pas obligatoire, vous devez donc choisir leur produit sous la forme 3 x 7 + 2 · 2, puis choisir x 7 + 2 · 2 pour la première fraction comme facteur supplémentaire, et 3 pour la seconde. En multipliant, on obtient une fraction de la forme x 3 + 1 x 7 + 2 2 = x x 7 + 2 2 3 x 7 + 2 2 + 3 1 3 x 7 + 2 2 = = x x 7 + 2 2 + 3 3 x 7 + 2 2 = x x 7 + 2 2 x + 3 3 x 7 + 2 2
2. On constate que les dénominateurs sont présentés sous la forme d'un produit, ce qui signifie que des transformations supplémentaires ne sont pas nécessaires. Le dénominateur commun sera considéré comme un produit de la forme x 5 · ln 2 x + 1 · 2 x - 4 . Donc x4 est un facteur supplémentaire à la première fraction, et ln(x + 1) à la seconde. Ensuite on soustrait et on obtient :
   x + 1 x · ln 2 (x + 1) · 2 x - 4 - péché x x 5 · ln (x + 1) · 2 x - 4 = = x + 1 · x 4 x 5 · ln 2 (x + 1) ) · 2 x - 4 - péché x · ln x + 1 x 5 · ln 2 (x + 1) · (2 ​​​​​​x - 4) = = x + 1 · x 4 - péché x · ln (x + 1 ) x 5 · ln 2 (x + 1) · (2 ​​​​​​x - 4) = x · x 4 + x 4 - sin x · ln (x + 1) x 5 · ln 2 (x + 1) · ( 2x-4)
3. Cet exemple est logique lorsque l’on travaille avec des dénominateurs de fractions. Il faut appliquer les formules de la différence des carrés et du carré de la somme, puisqu'elles permettront de passer à une expression de la forme 1 cos x - x · cos x + x + 1 (cos x + x) 2. On voit que les fractions sont réduites à un dénominateur commun. Nous obtenons cela cos x - x · cos x + x 2 .

Ensuite, nous obtenons cela

1 cos 2 x - x + 1 cos 2 x + 2 cos x x + x = = 1 cos x - x cos x + x + 1 cos x + x 2 = = cos x + x cos x - x cos x + x 2 + cos x - x cos x - x cos x + x 2 = = cos x + x + cos x - x cos x - x cos x + x 2 = 2 cos x cos x - x cos x + x 2

Répondre:

1) x 3 + 1 x 7 + 2 2 = x x 7 + 2 2 x + 3 3 x 7 + 2 2, 2) x + 1 x ln 2 (x + 1) 2 x - 4 - sin x x 5 · ln (x + 1) · 2 x - 4 = = x · x 4 + x 4 - sin x · ln (x + 1) x 5 · ln 2 (x + 1) · ( 2 x - 4) , 3) ​​​​1 cos 2 x - x + 1 cos 2 x + 2 · cos x · x + x = 2 · cos x cos x - x · cos x + x 2 .

Exemples de multiplication de fractions avec des variables

Lors de la multiplication de fractions, le numérateur est multiplié par le numérateur et le dénominateur par le dénominateur. Ensuite, vous pouvez appliquer la propriété de réduction.

Exemple 8

Multipliez les fractions x + 2 · x x 2 · ln x 2 · ln x + 1 et 3 · x 2 1 3 · x + 1 - 2 sin 2 · x - x.

Solution

Il faut faire une multiplication. Nous obtenons cela

x + 2 x x 2 ln x 2 ln x + 1 3 x 2 1 3 x + 1 - 2 sin (2 x - x) = = x - 2 x 3 x 2 1 3 x + 1 - 2 x 2 ln x 2 ln x + 1 péché (2 x - x)

Le nombre 3 est déplacé à la première place pour la commodité des calculs, et vous pouvez réduire la fraction de x 2, nous obtenons alors une expression de la forme

3 x - 2 x x 1 3 x + 1 - 2 ln x 2 ln x + 1 péché (2 x - x)

Répondre: x + 2 x x 2 ln x 2 ln x + 1 3 x 2 1 3 x + 1 - 2 sin (2 x - x) = 3 x - 2 x x 1 3 x + 1 - 2 ln x 2 · ln x + 1 · péché (2 · x - x) .

Division

La division des fractions est similaire à la multiplication, puisque la première fraction est multipliée par la seconde réciproque. Si nous prenons par exemple la fraction x + 2 x x 2 ln x 2 ln x + 1 et divisons par 3 x 2 1 3 x + 1 - 2 sin 2 x - x, alors cela peut s'écrire

x + 2 · x x 2 · ln x 2 · ln x + 1 : 3 · x 2 1 3 · x + 1 - 2 sin (2 · x - x) , puis remplacer par un produit de la forme x + 2 · x x 2 · ln x 2 ln x + 1 3 x 2 1 3 x + 1 - 2 péché (2 x - x)

Exponentiation

Passons à l'examen des opérations avec des fractions générales avec exponentiation. S'il existe une puissance avec un exposant naturel, alors l'action est considérée comme une multiplication de fractions égales. Mais il est recommandé d’utiliser une approche générale basée sur les propriétés des diplômes. Toutes les expressions A et C, où C n'est pas identiquement égal à zéro, et tout réel r sur l'ODZ pour une expression de la forme A C r l'égalité A C r = A r C r est valide. Le résultat est une fraction élevée à une puissance. Par exemple, considérez :

x 0, 7 - π · ln 3 x - 2 - 5 x + 1 2, 5 = = x 0, 7 - π · ln 3 x - 2 - 5 2, 5 x + 1 2, 5

Procédure pour effectuer des opérations avec des fractions

Les opérations sur les fractions sont effectuées selon certaines règles. En pratique, on remarque qu'une expression peut contenir plusieurs fractions ou expressions fractionnaires. Ensuite, il faut effectuer toutes les actions dans un ordre strict : élever à une puissance, multiplier, diviser, puis additionner et soustraire. S'il y a des parenthèses, la première action y est effectuée.

Exemple 9

Calculez 1 - x cos x - 1 c o s x · 1 + 1 x .

Solution

Depuis que nous avons même dénominateur, puis 1 - x cos x et 1 c o s x , mais les soustractions ne peuvent pas être effectuées selon la règle : on effectue d'abord les opérations entre parenthèses, puis la multiplication, puis l'addition. Ensuite, en calculant, nous obtenons cela

1 + 1 x = 1 1 + 1 x = x x + 1 x = x + 1 x

En remplaçant l'expression par celle d'origine, nous obtenons que 1 - x cos x - 1 cos x · x + 1 x. En multipliant des fractions, nous avons : 1 cos x · x + 1 x = x + 1 cos x · x. Après avoir effectué toutes les substitutions, nous obtenons 1 - x cos x - x + 1 cos x · x. Vous devez maintenant travailler avec des fractions qui ont des dénominateurs différents. On a:

x · 1 - x cos x · x - x + 1 cos x · x = x · 1 - x - 1 + x cos x · x = = x - x - x - 1 cos x · x = - x + 1 cos xx

Répondre: 1 - x cos x - 1 c o s x · 1 + 1 x = - x + 1 cos x · x .

Si vous remarquez une erreur dans le texte, veuillez la surligner et appuyer sur Ctrl+Entrée