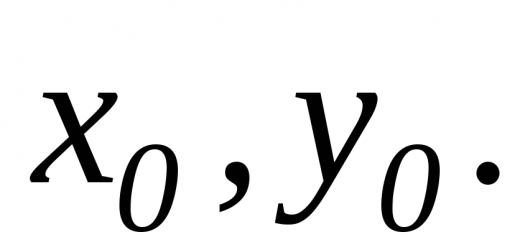Harmonie divine : quel est le nombre d'or en termes simples. Les secrets de l'univers en chiffres. Shkrudnev Fedor Dmitrievich Nombre d'or d'un triangle

Nombre d'or - proportion harmonique

Au cours de la période de développement de l'architecture, lorsque les caractéristiques physiques et mécaniques des matériaux de construction étaient peu étudiées, il n'existait aucune méthode éprouvée pour calculer les structures des bâtiments - l'expérience empirique et le strict respect des proportions harmoniques du « nombre d'or » prévalaient.

En mathématiques, la proportion (lat. proportio) est l'égalité de deux rapports : a : b = c : d.

Un segment de droite AB peut être divisé en deux parties de la manière suivante :
en deux parties égales – AB : AC = AB : BC ;
en deux parties inégales à tous égards (ces parties ne forment pas de proportions) ;
ainsi, quand AB : AC = AC : BC.

Cette dernière est la division dorée ou division d'un segment en rapport extrême et moyen.

Le nombre d'or est une telle division proportionnelle d'un segment en parties inégales, dans laquelle le segment entier est lié à la plus grande partie comme la plus grande partie elle-même est liée à la plus petite ; ou en d’autres termes, le plus petit segment est au plus grand ce que le plus grand est au tout.

a : b = b : c ou c : b = b : a.

La connaissance pratique du nombre d'or commence par la division d'un segment de ligne droite dans la proportion d'or à l'aide d'un compas et d'une règle.

Du point B on restitue une perpendiculaire égale à la moitié AB. Le point résultant C est relié par une ligne au point A. Sur la ligne résultante, un segment BC est posé, se terminant par le point D. Le segment AD est transféré à la droite AB. Le point E résultant divise le segment AB dans la proportion d'or.

Les segments de la proportion d'or sont exprimés par la fraction irrationnelle infinie AE = 0,618..., si AB est pris comme un, BE = 0,382... À des fins pratiques, des valeurs approximatives de 0,62 et 0,38 sont souvent utilisées. Si le segment AB est considéré comme étant composé de 100 parties, alors la plus grande partie du segment est de 62 parties et la plus petite partie est de 38 parties.

Les propriétés du nombre d'or sont décrites par l'équation :

x2 – x – 1 = 0.

Solution à cette équation :

Les propriétés du nombre d’or ont créé une aura romantique de mystère et de culte presque mystique autour de ce nombre.

Deuxième nombre d'or

Le magazine bulgare « Patrie » (n° 10, 1983) a publié un article de Tsvetan Tsekov-Karandash « Sur le deuxième nombre d'or », qui découle de la section principale et donne un autre rapport de 44 : 56.

La division s'effectue comme suit. Le segment AB est divisé proportionnellement au nombre d'or. A partir du point C, un CD perpendiculaire est restitué. Le rayon AB est le point D, qui est relié par une ligne au point A. L'angle droit ACD est divisé en deux. Une ligne est tracée du point C jusqu'à l'intersection avec la ligne AD. Le point E divise le segment AD dans le rapport 56:44.

La figure montre la position de la ligne du deuxième nombre d'or. Il est situé à mi-chemin entre la ligne du nombre d’or et la ligne médiane du rectangle.

triangle d'or

Pour trouver des segments de la proportion d'or des séries ascendantes et descendantes, vous pouvez utiliser le pentagramme.

Pour construire un pentagramme, vous devez construire un pentagone régulier. La méthode de construction a été développée par le peintre et graphiste allemand Albrecht Dürer (1471...1528). Soit O le centre du cercle, A un point du cercle et E le milieu du segment OA. La perpendiculaire au rayon OA, restituée au point O, coupe le cercle au point D. A l'aide d'un compas, tracez le segment CE = ED sur le diamètre. La longueur du côté d’un pentagone régulier inscrit dans un cercle est égale à DC. Nous traçons les segments DC sur le cercle et obtenons cinq points pour dessiner un pentagone régulier. Nous connectons les coins du pentagone les uns aux autres avec des diagonales et obtenons un pentagramme. Toutes les diagonales du pentagone se divisent en segments reliés par le nombre d'or.

Nous dessinons directement AB. A partir du point A, nous y déposons trois fois un segment O de taille arbitraire, passant par le point P résultant nous traçons une perpendiculaire à la ligne AB, sur la perpendiculaire à droite et à gauche du point P nous déposons les segments O. Nous connectons les points résultants d et d1 avec des lignes droites jusqu'au point A. Nous plaçons le segment dd1 sur la ligne Ad1, obtenant le point C. Elle a divisé la ligne Ad1 proportionnellement au nombre d'or. Les lignes Ad1 et dd1 sont utilisées pour construire un rectangle « doré ».

Riz. 5. Construction d'un pentagone régulier et d'un pentagramme

Riz. 6. Construction du triangle d'or

Histoire du nombre d'or

Il est généralement admis que le concept de division d'or a été introduit dans l'usage scientifique par Pythagoras, philosophe et mathématicien grec ancien (VIe siècle avant JC). On suppose que Pythagore a emprunté sa connaissance de la division en or aux Égyptiens et aux Babyloniens. En effet, les proportions de la pyramide de Khéops, des temples, des bas-reliefs, des objets ménagers et des bijoux du tombeau de Toutankhamon indiquent que les artisans égyptiens ont utilisé les rapports de la division d'or lors de leur création. architecte français le Corbusier a constaté que dans le relief du temple du pharaon Seti I à Abydos et dans le relief représentant le pharaon Ramsès, les proportions des figures correspondent aux valeurs de la division dorée. L'architecte Khesira, représenté sur un relief d'une planche de bois provenant d'une tombe qui porte son nom, tient dans ses mains des instruments de mesure dans lesquels sont enregistrées les proportions de la division d'or.

Les Grecs étaient de talentueux géomètres. Ils enseignaient même l’arithmétique à leurs enfants en utilisant des figures géométriques. Le carré de Pythagore et la diagonale de ce carré ont servi de base à la construction de rectangles dynamiques.

Platon(427...347 avant JC) connaissait également la division d'or. Ses dialogues" Timée"est consacré aux vues mathématiques et esthétiques de l'école pythagoricienne et, en particulier, aux questions de la division d'or.

La façade de l'ancien temple grec du Parthénon présente des proportions dorées. Lors de ses fouilles, on a découvert des boussoles utilisées par les architectes et les sculpteurs du monde antique. La boussole pompéienne (musée de Naples) contient également les proportions de la division dorée.

Riz. 7. Rectangles dynamiques

Riz. 8. Boussole antique au nombre d’or

Dans la littérature ancienne qui nous est parvenue, la division dorée a été mentionnée pour la première fois dans « Les débuts» Euclide. Dans le 2ème livre des «Principes», la construction géométrique de la division d'or est donnée. Après Euclide, l'étude de la division d'or a été réalisée par Hypsiclès (2ème siècle avant JC), Pappus (IIIème siècle après JC) et d'autres. L’Europe médiévale, avec la division d’or Nous nous sommes rencontrés à travers les traductions arabes des Éléments d’Euclide. Le traducteur J. Campano de Navarre (IIIe siècle) a fait des commentaires sur la traduction. Les secrets de la division dorée étaient jalousement gardés et gardés dans le plus strict secret. Ils n'étaient connus que des initiés.

Au cours de la Renaissance, l'intérêt pour la division dorée s'est accru parmi les scientifiques et les artistes en raison de son utilisation à la fois en géométrie et en art, notamment en architecture. Léonard de Vinci, artiste et scientifique, a constaté que les artistes italiens ont beaucoup d'expérience empirique, mais peu de connaissances. Il conçut et commença à écrire un livre sur la géométrie, mais à cette époque parut un livre de moine Luca Pacioli, et Leonardo a abandonné son idée. Selon les contemporains et les historiens des sciences, Luca Pacioli était une véritable sommité, le plus grand mathématicien d'Italie entre Fibonacci et Galilée. Luca Pacioli était l'élève de l'artiste Piero della Franceschi, qui a écrit deux livres, dont l'un s'intitulait « De la perspective dans la peinture ». Il est considéré comme le créateur de la géométrie descriptive.

Luca Pacioli a parfaitement compris l'importance de la science pour l'art. En 1496, à l'invitation du duc de Moreau, il vient à Milan, où il donne des cours de mathématiques. Léonard de Vinci travaillait également à Milan à la cour de Moro à cette époque. En 1509, le livre de Luca Pacioli « La Divine Proportion » fut publié à Venise avec des illustrations brillamment exécutées, c'est pourquoi on pense qu'elles ont été réalisées par Léonard de Vinci. Le livre était un hymne enthousiaste au nombre d’or. Parmi les nombreux avantages de la proportion dorée, le moine Luca Pacioli n'a pas manqué de nommer son « essence divine » comme expression de la trinité divine - Dieu le fils, Dieu le père et Dieu le Saint-Esprit (il était sous-entendu que le petit le segment est la personnification de Dieu le fils, le segment le plus grand est le dieu du père et le segment entier est le Dieu du Saint-Esprit).

Léonard de Vinci a également accordé beaucoup d'attention à l'étude de la division d'or. Il réalisa des sections d'un corps stéréométrique formé de pentagones réguliers, et à chaque fois il obtint des rectangles avec des proportions dans la division d'or. C’est pourquoi il a donné à cette division le nom de nombre d’or. Il reste donc le plus populaire.

Au même moment, dans le nord de l'Europe, en Allemagne, il travaillait sur les mêmes problèmes Albrecht Dürer. Il esquisse l'introduction de la première version du traité sur les proportions. Dürer écrit. « Il est nécessaire que quelqu’un qui sait faire quelque chose l’enseigne à ceux qui en ont besoin. C’est ce que j’ai décidé de faire.

À en juger par l'une des lettres de Dürer, il a rencontré Luca Pacioli alors qu'il était en Italie. Albrecht Dürer développe en détail la théorie des proportions du corps humain. Dürer accordait une place importante dans son système de relations au nombre d'or. La taille d'une personne est divisée en proportions dorées par la ligne de la ceinture, ainsi que par une ligne tracée à travers le bout du majeur des mains baissées, la partie inférieure du visage par la bouche, etc. Le compas proportionnel de Dürer est bien connu.

Grand astronome du XVIe siècle. Johann Kepler a appelé le nombre d'or l'un des trésors de la géométrie. Il fut le premier à attirer l'attention sur l'importance de la proportion d'or pour la botanique (la croissance des plantes et leur structure).

Cette proportion se retrouve en architecture et se produit également lors de la construction de compositions d'images de format horizontal allongé.

La figure montre la position de la ligne du deuxième nombre d'or. Il est situé à mi-chemin entre la ligne du nombre d’or et la ligne médiane du rectangle.

triangle d'or

Pour trouver des segments de la proportion d'or des séries ascendantes et descendantes, vous pouvez utiliser pentacle.

Pour construire un pentagramme, vous devez construire un pentagone régulier. La méthode de construction a été développée par le peintre et graphiste allemand Albrecht Dürer (1471...1528). Laisser Ô- centre du cercle, UN- un point sur un cercle et E- le milieu du segment OA. Perpendiculaire au rayon OA, restauré au point À PROPOS, coupe le cercle au point D. A l'aide d'un compas, tracez un segment sur le diamètre C.E. = ED. La longueur du côté d’un pentagone régulier inscrit dans un cercle est CC. Disposez les segments sur le cercle CC et nous obtenons cinq points pour dessiner un pentagone régulier. Nous connectons les coins du pentagone les uns aux autres avec des diagonales et obtenons un pentagramme. Toutes les diagonales du pentagone se divisent en segments reliés par le nombre d'or.

Nous effectuons un direct UN B. Du point UN on y trace trois fois un segment O de taille arbitraire, passant par le point résultant R. tracer une perpendiculaire à la ligne UN B, sur la perpendiculaire à droite et à gauche du point R. mettre de côté les segments À PROPOS. Points reçus d Et d1 relier par des lignes droites à un point UN. Segment de ligne dd1 mettre en ligne Annonce1, j'obtiens un point AVEC. Elle a divisé la ligne Annonce1 proportionnellement au nombre d'or. Lignes Annonce1 Et dd1 utilisé pour construire un rectangle « doré ».

Cette harmonie frappe par son ampleur...

Bonjour les amis!

Avez-vous entendu parler de l'Harmonie Divine ou du Nombre d'Or ? Avez-vous déjà réfléchi à la raison pour laquelle quelque chose nous semble idéal et beau, mais quelque chose nous repousse ?

Si ce n'est pas le cas, alors vous êtes parvenu à cet article avec succès, car nous y discuterons du nombre d'or, découvrirons ce que c'est, à quoi il ressemble dans la nature et chez l'homme. Parlons de ses principes, découvrons ce qu'est la série de Fibonacci et bien plus encore, notamment le concept du rectangle d'or et de la spirale d'or.

Oui, l'article contient beaucoup d'images, de formules, après tout, le nombre d'or, c'est aussi des mathématiques. Mais tout est décrit dans un langage assez simple, clair. Et à la fin de l'article, vous découvrirez pourquoi tout le monde aime tant les chats =)

Qu'est-ce que le nombre d'or ?

Pour faire simple, le nombre d’or est une certaine règle de proportion qui crée l’harmonie ?. Autrement dit, si nous ne violons pas les règles de ces proportions, nous obtenons alors une composition très harmonieuse.

La définition la plus complète du nombre d’or stipule que la plus petite partie est liée à la plus grande, tout comme la plus grande partie l’est au tout.

Mais à part cela, le nombre d’or est mathématique : il a une formule spécifique et un nombre spécifique. De nombreux mathématiciens, en général, la considèrent comme la formule de l'harmonie divine et l'appellent « symétrie asymétrique ».

Le nombre d'or a atteint nos contemporains depuis l'époque de la Grèce antique, cependant, il existe une opinion selon laquelle les Grecs eux-mêmes avaient déjà repéré le nombre d'or parmi les Égyptiens. Car de nombreuses œuvres d’art de l’Egypte ancienne sont clairement construites selon les canons de cette proportion.

On pense que Pythagore fut le premier à introduire le concept du nombre d’or. Les œuvres d'Euclide ont survécu jusqu'à nos jours (il a utilisé le nombre d'or pour construire des pentagones réguliers, c'est pourquoi un tel pentagone est appelé « d'or »), et le nombre du nombre d'or porte le nom de l'ancien architecte grec Phidias. C'est-à-dire qu'il s'agit de notre nombre « phi » (désigné par la lettre grecque φ), et il est égal à 1,6180339887498948482... Naturellement, cette valeur est arrondie : φ = 1,618 ou φ = 1,62, et en pourcentage le nombre d'or on dirait 62% et 38%.

Qu’y a-t-il d’unique dans cette proportion (et croyez-moi, elle existe) ? Essayons d'abord de le comprendre en utilisant un exemple de segment. Ainsi, nous prenons un segment et le divisons en parties inégales de telle manière que sa plus petite partie se rapporte à la plus grande, comme la plus grande partie se rapporte au tout. Je comprends, ce n'est pas encore très clair de quoi il s'agit, je vais essayer de l'illustrer plus clairement en utilisant l'exemple des segments :

Ainsi, nous prenons un segment et le divisons en deux autres, de sorte que le plus petit segment a se rapporte au plus grand segment b, tout comme le segment b se rapporte au tout, c'est-à-dire à la ligne entière (a + b). Mathématiquement, cela ressemble à ceci :

Cette règle fonctionne indéfiniment ; vous pouvez diviser les segments aussi longtemps que vous le souhaitez. Et voyez comme c’est simple. L’essentiel est de comprendre une fois et c’est tout.

Mais regardons maintenant un exemple plus complexe, qui revient très souvent, puisque le nombre d'or est également représenté sous la forme d'un rectangle d'or (dont le rapport d'aspect est φ = 1,62). C'est un rectangle très intéressant : si on en « coupe » un carré, on obtiendra à nouveau un rectangle doré. Et ainsi de suite sans fin. Voir:

Mais les mathématiques ne seraient pas des mathématiques si elles n’avaient pas de formules. Alors, mes amis, maintenant ça va faire un peu mal. J'ai caché la solution du nombre d'or sous un spoiler ; il existe de nombreuses formules, mais je ne veux pas quitter l'article sans elles.

Série de Fibonacci et nombre d'or

Nous continuons à créer et à observer la magie des mathématiques et du nombre d'or. Au Moyen Âge, il y avait un tel camarade - Fibonacci (ou Fibonacci, ils l'écrivent différemment partout). Il aimait les mathématiques et les problèmes, il avait aussi un problème intéressant avec la reproduction des lapins =) Mais ce n'est pas le sujet. Il a découvert une suite de nombres dont les nombres sont appelés « nombres de Fibonacci ».

La séquence elle-même ressemble à ceci :

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233... et ainsi de suite à l'infini.

En d’autres termes, la suite de Fibonacci est une suite de nombres où chaque nombre suivant est égal à la somme des deux précédents.

Qu’est-ce que le nombre d’or a à voir là-dedans ? Vous verrez maintenant.

Spirale de Fibonacci

Pour voir et ressentir tout le lien entre la série de nombres de Fibonacci et le nombre d'or, vous devez revoir les formules.

Autrement dit, à partir du 9ème terme de la suite de Fibonacci on commence à obtenir les valeurs du nombre d'or. Et si nous visualisons cette image dans son ensemble, nous verrons comment la séquence de Fibonacci crée des rectangles de plus en plus proches du rectangle d'or. C'est la connexion.

Parlons maintenant de la spirale de Fibonacci, elle est aussi appelée « spirale dorée ».

La spirale d'or est une spirale logarithmique dont le coefficient de croissance est φ4, où φ est le nombre d'or.

En général, d'un point de vue mathématique, le nombre d'or est une proportion idéale. Mais ce n'est que le début de ses miracles. Presque le monde entier est soumis aux principes du nombre d’or ; la nature elle-même a créé cette proportion. Même les ésotéristes y voient un pouvoir numérique. Mais nous n'en parlerons certainement pas dans cet article, alors pour ne rien manquer, vous pouvez vous abonner aux mises à jour du site.

Nombre d'or dans la nature, l'homme, l'art

Avant de commencer, je voudrais clarifier un certain nombre d'inexactitudes. Premièrement, la définition même du nombre d’or dans ce contexte n’est pas tout à fait correcte. Le fait est que le concept même de « section » est un terme géométrique, désignant toujours un plan, mais pas une séquence de nombres de Fibonacci.

Et, deuxièmement, les séries de nombres et le rapport de l'un à l'autre, bien sûr, ont été transformés en une sorte de pochoir qui peut être appliqué à tout ce qui semble suspect, et on peut être très heureux quand il y a des coïncidences, mais quand même , il ne faut pas perdre le bon sens.

Cependant, « tout se mélangeait dans notre royaume » et l’un devint synonyme de l’autre. Donc, en général, le sens n’en est pas perdu. Passons maintenant aux choses sérieuses.

Vous serez surpris, mais le nombre d'or, ou plutôt les proportions qui s'en rapprochent le plus possible, se voient presque partout, même dans le miroir. Vous ne me croyez pas ? Commençons par ceci.

Vous savez, quand j’apprenais à dessiner, on nous expliquait à quel point il était plus facile de construire le visage d’une personne, son corps, etc. Tout doit être calculé par rapport à autre chose.

Tout, absolument tout est proportionnel : les os, nos doigts, nos paumes, les distances sur le visage, la distance des bras tendus par rapport au corps, etc. Mais même cela n’est pas tout, la structure interne de notre corps, même cela, est égale ou presque égale à la formule du nombre d’or. Voici les distances et proportions :

des épaules à la couronne en passant par la taille de la tête = 1:1,618

du nombril à la couronne jusqu'au segment des épaules à la couronne = 1:1,618

du nombril aux genoux et des genoux aux pieds = 1:1,618

du menton jusqu'à l'extrémité de la lèvre supérieure et de celle-ci jusqu'au nez = 1:1,618

N'est-ce pas incroyable !? L'harmonie à l'état pur, tant à l'intérieur qu'à l'extérieur. Et c'est pourquoi, à un certain niveau subconscient, certaines personnes ne nous semblent pas belles, même si elles ont un corps fort et tonique, une peau veloutée, de beaux cheveux, de beaux yeux, etc., et tout le reste. Mais, tout de même, la moindre violation des proportions du corps, et l'apparence déjà légèrement "fait mal aux yeux".

Bref, plus une personne nous paraît belle, plus ses proportions se rapprochent de l'idéal. Et cela, d'ailleurs, ne peut pas être attribué uniquement au corps humain.

Nombre d'or dans la nature et ses phénomènes

Un exemple classique du nombre d’or dans la nature est la coquille du mollusque Nautilus pompilius et l’ammonite. Mais ce n’est pas tout, il existe bien d’autres exemples :

dans les boucles de l’oreille humaine, nous pouvons voir une spirale dorée ;

il en est de même (ou presque) dans les spirales le long desquelles les galaxies se tordent ;

et dans la molécule d'ADN ;

Selon la série de Fibonacci, le centre d'un tournesol est disposé, des cônes poussent, le milieu des fleurs, un ananas et bien d'autres fruits.

Mes amis, il y a tellement d'exemples que je vais juste laisser la vidéo ici (elle est juste en dessous) pour ne pas surcharger l'article de texte. Parce que si vous approfondissez ce sujet, vous pouvez approfondir la jungle suivante : même les anciens Grecs ont prouvé que l'Univers et, en général, tout l'espace est planifié selon le principe du nombre d'or.

Vous serez surpris, mais ces règles se retrouvent même dans le son. Voir:

Le niveau sonore le plus élevé qui provoque de la douleur et de l'inconfort dans nos oreilles est de 130 décibels.

Nous divisons la proportion 130 par le nombre d'or φ = 1,62 et nous obtenons 80 décibels - le son d'un cri humain.

Nous continuons à diviser proportionnellement et obtenons, disons, le volume normal de la parole humaine : 80 / φ = 50 décibels.

Eh bien, le dernier son que nous obtenons grâce à la formule est un agréable murmure = 2,618.

En utilisant ce principe, il est possible de déterminer les valeurs optimales de confort, minimales et maximales de température, de pression et d'humidité. Je ne l’ai pas testé et je ne sais pas à quel point cette théorie est vraie, mais vous devez en convenir, cela semble impressionnant.

On peut lire la plus haute beauté et l’harmonie dans absolument tout ce qui est vivant et non vivant.

L'essentiel est de ne pas se laisser emporter par cela, car si nous voulons voir quelque chose dans quelque chose, nous le verrons, même s'il n'est pas là. Par exemple, j'ai prêté attention au design de la PS4 et j'y ai vu le nombre d'or =) Cependant, cette console est tellement cool que je ne serais pas surpris si le concepteur y faisait vraiment quelque chose d'intelligent.

Le nombre d’or dans l’art

Il s’agit également d’un sujet très vaste et vaste qui mérite d’être examiné séparément. Ici, je me contenterai de noter quelques points fondamentaux. Le plus remarquable est que de nombreuses œuvres d'art et chefs-d'œuvre architecturaux de l'Antiquité (et pas seulement) ont été réalisés selon les principes du nombre d'or.

Pyramides égyptiennes et mayas, Notre Dame de Paris, Parthénon grec, etc.

Dans les œuvres musicales de Mozart, Chopin, Schubert, Bach et autres.

En peinture (cela se voit bien) : tous les tableaux les plus célèbres d'artistes célèbres sont réalisés en tenant compte des règles du nombre d'or.

Ces principes se retrouvent dans les poèmes de Pouchkine et dans le buste de la belle Néfertiti.

Même aujourd'hui, les règles du nombre d'or sont utilisées, par exemple, en photographie. Eh bien, et bien sûr, dans tous les autres arts, y compris le cinéma et le design.

Chats dorés de Fibonacci

Et enfin, à propos des chats ! Vous êtes-vous déjà demandé pourquoi tout le monde aime tant les chats ? Ils ont envahi Internet ! Les chats sont partout et c'est merveilleux =)

Et le fait est que les chats sont parfaits ! Vous ne me croyez pas ? Maintenant, je vais vous le prouver mathématiquement !

Est-ce que tu vois? Le secret est révélé ! Les chats sont idéaux du point de vue des mathématiques, de la nature et de l'Univers =)

*Je plaisante, bien sûr. Non, les chats sont vraiment idéaux.) Mais personne ne les a probablement mesurés mathématiquement.

C'est essentiellement ça, les amis ! Nous nous reverrons dans les prochains articles. Bonne chance à toi!

P.S. Images tirées de medium.com.

nombre d'or

Une personne distingue les objets qui l'entourent par leur forme. L’intérêt pour la forme d’un objet peut être dicté par une nécessité vitale, ou bien il peut être provoqué par la beauté de la forme. La forme, dont la construction repose sur une combinaison de symétrie et de nombre d'or, contribue à la meilleure perception visuelle et à l'apparition d'un sentiment de beauté et d'harmonie. Le tout est toujours constitué de parties, des parties de tailles différentes sont dans une certaine relation les unes avec les autres et avec le tout. Le principe du nombre d’or est la plus haute manifestation de la perfection structurelle et fonctionnelle de l’ensemble et de ses parties dans l’art, la science, la technologie et la nature.

Nombre d'or - proportion harmonique

En mathématiques proportion(lat. proportion) appelle l'égalité de deux relations : un : b = c : d.

Segment droit UN B peut être divisé en deux parties de la manière suivante :

en deux parties égales - UN B : CA = UN B : Soleil;
en deux parties inégales à tous égards (ces parties ne forment pas de proportions) ;
ainsi, quand UN B : CA = CA : Soleil.

Cette dernière est la division dorée ou division d'un segment en rapport extrême et moyen.

un : b = b : c ou Avec : b = b : UN.

Riz. 1.Image géométrique du nombre d'or

La connaissance pratique du nombre d'or commence par la division d'un segment de ligne droite dans la proportion d'or à l'aide d'un compas et d'une règle.

Riz. 2.Diviser un segment de ligne droite à l'aide du nombre d'or. AVANT JC. = 1/2 UN B; CD = AVANT JC.

Du point DANS une perpendiculaire égale à la moitié est restituée UN B. Point reçu AVEC relié par une ligne à un point UN. Un segment est tracé sur la ligne résultante Soleil se terminant par un point D. Segment de ligne ANNONCE transféré à diriger UN B. Le point résultant E divise un segment UN B dans le nombre d’or.

Les segments du nombre d'or sont exprimés comme une fraction irrationnelle infinie A.E.= 0,618..., si UN B prendre pour un ÊTRE= 0,382... À des fins pratiques, des valeurs approximatives de 0,62 et 0,38 sont souvent utilisées. Si le segment UN B pris comme 100 parties, alors la plus grande partie du segment est égale à 62 et la plus petite partie est à 38 parties.

Les propriétés du nombre d'or sont décrites par l'équation :

X 2 - X - 1 = 0.

Solution à cette équation :

Les propriétés du nombre d’or ont créé une aura romantique de mystère et de culte presque mystique autour de ce nombre.

Deuxième nombre d'or

Le magazine bulgare « Patrie » (n° 10, 1983) a publié un article de Tsvetan Tsekov-Karandash « Sur le deuxième nombre d'or », qui découle de la section principale et donne un rapport différent 44:56.

Cette proportion se retrouve en architecture et se produit également lors de la construction de compositions d'images de format horizontal allongé.

Riz. 3.Construction du deuxième nombre d'or

La division s'effectue comme suit. Segment de ligne UN B divisé selon le nombre d’or. Du point AVEC la perpendiculaire est restaurée CD. Rayon UN B il y a un point D, qui est relié par une ligne à un point UN. Angle droit ACD est divisé en deux. Du point AVEC une ligne est tracée jusqu'à ce qu'elle croise la ligne ANNONCE. Point E divise un segment ANNONCE dans le rapport 56:44.

Riz. 4.Diviser un rectangle avec la ligne du deuxième nombre d'or

La figure montre la position de la ligne du deuxième nombre d'or. Il est situé à mi-chemin entre la ligne du nombre d’or et la ligne médiane du rectangle.

triangle d'or

Pour trouver des segments de la proportion d'or des séries ascendantes et descendantes, vous pouvez utiliser pentacle.

Riz. 5.Construction d'un pentagone régulier et d'un pentagramme

Pour construire un pentagramme, vous devez construire un pentagone régulier. La méthode de construction a été développée par le peintre et graphiste allemand Albrecht Dürer (1471...1528). Laisser Ô- centre du cercle, UN- un point sur un cercle et E- le milieu du segment OA. Perpendiculaire au rayon OA, restauré au point À PROPOS, coupe le cercle au point D. A l'aide d'un compas, tracez un segment sur le diamètre C.E. = ED. La longueur du côté d’un pentagone régulier inscrit dans un cercle est CC. Disposez les segments sur le cercle CC et nous obtenons cinq points pour dessiner un pentagone régulier. Nous connectons les coins du pentagone les uns aux autres avec des diagonales et obtenons un pentagramme. Toutes les diagonales du pentagone se divisent en segments reliés par le nombre d'or.

Riz. 6.Construire un doré
Triangle

Nous effectuons un direct UN B. Du point UN posez un segment dessus trois fois À PROPOS valeur arbitraire, passant par le point résultant R. tracer une perpendiculaire à la ligne UN B, sur la perpendiculaire à droite et à gauche du point R. mettre de côté les segments À PROPOS. Points reçus d Et d 1 relier par des lignes droites à un point UN. Segment de ligne jj 1 mettre en ligne Annonce 1 , j'obtiens un point AVEC. Elle a divisé la ligne Annonce 1 proportionnellement au nombre d'or. Lignes Annonce 1 et jj 1 utilisé pour construire un rectangle « doré ».

Histoire du nombre d'or

Il est généralement admis que le concept de division d'or a été introduit dans l'usage scientifique par Pythagore, philosophe et mathématicien grec ancien (VIe siècle avant JC). On suppose que Pythagore a emprunté sa connaissance de la division en or aux Égyptiens et aux Babyloniens. En effet, les proportions de la pyramide de Khéops, des temples, des bas-reliefs, des objets ménagers et des bijoux du tombeau de Toutankhamon indiquent que les artisans égyptiens ont utilisé les rapports de la division d'or lors de leur création. L'architecte français Le Corbusier a constaté que dans le relief du temple du pharaon Séti Ier à Abydos et dans le relief représentant le pharaon Ramsès, les proportions des figures correspondent aux valeurs de la division d'or. L'architecte Hesira, représenté sur un relief d'une planche de bois provenant d'une tombe portant son nom, tient dans ses mains des instruments de mesure dans lesquels sont enregistrées les proportions de la division d'or.

Riz. 7.Rectangles dynamiques

Platon (427...347 avant JC) connaissait également la division en or. Son dialogue « Timée » est consacré aux vues mathématiques et esthétiques de l'école pythagoricienne et, en particulier, aux questions de la division d'or.

Riz. 8.Boussole antique de nombre d'or

Dans la littérature ancienne qui nous est parvenue, la division dorée a été mentionnée pour la première fois dans les Éléments d’Euclide. Dans le 2ème livre des "Principes", une construction géométrique de la division d'or est donnée. Après Euclide, l'étude de la division d'or a été réalisée par Hypsiclès (IIe siècle avant JC), Pappus (IIIe siècle après JC) et d'autres. L’Europe médiévale, avec la division de l’or, nous avons fait connaissance grâce aux traductions arabes des Éléments d’Euclide. Le traducteur J. Campano de Navarre (IIIe siècle) a fait des commentaires sur la traduction. Les secrets de la division dorée étaient jalousement gardés et gardés dans le plus strict secret. Ils n'étaient connus que des initiés.

Au cours de la Renaissance, l'intérêt pour la division d'or s'est accru parmi les scientifiques et les artistes en raison de son utilisation à la fois dans la géométrie et dans l'art, notamment en architecture. Léonard de Vinci, artiste et scientifique, a vu que les artistes italiens avaient beaucoup d'expérience empirique, mais peu connaissance . Il conçut et commença à écrire un livre sur la géométrie, mais à cette époque parut un livre du moine Luca Pacioli et Léonard abandonna son idée. Selon les contemporains et les historiens des sciences, Luca Pacioli était une véritable sommité, le plus grand mathématicien d'Italie entre Fibonacci et Galilée. Luca Pacioli fut l'élève du peintre Piero della Francesca, qui écrivit deux livres, dont l'un intitulé "De la perspective dans la peinture". Il est considéré comme le créateur de la géométrie descriptive.

Luc Pacioli a parfaitement compris l'importance de la science pour l'art. En 1496, à l'invitation du duc de Moreau, il vient à Milan, où il donne des cours de mathématiques. Léonard de Vinci travaillait également à Milan à la cour de Moro à cette époque. En 1509, le livre de Luca Pacioli « La Divine Proportion » fut publié à Venise avec des illustrations brillamment exécutées, c'est pourquoi on pense qu'elles ont été réalisées par Léonard de Vinci. Le livre était un hymne enthousiaste au nombre d’or. Parmi les nombreux avantages de la proportion dorée, le moine Luca Pacioli n'a pas manqué de nommer son « essence divine » comme expression de la trinité divine - Dieu le fils, Dieu le père et Dieu le Saint-Esprit (il était sous-entendu que le petit le segment est la personnification de Dieu le fils, le segment plus grand est Dieu le père et le segment entier est le Dieu du Saint-Esprit).

Léonard de Vinci a également accordé beaucoup d'attention à l'étude de la division d'or. Il réalisa des sections d'un corps stéréométrique formé de pentagones réguliers, et à chaque fois il obtint des rectangles avec des proportions dans la division d'or. C'est pourquoi il a donné le nom à cette division nombre d'or. Il reste donc le plus populaire.

Au même moment, dans le nord de l’Europe, en Allemagne, Albrecht Dürer travaillait sur les mêmes problématiques. Il esquisse l'introduction de la première version du traité sur les proportions. Dürer écrit. « Il est nécessaire que quelqu’un qui sait faire quelque chose l’enseigne à ceux qui en ont besoin. C’est ce que j’ai décidé de faire.

Grand astronome du XVIe siècle. Johannes Kepler a qualifié le nombre d'or de l'un des trésors de la géométrie. Il fut le premier à attirer l'attention sur l'importance de la proportion d'or pour la botanique (la croissance des plantes et leur structure).

Kepler a qualifié la proportion d'or d'auto-continue. « Elle est structurée de telle manière », écrit-il, « que les deux termes les plus bas de cette proportion sans fin s'additionnent pour former le troisième terme, et les deux derniers termes, s'ils sont additionnés. , donnez le terme suivant, et la même proportion demeure jusqu'à l'infini.

La construction d'une série de segments de la proportion d'or peut se faire aussi bien dans le sens croissant (série croissante) que dans le sens décroissant (série décroissante).

Si vous êtes sur une ligne droite de longueur arbitraire, mettez de côté le segment m, placez le segment à côté M. A partir de ces deux segments, nous construisons une échelle de segments de la proportion d'or des séries ascendantes et descendantes

Riz. 9.Construction d'une échelle de segments de proportion d'or

Au cours des siècles suivants, la règle de la proportion d’or est devenue un canon académique et, au fil du temps, la lutte contre la routine académique a commencé dans l’art, dans le feu de la lutte « ils ont jeté le bébé avec l’eau du bain ». Le nombre d’or a été à nouveau « découvert » au milieu du XIXe siècle. En 1855, le chercheur allemand sur le nombre d'or, le professeur Zeising, publie son ouvrage « Aesthetic Studies ». Ce qui est arrivé à Zeising est exactement ce qui devrait inévitablement arriver à un chercheur qui considère un phénomène comme tel, sans lien avec d’autres phénomènes. Il a absolutisé la proportion du nombre d'or, la déclarant universelle pour tous les phénomènes de la nature et de l'art. Zeising avait de nombreux adeptes, mais il y avait aussi des opposants qui qualifiaient sa doctrine des proportions d’« esthétique mathématique ».

Riz. dix.Proportions dorées dans certaines parties du corps humain

Riz. onze.Des proportions dorées dans la figure humaine

Zeisinga fait un travail formidable. Il mesura environ deux mille corps humains et arriva à la conclusion que le nombre d'or exprime la loi statistique moyenne. La division du corps par la pointe du nombril est l'indicateur le plus important du nombre d'or. Les proportions du corps masculin fluctuent dans le rapport moyen de 13 : 8 = 1,625 et sont un peu plus proches du nombre d'or que les proportions du corps féminin, pour lesquelles la proportion moyenne est exprimée dans le rapport 8 : 5 = 1,6. Chez un nouveau-né, la proportion est de 1:1 ; à 13 ans, elle est de 1,6 et à 21 ans, elle est égale à celle d'un homme. Les proportions du nombre d'or apparaissent également par rapport à d'autres parties du corps - la longueur de l'épaule, de l'avant-bras et de la main, de la main et des doigts, etc.

Zeising testa la validité de sa théorie sur les statues grecques. Il a développé les proportions d'Apollo Belvedere de manière très détaillée. Des vases grecs, des structures architecturales de différentes époques, des plantes, des animaux, des œufs d'oiseaux, des sons musicaux et des mètres poétiques ont été étudiés. Zeising a donné une définition du nombre d'or et a montré comment il s'exprime en segments de droite et en nombres. Lorsqu'on obtint les nombres exprimant les longueurs des segments, Zeising vit qu'ils constituaient une série de Fibonacci, qui pouvait se poursuivre indéfiniment dans un sens ou dans l'autre. Son livre suivant s'intitulait « La division d'or comme loi morphologique fondamentale dans la nature et l'art ». En 1876, un petit livre, presque une brochure, fut publié en Russie, décrivant l'œuvre de Zeising. L'auteur s'est réfugié sous les initiales Yu.F.V. Cette édition ne mentionne aucune œuvre de peinture.

Fin XIXème – début XXème siècles. De nombreuses théories purement formalistes sont apparues sur l’utilisation du nombre d’or dans les œuvres d’art et d’architecture.Avec le développement du design et de l’esthétique technique, la loi du nombre d’or s’est étendue au design des voitures, des meubles, etc.

Série de Fibonacci

Le nom du moine mathématicien italien Léonard de Pise, mieux connu sous le nom de Fibonacci (fils de Bonacci), est indirectement lié à l'histoire du nombre d'or. Il a beaucoup voyagé à l'Est, a fait découvrir à l'Europe les chiffres indiens (arabes). En 1202, fut publié son ouvrage mathématique « Le Livre du Boulier » (tableau de comptage), qui rassemblait tous les problèmes connus à cette époque. L’un des problèmes disait « Combien de couples de lapins naîtront d’un couple en un an ». En réfléchissant à ce sujet, Fibonacci a construit la série de nombres suivante :

Mois

etc.

Des couples de lapins

etc.

Une série de nombres 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, etc. connue sous le nom de série de Fibonacci. La particularité de la séquence de nombres est que chacun de ses membres, à partir du troisième, est égal à la somme des deux précédents 2 + 3 = 5 ; 3 + 5 = 8 ; 5 + 8 = 13, 8 + 13 = 21 ; 13 + 21 = 34, etc., et le rapport des nombres adjacents dans la série se rapproche du rapport de la division d'or. Donc, 21 : 34 = 0,617 et 34 : 55 = 0,618. Cette relation est désignée par le symbole F. Seul ce rapport - 0,618 : 0,382 - donne une division continue d'un segment de droite dans la proportion d'or, en l'augmentant ou en la diminuant jusqu'à l'infini, lorsque le plus petit segment est lié au plus grand comme le plus grand l'est au tout.

Fibonacci a également abordé les besoins pratiques du commerce : quel est le plus petit nombre de poids pouvant être utilisé pour peser un produit ? Fibonacci prouve que le système de poids optimal est : 1, 2, 4, 8, 16...

Nombre d'or généralisé

La série de Fibonacci n'aurait pu rester qu'un incident mathématique, sans le fait que tous les chercheurs de la division d'or dans le monde végétal et animal, sans parler de l'art, en venaient invariablement à cette série comme une expression arithmétique de la loi de l'or. division.

Les scientifiques ont continué à développer activement la théorie des nombres de Fibonacci et du nombre d'or. Yu. Matiyasevich résout le 10ème problème de Hilbert en utilisant les nombres de Fibonacci. Des méthodes élégantes émergent pour résoudre un certain nombre de problèmes cybernétiques (théorie de la recherche, jeux, programmation) en utilisant les nombres de Fibonacci et le nombre d'or. Aux États-Unis, même la Mathematical Fibonacci Association est en cours de création, qui publie une revue spéciale depuis 1963.

L'une des réalisations dans ce domaine est la découverte des nombres de Fibonacci généralisés et des nombres d'or généralisés.

La série de Fibonacci (1, 1, 2, 3, 5, 8) et la série « binaire » de poids découverte par lui 1, 2, 4, 8, 16... à première vue sont complètement différentes. Mais les algorithmes pour leur construction sont très similaires les uns aux autres : dans le premier cas, chaque nombre est la somme du nombre précédent avec lui-même 2 = 1 + 1 ; 4 = 2 + 2..., dans le second - c'est la somme des deux nombres précédents 2 = 1 + 1, 3 = 2 + 1, 5 = 3 + 2.... Est-il possible de trouver un général formule mathématique à partir de laquelle on obtient « les séries binaires et les séries de Fibonacci ? Ou peut-être que cette formule nous donnera de nouveaux ensembles numériques dotés de nouvelles propriétés uniques ?

En effet, fixons le paramètre numérique S, qui peut prendre n'importe quelle valeur : 0, 1, 2, 3, 4, 5... Considérons la série de nombres, S+ 1 des premiers termes dont sont des unités, et chacun des suivants est égal à la somme de deux termes du précédent et séparé du précédent par S pas. Si n On note le ième terme de cette série par φ S (n), alors on obtient la formule générale φ S (n) = φ S (n- 1) + φ S (n - S - 1).

Il est évident que lorsque S= 0 de cette formule on obtient une série « binaire », avec S= 1 - Série de Fibonacci, avec S= 2, 3, 4. nouvelle série de nombres, appelés S-Nombres de Fibonacci.

Globalement doré S-la proportion est la racine positive de l'équation d'or S-sections x S+1 - X S - 1 = 0.

Il est facile de montrer que lorsque S= 0, le segment est divisé en deux, et lorsque S= 1 - le nombre d'or classique familier.

Relations entre voisins S- Les nombres de Fibonacci coïncident avec une précision mathématique absolue dans la limite de l'or S-les proportions ! Les mathématiciens disent dans de tels cas que l'or S-les sections sont des invariants numériques S-Nombres de Fibonacci.

Faits confirmant l'existence de l'or S-sections dans la nature, cite le scientifique biélorusse E.M. Soroko dans le livre « Structurel Harmony of Systems » (Minsk, « Science and Technology », 1984). Il s'avère, par exemple, que les alliages binaires bien étudiés n'ont des propriétés fonctionnelles particulières et prononcées (thermiquement stables, durs, résistants à l'usure, résistants à l'oxydation, etc.) que si les densités des composants d'origine sont liées les unes aux autres. par un d'or S-les proportions. Cela a permis à l'auteur d'émettre des hypothèses e sur le fait qu'ils sont dorés S-les sections sont des invariants numériques de systèmes auto-organisés. Une fois confirmée expérimentalement, cette hypothèse pourrait revêtir une importance fondamentale pour le développement de la synergie, un nouveau domaine scientifique qui étudie les processus dans les systèmes auto-organisés.

Utiliser des codes dorés S-les proportions peuvent être exprimées par n'importe quel nombre réel comme une somme de puissances d'or S-proportions à coefficients entiers.

La différence fondamentale entre cette méthode de codage des nombres est que les bases des nouveaux codes, qui sont en or S-les proportions, avec S> 0 s'avèrent être des nombres irrationnels. Ainsi, les nouveaux systèmes numériques dotés de bases irrationnelles semblent placer la hiérarchie historiquement établie des relations entre nombres rationnels et irrationnels « de la tête aux pieds ». Le fait est que les nombres naturels ont été « découverts » pour la première fois ; alors leurs rapports sont des nombres rationnels. Et ce n'est que plus tard - après la découverte des segments incommensurables par les Pythagoriciens - que les nombres irrationnels sont nés. Par exemple, dans les systèmes de nombres décimaux, quinaires, binaires et autres systèmes de nombres positionnels classiques, les nombres naturels ont été choisis comme une sorte de principe fondamental - 10, 5, 2 - à partir duquel, selon certaines règles, tous les autres nombres naturels, ainsi que les nombres rationnels et des nombres irrationnels, ont été construits.

Une sorte d'alternative aux méthodes de notation existantes est un nouveau système irrationnel, comme principe fondamental, dont le début est un nombre irrationnel (qui, rappelons-le, est la racine de l'équation du nombre d'or) ; d'autres nombres réels s'expriment déjà à travers lui.

Dans un tel système numérique, tout nombre naturel peut toujours être représenté comme fini – et non comme infini, comme on le pensait auparavant ! - la somme des degrés de l'un des or S-les proportions. C’est l’une des raisons pour lesquelles l’arithmétique « irrationnelle », d’une simplicité et d’une élégance mathématiques étonnantes, semble avoir absorbé les meilleures qualités de l’arithmétique binaire classique et de « Fibonacci ».

Principes de formation dans la nature

Tout ce qui prenait une forme se formait, grandissait, s'efforçait de prendre place dans l'espace et de se conserver. Ce désir se réalise principalement selon deux options : grandir vers le haut ou s'étendre sur la surface de la terre et se tordre en spirale.

La coquille est tordue en spirale. Si vous le dépliez, vous obtenez une longueur légèrement plus courte que la longueur du serpent. Une petite coquille de dix centimètres a une spirale de 35 cm de long.Les spirales sont très courantes dans la nature. L’idée du nombre d’or sera incomplète sans parler de la spirale.

Riz. 12.Spirale d'Archimède

La forme de la coquille enroulée en spirale a attiré l’attention d’Archimède. Il l'a étudié et a trouvé une équation pour la spirale. La spirale dessinée selon cette équation porte son nom. L'augmentation de son pas est toujours uniforme. Actuellement, la spirale d'Archimède est largement utilisée en technologie.

Goethe a également souligné la tendance de la nature à la spirale. La disposition hélicoïdale et spirale des feuilles sur les branches des arbres a été remarquée il y a longtemps. La spirale a été vue dans la disposition des graines de tournesol, des pommes de pin, des ananas, des cactus, etc. Les travaux conjoints de botanistes et de mathématiciens ont mis en lumière ces phénomènes naturels étonnants. Il s'est avéré que la série de Fibonacci se manifeste dans la disposition des feuilles sur une branche (phylotaxie), des graines de tournesol et des pommes de pin, et par conséquent, la loi du nombre d'or se manifeste. L'araignée tisse sa toile en forme de spirale. Un ouragan tourne comme une spirale. Un troupeau de rennes effrayé se disperse en spirale. La molécule d'ADN est tordue en double hélice. Goethe appelait la spirale la « courbe de la vie ».

Parmi les herbes en bordure de route pousse une plante banale : la chicorée. Regardons-le de plus près. Une pousse s'est formée à partir de la tige principale. La première feuille se trouvait juste là.

Riz. 13. Chicorée

La pousse fait une forte éjection dans l'espace, s'arrête, libère une feuille, mais cette fois plus courte que la première, fait à nouveau une éjection dans l'espace, mais avec moins de force, libère une feuille encore plus petite et est à nouveau éjectée. . Si la première émission est considérée comme égale à 100 unités, alors la seconde est égale à 62 unités, la troisième à 38, la quatrième à 24, etc. La longueur des pétales dépend également de la proportion d’or. En grandissant et en conquérant l’espace, la plante a conservé certaines proportions. Les impulsions de sa croissance ont progressivement diminué proportionnellement au nombre d'or.

Riz. 14.Lézard vivipare

À première vue, le lézard a des proportions agréables à nos yeux - la longueur de sa queue est liée à la longueur du reste du corps comme 62 à 38.

Dans le monde végétal comme dans le monde animal, la tendance formatrice de la nature se manifeste de manière persistante : la symétrie dans la direction de la croissance et du mouvement. Ici, le nombre d'or apparaît dans les proportions des parties perpendiculaires à la direction de croissance.

La nature a procédé à une division en parties symétriques et en proportions dorées. Les parties révèlent une répétition de la structure de l’ensemble.

Riz. 15. oeuf d'oiseau

Le grand Goethe, poète, naturaliste et artiste (il dessinait et peignait à l'aquarelle), rêvait de créer une doctrine unifiée sur la forme, la formation et la transformation des corps organiques. C'est lui qui a introduit le terme morphologie dans l'usage scientifique.

Pierre Curie a formulé au début de ce siècle un certain nombre d'idées profondes sur la symétrie. Il a soutenu qu’on ne peut considérer la symétrie d’un corps sans prendre en compte la symétrie de l’environnement.

Les lois de la symétrie « d'or » se manifestent dans les transitions énergétiques des particules élémentaires, dans la structure de certains composés chimiques, dans les systèmes planétaires et cosmiques, dans les structures génétiques des organismes vivants. Ces modèles, comme indiqué ci-dessus, existent dans la structure des organes humains individuels et du corps dans son ensemble, et se manifestent également dans les biorythmes et le fonctionnement du cerveau et dans la perception visuelle.

Nombre d'or et symétrie

Le nombre d’or ne peut être considéré seul, séparément, sans lien avec la symétrie. Le grand cristallographe russe G.V. Wulf (1863...1925) considérait le nombre d'or comme l'une des manifestations de la symétrie.

La division dorée n'est pas une manifestation d'asymétrie, quelque chose d'opposé à la symétrie. Selon les idées modernes, la division dorée est une symétrie asymétrique. La science de la symétrie comprend des concepts tels que statique Et symétrie dynamique. La symétrie statique caractérise la paix et l'équilibre, tandis que la symétrie dynamique caractérise le mouvement et la croissance. Ainsi, dans la nature, la symétrie statique est représentée par la structure des cristaux, et dans l'art, elle caractérise la paix, l'équilibre et l'immobilité. La symétrie dynamique exprime l'activité, caractérise le mouvement, le développement, le rythme, elle est témoignage de la vie. La symétrie statique est caractérisée par des segments égaux et des valeurs égales. La symétrie dynamique se caractérise par une augmentation des segments ou leur diminution, et elle s'exprime dans les valeurs du nombre d'or d'une série croissante ou décroissante.

Nombre de lectures : 7654

On le savait même dans l'Egypte ancienne nombre d'or, Léonard de Vinci et Euclide étudièrent ses propriétés.La perception visuelle d’une personne est conçue de telle manière qu’elle distingue par sa forme tous les objets qui l’entourent. Son intérêt pour un objet ou sa forme est parfois dicté par la nécessité, ou encore cet intérêt peut être provoqué par la beauté de l'objet. Si à la base même de la construction du formulaire, une combinaison est utilisée nombre d'or et les lois de la symétrie, alors c'est la meilleure combinaison pour la perception visuelle par une personne qui ressent l'harmonie et la beauté. Le tout est constitué de parties, grandes et petites, et ces parties de différentes tailles ont une certaine relation, à la fois entre elles et avec le tout. Et la plus haute manifestation de la perfection fonctionnelle et structurelle dans la nature, la science, l'art, l'architecture et la technologie est le Principe. nombre d'or. Concept de nombre d'or introduit dans l'usage scientifique par le mathématicien et philosophe grec ancien (VIe siècle avant JC) Pythagore. Mais la connaissance même de nombre d'or il a emprunté aux anciens Égyptiens. Les proportions de tous les bâtiments du temple, de la pyramide de Khéops, des bas-reliefs, des articles ménagers et des décorations des tombes montrent que le rapport nombre d'orétait activement utilisé par les maîtres anciens bien avant Pythagore. A titre d'exemple : le bas-relief du temple de Séthi Ier à Abydos et le bas-relief de Ramsès reprennent le principe nombre d'or dans les proportions des personnages. L'architecte Le Corbusier l'a découvert. Sur une planche de bois récupérée dans la tombe de l'architecte Khesir, il y a un dessin en relief sur lequel l'architecte lui-même est visible, tenant dans ses mains des instruments de mesure, qui sont représentés dans une position fixant les principes. nombre d'or. Connaissait les principes nombre d'or et Platon (427...347 avant JC). Le dialogue « Timée » en est la preuve, puisqu'il est consacré aux questions division dorée, vues esthétiques et mathématiques de l’école pythagoricienne. Des principes nombre d'or utilisé par les architectes grecs antiques dans la façade du temple du Parthénon. Les boussoles que les anciens architectes et sculpteurs du monde antique utilisaient dans leur travail ont été découvertes lors des fouilles du temple du Parthénon.

Parthénon, Acropole, Athènes Dans les proportions de Pompéi (musée de Naples) division dorée aussi disponible.Dans la littérature ancienne qui nous est parvenue, le principe nombre d'or mentionné pour la première fois dans les Éléments d'Euclide. Dans le livre "Débuts" dans la deuxième partie, le principe géométrique est donné nombre d'or. Les adeptes d'Euclide furent Pappus (IIIe siècle après J.-C.), Hypsiclès (IIe siècle av. J.-C.) et d'autres. Vers l'Europe médiévale avec le principe nombre d'or Nous nous sommes rencontrés grâce aux traductions de l'arabe des Éléments d'Euclide. Des principes nombre d'or n'étaient connus que d'un cercle restreint d'initiés, ils étaient jalousement gardés et gardés dans la plus stricte confidentialité. L’ère de la renaissance et de l’intérêt pour les principes est arrivée nombre d'or augmente parmi les scientifiques et les artistes, puisque ce principe est applicable dans la science, l’architecture et l’art. Et Léonard de Vinci a commencé à utiliser ces principes dans ses œuvres, de plus, il a commencé à écrire un livre sur la géométrie, mais à cette époque est apparu un livre du moine Luca Pacioli, qui l'a précédé et a publié le livre « Divine Proportion », après quoi Léonard a laissé son œuvre inachevée. Selon les historiens des sciences et ses contemporains, Luca Pacioli était une véritable sommité, un brillant mathématicien italien qui a vécu entre Galilée et Fibonacci. Élève de l'artiste Piero della Francesca, Luca Pacioli a écrit deux livres, « De la perspective dans la peinture », le titre de l'un d'eux. Il est considéré par beaucoup comme le créateur de la géométrie descriptive. Luca Pacioli, à l'invitation du duc de Moro, vint à Milan en 1496 et y donna des cours de mathématiques. Léonard de Vinci travaillait à cette époque à la cour de Moro. Le livre de Luca Pacioli, La Divine Proportion, publié à Venise en 1509, devient un hymne enthousiaste. nombre d'or, avec des illustrations magnifiquement exécutées, il y a tout lieu de croire que les illustrations ont été réalisées par Léonard de Vinci lui-même. Le moine Luca Pacioli, comme l'une des vertus nombre d'or a souligné son « essence divine ». Comprenant la valeur scientifique et artistique du nombre d'or, Léonard de Vinci a consacré beaucoup de temps à son étude. En effectuant une section d'un corps stéréométrique constitué de pentagones, il a obtenu des rectangles avec des rapports d'aspect conformes à nombre d'or. Et il lui a donné le nom « nombre d'or" Ce qui tient encore aujourd’hui. Albrecht Dürer, étudiant également nombre d'or en Europe, rencontre le moine Luca Pacioli. Johannes Kepler, le plus grand astronome de son temps, fut le premier à attirer l'attention sur la signification nombre d'or pour la botanique, il l'appelle le trésor de la géométrie. Il a appelé la proportion d'or auto-continue. "Elle est structurée de cette façon", a-t-il dit, "la somme des deux termes juniors d'une proportion infinie donne le troisième terme, et deux derniers termes quelconques, s'ils sont ajoutés, donnent le terme suivant. , et la même proportion est maintenue à l’infini.

Triangle d'or : Nombre d'or et nombre d'or : Rectangle d'or : Spirale d'or

triangle d'or

Pour retrouver les segments de la proportion d'or des rangées descendantes et ascendantes, nous utiliserons un pentagramme.

Riz. 5. Construction d'un pentagone régulier et d'un pentagramme

Pour construire un pentagramme, il faut dessiner un pentagone régulier selon la méthode de construction développée par le peintre et graphiste allemand Albrecht Durer. Si O est le centre du cercle, A est un point du cercle et E est le milieu du segment OA. La perpendiculaire au rayon OA, restituée au point O, coupe le cercle au point D. A l'aide d'un compas, marquez un segment sur le diamètre CE = ED. Alors la longueur du côté d’un pentagone régulier inscrit dans un cercle est égale à DC. Nous traçons les segments DC sur le cercle et obtenons cinq points pour dessiner un pentagone régulier. Ensuite, par un coin, nous connectons les coins du pentagone avec des diagonales et obtenons un pentagramme. Toutes les diagonales du pentagone se divisent en segments reliés par le nombre d'or.

Chaque extrémité de l'étoile pentagonale représente un triangle d'or. Ses côtés forment un angle de 36° au sommet, et la base, posée sur le côté, le divise dans la proportion du nombre d'or. Nous dessinons directement AB. A partir du point A, nous y déposons trois fois un segment O de taille arbitraire, passant par le point P résultant nous traçons une perpendiculaire à la ligne AB, sur la perpendiculaire à droite et à gauche du point P nous déposons les segments O. Nous connectons les points résultants d et d1 avec des lignes droites jusqu'au point A. Nous plaçons le segment dd1 sur la ligne Ad1, obtenant le point C. Elle a divisé la ligne Ad1 proportionnellement au nombre d'or. Les lignes Ad1 et dd1 sont utilisées pour construire un rectangle « doré ».

Riz. 6. Construire de l’or

Triangle

Nombre d'or et nombre d'or

En mathématiques et en art, deux quantités sont dans le nombre d'or si le rapport entre la somme de ces quantités et la plus grande est le même que le rapport entre la plus grande et la plus petite. Exprimé algébriquement : Le nombre d'or est souvent désigné par la lettre grecque phi (? ou ?). La figure du nombre d'or illustre les relations géométriques qui définissent cette constante. Le nombre d'or est une constante mathématique irrationnelle, d'environ 1,6180339887.

rectangle doré

Un rectangle doré est un rectangle dont les longueurs des côtés sont dans le nombre d'or, 1 :? (un à fi), soit 1 : ou environ 1 : 1,618. Le rectangle d'or ne peut être construit qu'avec une règle et une boussole : 1. Construisez un carré simple 2. Tracez une ligne du milieu d'un côté de la zone jusqu'au coin opposé 3. Utilisez cette ligne comme rayon pour tracer un arc qui définit la hauteur du rectangle 4. Complétez le rectangle doré

Spirale dorée

En géométrie, la spirale d'or est une spirale logarithmique dont le facteur de croissance b est lié à? , nombre d'or. En particulier, la spirale dorée s'élargit (plus loin de son origine) d'un facteur ? pour chaque quart de tour qu'il fait.

Les points consécutifs de division du rectangle d'or en carrés se trouvent sur spirale logarithmique, parfois connue sous le nom de spirale dorée.

Nombre d’or en architecture et en art.

De nombreux architectes et artistes ont exécuté leurs œuvres conformément aux proportions du nombre d'or, notamment sous la forme d'un rectangle d'or, dans lequel le rapport du plus grand côté au plus petit côté a les proportions du nombre d'or, estimant que ce rapport serait esthétiquement agréable. [Source : Wikipédia.org ]

Voici quelques exemples:

Parthénon, Acropole, Athènes . Cet ancien temple s’inscrit presque exactement dans le rectangle d’or.

L'Homme de Vitruve de Léonard de Vinci vous pouvez créer de nombreuses lignes de rectangles sur cette figure. Ensuite, il y a trois ensembles différents de rectangles dorés : Chaque ensemble est destiné à la zone de la tête, du torse et des jambes. Le dessin de l'Homme de Vitruve de Léonard de Vinci est parfois confondu avec les principes du Rectangle d'Or, cependant ce n'est pas le cas. La construction de l'Homme de Vitruve consiste à tracer un cercle d'un diamètre égal à la diagonale du carré, en le déplaçant vers le haut pour qu'il touche la base du carré et en traçant un cercle final entre la base du carré et le milieu entre l'aire du centre du carré et du centre du cercle : Explication détaillée sur la construction géométrique >>

Nombre d'or dans la nature.

Adolf Zeising, dont les principaux intérêts étaient les mathématiques et la philosophie, a trouvé la proportion dorée dans la disposition des branches le long de la tige d'une plante et dans les nervures des feuilles. Il élargit ses recherches et passe des plantes aux animaux, étudiant les squelettes des animaux et les branches de leurs veines et nerfs, ainsi que les proportions de composés chimiques et la géométrie des cristaux, jusqu'à l'utilisation du nombre d'or dans l'image visuelle. arts. Dans ces phénomènes, il a vu que le nombre d'or était utilisé partout comme une loi universelle, écrivait Zeising en 1854 : Le nombre d'or est une loi universelle qui contient le principe de base qui façonne le désir de beauté et d'intégralité dans des domaines tels que la nature et l'art, qui imprègne, en tant qu'idéal spirituel primaire, toutes les structures, formes et proportions, qu'elles soient cosmiques ou physiques, organiques. ou inorganique, acoustique ou optique, mais le principe du nombre d'or trouve sa réalisation la plus complète dans la forme humaine.

Exemples:

La découpe de la coquille du Nautilus révèle le principe doré de la construction en spirale.

Mozart a divisé ses sonates en deux parties, dont la durée reflète nombre d'or, bien qu'il y ait beaucoup de débats quant à savoir s'il l'a fait délibérément. À des époques plus modernes, le compositeur hongrois Béla Bartók et l'architecte français Le Corbusier ont délibérément intégré le principe du nombre d'or dans leurs œuvres. Même aujourd'hui nombre d'or nous entoure partout d’objets artificiels. Regardez presque toutes les croix chrétiennes, le rapport entre la partie verticale et la partie horizontale est la proportion d'or. Pour trouver le rectangle doré, regardez dans votre portefeuille et vous y trouverez des cartes de crédit. Malgré ces nombreuses preuves provenant d'œuvres d'art créées au fil des siècles, il y a actuellement un débat parmi les psychologues pour savoir si les gens perçoivent réellement les proportions dorées, en particulier le rectangle doré, comme plus belles que les autres formes. Dans un article de revue de 1995, le professeur Christopher Green, de l'Université York à Toronto, discute d'un certain nombre d'expériences menées au fil des ans qui n'ont montré aucune préférence pour la forme du rectangle d'or, mais note que plusieurs autres ont fourni la preuve qu'une telle préférence ne exister. . Mais quelle que soit la science, le nombre d’or conserve son caractère mystique, en partie parce qu’il trouve d’excellentes applications dans de nombreux endroits inattendus de la nature. Spirale Les coquilles de Nautilus sont étonnamment proches de nombre d'or, et le rapport entre la longueur de la poitrine et de l'abdomen chez la plupart des abeilles est presque nombre d'or. Même un échantillon représentatif des formes les plus courantes d’ADN humain s’intègre parfaitement dans le décagone doré. nombre d'or et ses parents apparaissent également dans de nombreux contextes inattendus en mathématiques, et ils continuent de susciter l'intérêt des communautés mathématiques. Le Dr Steven Marquardt, ancien chirurgien plasticien, a utilisé cette mystérieuse proportion nombre d'or, dans son travail, longtemps responsable de la beauté et de l'harmonie, pour réaliser un masque qu'il considérait comme la plus belle forme de visage humain qui puisse être.