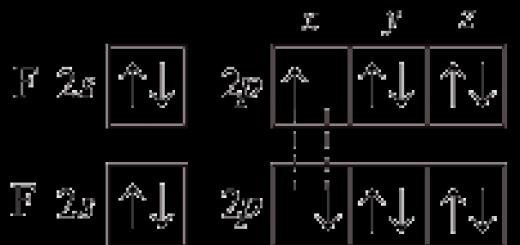
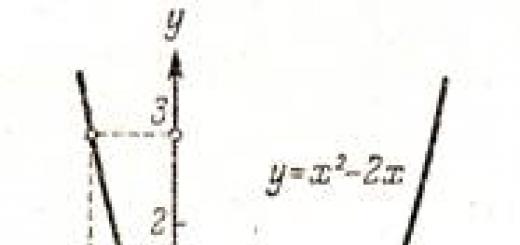قضیه 3.1.اتحاد هر تعداد مجموعه باز یک مجموعه باز است.

اجازه دهید Gk، که در آن k О N مجموعه های باز هستند.

3 هر نقطه ای را انتخاب کنید ایکس O ÎG. با تعریف اتحاد مجموعه ها، نقطه ایکس o متعلق به یکی از مجموعه هاست Gk. از آنجا که Gkیک مجموعه باز است، پس وجود دارد الکترونیکیهمسایگی یک نقطه x o، که به طور کامل در مجموعه نهفته است Gk: U(x o، e)Ì G k Þ U(x o، e)Ì G.

هر نکته ای را فهمیدم x o ÎG- داخلی، که به این معنی است جی- مجموعه باز 4

قضیه 3.2 . محل تقاطع تعداد محدودی از مجموعه های غیر خالی باز یک مجموعه باز است.

اجازه دهید Gk (k = 1,2, …,n) مجموعه های باز هستند.

اجازه دهید ثابت کنیم که یک مجموعه باز است.

3 هر نقطه ای را انتخاب کنید ایکس O ÎG. با تعریف تقاطع مجموعه ها ایکس o به هر یک از مجموعه ها تعلق دارد Gk. از آنجایی که هر مجموعه Gkباز، سپس در هر مجموعه Gkوجود دارد e k- همسایگی یک نقطه ایکس O : U(ایکس o ، e k)Ì G k. تعداد زیادی اعداد ( ه 1 ، ه 2 ,…, e n) محدود است، بنابراین یک عدد وجود دارد e = حداقل{ه 1 ، ه 2 ,…,e n). سپس ه- همسایگی یک نقطه ایکس o در هر e k- همسایگی نقطه ایکس O : U(ایکس o ، ه)M U e(ایکس o ، e k) Þ U(ایکس o ، ه)Ì G.

گرفتش ایکس o – نقطه داخلی مجموعه جی، که به این معنی است جی- مجموعه باز 4

نکته 3.1.محل تقاطع تعداد نامتناهی مجموعه باز ممکن است یک مجموعه باز نباشد.

مثال 3.1. اجازه دهید در فضا R G k =(2 – 1/k; 4+ 1/k)، جایی که k= 1,2,…,n…. G 1 =(1;5)، G 2(1.5;4.5)، بخش Ì G kو یک مجموعه باز نیست، نقاط 2 و 4 داخلی نیستند.

قضیه 3.3 . محل تقاطع هر مجموعه ای از مجموعه های غیر خالی بسته یک مجموعه بسته است.

اجازه دهید Fk- مجموعه های بسته

اجازه دهید ثابت کنیم که مجموعه بسته است، i.e. این شامل تمام نقاط حد خود است.

3 اجازه دهید ایکس اف.از تعریف تقاطع مجموعه ها چنین بر می آید که در هر ه- همسایگی نقطه ایکس o بی نهایت نقاط هر مجموعه وجود دارد Fk، که به این معنی است ایکس o – نقطه حد هر مجموعه Fk. به دلیل بسته بودن مجموعه ها Fkنقطه

ایکس O О F k "k Þ x O Î F.از آنجا که نقطه ایکس اف، و این به معنای زیادی است افبسته 4

قضیه 3.4.اتحاد تعداد محدودی از مجموعه های بسته یک مجموعه بسته است.

اجازه دهید هر مجموعه Fkبسته

اجازه دهید ثابت کنیم که مجموعه بسته است، یعنی اگر ایکس o – نقطه حدی مجموعه اف، آن ایکس O О F.

3 اجازه دهید ایکس o – هر نقطه حدی از مجموعه اف، سپس در هر ه- همسایگی نقطه ایکس o بی نهایت نقاط مجموعه وجود دارد. از آنجایی که تعداد مجموعه ها F kمحدود است، پس ایکس o حداقل به یکی از مجموعه ها تعلق دارد F k، یعنی ایکس o نقطه حد برای این مجموعه است.

به دلیل انزوا Fkنقطه ایکس o متعلق است F kو بنابراین بسیاری از آنها. از آنجا که نقطه ایکس o به طور دلخواه انتخاب می شود، سپس تمام نقاط حد متعلق به مجموعه هستند اف، که معنی زیادی دارد افبسته 4

نکته 3.2.اتحاد تعداد نامتناهی مجموعه بسته می تواند یک مجموعه باز باشد.

مثال 3.2 . در فضای آر: F k =

F 1 =; F 2 = ; …. فاصله (2;5) یک مجموعه باز است.

اجازه دهید بدون اثبات قضایای 3.5 و 3.6 مربوط به متمم مجموعه را بپذیریم Eبه بسیاری X: C x E=CE.

قضیه 3.5 . اگر مجموعه Eبسته، سپس مکمل آن SEمجموعه باز

مثال 3.3 . E=، C R E =(- ¥, 2)È (5,+¥ ).

قضیه 3.6 . اگر مجموعه Eباز، سپس مکمل آن SEمجموعه بسته

مثال 3.4 . E=(2,5)، C R E =(-¥, 2]È[ 5, +¥ ).

اثبات.

1) در واقع، اگر نکته آمتعلق به اتحاد مجموعه‌های باز است، پس حداقل به یکی از این مجموعه‌ها تعلق دارد که طبق شرایط قضیه، باز است. این بدان معنی است که به یک محله خاص O(a) نقطه تعلق دارد آ، اما پس از آن این محله نیز متعلق به اتحادیه همه مجموعه های باز است. بنابراین، نکته آنقطه اتحاد داخلی است. زیرا آیک نقطه اتحاد دلخواه است، پس فقط از نقاط داخلی تشکیل شده است، و بنابراین، طبق تعریف، یک مجموعه باز است.

2) اکنون اجازه دهید ایکس- تقاطع تعداد محدودی از مجموعه های باز. اگر آیک نقطه تنظیم است ایکس، سپس به هر یک از مجموعه های باز تعلق دارد و بنابراین یک نقطه داخلی هر یک از مجموعه های باز است. به عبارت دیگر، فواصل زمانی وجود دارد که به طور کامل در مجموعه ها وجود دارد. اجازه دهید با کوچکترین اعداد نشان دهیم. سپس بازه به طور همزمان در تمام فواصل، یعنی. به طور کامل شامل خواهد شد ، و در،...، و در، i.e. . از اینجاو نتیجه می گیریم که هر نقطه یک نقطه داخلی مجموعه است ایکس، یعنی یک دسته از ایکسباز است.

از این قضیه به دست می آید که تقاطع تعداد محدودی از همسایگی های یک نقطه a دوباره همسایگی این نقطه است. توجه داشته باشید که محل تلاقی تعداد نامتناهی مجموعه باز همیشه یک مجموعه باز نیست. به عنوان مثال، تقاطع فواصل، ... مجموعه ای متشکل از یک نقطه a است که یک مجموعه باز نیست (چرا؟).

نقطه a را نقطه حدی از مجموعه X می نامند اگر در هر همسایگی سوراخ شده این نقطه حداقل یک نقطه از مجموعه X وجود داشته باشد.

بنابراین، نقطه نقطه حدی قطعه است , از آنجایی که در هر بازه سوراخ شده یک نقطه، یک نقطه متعلق به این بخش وجود دارد. به عنوان مثال، نقطه ای که نابرابری را برآورده می کند. و بدیهی است که بسیاری از این نکات وجود دارد.

اثبات اینکه هر نقطه از بخش [ 0, 1] است نهایینقطه این بخش به عبارت دیگر، بخش به طور کامل از نقاط حد آن تشکیل شده است. یک عبارت مشابه برای هر بخش صادق است. در اینجا توجه داشته باشید که تمام نقاط محدود مجموعه متعلق به این بخش است. همچنین بدیهی است که تمام نقاط قطعه، نقاط حدی برای بازه خواهند بود (0, 1 ) (اثباتش کن!). با این حال، در حال حاضر دو نقطه محدود وجود دارد 0 و 1به فاصله تعلق ندارند (0, 1). در این مثال ها می بینیم که

نقاط حد یک مجموعه ممکن است متعلق به آن باشد یا نباشد. می توان ثابت کرد که در هر محله سوراخ شده نقطه حدی a از مجموعه X بی نهایت نقاط مجموعه X وجود دارد.

مجموعه X در صورتی مجموعه بسته نامیده می شود که تمام نقاط حد خود را داشته باشد.

بنابراین، هر بخش یک مجموعه بسته است. فاصله (0, 1) یک مجموعه بسته نیست، زیرا دو نقطه حد آن به آن تعلق ندارد 0 و 1. مجموعه تمام اعداد گویا سبسته نیست، زیرا برخی از نقاط حد آن را شامل نمی شود. به طور خاص، عدد نقطه حدی مجموعه است س(اثبات کن!) اما س.

از آنجایی که هر نقطه از مجموعه آرنقطه حد این مجموعه است و به آن تعلق دارد، پس R - مجموعه بسته.

هر مجموعه محدود بسته است،از آنجایی که مجموعه نقاط حد آن مجموعه خالی است Æ ، که متعلق به خود مجموعه است.

مجموعه های بسته را می توان محدود کرد، به عنوان مثال، بخش، و نامحدود، برای مثال، مجموعه اعداد واقعی R. True

طرح

1. فضای برداری .
2. نقطه داخلی یک مجموعه باز در فضا
3. ویژگی های مجموعه های باز
4. نقطه حد یک مجموعه مجموعه های بسته در فضا
5. ویژگی های مجموعه های بسته در فضا

1. فضای برداری . مفهوم متریک. خواص متریک

بگذار باشد. عناصر فضا بردار هستند، جایی که. دو عمل در فضا معرفی شده است: جمع بردارها و ضرب یک بردار در یک اسکالر که خصوصیات آنها در درس جبر و هندسه مورد بحث قرار گرفته است.

بیایید هنجار برداری را به عنوان یک تابع تعریف کنیم:

تابع هنجار برداری ویژگی های زیر را برآورده می کند:

تعریف 1. فاصلهدر فضای بین بردارها نامیده می شود

ویژگی های فاصله:

1. من اگر و فقط اگر;

تعریف 2. بگذار باشد. یک توپ باز با شعاع در مرکز یک نقطه (نشان داده شده) مجموعه نقاطی است که

مثال. - این فاصله زمانی است (شکل 1).

مثال. (شکل 2).

تعریف 3. بگذار باشد. یک توپ بسته با شعاع با مرکز در یک نقطه (نشان داده شده) مجموعه ای از نقاط است به طوری که

تعریف 4. نقطه ای را نقطه داخلی این مجموعه می نامند اگر یک توپ باز وجود داشته باشد که به طور کامل در مجموعه وجود داشته باشد.

تعریف 5. یک مجموعه در صورتی مجموعه باز نامیده می شود که هر یک از نقاط آن یک نقطه داخلی باشد.

مثال. مجموعه خالی و مجموعه مجموعه های باز هستند.

مثال. ثابت کنید که یک مجموعه باز است (شکل 3).

آن را بگیریم. این به آن معنا است. بیایید نشان دهیم یک توپ باز را در نظر بگیرید. این را ثابت کنیم. برای انجام این کار، اجازه دهید نشان دهیم که به طور همزمان به چه چیزی تعلق دارد:

بنابراین، و این بدان معنی است که.

تعریف 6. متوازی الاضلاع باز مجموعه ای از نقاط است که نابرابری های زیر برای آنها برقرار است:

ورزش. نشان دهید که یک متوازی الاضلاع باز یک مجموعه باز است.

قضیه 1. محل تقاطع هر تعداد محدودی از مجموعه های باز یک مجموعه باز است.

اثبات. اجازه دهید مجموعه باز باشد، . اجازه دهید نشان دهیم که یک مجموعه باز است. برای انجام این کار، بیایید بگیریم و نشان دهیم که این نقطه درونی است:

از آنجایی که هر ست باز است، یک توپ باز برای وجود دارد. بیایید نشان دهیم سپس

بنابراین، برای این مجموعه داخلی است و خود مجموعه باز است.

اظهار نظر. محل تقاطع بی نهایت مجموعه باز ممکن است یک مجموعه باز نباشد.

مثال. اجازه دهید یک مجموعه بی نهایت از مجموعه های باز را برای آنها در نظر بگیریم. مجموعه ای که حاوی یک نقطه است باز نیست.

قضیه 2. اتحاد هر تعداد مجموعه باز یک مجموعه باز است.

اثبات. اجازه دهید مجموعه ای از شاخص ها باشد. بگذارید مجموعه برای باز باشد. در نظر بگیریم. اجازه دهید نشان دهیم که باز است. برای انجام این کار، بیایید بگیریم و نشان دهیم که این نقطه درونی است:

از آنجا که یک مجموعه باز است، پس، و این به این معنی است که یک مجموعه باز است.

یکی از وظایف اصلی تئوری مجموعه های نقطه، بررسی خواص انواع مجموعه نقطه است. بیایید با استفاده از دو مثال با این نظریه آشنا شویم و ویژگی های مجموعه های به اصطلاح بسته و باز را بررسی کنیم.

مجموعه نامیده می شود بسته ، اگر شامل تمام نقاط حد خود باشد. اگر مجموعه ای یک نقطه حدی واحد نداشته باشد، بسته نیز در نظر گرفته می شود. یک مجموعه بسته علاوه بر نقاط حدی خود می تواند حاوی نقاط ایزوله نیز باشد. مجموعه نامیده می شود باز کن ، اگر هر یک از نقاط آن برای آن داخلی باشد.

بدهیم نمونه هایی از مجموعه های بسته و باز .

هر بخش یک مجموعه بسته است و هر بازه (a, b) یک مجموعه باز است. نیم فواصل نامناسب و بسته، و فواصل نامناسب و باز کن. کل خط هم یک مجموعه بسته و هم باز است. راحت است که مجموعه خالی را همزمان بسته و باز در نظر بگیرید. هر مجموعه محدودی از نقاط روی یک خط بسته است، زیرا هیچ نقطه حدی ندارد.

مجموعه ای متشکل از نکات:

بسته این مجموعه دارای یک نقطه حد منحصر به فرد x=0 است که متعلق به مجموعه است.

وظیفه اصلی این است که بفهمیم یک مجموعه بسته یا باز دلخواه چگونه ساختار یافته است. برای این کار به تعدادی واقعیت کمکی نیاز خواهیم داشت که بدون اثبات آنها را می پذیریم.

• 1. محل تقاطع هر تعداد مجموعه بسته بسته است.
• 2. مجموع هر تعداد مجموعه باز یک مجموعه باز است.
• 3. اگر یک مجموعه بسته در بالا محصور شود، آنگاه دارای supremum است. به طور مشابه، اگر یک مجموعه بسته در زیر محدود شود، آنگاه حاوی infimum خود است.

فرض کنید E یک مجموعه دلخواه از نقاط روی یک خط باشد. اجازه دهید مکمل مجموعه را E بنامیم و با CE مجموعه تمام نقاط روی خط را که به مجموعه E تعلق ندارند نشان دهیم. واضح است که اگر x یک نقطه خارجی برای E باشد، آنگاه یک نقطه داخلی برای E است. مجموعه CE و بالعکس.

4. اگر یک مجموعه F بسته باشد، مکمل آن CF باز است و بالعکس.

گزاره 4 نشان می دهد که ارتباط بسیار نزدیکی بین مجموعه های بسته و باز وجود دارد: برخی مکمل های دیگر هستند. به همین دلیل، مطالعه فقط مجموعه های بسته یا فقط باز کافی است. دانستن ویژگی‌های مجموعه‌های یک نوع به شما این امکان را می‌دهد که فوراً ویژگی‌های مجموعه‌های نوع دیگر را دریابید. به عنوان مثال، هر مجموعه باز با حذف مقداری مجموعه بسته از یک خط به دست می آید.

بیایید شروع به مطالعه خواص مجموعه های بسته کنیم. بیایید یک تعریف را معرفی کنیم. فرض کنید F یک مجموعه بسته باشد. بازه ای (a, b) که این ویژگی را داشته باشد که هیچ یک از نقاط آن متعلق به مجموعه F نباشد، اما نقاط a و b متعلق به F باشد، فاصله مجاور مجموعه F نامیده می شود.

همچنین فواصل نامناسب را در بین فواصل مجاور قرار می دهیم، یا اگر نقطه a یا نقطه b متعلق به مجموعه F باشد و خود فواصل با F تلاقی نداشته باشند. اجازه دهید نشان دهیم که اگر یک نقطه x متعلق به یک مجموعه بسته F نباشد، به یکی از فواصل مجاور آن تعلق دارد.

اجازه دهید با بخشی از مجموعه F که در سمت راست نقطه x قرار دارد نشان دهیم. از آنجایی که نقطه x خود به مجموعه F تعلق ندارد، می توان آن را به صورت تقاطع نشان داد:

هر یک از مجموعه ها F و بسته است. بنابراین، با گزاره 1، مجموعه بسته می شود. اگر مجموعه خالی باشد، کل نیم فاصله به مجموعه F تعلق ندارد. اکنون فرض می کنیم که مجموعه خالی نیست. از آنجایی که این مجموعه کاملاً در یک نیم فاصله قرار دارد، در زیر محدود شده است. اجازه دهید کران پایین آن را با b نشان دهیم. با توجه به گزاره 3 که به معنای. بعلاوه، از آنجایی که b پایین مجموعه است، نیمه بازه (x, b) که در سمت چپ نقطه b قرار دارد شامل نقاط مجموعه نیست و بنابراین شامل نقاط مجموعه F نمی شود. ما یک نیم بازه (x, b) ساخته ایم که حاوی نقاط مجموعه F نیست، و هر یک یا نقطه b متعلق به مجموعه F است. به همین ترتیب، یک نیم فاصله (a, x) ساخته شده است که حاوی نقاطی نیست. از مجموعه F، و یا یا. اکنون مشخص است که بازه (a, b) حاوی نقطه x است و یک فاصله مجاور از مجموعه F است. به راحتی می توان فهمید که اگر و دو بازه مجاور مجموعه F باشند، این فواصل یا منطبق هستند یا انجام می دهند. قطع نمی شود

از موارد قبلی چنین استنباط می شود که هر مجموعه بسته روی یک خط با حذف تعداد معینی از بازه ها از خط به دست می آید، یعنی فواصل مجاور مجموعه F. از آنجایی که هر بازه حاوی حداقل یک نقطه گویا است، و مجموعه ای قابل شمارش وجود دارد. تمام نقاط منطقی روی خط، آسان است مطمئن شوید که تعداد تمام فواصل مجاور حداکثر قابل شمارش است. از اینجا به نتیجه نهایی می رسیم. هر مجموعه بسته روی یک خط با حذف حداکثر یک مجموعه قابل شمارش از فواصل غیرمتناسب از خط به دست می آید.

به موجب گزاره 4، بلافاصله نتیجه می شود که هر مجموعه باز روی یک خط چیزی بیش از مجموع قابل شمارش فواصل غیرمتناسب نیست. به موجب گزاره‌های 1 و 2، همچنین واضح است که هر مجموعه‌ای که همانطور که در بالا نشان داده شد، در واقع بسته (باز) است.

همانطور که از مثال زیر مشاهده می شود، مجموعه های بسته می توانند ساختار بسیار پیچیده ای داشته باشند.

§6. قضایای مجموعه های باز و بسته

قضیه 1. اتحاد هر تعداد مجموعه باز یک مجموعه باز است.

اجازه دهید جی ک - مجموعه های باز

اجازه دهید ثابت کنیم که یک مجموعه باز است.

هر نکته ای را در نظر بگیرید ایکس O  جی. با تعریف اتحاد مجموعه ها، نقطه ایکس Oحداقل به یکی از مجموعه ها تعلق خواهد داشت جی ک . زیرا جی کمجموعه های باز هستند، پس وجود دارد  - همسایگی یک نقطه ایکس O، که کاملاً متعلق به مجموعه است جی ک :

هر نکته ای را فهمیدم ایکس O  جی - داخلی، که به این معنی است جی- مجموعه باز 

قضیه 2 . محل تقاطع تعداد محدودی از مجموعه های غیر خالی باز یک مجموعه باز است.

اجازه دهید جی ک ( ک = 1,2, …,n) مجموعه های باز هستند.

این را ثابت کنیم
- مجموعه باز

هر نکته ای را در نظر بگیرید ایکس O  جی. با تعریف تقاطع مجموعه ها ایکس Oمتعلق به هر یک از مجموعه ها است جی ک. زیرا مجموعه ها جی کباز، سپس در هر مجموعه جی کوجود دارد  ک- همسایگی یک نقطه ایکس O : U( ایکس o ,  ک)  جی ک. تعداد زیادی اعداد { 1 ,  2 ,…,  n ) متناهی است، بنابراین   = دقیقه { 1 ,  2 ,…,  n). سپس  - همسایگی یک نقطه ایکس O متعلق به همه است  ک- همسایگی نقطه ایکس O :

گرفتش ایکس O– نقطه داخلی مجموعه جی، که به این معنی است جی- مجموعه باز 

یادداشت 1.محل تقاطع بی نهایت مجموعه باز ممکن است یک مجموعه باز نباشد.

مثال 1 . اجازه دهید در فضا آر جایی که ک= 1,2,…,n, ….

قضیه 3 . محل تقاطع بی نهایت مجموعه غیر خالی بسته یک مجموعه بسته است.

اجازه دهید اف ک- مجموعه های بسته

اجازه دهید ثابت کنیم که مجموعه ها
بسته، یعنی این شامل تمام نقاط حد خود است.

قضیه 4. اتحاد تعداد محدودی از مجموعه های غیر خالی بسته یک مجموعه بسته است.

بگذارید مجموعه ها اف ک- بسته

اجازه دهید ثابت کنیم که مجموعه
بسته، یعنی اگر ایکس O اف، آن ایکس O  اف.

تبصره 2.اتحاد تعداد نامتناهی مجموعه بسته می تواند یک مجموعه باز باشد.

مثال 2 . در فضای آر: اف ک =

قضیه 5 . اگر مجموعه Eبسته، سپس مکمل آن مجموعه است X: C ایکس E=CE -مجموعه باز

مثال .3 . E=, سی آر E =

قضیه 6 . اگر مجموعه Eباز شود، سپس مکمل آن مجموعه است X: C ایکس E=CE -مجموعه بسته

مثال 4 . E=(2,5), سی آر E =

§7. دنباله ای از نقاط در فضای متریک

تعریف 1 . دنباله ای از نقاط در یک فضای متریک (ایکس،  ) نقشه برداری نامیده می شود fمجموعه ای از اعداد طبیعی نبه انبوه ایکس: f: نایکس.

ارزش این نگاشت در نقطه n  ن تماس گرفت n-عضو دنباله نقاط در فضای متریک است و با نشان داده می شود ایکس n = f(n). دنباله را مشخص می کنیم (ایکس n) یا ( ایکس 1 ،ایکس 2 ،…، ایکس n … ).

مثال 1. در فضای آر 2 : ایکس n = (1 n, n+ 1/ n));

مثال 2 . در فضای با: (ایکس n = (1/ nx + n 2 ایکس)) کجا  آ,b حاوی 0 نیست.

تعریف 2 . اجازه دهید ( ایکس nایکس، ), (ک 1 , ک 2 ,…, ک n ,… ) دنباله فزاینده ای از اعداد طبیعی است. سپس دنباله (ایکس kn) نامیده میشود دنباله بعدی دنباله (ایکس n).

مثال 3. دنباله (1 / n 2 ) – دنباله ای از دنباله (1 / n).

تعریف 3 . اجازه دهید ( ایکس n) ایکس، ), دنباله (ایکس n) نامیده میشود محدود ، اگر یک توپ بسته با مرکز وجود داشته باشد آو یک شعاع نهایی R، که شامل تمام اعضای دنباله است، یعنی.

.

یادداشت 1 . مفهوم توالی یکنواخت را نمی توان در همه فضاهای متریک معرفی کرد.

تعریف 4. اجازه دهید ( ایکس n) - دنباله ای از نقاط فضای متریک ( ایکس، ). نقطه آ ایکستماس گرفت محدودیت دنباله (ایکس n) اگر:

  (    ن   n   ( , n  ن   ایکس n , آ  

یا، که همان چیزی است، یک دنباله اعداد (  ایکس n , آ)) - بی نهایت کوچک (به 0 تمایل دارد)، با n ، آن ها

و abazanaetstsa

توسط متریک  یا
، در n .

اگر دنباله ( ایکس n) حد محدود دارد سپس همگرا و در غیر این صورت واگرا می گویند.

اگر ( ایکس n) – دنباله ای از نقاط فضای متریک ( ایکس، ) به یک نقطه همگرا می شود آ ایکس، آن آ- نقطه حدی دنباله ( ایکس n).

برعکس همیشه صادق نیست.

تبصره 2 . توالی یکسان در فضاهای متریک مختلف می تواند همگرا و واگرا باشد

مثال 4. دنباله (1 / n) در فضای R همگرا می شود، اما در فضا واگرا می شود ( ایکس, ), جایی که
 (ایکس, y)=  ایکس در، زیرا 0
.

قضایا برای دنباله های همگرا صدق می کنند.

قضیه 1. اگر ( ایکس n) – دنباله همگرا فضای متریک ( ایکس، ) پس حد آن منحصر به فرد است.

  ایکس n ،آ 0 و
  ایکس n ، ب 0.

با توجه به بدیهیات متریک 0   آ, ب    ایکس n , آ +  ایکس n , ب. ما به مرز عبور می کنیم، در n ، ما گرفتیم  آ, ب = 0  آ= ب. 

قضیه 2 . اگر ( ایکس n) – دنباله ای از نقاط فضای متریک ( ایکس، ) – همگرا، سپس محدود می شود.

اجازه دهید
.

قضیه 3 . اگر ( ایکس n) – دنباله ای از نقاط فضای متریک ( ایکس، ) به یک نقطه همگرا می شود آ ایکس، سپس هر یک از دنباله های آن به همگرا می شود آ.

اجازه دهید
- هر دنباله ای از دنباله (ایکس n). با شرط. این به آن معنا است:      n    ایکس n ،آ   .

زیرا ک n  n، سپس برای همه n> ن درست ک n > ن و بنابراین 
.

بنابراین ما این را ثابت کرده ایم     n   ، این به آن معنا است
.

§8. خواص دنباله های همگرا در برخی

فضاهای متریک

قضیه 1 (در مورد همگرایی مختصات یک دنباله در pr.آر متر ). به منظور دنباله ای از نقاط در یک فضای متریک آر متر

(ایکس n = (ایکس 1 ( n ) ،ایکس 2 ( n ) ،…، ایکس متر ( n ) ) به یک نقطه همگرا شد آ = (آ 1 ،آ 2 ،…، آ متر) این فضا برای دنباله های عددی لازم و کافی است ( ایکس 1 ( n ) ), (ایکس 2 ( n ) ),…, (ایکس متر ( n ) ) (مختصات مربوطه) مطابق با اعداد تمایل داشت آ 1 ،آ 2 ،…، آ متر ، یعنی

,
,...,
(1)

اگر برابری های (1) برآورده شوند، می گوییم دنباله ( ایکس n) به یک نقطه همگرا می شود آهماهنگ کردن با مختصات

1. اجازه دهید در m.pr. آر متر . (2)

اجازه دهید ثابت کنیم که برابری های (1) برآورده می شوند.

به موجب تساوی (2) (با تعریف حد یک دنباله) در m.p. آر مترخواهد داشت:

  n    ایکس n ،آ ,

جایی که  - متریک فضای متریک آر متر :

x، y آر متر .

2. اجازه دهید برابری های (1) برآورده شود.

اجازه دهید که (2) را در فضای متریک ثابت کنیم آر متر .

اجازه دهید  - هر عدد مثبتی عدد محسوب می شود
. سپس

مثال 1 . حد را پیدا کنید آ = (آ 1 , آ 2 ) دنباله ها

در فضای آر 2 .

بدین ترتیب، = (1/4;3).

قضیه 2 (Bolzana-Weierstrasse در m.pr.آر متر ). از هر توالی محدودی از فضا آر متریک دنباله همگرا قابل شناسایی است.

یک مورد خاص از این قضیه برای فضا آر 1 در سال اول ثابت شد.

قضیه 3 . به منظور دنباله ( ایکس n) نقاط m.pr. با [ آ , ب] با متریک چبیشف به عنصر همگرا شده است ایکساین و غیره برای توالی عملکردی لازم و کافی است ( ایکس n) به طور یکنواخت به ایکسبر [ آ, ب].

اجازه دهید آن را با استفاده از معیار همگرایی یکنواخت ثابت کنیم.

مشخص است که توالی عملکردی ( ایکس n) به طور یکنواخت به تابع حد همگرا می شود ایکسآن وقت و فقط وقتی

با در نظر گرفتن تعریف متریک در m.pr. با[آ, ب] برابری می گیریم

(به تعریف 4 §7 مراجعه کنید)
توسط متریک  در m.pr. با[آ, ب]. 

مثال 2. ایکس n (تی) = تی n  تی ;   n ن. مشخص است که در ;/2 دنباله تابعی ایکس n (تی) = تی nبه طور یکنواخت به تابع حد همگرا می شود ایکس (تی) = 0. بنابراین  تی دنباله ; ( ایکس n) به تابع همگرا می شود x = 0 در m.pr. با.

قضیه 4. اگر آ– نقطه حدی مجموعه Eفضای متریک ( ایکس,  ، سپس یک دنباله وجود دارد ( ایکس n), که اعضای آن تعلق دارند Eو برابر نیستند آ، و ( ایکس n), همگرا می شود آدر این فضای متریک

اثبات شبیه اثبات در فضا است آر.

یادداشت 1. از آنجایی که هر هنجاری یک متریک را مشخص می کند،

 o ( ایکس, y) =

سپس در فضای نرمال شده آهمچنین می توان حد یک دنباله از عناصر یک فضای هنجاری را تعریف کرد.

تبصره 2. از آنجایی که یک فضای پیش از هیلبرت یک فضای هنجاردار با هنجار است
، سپس در یک فضای پیش هیلبرت می توان حد توالی عناصر یک فضای پیش هیلبرت را نیز تعریف کرد.

§9. فضاهای متریک کامل

تعریف 1 . دنباله ( ایکس n) فضای متریک ( ایکس، ) اگر اساسی نامیده می شود

یک مثال از یک دنباله اساسی هر دنباله همگرا از نقاط در یک فضای متریک است.

در فضای آرهر دنباله اساسی همگرا است. اما برای هر m.pr. نه هر دنباله اساسی از یک فضای متریک ( ایکس،  ) در این فضا همگرا می شود.

مثال 1 . در m.pr. ایکس = (س;  =  ایکس در) دنباله بنیادی است، اما از سال اول مشخص می شود که اما ه ایکس(ه من ).

تعریف 2 . فضای متریک نامیده می شود فضای متریک کامل ، اگر هر دنباله اساسی از نقاط این فضا در آن همگرا شود.

مثال 2 . فضای متریک آریک فضای متریک کامل است، زیرا هر دنباله اساسی از فضا به عددی همگرا می شود آر. این از معیار کوشی ناشی می شود (به دوره اول مراجعه کنید).

مثال 3 . اجازه دهید آن فضا را ثابت کنیم آر متر- فضای متریک کامل

به دنباله اجازه دهید( ایکس n= ایکس 1 (n) , ایکس 2 (n) ,…, ایکسمتر ( n)) (1)

هر توالی اساسی از فضا آر متر . اجازه دهید نشان دهیم که این دنباله همگرا است و حد آن به فضا تعلق دارد آر متر .

در مورد تعریف دنباله اساسی و تعریف متریک در فضا آر متر

0 N( ) ن  p,n > N  (ایکس پ ،ایکس n) 

با توجه به اثبات قضیه 1 §8، بنابراین، ماهیت بنیادی دنباله های اعداد ( ایکس 1 ( n ) ), (ایکس 2 ( n ) ),…, (ایکس متر ( n ) ، و از این رو همگرایی آنها (بر اساس معیار کوشی).

اجازه دهید

نکته را در نظر بگیرید a =(آ 1 ، آ 2 ، …، آ متر). زیرا آ 1 ، آ 2 ، …، آ متر  آر, که آ آر متر. با قضیه 1 §8 به دست می آوریم که در m.pr. آر متر دنباله ( ایکس n) همگرا می شود آ آر متر . این یعنی آن فضا آر متر فضای متریک کامل 

مثال 4 . اجازه دهید ثابت کنیم که فضای متریک با[آ, ب] کامل است.

اجازه دهید ( ایکس n) - هر دنباله اساسی در m.p. با[آ, ب]، شرایط آن در [ آ, ب] کارکرد.

اجازه دهید ثابت کنیم که دنباله ( ایکس n) در فضای متریک همگرا می شود با [ آ , ب] . ابتدا نشان می دهیم که به تابع حد همگرا می شود ایکسدر بخش [ آ, ب].

با تعریف دنباله بنیادی

این به آن معنا است  تی [آ, ب] (ثابت تی) اساسی دنباله اعداد است ( ایکس n (تی) ). این بدان معنی است که یک حد دارد که ما با آن نشان می دهیم
برای هر ثابت تی [آ, ب].

اجازه دهید نشان دهیم که تابع حد است ایکس(تی) پیوسته در [ آ, ب]. برای انجام این کار، در نابرابری (2) به حد حد در می رویم متر . ما گرفتیم

 ایکس (تی) ایکس n (تی)   n>N تی [الف، ب].

بنابراین، ما این را ثابت کرده ایم

0 نن  m,n > N ایکس (تی) ایکس n (تی)   تی [الف، ب].

این بدان معنی است که دنباله ( ایکس n) به طور یکنواخت به تابع همگرا می شود ایکسبر [ آ, ب]. زیرا همه اعضای دنباله ( ایکس n) پیوسته در [ آ, ب] تابع، پس تابع حد نیز روی این قطعه پیوسته است، یعنی عنصری از فضای متریک است با [ آ , ب]. توسط قضیه 2 §8 در این فضا دنباله ( ایکس n) همگرا می شود ایکس. این یعنی فضا با [ آ , ب] – فضای متریک کامل. 

تعریف 3. فضای هنجاری کامل نامیده می شود بانوهاو هفتم فضا متر .

فضاهای بانوهاویی فضاهای زیر هستند:

آر پبا استانداردها
,
;

ل 2 با هنجار برداری ایکس = (ایکس n) = (ایکس 1 , ایکس 2 , … )

سی[ آ, ب] با هنجار توابع ایکس(تی)
.

و فضا سی 1 [آ, ب] با هنجار بانوچ نیست.

تعریف 2 . یک فضای کامل قبل از هیلبرت با توجه به هنجار (2) §3 نامیده می شود فضای هیلبرت .

نمونه هایی از فضاهای هیلبرت، فضاهای فهرست شده از نمونه های §4 هستند. فضای پیش از هیلبرت از مثال 3 از §4 با توجه به هنجار (2) کامل نیست و بنابراین هیلبرت نیست.

انفورماتیک، 4 سال، 1-2 ماژول) تعریفمتریکفضا(m.p.). مثال ها. ست های باز و بسته در m.p. همگرایی ... نگاشتهای خطی نرمال شده فضاها. مثال ها. عادی شده است فضانگاشت های خطی قضیه...

سخنرانی شماره 3 فضاهای متریک مجموعه های باز و بسته

سخنرانی

... فضاها. تعریف 4. متریکفضااگر دنباله ای بنیادی در آن همگرا شود (به عنصری از این، کامل می گویند فضا!). مثال ها. 9) ب فضا ...

برای مطالعه فضاهای متریک

سند

چیزی که به دست می آوریم معادل است تعریفمتریکفضا. 4. ثابت کنید که برای یک دلخواه متریکفضاáX، rñ معادل عبارت... نگاشت های پیوسته هستند متریکفضاهامداوم. اشاره به مثال، چی...