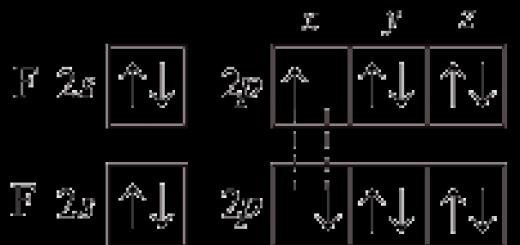
مبانی نظریه ماکسول برای میدان الکترومغناطیسی

میدان الکتریکی گرداب

از قانون فارادی ξ=dФ/dtبه دنبال آن است هرتغییر در شار القایی مغناطیسی مرتبط با مدار منجر به ظهور یک نیروی القایی الکتروموتور می شود و در نتیجه یک جریان القایی ظاهر می شود. در نتیجه، وقوع emf. القای الکترومغناطیسی در یک مدار ثابت واقع در یک میدان مغناطیسی متناوب نیز امکان پذیر است. با این حال، e.m.f. در هر مدار فقط زمانی اتفاق می افتد که نیروهای خارجی بر حامل های جریان در آن - نیروهای با منشاء غیرالکترواستاتیکی (نگاه کنید به § 97) وارد می شوند. بنابراین، این سؤال در مورد ماهیت نیروهای خارجی در این مورد مطرح می شود.

تجربه نشان می دهد که این نیروهای خارجی با فرآیندهای حرارتی یا شیمیایی در مدار مرتبط نیستند. وقوع آنها نیز نمی تواند توسط نیروهای لورنتز توضیح داده شود، زیرا آنها بر روی بارهای ثابت عمل نمی کنند. ماکسول فرض کرد که هر میدان مغناطیسی متناوب، یک میدان الکتریکی در فضای اطراف را تحریک می کند، که

و علت وقوع جریان القایی در مدار است. با توجه به ایده های ماکسول، مداری که در آن emf ظاهر می شود نقش ثانویه ایفا می کند، و تنها نوعی "دستگاه" است که این میدان را تشخیص می دهد.

معادله اولماکسول بیان می کند که تغییرات میدان الکتریکی یک میدان مغناطیسی گردابی ایجاد می کند.

معادله دومقانون ماکسول بیان می کند القای الکترومغناطیسیفارادی: emf در هر حلقه بسته برابر است با نرخ تغییر (یعنی مشتق زمانی) شار مغناطیسی. اما EMF برابر با مولفه مماسی بردار شدت میدان الکتریکی E است که در طول مدار ضرب می شود. برای رفتن به روتور، مانند معادله اول ماکسول، کافی است emf را بر مساحت کانتور تقسیم کرده و دومی را روی صفر هدایت کنید، یعنی یک کانتور کوچک که نقطه در فضای مورد نظر را پوشش می دهد (شکل) 9، ج). سپس در سمت راست معادله دیگر یک شار وجود نخواهد داشت، بلکه یک القای مغناطیسی وجود خواهد داشت، زیرا شار برابر است با القایی ضرب شده در مساحت مدار.
بنابراین، ما دریافت می کنیم: rotE = - dB/dt.
بنابراین، میدان الکتریکی گرداب با تغییرات میدان مغناطیسی ایجاد می‌شود که در شکل نشان داده شده است. 9,c و با فرمول ارائه شده نشان داده می شود.
معادلات سوم و چهارمماکسول با اتهامات و زمینه های تولید شده توسط آنها سروکار دارد. آنها بر اساس قضیه گاوس هستند، که بیان می کند که شار بردار القای الکتریکی از طریق هر سطح بسته برابر با بار داخل آن سطح است.

کل علم مبتنی بر معادلات ماکسول - الکترودینامیک است که حل بسیاری از مسائل کاربردی مفید را با استفاده از روش‌های ریاضی دقیق ممکن می‌سازد. برای مثال، می توان میدان تابش آنتن های مختلف را هم در فضای آزاد و هم در نزدیکی سطح زمین یا نزدیک بدن هر یک محاسبه کرد. هواپیمامثلاً یک هواپیما یا یک موشک. الکترودینامیک امکان محاسبه طراحی موجبرها و تشدید کننده‌های حفره را فراهم می‌کند - دستگاه‌هایی که در فرکانس‌های بسیار بالا در محدوده‌های موج سانتی‌متری و میلی‌متری استفاده می‌شوند، جایی که خطوط انتقال معمولی و مدارهای نوسانی دیگر مناسب نیستند. بدون الکترودینامیک، توسعه رادار، ارتباطات رادیویی فضایی، فناوری آنتن و بسیاری دیگر از حوزه‌های مهندسی رادیویی مدرن غیرممکن خواهد بود.

جریان بایاس

DISPLACEMENT CURRENT، مقداری متناسب با سرعت تغییر میدان الکتریکی متناوب در دی الکتریک یا خلاء. نام "جریان" به این دلیل است که جریان جابجایی، مانند جریان هدایت، یک میدان مغناطیسی ایجاد می کند.

هنگام ساخت نظریه میدان الکترومغناطیسی، جی سی ماکسول فرضیه ای را مطرح کرد (که بعداً به طور تجربی تأیید شد) که میدان مغناطیسی نه تنها با حرکت بارها (جریان رسانش یا صرفاً جریان)، بلکه با هر تغییر در زمان ایجاد می شود. میدان الکتریکی

مفهوم جریان جابجایی توسط ماکسول برای ایجاد روابط کمی بین تغییر معرفی شد میدان الکتریکیو میدان مغناطیسی ناشی از آن

طبق نظریه ماکسول، در یک مدار جریان متناوب حاوی یک خازن، میدان الکتریکی متناوب در خازن در هر لحظه از زمان، همان میدان مغناطیسی را ایجاد می کند که توسط جریان (به نام جریان جابجایی) ایجاد می شود، اگر بین صفحات جریان پیدا کند. خازن از این تعریف چنین بر می آید که J cm = J(یعنی مقادیر عددیچگالی جریان هدایت و چگالی جریان جابجایی برابر است)، و بنابراین، خطوط چگالی جریان رسانایی در داخل هادی به طور مداوم به خطوط چگالی جریان جابه‌جایی بین صفحات خازن تبدیل می‌شوند. چگالی جریان بایاس j سانتی مترمیزان تغییر القای الکتریکی را مشخص می کند دیبه موقع:

J cm = + ?D/?t.

جریان جابجایی گرمای اصلی خود را ژول تولید نمی کند دارایی فیزیکی- قابلیت ایجاد میدان مغناطیسی در فضای اطراف.

یک میدان مغناطیسی گردابی توسط جریان کل ایجاد می شود که چگالی آن برابر است j، برابر است با مجموع چگالی جریان هدایت و جریان جابجایی؟D/?t. به همین دلیل نام جریان برای کمیت ?D/?t معرفی شد.

نوسان ساز هارمونیکسیستمی است که در نوسان است که با بیانی به شکل d 2 s/dt 2 + ω 0 2 s = 0 یا

که در آن دو نقطه بالا به معنای تمایز مضاعف در زمان است. نوسانات نوسانگر هارمونیک وجود دارد مثال مهمحرکت تناوبی و به عنوان یک مدل دقیق یا تقریبی در بسیاری از مسائل کلاسیک و فیزیک کوانتوم. نمونه هایی از نوسان ساز هارمونیک شامل فنر، فیزیکی و آونگ ریاضیو یک مدار نوسانی (برای جریانها و ولتاژهای آنقدر کوچک که عناصر مدار را می توان خطی در نظر گرفت).

ارتعاشات هارمونیک

همراه با حرکات انتقالی و چرخشی اجسام در مکانیک، حرکات نوسانی. ارتعاشات مکانیکی نامیده می شود حرکات اجسامی که دقیقاً (یا تقریباً) در فواصل زمانی مساوی تکرار می شوند. قانون حرکت یک جسم در حال نوسان با استفاده از یک معین مشخص می شود تابع دوره ایزمان ایکس = f (تی). تصویر گرافیکیاین تابع یک نمایش بصری از روند فرآیند نوسانی در طول زمان می دهد.

نمونه هایی از سیستم های نوسانی ساده، بار روی فنر یا آونگ ریاضی هستند (شکل 2.1.1).

ارتعاشات مکانیکی، مانند فرآیندهای نوسانی با هر ماهیت فیزیکی دیگری، می توانند باشند رایگانو مجبور شد. ارتعاشات رایگان تحت تأثیر متعهد می شوند نیروهای داخلیسیستم پس از خروج سیستم از حالت تعادل. نوسانات وزنه روی فنر یا نوسانات آونگ نوسانات آزاد هستند. ارتعاشات تحت تأثیر رخ می دهد خارجینیروهای متغییر دوره ای نامیده می شوند مجبور شد ساده ترین نوع فرآیند نوسانی ساده است ارتعاشات هارمونیک ، که با معادله توصیف می شوند

فرکانس نوسان fنشان می دهد که در 1 ثانیه چند نوسان رخ می دهد. واحد فرکانس - هرتز(هرتز). فرکانس نوسان fمربوط به فرکانس چرخه ای ω و دوره نوسان است تینسبت ها:

وابستگی کمیت نوسان را نشان می دهد اساز زمان تی; این معادله نوسانات هارمونیک آزاد به صورت صریح است. با این حال، معمولا معادله ارتعاش به عنوان یک نمایش متفاوت از این معادله، به شکل دیفرانسیل درک می شود. برای قطعیت، معادله (1) را به شکل در نظر می گیریم

بیایید آن را دو بار از نظر زمان متمایز کنیم:

مشاهده می شود که رابطه زیر برقرار است:

که معادله نوسانات هارمونیک آزاد (به صورت دیفرانسیل) نامیده می شود. معادله (1) حل معادله دیفرانسیل (2) است. از آنجایی که معادله (2) است معادله دیفرانسیلمرتبه دوم، دو شرط اولیه برای به دست آوردن مورد نیاز است راه حل کامل(یعنی تعاریف ثابت های موجود در رابطه (1) آو j 0)؛ به عنوان مثال، موقعیت و سرعت سیستم نوسانی در تی = 0.

افزودن ارتعاشات هارمونیک هم جهت و هم فرکانس. می زند

بگذارید دو نوسان هارمونیک هم جهت و یک فرکانس وجود داشته باشد

معادله نوسان حاصل شکل خواهد داشت

اجازه دهید این را با اضافه کردن معادلات سیستم (4.1) تأیید کنیم.

بکار بردن قضیه مجموع کسینوس و تبدیل جبری:

می توان مقادیر A و φ0 را به گونه ای یافت که معادلات برآورده شوند

با در نظر گرفتن (4.3) به عنوان دو معادله با دو مجهول A و φ0، با مجذور کردن آنها و جمع آنها و سپس تقسیم دومی بر اولی آنها را پیدا می کنیم:

با جایگزینی (4.3) به (4.2)، دریافت می کنیم:

یا در نهایت با استفاده از قضیه مجموع کسینوس، داریم:

بدن شرکت کننده در دو ارتعاشات هارمونیکهمان جهت و فرکانس یکسان، همچنین یک نوسان هارمونیک را در همان جهت و با همان فرکانس نوسانات اضافه انجام می دهد. دامنه نوسان حاصل به اختلاف فاز (φ2-φ1) نوسانات هموار بستگی دارد.

بسته به اختلاف فاز (φ2-φ1):

1) (φ2-φ1) = ± 2mπ (m=0، 1، 2، …)، سپس A= A1+A2، یعنی دامنه نوسان حاصل A برابر است با مجموع دامنه های نوسانات اضافه شده.

2) (φ2-φ1) = ±(2m+1)π (m=0، 1، 2، ...)، سپس A= |A1-A2|، یعنی دامنه نوسان حاصل برابر با اختلاف است. در دامنه های نوسانات اضافه شده

تغییرات دوره ای در دامنه ارتعاشات که با اضافه شدن دو ارتعاش هارمونیک با فرکانس های مشابه رخ می دهد، ضرب نامیده می شود.

بگذارید دو نوسان از نظر فرکانس کمی متفاوت باشند. سپس دامنه نوسانات اضافه شده برابر با A و فرکانسها برابر با ω و ω+Δω است و Δω بسیار کمتر از ω است. نقطه شروع را طوری انتخاب می کنیم که فازهای اولیه هر دو نوسان برابر با صفر باشد:

بیایید سیستم را حل کنیم

راه حل سیستم:

نوسان حاصل را می توان به صورت هارمونیک با فرکانس ω، دامنه A در نظر گرفت که به صورت زیر تغییر می کند. قانون دوره ای:

فرکانس تغییر A دو برابر فرکانس تغییر کسینوس است. فرکانس ضربان برابر است با اختلاف فرکانس نوسانات اضافه شده: ωb = Δω

دوره ضرب و شتم:

تعیین فرکانس یک تن (صدایی با ارتفاع ضرب معین توسط مرجع و ارتعاشات اندازه گیری شده پرکاربردترین روش برای مقایسه مقدار اندازه گیری شده با مقدار مرجع است. روش بیت برای کوک آلات موسیقی، تجزیه و تحلیل شنوایی و غیره استفاده می شود. .

اطلاعات مربوطه.

نوسان هارمونیک پدیده ای از تغییر دوره ای از هر کمیت است که در آن وابستگی به آرگومان دارای ویژگی تابع سینوسی یا کسینوس است. به عنوان مثال، یک کمیت به طور هماهنگ نوسان می کند و در طول زمان به صورت زیر تغییر می کند:

که در آن x مقدار کمیت متغیر است، t زمان است، پارامترهای باقیمانده ثابت هستند: A دامنه نوسانات، ω فرکانس چرخه ای نوسانات است، - فاز کاملتردید - فاز اولیهتردید.

نوسان هارمونیک تعمیم یافته به شکل دیفرانسیل

(هر راه حل غیر بی اهمیت برای این معادله دیفرانسیل یک نوسان هارمونیک با فرکانس چرخه ای است)

انواع ارتعاشات

ارتعاشات آزاد تحت تأثیر نیروهای داخلی سیستم پس از خارج شدن سیستم از وضعیت تعادل خود رخ می دهد. برای هارمونیک بودن نوسانات آزاد، لازم است که سیستم نوسانی خطی باشد (که با معادلات حرکتی خطی توصیف می شود) و هیچ اتلاف انرژی در آن وجود نداشته باشد (این دومی باعث میرایی می شود).

ارتعاشات اجباری تحت تأثیر یک نیروی تناوبی خارجی رخ می دهد. برای هارمونیک بودن آنها کافی است که سیستم نوسانی خطی باشد (که با معادلات خطی حرکت توصیف می شود) و نیروی خارجیخود در طول زمان به عنوان یک نوسان هارمونیک تغییر کرد (یعنی به طوری که وابستگی زمانی این نیرو سینوسی بود).

معادله هارمونیک

معادله 1)

وابستگی مقدار نوسان S را به زمان t نشان می دهد. این معادله نوسانات هارمونیک آزاد به صورت صریح است. با این حال، معمولا معادله ارتعاش به عنوان یک نمایش متفاوت از این معادله، به شکل دیفرانسیل درک می شود. برای قطعیت، معادله (1) را به شکل در نظر می گیریم

بیایید آن را دو بار از نظر زمان متمایز کنیم:

مشاهده می شود که رابطه زیر برقرار است:

که معادله نوسانات هارمونیک آزاد (به صورت دیفرانسیل) نامیده می شود. معادله (1) حل معادله دیفرانسیل (2) است. از آنجایی که معادله (2) یک معادله دیفرانسیل مرتبه دوم است، برای به دست آوردن یک جواب کامل، دو شرط اولیه لازم است (یعنی تعیین ثابت های A و   موجود در رابطه (1). به عنوان مثال، موقعیت و سرعت سیستم نوسانی در t = 0.

آونگ ریاضی یک نوسان ساز است که یک سیستم مکانیکی متشکل از یک نقطه مادی است که روی یک رشته غیر قابل امتداد بی وزن یا روی یک میله بی وزن در میدان یکنواخت نیروهای گرانشی قرار دارد. دوره نوسانات طبیعی کوچک یک آونگ ریاضی به طول l که بدون حرکت در یک میدان گرانشی یکنواخت با شتاب سقوط آزاد g معلق است، برابر است با

و به دامنه و جرم آونگ بستگی ندارد.

آونگ فیزیکی یک نوسان ساز است که جسم جامدی است که در میدانی از هر نیرو نسبت به نقطه ای که مرکز جرم این جسم نیست، یا یک محور ثابت عمود بر جهت عمل نیروها و نه نوسان می کند. از مرکز جرم این جسم عبور می کند.

دارند بیان ریاضی. ویژگی های آنها با مجموعه ای از معادلات مثلثاتی مشخص می شود که پیچیدگی آنها با پیچیدگی خود فرآیند نوسانی، ویژگی های سیستم و محیطی که در آن رخ می دهند، یعنی عوامل خارجی موثر بر فرآیند نوسانی تعیین می شود.

به عنوان مثال، در مکانیک، یک نوسان هارمونیک حرکتی است که با:

شخصیت مستقیم؛

ناهمواری؛

حرکت یک جسم فیزیکی که بسته به زمان در امتداد یک مسیر سینوسی یا کسینوس رخ می دهد.

بر اساس این ویژگی ها، می توانیم معادله ای برای ارتعاشات هارمونیک ارائه دهیم که به شکل زیر است:

x = A cos ωt یا شکل x = A sin ωt، که x مقدار مختصات است، A مقدار دامنه ارتعاش، ω ضریب است.

این معادله ارتعاشات هارمونیک برای همه ارتعاشات هارمونیک که در سینماتیک و مکانیک مورد توجه قرار می گیرند، اساسی است.

نشانگر ωt که در این فرمول زیر علامت است تابع مثلثاتی، فاز نامیده می شود و محل نوسان را تعیین می کند نقطه مادیدر یک لحظه خاص در زمان در یک دامنه معین. هنگام در نظر گرفتن نوسانات چرخه ای، این نشانگر برابر با 2 لیتر است، مقدار را در چرخه زمانی نشان می دهد و با w نشان داده می شود. در این مورد، معادله نوسانات هارمونیک آن را به عنوان شاخصی از بزرگی فرکانس چرخه ای (دایره ای) در خود دارد.

معادله نوسانات هارمونیک که ما در نظر می گیریم، همانطور که قبلا ذکر شد، بسته به عوامل متعددی می تواند اشکال مختلفی داشته باشد. به عنوان مثال، در اینجا این گزینه است. برای در نظر گرفتن نوسانات هارمونیک آزاد، باید این واقعیت را در نظر گرفت که همه آنها با میرایی مشخص می شوند. در کشورهای مختلف، این پدیده به روش های مختلف خود را نشان می دهد: توقف یک جسم متحرک، توقف تشعشع در سیستم های الکتریکی. ساده ترین مثالی که کاهش پتانسیل نوسانی را نشان می دهد، تبدیل آن به انرژی حرارتی است.

معادله مورد بررسی به شکل: d²s/dt² + 2β x ds/dt + ω²s = 0 است. در این فرمول: s مقدار کمیت نوسانی است که ویژگی های یک سیستم خاص را مشخص می کند، β ثابتی است که میرایی را نشان می دهد. ضریب، ω فرکانس چرخه ای است.

استفاده از این فرمول به ما امکان می دهد به توضیحات نزدیک شویم فرآیندهای نوسانی V سیستم های خطیاز یک دیدگاه واحد و همچنین طراحی و شبیه سازی فرآیندهای نوسانی در سطح علمی و تجربی.

مثلاً معلوم است که مرحله نهاییمظاهر آنها از هارمونیک بودن خود متوقف می شود، یعنی مقوله های فرکانس و دوره برای آنها به سادگی بی معنی می شوند و در فرمول منعکس نمی شوند.

روش کلاسیک برای مطالعه نوسانات هارمونیک در ساده ترین شکل آن است، که سیستمی را نشان می دهد که با معادله دیفرانسیل زیر از نوسانات هارمونیک توصیف می شود: ds/dt + ω²s = 0. اما تنوع فرآیندهای نوسانی به طور طبیعی منجر به این واقعیت می شود که وجود دارد. تعداد زیادی ازاسیلاتورها ما انواع اصلی آنها را لیست می کنیم:

نوسان ساز فنری یک بار معمولی با جرم معین m است که بر روی یک فنر الاستیک معلق است. این نوع هارمونیک را انجام می دهد که با فرمول F = - kx توصیف می شود.

نوسانگر فیزیکی (آونگ) - جامدانجام حرکات نوسانی حول محور ایستا تحت تاثیر نیروی معین.

- (عملاً در طبیعت یافت نمی شود). این نشان دهنده یک مدل ایده آل از یک سیستم است که شامل یک جسم فیزیکی نوسانی با جرم مشخص است که بر روی یک نخ سفت و سخت بدون وزن معلق است.

نوسانات اینها فرآیندهایی هستند که در آن یک سیستم، با تناوب بیشتر یا کمتر، مکرراً از یک موقعیت تعادلی عبور می کند.

طبقه بندی نوسان:

آ) طبیعتا (مکانیکی، الکترومغناطیسی، نوسانات غلظت، دما و غیره)؛

ب) با توجه به فرم (ساده = هارمونیک؛ پیچیده، مجموع ارتعاشات هارمونیک ساده)؛

V) بر اساس درجه فرکانس = دوره ای (ویژگی های سیستم پس از یک دوره زمانی کاملاً تعریف شده تکرار می شود) و غیر پریودیک.

ز) در رابطه با زمان (بدون میرا = دامنه ثابت؛ میرا = کاهش دامنه).

ز) روی انرژی - رایگان (یک بار ورودی انرژی به سیستم از خارج = یک بار تاثیر خارجی)؛ اجباری (ورودی چندگانه (دوره ای) انرژی از خارج به سیستم = تأثیر خارجی دوره ای). خود نوسانات (نوسانات بدون میرایی که به دلیل توانایی سیستم در تنظیم تامین انرژی از یک منبع ثابت ایجاد می شود).

شرایط وقوع نوسانات.

الف) وجود یک سیستم نوسانی (آونگ معلق، آونگ فنری، مدار نوسانی و غیره)؛

ب) وجود یک منبع انرژی خارجی که بتواند حداقل یکبار سیستم را از حالت تعادل خارج کند.

ج) ظهور یک نیروی بازگردان شبه الاستیک (یعنی نیرویی متناسب با جابجایی) در سیستم؛

د) وجود اینرسی (عنصر اینرسی) در سیستم.

به عنوان یک مثال گویا، حرکت یک آونگ ریاضی را در نظر بگیرید. آونگ ریاضیجسم کوچکی را می گویند که بر روی یک نخ نازک غیر قابل امتداد معلق است که جرم آن در مقایسه با جرم بدن ناچیز است. در حالت تعادل، هنگامی که آونگ شاقول را آویزان می کند، نیروی گرانش با نیروی کشش نخ متعادل می شود.
. هنگامی که آونگ با زاویه معینی از وضعیت تعادل منحرف می شود α یک جزء مماسی از گرانش ظاهر می شود اف=- میلی گرم sina. علامت منفی در این فرمول به این معنی است که جزء مماسی در جهت مخالف انحراف آونگ هدایت می شود. او یک نیروی ترمیم کننده است. در زوایای کوچک α (حدود 15-20 درجه) این نیرو متناسب با جابجایی آونگ است، یعنی. شبه الاستیک است و نوسانات آونگ هارمونیک است.

هنگامی که آونگ منحرف می شود، تا ارتفاع معینی بالا می رود، یعنی. ذخیره معینی از انرژی پتانسیل به او داده می شود ( E عرق = mgh). وقتی آونگ به حالت تعادل حرکت می کند، انرژی پتانسیل به انرژی جنبشی تبدیل می شود. در لحظه ای که آونگ از موقعیت تعادل عبور می کند، انرژی پتانسیل صفر و انرژی جنبشی حداکثر است. به دلیل وجود جرم متر(وزن - کمیت فیزیکیکه خواص اینرسی و گرانشی ماده را تعیین می کند، آونگ از موقعیت تعادل عبور کرده و در جهت مخالف منحرف می شود. اگر اصطکاک در سیستم وجود نداشته باشد، نوسانات آونگ به طور نامحدود ادامه می یابد.

معادله ارتعاش هارمونیک به شکل زیر است:

x(t) = x متر cos(ω 0 t+φ 0 ),

جایی که ایکس- جابجایی بدن از وضعیت تعادل؛

ایکس متر (آ) - دامنه نوسانات، یعنی مدول حداکثر جابجایی،

ω 0 - فرکانس چرخه ای (یا دایره ای) نوسانات،

تی- زمان.

کمیت زیر علامت کسینوس φ = ω 0 t + φ 0 تماس گرفت فازارتعاش هارمونیک فاز افست در را تعیین می کند این لحظهزمان تی. فاز در واحدهای زاویه ای (رادیان) بیان می شود.

در تی= 0 φ = φ 0 ، از همین رو φ 0 تماس گرفت فاز اولیه.

دوره زمانی که در طی آن حالت های خاصی از سیستم نوسانی تکرار می شود نامیده می شود دوره نوسانتی.

کمیت فیزیکی معکوس دوره نوسان نامیده می شود فرکانس نوسان:
. فرکانس نوسان ν نشان می دهد که در واحد زمان چند نوسان رخ می دهد. واحد فرکانس - هرتز (هرتز) -یک ارتعاش در ثانیه

فرکانس نوسان ν مربوط به فرکانس چرخه ای ω و دوره نوسان تینسبت ها:
.

یعنی فرکانس دایره ای تعداد نوسانات کاملی است که در 2π واحد زمان رخ می دهد.

از نظر گرافیکی، نوسانات هارمونیک را می توان به عنوان یک وابستگی نشان داد ایکساز جانب تی و روش نمودار برداری.

روش نمودار برداری به شما امکان می دهد تمام پارامترهای موجود در معادله نوسانات هارمونیک را به وضوح ارائه دهید. در واقع، اگر بردار دامنه آ در یک زاویه قرار دارد φ به محور ایکس، سپس آن را بر روی محور برجسته می کند ایکسبرابر خواهد بود با: x = Acos(φ ) . گوشه φ و مرحله اولیه وجود دارد. اگر بردار آدر چرخش با سرعت زاویهایω 0 برابر با فرکانس دایره ای نوسانات است، سپس برآمدگی انتهای بردار در امتداد محور حرکت می کند. ایکسو مقادیری از -آقبل از +Aو مختصات این پیش بینی طبق قانون به مرور زمان تغییر می کند: ایکس(تی) = آcos(ω 0 تی+ φ) . مدت زمانی که طول می کشد تا بردار دامنه یک دور کامل انجام دهد برابر با دوره است تیارتعاشات هارمونیک تعداد دورهای برداری در ثانیه برابر با فرکانس نوسان است ν .

بر اساس قانون سینوسی در طول زمان تغییر می کند:

جایی که ایکس- مقدار کمیت در حال نوسان در لحظه زمان تی, آ- دامنه، ω - فرکانس دایره ای، φ - فاز اولیه نوسانات، ( φt + φ ) - فاز کامل نوسانات. در عین حال، ارزش ها آ, ω و φ - دائمی

برای ارتعاشات مکانیکیارزش نوسان ایکسبه ویژه، جابجایی و سرعت، برای ارتعاشات الکتریکی - ولتاژ و جریان.

نوسانات هارمونیک جایگاه ویژه ای را در بین انواع نوسانات به خود اختصاص می دهد، زیرا این تنها نوع نوسان است که شکل آن هنگام عبور از هر محیط همگن تغییر نمی کند، یعنی امواج منتشر شده از منبع نوسانات هارمونیک نیز هارمونیک خواهند بود. هر نوسان غیر هارمونیک را می توان به صورت مجموع (انتگرال) نوسانات هارمونیک مختلف (به شکل طیفی از نوسانات هارمونیک) نشان داد.

تبدیل انرژی در طی ارتعاشات هارمونیک

در طول فرآیند نوسان، انتقال انرژی پتانسیل رخ می دهد Wpبه جنبشی هفتهو بالعکس. در موقعیت حداکثر انحراف از موقعیت تعادل، انرژی پتانسیل حداکثر است، انرژی جنبشی صفر است. با بازگشت به حالت تعادل، سرعت جسم در حال نوسان افزایش می یابد و با آن انرژی جنبشی نیز افزایش می یابد و در موقعیت تعادل به حداکثر می رسد. انرژی پتانسیل به صفر می رسد. حرکت بیشتر با کاهش سرعت اتفاق می‌افتد که وقتی انحراف به حداکثر دوم خود می‌رسد به صفر می‌رسد. انرژی پتانسیل در اینجا به مقدار اولیه (حداکثر) خود (در صورت عدم وجود اصطکاک) افزایش می یابد. بنابراین، نوسانات انرژی جنبشی و پتانسیل با فرکانس دو برابر (در مقایسه با نوسانات خود آونگ) رخ می دهد و در پادفاز است (یعنی بین آنها یک تغییر فاز برابر با π ). کل انرژی ارتعاشی دبلیوبدون تغییر باقی می ماند. برای جسمی که تحت اثر نیروی کشسان در حال نوسان است برابر است با:

جایی که v m — حداکثر سرعت، بیشینه سرعتبدن (در موقعیت تعادل)، x m = آ- دامنه

به دلیل وجود اصطکاک و مقاومت محیط، ارتعاشات آزاد کاهش می یابد: انرژی و دامنه آنها با گذشت زمان کاهش می یابد. بنابراین، در عمل، از نوسانات اجباری بیشتر از نوسانات آزاد استفاده می شود.