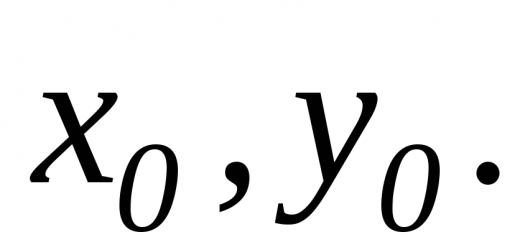حل مسائل یا مثال های فیزیکی در ریاضیات بدون آگاهی از مشتق و روش های محاسبه آن کاملاً غیرممکن است. مشتق یکی از مهمترین مفاهیم در تحلیل ریاضی است. ما تصمیم گرفتیم مقاله امروز را به این موضوع اساسی اختصاص دهیم. مشتق چیست، معنای فیزیکی و هندسی آن چیست، مشتق تابع را چگونه محاسبه کنیم؟ همه این سؤالات را می توان در یکی ترکیب کرد: چگونه مشتق را درک کنیم؟
معنای هندسی و فیزیکی مشتق
اجازه دهید یک تابع وجود داشته باشد f(x) ، در یک بازه زمانی مشخص مشخص شده است (الف، ب) . نقاط x و x0 متعلق به این بازه هستند. وقتی x تغییر می کند، خود تابع تغییر می کند. تغییر استدلال - تفاوت در مقادیر آن x-x0 . این تفاوت به صورت نوشته شده است دلتا x و افزایش آرگومان نامیده می شود. تغییر یا افزایش یک تابع، تفاوت بین مقادیر یک تابع در دو نقطه است. تعریف مشتق:
مشتق یک تابع در یک نقطه حد نسبت افزایش تابع در یک نقطه معین به افزایش آرگومان زمانی است که دومی به سمت صفر میل می کند.
در غیر این صورت می توان اینگونه نوشت:

یافتن چنین محدودیتی چه فایده ای دارد؟ و در اینجا چیست:
مشتق تابع در یک نقطه برابر است با مماس زاویه بین محور OX و مماس بر نمودار تابع در یک نقطه معین.

معنای فیزیکیمشتق: مشتق مسیر نسبت به زمان برابر است با سرعت حرکت مستقیم.
در واقع، از دوران مدرسه همه می دانند که سرعت یک مسیر خاص است x=f(t) و زمان تی . سرعت متوسطبرای مدت معین:

برای پی بردن به سرعت حرکت در یک لحظه از زمان t0 شما باید حد را محاسبه کنید:

قانون اول: یک ثابت تنظیم کنید
ثابت را می توان از علامت مشتق خارج کرد. علاوه بر این، این باید انجام شود. هنگام حل مثال هایی در ریاضیات، آن را به عنوان یک قاعده در نظر بگیرید - اگر می توانید یک عبارت را ساده کنید، حتما آن را ساده کنید .
مثال. بیایید مشتق را محاسبه کنیم:

قانون دوم: مشتق از مجموع توابع
مشتق مجموع دو تابع برابر است با مجموع مشتقات این توابع. همین امر در مورد مشتق تفاوت توابع نیز صادق است.

ما برای این قضیه اثبات نمی کنیم، بلکه یک مثال عملی را در نظر می گیریم.
مشتق تابع را پیدا کنید:


قانون سوم: مشتق حاصلضرب توابع
مشتق حاصل ضرب دو تابع متمایز با فرمول محاسبه می شود:

مثال: مشتق یک تابع را پیدا کنید:

راه حل: 
در اینجا مهم است که در مورد محاسبه مشتقات توابع پیچیده صحبت کنیم. مشتق تابع مختلط با حاصلضرب مشتق این تابع نسبت به آرگومان میانی و مشتق آرگومان میانی نسبت به متغیر مستقل برابر است.
در مثال بالا به این عبارت برخورد می کنیم:

در این حالت، آرگومان میانی 8 برابر به توان پنجم است. برای محاسبه مشتق چنین عبارتی، ابتدا مشتق تابع خارجی را با توجه به آرگومان میانی محاسبه می کنیم و سپس با توجه به متغیر مستقل در مشتق خود آرگومان میانی ضرب می کنیم.
قانون چهارم: مشتق ضریب دو تابع
فرمول تعیین مشتق ضریب دو تابع:



ما سعی کردیم در مورد مشتقات برای آدمک ها از ابتدا صحبت کنیم. این موضوع آنقدرها هم که به نظر می رسد ساده نیست، پس اخطار داشته باشید: در مثال ها اغلب مشکلاتی وجود دارد، بنابراین هنگام محاسبه مشتقات مراقب باشید.
در صورت داشتن هرگونه سوال در این زمینه و موضوعات دیگر، می توانید با خدمات دانشجویی تماس بگیرید. در مدت زمان کوتاهی، ما به شما کمک می کنیم تا سخت ترین آزمون را حل کنید و وظایف را درک کنید، حتی اگر قبلاً محاسبات مشتق را انجام نداده باشید.
برای راحتی و وضوح در هنگام مطالعه موضوع، یک جدول خلاصه ارائه می دهیم.
|
ثابتy = C تابع توان y = x p (x p) " = p x p - 1 |
تابع نماییy = تبر (a x) " = a x ln a به ویژه، زمانی کهa = eما داریم y = e x (e x) " = e x |
|
تابع لگاریتمی (log a x) " = 1 x ln a به ویژه، زمانی کهa = eما داریم y = logx (ln x) " = 1 x |
توابع مثلثاتی (sin x) " = cos x (cos x) " = - sin x (t g x) " = 1 cos 2 x (c t g x) " = - 1 sin 2 x |
|
توابع مثلثاتی معکوس (a r c sin x) " = 1 1 - x 2 (a r c cos x) " = - 1 1 - x 2 (a r c t g x) " = 1 1 + x 2 (a r c c t g x) " = - 1 1 + x 2 |
توابع هذلولی (s h x) " = c h x (c h x) " = s h x (t h x) " = 1 c h 2 x (c t h x) " = - 1 s h 2 x |
اجازه دهید نحوه به دست آوردن فرمول های جدول مشخص شده را تجزیه و تحلیل کنیم یا به عبارت دیگر، مشتق فرمول های مشتق را برای هر نوع تابع ثابت کنیم.
مشتق از یک ثابت
شواهد 1به منظور عقب نشینی این فرمول، اجازه دهید تعریف مشتق یک تابع را در یک نقطه به عنوان مبنایی در نظر بگیریم. ما از x 0 = x، که در آن استفاده می کنیم ایکسمقدار هر عدد واقعی را می گیرد، یا به عبارت دیگر، ایکسهر عددی از دامنه تابع f (x) = C است. اجازه دهید حد نسبت افزایش یک تابع به افزایش آرگومان را به صورت ∆ x → 0 بنویسیم:
lim ∆ x → 0 ∆ f (x) ∆ x = lim ∆ x → 0 C - C ∆ x = lim ∆ x → 0 0 ∆ x = 0
لطفاً توجه داشته باشید که عبارت 0 ∆ x تحت علامت حد قرار می گیرد. این عدم قطعیت «صفر تقسیم بر صفر» نیست، زیرا شمارش حاوی یک مقدار بی نهایت کوچک نیست، بلکه دقیقاً صفر است. به عبارت دیگر، افزایش یک تابع ثابت همیشه صفر است.
بنابراین، مشتق تابع ثابت f (x) = C در کل دامنه تعریف برابر با صفر است.
مثال 1
توابع ثابت داده شده است:
f 1 (x) = 3، f 2 (x) = a، a ∈ R، f 3 (x) = 4. 13 7 22، f 4 (x) = 0، f 5 (x) = - 8 7
راه حل
اجازه دهید شرایط داده شده را شرح دهیم. در تابع اول مشتق عدد طبیعی 3 را می بینیم. در مثال زیر باید مشتق از را بگیرید آ، جایی که آ- هر عدد واقعی مثال سوم مشتق عدد غیر منطقی 4 را به ما می دهد. 13 7 22، چهارم مشتق صفر است (صفر یک عدد صحیح است). در نهایت در مورد پنجم مشتق را داریم کسر گویا - 8 7 .
پاسخ:مشتقات توابع مشخص شدهبرای هر واقعی صفر است ایکس(در کل منطقه تعریف)
f 1 " (x) = (3) " = 0 , f 2 " (x) = (a) " = 0 , a ∈ R , f 3 " (x) = 4 . 13 7 22 " = 0 , f 4 " (x) = 0" = 0، f 5" (x) = - 8 7" = 0
مشتق تابع توان
بیایید به ادامه مطلب برویم تابع توانو فرمول مشتق آن، که به شکل: (x p) " = p x p - 1، که در آن توان پهر عدد واقعی است
شواهد 2
اجازه دهید زمانی که توان این فرمول است، اثبات کنیم عدد طبیعی: p = 1، 2، 3، …
ما دوباره بر تعریف مشتق تکیه می کنیم. اجازه دهید حد نسبت افزایش یک تابع توان به افزایش آرگومان را بنویسیم:
(x p) " = lim ∆ x → 0 = ∆ (x p) ∆ x = lim ∆ x → 0 (x + ∆ x) p - x p ∆ x
برای ساده کردن عبارت در عدد، از فرمول دو جمله ای نیوتن استفاده می کنیم:
(x + ∆ x) p - x p = C p 0 + x p + C p 1 · x p - 1 · ∆ x + C p 2 · x p - 2 · (∆ x) 2 + . . . + + C p p - 1 x (∆ x) p - 1 + C p p (∆ x) p - x p = = C p 1 x p - 1 ∆ x + C p 2 x p - 2 (∆ x) 2 + . . . + C p p - 1 x (∆ x) p - 1 + C p p (∆ x) p
بدین ترتیب:
(x p) " = lim ∆ x → 0 ∆ (x p) ∆ x = lim ∆ x → 0 (x + ∆ x) p - x p ∆ x = = lim ∆ x → 0 (C p 1 x p - 1 ∆ x + C p 2 x p - 2 (∆ x) 2 + ... + C p p - 1 x (∆ x) p - 1 + C p p (∆ x) p) ∆ x = = lim ∆ x → 0 (C p 1 x p - 1 + C p 2 x p - 2 ∆ x + . . + C p p - 1 x (∆ x) p - 2 + C p p (∆ x) p - 1) = = C p 1 · x p - 1 + 0 + 0 + . . . + 0 = p ! 1 ! · (p - 1) ! · x p - 1 = p · x p - 1
بنابراین، ما فرمول مشتق یک تابع توان را زمانی که توان یک عدد طبیعی باشد، ثابت کردهایم.
شواهد 3
برای ارائه مدرک برای پرونده زمانی که پ-هر عدد واقعی غیر از صفر، از مشتق لگاریتمی استفاده می کنیم (در اینجا باید تفاوت را با مشتق یک تابع لگاریتمی درک کنیم). برای درک کامل تر، توصیه می شود مشتق یک تابع لگاریتمی را مطالعه کنید و علاوه بر آن مشتق یک تابع ضمنی و مشتق یک تابع مختلط را درک کنید.
بیایید دو مورد را در نظر بگیریم: چه زمانی ایکسمثبت و چه زمانی ایکسمنفی.
بنابراین x> 0. سپس: x p > 0 . اجازه دهید برابری y = x p را بر مبنای e لگاریتم کنیم و خاصیت لگاریتم را اعمال کنیم:
y = x p ln y = ln x p ln y = p · ln x
در این مرحله، یک تابع به طور ضمنی مشخص شده به دست آورده ایم. بیایید مشتق آن را تعریف کنیم:
(ln y) " = (p · ln x) 1 y · y " = p · 1 x ⇒ y " = p · y x = p · x p x = p · x p - 1
اکنون موردی را در نظر می گیریم که ایکس -یک عدد منفی
اگر نشانگر پوجود دارد عدد زوج، سپس تابع توان برای x تعریف می شود< 0 , причем является четной: y (x) = - y ((- x) p) " = - p · (- x) p - 1 · (- x) " = = p · (- x) p - 1 = p · x p - 1
سپس x p< 0 и возможно составить доказательство, используя логарифмическую производную.
اگر پیک عدد فرد است، سپس تابع توان برای x تعریف می شود< 0 , причем является нечетной: y (x) = - y (- x) = - (- x) p . Тогда x p < 0 , а значит логарифмическую производную задействовать нельзя. В такой ситуации возможно взять за основу доказательства правила дифференцирования и правило нахождения производной сложной функции:
y " (x) = (- (- x) p) " = - ((- x) p) " = - p · (- x) p - 1 · (- x) " = = p · (- x) p - 1 = p x p - 1
آخرین انتقال به این دلیل امکان پذیر است که اگر پیک عدد فرد است، پس p - 1یا یک عدد زوج یا صفر (برای p = 1)، بنابراین برای منفی ایکسبرابری (- x) p - 1 = x p - 1 درست است.
بنابراین، ما فرمول مشتق تابع توان را برای هر p واقعی ثابت کردهایم.
مثال 2
توابع داده شده:
f 1 (x) = 1 x 2 3، f 2 (x) = x 2 - 1 4، f 3 (x) = 1 x log 7 12
مشتقات آنها را تعیین کنید.
راه حل
برخی از توابع داده شده را بر اساس ویژگی های درجه به شکل جدولی y = x p تبدیل می کنیم و سپس از فرمول استفاده می کنیم:
f 1 (x) = 1 x 2 3 = x - 2 3 ⇒ f 1 " (x) = - 2 3 x - 2 3 - 1 = - 2 3 x - 5 3 f 2 " (x) = x 2 - 1 4 = 2 - 1 4 x 2 - 1 4 - 1 = 2 - 1 4 x 2 - 5 4 f 3 (x) = 1 x log 7 12 = x - log 7 12 ⇒ f 3" ( x) = - log 7 12 x - log 7 12 - 1 = - log 7 12 x - log 7 12 - log 7 7 = - log 7 12 x - log 7 84
مشتق تابع نمایی
اثبات 4اجازه دهید فرمول مشتق را با استفاده از تعریف به عنوان پایه استخراج کنیم:
(a x) " = lim ∆ x → 0 a x + ∆ x - a x ∆ x = lim ∆ x → 0 a x (a ∆ x - 1) ∆ x = a x lim ∆ x → 0 a ∆ x - 1 ∆ x = 0 0
دچار بلاتکلیفی شدیم. برای گسترش آن، اجازه دهید یک متغیر جدید z = a ∆ x - 1 بنویسیم (z → 0 به عنوان ∆ x → 0). در این مورد، ∆ x = z + 1 ⇒ ∆ x = log a (z + 1) = ln (z + 1) ln a . برای آخرین انتقال، از فرمول انتقال به یک پایه لگاریتمی جدید استفاده شد.
اجازه دهید حد اصلی را جایگزین کنیم:
(a x) " = a x · lim ∆ x → 0 a ∆ x - 1 ∆ x = a x · ln a · lim ∆ x → 0 1 1 z · ln (z + 1) = = a x · ln a · lim ∆ x → 0 1 ln (z + 1) 1 z = a x · ln a · 1 ln lim ∆ x → 0 (z + 1) 1 z
اجازه دهید حد قابل توجه دوم را به خاطر بسپاریم و سپس فرمول مشتق را بدست آوریم تابع نمایی:
(a x) " = a x · ln a · 1 ln lim z → 0 (z + 1) 1 z = a x · ln a · 1 ln e = a x · ln a
مثال 3
توابع نمایی داده شده است:
f 1 (x) = 2 3 x , f 2 (x) = 5 3 x , f 3 (x) = 1 (e) x
باید مشتقات آنها را پیدا کرد.
راه حل
ما از فرمول برای مشتق تابع نمایی و خواص لگاریتم استفاده می کنیم:
f 1 " (x) = 2 3 x " = 2 3 x ln 2 3 = 2 3 x (ln 2 - ln 3) f 2 " (x) = 5 3 x " = 5 3 x ln 5 1 3 = 1 3 5 3 x ln 5 f 3 " (x) = 1 (e) x " = 1 e x " = 1 e x ln 1 e = 1 e x ln e - 1 = - 1 e x
مشتق تابع لگاریتمی
شواهد 5اجازه دهید اثباتی از فرمول برای مشتق تابع لگاریتمی برای هر کدام ارائه کنیم ایکسدر زمینه تعریف و هر ارزش های قابل قبولپایه a لگاریتم بر اساس تعریف مشتق، به دست می آوریم:
(log a x) " = lim ∆ x → 0 log a (x + ∆ x) - log a x ∆ x = lim ∆ x → 0 log a x + ∆ x x ∆ x = = lim ∆ x → 0 1 ∆ x log a 1 + ∆ x x = lim ∆ x → 0 log a 1 + ∆ x x 1 ∆ x = = lim ∆ x → 0 log a 1 + ∆ x x 1 ∆ x · x x = lim ∆ x → 0 1 x · log a 1 + ∆ x x x ∆ x = = 1 x · log a lim ∆ x → 0 1 + ∆ x x x ∆ x = 1 x · log a e = 1 x · ln e ln a = 1 x · ln a
از زنجیره برابری های نشان داده شده مشخص است که تبدیل ها بر اساس خاصیت لگاریتم بوده اند. مرز تساوی ∆ x → 0 1 + ∆ x x x ∆ x = e مطابق با حد قابل توجه دوم صادق است.
مثال 4
توابع لگاریتمی داده شده است:
f 1 (x) = log ln 3 x , f 2 (x) = ln x
محاسبه مشتقات آنها ضروری است.
راه حل
بیایید فرمول مشتق شده را اعمال کنیم:
f 1 " (x) = (log ln 3 x) " = 1 x · ln (ln 3) ; f 2 " (x) = (ln x)" = 1 x ln e = 1 x
بنابراین، مشتق لگاریتم طبیعی یک تقسیم بر است ایکس.
مشتقات توابع مثلثاتی
اثبات 6از مقداری استفاده کنیم فرمول های مثلثاتیو اولین حد قابل توجه برای استخراج فرمول مشتق یک تابع مثلثاتی.
با توجه به تعریف مشتق تابع سینوس، به دست می آوریم:
(sin x) " = lim ∆ x → 0 sin (x + ∆ x) - sin x ∆ x
فرمول تفاوت سینوس ها به ما امکان می دهد اقدامات زیر را انجام دهیم:
(sin x) " = lim ∆ x → 0 sin (x + ∆ x) - sin x ∆ x = = lim ∆ x → 0 2 sin x + ∆ x - x 2 cos x + ∆ x + x 2 ∆ x = = lim ∆ x → 0 sin ∆ x 2 · cos x + ∆ x 2 ∆ x 2 = = cos x + 0 2 · lim ∆ x → 0 sin ∆ x 2 ∆ x 2
در نهایت، از اولین محدودیت فوق العاده استفاده می کنیم:
sin " x = cos x + 0 2 · lim ∆ x → 0 sin ∆ x 2 ∆ x 2 = cos x
بنابراین، مشتق تابع گناه xاراده cos x.
ما همچنین فرمول مشتق کسینوس را ثابت خواهیم کرد:
cos "x = lim ∆ x → 0 cos (x + ∆ x) - cos x ∆ x = = lim ∆ x → 0 - 2 sin x + ∆ x - x 2 sin x + ∆ x + x 2 ∆ x = = - lim ∆ x → 0 sin ∆ x 2 sin x + ∆ x 2 ∆ x 2 = = - sin x + 0 2 lim ∆ x → 0 sin ∆ x 2 ∆ x 2 = - sin x
آن ها مشتق توابع cos x خواهد بود - گناه x.
ما فرمول های مشتقات مماس و کتانژانت را بر اساس قوانین تمایز استخراج می کنیم:
t g " x = گناه x cos x " = گناه " x · cos x - sin x · cos " x cos 2 x = = cos x · cos x - sin x · (- گناه x) cos 2 x = گناه 2 x + cos 2 x cos 2 x = 1 cos 2 x c t g " x = cos x sin x " = cos " x · sin x - cos x · sin " x sin 2 x = = - sin x · sin x - cos x · cos x sin 2 x = - sin 2 x + cos 2 x sin 2 x = - 1 sin 2 x
مشتقات توابع مثلثاتی معکوس
بخش مشتق توابع معکوس اطلاعات جامعی در مورد اثبات فرمول های مشتقات آرکسین، آرکوزین، آرکتتانژانت و آرکوتانژانت ارائه می دهد، بنابراین ما در اینجا مطالب را تکرار نمی کنیم.
مشتقات توابع هذلولی
شواهد 7با استفاده از قانون تمایز و فرمول مشتق تابع نمایی میتوانیم فرمولهای مشتقات سینوس هذلولی، کسینوس، مماس و کوتانژانت را استخراج کنیم:
s h " x = e x - e - x 2 " = 1 2 e x " - e - x " = = 1 2 e x - - e - x = e x + e - x 2 = c h x c h " x = e x + e - x 2 " = 1 2 e x " + e - x " = = 1 2 e x + - e - x = e x - e - x 2 = s h x t h " x = s h x c h x " = s h " x · c h x - s h x · c h " x c h 2 x = c h 2 x - s h 2 x c h 2 x = 1 c h 2 x c t h " x = c h x s h x " = c h " x · s h x - c h x · s h " x s h 2 x = s h 2 x - c h 2 x s h x s h x h
در صورت مشاهده خطایی در متن، لطفاً آن را برجسته کرده و Ctrl+Enter را فشار دهید
حل مسائل یا مثال های فیزیکی در ریاضیات بدون آگاهی از مشتق و روش های محاسبه آن کاملاً غیرممکن است. مشتق یکی از مهمترین مفاهیم در تحلیل ریاضی است. ما تصمیم گرفتیم مقاله امروز را به این موضوع اساسی اختصاص دهیم. مشتق چیست، معنای فیزیکی و هندسی آن چیست، مشتق تابع را چگونه محاسبه کنیم؟ همه این سؤالات را می توان در یکی ترکیب کرد: چگونه مشتق را درک کنیم؟
معنای هندسی و فیزیکی مشتق
اجازه دهید یک تابع وجود داشته باشد f(x) ، در یک بازه زمانی مشخص مشخص شده است (الف، ب) . نقاط x و x0 متعلق به این بازه هستند. وقتی x تغییر می کند، خود تابع تغییر می کند. تغییر استدلال - تفاوت در مقادیر آن x-x0 . این تفاوت به صورت نوشته شده است دلتا x و افزایش آرگومان نامیده می شود. تغییر یا افزایش یک تابع، تفاوت بین مقادیر یک تابع در دو نقطه است. تعریف مشتق:
مشتق یک تابع در یک نقطه حد نسبت افزایش تابع در یک نقطه معین به افزایش آرگومان زمانی است که دومی به سمت صفر میل می کند.
در غیر این صورت می توان اینگونه نوشت:

یافتن چنین محدودیتی چه فایده ای دارد؟ و در اینجا چیست:
مشتق تابع در یک نقطه برابر است با مماس زاویه بین محور OX و مماس بر نمودار تابع در یک نقطه معین.

معنای فیزیکی مشتق: مشتق مسیر نسبت به زمان برابر است با سرعت حرکت مستقیم.
در واقع، از دوران مدرسه همه می دانند که سرعت یک مسیر خاص است x=f(t) و زمان تی . سرعت متوسط در یک بازه زمانی معین:

برای پی بردن به سرعت حرکت در یک لحظه از زمان t0 شما باید حد را محاسبه کنید:

قانون اول: یک ثابت تنظیم کنید
ثابت را می توان از علامت مشتق خارج کرد. علاوه بر این، این باید انجام شود. هنگام حل مثال هایی در ریاضیات، آن را به عنوان یک قاعده در نظر بگیرید - اگر می توانید یک عبارت را ساده کنید، حتما آن را ساده کنید .
مثال. بیایید مشتق را محاسبه کنیم:

قانون دوم: مشتق از مجموع توابع
مشتق مجموع دو تابع برابر است با مجموع مشتقات این توابع. همین امر در مورد مشتق تفاوت توابع نیز صادق است.

ما برای این قضیه اثبات نمی کنیم، بلکه یک مثال عملی را در نظر می گیریم.
مشتق تابع را پیدا کنید:


قانون سوم: مشتق حاصلضرب توابع
مشتق حاصل ضرب دو تابع متمایز با فرمول محاسبه می شود:

مثال: مشتق یک تابع را پیدا کنید:

راه حل: 
در اینجا مهم است که در مورد محاسبه مشتقات توابع پیچیده صحبت کنیم. مشتق تابع مختلط با حاصلضرب مشتق این تابع نسبت به آرگومان میانی و مشتق آرگومان میانی نسبت به متغیر مستقل برابر است.
در مثال بالا به این عبارت برخورد می کنیم:

در این حالت، آرگومان میانی 8 برابر به توان پنجم است. برای محاسبه مشتق چنین عبارتی، ابتدا مشتق تابع خارجی را با توجه به آرگومان میانی محاسبه می کنیم و سپس با توجه به متغیر مستقل در مشتق خود آرگومان میانی ضرب می کنیم.
قانون چهارم: مشتق ضریب دو تابع
فرمول تعیین مشتق ضریب دو تابع:



ما سعی کردیم در مورد مشتقات برای آدمک ها از ابتدا صحبت کنیم. این موضوع آنقدرها هم که به نظر می رسد ساده نیست، پس اخطار داشته باشید: در مثال ها اغلب مشکلاتی وجود دارد، بنابراین هنگام محاسبه مشتقات مراقب باشید.
در صورت داشتن هرگونه سوال در این زمینه و موضوعات دیگر، می توانید با خدمات دانشجویی تماس بگیرید. در مدت زمان کوتاهی، ما به شما کمک می کنیم تا سخت ترین آزمون را حل کنید و وظایف را درک کنید، حتی اگر قبلاً محاسبات مشتق را انجام نداده باشید.
خیلی راحت به خاطر سپردن
خوب، بیایید دور نرویم، بیایید فوراً به آن نگاه کنیم تابع معکوس. کدام تابع معکوس تابع نمایی است؟ لگاریتم:
در مورد ما، پایه عدد است:
چنین لگاریتمی (یعنی لگاریتمی با پایه) "طبیعی" نامیده می شود و ما از نماد خاصی برای آن استفاده می کنیم: به جای آن می نویسیم.
با چه چیزی برابر است؟ البته، .
مشتق لگاریتم طبیعی نیز بسیار ساده است:
مثال ها:
- مشتق تابع را بیابید.
- مشتق تابع چیست؟
پاسخ ها: غرفه دار و لگاریتم طبیعی- توابع از نظر مشتقات به طور منحصر به فردی ساده هستند. توابع نمایی و لگاریتمی با هر پایه دیگری مشتق متفاوتی خواهند داشت که بعد از مرور قوانین تمایز آن را تحلیل خواهیم کرد.
قوانین تمایز
قوانین چی؟ بازم یه ترم جدید دیگه؟!...
تفکیکفرآیند یافتن مشتق است.
همین. این فرآیند را در یک کلمه چه چیز دیگری میتوان نامید؟ نه مشتق... ریاضیدانان دیفرانسیل را همان افزایش یک تابع در می نامند. این اصطلاح از دیفرانسیل لاتین - تفاوت می آید. اینجا.
هنگام استخراج همه این قوانین، از دو تابع به عنوان مثال و. ما همچنین به فرمول هایی برای افزایش آنها نیاز خواهیم داشت:
در کل 5 قانون وجود دارد.
ثابت از علامت مشتق خارج می شود.
اگر - برخی عدد ثابت(ثابت)، سپس.
بدیهی است که این قانون برای تفاوت نیز کار می کند: .
بیایید ثابت کنیم. بگذارید باشد یا ساده تر.
مثال ها.
مشتقات توابع را پیدا کنید:
- در یک نقطه؛
- در یک نقطه؛
- در یک نقطه؛
- در نقطه
راه حل ها:
- (مشتق در همه نقاط یکسان است، زیرا این تابع خطی، یاد آوردن؟)؛
مشتق محصول
همه چیز در اینجا مشابه است: بیایید یک تابع جدید معرفی کنیم و افزایش آن را پیدا کنیم:
مشتق:
مثال ها:
- مشتقات توابع را پیدا کنید و
- مشتق تابع را در یک نقطه پیدا کنید.
راه حل ها:
مشتق تابع نمایی
اکنون دانش شما کافی است تا بیاموزید چگونه مشتق هر تابع نمایی را بیابید، و نه فقط نماها (آیا هنوز فراموش کرده اید که چیست؟).
بنابراین، برخی از شماره ها کجاست.
ما قبلاً مشتق تابع را می دانیم، بنابراین بیایید سعی کنیم تابع خود را به یک پایه جدید کاهش دهیم:
برای این ما استفاده خواهیم کرد قانون ساده: . سپس:
خوب، کار کرد. حالا سعی کنید مشتق را پیدا کنید و فراموش نکنید که این تابع پیچیده است.
اتفاق افتاد؟
در اینجا، خود را بررسی کنید:
فرمول بسیار شبیه به مشتق یک توان است: همانطور که بود، ثابت می ماند، فقط یک عامل ظاهر شد که فقط یک عدد است، اما یک متغیر نیست.
مثال ها:
مشتقات توابع را پیدا کنید:
پاسخ ها:
این فقط یک عدد است که بدون ماشین حساب نمی توان آن را محاسبه کرد، یعنی نمی توان آن را به شکل ساده تر یادداشت کرد. لذا در جواب به این شکل می گذاریم.
توجه داشته باشید که در اینجا ضریب دو تابع است، بنابراین قانون تمایز مربوطه را اعمال می کنیم:
در این مثال حاصل ضرب دو تابع:
مشتق تابع لگاریتمی
در اینجا مشابه است: شما قبلاً مشتق لگاریتم طبیعی را می دانید:
بنابراین، برای پیدا کردن یک لگاریتم دلخواه با پایه متفاوت، به عنوان مثال:
باید این لگاریتم را به پایه کاهش دهیم. چگونه پایه لگاریتم را تغییر می دهید؟ امیدوارم این فرمول را به خاطر داشته باشید:
فقط اکنون به جای آن می نویسیم:
مخرج به سادگی یک ثابت است (عددی ثابت، بدون متغیر). مشتق بسیار ساده به دست می آید:
مشتقات نمایی و توابع لگاریتمیتقریباً هرگز در آزمون یکپارچه ایالت ظاهر نمی شوند، اما دانستن آنها ضرری ندارد.
مشتق تابع مختلط
چه اتفاقی افتاده است " تابع پیچیده"؟ نه، این یک لگاریتم نیست و نه یک تانژانت. درک این توابع ممکن است دشوار باشد (البته اگر لگاریتم را دشوار میدانید، مبحث "لگاریتم" را بخوانید و خوب خواهید شد)، اما از نظر ریاضی، کلمه "پیچیده" به معنای "دشوار" نیست.
یک تسمه نقاله کوچک را تصور کنید: دو نفر نشسته اند و با برخی از اشیا کارهایی را انجام می دهند. به عنوان مثال، اولی یک تخته شکلات را در یک بسته بندی می پیچد و دومی آن را با یک روبان می بندد. نتیجه یک شی ترکیبی است: یک شکلات که با روبان بسته شده و بسته شده است. برای خوردن یک شکلات تخته ای، باید مراحل معکوس را به ترتیب معکوس انجام دهید.
بیایید یک خط لوله ریاضی مشابه ایجاد کنیم: ابتدا کسینوس یک عدد را پیدا می کنیم و سپس عدد حاصل را مربع می کنیم. بنابراین، یک عدد (شکلاتی) به ما داده می شود، من کسینوس آن را پیدا می کنم (لفاف بندی)، و سپس شما آنچه را که به دست آوردم مربع می کنید (آن را با یک روبان ببندید). چی شد؟ تابع. این مثالی از یک تابع پیچیده است: زمانی که برای یافتن مقدار آن، اولین عمل را مستقیماً با متغیر انجام می دهیم، و سپس یک عمل دوم را با آنچه که از اولی حاصل می شود، انجام می دهیم.
به عبارت دیگر، تابع پیچیده تابعی است که آرگومان آن تابع دیگری است: .
برای مثال ما، .
ما به راحتی میتوانیم همان مراحل را به ترتیب معکوس انجام دهیم: ابتدا آن را مربع میکنید و من به دنبال کسینوس عدد حاصل میگردم: . به راحتی می توان حدس زد که نتیجه تقریباً همیشه متفاوت خواهد بود. یک ویژگی مهم توابع پیچیده: وقتی ترتیب اعمال تغییر می کند، تابع تغییر می کند.
مثال دوم: (همان چیز). .
اقدامی که آخرین بار انجام می دهیم نامیده می شود عملکرد "خارجی".، و عمل انجام شد - بر این اساس عملکرد "داخلی".(این اسامی غیر رسمی هستند، من از آنها فقط برای توضیح مطالب به زبان ساده استفاده می کنم).
سعی کنید خودتان تعیین کنید کدام تابع خارجی و کدام داخلی است:
پاسخ ها:جداسازی توابع داخلی و خارجی بسیار شبیه به تغییر متغیرها است: به عنوان مثال، در یک تابع
- ابتدا چه اقدامی را انجام خواهیم داد؟ ابتدا بیایید سینوس را محاسبه کنیم و فقط آن را مکعب کنیم. این بدان معنی است که یک عملکرد داخلی است، اما یک عملکرد خارجی.
و کارکرد اصلی ترکیب آنهاست: . - درونی؛ داخلی: ؛ خارجی: .
معاینه: . - درونی؛ داخلی: ؛ خارجی: .
معاینه: . - درونی؛ داخلی: ؛ خارجی: .
معاینه: . - درونی؛ داخلی: ؛ خارجی: .
معاینه: .
متغیرها را تغییر می دهیم و تابع می گیریم.
خوب، حالا شکلاتمان را استخراج میکنیم و به دنبال مشتق آن میگردیم. روال همیشه برعکس است: ابتدا مشتق تابع بیرونی را جستجو می کنیم، سپس نتیجه را در مشتق تابع درونی ضرب می کنیم. در رابطه با نمونه اصلی، به این صورت است:
مثالی دیگر:
بنابراین، اجازه دهید در نهایت قانون رسمی را فرموله کنیم:
الگوریتم یافتن مشتق تابع مختلط:
ساده به نظر می رسد، درست است؟
بیایید با مثال ها بررسی کنیم:
راه حل ها:
1) داخلی:
خارجی: ;
2) داخلی:
(فقط سعی نکنید تا الان آن را قطع کنید! چیزی از زیر کسینوس بیرون نمی آید، یادتان هست؟)
3) داخلی:
خارجی: ;
بلافاصله مشخص می شود که این یک عملکرد پیچیده سه سطحی است: از این گذشته ، این به خودی خود یک عملکرد پیچیده است و ما ریشه را نیز از آن استخراج می کنیم ، یعنی عمل سوم را انجام می دهیم (شکلات را در یک بسته بندی قرار می دهیم. و با یک روبان در کیف). اما دلیلی برای ترس وجود ندارد: ما همچنان این عملکرد را به همان ترتیب معمول "باز کردن" خواهیم کرد: از پایان.
یعنی ابتدا ریشه و بعد کسینوس و فقط بعد عبارت داخل پرانتز را متمایز می کنیم. و سپس همه را ضرب می کنیم.
در چنین مواردی، شماره گذاری اقدامات راحت است. یعنی آنچه را که می دانیم تصور کنیم. به چه ترتیبی اقداماتی را برای محاسبه مقدار این عبارت انجام خواهیم داد؟ بیایید به یک مثال نگاه کنیم:
هرچه این عمل دیرتر انجام شود، عملکرد مربوطه "خارجی" تر خواهد بود. توالی اقدامات مانند قبل است:
در اینجا لانه سازی به طور کلی 4 سطح است. بیایید مسیر عمل را مشخص کنیم.
1. بیان رادیکال. .
2. ریشه. .
3. سینوس. .
4. مربع. .
5. کنار هم گذاشتن همه:
مشتق. به طور خلاصه در مورد چیزهای اصلی
مشتق یک تابع- نسبت افزایش تابع به افزایش آرگومان برای افزایش بی نهایت کوچک آرگومان:
مشتقات پایه:
قوانین تمایز:
ثابت از علامت مشتق خارج می شود:
مشتق جمع:
مشتقات محصول:
مشتق ضریب:
مشتق تابع مختلط:
الگوریتم یافتن مشتق تابع مختلط:
- ما تابع "داخلی" را تعریف کرده و مشتق آن را پیدا می کنیم.
- ما تابع "خارجی" را تعریف می کنیم و مشتق آن را پیدا می کنیم.
- نتایج نقطه اول و دوم را ضرب می کنیم.
مشتق اول
مشتق اول
(مشتق اول)نرخی که مقدار یک تابع با افزایش آرگومان آن در هر نقطه افزایش می یابد، اگر خود تابع در آن نقطه تعریف شده باشد. در نمودار، اولین مشتق یک تابع، شیب آن را نشان می دهد. اگر y=f(x)،اولین مشتق آن در نقطه x0حدی است که به آن تمایل دارد f(x0+а)–f(x0)/аمانند آبه بی نهایت تمایل دارد اندازه کوچک. مشتق اول را می توان نشان داد dy/dxیا y'(x).تابع y(x)این دارد مقدار ثابتدر نقطه x0،اگر dy/dxدر نقطه x0برابر با صفر است. یک مشتق اول برابر با صفر شرط لازم اما کافی نیست تا تابع در یک نقطه به حداکثر یا حداقل خود برسد.
اقتصاد. فرهنگ لغت. - م.: "INFRA-M"، انتشارات "وس میر". جی. بلک. سردبیر: دکترای اقتصاد Osadchaya I.M.. 2000 .
فرهنگ لغت اقتصادی. 2000 .
ببینید "FIRST DERIVATIV" در فرهنگ های دیگر چیست:
- (مشتق) نرخی که مقدار یک تابع با افزایش آرگومان آن در هر نقطه افزایش می یابد، اگر خود تابع در این نقطه تعریف شده باشد. در نمودار، اولین مشتق یک تابع، شیب آن را نشان می دهد. اگر y=f(x)، اولین مشتق آن در نقطه... ... فرهنگ لغت اقتصادی
این اصطلاح معانی دیگری دارد، به مشتق مراجعه کنید. تصویری از مفهوم مشتق مشتق ... ویکی پدیا
مشتق مفهوم اساسی حساب دیفرانسیل است که میزان تغییر یک تابع را مشخص می کند. به عنوان حد نسبت افزایش یک تابع به افزایش آرگومان آن تعریف می شود زیرا افزایش آرگومان به صفر میل می کند، اگر چنین حدی... ... ویکی پدیا
مشکل ارزش مرزی نوع خاص; شامل یافتن راه حل در حوزه متغیرهای x=(x1,..., x n) است. معادله دیفرانسیل(1) حتی 2 متر اینچ سفارش دهید مقادیر داده شدهتمام مشتقات مرتبه ای که بالاتر از m در مرز S منطقه D (یا بخشی از آن) نیستند ... دایره المعارف ریاضی
- (مشتق دوم) اولین مشتق از اولین مشتق تابع. اولین مشتق شیب تابع را اندازه گیری می کند. مشتق دوم نحوه تغییر شیب را با افزایش آرگومان اندازه گیری می کند. مشتق دوم y = f(x)…… فرهنگ لغت اقتصادی
این مقاله یا بخش نیاز به بازبینی دارد. لطفاً مقاله را مطابق با قوانین مقاله نویسی بهبود ببخشید. کسری در مورد ... ویکی پدیا
- (مشتق جزئی متقاطع) اثر تغییر یک آرگومان یک تابع از دو یا چند متغیر بر مشتق یک تابع معین که با توجه به آرگومان دیگر گرفته شده است. اگر y=f(x,z)، مشتق آن یا اولین مشتق تابع y نسبت به آرگومان x برابر است با... ... فرهنگ لغت اقتصادی
آنالوگ سرعت نقطه- اولین مشتق حرکت یک نقطه در امتداد مختصات تعمیم یافته مکانیسم ...
آنالوگ سرعت زاویه ای پیوند- اولین مشتق زاویه چرخش پیوند با توجه به مختصات تعمیم یافته مکانیسم ... فرهنگ لغت توضیحی اصطلاحات پلی تکنیک
سرعت کلی مکانیسم- اولین مشتق مختصات تعمیم یافته مکانیسم با توجه به زمان ... فرهنگ لغت توضیحی اصطلاحات پلی تکنیک
کتاب ها
- مجموعه مسائل هندسه و توپولوژی دیفرانسیل، Mishchenko A.S.. این مجموعه از مسائل در نظر گرفته شده است تا حد ممکن الزامات موجود برای دروس هندسه دیفرانسیل و توپولوژی، هم از برنامه های جدید و هم از دروس دیگر را منعکس کند.
- مقالات علمی من کتاب 3. روش ماتریس های چگالی در نظریه های کوانتومی یک لیزر، یک اتم دلخواه، بوندارف بوریس ولادیمیرویچ. این کتاب به بررسی مقالات علمی منتشر شده می پردازد که در آنها با استفاده از روش ماتریس چگالی، جدید نظریه های کوانتومیلیزر، اتم دلخواه و نوسان ساز کوانتومی با میرایی...