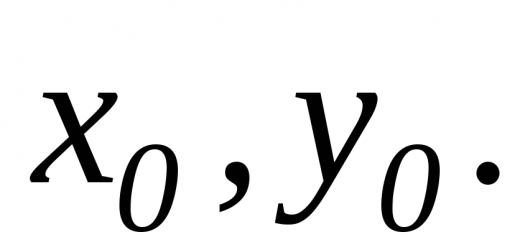محدودیت ها برای همه دانش آموزان ریاضی دردسرهای زیادی ایجاد می کند. برای حل یک محدودیت، گاهی اوقات باید از ترفندهای زیادی استفاده کنید و از بین انواع روش های حل، دقیقاً روشی را انتخاب کنید که برای یک مثال خاص مناسب است.

در این مقاله به شما در درک محدودیت‌های توانایی‌های خود یا درک محدودیت‌های کنترل کمک نمی‌کنیم، اما سعی می‌کنیم به این سوال پاسخ دهیم: چگونه محدودیت‌ها را در ریاضیات بالاتر درک کنیم؟ درک با تجربه حاصل می شود، بنابراین در عین حال چند مورد را ارائه خواهیم کرد نمونه های دقیقحل حدود با توضیحات

مفهوم حد در ریاضیات

سؤال اول این است: این حد چیست و حد چیست؟ ما می توانیم در مورد محدودیت های دنباله های عددی و توابع صحبت کنیم. ما به مفهوم حد یک تابع علاقه مندیم، زیرا این همان چیزی است که دانش آموزان اغلب با آن مواجه می شوند. اما ابتدا کلی ترین تعریف از حد:

فرض کنید مقداری متغیر وجود دارد. اگر این مقدار در فرآیند تغییر به طور نامحدود به عدد خاصی نزدیک شود آ ، آن آ - حد این مقدار

برای تابعی که در یک بازه مشخص تعریف شده است f(x)=y چنین عددی حد نامیده می شود آ ، که تابع زمانی به آن تمایل دارد ایکس ، به یک نقطه خاص تمایل دارد آ . نقطه آ متعلق به بازه ای است که تابع در آن تعریف می شود.

دست و پا گیر به نظر می رسد، اما بسیار ساده نوشته شده است:

لیم- از انگلیسی حد- حد.

یک توضیح هندسی نیز برای تعیین حد وجود دارد، اما در اینجا ما به تئوری نمی پردازیم، زیرا ما بیشتر به جنبه عملی موضوع علاقه داریم تا جنبه نظری. وقتی این را می گوییم ایکس به مقداری تمایل دارد، این بدان معناست که متغیر مقدار یک عدد را نمی گیرد، بلکه به آن بی نهایت نزدیک می شود.

بدهیم مثال خاص. وظیفه یافتن حد است.

برای حل این مثال، مقدار را جایگزین می کنیم x=3 به یک تابع ما گرفتیم:

به هر حال، اگر به عملیات پایه روی ماتریس ها علاقه دارید، مقاله جداگانه ای در این زمینه بخوانید.

در نمونه ها ایکس می تواند به هر ارزشی گرایش داشته باشد. می تواند هر عدد یا بی نهایت باشد. در اینجا یک مثال زمانی است ایکس به بی نهایت تمایل دارد:

به طور شهودی مشخص است که چیست تعداد بزرگتردر مخرج، مقدار تابع کوچکتر خواهد بود. بنابراین، با رشد نامحدود ایکس معنی 1/x کاهش می یابد و به صفر نزدیک می شود.

همانطور که می بینید، برای حل محدودیت، فقط باید مقدار مورد نظر را در تابع جایگزین کنید ایکس . با این حال، این ساده ترین مورد است. اغلب یافتن محدودیت چندان واضح نیست. در محدوده ها عدم قطعیت هایی از نوع وجود دارد 0/0 یا بی نهایت/بی نهایت . در چنین مواقعی چه باید کرد؟ توسل به ترفندها!

عدم قطعیت های درون

عدم قطعیت شکل بی نهایت/بی نهایت

بگذارید یک محدودیت وجود داشته باشد:

اگر بخواهیم بی نهایت را جایگزین تابع کنیم، هم در صورت و هم در مخرج بی نهایت می گیریم. به طور کلی، شایان ذکر است که عنصر خاصی از هنر در حل چنین عدم قطعیت هایی وجود دارد: باید توجه داشته باشید که چگونه می توانید عملکرد را به گونه ای تغییر دهید که عدم قطعیت از بین برود. در مورد ما، صورت و مخرج را بر تقسیم می کنیم ایکس در مقطع ارشد چه اتفاقی خواهد افتاد؟

از مثالی که قبلاً در بالا توضیح داده شد، می دانیم که عبارت های حاوی x در مخرج به صفر تمایل دارند. سپس راه حل حد این است:

برای حل عدم قطعیت نوع بی نهایت/بی نهایتصورت و مخرج را تقسیم بر ایکسبه بالاترین درجه

راستی! برای خوانندگان ما اکنون 10٪ تخفیف در نظر گرفته شده است هر نوع کاری

نوع دیگری از عدم قطعیت: 0/0

مثل همیشه، جایگزینی مقادیر در تابع x=-1 می دهد 0 در صورت و مخرج کمی دقیق تر نگاه کنید و متوجه خواهید شد که در شمارشگر ما معادله درجه دوم. بیایید ریشه ها را پیدا کنیم و بنویسیم:

کم کنیم و بگیریم:

بنابراین، اگر با عدم قطعیت نوع مواجه هستید 0/0 - صورت و مخرج را فاکتور بگیرید.

برای آسان‌تر کردن حل مثال‌ها، جدولی با محدودیت‌های برخی از توابع ارائه می‌کنیم:

حکومت L'Hopital در داخل

راه قدرتمند دیگری برای از بین بردن هر دو نوع عدم قطعیت. ماهیت روش چیست؟

در صورت عدم قطعیت در حد، مشتق صورت و مخرج را بگیرید تا عدم قطعیت از بین برود.

قانون L'Hopital به این صورت است:

نکته مهم : حدی که در آن مشتقات صورت و مخرج به جای مصدر و مخرج قرار می گیرند باید وجود داشته باشد.

و اکنون - یک مثال واقعی:

عدم قطعیت معمولی وجود دارد 0/0 . بیایید مشتقات صورت و مخرج را در نظر بگیریم:

Voila، عدم قطعیت به سرعت و با ظرافت حل می شود.

امیدواریم بتوانید این اطلاعات را در عمل به کار ببرید و پاسخ سوال «چگونه محدودیت ها را در ریاضیات بالاتر حل کنیم» بیابید. اگر نیاز به محاسبه حد یک دنباله یا حد یک تابع در یک نقطه دارید، و مطلقاً زمانی برای این کار وجود ندارد، برای یک راه حل سریع و دقیق با یک سرویس دانشجویی حرفه ای تماس بگیرید.

تعریف داده شده است حد نهاییدنباله ها ویژگی های مرتبط و تعریف معادل مورد بحث قرار می گیرد. تعریفی ارائه شده است که نقطه a حد دنباله نیست. نمونه هایی در نظر گرفته می شود که در آنها وجود حد با استفاده از تعریف ثابت می شود.

محتوا

همچنین ببینید: محدودیت دنباله - قضایای اساسی و خواص
انواع اصلی نابرابری ها و خواص آنها

در اینجا به تعریف حد محدود یک دنباله خواهیم پرداخت. مورد یک دنباله همگرا به بی نهایت در صفحه "تعریف یک دنباله بی نهایت بزرگ" بحث شده است.

حد یک دنباله یک عدد a if برای هر عدد مثبت ε است > 0 چنین چیزی وجود دارد عدد طبیعی N ε بسته به ε به طوری که برای همه n طبیعی > N ε نابرابری است
| x n - a|< ε .
در اینجا x n عنصر دنباله با عدد n است. محدودیت توالیبه صورت زیر مشخص می شود:
.
یا در .

بیایید نابرابری را تبدیل کنیم:
;
;
.

ε - همسایگی یک نقطه a - یک بازه باز است (a - ε، a + ε). دنباله همگرا دنباله ای است که حدی دارد. همچنین گفته می شود که دنباله همگرا می شودبه a. دنباله واگرا دنباله ای است که محدودیتی ندارد.

از تعریف چنین برمی‌آید که اگر دنباله‌ای دارای حد a باشد، مهم نیست که کدام ε-همسایگی نقطه a را انتخاب کنیم، فقط شماره نهاییعناصر توالی، یا اصلاً هیچ ( مجموعه تهی). و هر همسایگی ε شامل تعداد نامتناهی عنصر است. در واقع، با دادن عدد مشخصی ε، به این ترتیب عدد . بنابراین تمام عناصر دنباله با اعداد، طبق تعریف، در همسایگی ε نقطه a قرار دارند. اولین عناصر را می توان در هر جایی قرار داد. یعنی خارج از همسایگی ε نمی تواند بیشتر از عناصر وجود داشته باشد - یعنی یک عدد محدود.

ما همچنین توجه می کنیم که تفاوت مجبور نیست به طور یکنواخت به سمت صفر گرایش داشته باشد، یعنی همیشه کاهش یابد. می تواند به صورت غیر یکنواخت به صفر گرایش پیدا کند: می تواند افزایش یا کاهش یابد، با داشتن حداکثرهای محلی. با این حال، این ماکزیمم ها، با افزایش n، باید به سمت صفر (احتمالاً نه یکنواخت) تمایل داشته باشند.

با استفاده از نمادهای منطقی وجود و جهان شمول، تعریف حد را می توان به صورت زیر نوشت:
(1) .

تعیین اینکه a حد نیست

حال عبارت معکوس را در نظر بگیرید که عدد a حد دنباله نیست.

شماره a حد توالی نیست، اگر چنین باشد که برای هر عدد طبیعی n چنین m طبیعی وجود داشته باشد > n، چی
.

بیایید این عبارت را با استفاده از نمادهای منطقی بنویسیم.
(2) .

بیانیه که عدد a حد دنباله نیست، یعنی که
می توانید چنین همسایگی ε - نقطه a را انتخاب کنید که خارج از آن تعداد نامحدودی از عناصر دنباله وجود خواهد داشت..

بیایید به یک مثال نگاه کنیم. اجازه دهید یک دنباله با یک عنصر مشترک داده شود
(3)
هر همسایگی یک نقطه شامل بی نهایت عنصر است. با این حال، این نقطه محدودیت دنباله نیست، زیرا هر همسایگی نقطه نیز شامل تعداد نامحدودی از عناصر است. بیایید ε - همسایگی یک نقطه با ε = را در نظر بگیریم 1 . این فاصله زمانی خواهد بود (-1, +1) . همه عناصر به جز اولین عنصر با n زوج به این بازه تعلق دارند. اما همه عناصر با n فرد خارج از این بازه هستند، زیرا نابرابری x n را برآورده می کنند. > 2 . از آنجایی که تعداد عناصر فرد بی نهایت است، تعداد نامتناهی عنصر در خارج از محله انتخابی وجود خواهد داشت. بنابراین، نقطه محدودیت دنباله نیست.

اکنون ما این را با رعایت دقیق بیانیه (2) نشان خواهیم داد. نقطه حدی از دنباله (3) نیست، زیرا چنین وجود دارد که برای هر n طبیعی، یک فرد وجود دارد که نابرابری برای آن برقرار است.
.

همچنین می توان نشان داد که هر نقطه a نمی تواند حدی برای این دنباله باشد. ما همیشه می‌توانیم یک همسایگی ε - از نقطه a را انتخاب کنیم که حاوی نقطه 0 یا 2 نباشد. سپس در خارج از همسایگی انتخاب شده تعداد نامحدودی از عناصر دنباله وجود خواهد داشت.

تعریف معادل محدودیت توالی

اگر مفهوم ε - همسایگی را گسترش دهیم، می‌توانیم تعریفی معادل از حد یک دنباله ارائه دهیم. اگر به جای ε-همسایگی، هر همسایگی نقطه a را داشته باشد، تعریفی معادل به دست خواهیم آورد. همسایگی یک نقطه هر بازه باز حاوی آن نقطه است. از نظر ریاضی همسایگی یک نقطهبه صورت زیر تعریف می شود: ، جایی که ε 1 و ε 2 - اعداد مثبت دلخواه

سپس تعریف معادل از حد به شرح زیر است.

حد یک دنباله عدد a است اگر برای هر همسایگی آن عدد طبیعی N وجود داشته باشد به طوری که همه عناصر دنباله دارای اعداد متعلق به این همسایگی باشند.

این تعریف را می توان به صورت بسط یافته نیز ارائه کرد.

حد یک دنباله یک عدد اگر برای هر اعداد مثبت است و یک عدد طبیعی N وجود دارد بسته به این که نابرابری ها برای همه اعداد طبیعی برقرار باشد.
.

اثبات معادل بودن تعاریف

اجازه دهید ثابت کنیم که دو تعریف از حد یک دنباله ارائه شده در بالا معادل هستند.

طبق تعریف اول عدد a حد دنباله باشد. این بدان معنی است که یک تابع وجود دارد، به طوری که برای هر عدد مثبت ε نابرابری های زیر برآورده می شود:
(4) در .

اجازه دهید نشان دهیم که عدد a حد دنباله با تعریف دوم است. یعنی باید نشان دهیم که چنین تابعی وجود دارد که برای هر عدد مثبت ε 1 و ε 2 نابرابری های زیر برآورده می شوند:
(5) در .

دو عدد مثبت داشته باشیم: ε 1 و ε 2 . و اجازه دهید ε کوچکترین آنها باشد: . سپس ؛ ; . بیایید از این در (5) استفاده کنیم:
.
اما نابرابری ها برای . سپس نابرابری های (5) نیز برای .

یعنی تابعی را پیدا کرده ایم که نابرابری (5) برای هر عدد مثبت ε ارضا می شود. 1 و ε 2 .
قسمت اول ثابت شده است.

حالا طبق تعریف دوم عدد a حد دنباله باشد. این بدان معنی است که تابعی وجود دارد که برای هر عدد مثبت ε 1 و ε 2 نابرابری های زیر برآورده می شوند:
(5) در .

اجازه دهید نشان دهیم که عدد a حد دنباله با تعریف اول است. برای این کار باید قرار دهید. سپس هنگامی که نابرابری های زیر برقرار است:
.
این با تعریف اول مطابقت دارد.
هم ارزی تعاریف ثابت شده است.

مثال ها

مثال 1

ثابت کنیم که .

(1) .
در مورد ما ؛
.

.
بیایید از خواص نامساوی استفاده کنیم. سپس اگر و، پس
.

.
سپس
در .
این به این معنی است که عدد حد توالی داده شده است:
.

مثال 2

با استفاده از تعریف حد یک دنباله، آن را ثابت کنید
.

اجازه دهید تعریف حد یک دنباله را بنویسیم:
(1) .
در مورد ما ، ؛
.

اعداد مثبت را وارد کنید و:
.
بیایید از خواص نامساوی استفاده کنیم. سپس اگر و، پس
.

یعنی برای هر مثبتی می توانیم هر عدد طبیعی را بزرگتر یا مساوی بگیریم:
.
سپس
در .
.

مثال 3

.

ما نماد , .
بیایید تفاوت را تغییر دهیم:
.
برای n طبیعی = 1, 2, 3, ... ما داریم:
.

اجازه دهید تعریف حد یک دنباله را بنویسیم:
(1) .
اعداد مثبت را وارد کنید و:
.
سپس اگر و، پس
.

یعنی برای هر مثبتی می توانیم هر عدد طبیعی را بزرگتر یا مساوی بگیریم:
.
که در آن
در .
این به این معنی است که تعداد محدودیت دنباله است:
.

مثال 4

با استفاده از تعریف حد یک دنباله، آن را ثابت کنید
.

اجازه دهید تعریف حد یک دنباله را بنویسیم:
(1) .
در مورد ما ، ؛
.

اعداد مثبت را وارد کنید و:
.
سپس اگر و، پس
.

یعنی برای هر مثبتی می توانیم هر عدد طبیعی را بزرگتر یا مساوی بگیریم:
.
سپس
در .
این به این معنی است که تعداد محدودیت دنباله است:
.

منابع:
L.D. کودریاوتسف. دوره تحلیل ریاضی. جلد 1. مسکو، 2003.
سانتی متر. نیکولسکی. دوره تحلیل ریاضی. جلد 1. مسکو، 1983.

همچنین ببینید:

تعاریف حد یک تابع با توجه به هاینه (از طریق دنباله ها) و با توجه به کوشی (از طریق همسایگی اپسیلون و دلتا) ارائه شده است. تعاریف به شکل جهانی ارائه شده است که برای محدودیت های دو طرفه و یک طرفه در نقاط محدود و بی نهایت دور قابل استفاده است. این تعریف که نقطه a حد یک تابع نیست در نظر گرفته می شود. اثبات هم ارزی تعاریف هاینه و کوشی.

محتوا

همچنین ببینید: همسایگی یک نقطه
تعیین حد یک تابع در یک نقطه پایانی
تعیین حد تابع در بی نهایت

اولین تعریف حد یک تابع (طبق گفته هاینه)

(ایکس)در نقطه x 0 :
,
اگر
1) چنین همسایگی سوراخ شده ای از نقطه x وجود دارد 0
2) برای هر دنباله ای (xn)، همگرا به x 0 :
، که عناصر آن متعلق به محله است،
دنباله (f(xn))به یک همگرا می شود:
.

اینجا x 0 و a می تواند اعداد متناهی یا نقاطی در بی نهایت باشد. محله می تواند دو طرفه یا یک طرفه باشد.

.

تعریف دوم از حد یک تابع (طبق نظر کوشی)

عدد a را حد تابع f می نامند (ایکس)در نقطه x 0 :
,
اگر
1) چنین همسایگی سوراخ شده ای از نقطه x وجود دارد 0 ، که تابع بر روی آن تعریف شده است.
2) برای هر عدد مثبت ε > 0 چنین عدد δ ε وجود دارد > 0 بسته به ε، که برای همه x متعلق به δ ε سوراخ شده - همسایگی نقطه x 0 :
,
مقادیر تابع f (ایکس)متعلق به همسایگی ε نقطه a:
.

امتیاز x 0 و a می تواند اعداد متناهی یا نقاطی در بی نهایت باشد. محله نیز می تواند دو طرفه یا یک طرفه باشد.

اجازه دهید این تعریف را با استفاده از نمادهای منطقی وجود و جهان شمول بنویسیم:
.

این تعریف از محله هایی با انتهای مساوی استفاده می کند. یک تعریف معادل را می توان با استفاده از همسایگی دلخواه نقاط ارائه داد.

تعریف با استفاده از محله های دلخواه
عدد a را حد تابع f می نامند (ایکس)در نقطه x 0 :
,
اگر
1) چنین همسایگی سوراخ شده ای از نقطه x وجود دارد 0 ، که تابع بر روی آن تعریف شده است.
2) برای هر محله U (آ)از نقطه a چنین همسایگی سوراخ شده ای از نقطه x وجود دارد 0 که برای تمام x متعلق به همسایگی سوراخ شده نقطه x 0 :
,
مقادیر تابع f (ایکس)متعلق به محله U (آ)نکات الف:
.

با استفاده از نمادهای منطقی هستی و جهان شمول می توان این تعریف را به صورت زیر نوشت:
.

محدودیت های یک طرفه و دو طرفه

تعاریف فوق از این نظر جهانی هستند که می توان از آنها برای هر نوع محله استفاده کرد. اگر به عنوان محله سوراخ شده سمت چپ نقطه پایانی استفاده کنیم، تعریف حد سمت چپ را به دست می آوریم. اگر همسایگی یک نقطه در بینهایت را به عنوان همسایگی استفاده کنیم، تعریف حد در بینهایت را بدست می آوریم.

برای تعیین حد هاینه، این به این واقعیت مربوط می شود که یک محدودیت اضافی بر روی یک دنباله دلخواه که به همگرا می شود اعمال می شود: عناصر آن باید به همسایگی سوراخ شده مربوطه در نقطه تعلق داشته باشند.

برای تعیین حد کوشی، در هر مورد باید با استفاده از تعاریف مناسب همسایگی یک نقطه، عبارات را به نابرابری تبدیل کرد.
به "همسایگی یک نقطه" مراجعه کنید.

تعیین اینکه نقطه a حد تابع نیست

اغلب لازم است از شرطی استفاده کنیم که نقطه a حد تابع در نباشد. اجازه دهید برای تعاریف بالا نفی بسازیم. در آنها فرض می کنیم که تابع f (ایکس)بر روی برخی از محله های سوراخ شده نقطه x تعریف شده است 0 . نقاط a و x 0 می تواند اعداد متناهی یا بی نهایت دور باشد. همه موارد ذکر شده در زیر برای محدودیت های دوجانبه و یک جانبه اعمال می شود.

به گفته هاینه.
شماره a نیستحد تابع f (ایکس)در نقطه x 0 : ,
اگر چنین دنباله ای وجود داشته باشد (xn)، همگرا به x 0 :
,
که عناصر آن متعلق به محله است،
دنباله چیست (f(xn))به یک همگرا نمی شود:
.
.

به گفته کوشی.
شماره a نیستحد تابع f (ایکس)در نقطه x 0 :
,
اگر چنین عدد مثبت ε وجود داشته باشد > 0 بنابراین برای هر عدد مثبت δ > 0 ، یک x وجود دارد که متعلق به همسایگی δ سوراخ شده نقطه x است. 0 :
,
که مقدار تابع f (ایکس)به همسایگی ε نقطه a تعلق ندارد:
.
.

البته اگر نقطه a حد یک تابع در نباشد، به این معنی نیست که نمی تواند محدودیت داشته باشد. ممکن است حدی وجود داشته باشد، اما برابر با a نیست. همچنین ممکن است که تابع در یک محله سوراخ شده از نقطه تعریف شده باشد، اما محدودیتی در آن نداشته باشد.

تابع f(x) = sin(1/x)هیچ محدودیتی به عنوان x → 0 ندارد.

به عنوان مثال، یک تابع در تعریف شده است، اما هیچ محدودیتی وجود ندارد. برای اثبات آن، بیایید دنباله را در نظر بگیریم. به یک نقطه همگرا می شود 0 : . چون پس .
بیایید دنباله را در نظر بگیریم. همچنین به نقطه همگرا می شود 0 : . اما از آن پس .
آنگاه حد نمی تواند با هیچ عدد a برابر باشد. در واقع، برای، دنباله ای وجود دارد که با آن . بنابراین، هر عدد غیر صفر محدودیت نیست. اما این محدودیت نیز نیست، زیرا دنباله ای وجود دارد که با آن .

هم ارزی تعاریف هاینه و کوشی از حد

قضیه
تعاریف هاینه و کوشی از حد یک تابع معادل هستند.

اثبات

در اثبات، فرض می کنیم که تابع در برخی از همسایگی های سوراخ شده یک نقطه (محدود یا در بی نهایت) تعریف شده است. نقطه a همچنین می تواند متناهی یا در بی نهایت باشد.

اثبات هاینه ⇒ کوشی

اجازه دهید تابع در یک نقطه با توجه به تعریف اول (طبق تعریف هاینه) حد a داشته باشد. یعنی برای هر دنباله ای که به محله سوراخ شده یک نقطه تعلق دارد و حدی دارد
(1) ,
حد دنباله عبارت است از:
(2) .

اجازه دهید نشان دهیم که تابع در یک نقطه دارای حد کوشی است. یعنی برای همه چیزی هست که برای همه است.

بیایید برعکس فرض کنیم. اجازه دهید شرایط (1) و (2) برآورده شود، اما تابع محدودیت کوشی ندارد. یعنی چیزی وجود دارد که برای هر کسی وجود دارد، بنابراین
.

بیایید، جایی که n یک عدد طبیعی است. سپس وجود دارد، و
.
بنابراین ما یک دنباله همگرا ساخته ایم، اما حد دنباله برابر با a نیست. این با شرایط قضیه در تضاد است.

قسمت اول ثابت شده است.

اثبات کوشی ⇒ اثبات هاینه

طبق تعریف دوم (طبق گفته کوشی) اجازه دهید تابع در نقطه ای یک حد داشته باشد. یعنی برای هر کسی که وجود دارد
(3) برای همه .

اجازه دهید نشان دهیم که تابع یک حد a در نقطه ای مطابق با هاینه دارد.
بیایید یک عدد دلخواه بگیریم. طبق تعریف کوشی، عدد وجود دارد، بنابراین (3) برقرار است.

اجازه دهید یک دنباله دلخواه بگیریم که متعلق به محله سوراخ شده و همگرا به . با تعریف یک دنباله همگرا، برای هر چیزی وجود دارد که وجود دارد
در .
سپس از (3) چنین می شود که
در .
از آنجایی که این برای هر کسی صدق می کند، پس
.

قضیه ثابت شده است.

منابع:
L.D. کودریاوتسف. دوره تحلیل ریاضی. جلد 1. مسکو، 2003.

همچنین ببینید:

امروز در کلاس نگاه خواهیم کرد توالی دقیقو تعریف دقیق حد یک تابع، و همچنین حل مسائل مربوط به ماهیت نظری را بیاموزید. این مقاله در درجه اول برای دانشجویان سال اول علوم طبیعی و تخصص های مهندسی است که شروع به مطالعه تئوری تجزیه و تحلیل ریاضی کردند و در درک این بخش از ریاضیات عالی با مشکلاتی مواجه شدند. علاوه بر این، مطالب برای دانش آموزان دبیرستانی کاملاً در دسترس است.

در طول سال‌های فعالیت سایت، ده‌ها نامه با این مضمون دریافت کرده‌ام: «من تحلیل ریاضی را خوب نمی‌فهمم، چه کار کنم؟»، «اصلاً ریاضی را نمی‌فهمم، به ترک تحصیل فکر می کنم و غیره. و در واقع، این متان است که اغلب پس از جلسه اول، گروه دانشجو را نازک می کند. چرا این طور است؟ چون موضوع به طرز غیرقابل تصوری پیچیده است؟ اصلا! تئوری تجزیه و تحلیل ریاضی آنقدرها هم که عجیب است دشوار نیست. و باید او را همان طور که هست بپذیری و دوستش داشته باشی =)

بیایید با سخت ترین مورد شروع کنیم. اولین و مهمترین چیز این است که شما مجبور نیستید تحصیل خود را رها کنید. به درستی درک کنید، همیشه می توانید ترک کنید؛-) البته، اگر بعد از یک یا دو سال از تخصص انتخابی خود احساس بیماری کردید، بله، باید در مورد آن فکر کنید. (و عصبانی نشو!)در مورد تغییر فعالیت اما در حال حاضر ارزش ادامه دادن را دارد. و لطفاً عبارت "من چیزی نمی فهمم" را فراموش کنید - این اتفاق نمی افتد که شما اصلاً چیزی را نمی فهمید.

اگر تئوری بد بود چه باید کرد؟ به هر حال، این نه تنها در مورد تجزیه و تحلیل ریاضی صدق می کند. اگر تئوری بد است، ابتدا باید به طور جدی روی تمرین تمرکز کنید. در این مورد، دو وظیفه استراتژیک به طور همزمان حل می شود:

- اولاً سهم قابل توجهی دانش نظریاز طریق تمرین به وجود آمد. و به همین دلیل است که بسیاری از مردم این نظریه را از طریق ... درک می کنند - درست است! نه، نه، تو به این فکر نمی کنی =)

– و ثانیاً، مهارت‌های عملی به احتمال زیاد شما را از امتحان «کشش» می‌کند، حتی اگر... اما اجازه دهید اینقدر هیجان زده نشویم! همه چیز واقعی است و همه چیز را می توان در یک زمان نسبتاً کوتاه "بالا" کرد. تجزیه و تحلیل ریاضی بخش مورد علاقه من در ریاضیات عالی است و بنابراین نمی توانم کمکی به شما نکنم:

در ابتدای ترم 1، محدودیت های توالی و محدودیت های عملکرد معمولا پوشش داده می شود. نمی دانید اینها چیست و نمی دانید چگونه آنها را حل کنید؟ با مقاله شروع کنید محدودیت های عملکرد، که در آن خود مفهوم "روی انگشتان" بررسی می شود و ساده ترین نمونه ها تجزیه و تحلیل می شود. در مرحله بعد، درس های دیگر را در مورد موضوع، از جمله درسی در مورد آن کار کنید در سکانس ها، که من در واقع قبلاً تعریف دقیقی از آن ارائه کرده ام.

به جز علائم نابرابری و مدول چه نمادهایی را می شناسید؟

- یک چوب بلند عمودی به این صورت است: "چنین آن"، "چنین آن"، "چنین آن" یا "چنین آن"در مورد ما، بدیهی است که ما در مورد یک عدد صحبت می کنیم - بنابراین "چنین"؛

– برای همه «en» بزرگتر از ;

– علامت مدول به معنای فاصله است، یعنی این مدخل به ما می گوید که فاصله بین مقادیر کمتر از اپسیلون است.

خوب، کشنده سخت است؟ =)

پس از تسلط بر تمرین، مشتاقانه منتظر دیدار شما در پاراگراف بعدی هستم:

و در واقع، بیایید کمی فکر کنیم - چگونه یک تعریف دقیق از دنباله را تدوین کنیم؟ ... اولین چیزی که در دنیا به ذهن می رسد درس عملی: "حد یک دنباله عددی است که اعضای دنباله بی نهایت به آن نزدیک می شوند."

خوب، بیایید آن را بنویسیم دنباله :

درک آن کار سختی نیست دنباله بی نهایت نزدیک به عدد -1 و اصطلاحات زوج است - به یک".

یا شاید دو حد وجود دارد؟ اما پس چرا هیچ سکانسی نمی تواند ده یا بیست عدد از آنها را داشته باشد؟ شما می توانید از این راه دور بروید. در این زمینه منطقی است که چنین فرض کنیم اگر یک دنباله دارای محدودیت باشد، پس منحصر به فرد است.

توجه داشته باشید : دنباله محدودیتی ندارد، اما دو دنباله فرعی از آن قابل تشخیص است (به بالا مراجعه کنید) که هر کدام حد خود را دارند.

بنابراین، تعریف فوق غیرقابل دفاع است. بله، برای مواردی از این قبیل کار می کند (که من در توضیح ساده مثال های کاربردی به درستی استفاده نکردم)، اما اکنون باید یک تعریف دقیق پیدا کنیم.

تلاش دوم: "محدودیت یک دنباله، عددی است که همه اعضای دنباله به آن نزدیک می شوند، به جز شاید آنها نهاییمقادیر." این به حقیقت نزدیک‌تر است، اما هنوز کاملاً دقیق نیست. بنابراین، برای مثال، دنباله نیمی از عبارات به هیچ وجه به صفر نزدیک نمی شوند - آنها به سادگی با آن برابر هستند =) به هر حال، "چراغ چشمک زن" معمولاً دو مقدار ثابت می گیرد.

توضیح این فرمول دشوار نیست، اما سؤال دیگری مطرح می شود: چگونه تعریف را در آن بنویسیم نشانه های ریاضی? دنیای علمیمن مدت زیادی با این مشکل دست و پنجه نرم کردم تا اینکه وضعیت را حل کردم استاد معروف، که در اصل آنالیز ریاضی کلاسیک را با تمام سختی آن رسمیت بخشید. کوشی عمل جراحی را پیشنهاد کرد محیط اطراف ، که به طور قابل توجهی این نظریه را پیش برد.

یک نکته و آن را در نظر بگیرید دلخواه-محیط اطراف:

ارزش "epsilon" همیشه مثبت است، و علاوه بر این، ما این حق را داریم که خودمان آن را انتخاب کنیم. بیایید فرض کنیم که در این محله اعضای زیادی وجود دارد (نه لزوما همه)چند دنباله اینکه مثلاً ترم دهم در همسایگی است چگونه یادداشت کنیم؟ بگذارید در سمت راست آن باشد. سپس فاصله بین نقاط و باید کمتر از “epsilon” باشد: . اما اگر "x دهم" در سمت چپ نقطه "الف" قرار داشته باشد، این تفاوت منفی خواهد بود و بنابراین علامت باید به آن اضافه شود. مدول: .

تعریف: یک عدد را حد یک دنباله اگر می گویند برای هرچیاطراف آن (از پیش انتخاب شده)یک عدد طبیعی وجود دارد که همهاعضای دنباله با اعداد بالاتر در داخل محله خواهند بود:

یا به طور خلاصه: اگر

به عبارت دیگر، مهم نیست که چقدر مقدار "اپسیلون" را کوچک می گیریم، دیر یا زود "دم بی نهایت" دنباله به طور کامل در این همسایگی خواهد بود.

به عنوان مثال، "دم بی نهایت" دنباله به طور کامل وارد هر محله کوچک دلخواه نقطه می شود. بنابراین این مقدار طبق تعریف، حد توالی است. به شما یادآوری می کنم که دنباله ای که حد آن صفر است نامیده می شود بی نهایت کوچک.

لازم به ذکر است که برای یک سکانس دیگر نمی توان گفت "دم بی پایان" وارد خواهد شد"- اعضای با اعداد فرد در واقع برابر با صفر هستند و "هیچ جا نمی روند" =) به همین دلیل است که در تعریف از فعل "ظاهر می شود" استفاده می شود. و البته اعضای سکانسی مانند این نیز «به جایی نمی‌رسند». به هر حال، بررسی کنید که آیا تعداد محدودیت آن است یا خیر.

اکنون نشان خواهیم داد که دنباله محدودیتی ندارد. برای مثال، همسایگی نقطه را در نظر بگیرید. کاملاً واضح است که چنین عددی وجود ندارد که پس از آن همه عبارت‌ها در یک محله مشخص به پایان برسند - عبارت‌های فرد همیشه به «منهای یک» «بیرون می‌روند». به همین دلیل، هیچ محدودیتی در نقطه وجود ندارد.

بیایید مطالب را با تمرین ادغام کنیم:

مثال 1

ثابت کنید که حد دنباله صفر است. عددی را مشخص کنید که پس از آن همه اعضای دنباله تضمین می‌شوند که در هر محله کوچک دلخواه نقطه قرار دارند.

توجه داشته باشید : برای بسیاری از دنباله ها، عدد طبیعی مورد نیاز به مقدار بستگی دارد - از این رو نماد .

راه حل: در نظر گرفتن دلخواه هستتعداد - به طوری که همه اعضای با تعداد بالاتر در این محله باشند:

برای نشان دادن وجود عدد مورد نیاز، آن را از طریق بیان می کنیم.

از آنجایی که برای هر مقدار "en"، علامت مدول را می توان حذف کرد:

ما از اقدامات "مدرسه ای" با نابرابری هایی استفاده می کنیم که در کلاس تکرار کردم نابرابری های خطیو دامنه تابع. در این مورد، یک شرایط مهم این است که "epsilon" و "en" مثبت هستند:

از آنجایی که در سمت چپ ما در مورد اعداد طبیعی صحبت می کنیم، و قسمت راست V مورد کلیکسری است، پس باید گرد شود:

توجه داشته باشید : گاهی اوقات یک واحد به سمت راست اضافه می شود تا در سمت امن باشد، اما در واقع این بیش از حد است. به طور نسبی، اگر نتیجه را با گرد کردن به پایین تضعیف کنیم، نزدیکترین عدد مناسب ("سه") همچنان نابرابری اصلی را برآورده می کند.

اکنون به نابرابری نگاه می کنیم و آنچه را در ابتدا در نظر گرفتیم به یاد می آوریم دلخواه- همسایگی، یعنی "epsilon" می تواند برابر باشد هر کسییک عدد مثبت

نتیجه: برای هر محله کوچک دلخواه یک نقطه، مقدار پیدا شد . بنابراین، عدد بر اساس تعریف، حد یک دنباله است. Q.E.D.

به هر حال، از نتیجه به دست آمده یک الگوی طبیعی به وضوح قابل مشاهده است: هر چه محله کوچکتر باشد، تعداد آن بزرگتر است، پس از آن همه اعضای دنباله در این محله خواهند بود. اما مهم نیست که "اپسیلون" چقدر کوچک باشد، همیشه یک "دم بی نهایت" در داخل و خارج وجود خواهد داشت - حتی اگر بزرگ باشد. نهاییتعداد اعضا

برداشت شما چگونه است؟ =) موافقم که کمی عجیب است. اما به شدت!لطفا دوباره بخوانید و دوباره به همه چیز فکر کنید.

بیایید به یک مثال مشابه نگاه کنیم و دیگران را بشناسیم روش های فنی:

مثال 2

راه حل: با تعریف یک دنباله اثبات آن ضروری است (این را بلند بگو!!!).

در نظر بگیریم دلخواه- همسایگی نقطه و بررسی، آیا وجود داردعدد طبیعی - به طوری که برای همه اعداد بزرگتر نابرابری زیر برقرار است:

برای نشان دادن وجود چنین، باید "en" را از طریق "epsilon" بیان کنید. عبارت زیر علامت مدول را ساده می کنیم:

ماژول علامت منفی را از بین می برد:

مخرج برای هر "en" مثبت است، بنابراین، میله ها را می توان حذف کرد:

بر زدن:

حالا باید استخراج کنیم ریشه دوم، اما نکته مهم این است که برای برخی از "اپسیلون" سمت راست منفی خواهد بود. برای جلوگیری از این دردسر تقویت کنیمنابرابری بر اساس مدول:

چرا می توان این کار را انجام داد؟ اگر، به طور نسبی، معلوم شود که، آنگاه شرط نیز برآورده می شود. ماژول می تواند فقط افزایش دهیدشماره مورد نظر، و این برای ما نیز مناسب خواهد بود! به طور کلی اگر صدم مناسب است، دو صدم هم مناسب است! طبق تعریف، باید نشان دهید حقیقت وجود عدد(حداقل برخی)، پس از آن همه اعضای دنباله در همسایگی خواهند بود. به هر حال، به همین دلیل است که ما از گرد شدن نهایی سمت راست به سمت بالا نمی ترسیم.

استخراج ریشه:

و نتیجه را گرد کنید:

نتیجه: زیرا مقدار "epsilon" به طور دلخواه انتخاب شد، سپس برای هر محله کوچک دلخواه نقطه، مقدار آن پیدا شد. ، به طوری که برای همه اعداد بزرگتر نابرابری برقرار است . بدین ترتیب، اولی. Q.E.D.

من توصیه میکنم بخصوصدرک تقویت و تضعیف نابرابری ها یک تکنیک معمولی و بسیار رایج در تحلیل ریاضی است. تنها چیزی که باید نظارت کنید صحت این یا آن عمل است. بنابراین، برای مثال، نابرابری تحت هیچ شرایطی امکان پذیر نیست شل کردن، تفریق، بگویید، یک:

باز هم به صورت مشروط: اگر عدد دقیقاً مطابقت داشته باشد، ممکن است شماره قبلی دیگر مناسب نباشد.

مثال زیر برای یک راه حل مستقل:

مثال 3

با استفاده از تعریف یک دنباله، آن را ثابت کنید

راه حل و پاسخ کوتاه در پایان درس.

اگر دنباله بی نهایت بزرگ، سپس تعریف یک حد به روشی مشابه فرموله می شود: یک نقطه حد یک دنباله نامیده می شود اگر وجود داشته باشد، به اندازه ای که دوست داریدعدد، عددی وجود دارد که برای همه اعداد بزرگتر، نابرابری برآورده می شود. شماره تماس گرفته می شود مجاورت نقطه "به علاوه بی نهایت":

به عبارت دیگر، هر چه باشد پراهمیتمهم نیست که چه اتفاقی می افتد، "دم نامتناهی" دنباله قطعاً به همسایگی نقطه می رود و فقط تعداد محدودی از عبارت ها در سمت چپ باقی می ماند.

مثال استاندارد:

و علامت کوتاه شده: , if

برای مورد، تعریف را خودتان بنویسید. نسخه صحیح در انتهای درس آمده است.

پس از بررسی مثال‌های عملی و فهمیدن تعریف حد یک دنباله، می‌توانید به ادبیات حسابان و/یا دفتر سخنرانی خود مراجعه کنید. توصیه می کنم جلد 1 بوهان را دانلود کنید (ساده تر - برای دانشجویان مکاتبه ای)و فیختنهولتز (با جزئیات و جزئیات بیشتر). در میان نویسندگان دیگر، من Piskunov را توصیه می کنم، که دوره اش برای دانشگاه های فنی است.

سعی کنید با وجدان قضایایی را که مربوط به حد توالی، اثبات آنها، پیامدها است، مطالعه کنید. در ابتدا، این نظریه ممکن است "ابری" به نظر برسد، اما این طبیعی است - فقط باید به آن عادت کنید. و بسیاری حتی طعم آن را خواهند چشید!

تعریف دقیق حد یک تابع

بیایید با همین موضوع شروع کنیم - چگونه این مفهوم را فرموله کنیم؟ تعریف شفاهی حد یک تابع بسیار ساده تر است: "عدد حد یک تابع است اگر "x" تمایل به (هم چپ و هم راست)، مقادیر تابع مربوطه به » (نقاشی را ببینید). به نظر می رسد همه چیز عادی است، اما کلمات کلمه هستند، معنی معنی است، نماد یک نماد است، و نمادهای ریاضی دقیق کافی وجود ندارد. و در پاراگراف دوم با دو رویکرد برای حل این موضوع آشنا می شویم.

اجازه دهید تابع در یک بازه زمانی مشخص، به استثنای نقطه، تعریف شود. که در ادبیات آموزشیبه طور کلی پذیرفته شده است که تابع وجود دارد نهتعریف شده است:

این انتخاب تاکید می کند ماهیت حد یک تابع: "ایکس" بی نهایت نزدیکرویکردها و مقادیر مربوط به تابع هستند بی نهایت نزدیکبه . به عبارت دیگر، مفهوم حد به معنای «رویکرد دقیق» به نقاط نیست، بلکه به معنای آن است تقریب بی نهایت نزدیک، فرقی نمی کند که تابع در نقطه تعریف شده باشد یا خیر.

تعریف اول از حد یک تابع، تعجب آور نیست، با استفاده از دو دنباله فرموله شده است. اولاً، مفاهیم مرتبط هستند، و ثانیاً، حدود توابع معمولاً پس از محدودیت‌های توالی مورد مطالعه قرار می‌گیرند.

دنباله را در نظر بگیرید نکته ها (روی نقاشی نیست), متعلق به فاصلهو متفاوت از، که همگرا می شودبه . سپس مقادیر تابع مربوطه نیز یک دنباله عددی را تشکیل می دهند که اعضای آن در محور ارتین قرار دارند.

حد یک تابع طبق هاینه برای هرچیدنباله ای از نقاط (متعلق و متفاوت از)، که به نقطه همگرا می شود، دنباله مربوط به مقادیر تابع به همگرا می شود.

ادوارد هاینه یک ریاضیدان آلمانی است. ... و نیازی به چنین چیزی نیست، فقط یک همجنسگرا در اروپا وجود دارد - گی-لوساک =)

تعریف دوم حد ایجاد شد... بله بله درست می فرمایید. اما ابتدا بیایید طراحی آن را درک کنیم. یک همسایگی دلخواه نقطه را در نظر بگیرید (محله "سیاه"). بر اساس پاراگراف قبل، مدخل به این معناست که مقداری ارزشتابع در داخل محله "epsilon" واقع شده است.

اکنون - همسایگی را می یابیم که با - همسایگی داده شده مطابقت دارد (خطوط نقطه چین سیاه را از چپ به راست و سپس از بالا به پایین بکشید). توجه داشته باشید که مقدار انتخاب شده است در طول بخش کوچکتر، در این مورد - در امتداد طول بخش سمت چپ کوتاهتر. علاوه بر این، "تمشک" - همسایگی یک نقطه حتی می تواند کاهش یابد، زیرا در تعریف زیر حقیقت وجود مهم استاین محله و به طور مشابه، نماد به این معنی است که مقداری در همسایگی "دلتا" قرار دارد.

محدودیت عملکرد کوشی: یک عدد حد تابع در یک نقطه if نامیده می شود برای هرچی از پیش انتخاب شدهمحله (هرچقدر که دوست دارید کوچک), وجود دارد-همسایگی نقطه، چنین، که: AS ONLY مقادیر (متعلق به)در این حوزه گنجانده شده است: (فلش های قرمز)- بنابراین بلافاصله مقادیر تابع مربوطه برای وارد کردن - همسایگی تضمین می شود: (فلش های آبی).

باید به شما هشدار بدهم که برای شفافیت، کمی بداهه نوشتم، پس زیاده روی نکنید =)

ورودی کوتاه:، اگر

اصل تعریف چیست؟ به بیان تصویری، با کاهش بی‌نهایت همسایگی، مقادیر تابع را تا حد آنها «همراه» می‌کنیم و هیچ جایگزینی برای نزدیک شدن به جای دیگری باقی نمی‌گذاریم. کاملا غیر معمول، اما باز هم سختگیرانه! برای درک کامل ایده، عبارت را دوباره بخوانید.

! توجه: اگر فقط نیاز به فرمول بندی دارید تعریف هاینهیا فقط تعریف کوشیلطفا در مورد را فراموش نکنید قابل توجهنظرات اولیه: "یک تابع را در نظر بگیرید که در یک بازه زمانی مشخص تعریف شده است، به استثنای یک نقطه". این را در همان ابتدا یک بار گفتم و هر بار تکرار نکردم.

با توجه به قضیه مربوط به تحلیل ریاضی، تعاریف هاینه و کوشی معادل هستند، اما گزینه دوم معروف ترین است. (هنوز این کار را انجام می دهد!)، که به آن "محدودیت زبان" نیز می گویند:

مثال 4

با استفاده از تعریف حد، آن را ثابت کنید

راه حل: تابع در کل خط عددی به جز نقطه تعریف شده است. با استفاده از تعریف، وجود یک حد را در یک نقطه معین اثبات می کنیم.

توجه داشته باشید : ارزش محله "دلتا" به "epsilon" بستگی دارد، از این رو تعیین می شود

در نظر بگیریم دلخواه-محیط اطراف. وظیفه این است که از این مقدار برای بررسی اینکه آیا استفاده کنید آیا وجود دارد-محیط اطراف، چنین، که از نابرابری نابرابری به دنبال دارد .

با این فرض، آخرین نابرابری را تبدیل می کنیم:
(سه جمله ای درجه دوم را گسترش داد)

تعریف 1. اجازه دهید E- یک عدد بی نهایت اگر هر محله ای حاوی نقاطی از مجموعه باشد E، متفاوت از نقطه آ، آن آتماس گرفت نهایی نقطه مجموعه E.

تعریف 2. (هاینریش هاینه (1821-1881)). اجازه دهید تابع
در مجموعه تعریف شده است ایکسو آتماس گرفت حد کارکرد
در نقطه (یا چه زمانی
، اگر برای هر دنباله ای از مقادیر آرگومان باشد
، همگرا به ، دنباله مربوط به مقادیر تابع به عدد همگرا می شود آ. آنها می نویسند:
.

مثال ها. 1) عملکرد
دارای حدی برابر با با، در هر نقطه از خط اعداد.

در واقع، برای هر نقطه و هر دنباله ای از مقادیر آرگومان
، همگرا به و متشکل از اعدادی غیر از ، دنباله مربوط به مقادیر تابع دارای شکل است
، و می دانیم که این دنباله به همگرا می شود با. از همین رو
.

2) برای عملکرد

.

این بدیهی است، زیرا اگر
، سپس
.

3) تابع دیریکله
هیچ محدودیتی در هیچ نقطه ای ندارد

در واقع، اجازه دهید
و
، و همه - اعداد گویا. سپس
برای همه n، از همین رو
. اگر
و این همه است پس اعداد غیر منطقی هستند
برای همه n، از همین رو
. بنابراین می بینیم که شرایط تعریف 2 برآورده نمی شود
وجود ندارد.

4)
.

در واقع، اجازه دهید یک توالی دلخواه در نظر بگیریم
، همگرا به

شماره 2. سپس . Q.E.D.

تعریف 3. (کوشی (1789-1857)). اجازه دهید تابع
در مجموعه تعریف شده است ایکسو نقطه حد این مجموعه است. عدد آتماس گرفت حد کارکرد
در نقطه (یا چه زمانی
، در صورت وجود
خواهد بود
، به طوری که برای تمام مقادیر آرگومان ایکس، ارضای نابرابری

,

نابرابری درست است

.

آنها می نویسند:
.

تعریف کوشی را می توان با استفاده از همسایگی ها نیز ارائه داد، اگر توجه داشته باشیم که:

اجازه دهید عملکرد داشته باشد
در مجموعه تعریف شده است ایکسو نقطه حد این مجموعه است. عدد آحد نامیده می شود کارکرد
در نقطه ، در صورت وجود -همسایگی یک نقطه آ
سوراخ شده وجود دارد - همسایگی یک نقطه
،به طوری که
.

توضیح این تعریف با یک نقاشی مفید است.

مثال 5.
.

در واقع، بیایید بگیریم
به صورت تصادفی و پیدا کنید
، به طوری که برای همه ایکس، ارضای نابرابری
نابرابری برقرار است
. آخرین نابرابری معادل نابرابری است
، پس می بینیم که گرفتن کافی است
. بیانیه ثابت شده است.

نمایشگاه

قضیه 1. تعاریف حد تابع از نظر هاینه و کوشی معادل هستند.

اثبات. 1) اجازه دهید
به گفته کوشی بیایید ثابت کنیم که همان عدد از نظر هاینه نیز یک حد است.

بگیریم
خودسرانه طبق تعریف 3 وجود دارد
، به طوری که برای همه
نابرابری برقرار است
. اجازه دهید
– یک توالی دلخواه به گونه ای که
در
. سپس یک عدد وجود دارد نطوری که برای همه
نابرابری برقرار است
، از همین رو
برای همه
، یعنی

به گفته هاینه

2) اکنون اجازه دهید
به گفته هاینه این را ثابت کنیم
و به گفته کوشی.

بیایید برعکس را فرض کنیم، یعنی. چی
به گفته کوشی سپس وجود دارد
طوری که برای هر کسی
خواهد بود
,
و
. دنباله را در نظر بگیرید
. برای مشخص شده
و هر nوجود دارد

و
. این به آن معنا است
، با اينكه
، یعنی عدد آحد نیست
در نقطه به گفته هاینه ما به تناقضی دست یافته ایم که این گفته را ثابت می کند. قضیه ثابت شده است.

قضیه 2 (در منحصر به فرد بودن حد). اگر محدودیتی برای یک تابع در یک نقطه وجود داشته باشد ، پس او تنها است.

اثبات. اگر حدی طبق هاینه تعریف شود، منحصر به فرد بودن آن از منحصر به فرد بودن حد دنباله ناشی می شود. اگر حدی بر اساس کوشی تعریف شود، منحصر به فرد بودن آن از هم ارزی تعاریف حد بر اساس کوشی و هاینه ناشی می شود. قضیه ثابت شده است.

مشابه معیار کوشی برای دنباله ها، معیار کوشی برای وجود حد یک تابع برقرار است. قبل از فرمول بندی، اجازه دهید ارائه دهیم

تعریف 4. می گویند که تابع
شرایط کوشی را در نقطه ارضا می کند ، در صورت وجود
وجود دارد

، به طوری که
و
، نابرابری برقرار است
.

قضیه 3 (معیار کوشی برای وجود حد). به منظور عملکرد
در نقطه داشت حد محدود، لازم و کافی است که در این مرحله تابع شرط کوشی را برآورده کند.

اثبات.ضرورت. اجازه دهید
. ما باید این را ثابت کنیم
در نقطه ارضا می کند حالت کوشی

بگیریم
خودسرانه و قرار داده است
. با تعریف حد برای وجود دارد
، به طوری که برای هر مقدار
، ارضای نابرابری ها
و
، نابرابری ها ارضا می شوند
و
. سپس

نیاز ثابت شده است.

کفایت. اجازه دهید تابع
در نقطه ارضا می کند حالت کوشی ما باید ثابت کنیم که آن را در نقطه است حد نهایی

بگیریم
خودسرانه طبق تعریف 4 وجود دارد
، به طوری که از نابرابری ها
,
به دنبال آن است
- این داده شده است.

اجازه دهید ابتدا آن را برای هر دنباله ای نشان دهیم
، همگرا به ، دنباله
مقادیر تابع همگرا می شوند. در واقع، اگر
، سپس، به موجب تعریف حد دنباله، برای یک معین
یک عدد وجود دارد ن، به طوری که برای هر

و
. از آنجا که
در نقطه شرایط کوشی را برآورده می کند، ما داریم
. سپس با معیار کوشی برای دنباله ها، دنباله
همگرا می شود. اجازه دهید نشان دهیم که تمام این دنباله ها
به همان حد همگرا می شوند. بیایید برعکس را فرض کنیم، یعنی. دنباله ها چیست
و
,
,
، به طوری که. بیایید دنباله را در نظر بگیریم. واضح است که همگرا می شود بنابراین، با آنچه در بالا ثابت شد، توالی همگرا می شود، که غیرممکن است، زیرا دنباله های بعدی
و
محدودیت های متفاوتی دارند و . تناقض حاصل نشان می دهد که =. بنابراین، طبق تعریف هاینه، تابع در نقطه است حد نهایی کفایت و از این رو قضیه ثابت شده است.