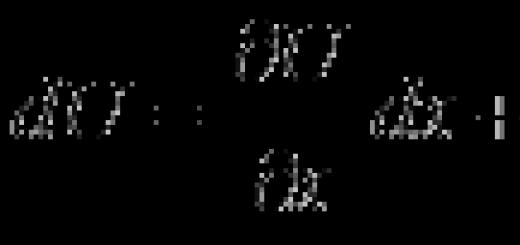Das 19. Jahrhundert ist der Beginn einer neuen, vierten Periode in der Geschichte der Mathematik – der Periode der modernen Mathematik.

Wir wissen bereits, dass eine der Hauptrichtungen in der Entwicklung der Mathematik in der vierten Periode die Stärkung der Beweisgenauigkeit in der gesamten Mathematik ist, insbesondere die Umstrukturierung der mathematischen Analyse auf logischer Grundlage. In der zweiten Hälfte des 18. Jahrhunderts. Es wurden zahlreiche Versuche unternommen, die mathematische Analyse neu aufzubauen: die Einführung der Definition eines Grenzwerts (D'Alembert et al.), die Definition der Ableitung als Grenzwert eines Verhältnisses (Euler et al.), die Ergebnisse von Lagrange und Carnot usw., aber diesen Werken fehlte ein System, und manchmal waren sie erfolglos. Sie bereiteten jedoch den Boden für die Perestroika im 19. Jahrhundert. umgesetzt werden konnte. Im 19. Jahrhundert Diese Entwicklungsrichtung der mathematischen Analyse wurde zur führenden. Es wurde von O. Cauchy, B. Bolzano, K. Weierstrass und anderen aufgegriffen.

1. Augustin Louis Cauchy (1789–1857) absolvierte die Ecole Polytechnique und das Institut für Kommunikation in Paris. Seit 1816 Mitglied der Pariser Akademie und Professor an der Ecole Polytechnique. 1830–1838 Während der Jahre der Republik befand er sich wegen seiner monarchistischen Überzeugung im Exil. Seit 1848 war Cauchy Professor an der Sorbonne-Universität Paris. Er veröffentlichte mehr als 800 Arbeiten über mathematische Analyse, Differentialgleichungen, Funktionstheorie einer komplexen Variablen, Algebra, Zahlentheorie, Geometrie, Mechanik, Optik usw. Die Hauptgebiete seiner wissenschaftlichen Interessen waren mathematische Analyse und Funktionentheorie einer komplexe Variable.

Cauchy veröffentlichte seine an der Ecole Polytechnique gehaltenen Vorlesungen über Analysis in drei Werken: „Course of Analysis“ (1821), „Summary of Lectures on Infinitesimal Calculus“ (1823), „Lecture on Applications of Analysis to Geometry“, 2 Bände (1826, 1828). In diesen Büchern wird erstmals die mathematische Analyse auf der Grundlage der Grenzwerttheorie aufgebaut. Sie markierten den Beginn einer radikalen Umstrukturierung der mathematischen Analyse.

Cauchy gibt die folgende Definition des Grenzwerts einer Variablen: „Wenn sich die Werte, die nacheinander derselben Variablen zugewiesen werden, einem festen Wert auf unbestimmte Zeit nähern, so dass sie am Ende so wenig wie möglich von diesem abweichen, dann nennt man letzteren den Grenze aller anderen.“ Der Kern der Sache wird hier gut ausgedrückt, aber die Worte „so wenig wie gewünscht“ selbst bedürfen einer Definition, und außerdem wird hier die Definition des Grenzwerts einer Variablen und nicht des Grenzwerts einer Funktion formuliert. Als nächstes beweist der Autor verschiedene Eigenschaften von Grenzwerten.

Dann gibt Cauchy die folgende Definition der Stetigkeit einer Funktion: Eine Funktion heißt stetig (an einem Punkt), wenn ein infinitesimales Inkrement im Argument ein infinitesimales Inkrement in der Funktion erzeugt, d. h. in der modernen Sprache

Dann hat er verschiedene Eigenschaften stetiger Funktionen.

Das erste Buch befasst sich auch mit der Reihentheorie: Es definiert die Summe einer Zahlenreihe als Grenze ihrer Teilsumme und führt eine Reihe hinreichender Kriterien für die Konvergenz von Zahlenreihen sowie Potenzreihen und die Region ein ihrer Konvergenz - und das sowohl im realen als auch im komplexen Bereich.

In seinem zweiten Buch stellt er Differential- und Integralrechnung vor.

Cauchy definiert die Ableitung einer Funktion als Grenze des Verhältnisses des Inkrements der Funktion zum Inkrement des Arguments, wenn das Inkrement des Arguments gegen Null tendiert, und das Differential als Grenze des Verhältnisses Daraus folgt das. Als nächstes werden die üblichen Ableitungsformeln besprochen; In diesem Fall verwendet der Autor häufig den Mittelwertsatz von Lagrange.

In der Integralrechnung stellt Cauchy zunächst das bestimmte Integral als Grundbegriff vor. Er führt ihn auch erstmals als Grenzwert ganzzahliger Summen ein. Hier beweisen wir einen wichtigen Satz über die Integrierbarkeit einer stetigen Funktion. Sein unbestimmtes Integral wird als Funktion des Arguments definiert. Darüber hinaus werden hier Entwicklungen von Funktionen in Taylor- und Maclaurin-Reihen betrachtet.

In der zweiten Hälfte des 19. Jahrhunderts. Eine Reihe von Wissenschaftlern: B. Riemann, G. Darboux und andere fanden neue Bedingungen für die Integrierbarkeit einer Funktion und änderten sogar die Definition eines bestimmten Integrals selbst, sodass sie auf die Integration einiger diskontinuierlicher Funktionen angewendet werden konnte.

In der Theorie der Differentialgleichungen beschäftigte sich Cauchy hauptsächlich mit Beweisen grundlegend wichtiger Existenzsätze: der Existenz einer Lösung einer gewöhnlichen Differentialgleichung, zunächst erster und dann dritter Ordnung; Existenz einer Lösung für ein lineares System partieller Differentialgleichungen.

In der Theorie der Funktionen einer komplexen Variablen ist Cauchy der Begründer; Viele seiner Artikel sind diesem Thema gewidmet. Im 18. Jahrhundert Euler und d'Alembert legten nur den Anfang dieser Theorie. Im Universitätskurs zur Theorie der Funktionen einer komplexen Variablen stoßen wir ständig auf den Namen Cauchy: die Cauchy-Riemann-Bedingungen für die Existenz einer Ableitung, das Cauchy-Integral, die Cauchy-Integralformel usw.; Viele Sätze über Reste einer Funktion gehen ebenfalls auf Cauchy zurück. Auch B. Riemann, K. Weierstrass, P. Laurent und andere erzielten auf diesem Gebiet sehr wichtige Ergebnisse.

Kehren wir zu den Grundkonzepten der mathematischen Analyse zurück. In der zweiten Hälfte des Jahrhunderts wurde deutlich, dass der tschechische Wissenschaftler Bernard Bolzano (1781 – 1848) vor Cauchy und Weierschtrass viel auf dem Gebiet der fundierten Analyse geleistet hatte. Vor Cauchy definierte er den Grenzwert, die Stetigkeit einer Funktion und die Konvergenz einer Zahlenreihe, bewies ein Kriterium für die Konvergenz einer Zahlenfolge und auch, lange bevor er bei Weierstrass erschien, den Satz: Wenn eine Zahl gesetzt ist nach oben (unten) begrenzt ist, dann hat es eine exakte obere (genaue untere) Kante. Er betrachtete eine Reihe von Eigenschaften stetiger Funktionen; Erinnern wir uns daran, dass es im Universitätskurs der mathematischen Analysis die Sätze von Bolzano-Cauchy und Bolzano-Weierstrass über in einem Intervall stetige Funktionen gibt. Bolzano untersuchte auch einige Fragen der mathematischen Analyse. Beispielsweise konstruierte er das erste Beispiel einer Funktion, die auf einem Segment stetig ist, aber an keinem Punkt des Segments eine Ableitung aufweist. Da Bozen zu seinen Lebzeiten nur fünf kleinere Werke veröffentlichen konnte, wurden seine Ergebnisse zu spät bekannt.

2. In der mathematischen Analyse wurde das Fehlen einer klaren Definition einer Funktion immer deutlicher spürbar. Einen wesentlichen Beitrag zur Lösung des Streits darüber, was unter Funktion zu verstehen ist, leistete der französische Wissenschaftler Jean Fourier. Er studierte die mathematische Theorie der Wärmeleitfähigkeit in Festkörpern und verwendete in diesem Zusammenhang trigonometrische Reihen (Fourier-Reihen).

Diese Reihen fanden später breite Anwendung in der mathematischen Physik, einer Wissenschaft, die sich mit mathematischen Methoden zur Untersuchung partieller Differentialgleichungen aus der Physik befasst. Fourier hat bewiesen, dass jede kontinuierliche Kurve, unabhängig davon, aus welchen unterschiedlichen Teilen sie besteht, durch einen einzigen analytischen Ausdruck – eine trigonometrische Reihe – definiert werden kann, und dass dies auch für einige Kurven mit Diskontinuitäten möglich ist. Fouriers Untersuchung solcher Reihen warf erneut die Frage auf, was unter einer Funktion zu verstehen ist. Kann eine solche Kurve als Definition einer Funktion angesehen werden? (Dies ist eine Erneuerung der alten Debatte des 18. Jahrhunderts über die Beziehung zwischen Funktion und Formel auf einer neuen Ebene.)

Im Jahr 1837 gab der deutsche Mathematiker P. Direchle erstmals eine moderne Definition einer Funktion: „ist eine Funktion einer Variablen (in einem Intervall, wenn jeder Wert (in diesem Intervall) einem ganz bestimmten Wert entspricht, und es spielt keine Rolle, wie Diese Entsprechung wird festgestellt – durch eine analytische Formel, eine Grafik, eine Tabelle oder auch nur in Worten.“ Der Zusatz ist bemerkenswert: „Es spielt keine Rolle, wie diese Entsprechung festgestellt wird.“

3. Der moderne Standard der Genauigkeit in der mathematischen Analyse taucht erstmals in den Werken von Weierstrass (1815–1897) auf. Er arbeitete lange Zeit als Mathematiklehrer an Gymnasien und wurde 1856 Professor an der Universität Berlin. Die Zuhörer seiner Vorlesungen veröffentlichten sie nach und nach in Form separater Bücher, wodurch der Inhalt der Vorlesungen von Weierstrass in Europa bekannt wurde. Es war Weierstrass, der begann, Sprache systematisch in der mathematischen Analyse zu verwenden. Er gab eine Definition des Grenzwerts einer Folge, eine Definition des Grenzwerts einer Funktion in der Sprache (die fälschlicherweise oft als Cauchy-Definition bezeichnet wird) und bewies rigoros Sätze über Grenzwerte und der sogenannte Weierstrass-Satz über den Grenzwert einer monotonen Folge: Eine steigende (abfallende) Folge, die von oben (von unten) begrenzt ist, hat einen endlichen Grenzwert. Er begann, die Konzepte der exakten oberen und exakten unteren Grenzen einer numerischen Menge zu verwenden, das Konzept eines Grenzpunkts einer Menge, bewies den Satz (der einen anderen Autor hat – Bolzano): Eine begrenzte numerische Menge hat einen Grenzpunkt, und untersuchte einige Eigenschaften stetiger Funktionen. Weierstrass widmete viele Arbeiten der Theorie der Funktionen einer komplexen Variablen und untermauerte sie mit Hilfe von Potenzreihen. Er studierte auch Variationsrechnung, Differentialgeometrie und lineare Algebra.

4. Bleiben wir bei der Theorie der unendlichen Mengen. Sein Schöpfer war der deutsche Mathematiker Cantor. Georg Kantor (1845–1918) war viele Jahre als Professor an der Universität Halle tätig. Ab 1870 veröffentlichte er Arbeiten zur Mengenlehre. Er bewies die Unabzählbarkeit der Menge der reellen Zahlen und bewies damit die Existenz nichtäquivalenter unendlicher Mengen, führte das allgemeine Konzept der Potenz einer Menge ein und erläuterte die Prinzipien für den Vergleich von Potenzen. Cantor entwickelte eine Theorie der transfiniten, „uneigentlichen“ Zahlen, indem er die niedrigste, kleinste transfinite Zahl der Potenz einer abzählbaren Menge (insbesondere der Menge der natürlichen Zahlen) und der Potenz der Menge der reellen Zahlen zuschrieb – einer höheren, größere transfinite Zahl usw.; Dies gab ihm die Möglichkeit, eine Arithmetik transfiniter Zahlen zu konstruieren, ähnlich der gewöhnlichen Arithmetik natürlicher Zahlen. Cantor nutzte die tatsächliche Unendlichkeit, beispielsweise die Möglichkeit, die natürliche Zahlenreihe vollständig zu „ausschöpfen“, schon vor ihm in der Mathematik des 19. Jahrhunderts systematisch. Es wurde nur die potenzielle Unendlichkeit verwendet.

Cantors Mengenlehre löste bei ihrem Erscheinen bei vielen Mathematikern Einwände aus, doch die Anerkennung kam nach und nach, als ihre enorme Bedeutung für die Begründung der Topologie und der Funktionentheorie einer reellen Variablen klar wurde. Es blieben jedoch logische Lücken in der Theorie selbst; insbesondere wurden Paradoxien der Mengenlehre entdeckt. Hier ist eines der berühmtesten Paradoxien. Mit der Menge bezeichnen wir alle solchen Mengen, die keine Elemente ihrer selbst sind. Gilt die Einbeziehung auch und ist sie kein Element, da bedingt nur solche Mengen als Elemente enthalten sind, die keine Elemente ihrer selbst sind? Wenn die Bedingung zutrifft, ist die Einbeziehung in beiden Fällen ein Widerspruch.

Diese Paradoxien waren mit der internen Inkonsistenz einiger Mengen verbunden. Es wurde deutlich, dass in der Mathematik nicht beliebige Mengen verwendet werden können. Die Existenz von Paradoxien wurde durch die Schöpfung bereits zu Beginn des 20. Jahrhunderts überwunden. axiomatische Mengenlehre (E. Zermelo, A. Frenkel, D. Neumann usw.), die insbesondere die Frage beantwortete: Welche Mengen können in der Mathematik verwendet werden? Es stellt sich heraus, dass Sie die leere Menge, die Vereinigung gegebener Mengen, die Menge aller Teilmengen einer gegebenen Menge usw. verwenden können.

Die Philosophie gilt als Mittelpunkt aller Wissenschaften, da sie die ersten Zweige der Literatur, Astronomie, Literatur, Naturwissenschaften, Mathematik und anderer Bereiche umfasste. Im Laufe der Zeit entwickelte sich jedes Fachgebiet unabhängig voneinander, die Mathematik bildete da keine Ausnahme. Als erster „Hinweis“ der Analyse gilt die Theorie der Zerlegung in unendlich kleine Größen, an die sich viele Köpfe zu nähern versuchten, die jedoch vage war und keine Grundlage hatte. Dies ist auf eine Bindung an die alte Schule der Wissenschaft zurückzuführen, die in ihren Formulierungen streng war. Isaac Newton war kurz davor, den Grundstein zu legen, aber es war zu spät. Infolgedessen verdankt die mathematische Analyse ihre Entstehung als eigenständiges System dem Philosophen Gottfried Leibniz. Er war es, der Konzepte wie Minimum und Maximum, Wendepunkte und Konvexität des Funktionsgraphen in die wissenschaftliche Welt einführte und die Grundlagen der Differentialrechnung formulierte. Von diesem Moment an ist die Mathematik offiziell in Grund- und höhere Mathematik unterteilt.

Mathematische Analyse. Unsere Tage

Jedes Fachgebiet, sei es technischer oder humanitärer Natur, beinhaltet die Analyse im Rahmen des Studiums. Die Tiefe des Studiums variiert, aber das Wesentliche bleibt dasselbe. Bei aller „Abstraktheit“ ist sie eine der Säulen, auf denen die Naturwissenschaft in ihrem modernen Verständnis ruht. Mit seiner Hilfe ist er in der Lage, die Aktivitäten der Börse zu beschreiben und vorherzusagen und dabei zu helfen, ein optimales Aktienportfolio aufzubauen. Die Einführung in die mathematische Analyse basiert auf elementaren Konzepten:

• Massen;
• grundlegende Operationen an Mengen;
• Eigenschaften von Operationen auf Mengen;
• Funktionen (auch als Mappings bekannt);
• Arten von Funktionen;
• Sequenzen;
• Zahlenlinien;
• Sequenzlimit;
• Eigenschaften von Grenzwerten;
• Kontinuität der Funktion.

Es lohnt sich, Konzepte wie Menge, Punkt, Gerade, Ebene gesondert hervorzuheben. Für alle gibt es keine Definitionen, da es sich um die Grundkonzepte handelt, auf denen die gesamte Mathematik aufbaut. Dabei kann lediglich erläutert werden, was im Einzelfall genau gemeint ist.

Limit als Fortsetzung

Zu den Grundlagen der mathematischen Analyse gehört die Begrenzung. In der Praxis stellt er den Wert dar, den eine Folge oder Funktion anstrebt, dem gewünschten Wert nahe kommt, ihn aber nicht erreicht. Es wird als lim bezeichnet; betrachten Sie einen Sonderfall des Grenzwerts der Funktion: lim (x-1)= 0 für x→1. Anhand dieses einfachsten Beispiels wird deutlich, dass bei x→1 die gesamte Funktion gegen 0 tendiert, denn wenn wir den Grenzwert in die Funktion selbst einsetzen, erhalten wir (1-1)=0. Detailliertere Informationen, von elementaren bis hin zu komplexen Spezialfällen, werden in einer Art „Bibel“ der Analyse präsentiert – den Werken von Fichtenholtz. Es untersucht mathematische Analysen, Grenzwerte, deren Ableitung und weitere Anwendung. Beispielsweise wäre die Ableitung der Zahl e (Eulersche Konstante) ohne die Grenzwerttheorie unmöglich. Trotz der dynamischen Abstraktheit der Theorie werden Grenzen in der Praxis in den Wirtschaftswissenschaften und der Soziologie aktiv genutzt. Sie können beispielsweise bei der Berechnung der Zinsen für eine Bankeinlage nicht darauf verzichten.

Englisch: Wikipedia macht die Seite sicherer. Sie verwenden einen alten Webbrowser, der in Zukunft keine Verbindung zu Wikipedia herstellen kann. Bitte aktualisieren Sie Ihr Gerät oder wenden Sie sich an Ihren IT-Administrator.

中文: 的浏览器,这在将来无法连接维基百科.请更新IT ）.

Spanisch: Wikipedia ist der Standort am sichersten. Ich verwende derzeit einen Web-Navigator, der in Zukunft keine Verbindung zu Wikipedia herstellen kann. Bitte kontaktieren Sie Ihren Administrator oder wenden Sie sich an Ihren Administrator. Es gab noch mehr Aktualisierungen und mehr Technik auf Englisch.

ﺎﻠﻋﺮﺒﻳﺓ: ويكيبيديا تسعى لتأمين الموقع أكثر من ذي قبل. أنت تستخدم متصفح وب قديم لن يتمكن من الاتصال بموقع ويكيبيديا في المستقبل. يرجى تحديث جهازك أو الاتصال بغداري تقنية المعلومات الخاص بك. يوجد تحديث فني أطول ومغرق في التقنية باللغة الإنجليزية تاليا.

Französisch: Wikipédia erweitert die Sicherheit seiner Website. Sie nutzen derzeit einen alten Web-Navigator, der sich nicht mehr mit Wikipedia verbinden muss, bevor er fertig ist. Vielen Dank für Ihren Besuch oder wenden Sie sich an Ihren Informatikadministrator. Zusätzliche Informationen sowie Techniken und Englisch sind hier verfügbar.

日本語: 利用のブラウザはバージョン???

Deutsch: Wikipedia erhöht die Sicherheit der Webseite. Du benutzt einen alten Webbrowser, der in Zukunft nicht mehr auf Wikipedia zugreifen kann. Bitte aktualisieren Sie Ihr Gerät oder sprechen Sie mit Ihrem IT-Administrator. Ausführlichere (und technisch detaillierte) Hinweise finden Sie unten in englischer Sprache.

Italienisch: Wikipedia stellt die sicherere Website wieder her. Bleiben Sie in einem Webbrowser, der Sie in Zukunft nicht mehr mit Wikipedia verbinden wird. Bitte kontaktieren Sie Ihren Informatiker oder kontaktieren Sie ihn. Für mehr Bass ist eine Erweiterung mit mehr Details und Technik in Englisch verfügbar.

Magyar: Biztonságosabb auf Wikipédia gelesen. Ein toller, mit Használsz, nem lesz képes kapcsolódni a jövőben. Die meisten modernen Geräte haben ein Problem mit der Reparatur verursacht. Alább olvashatod a részletesebb magyarázatot (angolul).

Schweden: Wikipedia wird nicht mehr gefunden. Sie nutzen ein älteres Webbrowser, der Ihnen die Möglichkeit gibt, Wikipedia aus der Community zu lesen. Aktualisieren Sie Ihr Gerät oder wenden Sie sich an Ihren IT-Administrator. Es ist eine lange Zeit und es gibt noch mehr technische Erläuterungen auf Englisch.

हिन्दी: विकिपीडिया साइट को और अधिक सुरक्षित बना रहा है। आप एक पुराने वेब ब्राउज़र का उपयोग कर रहे हैं जो भविष्य में विकिपीडिया से कनेक्ट नहीं हो पाएगा। कृपया अपना डिवाइस अपडेट करें या अपने आईटी व्यवस्थापक से संपर्क करें। नीचे अंग्रेजी में एक लंबा और अधिक तकनीकी अद्यतन है।

Wir entfernen die Unterstützung für unsichere TLS-Protokollversionen, insbesondere TLSv1.0 und TLSv1.1, auf die Ihre Browsersoftware für die Verbindung zu unseren Websites angewiesen ist. Die Ursache dafür sind meist veraltete Browser oder ältere Android-Smartphones. Oder es könnte sich um einen Eingriff durch Unternehmens- oder Privatsoftware „Web Security“ handeln, die die Verbindungssicherheit tatsächlich herabsetzt.

Sie müssen Ihren Webbrowser aktualisieren oder dieses Problem auf andere Weise beheben, um auf unsere Websites zugreifen zu können. Diese Meldung bleibt bis zum 1. Januar 2020 bestehen. Nach diesem Datum kann Ihr Browser keine Verbindung mehr zu unseren Servern herstellen.

In der Geschichte der Mathematik können wir grob zwei Hauptperioden unterscheiden: die Elementarmathematik und die moderne Mathematik. Der Meilenstein, von dem aus die Ära der neuen (manchmal auch höheren) Mathematik gezählt wird, war das 17. Jahrhundert – das Jahrhundert der Entstehung der mathematischen Analyse. Bis zum Ende des 17. Jahrhunderts. I. Newton, G. Leibniz und ihre Vorgänger schufen den Apparat einer neuen Differentialrechnung und Integralrechnung, der die Grundlage der mathematischen Analyse und vielleicht sogar die mathematische Grundlage aller modernen Naturwissenschaften bildet.

Die mathematische Analysis ist ein weites Feld der Mathematik mit einem charakteristischen Untersuchungsgegenstand (variable Größe), einer einzigartigen Forschungsmethode (Analyse mittels Infinitesimalzahlen oder mittels Grenzwertübergängen) und einem bestimmten System grundlegender Konzepte (Funktion, Grenzwert, Ableitung). , Differential, Integral, Reihe) und ein sich ständig verbessernder und sich weiterentwickelnder Apparat, dessen Grundlage die Differential- und Integralrechnung ist.

Versuchen wir, eine Vorstellung davon zu geben, welche Art von mathematischer Revolution im 17 grundlegende Rolle im gesamten modernen System des theoretischen und angewandten Wissens.

Stellen Sie sich vor, vor Ihnen liegt ein wunderschön ausgeführtes Farbfoto einer stürmischen Meereswelle, die ans Ufer strömt: ein kraftvoll gebeugter Rücken, eine steile, aber leicht eingesunkene Brust, ein bereits nach vorne geneigter und zum Fallen bereiter Kopf mit einer grauen Mähne, die von den Wellen gepeinigt wird Wind. Sie haben den Moment angehalten, es ist Ihnen gelungen, die Welle einzufangen, und Sie können sie nun ohne Eile sorgfältig und bis ins kleinste Detail studieren. Eine Welle kann gemessen werden, und mit den Werkzeugen der elementaren Mathematik können Sie viele wichtige Schlussfolgerungen über diese Welle und damit über alle ihre Schwestern im Ozean ziehen. Aber indem Sie die Welle gestoppt haben, haben Sie ihr Bewegung und Leben genommen. Sein Ursprung, seine Entwicklung, sein Verlauf, die Wucht, mit der es auf das Ufer trifft – all das lag außerhalb Ihres Blickfeldes, denn Sie verfügen noch nicht über eine Sprache oder einen mathematischen Apparat, der zum Beschreiben und Studieren geeignet ist, nicht statisch, sondern sich entwickelnde, dynamische Prozesse, Variablen und deren Beziehungen.

„Die mathematische Analyse ist nicht weniger umfassend als die Natur selbst: Sie ermittelt alle greifbaren Zusammenhänge, misst Zeiten, Räume, Kräfte, Temperaturen.“ J. Fourier

Bewegung, Variablen und ihre Beziehungen umgeben uns überall. Verschiedene Arten von Bewegungen und ihre Muster bilden den Hauptgegenstand des Studiums bestimmter Wissenschaften: Physik, Geologie, Biologie, Soziologie usw. Daher erwiesen sich in allen Bereichen der Wissenschaft eine präzise Sprache und entsprechende mathematische Methoden zur Beschreibung und Untersuchung variabler Größen als notwendig Für die Beschreibung quantitativer Zusammenhänge sind Kenntnisse in etwa dem gleichen Umfang erforderlich wie Zahlen und Rechnen. Die mathematische Analyse bildet also die Grundlage der Sprache und der mathematischen Methoden zur Beschreibung von Variablen und ihren Beziehungen. Heutzutage ist es ohne mathematische Analyse nicht nur unmöglich, Weltraumflugbahnen, den Betrieb von Kernreaktoren, die Bewegung von Meereswellen und Muster der Zyklonentwicklung zu berechnen, sondern auch die Produktion, die Ressourcenverteilung, die Organisation technologischer Prozesse wirtschaftlich zu verwalten und vorherzusagen Ablauf chemischer Reaktionen oder Veränderungen in der Anzahl verschiedener in der Natur miteinander verbundener Tier- und Pflanzenarten, da es sich bei all diesen um dynamische Prozesse handelt.

Die Elementarmathematik war hauptsächlich die Mathematik konstanter Größen, sie untersuchte hauptsächlich die Beziehungen zwischen den Elementen geometrischer Figuren, die arithmetischen Eigenschaften von Zahlen und algebraische Gleichungen. Seine Einstellung zur Realität lässt sich gewissermaßen mit einer aufmerksamen, ja sogar gründlichen und vollständigen Untersuchung jedes festen Bildes eines Films vergleichen, das die sich verändernde, sich entwickelnde Lebenswelt in ihrer Bewegung einfängt, die jedoch nicht in einem separaten Bild sichtbar ist und Dies kann nur beobachtet werden, wenn man das Band als Ganzes betrachtet. Aber so wie das Kino ohne Fotografie undenkbar ist, so ist die moderne Mathematik ohne den Teil davon, den wir gemeinhin als elementar bezeichnen, ohne die Ideen und Errungenschaften vieler herausragender Wissenschaftler, die manchmal Jahrzehnte voneinander entfernt sind, unmöglich.

Die Mathematik ist vereint, und ihr „höherer“ Teil ist mit dem „elementaren“ Teil auf die gleiche Weise verbunden, wie die nächste Etage eines im Bau befindlichen Hauses mit der vorherigen verbunden ist und wie weit die Horizonte sind, die die Mathematik eröffnet Für uns in der Welt um uns herum hängt es davon ab, welche Etage dieses Gebäudes wir erreichen konnten. Geboren im 17. Jahrhundert. Die mathematische Analyse hat uns Möglichkeiten eröffnet, Variablen und Bewegung im weitesten Sinne des Wortes wissenschaftlich zu beschreiben, quantitativ und qualitativ zu untersuchen.

Was sind die Voraussetzungen für die Entstehung der mathematischen Analysis?

Bis zum Ende des 17. Jahrhunderts. Es ist folgende Situation eingetreten. Erstens haben sich im Rahmen der Mathematik selbst über viele Jahre hinweg einige wichtige Klassen von Problemen der gleichen Art angesammelt (z. B. Probleme beim Messen von Flächen und Volumina nicht standardmäßiger Figuren, Probleme beim Zeichnen von Tangenten an Kurven) und Methoden für Lösungsansätze für verschiedene Sonderfälle sind erschienen. Zweitens stellte sich heraus, dass diese Probleme eng mit den Problemen der Beschreibung einer beliebigen (nicht unbedingt gleichmäßigen) mechanischen Bewegung und insbesondere mit der Berechnung ihrer momentanen Eigenschaften (Geschwindigkeit, Beschleunigung zu jedem Zeitpunkt) sowie mit der Suche nach der Bewegung zusammenhängen zurückgelegte Distanz für eine Bewegung, die mit einer bestimmten variablen Geschwindigkeit erfolgt. Die Lösung dieser Probleme war für die Entwicklung von Physik, Astronomie und Technologie notwendig.

Drittens schließlich bis zur Mitte des 17. Jahrhunderts. Die Arbeiten von R. Descartes und P. Fermat legten den Grundstein für die analytische Methode der Koordinaten (die sogenannte analytische Geometrie), die es ermöglichte, geometrische und physikalische Probleme heterogenen Ursprungs in der allgemeinen (analytischen) Zahlensprache zu formulieren und numerische Abhängigkeiten, oder, wie wir jetzt sagen, numerische Funktionen.

Das Zusammentreffen dieser Umstände führte dazu, dass am Ende des 17. Jahrhunderts. zwei Wissenschaftlern – I. Newton und G. Leibniz – gelang es unabhängig voneinander, einen mathematischen Apparat zur Lösung dieser Probleme zu schaffen, indem sie einzelne Ergebnisse ihrer Vorgänger, darunter des antiken Wissenschaftlers Archimedes und der Zeitgenossen von Newton und Leibniz – B., zusammenfassten und verallgemeinerten. Cavalieri, B. Pascal, D. Gregory, I. Barrow. Dieser Apparat bildete die Grundlage der mathematischen Analysis – einem neuen Zweig der Mathematik, der verschiedene Entwicklungsprozesse untersucht, d.h. Beziehungen zwischen Variablen, die in der Mathematik funktionale Abhängigkeiten oder mit anderen Worten Funktionen genannt werden. Der Begriff „Funktion“ selbst war übrigens genau im 17. Jahrhundert notwendig und natürlich entstanden und hat inzwischen nicht nur allgemeine mathematische, sondern auch allgemeine wissenschaftliche Bedeutung erlangt.

Erste Informationen zu den Grundkonzepten und dem mathematischen Apparat der Analyse finden Sie in den Artikeln „Differentialrechnung“ und „Integralrechnung“.

Abschließend möchte ich nur auf ein Prinzip der mathematischen Abstraktion eingehen, das der gesamten Mathematik gemeinsam ist und für die Analyse charakteristisch ist, und in diesem Zusammenhang erklären, in welcher Form die mathematische Analyse Variablen untersucht und was das Geheimnis dieser Universalität ihrer Untersuchungsmethoden ist allerlei spezifische Entwicklungsprozesse und deren Zusammenhänge.

Schauen wir uns einige anschauliche Beispiele und Analogien an.

Manchmal ist uns nicht mehr bewusst, dass beispielsweise eine mathematische Beziehung, die nicht für Äpfel, Stühle oder Elefanten, sondern in abstrakter Form abstrahiert von bestimmten Objekten geschrieben wurde, eine herausragende wissenschaftliche Leistung ist. Dabei handelt es sich um ein mathematisches Gesetz, das erfahrungsgemäß auf verschiedene spezifische Objekte anwendbar ist. Das bedeutet, dass wir durch das Studium der allgemeinen Eigenschaften abstrakter, abstrakter Zahlen in der Mathematik die quantitativen Beziehungen der realen Welt untersuchen.

Aus einem Schulmathematikkurs ist beispielsweise bekannt, dass man daher in einer konkreten Situation sagen könnte: „Wenn sie mir nicht zwei Sechs-Tonnen-Muldenkipper geben, um 12 Tonnen Erde zu transportieren, dann kann ich fragen.“ für drei Vier-Tonnen-Muldenkipper und die Arbeit ist erledigt, und wenn sie mir nur einen Vier-Tonnen-Muldenkipper geben, muss sie drei Flüge machen.“ So werden den uns heute bekannten abstrakten Zahlen und Zahlenmustern ihre spezifischen Erscheinungsformen und Anwendungen zugeordnet.

Die Gesetze der Veränderung bestimmter Variablen und sich entwickelnder Prozesse der Natur hängen in etwa in gleicher Weise mit der abstrakten, abstrakten Form-Funktion zusammen, in der sie auftreten und in der mathematischen Analyse untersucht werden.

Ein abstraktes Verhältnis kann beispielsweise die Abhängigkeit der Kinokassen von der Anzahl der verkauften Eintrittskarten widerspiegeln, wenn 20 20 Kopeken sind – der Preis einer Eintrittskarte. Wenn wir jedoch mit dem Fahrrad auf einer Autobahn unterwegs sind und 20 km pro Stunde zurücklegen, kann dieses Verhältnis als Verhältnis zwischen der Zeit (Stunden) unserer Radtour und der in dieser Zeit zurückgelegten Strecke (Kilometer) interpretiert werden Sagen Sie immer, dass zum Beispiel eine Änderung um mehrere Male zu einer proportionalen (d. h. gleich oft) Änderung des Wertes von führt, und wenn , dann ist auch die umgekehrte Schlussfolgerung wahr. Das bedeutet insbesondere: Um die Kinokassen zu verdoppeln, muss man doppelt so viele Zuschauer anlocken, und um mit dem Fahrrad doppelt so weit bei gleicher Geschwindigkeit zurückzulegen, muss man doppelt so lange fahren .

Die Mathematik untersucht sowohl die einfachste Abhängigkeit als auch andere, viel komplexere Abhängigkeiten in einer allgemeinen, abstrakten Form, abstrahiert von einer bestimmten Interpretation. Die Eigenschaften einer Funktion oder Methoden zur Untersuchung dieser Eigenschaften, die in einer solchen Studie identifiziert werden, werden von der Natur allgemeiner mathematischer Techniken, Schlussfolgerungen, Gesetze und Schlussfolgerungen sein, die auf jedes spezifische Phänomen anwendbar sind, in dem die in abstrakter Form untersuchte Funktion auftritt, unabhängig davon, in welchem ​​Bereich Wissensstand gehört dieses Phänomen dazu.

So nahm die mathematische Analyse als Zweig der Mathematik Ende des 17. Jahrhunderts Gestalt an. Gegenstand des Studiums der mathematischen Analyse (wie sie aus modernen Sichtweisen erscheint) sind Funktionen, oder mit anderen Worten, Abhängigkeiten zwischen variablen Größen.

Mit dem Aufkommen der mathematischen Analyse wurde die Mathematik für das Studium und die Reflexion sich entwickelnder Prozesse in der realen Welt zugänglich; Die Mathematik umfasste Variablen und Bewegung.

Antike

Während der Antike tauchten einige Ideen auf, die später zur Integralrechnung führten, aber in dieser Zeit wurden diese Ideen nicht auf strenge, systematische Weise entwickelt. Berechnungen von Volumina und Flächen, einer der Zwecke der Integralrechnung, finden sich im Moskauer mathematischen Papyrus aus Ägypten (ca. 1820 v. Chr.), aber die Formeln ähneln eher Anweisungen, ohne Angabe der Methode, und einige sind einfach fehlerhaft. Im Zeitalter der griechischen Mathematik verwendete Eudoxos (ca. 408–355 v. Chr.) die Erschöpfungsmethode zur Berechnung von Flächen und Volumina, was das Konzept der Grenze vorwegnahm. Später wurde diese Idee von Archimedes (ca. 287–212 v. Chr.) weiterentwickelt. , indem er Heuristiken erfand, die Methoden der Integralrechnung ähneln. Die Erschöpfungsmethode wurde später im 3. Jahrhundert n. Chr. in China von Liu Hui erfunden, mit der er die Fläche eines Kreises berechnete. Im 5. n. Chr. entwickelte Zu Chongzhi eine Methode zur Berechnung des Volumens einer Kugel, die später als Cavalieri-Prinzip bezeichnet wurde.

Mittelalter

Im 14. Jahrhundert führten der indische Mathematiker Madhava Sangamagrama und die Kerala School of Astronomy and Mathematics viele Komponenten der Analysis ein, wie z. B. Taylor-Reihen, Approximation unendlicher Reihen, integrale Konvergenztests, frühe Formen der Differentiation, termweise Integration, iterative Methoden zum Lösen nichtlinearer Gleichungen und zur Bestimmung der Fläche unter der Kurve, deren Integral sie ist. Einige betrachten Yuktibhāṣā als das erste Werk zur mathematischen Analyse.

Moderne Ära

In Europa war das wegweisende Werk die Abhandlung von Bonaventura Cavalieri, in der er argumentierte, dass Volumina und Flächen als Summe der Volumina und Flächen eines unendlich dünnen Abschnitts berechnet werden können. Die Ideen ähnelten denen, die Archimedes in seiner Methode skizzierte, aber diese Abhandlung von Archimedes ging bis zur ersten Hälfte des 20. Jahrhunderts verloren. Cavalieris Arbeit wurde nicht anerkannt, weil seine Methoden zu fehlerhaften Ergebnissen führen konnten, und er gab den Infinitesimalen einen zweifelhaften Ruf.

Zu dieser Zeit fand in Europa formale Forschung zur Infinitesimalrechnung statt, die Cavalieri mit der Finite-Differenzen-Rechnung kombinierte. Pierre Fermat, der behauptete, er habe es von Diophantus übernommen, führte das Konzept der „Quasi-Gleichheit“ (englisch: adequality) ein, das Gleichheit bis zu einem verschwindend kleinen Fehler bedeutete. Auch John Wallis, Isaac Barrow und James Gregory leisteten wichtige Beiträge. Die letzten beiden, um 1675, bewiesen den zweiten Grundsatz der Analysis.

Gründe

In der Mathematik beziehen sich Grundlagen auf eine strenge Definition eines Themas, ausgehend von präzisen Axiomen und Definitionen. In der Anfangsphase der Entwicklung der Infinitesimalrechnung galt die Verwendung von Infinitesimalgrößen als lax und wurde von einer Reihe von Autoren, insbesondere Michel Rolle und Bishop Berkeley, heftig kritisiert. Berkeley beschrieb die Infinitesimalzahlen in seinem Buch The Analyst aus dem Jahr 1734 hervorragend als „Geister toter Größen“. Die Entwicklung einer strengen Grundlage für die Infinitesimalrechnung beschäftigte die Mathematiker nach Newton und Leibniz mehr als ein Jahrhundert lang und ist zum Teil auch heute noch ein aktives Forschungsgebiet.

Mehrere Mathematiker, darunter Maclaurin, versuchten, die Gültigkeit der Verwendung von Infinitesimalzahlen zu beweisen, aber dies gelang erst 150 Jahre später mit der Arbeit von Cauchy und Weierstrass, die schließlich einen Weg fanden, die einfachen „Kleinigkeiten“ von Infinitesimalzahlen zu umgehen Die Anfänge wurden in der Differential- und Integralrechnung gemacht. In Cauchys Schriften finden wir eine universelle Palette grundlegender Ansätze, darunter die Definition der Kontinuität in Bezug auf Infinitesimalzahlen und den (etwas ungenauen) Prototyp der (ε, δ)-Grenzdefinition in der Definition der Differentiation. In seiner Arbeit formalisiert Weierstrass den Grenzwertbegriff und eliminiert Infinitesimalmengen. Nach dieser Arbeit von Weierstrass wurden die allgemeinen Grundlagen der Infinitesimalrechnung zu Grenzwerten und nicht zu Infinitesimalgrößen. Bernhard Riemann nutzte diese Ideen, um eine genaue Definition des Integrals zu geben. Darüber hinaus wurden in dieser Zeit die Ideen der Infinitesimalrechnung auf den euklidischen Raum und die komplexe Ebene verallgemeinert.

In der modernen Mathematik sind die Grundlagen der Infinitesimalrechnung im Zweig der reellen Analysis enthalten, der vollständige Definitionen und Beweise der Theoreme der Infinitesimalrechnung enthält. Der Umfang der Analysisforschung ist viel breiter geworden. Henri Lebesgue entwickelte die Theorie der Mengenmaße und verwendete sie zur Bestimmung von Integralen aller bis auf die exotischsten Funktionen. Laurent Schwartz führte verallgemeinerte Funktionen ein, mit denen sich allgemein die Ableitungen jeder Funktion berechnen lassen.

Die Einführung von Grenzwerten bestimmte nicht die einzige strikte Herangehensweise an die Grundlagen der Infinitesimalrechnung. Eine Alternative wäre beispielsweise die nichtstandardisierte Analyse von Abraham Robinson. Robinsons in den 1960er Jahren entwickelter Ansatz nutzt technische Hilfsmittel der mathematischen Logik, um das System der reellen Zahlen auf unendlich kleine und unendlich große Zahlen zu erweitern, wie im ursprünglichen Newton-Leibniz-Konzept. Diese Zahlen, sogenannte hyperreale Zahlen, können in den gewöhnlichen Regeln der Analysis verwendet werden, ähnlich wie Leibniz es tat.

Bedeutung

Obwohl einige Ideen der Infinitesimalrechnung bereits zuvor in Ägypten, Griechenland, China, Indien, Irak, Persien und Japan entwickelt worden waren, begann die moderne Verwendung der Infinitesimalrechnung in Europa im 17. Jahrhundert, als Isaac Newton und Gottfried Wilhelm Leibniz auf der Arbeit von bauten frühere Mathematiker, auf seinen Grundprinzipien aufzubauen. Die Entwicklung der Analysis basierte auf den früheren Konzepten der Momentanbewegung und der Fläche unter einer Kurve.

Die Differentialrechnung wird bei Berechnungen im Zusammenhang mit Geschwindigkeit und Beschleunigung, Kurvensteigung und Optimierung verwendet. Zu den Anwendungen der Integralrechnung gehören Berechnungen mit Flächen, Volumina, Bogenlängen, Massenschwerpunkten, Arbeit und Druck. Zu komplexeren Anwendungen gehören Berechnungen von Potenzreihen und Fourierreihen.

Infinitesimalrechnung [ ] wird auch verwendet, um ein genaueres Verständnis der Natur von Raum, Zeit und Bewegung zu erlangen. Seit Jahrhunderten kämpfen Mathematiker und Philosophen mit den Paradoxien, die mit der Division durch Null oder der Ermittlung der Summe einer unendlichen Zahlenreihe verbunden sind. Diese Fragen stellen sich, wenn man Bewegungen untersucht und Flächen berechnet. Der antike griechische Philosoph Zenon von Elea nannte mehrere berühmte Beispiele für solche Paradoxien. Die Infinitesimalrechnung bietet Werkzeuge zur Lösung dieser Paradoxien, insbesondere von Grenzwerten und unendlichen Reihen.

Grenzen und Infinitesimalzahlen

Anmerkungen

1. Morris Kline, Mathematische Gedanken von der Antike bis zur Neuzeit, Bd. ICH
2. Archimedes, Methode, In Die Werke von Archimedes ISBN 978-0-521-66160-7
3. Dun, Liu; Fan, Dainian; Cohen, Sohn Robertne. Ein Vergleich der Kreisstudien von Archimdes und Liu Hui (Englisch): Zeitschrift. - Springer, 1966. - Bd. 130. - S. 279. - ISBN 0-792-33463-9., Kapitel, S. 279
4. Zill, Dennis G.; Wright, Scott; Wright, Warren S. Infinitesimalrechnung: Frühe Transzendentale (undefiniert). - 3. - Jones & Bartlett Learning (Englisch)Russisch, 2009. - S. xxvii. - ISBN 0-763-75995-3.,Auszug aus Seite 27
5. Indische Mathematik
6. von Neumann, J., „The Mathematician“, in Heywood, R. B., Hrsg., Die Werke des Geistes, University of Chicago Press, 1947, S. 180-196. Nachdruck in Brody, F., Vámos, T., Hrsg., Das Neumann-Kompedium, World Scientific Publishing Co. Pte. Ltd., 1995, ISBN 9810222017, S. 618-626.
7. André Weil: Zahlentheorie. Eine Annäherung durch die Geschichte. Von Hammurapi nach Legendre. Birkhauser Boston, Inc., Boston, MA, 1984, ISBN 0-8176-4565-9, S. 28.
8. Leibniz, Gottfried Wilhelm. Die frühen mathematischen Manuskripte von Leibniz. Cosimo, Inc., 2008. Seite 228. Kopie
9. Unlu, Elif Maria Gaetana Agnesi (nicht definiert) . Agnes Scott College (April 1995). Archiviert vom Original am 5. September 2012.

Links

• Ron Larson, Bruce H. Edwards (2010). „Calculus“, 9. Auflage, Brooks Cole Cengage Learning. ISBN 978-0-547-16702-2
• McQuarrie, Donald A. (2003). Mathematische Methoden für Wissenschaftler und Ingenieure, Wissenschaftsbücher der Universität. ISBN 978-1-891389-24-5
• James Stewart (2008). Infinitesimalrechnung: Frühe Transzendentale, 6. Auflage, Brooks Cole Cengage Learning.