Ausreichende Anzeichen eines Extremums einer Funktion. Anzeichen einer lokalen Zunahme und Abnahme einer Funktion. Notwendige und hinreichende Bedingungen für die Existenz eines Extremums einer Funktion an einem Punkt. Ein hinreichendes Zeichen für die Existenz eines Extremums

Die Funktion y = f(x) wird aufgerufen zunehmend (abnehmend) in einem bestimmten Intervall, wenn für x 1< x 2 выполняется неравенство (f(x 1) < f (x 2) (f(x 1) >f(x 2)).

Wenn die differenzierbare Funktion y = f(x) in einem Intervall zunimmt (abnimmt), dann ist ihre Ableitung in diesem Intervall f " (x) > 0

(f" (x)< 0).

Punkt x o angerufen lokaler Maximalpunkt (Minimum) Funktion f(x), wenn es eine Umgebung des Punktes gibt x o, für alle Punkte, für die die Ungleichung f(x) ≤ f(x о) (f(x) ≥ f(x о)) gilt.

Es werden die Maximal- und Minimalpunkte aufgerufen Extrempunkte, und die Werte der Funktion an diesen Punkten sind ihre Extreme.

Notwendige Bedingungen für ein Extremum. Wenn der Punkt x o ist ein Extrempunkt der Funktion f(x), dann ist entweder f " (x o) = 0, oder f (x o) existiert nicht. Solche Punkte werden aufgerufen kritisch, und die Funktion selbst ist am kritischen Punkt definiert. Die Extrema einer Funktion sollten unter ihren kritischen Punkten gesucht werden.

Die erste hinreichende Bedingung. Lassen x o- kritischer Punkt. Wenn f "(x) beim Durchgang durch einen Punkt x oÄndert das Pluszeichen in Minus, dann am Punkt x o Die Funktion hat ein Maximum, andernfalls hat sie ein Minimum. Wenn die Ableitung beim Durchlaufen des kritischen Punktes das Vorzeichen nicht ändert, dann an dem Punkt x o es gibt kein Extrem.

Zweite ausreichende Bedingung. Die Funktion f(x) habe eine Ableitung
f "(x) in der Nähe des Punktes x o und die zweite Ableitung am Punkt selbst x o. Wenn f "(x o) = 0, >0 (<0), то точка x o ist der lokale minimale (maximale) Punkt der Funktion f(x). Wenn =0, müssen Sie entweder die erste ausreichende Bedingung verwenden oder höhere Ableitungen verwenden.

Auf einem Segment kann die Funktion y = f(x) ihren minimalen oder maximalen Wert entweder an kritischen Punkten oder an den Enden des Segments erreichen.

Studieren von Bedingungen und Zeichnen von Diagrammen.

Finden Sie den Definitionsbereich einer Funktion

Finden Sie die Schnittpunkte des Diagramms mit den Koordinatenachsen

Finden Sie Intervalle des Konstanzzeichens

Auf Gleichmäßigkeit und Ungeradheit prüfen

Finden Sie Asymptoten des Graphen einer Funktion

Finden Sie Intervalle der Monotonie einer Funktion

Finden Sie die Extrema der Funktion

Finden Sie Konvexitätsintervalle und Wendepunkte

Asymptoten von Funktionsgraphen. Allgemeines Schema zum Studieren und Zeichnen von Funktionsgraphen. Beispiele.

Vertikal

Vertikale Asymptote – eine gerade Linie, vorbehaltlich der Existenz einer Grenze .

Bei der Bestimmung der vertikalen Asymptote wird in der Regel nicht nach einer Grenze gesucht, sondern nach zwei einseitigen (links und rechts). Dies geschieht, um zu bestimmen, wie sich die Funktion verhält, wenn sie sich der vertikalen Asymptote aus verschiedenen Richtungen nähert. Zum Beispiel:

Hinweis: Achten Sie bei diesen Gleichungen auf die Unendlichkeitszeichen.

[Bearbeiten]Horizontal

Horizontale Asymptote – eine gerade Linie, vorbehaltlich der Existenz einer Grenze

[Bearbeiten] Schräg

Schräge Asymptote – eine gerade Linie, vorbehaltlich der Existenz von Grenzen

Beispiel einer schrägen Asymptote

Hinweis: Eine Funktion kann nicht mehr als zwei schräge (horizontale) Asymptoten haben!

Hinweis: Wenn mindestens einer der beiden oben genannten Grenzwerte nicht existiert (oder gleich ist), dann existiert die schräge Asymptote bei (oder ) nicht!

Beziehung zwischen schrägen und horizontalen Asymptoten

Wenn bei der Berechnung des Limits , dann ist es offensichtlich, dass die schräge Asymptote mit der horizontalen zusammenfällt. Welcher Zusammenhang besteht zwischen diesen beiden Arten von Asymptoten?

Die Sache ist, dass die horizontale Asymptote ein Sonderfall der schrägen ist bei , und aus den obigen Kommentaren folgt dies

1. Die Funktion hat entweder nur eine schräge Asymptote oder eine vertikale Asymptote oder eine schräge und eine vertikale oder zwei schräge oder zwei vertikale oder hat überhaupt keine Asymptoten.

2. Die Existenz der in Absatz 1.) genannten Asymptoten steht in direktem Zusammenhang mit der Existenz der entsprechenden Grenzen.

Graph einer Funktion mit zwei horizontalen Asymptoten

]Asymptoten finden

Die Reihenfolge, in der Asymptoten gefunden werden

1. Vertikale Asymptoten finden.

2. Zwei Grenzen finden

3. Zwei Grenzen finden:

wenn in Punkt 2.), dann , und der Grenzwert wird mit der horizontalen Asymptotenformel gesucht, .

Der Extrempunkt einer Funktion ist der Punkt im Definitionsbereich der Funktion, an dem der Wert der Funktion einen minimalen oder maximalen Wert annimmt. Die Werte der Funktion an diesen Punkten werden Extrema (Minimum und Maximum) der Funktion genannt.

Definition. Punkt X1 Funktionsdomäne F(X) wird genannt Maximalpunkt der Funktion , wenn der Wert der Funktion an diesem Punkt größer ist als die Werte der Funktion an Punkten, die ausreichend nahe daran liegen, rechts und links davon liegen (d. h. die Ungleichung gilt). F(X0 ) > F(X 0 + Δ X) X1 maximal.

Definition. Punkt X2 Funktionsdomäne F(X) wird genannt Minimalpunkt der Funktion, wenn der Wert der Funktion an diesem Punkt kleiner ist als die Werte der Funktion an Punkten, die ausreichend nahe daran liegen, rechts und links davon liegen (d. h. die Ungleichung gilt). F(X0 ) < F(X 0 + Δ X) ). In diesem Fall sagen wir, dass die Funktion den Punkt hat X2 Minimum.

Sagen wir Punkt X1 - Maximalpunkt der Funktion F(X). Dann im Intervall bis X1 Funktion erhöht, daher ist die Ableitung der Funktion größer als Null ( F "(X) > 0 ), und im Intervall danach X1 die Funktion nimmt also ab, Ableitung einer Funktion weniger als Null ( F "(X) < 0 ). Тогда в точке X1

Nehmen wir auch an, dass der Punkt X2 - Minimalpunkt der Funktion F(X). Dann im Intervall bis X2 Die Funktion nimmt ab und die Ableitung der Funktion ist kleiner als Null ( F "(X) < 0 ), а в интервале после X2 Die Funktion nimmt zu und die Ableitung der Funktion ist größer als Null ( F "(X) > 0 ). In diesem Fall auch an der Stelle X2 Die Ableitung der Funktion ist Null oder existiert nicht.

Satz von Fermat (ein notwendiges Zeichen für die Existenz eines Extremums einer Funktion). Wenn der Punkt X0 - Extrempunkt der Funktion F(X) dann ist an diesem Punkt die Ableitung der Funktion gleich Null ( F "(X) = 0 ) oder existiert nicht.

Definition. Es werden die Punkte aufgerufen, an denen die Ableitung einer Funktion Null ist oder nicht existiert kritische Punkte .

Beispiel 1. Betrachten wir die Funktion.

Am Punkt X= 0 ist die Ableitung der Funktion Null, also der Punkt X= 0 ist der kritische Punkt. Wie man jedoch am Graphen der Funktion erkennen kann, nimmt sie über den gesamten Definitionsbereich, also den Punkt, zu X= 0 ist nicht der Extrempunkt dieser Funktion.

Somit sind die Bedingungen, dass die Ableitung einer Funktion an einem Punkt gleich Null ist oder nicht existiert, notwendige Bedingungen für ein Extremum, aber nicht ausreichend, da außer der Funktion auch andere Beispiele für Funktionen angegeben werden können, für die diese Bedingungen erfüllt sind hat am entsprechenden Punkt kein Extremum. Deshalb Es müssen ausreichende Beweise vorliegen Dies ermöglicht die Beurteilung, ob an einem bestimmten kritischen Punkt ein Extremum vorliegt und um welche Art von Extremum es sich handelt – Maximum oder Minimum.

Satz (das erste hinreichende Zeichen für die Existenz eines Extremums einer Funktion). Kritischer Punkt X0 F(X) Wenn beim Durchlaufen dieses Punktes die Ableitung der Funktion das Vorzeichen ändert und wenn sich das Vorzeichen von „Plus“ nach „Minus“ ändert, dann handelt es sich um einen Maximalpunkt, und wenn von „Minus“ nach „Plus“, dann es ist ein Mindestpunkt.

Wenn in der Nähe des Punktes X0 , links und rechts davon behält die Ableitung ihr Vorzeichen, das bedeutet, dass die Funktion in einer bestimmten Umgebung des Punktes entweder nur abnimmt oder nur zunimmt X0 . In diesem Fall an der Stelle X0 es gibt kein Extrem.

Also, Um die Extrempunkte der Funktion zu bestimmen, müssen Sie Folgendes tun :

Finden Sie die Ableitung der Funktion.
Setzen Sie die Ableitung mit Null gleich und bestimmen Sie die kritischen Punkte.
Markieren Sie gedanklich oder auf Papier die kritischen Punkte auf der Zahlengeraden und bestimmen Sie die Vorzeichen der Ableitung der Funktion in den resultierenden Intervallen. Wenn sich das Vorzeichen der Ableitung von „Plus“ nach „Minus“ ändert, ist der kritische Punkt der Maximalpunkt, und wenn von „Minus“ nach „Plus“, dann der Minimalpunkt.
Berechnen Sie den Wert der Funktion an den Extrempunkten.

Beispiel 2. Finden Sie die Extrema der Funktion .

Lösung. Finden wir die Ableitung der Funktion:

Setzen wir die Ableitung mit Null gleich, um die kritischen Punkte zu finden:

Da für alle Werte von „x“ der Nenner ungleich Null ist, setzen wir den Zähler mit Null gleich:

Ich habe einen kritischen Punkt X= 3 . Bestimmen wir das Vorzeichen der Ableitung in den durch diesen Punkt begrenzten Intervallen:

im Bereich von minus unendlich bis 3 - ein Minuszeichen, d. h. die Funktion nimmt ab,

Im Intervall von 3 bis plus Unendlich gibt es ein Pluszeichen, das heißt, die Funktion nimmt zu.

Das heißt, Punkt X= 3 ist der Mindestpunkt.

Lassen Sie uns den Wert der Funktion am Minimalpunkt ermitteln:

Somit wird der Extrempunkt der Funktion gefunden: (3; 0) und es ist der Minimalpunkt.

Satz (das zweite hinreichende Zeichen für die Existenz eines Extremums einer Funktion). Kritischer Punkt X0 ist der Extrempunkt der Funktion F(X), wenn die zweite Ableitung der Funktion an dieser Stelle ungleich Null ist ( F ""(X) ≠ 0 ), und wenn die zweite Ableitung größer als Null ist ( F ""(X) > 0 ), dann der Maximalpunkt, und wenn die zweite Ableitung kleiner als Null ist ( F ""(X) < 0 ), то точкой минимума.

Hinweis 1. Wenn an der Stelle X0 Wenn sowohl die erste als auch die zweite Ableitung verschwinden, ist es zu diesem Zeitpunkt unmöglich, das Vorhandensein eines Extremums anhand des zweiten hinreichenden Kriteriums zu beurteilen. In diesem Fall müssen Sie das erste ausreichende Kriterium für das Extremum einer Funktion verwenden.

Bemerkung 2. Das zweite ausreichende Kriterium für das Extremum einer Funktion ist selbst dann nicht anwendbar, wenn die erste Ableitung an einem stationären Punkt nicht existiert (dann existiert auch die zweite Ableitung nicht). In diesem Fall müssen Sie auch das erste ausreichende Vorzeichen eines Extremums einer Funktion verwenden.

Lokale Natur der Extrema der Funktion

Aus den obigen Definitionen folgt, dass das Extremum einer Funktion lokaler Natur ist – es ist der größte und kleinste Wert der Funktion im Vergleich zu benachbarten Werten.

Nehmen wir an, Sie betrachten Ihre Einnahmen über einen Zeitraum von einem Jahr. Wenn Sie im Mai 45.000 Rubel, im April 42.000 Rubel und im Juni 39.000 Rubel verdient haben, dann ist der Mai-Verdienst das Maximum der Verdienstfunktion im Vergleich zu nahegelegenen Werten. Aber im Oktober haben Sie 71.000 Rubel verdient, im September 75.000 Rubel und im November 74.000 Rubel, sodass der Oktoberverdienst das Minimum der Verdienstfunktion im Vergleich zu nahegelegenen Werten darstellt. Und Sie können leicht erkennen, dass das Maximum der Werte von April-Mai-Juni unter dem Minimum von September-Oktober-November liegt.

Im Allgemeinen kann eine Funktion in einem Intervall mehrere Extrema haben, und es kann sich herausstellen, dass ein Minimum der Funktion größer als ein Maximum ist. Für die in der Abbildung oben gezeigte Funktion gilt also .

Das heißt, man sollte nicht denken, dass das Maximum und das Minimum einer Funktion deren größter bzw. kleinster Wert im gesamten betrachteten Segment sind. Am Maximalpunkt hat die Funktion den größten Wert nur im Vergleich zu den Werten, die sie an allen Punkten hat, die ausreichend nahe am Maximalpunkt liegen, und am Minimalpunkt hat sie den kleinsten Wert nur im Vergleich zu diesen Werten dass es an allen Punkten ausreichend nahe am Minimalpunkt liegt.

Daher können wir das obige Konzept der Extrempunkte einer Funktion klarstellen und Minimalpunkte als lokale Minimalpunkte und Maximalpunkte als lokale Maximalpunkte bezeichnen.

Wir suchen gemeinsam nach den Extrema der Funktion

Beispiel 3.

Lösung: Die Funktion ist auf dem gesamten Zahlenstrahl definiert und stetig. Seine Ableitung existiert auch auf dem gesamten Zahlenstrahl. Daher sind in diesem Fall die kritischen Punkte nur diejenigen, an denen, d. h. , von wo und . Kritische Punkte und unterteilen den gesamten Definitionsbereich der Funktion in drei Intervalle der Monotonie: . Wählen wir in jedem von ihnen einen Kontrollpunkt aus und ermitteln wir das Vorzeichen der Ableitung an diesem Punkt.

Für das Intervall kann der Kontrollpunkt sein: finden. Wenn wir einen Punkt im Intervall nehmen, erhalten wir, und wenn wir einen Punkt im Intervall nehmen, haben wir. Also, in den Intervallen und und im Intervall. Nach dem ersten hinreichenden Kriterium für ein Extremum gibt es an dem Punkt kein Extremum (da die Ableitung ihr Vorzeichen im Intervall behält) und an dem Punkt hat die Funktion ein Minimum (da die Ableitung beim Passieren ihr Vorzeichen von Minus nach Plus ändert). bis zu diesem Punkt). Finden wir die entsprechenden Werte der Funktion: , a . Im Intervall nimmt die Funktion ab, da in diesem Intervall , und im Intervall nimmt sie zu, da in diesem Intervall .

Um den Aufbau des Graphen zu verdeutlichen, ermitteln wir dessen Schnittpunkte mit den Koordinatenachsen. Wenn wir eine Gleichung erhalten, deren Wurzeln und sind, werden also zwei Punkte (0; 0) und (4; 0) des Funktionsgraphen gefunden. Aus allen erhaltenen Informationen erstellen wir ein Diagramm (siehe Anfang des Beispiels).

Zur Selbstkontrolle bei Berechnungen können Sie verwenden Online-Ableitungsrechner .

Beispiel 4. Finden Sie die Extrema der Funktion und erstellen Sie ihren Graphen.

Der Definitionsbereich einer Funktion ist der gesamte Zahlenstrahl mit Ausnahme des Punktes, d. h. .

Um die Studie zu verkürzen, können Sie die Tatsache nutzen, dass diese Funktion gerade ist, da . Daher ist sein Graph symmetrisch zur Achse Oy und die Studie kann nur für das Intervall durchgeführt werden.

Die Ableitung finden und kritische Punkte der Funktion:

1) ;

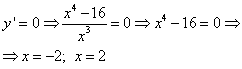2) ,

Da die Funktion an diesem Punkt jedoch eine Diskontinuität aufweist, kann es sich nicht um einen Extrempunkt handeln.

Somit hat die gegebene Funktion zwei kritische Punkte: und . Unter Berücksichtigung der Parität der Funktion prüfen wir nur den Punkt anhand des zweiten ausreichenden Kriteriums für ein Extremum. Dazu ermitteln wir die zweite Ableitung und bestimmen Sie sein Vorzeichen bei: Wir erhalten . Da und ist es der Minimalpunkt der Funktion und .

Um ein vollständigeres Bild des Graphen einer Funktion zu erhalten, wollen wir ihr Verhalten an den Grenzen des Definitionsbereichs herausfinden:

(Hier zeigt das Symbol den Wunsch an X von rechts auf Null und X bleibt positiv; bedeutet in ähnlicher Weise Streben X von links auf Null und X bleibt negativ). Also wenn, dann. Als nächstes finden wir

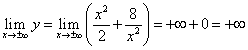diese. wenn, dann .

Der Graph einer Funktion hat keine Schnittpunkte mit den Achsen. Das Bild befindet sich am Anfang des Beispiels.

Zur Selbstkontrolle bei Berechnungen können Sie verwenden Online-Ableitungsrechner .

Wir suchen weiterhin gemeinsam nach Extrema der Funktion

Beispiel 8. Finden Sie die Extrema der Funktion.

Lösung. Finden wir den Definitionsbereich der Funktion. Da die Ungleichung erfüllt sein muss, erhalten wir aus .

Finden wir die erste Ableitung der Funktion.

Um die Maxima und Minima einer Funktion zu ermitteln, können Sie jedes der drei hinreichenden Vorzeichen eines Extremums verwenden. Obwohl die erste die gebräuchlichste und bequemste ist.

Die erste hinreichende Bedingung für ein Extremum.

Lassen Sie die Funktion y = f(x) ist in einer Umgebung des Punktes differenzierbar und am Punkt selbst stetig. Dann

Mit anderen Worten:

Algorithmus.

Wir finden den Definitionsbereich der Funktion.

Wir finden die Ableitung der Funktion im Definitionsbereich.

Wir bestimmen die Nullstellen des Zählers, die Nullstellen des Nenners der Ableitung und die Punkte des Definitionsbereichs, an denen die Ableitung nicht existiert (diese Punkte heißen Punkte möglichen Extremums Durch diese Punkte kann die Ableitung einfach ihr Vorzeichen ändern.

Diese Punkte unterteilen den Definitionsbereich der Funktion in Intervalle, in denen die Ableitung ihr Vorzeichen behält. Wir bestimmen die Vorzeichen der Ableitung in jedem der Intervalle (z. B. indem wir den Wert der Ableitung einer Funktion an einem beliebigen Punkt in einem bestimmten Intervall berechnen).

Wir wählen Punkte aus, an denen die Funktion stetig ist und durch die die Ableitung das Vorzeichen ändert.

Beispiel. Finden Sie die Extrema der Funktion.
Lösung.
Der Definitionsbereich einer Funktion ist die gesamte Menge der reellen Zahlen außer x = 2.
Finden der Ableitung:

Die Nullstellen des Zählers sind Punkte x = -1 Und x = 5, der Nenner geht bei Null auf Null x = 2. Markieren Sie diese Punkte auf der Zahlenachse

Wir bestimmen die Vorzeichen der Ableitung in jedem Intervall; dazu berechnen wir den Wert der Ableitung an einem beliebigen Punkt jedes Intervalls, beispielsweise an den Punkten x = -2, x = 0, x = 3 Und x=6.

Daher ist die Ableitung des Intervalls positiv (in der Abbildung haben wir über dieses Intervall ein Pluszeichen gesetzt). Ebenfalls

Deshalb setzen wir über das zweite Intervall ein Minus, über das dritte ein Minus und über das vierte ein Plus.

Es müssen noch Punkte ausgewählt werden, an denen die Funktion stetig ist und ihre Ableitung das Vorzeichen ändert. Dies sind die Extrempunkte.
Am Punkt x = -1 Die Funktion ist stetig und die Ableitung ändert das Vorzeichen von Plus nach Minus. Entsprechend dem ersten Vorzeichen eines Extremums gilt: x = -1 ist der Maximalpunkt; ihm entspricht das Maximum der Funktion.
Am Punkt x = 5 Die Funktion ist stetig und die Ableitung ändert das Vorzeichen von Minus nach Plus. x = -1 ist der Minimalpunkt; ihm entspricht das Minimum der Funktion.
Grafische Illustration.

Antwort: .

Das zweite ausreichende Zeichen für ein Extremum einer Funktion.
Lassen ,

wenn , dann ist der Mindestpunkt;

wenn , dann ist der maximale Punkt.

Wie Sie sehen, erfordert dieses Kriterium die Existenz einer Ableitung mindestens bis zur zweiten Ordnung im Punkt .
Beispiel. Finden Sie die Extrema der Funktion.
Lösung.
Beginnen wir mit dem Definitionsbereich:

Lassen Sie uns die ursprüngliche Funktion unterscheiden:

Die Ableitung geht bei Null auf Null x = 1, das heißt, dies ist ein möglicher Extrempunkt.
Wir finden die zweite Ableitung der Funktion und berechnen ihren Wert bei x = 1:

Daher gilt als zweite hinreichende Bedingung für ein Extremum: x = 1- Maximalpunkt. Dann - das Maximum der Funktion.
Grafische Illustration.

Antwort: .
Das dritte ausreichende Zeichen für ein Extremum einer Funktion.
Lassen Sie die Funktion y = f(x) hat Derivate bis zu N-te Ordnung in der -Nachbarschaft des Punktes und Ableitungen bis zu n+1-te Ordnung an der Stelle selbst. Lass es sein.
Dann,

Feierabend -

Dieses Thema gehört zum Abschnitt:

Algebra und analytische Geometrie. Das Konzept einer Matrix, Operationen auf Matrizen und ihre Eigenschaften

Das Konzept einer Matrix sind Operationen an Matrizen und ihren Eigenschaften. Eine Matrix ist eine rechteckige Tabelle, die aus Zahlen besteht, die nicht sein können. Und die Matrixaddition ist eine elementweise Operation.

Wenn Sie zusätzliches Material zu diesem Thema benötigen oder nicht gefunden haben, was Sie gesucht haben, empfehlen wir Ihnen die Suche in unserer Werkdatenbank:

Was machen wir mit dem erhaltenen Material:

Wenn dieses Material für Sie nützlich war, können Sie es auf Ihrer Seite in sozialen Netzwerken speichern:

Alle Themen in diesem Abschnitt:

Definition von Differenzierbarkeit
Die Operation, die Ableitung zu finden, nennt man Differentiation einer Funktion. Eine Funktion heißt an einem Punkt differenzierbar, wenn sie an diesem Punkt eine endliche Ableitung hat, und

Differenzierungsregel
Folgerung 1. Der konstante Faktor lässt sich aus dem Vorzeichen der Ableitung entnehmen:

Geometrische Bedeutung der Ableitung. Tangentengleichung
Der Neigungswinkel einer Geraden y = kx+b ist der von der Position aus gemessene Winkel

Geometrische Bedeutung der Ableitung einer Funktion an einem Punkt
Betrachten wir die Sekante AB des Graphen der Funktion y = f(x), sodass die Punkte A und B jeweils Koordinaten haben

Lösung
Die Funktion ist für alle reellen Zahlen definiert. Da (-1; -3) ein Tangentenpunkt ist

Notwendige Bedingungen für ein Extremum und hinreichende Bedingungen für ein Extremum
Definition einer steigenden Funktion. Die Funktion y = f(x) nimmt im Intervall X zu, wenn überhaupt

Bedingungen für Monotonie und Konstanz einer Funktion
Bedingung für die (nicht strikte) Monotonie einer Funktion auf einem Intervall. Die Funktion soll jeweils eine Ableitung haben

Definition von Stammfunktion
Eine Stammfunktion einer Funktion f(x) im Intervall (a; b) ist eine Funktion F(x) mit der Gleichheit

Untersuchung
Um das Ergebnis zu überprüfen, differenzieren wir den resultierenden Ausdruck: Als Ergebnis erhalten wir

Die Stammfunktion des Produkts einer Konstante und einer Funktion ist gleich dem Produkt einer Konstante und der Stammfunktion einer Funktion
Eine hinreichende Bedingung für die Existenz einer Stammfunktion einer auf einem Intervall gegebenen Funktion ist

Definition
Lassen Sie es definieren

Geometrische Bedeutung
Das bestimmte Integral ist numerisch gleich der Fläche der Figur, die durch die Abszissenachse und die Geraden begrenzt wird

Eigenschaften eines bestimmten Integrals
Grundlegende Eigenschaften eines bestimmten Integrals. Eigenschaft 1. Die Ableitung eines bestimmten Integrals nach der Obergrenze ist gleich dem Integranden, in den statt einer Variablen integriert wird

Newton-Leibniz-Formel (mit Beweis)
Newton-Leibniz-Formel. Sei die Funktion y = f(x) in einem Intervall stetig und F(x) eine der Stammfunktionen der Funktion in diesem Intervall, dann ergibt sich die Gleichung

Satz (die erste hinreichende Bedingung für ein Extremum). Die Funktion sei an einem Punkt stetig und die Ableitung ändere das Vorzeichen, wenn sie durch den Punkt geht. Dann ist der Extrempunkt: Maximum, wenn das Vorzeichen von „+“ auf „–“ wechselt, und Minimum, wenn von „–“ auf „+“ wechselt.

Nachweisen. Lass um und um .

Nach dem Satz von Lagrange , wo .Dann wenn , dann ; deshalb , somit, , oder . Wenn, dann; deshalb , somit, oder .

Damit ist bewiesen, dass an allen Punkten in der Nähe, d.h. – der Maximalpunkt der Funktion.

Der Beweis des Satzes für den Minimalpunkt erfolgt analog. Der Satz ist bewiesen.

Wenn die Ableitung beim Durchlaufen eines Punktes das Vorzeichen nicht ändert, gibt es an dem Punkt kein Extremum.

Satz (zweite hinreichende Bedingung für Extremum). Die Ableitung einer zweimal differenzierbaren Funktion an einem Punkt sei gleich 0 () und ihre zweite Ableitung an diesem Punkt sei von Null () verschieden und in einer Umgebung des Punktes stetig. Dann ist der Extrempunkt; an diesem Punkt ist der Minimalpunkt und an diesem Punkt ist der Maximalpunkt.

Ein Algorithmus zum Finden von Extrema einer Funktion unter Verwendung der ersten hinreichenden Bedingung für ein Extremum.

1. Finden Sie die Ableitung.

2. Finden Sie die kritischen Punkte der Funktion.

3. Untersuchen Sie das Vorzeichen der Ableitung links und rechts von jedem kritischen Punkt und ziehen Sie eine Schlussfolgerung über das Vorhandensein von Extrema.

4. Finden Sie Extremwerte der Funktion.

Ein Algorithmus zum Finden von Extrema einer Funktion unter Verwendung der zweiten hinreichenden Bedingung für ein Extremum.

1. Finden Sie die Ableitung.

2. Finden Sie die zweite Ableitung.

3. Finden Sie die Punkte, an denen .

4. Bestimmen Sie das Vorzeichen an diesen Punkten.

5. Ziehen Sie eine Schlussfolgerung über die Existenz und Natur von Extrema.

6. Finden Sie Extremwerte der Funktion.

Beispiel. Lassen Sie uns überlegen . Wir werden finden . Als nächstes, um und um . Lassen Sie uns die kritischen Punkte anhand der ersten hinreichenden Bedingung für das Extremum untersuchen. Wir haben das für und für und für . Bei Punkten ändert die Ableitung ihr Vorzeichen: bei von „+“ nach „–“ und bei bei von „–“ nach „+“. Das bedeutet, dass die Funktion an einem Punkt ein Maximum und an einem Punkt ein Minimum hat; . Zum Vergleich untersuchen wir die kritischen Punkte anhand der zweiten hinreichenden Bedingung für das Extremum. Finden wir die zweite Ableitung. Wir haben: , und das bedeutet, dass die Funktion an einem Punkt ein Maximum und an einem Punkt ein Minimum hat.

Das Konzept der Asymptote eines Funktionsgraphen. Horizontale, schräge und vertikale Asymptoten. Beispiele.

Definition. Eine Asymptote des Graphen einer Funktion ist eine gerade Linie, die die Eigenschaft hat, dass der Abstand von einem Punkt zu dieser geraden Linie gegen Null tendiert, wenn sich der Graphpunkt auf unbestimmte Zeit vom Ursprung entfernt.

Es gibt vertikale (Abb. 6.6 a), horizontale (Abb. 6.6 b) und geneigte (Abb. 6.6 c) Asymptoten.

In Abb. 6.6a ist dargestellt vertikale Asymptote.

In Abb. 6.6b - horizontale Asymptote.

In Abb. 6,6 V – schräge Asymptote.

Satz 1. An Punkten mit vertikalen Asymptoten (z. B. ) weist die Funktion eine Diskontinuität auf, ihr Grenzwert links und rechts vom Punkt ist gleich:

Satz 2. Die Funktion sei ausreichend groß definiert und es gebe endliche Grenzen

UND .

Dann ist die Gerade die schräge Asymptote des Funktionsgraphen.

Satz 3. Die Funktion sei hinreichend groß definiert und es gäbe einen Grenzwert der Funktion. Dann ist die Gerade die horizontale Asymptote des Funktionsgraphen.

Die horizontale Asymptote ist ein Sonderfall der schrägen Asymptote, wenn . Wenn also eine Kurve in irgendeiner Richtung eine horizontale Asymptote hat, dann gibt es in dieser Richtung keine geneigte und umgekehrt.

Beispiel. Finden Sie die Asymptoten des Funktionsgraphen.

Lösung. An dem Punkt, an dem die Funktion nicht definiert ist, ermitteln wir die Grenzen der Funktion links und rechts vom Punkt:

; .

Daher ist eine vertikale Asymptote.

Allgemeines Schema zum Studieren von Funktionen und zum Erstellen ihrer Graphen. Beispiel.

Allgemeines Schema der Funktionsforschung und es planen.

1. Finden Sie den Definitionsbereich.

2. Untersuchen Sie die Funktion auf Gleichmäßigkeit – Ungeradheit.

3. Finden Sie vertikale Asymptoten und Diskontinuitätspunkte (falls vorhanden).

4. Untersuchen Sie das Verhalten einer Funktion im Unendlichen; Finden Sie horizontale und schräge Asymptoten (falls vorhanden).

5. Finden Sie Extrema und Intervalle der Monotonie der Funktion.

6. Finden Sie die Schnittpunkte des Graphen mit den Koordinatenachsen und, falls für den schematischen Aufbau des Graphen erforderlich, zusätzliche Punkte.

7. Zeichnen Sie schematisch ein Diagramm.

Detailliertes Diagramm der Funktionsstudie und Plotten .

1. Finden Sie den Definitionsbereich .

A. Wenn y einen Nenner hat, sollte dieser nicht gegen 0 gehen.

B. Der Wurzelausdruck einer Wurzel geraden Grades darf nicht negativ sein (größer oder gleich Null).

C. Der Sublog-Ausdruck muss positiv sein.

2. Untersuchen Sie die Funktion auf Parität – Ungeradheit.

A. Wenn , dann ist die Funktion gerade.

B. Wenn , dann ist die Funktion ungerade.

C. Wenn weder , noch , dann ist eine Funktion der allgemeinen Form.

3. Finden Sie vertikale Asymptoten und Diskontinuitätspunkte (falls vorhanden).

A. Eine vertikale Asymptote kann nur am Rand des Definitionsbereichs der Funktion entstehen.

B. Wenn ( oder ), dann ist die vertikale Asymptote des Graphen.

4. Untersuchen Sie das Verhalten einer Funktion im Unendlichen; Finden Sie horizontale und schräge Asymptoten (falls vorhanden).

A. Wenn, dann ist die horizontale Asymptote des Graphen.

B. Wenn , dann ist die Gerade die geneigte Asymptote des Graphen.

C. Wenn die in den Absätzen a, b angegebenen Grenzen nur existieren, wenn einseitig gegen Unendlich tendiert ( oder ), dann sind die resultierenden Asymptoten einseitig: linkshändig bei und rechtshändig wenn .

5. Finden Sie Extrema und Intervalle der Monotonie der Funktion.

A. Finden Sie die Ableitung.

B. Finden Sie kritische Punkte (Punkte, die vorhanden sind oder nicht vorhanden sind).

C. Markieren Sie auf der Zahlenachse den Definitionsbereich und seine kritischen Punkte.

D. Bestimmen Sie für jedes der resultierenden numerischen Intervalle das Vorzeichen der Ableitung.

e. Ziehen Sie anhand der Vorzeichen der Ableitung eine Schlussfolgerung über das Vorhandensein von Extrema in y und deren Art.

F. Finden Sie Extremwerte.

G. Ziehen Sie anhand der Vorzeichen der Ableitung Rückschlüsse auf Zunahme und Abnahme.

6. Suchen Sie die Schnittpunkte des Diagramms mit den Koordinatenachsen und suchen Sie, falls für die schematische Darstellung des Diagramms erforderlich, zusätzliche Punkte.

A. Um die Schnittpunkte des Graphen mit der Achse zu finden, ist es notwendig, die Gleichung zu lösen. Die Punkte, an denen Nullen sind, sind die Schnittpunkte des Diagramms mit der Achse.

B. Der Schnittpunkt des Diagramms mit der Achse sieht wie folgt aus. Es existiert nur, wenn der Punkt innerhalb des Funktionsbereichs liegt.

8. Zeichnen Sie schematisch ein Diagramm.

A. Konstruieren Sie ein Koordinatensystem und Asymptoten.

B. Markieren Sie Extrempunkte.

C. Markieren Sie die Schnittpunkte des Diagramms mit den Koordinatenachsen.

D. Konstruieren Sie schematisch einen Graphen so, dass er durch die markierten Punkte verläuft und sich den Asymptoten nähert.

Beispiel. Erkunden Sie die Funktion und konstruieren Sie schematisch ihren Graphen.

2. – Funktion der allgemeinen Form.

3. Da und sind die Geraden und vertikale Asymptoten; Punkte sind Haltepunkte. , wenn es nicht im Definitionsbereich der Funktion enthalten ist

Ticket Nr. 1

StammfunktionSatzNachweisen unbestimmtes Integral

Der Punkt (X 0 ;Y 0) wird aufgerufen Maximalpunkt Mindestpunktzahl Funktionen: Für alle von (X 0 ;Y 0) verschiedenen Punkte (x;y) gilt aus der δ-Umgebung des Punktes (X 0 ;Y 0) die Ungleichung f(x;y)>f(X 0 ;Y 0) erfüllt ist.

Beweis:

Ticket Nr. 2

NachweisenGeometrische Bedeutung

privater Zuwachs partielle Ableitung Geometrische Bedeutung

Ticket Nr. 3

19. Bestimmung der Maximal- und Minimalpunkte der Funktion z=f(x,y). Der Punkt (X 0 ;Y 0) wird aufgerufen Maximalpunkt Funktion z=f(x;y), wenn es eine δ-Umgebung des Punktes (X 0 ;Y 0) gibt, so dass die Ungleichung f(x;y) gilt Mindestpunktzahl Funktionen: Für alle von (X 0 ;Y 0) verschiedenen Punkte (x;y) gilt aus der δ-Umgebung des Punktes (X 0 ;Y 0) die Ungleichung f(x;y)>f(X 0 ;Y 0) erfüllt ist. An einem stationären Punkt (X 0 ;Y 0) und einigen seiner Umgebungen soll die Funktion f(x;y) stetige partielle Ableitungen bis einschließlich zweiter Ordnung haben. Berechnen wir am Punkt (X 0 ;Y 0) die Werte A=f"" xx (X 0 ;Y 0), B=f"" xy (X 0 ;Y 0), C=f"" yy (X 0 ;Y 0). Bezeichnen wir Δ=|AB; BC|=AC-B^2. Dann: 1) wenn Δ><0; минимум, если A>0; 2) wenn Δ<0, то функция f(x;y) в точке (X 0 ;Y 0) экстремума не имеет. В случае Δ=0 экстремум в точке (X 0 ;Y 0) может быть, а может не быть. Необходимы дополнительные исследования.

Ticket Nr. 4 Durch ein bestimmtes Integral Eigenschaften Nachweisen. an einem Punkt mit den Koordinaten (x;y;z).Δu/Δl=LimΔl→0(Δ l u/Δl)=(δu/δx)*cosα+(δu/δy)*cosβ+(δu/δz)*cosγ . Angenommen, die Funktion u(x;y;z) ist stetig und hat stetige Ableitungen in Bezug auf ihre Argumente im Bereich D: Δu=(δu/δx)Δx+(δu/δy)Δy+(δu/δz)Δz+ E 1 Δx+E 2 Δy+E 3 Δz, wobei E 1, E 2, E 3 gegen Null tendieren, da Δl→0. Teilen wir die gesamte Gleichheit durch Δl. Δu/Δl=(δu/δx)(Δx/Δl)+(δu/δy)(Δy/Δl)+(δu/δz)(Δz/Δl)+E 1 (Δx/Δl)+E 2 (Δy/ Δl)+E 3 (Δz/Δl). Δx/Δl=cosα; Δy/Δl=cosβ; Δz/Δl=cosγ. Die Gleichheit kann wie folgt dargestellt werden: Δu/Δl=(δu/δx)cosα+(δu/δy)cosβ+(δu/δz)cosγ+E 1 cosα+E 2 cosβ+E 3 cosγ. Wenn wir uns dem Grenzwert nähern, erhalten wir Δu/Δl=LimΔl→0(Δ l u/Δl)=(δu/δx)*cosα+(δu/δy)*cosβ+(δu/δz)*cosγ.

Ticket Nr. 5

1. Stammfunktion. Satz über die Differenz zweier Stammfunktionen (mit Beweis). Unbestimmtes Integral: Definition Die Funktion F(x) wird aufgerufen Stammfunktion f(x) auf dem Intervall (a;b), wenn für jedes x∈(a;b) die Gleichheit F"(x)=f(x) gilt. Satz. Wenn die Funktion F(x) eine Stammfunktion der Funktion f(x) auf (a;b) ist, dann ist die Menge aller Stammfunktionen für f(x) durch die Formel F(x)+C gegeben, wobei C= const. Nachweisen. Die Funktion F(x)+C ist eine Stammfunktion von f(x). Tatsächlich ist (F(x)+C)"=F"(x)=f(x). Sei Ф(x) eine andere Stammfunktion f(x), die sich von F(x) unterscheidet, d. h. Ф"(x)=f(x). Dann gilt für jedes x∈(a;b) (Ф(х)-F(x))"=Ф"(x)-F"(x)=f( x )-f(x)=0. Und das bedeutet, dass Ф(x)-F(x)=C, C=const. Daher ist Ф(x)=F(x)+C. Die Menge aller Stammfunktionen F(x)+C für f(x) heißt unbestimmtes Integral der Funktion f(x) und wird mit dem Symbol ∫f(x)dx bezeichnet.

19. Bestimmung der Maximal- und Minimalpunkte der Funktion z=f(x,y). Der Punkt (X 0 ;Y 0) wird aufgerufen Maximalpunkt Funktion z=f(x;y), wenn es eine δ-Umgebung des Punktes (X 0 ;Y 0) gibt, so dass die Ungleichung f(x;y) gilt Mindestpunktzahl Funktionen: Für alle von (X 0 ;Y 0) verschiedenen Punkte (x;y) gilt aus der δ-Umgebung des Punktes (X 0 ;Y 0) die Ungleichung f(x;y)>f(X 0 ;Y 0) erfüllt ist. 20. Ein ausreichendes Zeichen für die Existenz eines Extremums der Funktion z=f(x;y). (Wortlaut). An einem stationären Punkt (X 0 ;Y 0) und einigen seiner Umgebungen soll die Funktion f(x;y) stetige partielle Ableitungen bis einschließlich zweiter Ordnung haben. Berechnen wir am Punkt (X 0 ;Y 0) die Werte A=f"" xx (X 0 ;Y 0), B=f"" xy (X 0 ;Y 0), C=f"" yy (X 0 ;Y 0). Bezeichnen wir Δ=|AB; BC|=AC-B^2. Dann: 1) wenn Δ>0, dann hat die Funktion f(x;y) am Punkt (X 0 ;Y 0) ein Extremum: Maximum, wenn A<0; минимум, если A>0; 2) wenn Δ<0, то функция f(x;y) в точке (X 0 ;Y 0) экстремума не имеет. В случае Δ=0 экстремум в точке (X 0 ;Y 0) может быть, а может не быть. Необходимы дополнительные исследования.

Ticket Nr. 6

3. Berechnung eines bestimmten Integrals über eine Strecke. Newton-Leibniz-Formel (Herleitung). Wenn die Funktion y=f(x) auf einem Intervall stetig ist und F(x) eine ihrer Stammfunktionen auf (F"(x)=f(x)) ist, dann gilt die Formel ∫(von a nach b) f( x) gilt )dx=F(b)-F(a). Diese Formel ist die Newton-Leibniz-Formel. Betrachten Sie die Identität: F(b)-F(a)=F(x n)-F(x 0)= (F(x n) -F(x n -1))+(f(x n -1)-F(x n -2))+…(F(x 2)-F(x 1))+(F(x 1 )-F(x 0)). Lassen Sie uns jede Differenz in Klammern mit der Lagrange-Formel transformieren: f(b)-f(a)=f'(c)*(b-a). Wir erhalten F(b)-F(a )=F'(c n)( x n -x n -1)+F'(c n -1)(x n -1 -x n -2)+F'(c 2)(x 2 -x 1)+F'(c 1)(x 1 -x 0 )= ΣF'(Ci)ΔXi=Σf(Ci)ΔXi, das heißt F(b)-F(a)= Σf(Ci)ΔXi, wobei Ci ein Punkt des Intervalls ist (X i -1 ,X i). Da also die Funktion y=f(x) auf stetig ist, ist sie auf integrierbar. Daher gibt es einen Grenzwert der Integralsumme, der dem bestimmten Integral von f(x) entspricht. weiter. Wenn wir zum Grenzwert bei λ=maxΔXi→0 übergehen, erhalten wir F(b)-F( a)=lim Σf(Ci)ΔXi, d. h. ∫(von a nach b) f(x)dx=F( b)-F(a).

Die Funktion z=f(x;y) wird aufgerufen differenzierbar

11. Eigenschaft einer differenzierbaren Funktion: Zusammenhang zwischen der Differenzierbarkeit der Funktion z=f(x;y) und der Stetigkeit der Funktion z=f(x;y) an einem Punkt (Formulierung, Beweis). Wenn die Funktion z=f(x;y) am Punkt M(x;y) differenzierbar ist, dann ist sie an diesem Punkt stetig und weist dort partielle Ableitungen auf. Nachweisen. Die Funktion y=f(x) sei am Punkt x 0 differenzierbar. An dieser Stelle geben wir dem Argument ein Inkrement Δx. Die Funktion erhält ein Inkrement Δу. Finden wir limΔx→0(Δy). limΔx→0(Δy)= limΔx→0((Δy*Δx)/Δx))= limΔx→0(Δy/Δx)* limΔx→0(Δx)=f"(x0)*0=0. Daher ist y =f(x) ist im Punkt x 0 stetig.

Ticket Nr. 7

Ein notwendiges Zeichen eines Extremums.

Wenn eine stetige Funktion z=z(x,y) ein Extremum am Punkt P0(x0,y0) hat, dann sind alle ihre partiellen Ableitungen erster Ordnung an diesem Punkt entweder gleich Null oder existieren nicht

Beweis: Die partielle Ableitung der Funktion z=f(x,y) nach x am Punkt P0(x0,y0) ist die Ableitung der Funktion einer Variablen φ(x)=f(x,y0) am Punkt x-x0. Aber an diesem Punkt hat die Funktion φ(x) offensichtlich ein Extremum. Daher ist φ'(x0)=0. Da φ'(x0)=f'x(x0,y0), dann ist f'x(x0,y0)=0. Ebenso kann gezeigt werden, dass f'y(x0, y0 )=0 . Der Satz ist bewiesen.

Ticket Nr. 8

6. Der Mittelwertsatz (Formulierung, Beweis, geometrische Bedeutung). Wenn die Funktion f(x) auf der Strecke stetig ist, dann gibt es einen Punkt C∈ mit ∫(von a nach b) f(x)dx=f(c)*(b-a). Nachweisen. Gemäß der Newton-Leibniz-Formel gilt ∫(von a nach b) f(x)dx=F(x)|(von a nach b)=F(b)-F(a), wobei F"(x )=f( x). Wenn wir den Satz von Lagrange (den Satz über das endliche Inkrement einer Funktion) auf die Differenz F(b)-F(a) anwenden, erhalten wir F(b)-F(a)=F"(c )*(b-a)=f(c) *(b-a). Geometrische Bedeutung. Der Satz für f(x)≥0 hat eine einfache geometrische Bedeutung: Der Wert des bestimmten Integrals ist für ein C∈ (a;b) gleich der Fläche eines Rechtecks mit der Höhe f(c) und der Grundfläche b-a. Die Zahl f(c)=1/(b-a)∫(von a nach b) f(x)dx wird als Durchschnittswert der Funktion f(x) auf dem Segment bezeichnet.

8. Teilinkremente der Funktion z=f(x;y). Partielle Ableitungen: Definition und ihre geometrische Bedeutung. Gegeben sei die Funktion z=f(x;y). Da x und y unabhängige Variablen sind, kann sich eine von ihnen ändern, während die andere konstant bleibt. Geben wir der Variablen x ein Inkrement ∆x und lassen den Wert der Variablen y unverändert. Dann erhält die Funktion z ein Inkrement, das wir aufrufen werden privater Zuwachs z in x und bezeichnen ∆ x z. Also, ∆ x z=f(x+∆x;y)–f(x;y). Auf ähnliche Weise erhalten wir das Teilinkrement von z in Bezug auf y: ∆ y z=f(x;ó+∆y)–f(x;y).Wenn es einen Grenzwert gibt lim∆x→0(∆ x z/∆x )=lim∆x→0( (f(x+∆x;y)-f(x;y))/∆x), dann heißt es partielle Ableitung Funktion z=f(x;y) am Punkt M(x;y) in der Variablen x und wird durch eines der Symbole bezeichnet: z" x, δz/δx; f" x, δf/δx. Geometrische Bedeutung. Der Graph der Funktion z=f(x;y) ist eine bestimmte Oberfläche. Der Graph der Funktion z=f(x 0 ;y 0) ist die Schnittlinie dieser Fläche mit der Ebene y=y 0. Basierend auf der geometrischen Bedeutung der Ableitung für eine Funktion einer Variablen schließen wir, dass f" x (x 0 ;y 0)=tgα, wobei α der Winkel zwischen der Ox-Achse und der an die Kurve gezogenen Tangente z=f ist (x 0 ;y 0) im Punkt M 0 (x 0 ;y 0 ;f(x 0 ;y 0)). Ähnlich wie f" y (x 0 ;y 0)=tgβ.

Ticket Nr. 9

Nachweisen Geometrische Bedeutung

Tangentialebene Normal zur Oberfläche

Ticket Nr. 10

10. Definition einer differenzierbaren Funktion z=f(x;y) an einem Punkt. Definition des Gesamtdifferentials dz und seiner Form. Die Funktion z=f(x;y) wird aufgerufen differenzierbar am Punkt M(x;y), wenn sein Gesamtinkrement an diesem Punkt dargestellt werden kann als: ∆z=A*∆x+B*∆y+α*∆x+β*∆y, wobei α=α(∆ x;∆y)→0 und β=β(∆x;∆y)→0 für ∆x→0 und ∆y→0. Der Hauptteil des Inkrements der Funktion z=f(x;y), linear bezüglich ∆x und ∆y, wird aufgerufen volles Differenzial Diese Funktion wird durch das Symbol dz bezeichnet: dz=A*∆x+B*∆y. dz=(δz/δx)dx+(δz/δy)dy.

Ticket Nr. 11

4. Definition eines bestimmten Integrals über ein Segment. Grundlegende Eigenschaften eines bestimmten Integrals über ein Segment (mit Beweis eines davon). Durch ein bestimmtes Integralüber einem Segment einer Funktion f(x) wird der Grenzwert der Integralsumme Σf(c i)Δx i genannt, wenn dieser Grenzwert existiert und weder von der Teilung des Segments in Teile noch von der Wahl der Punkte abhängt t innerhalb jedes der Teile, vorausgesetzt, dass die Länge der größten Teilsegmente (∆xi) gegen Null tendiert, d. h. ∫(von a nach b) f(x)dx=lim Δx i →0 Σf(c i)Δx i . Eigenschaften: 1) Wenn c eine konstante Zahl ist und die Funktion f(x) auf integrierbar ist, dann ist ∫(von a nach b) c*f(x)dx=c*∫(von a nach b) f(x)dx .2) Wenn die Funktionen f 1 (x) b f 2 (x) auf integrierbar sind, dann ist ihre Summe auch integrierbar ∫(von a nach b) (f 1 (x)+f 2 (x))dx=∫( von a nach b) f 1 (x)dx+∫(von a nach b) f 2 (x)dx. 3)∫(von a nach b) f(x)dx= -∫(von b nach a) f(x)dx. 4)Wenn die Funktion f(x) auf und a integrierbar ist

10. Definition einer differenzierbaren Funktion z=f(x;y) an einem Punkt. Die Funktion z=f(x;y) wird aufgerufen differenzierbar am Punkt M(x;y), wenn sein Gesamtinkrement an diesem Punkt dargestellt werden kann als: ∆z=A*∆x+B*∆y+α*∆x+β*∆y, wobei α=α(∆ x;∆y)→0 und β=β(∆x;∆y)→0 für ∆x→0 und ∆y→0.

12. Eigenschaft einer differenzierbaren Funktion: Zusammenhang zwischen der Differenzierbarkeit der Funktion z=f(x,y) und der Existenz partieller Ableitungen an einem Punkt (Formulierung, Beweis). Satz: Wenn eine Funktion an einem Punkt differenzierbar ist, dann gibt es an diesem Punkt endliche partielle Ableitungen, A und B sind numerisch gleich Gegeben: Δz=AΔx+BΔy+0(ρ) Beweisen Sie: Ǝ(δz/δx(x 0 ; y 0)=A Beweis: Gegeben sei x 0 →Δx, y=y 0 =>Δ x z=(A*Δx+0(│x│). ρ=√(Δx 2 +Δy 2)=│Δx│. Δ x z/Δx=A +0(│x│)/Δx. LimΔx→0 (Δ x z/Δx)=lim=A. δz/Δx(x 0 ;y 0)=A. Ähnlich: Y 0 →Δy, x=x 0 => Δ y Z. δz/Δy(x 0 ;y 0)=B.

Ticket Nr. 12

Nachweisen

Ticket Nr. 13

2. Das Problem der Fläche eines krummlinigen Trapezes, das zum Konzept eines bestimmten Integrals über einem Segment führt. Definition eines bestimmten Integrals über ein Segment. Auf dem Segment sei die Funktion y=f(x)≥0 gegeben. Eine Figur, die oben durch den Graphen der Funktion y=f(x), unten durch die Ox-Achse und seitlich durch Geraden x=a und x=b begrenzt wird, wird als krummliniges Trapez bezeichnet. Lassen Sie uns die Fläche dieses Trapezes ermitteln. f(c 1)Δx 1 +f(c 2)Δx 2 +..+f(c n)Δx n =Σf(c i)Δx i =Sn. Mit einer Abnahme aller Werte von Δx i steigt die Genauigkeit der Approximation eines krummlinigen Trapezes mit einer Stufenfigur und die Genauigkeit der resultierenden Formel. Daher nehmen wir für den genauen Wert der Fläche S eines krummlinigen Trapezes den Grenzwert S, zu dem die Fläche der Stufenfigur Sn tendiert, wenn n unbegrenzt zunimmt, sodass λ=maxΔx i →0: S=lim n →∞ Sn=lim n→∞(λ→0 ) Σf(c i)Δx i , also S=∫(von a nach b) f(x)dx. Das bestimmte Integral einer unbestimmten Funktion ist also numerisch gleich der Fläche eines krummlinigen Trapezes. Wenn die Integralsumme Sn einen Grenzwert I hat, der weder von der Methode der Aufteilung des Segments in numerische Segmente noch von der abhängt Wahl der Punkte in ihnen, dann heißt die Zahl I das bestimmte Integral der Funktion y=f(x) auf dem Segment und wird mit ∫(von a nach b) f(x)dx bezeichnet. Somit ist ∫(von a nach b) f(x)dx=lim n→∞(λ→0) Σf(c i)Δx i .

17. Tangente Ebene und Normale zur Oberfläche (Definition).Tangentialebene zu einer Fläche an einem Punkt M wird eine durch diesen Punkt der Fläche verlaufende Ebene genannt, wenn der Winkel zwischen dieser Ebene und der Sekante, die durch den Punkt M und jeden anderen Punkt M 1 der Fläche verläuft, gegen Null tendiert, da M gegen M tendiert 1. Normal zur Oberfläche an einem Punkt M ist eine gerade Linie, die durch diesen Punkt senkrecht zur Tangentenebene verläuft.

Ticket Nr. 14

5. Satz zur Schätzung eines bestimmten Integrals über eine Strecke (Formulierung, Beweis, geometrische Bedeutung). Schätzung des Integrals. Wenn m und M der kleinste bzw. größte Wert der Funktion y=f(x) auf dem Segment sind, (a Nachweisen. Da für jedes x∈ m≤f(x)≤M gilt, gilt ∫(von a nach b) mdx≤ ∫(von a nach b) f(x)dx≤∫(von a nach b) Mdx. Wir erhalten: m(b-a)≤∫(von a nach b) f(x)dx≤M(b-a). Geometrische Bedeutung. Die Fläche eines krummlinigen Trapezes wird zwischen den Flächen von Rechtecken eingeschlossen, deren Grundfläche m und m ist.

Ticket Nr. 15

Ticket Nr. 16

21. Ableitung der Funktion u=u(x;y;z) in Richtung l (Definition). Der Grenzwert LimΔl→0(Δu/Δl) heißt Ableitung der Funktion u(x;y;z) in Richtung des Vektors l an einem Punkt mit den Koordinaten (x;y;z).

22. Gradient der Funktion u=u(x;y;z) an einem Punkt (Definition). Ein Vektor mit den Koordinaten (δu/δx; δu/δy; δu/δz) wird aufgerufen

Ticket Nr. 17

7. Integral mit variabler Obergrenze. Satz über die Ableitung eines Integrals mit variabler Obergrenze (Formulierung, Beweis). Die Ableitung eines bestimmten Integrals nach einer Variablenobergrenze ist gleich dem Integranden, in dem die Integrationsvariable durch diese Grenze ersetzt wird, d. h. (∫(von a nach x) f(t)dt)" x =f (X). Nachweisen. Nach der Newton-Leibniz-Formel gilt: ∫(von a nach x) f(t)dt=F(t)|(von a nach x)=F(x)-F(a). Daher ist (∫(von a nach x) f(t)dt)" x =(F(x)-F(a))" x =F"(x)-0=f(x). Das bedeutet, dass a Bestimmtes Integral mit variabler Obergrenze ist eine der Stammfunktionen des Integranden.

volles Inkrement kontinuierlich kontinuierlich

Ticket Nr. 18

1. Stammfunktion. Satz über die Differenz zweier Stammfunktionen (mit Beweis). Unbestimmtes Integral: Definition, einfachste Eigenschaften des unbestimmten Integrals (mit Beweis einer davon). Die Funktion F(x) wird aufgerufen Stammfunktion f(x) auf dem Intervall (a;b), wenn für jedes x∈(a;b) die Gleichheit F"(x)=f(x) gilt. Satz. Wenn die Funktion F(x) eine Stammfunktion der Funktion f(x) auf (a;b) ist, dann ist die Menge aller Stammfunktionen für f(x) durch die Formel F(x)+C gegeben, wobei C= const. Nachweisen. Die Funktion F(x)+C ist eine Stammfunktion von f(x). Tatsächlich ist (F(x)+C)"=F"(x)=f(x). Sei Ф(x) eine andere Stammfunktion f(x), die sich von F(x) unterscheidet, d. h. Ф"(x)=f(x). Dann gilt für jedes x∈(a;b) (Ф(х)-F(x))"=Ф"(x)-F"(x)=f( x )-f(x)=0. Und das bedeutet, dass Ф(x)-F(x)=C, C=const. Daher ist Ф(x)=F(x)+C. Die Menge aller Stammfunktionen F(x)+C für f(x) heißt unbestimmtes Integral der Funktion f(x) und wird mit dem Symbol ∫f(x)dx bezeichnet. Eigenschaften: 1) Das Differential des unbestimmten Integrals ist gleich dem Integranden, und die Ableitung des unbestimmten Integrals ist gleich dem Integranden d(∫f(x)dx)=f(x)dx, (∫f(x)dx )"=f(x).d (∫f(x)dx)=d(F(x)+C)=dF(x)+dC=F"(x)dx=f(x)dx. und (∫f(x)dx)"=(F(x)+C)"=F"(x)+0=f(x).2) Das unbestimmte Integral des Differentials einer Funktion ist gleich der Summe dieser Funktion und einer beliebigen Konstante: ∫dF(x)=F(x)+C.∫dF(x)=F"(x)dx=∫f(x)dx=F(x)+C.3) Der konstante Faktor kann aus dem Integralzeichen entnommen werden: ∫af(x)dx=a∫f(x)dx.4) Das unbestimmte Integral der algebraischen Summe einer endlichen Anzahl stetiger Funktionen ist gleich der algebraischen Summe von die Integrale der Summanden der Funktionen: ∫(f(x)±g(x))dx=∫f (x)dx±∫g(x)dx.5) (Invarianz der Integrationsformel). Wenn ∫f(x)dx=F(x)+C, dann ∫f(u)du=F(u)+C, wobei u=φ(x) eine beliebige Funktion mit einer stetigen Ableitung ist.

22. Gradient der Funktion u=u(x;y;z) an einem Punkt (Definition, Eigenschaften). Zusammenhang zwischen Richtungsableitung und Gradient einer Funktion (Begründung). Ein Vektor mit den Koordinaten (δu/δx; δu/δy; δu/δz) wird aufgerufen Gradient der Funktion u=f(x;y;z) und wird mit gradU=(δu/δx; δu/δy; δu/δz) bezeichnet. gradU=(δu/δx)*i+(δu/δy)*j+(δu/δz)*k. Eigenschaften: 1)gradC=0; 2)grad(c*u)=c*gradU; 3)grad(u+v)=gradU+gradV; 4)grad(u*v)=u*gradV+v*gradU, wobei u*v Skalarprodukte der Vektoren u und v sind. Verbindung. Gegeben seien die Funktion u=u(x;y;z) und das Gradientenfeld gradU=(δu/δx)*i+(δu/δy)*j+(δu/δz)*k. Dann ist die Ableitung Δu/Δl in Richtung eines Vektors l gleich der Projektion des Vektors GradU auf den Vektor l.

Ticket Nr. 19

4. Definition eines bestimmten Integrals über ein Segment. Grundlegende Eigenschaften eines bestimmten Integrals über ein Segment (mit Beweis eines davon). Durch ein bestimmtes Integralüber einem Segment einer Funktion f(x) wird der Grenzwert der Integralsumme Σf(c i)Δx i genannt, wenn dieser Grenzwert existiert und weder von der Teilung des Segments in Teile noch von der Wahl der Punkte abhängt t innerhalb jedes der Teile, vorausgesetzt, dass die Länge der größten Teilsegmente (∆xi) gegen Null tendiert, d. h. ∫(von a nach b) f(x)dx=lim Δx i →0 Σf(c i)Δx i . Eigenschaften: 1) Wenn c eine konstante Zahl ist und die Funktion f(x) auf integrierbar ist, dann ist ∫(von a nach b) c*f(x)dx=c*∫(von a nach b) f(x)dx . Nachweisen. Lassen Sie uns die Integralsumme für die Funktion c*f(x) zusammenstellen. Wir haben Σс*f(c i)Δx i =с*Σf(c i)Δx i . Dann lim n→∞ Σс*f(c i)Δx i =c*lim n→∞ f(c i)=с*∫(von a nach b) f(x)dx. Daraus folgt, dass die Funktion с*f(x) auf integrierbar ist und die Formel ∫(von a nach b) с*f(x)dx= с*∫(von a nach b) f(x)dx.2) Wenn die Funktionen f 1 (x) b f 2 (x) auf integrierbar sind, dann ist ihre Summe integrierbar und ∫(von a nach b) (f 1 (x)+f 2 (x))dx=∫(von a nach b ) f 1 (x)dx+∫(von a nach b) f 2 (x)dx. 3)∫(von a nach b) f(x)dx= -∫(von b nach a) f(x)dx. 4)Wenn die Funktion f(x) auf und a integrierbar ist

17. Tangente Ebene und Normale zur Oberfläche (Definition). Satz über die Existenz einer Tangentialebene (Formulierung, Beweis). Tangentialebene zu einer Fläche an einem Punkt M wird eine durch diesen Punkt der Fläche verlaufende Ebene genannt, wenn der Winkel zwischen dieser Ebene und der Sekante, die durch den Punkt M und jeden anderen Punkt M 1 der Fläche verläuft, gegen Null tendiert, da M gegen M tendiert 1. Normal zur Oberfläche an einem Punkt M ist eine gerade Linie, die durch diesen Punkt senkrecht zur Tangentenebene verläuft. Satz. Wenn δF/δx; δF/δy; δF/δz in der Nähe des Punktes Mo definiert sind und im Punkt M 0 selbst stetig sind und gleichzeitig nicht verschwinden, dann liegen alle Tangenten an die Linien auf der Oberfläche in derselben Ebene. Nachweisen. L: System(x=x(t); y=y(t); z=z(t)). Tangente (M 0 ;P) y=(x"(t 0); y"(t o); z"(t 0)). L∈Q (Oberfläche). F(x(t), y(t) , z(t))=0 ist eine komplexe Funktion der Variablen t. Wir verwenden die Regel der Differenzierbarkeit einer komplexen Funktion: (δF/δx)*(dx/dt)+(δF/δy)*(dy/dt )+(δF/δz)*( dz/dt)=0; (δF(M 0)/δx)*x"(t 0)+(δF(M 0)/δy)*y"(t 0)+ (δF(M 0)/δz) *z"(t 0)=0; g=(x"(t 0),y"(t 0),z"(t 0)); bezeichnen n=(δF(M 0)/δx; δF(M 0)/δy; δF(M 0) /δz); n⊥g. Da durch einen gegebenen Punkt unendlich viele auf der Oberfläche liegende Geraden und unendlich viele Tangenten zu ihnen gezogen werden können, liegen alle Tangenten in derselben Ebene.

Ticket Nr. 20

9. Vollständiges Inkrement der Funktion z=f(x;y). Stetigkeit der Funktion z=f(x;y) an einem Punkt (zwei Definitionen). Gegeben sei die Funktion z=f(x;y). Geben wir der unabhängigen Variablen x ein Inkrement ∆x und der Variablen y ein Inkrement ∆y. Dann volles Inkrement∆z der Funktion wird durch die Gleichung bestimmt: ∆z=f(x+∆x;y+∆y)-f(x;y). 1)Die Funktion z=f(x;y) wird aufgerufen kontinuierlich am Punkt M 0 (x 0 ;y 0)∈ D(z), wenn sein Grenzwert an diesem Punkt mit dem Wert der Funktion an diesem Punkt übereinstimmt, d.h. limX→X 0 \Y→Y 0 (f(x;y))= f(x 0;y 0). 2) Funktion z=f(x;y) kontinuierlich auf einer Menge, wenn sie an jedem Punkt dieser Menge stetig ist

Ticket Nr. 21

21. Ableitung der Funktion u=u(x;y;z) in Richtung l (Definition, Berechnungsformel, Ableitung der Berechnungsformel). Der Grenzwert LimΔl→0(Δu/Δl) heißt Ableitung der Funktion u(x;y;z) in Richtung des Vektors l an einem Punkt mit den Koordinaten (x;y;z).Δu/Δl=LimΔl→0(Δ l u/Δl)=(δu/δx)*cosα+(δu/δy)*cosβ+(δu/δz)*cosγ . Angenommen, die Funktion u(x;y;z) ist stetig und hat stetige Ableitungen in Bezug auf ihre Argumente im Bereich D: Δu=(δu/δx)Δx+(δu/δy)Δy+(δu/δz)Δz+ E 1 Δx+E 2 Δy+E 3 Δz, wobei E 1, E 2, E 3 gegen Null tendieren, da Δl→0. Teilen wir die gesamte Gleichheit durch Δl. Δu/Δl=(δu/δx)(Δx/Δl)+(δu/δy)(Δy/Δl)+(δu/δz)(Δz/Δl)+E 1 (Δx/Δl)+E 2 (Δy/ Δl)+E 3 (Δz/Δl). Δx/Δl=cosα; Δy/Δl=cosβ; Δz/Δl=cosγ. Die Gleichheit kann wie folgt dargestellt werden: Δu/Δl=(δu/δx)cosα+(δu/δy)cosβ+(δu/δz)cosγ+E 1 cosα+E 2 cosβ+E 3 cosγ. Wenn wir uns dem Grenzwert nähern, erhalten wir Δu/Δl=LimΔl→0(Δ l u/Δl)=(δu/δx)*cosα+(δu/δy)*cosβ+(δu/δz)*cosγ.

Ticket Nr. 22

20. Ein ausreichendes Zeichen für die Existenz eines Extremums der Funktion z=f(x;y). (Wortlaut). An einem stationären Punkt (X 0 ;Y 0) und einigen seiner Umgebungen soll die Funktion f(x;y) stetige partielle Ableitungen bis einschließlich zweiter Ordnung haben. Berechnen wir am Punkt (X 0 ;Y 0) die Werte A=f"" xx (X 0 ;Y 0), B=f"" xy (X 0 ;Y 0), C=f"" yy (X 0 ;Y 0). Bezeichnen wir Δ=|AB; BC|=AC-B^2. Dann: 1) wenn Δ>0, dann hat die Funktion f(x;y) am Punkt (X 0 ;Y 0) ein Extremum: Maximum, wenn A<0; минимум, если A>0; 2) wenn Δ<0, то функция f(x;y) в точке (X 0 ;Y 0) экстремума не имеет. В случае Δ=0 экстремум в точке (X 0 ;Y 0) может быть, а может не быть. Необходимы дополнительные исследования.

Ticket Nr. 23

17. Tangentenebene an eine Fläche (Definition).Tangentialebene zu einer Fläche an einem Punkt M wird eine durch diesen Punkt der Fläche verlaufende Ebene genannt, wenn der Winkel zwischen dieser Ebene und der Sekante, die durch den Punkt M und jeden anderen Punkt M 1 der Fläche verläuft, gegen Null tendiert, da M gegen M tendiert 1.

18. Gleichungen einer Tangentenebene an eine explizit angegebene OberflächeOffensichtlich. z=f(x;y) am Punkt Mo(Xo;Yo;Zo). K: (δz/δx)|M 0 (X-X 0)+(δz/δy)|M 0 (Y-Y 0)-(Z-Z 0)=0

Ticket Nr. 24