Zeichnen Sie ein Diagramm des Systems und markieren Sie darauf den Schwerpunkt. Liegt der gefundene Schwerpunkt außerhalb des Objektsystems, haben Sie eine falsche Antwort erhalten. Möglicherweise haben Sie Entfernungen von verschiedenen Referenzpunkten gemessen. Wiederholen Sie die Messungen.
- Wenn Kinder beispielsweise auf einer Schaukel sitzen, liegt der Schwerpunkt irgendwo zwischen den Kindern und nicht rechts oder links von der Schaukel. Außerdem wird der Schwerpunkt nie mit dem Punkt übereinstimmen, an dem das Kind sitzt.
- Diese Argumente gelten im zweidimensionalen Raum. Zeichnen Sie ein Quadrat, das alle Objekte des Systems enthält. Der Schwerpunkt sollte innerhalb dieses Quadrats liegen.
Überprüfen Sie Ihre Mathematik, wenn Sie ein kleines Ergebnis erhalten. Wenn der Referenzpunkt an einem Ende des Systems liegt, liegt der Schwerpunkt bei einem kleinen Ergebnis nahe am Ende des Systems. Dies mag die richtige Antwort sein, aber in den allermeisten Fällen weist dieses Ergebnis auf einen Fehler hin. Haben Sie bei der Berechnung der Momente die entsprechenden Gewichte und Abstände multipliziert? Wenn Sie statt der Multiplikation die Gewichte und Abstände addieren würden, würden Sie ein viel kleineres Ergebnis erhalten.
Korrigieren Sie den Fehler, wenn Sie mehrere Schwerpunkte gefunden haben. Jedes System hat nur einen Schwerpunkt. Wenn Sie mehrere Schwerpunkte gefunden haben, haben Sie höchstwahrscheinlich nicht alle Momente addiert. Der Schwerpunkt ist gleich dem Verhältnis des „Gesamtmoments“ zum „Gesamtgewicht“. Es ist nicht nötig, „jeden“ Moment durch „jedes“ Gewicht zu dividieren: Auf diese Weise finden Sie die Position jedes Objekts.
Überprüfen Sie den Referenzpunkt, wenn die Antwort um einen ganzzahligen Wert abweicht. In unserem Beispiel ist die Antwort 3,4 m. Nehmen wir an, Sie haben die Antwort 0,4 m oder 1,4 m oder eine andere Zahl erhalten, die auf „.4“ endet. Dies liegt daran, dass Sie nicht das linke Ende des Bretts als Ausgangspunkt gewählt haben, sondern einen Punkt, der ein ganzes Stück rechts liegt. Tatsächlich ist Ihre Antwort richtig, egal welchen Bezugspunkt Sie wählen! Denken Sie daran: Der Referenzpunkt befindet sich immer an der Position x = 0. Hier ein Beispiel:
- In unserem Beispiel befand sich der Referenzpunkt am linken Ende des Bretts und wir stellten fest, dass der Schwerpunkt 3,4 m von diesem Referenzpunkt entfernt war.
- Wenn Sie als Bezugspunkt einen Punkt wählen, der 1 m rechts vom linken Ende der Tafel liegt, erhalten Sie als Antwort 2,4 m. Das heißt, der Schwerpunkt liegt 2,4 m vom neuen Bezugspunkt entfernt , wiederum befindet sich 1 m vom linken Ende der Tafel entfernt. Somit liegt der Schwerpunkt in einem Abstand von 2,4 + 1 = 3,4 m vom linken Ende des Bretts. Es stellte sich heraus, dass es sich um eine alte Antwort handelte!
- Hinweis: Beachten Sie beim Messen von Entfernungen, dass die Entfernungen zum „linken“ Referenzpunkt negativ und zum „rechten“ Referenzpunkt positiv sind.
Messen Sie Entfernungen in geraden Linien. Angenommen, es sitzen zwei Kinder auf einer Schaukel, aber ein Kind ist viel größer als das andere, oder ein Kind hängt unter dem Brett, anstatt darauf zu sitzen. Ignorieren Sie diesen Unterschied und messen Sie die Abstände entlang der geraden Linie der Platine. Das Messen von Entfernungen in Winkeln führt zu ähnlichen, aber nicht ganz genauen Ergebnissen.
- Denken Sie beim Problem mit dem Wippbrett daran, dass der Schwerpunkt zwischen dem rechten und dem linken Ende des Bretts liegt. Später lernen Sie, den Schwerpunkt komplexerer zweidimensionaler Systeme zu berechnen.
Vorlesung 4. Schwerpunkt.
In dieser Vorlesung werden folgende Themen behandelt
1. Schwerpunkt eines festen Körpers.
2. Koordinaten der Schwerpunkte inhomogener Körper.
3. Koordinaten der Schwerpunkte homogener Körper.
4. Methoden zur Bestimmung der Koordinaten von Schwerpunkten.
5. Schwerpunkte einiger homogener Körper.
Die Untersuchung dieser Fragen ist in Zukunft notwendig, um die Dynamik der Bewegung von Körpern unter Berücksichtigung von Gleit- und Rollreibung, die Dynamik der Bewegung des Massenschwerpunkts eines mechanischen Systems und kinetische Momente zu untersuchen und Probleme in der zu lösen Disziplin „Festigkeit der Werkstoffe“.
Parallele Kräfte bringen.
Nachdem wir darüber nachgedacht haben, ein flaches System und ein beliebiges räumliches Kräftesystem ins Zentrum zu bringen, kehren wir wieder zur Betrachtung des Sonderfalls eines Systems paralleler Kräfte zurück.
Bringt zwei parallele Kräfte.
Im Zuge der Betrachtung eines solchen Kräftesystems sind die folgenden drei Reduktionsfälle möglich.
1. System zweier kollinearer Kräfte. Betrachten wir ein System aus zwei parallelen Kräften, die in eine Richtung gerichtet sind P Und Q, punktuell angewendet A Und IN. Wir gehen davon aus, dass die Kräfte senkrecht zu diesem Segment wirken (Abb. 1, A).
MIT, zum Segment gehörend AB und die Bedingung erfüllen:
Wechselstrom/NE = Q/P.(1)
Hauptvektor des Systems R C = P + Q ist im Modul gleich der Summe dieser Kräfte: R C = P + Q.
MIT unter Berücksichtigung von (1) ist gleich Null:MC = P ∙ Wechselstrom- Q∙ CB = 0.
Als Ergebnis des Castings haben wir also Folgendes erhalten: R C ≠ 0, MC= 0. Dies bedeutet, dass der Hauptvektor der durch das Reduktionszentrum verlaufenden Resultierenden entspricht, d. h.:
Die Resultierende der kollinearen Kräfte ist im Modul gleich ihrer Summe, und ihre Wirkungslinie teilt das Segment, das die Punkte ihrer Anwendung verbindet, im umgekehrten Verhältnis zu den Modulen dieser Kräfte auf interne Weise.
Beachten Sie die Position des Punktes MIT wird sich nicht ändern, wenn die Kräfte R Und Q einen Winkel drehenα. Punkt MIT, das diese Eigenschaft hat, heißt Zentrum paralleler Kräfte.
2. Zweiersystem antikollinear und Kräfte, die nicht gleich groß sind. Möge die Stärke P Und Q, punktuell angewendet A Und IN, parallel, in entgegengesetzte Richtungen gerichtet und ungleich groß (Abb. 1, B).
Wählen wir einen Punkt als Reduktionszentrum MIT, die immer noch die Beziehung (1) erfüllt und auf derselben Linie, aber außerhalb des Segments liegt AB.
Der Hauptvektor dieses Systems R C = P + Q Der Modul ist nun gleich der Differenz zwischen den Modulen der Vektoren: R C = Q - P.
Der wichtigste Punkt bezüglich der Mitte MIT ist immer noch Null:MC = P ∙ Wechselstrom- Q∙ NE= 0, also
Resultierend antikollinear und Kräfte, deren Größe nicht gleich ist, sind gleich ihrer Differenz, auf die größere Kraft gerichtet, und ihre Wirkungslinie teilt das Segment, das die Punkte ihrer Anwendung verbindet, im umgekehrten Verhältnis zu den äußeren Modulen dieser Kräfte.
Abb.1
3. Zweiersystem antikollinear und Kräfte gleicher Größe. Nehmen wir den vorherigen Reduktionsfall als Ausgangsfall. Lasst uns die Kraft reparieren R, und Stärke Q Richten wir den Modul auf die Kraft aus R.
Dann um Q → R in Formel (1) die Beziehung Wechselstrom/NE → 1. Das bedeutet das Wechselstrom → NE, also die Entfernung Wechselstrom →∞ .
In diesem Fall das Modul des Hauptvektors R C → 0, und der Modul des Hauptmoments hängt nicht von der Position des Reduktionszentrums ab und bleibt gleich dem ursprünglichen Wert:
MC = P ∙ Wechselstrom- Q∙ NE = P ∙ ( Wechselstrom- NE) =P ∙ AB.
Im Grenzfall haben wir also ein Kräftesystem erhalten, für das R C = 0, MC≠ 0, und das Reduktionszentrum wird ins Unendliche verschoben, das nicht durch die Resultierende ersetzt werden kann. Es ist also nicht schwer, ein paar Kräfte in diesem System zu erkennen Ein Kräftepaar hat keine Resultierende.
Zentrum des Systems paralleler Kräfte.
Betrachten Sie das System N Stärke P ich, punktuell angewendetA i (x i , y i , z i) und parallel zur AchseOv mit orth l(Abb. 2).
Wenn wir den Fall eines Systems, das einem Kräftepaar entspricht, von vornherein ausschließen, ist es auf der Grundlage des vorherigen Absatzes nicht schwierig, die Existenz seiner Resultierenden zu beweisenR.
Bestimmen wir die Koordinaten des ZentrumsC(X C, j C, z C) parallele Kräfte, also die Koordinaten des Angriffspunkts der Resultierenden dieses Systems.
Zu diesem Zweck verwenden wir den Satz von Varignon, der darauf basiert:
M0 (R) = Σ M0(P ich).

Abb.2
Das Vektormoment einer Kraft kann als Vektorprodukt dargestellt werden, daher:
M 0 (R) = r c× R = Σ M0i(P ich) = Σ ( r i× P ich ).
Bedenkt, dass R = Rv ∙ l, A P ich = Pvi ∙ l und unter Verwendung der Eigenschaften des Vektorprodukts erhalten wir:
r c × Rv ∙ l = Σ ( r i × Pvi ∙ l),
r c ∙ R v× l = Σ ( r i ∙ Pvi × l) = Σ ( r i ∙ Pvi ) × l,
oder:
[ r c R v - Σ ( r i Pvi )] × l= 0.
Der letzte Ausdruck ist nur gültig, wenn der Ausdruck in eckigen Klammern gleich Null ist. Daher wird der Index weggelassenvund unter Berücksichtigung der resultierendenR = Σ P ich , von hier aus erhalten wir:
r c = (Σ P ich r i )/(Σ P ich ).
Indem wir die letzte Vektorgleichheit auf die Koordinatenachse projizieren, erhalten wir das erforderliche Ergebnis Ausdruck für die Koordinaten des Mittelpunkts paralleler Kräfte:
x c = (Σ P ich x i)/(Σ P ich );
y c = (Σ P ich y i )/(Σ P ich );(2)
z c = (Σ P ich z i )/(Σ P ich ).
Schwerpunkt der Körper.
Koordinaten der Schwerpunkte eines homogenen Körpers.
Stellen Sie sich eine starre Körperwägung vor P und Lautstärke V im Koordinatensystem Oxyz, wo sind die Achsen X Und j mit der Erdoberfläche und der Achse verbunden z auf den Zenit gerichtet.
Wenn wir den Körper in elementare Teile mit Volumen zerlegen∆ V ich , dann wirkt die Anziehungskraft auf jeden Teil davon∆ P ich, auf den Mittelpunkt der Erde gerichtet. Nehmen wir an, dass die Abmessungen des Körpers deutlich kleiner sind als die Abmessungen der Erde, dann kann das auf die Elementarteile des Körpers ausgeübte Kräftesystem als nicht konvergierend, sondern parallel betrachtet werden (Abb. 3) und alle Schlussfolgerungen des vorherigen Kapitels gelten hierfür.

Abb. 3
Definition . Der Schwerpunkt eines festen Körpers ist der Mittelpunkt paralleler Schwerkraftkräfte der Elementarteile dieses Körpers.
Wir möchten Sie daran erinnern spezifisches Gewicht eines elementaren Körperteils nennt man das Verhältnis seines Gewichts∆ P ich zum Volumen ∆ V ich : γ ich = ∆ P ich/ ∆ V ich . Für einen homogenen Körper ist dieser Wert konstant:γ ich = γ = P/ V.
Einsetzen von ∆ in (2) P ich = γ ich ∙∆ V ich anstatt P ich, unter Berücksichtigung der letzten Bemerkung und Reduzierung von Zähler und Nenner umG, wir bekommen Ausdrücke für die Koordinaten des Schwerpunkts eines homogenen Körpers:
x c = (Σ ∆ V i∙ x i)/(Σ ∆ V i);
y c = (Σ ∆ V i∙ y i )/(Σ ∆ V i);(3)
z c = (Σ ∆ V i∙ z i )/(Σ ∆ V i).
Zur Bestimmung des Schwerpunkts sind mehrere Theoreme hilfreich.
1) Wenn ein homogener Körper eine Symmetrieebene hat, liegt sein Schwerpunkt in dieser Ebene.
Wenn die Achsen X Und bei in dieser Symmetrieebene gelegen, dann für jeden Punkt mit Koordinaten. Und die Koordinate nach (3) wird gleich Null sein, weil in der Summe Alle Mitglieder mit entgegengesetzten Vorzeichen werden paarweise zerstört. Das bedeutet, dass der Schwerpunkt lokalisiert ist in der Symmetrieebene.
2) Wenn ein homogener Körper eine Symmetrieachse hat, dann liegt der Schwerpunkt des Körpers auf dieser Achse.
In diesem Fall nämlich, wenn die AchsezZeichnen Sie für jeden Punkt mit Koordinaten entlang der SymmetrieachseSie können einen Punkt mit Koordinaten finden und Koordinaten und , berechnet nach Formeln (3), ist gleich Null.
Der dritte Satz wird auf ähnliche Weise bewiesen.
3) Wenn ein homogener Körper ein Symmetriezentrum hat, dann liegt in diesem Punkt der Schwerpunkt des Körpers.
Und noch ein paar Kommentare.
Erste. Wenn der Körper in Teile zerlegt werden kann, für die Gewicht und Lage des Schwerpunkts bekannt sind, muss nicht jeder Punkt berücksichtigt werden, und in den Formeln (3) P ich – bestimmt als Gewicht des entsprechenden Teils und– als Koordinaten seines Schwerpunkts.
Zweite. Wenn der Körper homogen ist, dann das Gewicht eines einzelnen Teils davon, Wo - spezifisches Gewicht des Materials, aus dem der Körper besteht, und V i - das Volumen dieses Körperteils. Und Formeln (3) werden eine bequemere Form annehmen. Zum Beispiel,
Und ebenso, wo - Volumen des gesamten Körpers.
Dritte Anmerkung. Lassen Sie den Körper die Form einer dünnen Platte mit einer Fläche haben F und Dicke T, im Flugzeug liegend Oxy. Einsetzen in (3)∆ V ich =T ∙ ∆F ich , wir erhalten die Koordinaten des Schwerpunkts einer homogenen Platte:
x c = (Σ ∆ F i∙ x i) / (Σ ∆ F i);
y c = (Σ ∆ F i∙ y i ) / (Σ ∆ F i).
z c = (Σ ∆ F i∙ z ich ) / (Σ ∆ F i).
Wo – Koordinaten des Schwerpunkts einzelner Platten;– gesamter Körperbereich.
Vierte Anmerkung. Für einen Körper in Form eines dünnen, gebogenen Stabes der Länge L mit Querschnittsfläche A elementarer Band∆ V ich = A ∙∆ L ich , Deshalb Koordinaten des Schwerpunkts eines dünnen gebogenen Stabes wird gleich sein:
x c = (Σ ∆ L ich∙ x i)/(Σ ∆ L ich);
y c = (Σ ∆ L ich∙ y i )/(Σ ∆ L ich);(4)
z c = (Σ ∆ L ich∙ z i )/(Σ ∆ L ich).
Wo – Koordinaten des Schwerpunktsich-ter Abschnitt; .
Beachten Sie, dass der Schwerpunkt laut Definition ein geometrischer Punkt ist; es kann auch außerhalb der Grenzen eines bestimmten Körpers liegen (z. B. bei einem Ring).
Notiz.
In diesem Kursabschnitt wird nicht zwischen Schwerkraft, Schwerkraft und Körpergewicht unterschieden. In Wirklichkeit ist die Schwerkraft die Differenz zwischen der Gravitationskraft der Erde und der durch ihre Rotation verursachten Zentrifugalkraft.
Koordinaten der Schwerpunkte inhomogener Körper.
Schwerpunktkoordinaten inhomogener Feststoff(Abb.4) im gewählten Bezugssystem werden wie folgt ermittelt:

Abb.4



Wo - Gewicht pro Volumeneinheit eines Körpers (spezifisches Gewicht)
![]() - ganzes Körpergewicht.
- ganzes Körpergewicht.
ungleichmäßige Oberfläche(Abb. 5), dann werden die Koordinaten des Schwerpunkts im gewählten Bezugssystem wie folgt bestimmt:

Abb.5
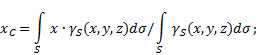

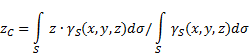
Wo - Gewicht pro Körperflächeneinheit,
![]() - ganzes Körpergewicht.
- ganzes Körpergewicht.
Wenn der Feststoff ist ungleichmäßige Linie(Abb. 6), dann werden die Koordinaten des Schwerpunkts im gewählten Bezugssystem wie folgt bestimmt:

Abb.6

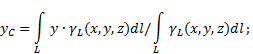

Wo - Gewicht pro Körperlänge,
Gesamtkörpergewicht.
Methoden zur Bestimmung der Koordinaten des Schwerpunkts.
Basierend auf den oben erhaltenen allgemeinen Formeln ist es möglich, spezifische Methoden anzugeben Bestimmung der Koordinaten der Schwerpunkte von Körpern.
1. Symmetrie. Besitzt ein homogener Körper eine Ebene, Achse oder ein Symmetriezentrum (Abb. 7), so liegt sein Schwerpunkt jeweils in der Symmetrieebene, Symmetrieachse bzw. im Symmetriezentrum.

Abb.7
2. Aufteilen. Der Körper ist in endlich viele Teile unterteilt (Abb. 8), für die jeweils die Lage des Schwerpunkts und die Fläche bekannt sind.

Abb.8
S =S 1 +S 2.
3.Negativflächenmethode. Ein Sonderfall der Partitionierungsmethode (Abb. 9). Sie gilt für Körper mit Aussparungen, wenn die Schwerpunkte des Körpers ohne Aussparung und des ausgeschnittenen Teils bekannt sind. Ein Körper in Form einer Platte mit Ausschnitt wird durch eine Kombination einer massiven Platte (ohne Ausschnitt) mit einer Fläche dargestellt S 1 und die Fläche des geschnittenen Teils S2.

Abb.9
S = S 1 - S 2.
4.Gruppierungsmethode. Es ist eine gute Ergänzung zu den letzten beiden Methoden. Nachdem man eine Figur in ihre Bestandteile zerlegt hat, ist es sinnvoll, einige davon wieder zu kombinieren, um dann die Lösung unter Berücksichtigung der Symmetrie dieser Gruppe zu vereinfachen.
Schwerpunkte einiger homogener Körper.
1) Schwerpunkt eines Kreisbogens. Betrachten Sie den Bogen AB RadiusR mit Zentralwinkel. Aus Symmetriegründen liegt der Schwerpunkt dieses Bogens auf der AchseOchse(Abb. 10).

Abb.10
Finden wir die Koordinate nach der Formel . Wählen Sie dazu den Bogen aus AB Element MM ’ Länge, dessen Position durch den Winkel bestimmt wird. Koordinate X Element MM' Wille. Ersetzen dieser Werte X Und D l und unter Berücksichtigung der Tatsache, dass das Integral über die gesamte Länge des Bogens ausgedehnt werden muss, erhalten wir:
![]()
wobei L die Länge des Bogens AB ist, gleich .
Von hier aus stellen wir schließlich fest, dass der Schwerpunkt eines Kreisbogens auf seiner Symmetrieachse im Abstand vom Mittelpunkt liegt O gleich
Wo ist der Winkel? gemessen im Bogenmaß.
2) Schwerpunkt der Dreiecksfläche. Betrachten Sie ein Dreieck, das in der Ebene liegt Oxy, deren Koordinaten der Eckpunkte bekannt sind: A i (x i,y i ), (ich= 1,2,3). Brechen Sie das Dreieck in schmale Streifen parallel zur Seite A 1 A 2 kommen wir zu dem Schluss, dass der Schwerpunkt des Dreiecks zum Median liegen muss A 3 M 3 (Abb. 11).

Abb.11
Ein Dreieck in seitlich parallele Streifen brechen A 2 A 3 können wir überprüfen, dass es auf dem Median liegen muss A 1 M 1 . Auf diese Weise, Der Schwerpunkt eines Dreiecks liegt im Schnittpunkt seiner Mediane, der bekanntlich von jedem Median einen dritten Teil abtrennt, gerechnet von der entsprechenden Seite.
Insbesondere für den Median A 1 M 1 erhalten wir unter Berücksichtigung der Koordinaten des Punktes M 1 - Dies ist das arithmetische Mittel der Koordinaten der Eckpunkte A 2 und A 3 :
x c = X 1 + (2/3) ∙ (XM 1 - X 1 ) = X 1 + (2/3) ∙ [(X 2 + X 3 )/2 - X 1 ] = (X 1 + X 2 + X 3 )/3.
Somit sind die Koordinaten des Schwerpunkts des Dreiecks das arithmetische Mittel der Koordinaten seiner Eckpunkte:
X C =(1/3) Σ x i ; j C =(1/3) Σ y i .
3) Schwerpunkt der Fläche eines Kreissektors. Betrachten Sie einen Kreissektor mit Radius R mit Zentrierwinkel 2α , symmetrisch um die Achse angeordnet Ochse (Abb. 12) .
Es ist klar, dass j C = 0, und der Abstand vom Mittelpunkt des Kreises, aus dem dieser Sektor geschnitten wird, zu seinem Schwerpunkt kann durch die Formel bestimmt werden:

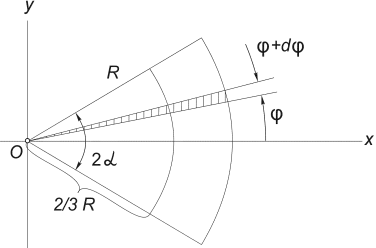
Abb.12
Der einfachste Weg, dieses Integral zu berechnen, besteht darin, das Integrationsgebiet in Elementarsektoren mit einem Winkel zu unterteilen Dφ . Auf Infinitesimalzahlen erster Ordnung genau kann ein solcher Sektor durch ein Dreieck mit einer Basis gleich ersetzt werden R × Dφ und Höhe R. Die Fläche eines solchen Dreiecks dF =(1/2)R 2 ∙ Dφ , und sein Schwerpunkt liegt in einem Abstand von 2/3 R vom Scheitelpunkt, deshalb setzen wir in (5). X = (2/3)R∙ cosφ. Einsetzen in (5) F= α R 2, wir erhalten:

Mit der letzten Formel berechnen wir insbesondere den Abstand zum Schwerpunkt Halbkreis.
Wenn wir α = π /2 in (2) einsetzen, erhalten wir: X C = (4 R)/(3π) ≅ 0,4 R .
Beispiel 1.Bestimmen wir den Schwerpunkt des in Abb. gezeigten homogenen Körpers. 13.

Abb.13
Lösung.Der Körper ist homogen und besteht aus zwei Teilen mit symmetrischer Form. Koordinaten ihrer Schwerpunkte:
Ihre Bände:
Daher die Koordinaten des Schwerpunkts des Körpers
Beispiel 2. Finden wir den Schwerpunkt einer im rechten Winkel gebogenen Platte. Die Abmessungen finden Sie in der Zeichnung (Abb. 14).

Abb.14
Lösung. Koordinaten der Schwerpunkte:
0.
Bereiche:
Deshalb:
Beispiel 3.
Auf einem quadratischen Blatt
cm quadratisches Loch schneiden
cm (Abb. 15). Lassen Sie uns den Schwerpunkt des Blattes ermitteln. Beispiel 4. Finden Sie die Position des Schwerpunkts der in Abb. gezeigten Platte. 16. Die Abmessungen werden in Zentimetern angegeben.

Abb.16
Lösung. Teilen wir die Platte in Figuren auf (Abb. 17), Zentren deren Schweregrad bekannt ist.
Die Flächen dieser Figuren und die Koordinaten ihrer Schwerpunkte:
1) ein Rechteck mit Seitenlängen von 30 und 40 cm,S 1 =30 ∙ 40=1200 cm 2 ; x 1=15 cm; bei 1 =20 cm.
2) ein rechtwinkliges Dreieck mit einer Grundfläche von 50 cm und einer Höhe von 40 cm;S 2 =0,5 ∙ 50 ∙ 40= 1000 cm 2 ; X 2 =30+50/3=46,7 cm; y 2 =40/3 =13,3 cm;
3) Halbkreisradiuskreis R = 20 cm;S 3 =0,5 ∙π∙ 20 2 =628 cm 2 ; X 3 =4 R /3 π =8,5 cm; bei
Lösung. Denken Sie daran, dass in der Physik die Dichte eines Körpers giltρ und sein spezifisches GewichtGhängen durch die Beziehung zusammen:γ = ρ G , WoG - Erdbeschleunigung. Um die Masse eines solchen homogenen Körpers zu ermitteln, müssen Sie die Dichte mit seinem Volumen multiplizieren.

Abb.19
Der Begriff „linear“ oder „lineare“ Dichte bedeutet, dass zur Bestimmung der Masse eines Halsstabes die lineare Dichte mit der Länge dieses Stabes multipliziert werden muss.
Um das Problem zu lösen, können Sie die Partitionierungsmethode verwenden. Wenn wir ein gegebenes Fachwerk als Summe von 6 einzelnen Stäben darstellen, erhalten wir:
WoL ich Längeich der Halsstab undx i , y i - Koordinaten seines Schwerpunkts.
Die Lösung dieses Problems kann durch die Gruppierung der letzten 5 Stäbe des Fachwerks vereinfacht werden. Es ist leicht zu erkennen, dass sie eine Figur bilden, deren Symmetriezentrum in der Mitte des vierten Stabes liegt, wo sich der Schwerpunkt dieser Stabgruppe befindet.
Somit kann ein gegebenes Fachwerk durch eine Kombination von nur zwei Stabgruppen dargestellt werden.
Die erste Gruppe besteht aus der ersten RuteL 1 = 4m,X 1 = 0 m,j 1 = 2 m. Die zweite Stabgruppe besteht aus fünf StäbenL 2 = 20 m,X 2 = 3m,j 2 = 2 m.
Die Koordinaten des Schwerpunkts des Fachwerks werden mit der Formel ermittelt:
X C = (L 1 ∙ X 1 + L 2 ∙ X 2 )/(L 1 + L 2 ) = (4∙0 + 20∙3)/24 = 5/2 m;
j C = (L 1 ∙ j 1 + L 2 ∙ j 2 )/(L 1 + L 2 ) = (4∙2 + 20∙2)/24 = 2 m.
Beachten Sie, dass die Mitte MIT liegt auf der Verbindungsgeraden MIT 1 und MIT 2 und teilt das Segment MIT 1 MIT 2 zu: MIT 1 MIT/SS 2 = (X C - X 1 )/(X 2 - X C ) = L 2 / L 1 = 2,5/0,5.
Fragen zum Selbsttest
- Wie nennt man das Zentrum paralleler Kräfte?
- Wie werden die Koordinaten des Mittelpunkts paralleler Kräfte bestimmt?
- Wie bestimmt man den Mittelpunkt paralleler Kräfte, deren Resultierende Null ist?
- Welche Eigenschaften hat der Mittelpunkt paralleler Kräfte?
- Mit welchen Formeln werden die Koordinaten des Mittelpunkts paralleler Kräfte berechnet?
- Wie nennt man den Schwerpunkt eines Körpers?
- Warum kann man die auf einen Punkt eines Körpers wirkenden Gravitationskräfte der Erde als ein System paralleler Kräfte auffassen?
- Schreiben Sie die Formel zur Bestimmung der Schwerpunktlage inhomogener und homogener Körper, die Formel zur Bestimmung der Schwerpunktlage flacher Abschnitte auf?
- Schreiben Sie die Formel zur Bestimmung der Schwerpunktlage einfacher geometrischer Formen auf: Rechteck, Dreieck, Trapez und Halbkreis?
- Was nennt man das statische Flächenmoment?
- Geben Sie ein Beispiel für einen Körper, dessen Schwerpunkt außerhalb des Körpers liegt.
- Wie werden die Eigenschaften der Symmetrie zur Bestimmung der Schwerpunkte von Körpern genutzt?
- Was ist das Wesentliche an der Methode der negativen Gewichte?
- Wo liegt der Schwerpunkt eines Kreisbogens?
- Mit welcher grafischen Konstruktion lässt sich der Schwerpunkt eines Dreiecks ermitteln?
- Schreiben Sie die Formel auf, die den Schwerpunkt eines Kreissektors bestimmt.
- Leiten Sie mithilfe von Formeln, die die Schwerpunkte eines Dreiecks und eines Kreissektors bestimmen, eine ähnliche Formel für ein Kreissegment ab.
- Mit welchen Formeln werden die Koordinaten der Schwerpunkte homogener Körper, flacher Figuren und Linien berechnet?
- Wie nennt man das statische Moment der Fläche einer ebenen Figur relativ zur Achse, wie berechnet man es und welche Dimension hat es?
- Wie lässt sich die Lage des Schwerpunkts einer Fläche bestimmen, wenn die Lage der Schwerpunkte ihrer einzelnen Teile bekannt ist?
- Welche Hilfssätze werden verwendet, um die Lage des Schwerpunkts zu bestimmen?
Autor: Nehmen wir einen Körper beliebiger Form. Ist es möglich, es an einem Faden aufzuhängen, damit es nach dem Aufhängen seine Position beibehält (d. h. nicht anfängt, sich zu drehen), wenn beliebig Erstorientierung (Abb. 27.1)?
Mit anderen Worten: Gibt es einen Punkt, relativ zu dem die Summe der auf verschiedene Körperteile wirkenden Schwerkraftmomente gleich Null wäre? beliebig Körperorientierung im Raum?
Leser: Ja, ich denke schon. Dieser Punkt heißt Schwerpunkt des Körpers.
Nachweisen. Betrachten wir der Einfachheit halber einen Körper in Form einer flachen Platte beliebiger Form, beliebig im Raum ausgerichtet (Abb. 27.2). Nehmen wir das Koordinatensystem X 0bei mit dem Anfang im Massenschwerpunkt - Punkt MIT, Dann x C = 0, bei C = 0.
 Stellen wir uns diesen Körper als eine Ansammlung einer großen Anzahl von Punktmassen vor m i, deren Position jeweils durch den Radiusvektor angegeben wird.
Stellen wir uns diesen Körper als eine Ansammlung einer großen Anzahl von Punktmassen vor m i, deren Position jeweils durch den Radiusvektor angegeben wird.
Per Definition ist der Schwerpunkt und die Koordinate x C = .
Da wir das Koordinatensystem übernommen haben x C= 0, dann . Multiplizieren wir diese Gleichheit mit G und wir bekommen
Wie aus Abb. ersichtlich ist. 27,2, | x i| - Das ist die Schulter der Macht. Und wenn x i> 0, dann das Kraftmoment M i> 0, und wenn x j < 0, то Mj < 0, поэтому с учетом знака можно утверждать, что для любого x i das Kraftmoment wird gleich sein M i = m i gx i . Dann ist Gleichheit (1) äquivalent zu Gleichheit, wobei M i– Moment der Schwerkraft. Dies bedeutet, dass bei beliebiger Ausrichtung des Körpers die Summe der auf den Körper einwirkenden Schwerkraftmomente relativ zu seinem Massenschwerpunkt gleich Null ist.
Damit der Körper, den wir betrachten, im Gleichgewicht ist, ist es notwendig, den Punkt auf ihn anzuwenden MIT Gewalt T = mg, senkrecht nach oben gerichtet. Das Moment dieser Kraft relativ zum Punkt MIT gleich Null.
Da unsere Überlegungen in keiner Weise davon abhingen, wie genau der Körper im Raum ausgerichtet ist, haben wir bewiesen, dass der Schwerpunkt mit dem Massenschwerpunkt zusammenfällt, was wir beweisen mussten.
Aufgabe 27.1. Finden Sie den Schwerpunkt eines schwerelosen Stabs der Länge l, an deren Enden zwei Punktmassen befestigt sind T 1 und T 2 .
| T 1 T 2 l | Lösung. Wir werden nicht nach dem Schwerpunkt suchen, sondern nach dem Massenschwerpunkt (da beides dasselbe ist). Lassen Sie uns die Achse vorstellen X(Abb. 27.3). |
| x C =? | |
Antwort: im Abstand von der Masse T 1 .
STOPPEN! Entscheiden Sie selbst: B1–B3.
Aussage 1 . Wenn ein homogener flacher Körper eine Symmetrieachse hat, liegt der Schwerpunkt auf dieser Achse.
Tatsächlich für jede Punktmasse m i, rechts von der Symmetrieachse gelegen, befindet sich die gleiche Punktmasse symmetrisch zur ersten (Abb. 27.4). In diesem Fall ist die Summe der Kraftmomente .
Da der gesamte Körper in gleichartige Punktpaare unterteilt dargestellt werden kann, ist das Gesamtschwerkraftmoment relativ zu jedem Punkt, der auf der Symmetrieachse liegt, gleich Null, was bedeutet, dass der Schwerpunkt des Körpers auf dieser Achse liegt . Dies führt zu einer wichtigen Schlussfolgerung: Besitzt ein Körper mehrere Symmetrieachsen, so liegt der Schwerpunkt im Schnittpunkt dieser Achsen(Abb. 27.5).
Reis. 27.5 
Aussage 2. Wenn zwei Körper Massen haben T 1 und T Wenn zwei Körper zu einem verbunden sind, liegt der Schwerpunkt eines solchen Körpers auf einem geraden Liniensegment, das die Schwerpunkte des ersten und zweiten Körpers verbindet (Abb. 27.6).
Reis. 27.6 ![]() Reis. 27.7
Reis. 27.7
Nachweisen. Positionieren wir den zusammengesetzten Körper so, dass das Segment, das die Schwerpunkte der Körper verbindet, vertikal ist. Dann die Summe der Schwerkraftmomente des ersten Körpers relativ zum Punkt MIT 1 ist gleich Null und die Summe der Schwerkraftmomente des zweiten Körpers relativ zum Punkt MIT 2 ist gleich Null (Abb. 27.7).
beachte das Schulter Schwerkraft einer Punktmasse t i das Gleiche gilt für jeden Punkt, der auf dem Segment liegt MIT 1 MIT 2 und damit das Schwerkraftmoment relativ zu jedem auf dem Segment liegenden Punkt MIT 1 MIT 2, das Gleiche. Folglich ist die Schwerkraft des gesamten Körpers relativ zu jedem Punkt auf dem Segment Null MIT 1 MIT 2. Somit liegt der Schwerpunkt des Verbundkörpers auf dem Segment MIT 1 MIT 2 .
Eine wichtige praktische Schlussfolgerung ergibt sich aus Aussage 2, die klar in Form einer Anleitung formuliert ist.
Anweisungen,
Wie findet man den Schwerpunkt eines festen Körpers, wenn dieser zerbrochen werden kann?
in Teile zerlegen, wobei die Lage der Schwerpunkte jedes einzelnen bekannt ist
1. Jedes Teil sollte durch eine Masse ersetzt werden, die sich im Schwerpunkt dieses Teils befindet.
2. Finden Massezentrum(und das ist dasselbe wie der Schwerpunkt) des resultierenden Systems von Punktmassen, wobei ein geeignetes Koordinatensystem gewählt wird X 0bei, nach den Formeln:
In der Tat ordnen wir den zusammengesetzten Körper so an, dass er segmentiert ist MIT 1 MIT 2 war horizontal und hängte es punktuell an Fäden auf MIT 1 und MIT 2 (Abb. 27.8, A). Es ist klar, dass der Körper im Gleichgewicht sein wird. Und dieses Gleichgewicht wird nicht gestört, wenn wir jeden Körper durch Punktmassen ersetzen T 1 und T 2 (Abb. 27.8, B).
 Reis. 27.8
Reis. 27.8
STOPPEN! Entscheiden Sie selbst: C3.
Aufgabe 27.2. Massenkugeln werden an zwei Eckpunkten eines gleichseitigen Dreiecks platziert T jeden. Am dritten Scheitelpunkt wird eine Kugel mit der Masse 2 platziert T(Abb. 27.9, A). Dreiecksseite A. Bestimmen Sie den Schwerpunkt dieses Systems.
| T 2T A |  Reis. 27.9 Reis. 27.9 |
| x C = ? bei C = ? | |
Lösung. Lassen Sie uns das Koordinatensystem vorstellen X 0bei(Abb. 27.9, B). Dann
![]() ,
,
 .
.
Antwort: x C = A/2; ; Der Schwerpunkt liegt auf halber Höhe ANZEIGE.
Lehrbuch für die 7. Klasse
§ 25.3. Wie findet man den Schwerpunkt eines Körpers?
Denken Sie daran, dass der Schwerpunkt der Punkt ist, an dem die Schwerkraft wirkt. Überlegen wir, wie wir experimentell die Lage des Schwerpunkts eines flachen Körpers ermitteln können – beispielsweise einer aus Pappe ausgeschnittenen Figur beliebiger Form (siehe Laborarbeit Nr. 12).
Wir hängen die Pappfigur mit einem Stift oder Nagel so auf, dass sie sich frei um eine horizontale Achse drehen kann, die durch den Punkt O verläuft (Abb. 25.4, a). Dann kann diese Figur als Hebel mit einem Drehpunkt O betrachtet werden.
Reis. 25.4. Wie man experimentell den Schwerpunkt einer flachen Figur ermittelt
Wenn eine Figur im Gleichgewicht ist, gleichen sich die auf sie einwirkenden Kräfte gegenseitig aus. Dies ist die Gravitationskraft F t, die am Schwerpunkt der Figur T wirkt, und die elastische Kraft F exr, die am Punkt O wirkt (diese Kraft wird von der Seite eines Stifts oder Nagels ausgeübt).
Diese beiden Kräfte gleichen sich nur dann aus, wenn die Angriffspunkte dieser Kräfte (Punkte T und O) auf derselben Vertikalen liegen (siehe Abb. 25.4, a). Andernfalls dreht die Schwerkraft die Figur um den Punkt O (Abb. 25.4, b).
Wenn die Figur also im Gleichgewicht ist, liegt der Schwerpunkt auf derselben Vertikalen wie der Aufhängepunkt O. Dadurch können wir die Position des Schwerpunkts der Figur bestimmen. Mit einem Lot zeichnen wir eine vertikale Linie durch den Aufhängepunkt (blaue Linie in Abb. 25.4, c). Der Schwerpunkt des Körpers liegt auf der eingezeichneten Linie. Wiederholen wir dieses Experiment mit einer anderen Position des Aufhängepunkts. Als Ergebnis erhalten wir eine zweite Linie, auf der der Schwerpunkt des Körpers liegt (grüne Linie in Abb. 25.4, d). Folglich liegt im Schnittpunkt dieser Linien der gewünschte Körperschwerpunkt (roter Punkt G in Abb. 25.4, d).
In der Ingenieurpraxis kommt es vor, dass die Koordinaten des Schwerpunkts einer komplexen flachen Figur berechnet werden müssen, die aus einfachen Elementen besteht, für die die Lage des Schwerpunkts bekannt ist. Diese Aufgabe ist Teil der Aufgabe der Ermittlung...
Geometrische Eigenschaften zusammengesetzter Querschnitte aus Balken und Stäben. Konstrukteure von Stanzformen stehen oft vor ähnlichen Fragen, wenn sie die Koordinaten des Druckzentrums bestimmen, Entwickler von Ladeplänen für verschiedene Fahrzeuge beim Platzieren von Ladung, Konstrukteure von Metallkonstruktionen bei der Auswahl von Elementquerschnitten und natürlich Studierende im Studium der Fachrichtungen „Theoretische Mechanik“ und „Festigkeitslehre“.
Bibliothek der Elementarfiguren.

Bei symmetrischen ebenen Figuren fällt der Schwerpunkt mit dem Symmetriezentrum zusammen. Die symmetrische Gruppe elementarer Objekte umfasst: Kreis, Rechteck (einschließlich Quadrat), Parallelogramm (einschließlich Raute), regelmäßiges Vieleck.
Von den zehn in der Abbildung oben dargestellten Zahlen sind nur zwei grundlegend. Das heißt, mit Hilfe von Dreiecken und Kreissektoren können Sie nahezu jede Figur von praktischem Interesse kombinieren. Beliebige Kurven können in Abschnitte unterteilt und durch Kreisbögen ersetzt werden.
Die übrigen acht Figuren sind die häufigsten und wurden deshalb in diese einzigartige Bibliothek aufgenommen. In unserer Klassifizierung sind diese Elemente nicht grundlegend. Aus zwei Dreiecken lassen sich ein Rechteck, ein Parallelogramm und ein Trapez bilden. Ein Sechseck ist die Summe von vier Dreiecken. Ein Kreissegment ist der Unterschied zwischen einem Kreissektor und einem Dreieck. Der ringförmige Sektor eines Kreises ist die Differenz zwischen zwei Sektoren. Ein Kreis ist ein Kreissektor mit einem Winkel α=2*π=360˚. Ein Halbkreis ist dementsprechend ein Kreissektor mit einem Winkel α=π=180˚.
Berechnung der Koordinaten des Schwerpunkts einer zusammengesetzten Figur in Excel.
Es ist immer einfacher, Informationen anhand eines Beispiels zu vermitteln und wahrzunehmen, als die Fragestellung anhand rein theoretischer Berechnungen zu untersuchen. Betrachten wir die Lösung des Problems „Wie findet man den Schwerpunkt?“ am Beispiel der zusammengesetzten Figur, die in der Abbildung unter diesem Text gezeigt wird.

Der zusammengesetzte Abschnitt ist ein Rechteck (mit Abmessungen). A1 =80 mm, B1 =40 mm), zu dem oben links ein gleichschenkliges Dreieck (in der Größe der Grundfläche) hinzugefügt wurde A2 =24 mm und Höhe H2 =42 mm) und aus dem von rechts oben ein Halbkreis ausgeschnitten wurde (mit der Mitte am Punkt mit Koordinaten). X03 =50 mm und j03 =40 mm, Radius R3 =26mm).
Zur Durchführung der Berechnungen nutzen wir ein Programm MS Excel oder Programm OOo Berech . Jeder von ihnen wird unsere Aufgabe problemlos bewältigen!
In Zellen mit Gelb wir werden es füllen Hilfsvorläufig Berechnungen .
Wir berechnen die Ergebnisse in hellgelb gefüllten Zellen.
Blau Schriftart ist Ausgangsdaten .
Schwarz Schriftart ist dazwischenliegend Berechnungsergebnisse .
Rot Schriftart ist Finale Berechnungsergebnisse .
Wir beginnen mit der Lösung des Problems – wir beginnen mit der Suche nach den Koordinaten des Schwerpunkts des Abschnitts.
Ausgangsdaten:
1. Wir werden die Namen der Elementarfiguren, die einen zusammengesetzten Abschnitt bilden, entsprechend schreiben
zu Zelle D3: Rechteck
zu Zelle E3: Dreieck
zu Zelle F3: Halbkreis
2. Mithilfe der in diesem Artikel vorgestellten „Bibliothek der Elementarfiguren“ ermitteln wir die Koordinaten der Schwerpunkte der Elemente des Verbundabschnitts xci Und yci in mm relativ zu willkürlich ausgewählten Achsen 0x und 0y und schreiben
zu Zelle D4: =80/2 = 40,000
xc 1 = A 1 /2
zu Zelle D5: =40/2 =20,000
yc 1 = B 1 /2
zu Zelle E4: =24/2 =12,000
xc 2 = A 2 /2
zu Zelle E5: =40+42/3 =54,000
yc 2 = B 1 + H 2 /3
zu Zelle F4: =50 =50,000
xc 3 = X03
zu Zelle F5: =40-4*26/3/PI() =28,965
yc 3 = j 03 -4* r3 /3/ π
3. Berechnen wir die Flächen der Elemente F 1 , F 2 , F3 in mm2, wiederum unter Verwendung der Formeln aus dem Abschnitt „Bibliothek der Elementarfiguren“
in Zelle D6: =40*80 =3200
F1 = A 1 * B1
in Zelle E6: =24*42/2 =504
F2 = a2 *h2 /2
in Zelle F6: =-PI()/2*26^2 =-1062
F3 =-π/2*r3 ^2
Die Fläche des dritten Elements – des Halbkreises – ist negativ, weil es ein Ausschnitt ist – ein leerer Raum!

Berechnung der Schwerpunktkoordinaten:
4. Bestimmen Sie die Gesamtfläche der endgültigen Figur F0 in mm2
in der zusammengeführten Zelle D8E8F8: =D6+E6+F6 =2642
F0 = F 1 + F 2 + F3
5. Berechnen wir die statischen Momente einer zusammengesetzten Figur Sx Und Sy in mm3 relativ zu den ausgewählten Achsen 0x und 0y
in der zusammengeführten Zelle D9E9F9: =D5*D6+E5*E6+F5*F6 =60459
Sx = yc1 * F1 + yc2 *F2 + yc3 *F3
in der zusammengeführten Zelle D10E10F10: =D4*D6+E4*E6+F4*F6 =80955
Sy = xc1 * F1 + xc2 *F2 + xc3 *F3
6. Und schließlich berechnen wir die Koordinaten des Schwerpunkts des Verbundabschnitts Xc Und Yc in mm im gewählten Koordinatensystem 0x - 0y
in der zusammengeführten Zelle D11E11F11: =D10/D8 =30,640
Xc = Sy / F0
in der zusammengeführten Zelle D12E12F12: =D9/D8 =22,883
Yc =Sx /F0
Das Problem ist gelöst, die Berechnung in Excel ist abgeschlossen – die aus drei einfachen Elementen zusammengestellten Koordinaten des Schwerpunkts des Abschnitts sind gefunden!
Abschluss.
Das Beispiel im Artikel wurde sehr einfach gewählt, um das Verständnis der Methodik zur Berechnung des Schwerpunkts eines komplexen Abschnitts zu erleichtern. Die Methode besteht darin, jede komplexe Figur in einfache Elemente mit bekannten Schwerpunktlagen zu zerlegen und abschließende Berechnungen für den gesamten Abschnitt durchzuführen.
Wenn der Abschnitt aus gewalzten Profilen – Winkeln und Kanälen – besteht, besteht keine Notwendigkeit, diese in Rechtecke und Quadrate mit ausgeschnittenen kreisförmigen „π/2“-Sektoren zu unterteilen. Die Koordinaten der Schwerpunkte dieser Profile sind in den GOST-Tabellen angegeben, d. Rohre, Stäbe und Sechsecke – das sind zentralsymmetrische Abschnitte).
Die Lage der Koordinatenachsen hat natürlich keinen Einfluss auf die Lage des Schwerpunkts der Figur! Wählen Sie daher ein Koordinatensystem, das Ihre Berechnungen vereinfacht. Wenn ich beispielsweise in unserem Beispiel das Koordinatensystem um 45˚ im Uhrzeigersinn drehen würde, würde die Berechnung der Koordinaten der Schwerpunkte eines Rechtecks, eines Dreiecks und eines Halbkreises zu einem weiteren separaten und umständlichen Berechnungsschritt werden, der nicht durchgeführt werden kann. im Kopf".
Die unten dargestellte Excel-Berechnungsdatei ist in diesem Fall kein Programm. Vielmehr handelt es sich um eine Skizze eines Rechners, eines Algorithmus, einer Vorlage, die im Einzelfall folgt Erstellen Sie Ihre eigene Formelfolge für Zellen mit einer leuchtend gelben Füllung.
Jetzt wissen Sie also, wie Sie den Schwerpunkt eines beliebigen Abschnitts ermitteln können! Die vollständige Berechnung aller geometrischen Eigenschaften beliebiger komplexer Verbundabschnitte wird in einem der kommenden Artikel im Abschnitt „“ behandelt. Verfolgen Sie die Neuigkeiten im Blog.
Für Empfang Informationen über die Veröffentlichung neuer Artikel und für Herunterladen funktionierender Programmdateien Ich bitte Sie, Ankündigungen im Fenster am Ende des Artikels oder im Fenster oben auf der Seite zu abonnieren.
Geben Sie Ihre E-Mail-Adresse ein und klicken Sie auf die Schaltfläche „Artikelankündigungen erhalten“. NICHT VERGESSEN BESTÄTIGE DEIN ABONNEMENT indem Sie auf den Link klicken in einem Brief, der Ihnen sofort an die angegebene E-Mail-Adresse (manchmal im Ordner) zugeht « Spam » )!
Ein paar Worte zum Glas, zur Münze und zu den beiden Gabeln, die im „Illustrationssymbol“ ganz am Anfang des Artikels abgebildet sind. Viele von Ihnen kennen sicherlich diesen „Trick“, der bei Kindern und uneingeweihten Erwachsenen bewundernde Blicke hervorruft. Das Thema dieses Artikels ist der Schwerpunkt. Er und sein Dreh- und Angelpunkt spielen mit unserem Bewusstsein und unserer Erfahrung und täuschen einfach unseren Verstand!
Der Schwerpunkt des Systems „Gabel+Münze“ liegt immer auf Fest Distanz senkrecht nach unten vom Rand der Münze, der wiederum der Drehpunkt ist. Dies ist eine Position des stabilen Gleichgewichts! Wenn man die Gabeln schüttelt, wird sofort deutlich, dass das System danach strebt, seine bisherige stabile Position einzunehmen! Stellen Sie sich ein Pendel vor – einen Befestigungspunkt (= der Auflagepunkt einer Münze auf dem Rand eines Glases), eine Stabachse des Pendels (= in unserem Fall ist die Achse virtuell, da die Masse der beiden Gabeln gleich ist). in verschiedene Raumrichtungen ausgebreitet) und einer Last am unteren Ende der Achse (= Schwerpunkt des gesamten „Gabel“-Systems + Münze“). Wenn Sie beginnen, das Pendel aus der Vertikalen in eine beliebige Richtung (vorwärts, rückwärts, links, rechts) auszulenken, kehrt es unter dem Einfluss der Schwerkraft zwangsläufig in seine ursprüngliche Position zurück. stabiler Gleichgewichtszustand(Das Gleiche passiert mit unseren Gabeln und unserer Münze)!
Wenn Sie es nicht verstehen, es aber verstehen wollen, finden Sie es selbst heraus. Es ist sehr interessant, selbst „dahin zu gelangen“! Ich möchte hinzufügen, dass das gleiche Prinzip der Verwendung eines stabilen Gleichgewichts auch im Spielzeug Vanka-Stand-up umgesetzt wird. Lediglich der Schwerpunkt dieses Spielzeugs liegt oberhalb des Drehpunkts, jedoch unterhalb der Mitte der Halbkugel der Auflagefläche.
Ich freue mich immer über Ihre Kommentare, liebe Leser!!!
Fragen, RESPEKTIEREN Werk des Autors, Datei herunterladen NACH DEM ABONNIEREN für Artikelankündigungen.










