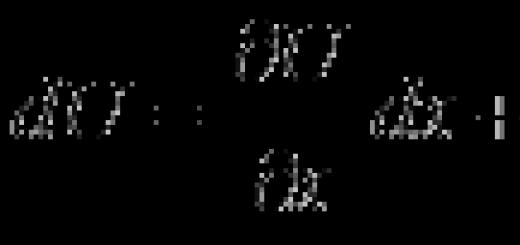Beim Studium verschiedener Teilgebiete der Physik, der Mechanik und der technischen Wissenschaften stößt man auf Größen, die durch die Angabe ihrer Zahlenwerte vollständig bestimmt werden. Solche Größen heißen Skalar oder, kurz gesagt, Skalare.

Skalare Größen sind Länge, Fläche, Volumen, Masse, Körpertemperatur usw. Neben skalaren Größen gibt es bei verschiedenen Problemen Größen, für die neben ihrem Zahlenwert auch die Richtung bekannt sein muss. Solche Größen heißen Vektor. Physikalische Beispiele für Vektorgrößen können die Verschiebung eines im Raum bewegten materiellen Punktes, die Geschwindigkeit und Beschleunigung dieses Punktes sowie die auf ihn wirkende Kraft sein.

Vektorgrößen werden durch Vektoren dargestellt.

Vektordefinition. Ein Vektor ist ein gerichteter Abschnitt einer Geraden mit einer bestimmten Länge.

Ein Vektor wird durch zwei Punkte charakterisiert. Ein Punkt ist der Anfangspunkt des Vektors, der andere Punkt ist der Endpunkt des Vektors. Wenn wir den Anfang des Vektors mit einem Punkt bezeichnen A , und das Ende des Vektors ist ein Punkt IN , dann wird der Vektor selbst bezeichnet. Ein Vektor kann auch durch einen kleinen lateinischen Buchstaben mit einem Balken darüber gekennzeichnet werden (z. B. ).

Grafisch wird ein Vektor durch ein Segment mit einem Pfeil am Ende dargestellt.

Der Anfang des Vektors wird aufgerufen sein Anwendungspunkt. Wenn der Punkt A ist der Anfang des Vektors , dann sagen wir, dass der Vektor an dem Punkt angewendet wird A.

Ein Vektor wird durch zwei Größen charakterisiert: Länge und Richtung.

Vektorlänge – der Abstand zwischen dem Startpunkt A und dem Endpunkt B. Ein anderer Name für die Länge eines Vektors ist der Modul des Vektors und wird durch das Symbol angezeigt . Bezeichnet wird der Vektormodul Vektor , dessen Länge 1 ist, heißt Einheitsvektor. Das ist die Bedingung für den Einheitsvektor

Ein Vektor mit der Länge Null wird Nullvektor genannt (gekennzeichnet mit). Offensichtlich hat der Nullvektor den gleichen Anfangs- und Endpunkt. Der Nullvektor hat keine bestimmte Richtung.

Definition kollinearer Vektoren. Vektoren, die auf derselben Geraden oder auf parallelen Geraden liegen, werden als kollinear bezeichnet .

Beachten Sie, dass kollineare Vektoren unterschiedliche Längen und unterschiedliche Richtungen haben können.

Bestimmung gleicher Vektoren. Zwei Vektoren heißen gleich, wenn sie kollinear sind, die gleiche Länge und die gleiche Richtung haben.

In diesem Fall schreiben sie:

Kommentar. Aus der Definition der Vektorgleichheit folgt, dass ein Vektor parallel übertragen werden kann, indem sein Ursprung an einem beliebigen Punkt im Raum (insbesondere einer Ebene) platziert wird.

Alle Nullvektoren gelten als gleich.

Bestimmung entgegengesetzter Vektoren. Zwei Vektoren heißen entgegengesetzt, wenn sie kollinear sind, die gleiche Länge, aber die entgegengesetzte Richtung haben.

In diesem Fall schreiben sie:

Mit anderen Worten, der dem Vektor entgegengesetzte Vektor wird als bezeichnet.

Ein Vektor ist ein gerichteter Abschnitt einer Geraden im euklidischen Raum, dessen eines Ende (Punkt A) als Anfang des Vektors und dessen anderes Ende (Punkt B) als Ende des Vektors bezeichnet wird (Abb. 1). Vektoren werden bezeichnet:

Wenn Anfang und Ende des Vektors zusammenfallen, wird der Vektor aufgerufen Nullvektor und ist bezeichnet 0 .

Beispiel. Der Anfang des Vektors im zweidimensionalen Raum soll Koordinaten haben A(12.6) und das Ende des Vektors sind die Koordinaten B(12.6). Dann ist der Vektor der Nullvektor.

Abschnittslänge AB angerufen Modul (Länge, Die Norm) Vektor und wird mit | bezeichnet A|. Ein Vektor mit der Länge eins heißt Einheitsvektor. Zusätzlich zum Modul wird der Vektor durch die Richtung charakterisiert: Der Vektor hat eine Richtung von A Zu B. Ein Vektor heißt Vektor, Gegenteil Vektor.

Die beiden Vektoren werden aufgerufen kollinear, wenn sie auf derselben Geraden oder auf parallelen Geraden liegen. Im Bild Abb. Die 3 roten Vektoren sind kollinear, weil sie liegen auf derselben Geraden und die blauen Vektoren sind kollinear, weil sie liegen auf parallelen Linien. Es werden zwei kollineare Vektoren aufgerufen gleichermaßen gerichtet, wenn ihre Enden auf derselben Seite der Geraden liegen, die ihre Anfänge verbindet. Es werden zwei kollineare Vektoren aufgerufen entgegengesetzt gerichtet, wenn ihre Enden auf gegenüberliegenden Seiten der geraden Linie liegen, die ihre Anfänge verbindet. Liegen zwei kollineare Vektoren auf derselben Geraden, so heißen sie identisch gerichtet, wenn einer der von einem Vektor gebildeten Strahlen den vom anderen Vektor gebildeten Strahl vollständig enthält. Ansonsten spricht man von entgegengesetzt gerichteten Vektoren. In Abbildung 3 sind die blauen Vektoren gleichgerichtet und die roten Vektoren entgegengesetzt gerichtet.

Die beiden Vektoren werden aufgerufen gleich wenn sie gleiche Module und gleiche Richtungen haben. In Abbildung 2 sind die Vektoren gleich, weil ihre Module sind gleich und haben die gleiche Richtung.

Die Vektoren heißen koplanar, wenn sie auf derselben Ebene oder in parallelen Ebenen liegen.

IN N Betrachten Sie in einem dimensionalen Vektorraum die Menge aller Vektoren, deren Startpunkt mit dem Koordinatenursprung zusammenfällt. Dann kann der Vektor in der folgenden Form geschrieben werden:

Wo x 1 , x 2 , ..., x n Vektorendpunktkoordinaten X.

Ein in der Form (1) geschriebener Vektor heißt Zeilenvektor und der im Formular geschriebene Vektor

angerufen Spaltenvektor.

Nummer N angerufen Abmessungen (in Ordnung) Vektor. Wenn dann heißt der Vektor Nullvektor(da der Startpunkt des Vektors ). Zwei Vektoren X Und j sind genau dann gleich, wenn ihre entsprechenden Elemente gleich sind.

Seite 1 von 2

Frage 1. Was ist ein Vektor? Wie werden Vektoren bezeichnet?
Antwort. Wir nennen ein gerichtetes Segment einen Vektor (Abb. 211). Die Richtung eines Vektors wird durch die Angabe seines Anfangs und Endes bestimmt. In der Zeichnung ist die Richtung des Vektors durch einen Pfeil angegeben. Um Vektoren zu bezeichnen, verwenden wir lateinische Kleinbuchstaben a, b, c, .... Sie können einen Vektor auch bezeichnen, indem Sie seinen Anfang und sein Ende angeben. In diesem Fall wird der Anfang des Vektors an erster Stelle platziert. Anstelle des Wortes „Vektor“ wird manchmal ein Pfeil oder eine Linie über der Buchstabenbezeichnung des Vektors platziert. Der Vektor in Abbildung 211 kann wie folgt bezeichnet werden:

\(\overline(a)\), \(\overrightarrow(a)\) oder \(\overline(AB)\), \(\overrightarrow(AB)\).

Frage 2. Welche Vektoren heißen gleichgerichtet (entgegengerichtet)?
Antwort. Die Vektoren \(\overline(AB)\) und \(\overline(CD)\) heißen gleich gerichtet, wenn die Halblinien AB und CD gleich gerichtet sind.
Die Vektoren \(\overline(AB)\) und \(\overline(CD)\) heißen entgegengesetzt gerichtet, wenn die Halblinien AB und CD entgegengesetzt gerichtet sind.
In Abbildung 212 sind die Vektoren \(\overline(a)\) und \(\overline(b)\) gleich gerichtet, und die Vektoren \(\overline(a)\) und \(\overline(c)\ ) sind entgegengesetzt gerichtet.

Frage 3. Was ist der absolute Betrag eines Vektors?
Antwort. Der Absolutwert (oder Modul) eines Vektors ist die Länge des Segments, das den Vektor darstellt. Der Absolutwert des Vektors \(\overline(a)\) wird mit |\(\overline(a)\)| bezeichnet.

Frage 4. Was ist ein Nullvektor?
Antwort. Der Anfang eines Vektors kann mit seinem Ende zusammenfallen. Wir nennen einen solchen Vektor den Nullvektor. Der Nullvektor wird durch eine Null mit Bindestrich (\(\overline(0)\)) bezeichnet. Sie sprechen nicht über die Richtung des Nullvektors. Der Absolutwert des Nullvektors wird als gleich Null betrachtet.

Frage 5. Welche Vektoren heißen gleich?
Antwort. Zwei Vektoren heißen gleich, wenn sie durch Parallelverschiebung kombiniert werden. Dies bedeutet, dass es eine parallele Übersetzung gibt, die den Anfang und das Ende eines Vektors jeweils zum Anfang und Ende eines anderen Vektors führt.

Frage 6. Beweisen Sie, dass gleiche Vektoren die gleiche Richtung haben und im Absolutwert gleich sind. Und umgekehrt: Gleichgerichtete Vektoren mit gleichem Absolutwert sind gleich.
Antwort. Bei der Parallelverschiebung behält der Vektor sowohl seine Richtung als auch seinen Absolutwert. Das bedeutet, dass gleiche Vektoren die gleiche Richtung haben und im Absolutwert gleich sind.
Seien \(\overline(AB)\) und \(\overline(CD)\) identisch gerichtete Vektoren mit gleichem Absolutwert (Abb. 213). Eine Parallelverschiebung, die Punkt C nach Punkt A verschiebt, kombiniert die Halblinie CD mit der Halblinie AB, da sie die gleiche Richtung haben. Und da die Segmente AB und CD gleich sind, fällt Punkt D mit Punkt B zusammen, d.h. Parallele Übersetzung transformiert den Vektor \(\overline(CD)\) in den Vektor \(\overline(AB)\). Das bedeutet, dass die Vektoren \(\overline(AB)\) und \(\overline(CD)\) gleich sind, was bewiesen werden musste.

Frage 7. Beweisen Sie, dass Sie von jedem Punkt aus einen Vektor zeichnen können, der einem gegebenen Vektor entspricht, und zwar nur einem.
Antwort. Sei CD eine Linie und der Vektor \(\overline(CD)\) Teil der Linie CD. Sei AB die Gerade, in die die Gerade CD bei paralleler Übertragung übergeht, \(\overline(AB)\) sei der Vektor, in den der Vektor \(\overline(CD)\) bei paralleler Übertragung übergeht, und daher der Die Vektoren \(\overline(AB)\) und \(\overline(CD)\) sind gleich und die Geraden AB und CD sind parallel (siehe Abb. 213). Wie wir wissen, kann man durch einen Punkt, der nicht auf einer gegebenen Geraden liegt, auf der Ebene höchstens eine Gerade parallel zu dieser zeichnen (Axiom paralleler Geraden). Das bedeutet, dass durch Punkt A eine Gerade parallel zur Geraden CD gezogen werden kann. Da der Vektor \(\overline(AB)\) Teil der Geraden AB ist, kann man durch Punkt A einen Vektor \(\overline(AB)\) zeichnen, der dem Vektor \(\overline(CD)\ entspricht ).

Frage 8. Was sind Vektorkoordinaten? Was ist der absolute Wert des Vektors mit den Koordinaten a 1, a 2?
Antwort. Der Vektor \(\overline(a)\) habe einen Anfangspunkt A 1 (x 1 ; y 1) und einen Endpunkt A 2 (x 2 ; y 2). Die Koordinaten des Vektors \(\overline(a)\) sind die Zahlen a 1 = x 2 - x 1 , a 2 = y 2 - y 1 . Wir werden die Koordinaten des Vektors neben die Buchstabenbezeichnung des Vektors setzen, in diesem Fall \(\overline(a)\) (a 1 ; a 2) oder einfach \((\overline(a 1 ; a 2 ) )\). Die Koordinaten des Nullvektors sind gleich Null.
Aus der Formel, die den Abstand zwischen zwei Punkten durch ihre Koordinaten ausdrückt, folgt, dass der Absolutwert des Vektors mit den Koordinaten a 1 , a 2 gleich \(\sqrt(a^2 1 + a^2 2 )\) ist.

Frage 9. Beweisen Sie, dass gleiche Vektoren jeweils gleiche Koordinaten haben und Vektoren mit jeweils gleichen Koordinaten gleich sind.
Antwort. Seien A 1 (x 1 ; y 1) und A 2 (x 2 ; y 2) der Anfang und das Ende des Vektors \(\overline(a)\). Da der ihm entsprechende Vektor \(\overline(a)\) aus dem Vektor \(\overline(a)\) durch Parallelverschiebung erhalten wird, sind Anfang und Ende A" 1 (x 1 + c; y 1). + d) bzw. ), A" 2 (x 2 + c; y 2 ​​​​+ d). Dies zeigt, dass beide Vektoren \(\overline(a)\) und \(\overline(a")\) die haben gleiche Koordinaten: x 2 - x 1, y 2 - y 1.
Beweisen wir nun die umgekehrte Aussage. Die entsprechenden Koordinaten der Vektoren \(\overline(A 1 A 2 )\) und \(\overline(A" 1 A" 2 )\) seien gleich. Beweisen wir, dass die Vektoren gleich sind.
Seien x" 1 und y" 1 die Koordinaten von Punkt A" 1 und x" 2, y" 2 die Koordinaten von Punkt A" 2. Gemäß den Bedingungen des Satzes ist x 2 - x 1 = x" 2 - x" 1, y 2 - y 1 = y" 2 - y" 1. Daher ist x" 2 = x 2 + x" 1 - x 1, y" 2 = y 2 + y" 1 - y 1. Parallelübertragung durch Formeln gegeben

x" = x + x" 1 - x 1 , y" = y + y" 1 - y 1 ,

überträgt Punkt A 1 auf Punkt A" 1 und Punkt A 2 auf Punkt A" 2, d.h. Die Vektoren \(\overline(A 1 A 2 )\) und \(\overline(A" 1 A" 2 )\) sind gleich, was bewiesen werden musste.

Frage 10. Definieren Sie die Summe der Vektoren.
Antwort. Die Summe der Vektoren \(\overline(a)\) und \(\overline(b)\) mit den Koordinaten a 1 , a 2 und b 1 , b 2 heißt der Vektor \(\overline(c)\) mit Koordinaten a 1 + b 1, a 2 + b a 2, d.h.

\(\overline(a) (a 1 ; a 2) + \overline(b)(b 1 ; b 2) = \overline(c) (a 1 + b 1 ; a 2 + b 2)\).