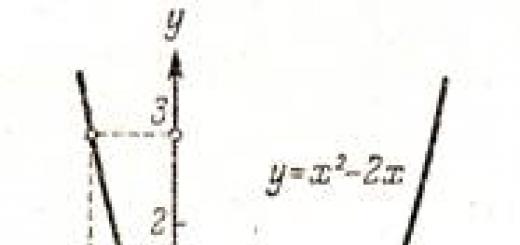3.3. Линейна независимост на векторите. Основа.

Линеен комбинация векторни системи

наречен вектор

където a 1 , a 2 , ..., a n - произволни числа.

Ако всички i = 0, тогава се извиква линейната комбинация тривиален . В този случай, очевидно

Определение 5.

Ако за система от вектори има нетривиална линейна комбинация (поне една ai¹ 0) равен на нулевия вектор: тогава системата от вектори се нарича линеен зависим. Ако равенството (1) е възможно само в случая, когато всички a i =0, тогава системата от вектори се извиква линеен независима .

Теорема 2 (Условия на линейна зависимост).

Определение 6.

От теорема 3 следва, че ако базата е дадена в пространството, тогава чрез добавяне на произволен вектор към нея, ние получаваме линейно зависима система от вектори. В съответствие съсТеорема 2 (1) , един от тях (може да се покаже, че векторът) може да бъде представен като линейна комбинация от останалите:

.

Определение 7.

Числа са наречени координати вектори в основата (означено

Ако векторите се разглеждат в равнината, тогава основата ще бъде подредена двойка неколинеарни вектори

и координатите на вектора в тази основа са двойка числа:

Бележка 3. Може да се покаже, че за даден базис координатите на вектора се определят еднозначно . От това по-специално следва, че ако векторите са равни, то съответните им координати са равни и обратно .

Така, ако базата е дадена в пространство, тогава всеки вектор от пространството съответства на подредена тройка от числа (координати на вектора в тази база) и обратно: всяка тройка от числа съответства на вектор.

В равнината подобно съответствие се установява между вектори и двойки числа.

Теорема 4 (Линейни операции чрез векторни координати).

Ако в някаква основа И а е произволно число, тогава в тази основа

С други думи:

Когато вектор се умножи по число, неговите координати се умножат по това число ;

при добавяне на вектори се добавят съответните им координати .

Пример 1 . В някаква основа векторитеимат координати

Покажете, че векторите образуват базис и намерете координатите на вектора в този базис.

Векторите формират основа, ако не са копланарни, следователно (в съответствие спо теорема 3(2) ) са линейно независими.

По дефиниция 5 това означава, че равенството

възможно само акох = г = z = 0.

Деф.множество w се нарича линейно пространство, а неговият елемент. -вектори, ако:

*законът е посочен (+) по кат. всеки два елемента x, y от w са свързани с елемент, наречен. тяхната сума [x + y]

*даден е закон (* за числото a), според cat елемента x от w и a се сравнява елемент от w, наречен продукт на x и a [ax];

* завършено

следните изисквания (или аксиоми):

Следа c1. нулев вектор (ctv 0 1 и 0 2. от a3: 0 2 + 0 1 = 0 2 и 0 1 + 0 2 = 0 1. от a1 0 1 + 0 2 = 0 2 + 0 1 => 0 1 = 0 2.)

в2. .(ctv, a4)

в3. 0 век.(a7)

c4. a(число)*0=0.(a6,c3)

c5. x (*) -1 =0 вектор, противоположен на x, т.е. (-1)x = -x. (a5,a6)

c6. В w е дефинирано действието на изваждане: векторът x се нарича разлика на вектори b и a, ако x + a = b, и се обозначава x = b - a.

Номер нНаречен измерение лин. пр-а Л , ако в Л има система от нлин. незав. вектори и всяка система от н+1 вектор - лин. зависим дим Л= н. пространство Л наречена n-мерна.

Подредена колекция от n реда. незав. вектори n мерно независими. пространство - база

Теорема. Всеки вектор X може да бъде представен единствения начинпод формата на линейни комбинации от базисни вектори

Нека (1) е основата на n-мерен линеар. пр-ва V, т.е. колекция от линейно независими вектори. Наборът от вектори ще бъде линеен. зависим, защото техен n+ 1.

Тези. има числа, които не всички са равни на нула едновременно, какво общо има това (иначе (1) са линейно зависими).

Тогава където е векторното разлагане хпо основа(1) .

Този израз е уникален, т.к ако съществува друг израз (**)

изваждане на равенство (**) от (*),

получаваме

защото са линейно независими, тогава . Chtd

Теорема. Ако - лин. независими векторипространство V и всеки вектор x от V може да бъде представен чрез , тогава тези вектори образуват основа на V

Документ: (1)-lin.independent =>документът остава, който е линейно независим. Според конвенцията Всеки вектор a се изразява чрез (1): , разгледайте , rang≤n => сред колоните не повече от n са линейно независими, но m > n=> m колони са линейно зависими => s=1, n

Тоест, векторите са линейно зависими

По този начин пространството V е n-мерно и (1) неговата база

№4Деф.Подмножество L lin. производство V се нарича лин. конд. на това пространство, ако по отношение на операциите (+) и (*a), посочени във V, подпространството L е линейно пространство

Теорема Множеството l от вектори на пространство V е линейно. Подпространство на това пространство изпълнява

(предварително) нека (1) и (2) са изпълнени, за да бъде L подпрост. V остава да докажем, че всички аксиоми на lin са изпълнени. пр-ва.

(-x): -x+x=0 д. a(x + y) = ax + ay;

(a-b) и (e-h) следва от валидността на V;

(необходимост) Нека L е lin. подпространство на това пространство, тогава (1) и (2) са удовлетворени по силата на дефиницията на линиите. пр-ва

Деф.Колекция от всякакви линии. комбинации от някои елементи (x j) линия. продуктът се нарича линейна обвивка

Теоремапроизволен набор от всички линии. комбинации от вектори V с реални. коефициентът е лин. субпр V (линейна обвивка дадена система от вектори lin. pr. е линейният subpr на този pr. )

ОПР.Непразно подмножество от L линейни вектори. производство V се нарича лин. подпространство, ако:

а) сумата от всички вектори от L принадлежи на L

б) произведението на всеки вектор от L с произволно число принадлежи на L

Сума от две подпространстваЛотново е подпространствоЛ

1) Нека y 1 + y 2 (L 1 + L 2)<=>y 1 =x 1 +x 2, y 2 =x’ 1 +x’ 2, където (x 1,x’ 1) L 1, (x 2,x’ 2) L 2. y 1 +y 2 =(x 1 +x 2)+(x' 1 +x' 2)=(x 1 +x' 1)+(x 2 +x' 2), където (x 1 +x' 1 ) L 1 , (x 2 +x' 2) L 2 => първото условие на линейно подпространство е изпълнено.

ay 1 =ax 1 +ax 2, където (ax 1) L 1, (ax 2) L 2 => защото (y 1 +y 2) (L 1 +L 2) , (ly 1) (L 1 +L 2) => условията са изпълнени => L 1 +L 2 е линейно подпространство.

Пресечната точка на две подразделенияЛ 1 ИЛ 2 лин. пр-ваЛ също е subsp. това пространство.

Да разгледаме два произволни вектора х,г, принадлежащи на пресечната точка на подпространства и две произволни числа а,b:.

Според деф. пресечни точки на множества:

=> по дефиниция на подпространство на линейно пространство:,.

T.K. вектор брадва + отпринадлежи на много Л 1, и много Л 2, то по дефиниция принадлежи на пресечната точка на тези множества. По този начин:

ОПР.Казват, че V е пряк сбор от своите подразделения. ако и б) това разлагане е уникално

б")Нека покажем, че b) е еквивалентно на b’)

Когато b) е вярно b’)

Всякакви видове (М, н) от се пресичат само по нулевия вектор

Нека ∃ z ∈

Справедлива връщанеЛ=

противоречие

Теорема за (*) е необходимо и достатъчно за обединението на бази ( формират основата на космоса

(Задължително)нека (*) и векторите са бази на подмножества. и има разширение в ; x се разширява върху базата L, за да се твърди, че ( представляват база, е необходимо да се докаже тяхната линейна независимост; всички те съдържат 0 0=0+...+0. Поради уникалността на разширението на 0 над : => поради линейната независимост на базиса => ( – базис

(Ext.)Нека ( формира основата на L уникално разлагане (**) съществува поне едно разлагане. Чрез уникалност (*) => уникалност (**)

Коментирайте. Размерността на пряката сума е равна на сумата от размерите на подпространството

Всяка неособена квадратна матрица може да служи като преходна матрица от една база към друга

Нека има две бази в n-мерно линейно пространство V и

(1) =A, където елементите * и ** не са числа, но ще разширим определени операции върху числова матрица до такива редове.

защото в противен случай векторите ** биха били линейно зависими

Обратно.Ако тогава колоните на A са линейно независими => образуват основа

Координати И свързани по отношение , Където преходни матрични елементи

Нека е известно разлагането на елементите на „новата” основа в „старата”.

Тогава равенствата са верни

Но ако линейна комбинация от линейно независими елементи е равна на 0, тогава =>

Основна теорема за линейна зависимост

Ако (*) се изразява линейно чрез (**) Чен<= м

Нека докажем чрез индукция по m

m=1: система (*) съдържа 0 и лин. управител - невъзможно

нека е вярно за m=k-1

нека докажем за m=k

Може да се окаже, че 1) , т.е. в-ри (1) са лин.комб. лин. in-ditch (2)Система (1) линейна ненадеждна, защото е част от лин.незав. системи (*). защото в система (2) има само k-1 вектора, тогава по индукционната хипотеза получаваме k+1

Теорема 1. (За линейната независимост на ортогоналните вектори). Нека Тогава системата от вектори е линейно независима.

Нека направим линейна комбинация ∑λ i x i =0 и да разгледаме скаларното произведение (x j , ∑λ i x i)=λ j ||x j || 2 =0, но ||x j || 2 ≠0⇒λ j =0.

Определение 1. Векторна системаили (e i ,e j)=δ ij - символ на Кронекер, наречено ортонормално (ONS).

Определение 2. За произволен елемент x от произволно безкрайномерно евклидово пространство и произволна ортонормална система от елементи, редът на Фурие на елемент x върху системата се нарича формално съставена безкрайна сума (серия) от формата , в които реалните числа λ i се наричат ​​коефициенти на Фурие на елемента x в системата, където λ i =(x,e i).

Коментар. (Естествено възниква въпросът за конвергенцията на тази серия. За да проучим този проблем, ние фиксираме произволно число n и откриваме какво отличава n-тата частична сума от реда на Фурие от всяка друга линейна комбинация от първите n елемента на ортонормалната система.)

Теорема 2. За всяко фиксирано число n, сред всички суми на формата, n-тата частична сума от реда на Фурие на елемента има най-малкото отклонение от елемента x според нормата на дадено евклидово пространство

Като вземем предвид ортонормалността на системата и дефиницията на коефициента на Фурие, можем да запишем

Минимумът на този израз се постига при c i =λ i, тъй като в този случай неотрицателната първа сума от дясната страна винаги се нулира, а останалите членове не зависят от c i.

Пример. Помислете за тригонометричната система

в пространството на всички интегрируеми на Риман функции f(x) на сегмента [-π,π]. Лесно се проверява, че това е ONS и тогава редът на Фурие на функцията f(x) има формата където .

Коментар. (Тригонометричният ред на Фурие обикновено се записва във формата Тогава )

Произволно ONS в безкрайномерно евклидово пространство без допълнителни предположения, най-общо казано, не е основа на това пространство. На интуитивно ниво, без да даваме строги определения, ще опишем същността на въпроса. В произволно безкрайномерно евклидово пространство E, разгледайте ONS, където (e i ,e j)=δ ij е символът на Кронекер. Нека M е подпространство на евклидовото пространство и k=M ⊥ е подпространство, ортогонално на M, така че евклидовото пространство E=M+M ⊥ . Проекцията на вектора x∈E върху подпространството M е векторът ∈M, където

Ще търсим онези стойности на коефициентите на разширение α k, за които остатъкът (остатъкът на квадрат) h 2 =||x-|| 2 ще бъде минимумът:

h 2 =||x-|| 2 =(x-,x-)=(x-∑α k e k,x-∑α k e k)=(x,x)-2∑α k (x,e k)+(∑α k e k,∑α k e k)= ||x|| 2 -2∑α k (x,e k)+∑α k 2 +∑(x,e k) 2 -∑(x,e k) 2 =||x|| 2 +∑(α k -(x,e k)) 2 -∑(x,e k) 2 .

Ясно е, че този израз ще приеме минимална стойност при α k =0, което е тривиално, и при α k =(x,e k). Тогава ρ min =||x|| 2 -∑α k 2 ≥0. От тук получаваме неравенството на Бесел ∑α k 2 ||x|| 2. При ρ=0 ортонормална система от вектори (ONS) се нарича пълна ортонормална система в смисъла на Стеклов (PONS).От тук можем да получим равенството на Стеклов-Парсевал ∑α k 2 =||x|| 2 - „Питагоровата теорема“ за безкрайномерни евклидови пространства, които са пълни по смисъла на Стеклов. Сега би било необходимо да се докаже, че за да може всеки вектор в пространството да бъде уникално представен под формата на ред на Фурие, сходен към него, е необходимо и достатъчно равенството на Стеклов-Парсевал да се изпълнява. Системата от вектори pic=""> ONB образува система от вектори. Помислете за частичната сума на серията Тогава като опашката на конвергентна серия. Така системата от вектори е PONS и образува ONB.

Пример.Тригонометрична система

в пространството на всички интегрируеми по Риман функции f(x) на сегмента [-π,π] е PONS и образува ONB.

Позволявам Л – линейно пространство над полето Р . Позволявам А1, а2, …, ан (*) крайна система от вектори от Л . вектор IN = a1× A1 + a2× A2 + … + an× Ан (16) се нарича Линейна комбинация от вектори ( *), или казват, че е вектор IN линейно изразено чрез система от вектори (*).

Определение 14. Системата от вектори (*) се нарича Линейно зависима , ако и само ако съществува ненулев набор от коефициенти a1, a2, … , такъв, че a1× A1 + a2× A2 + … + an× Ан = 0. Ако a1× A1 + a2× A2 + … + an× Ан = 0 Û a1 = a2 = … = an = 0, тогава се извиква системата (*). Линейно независим.

Свойства на линейна зависимост и независимост.

10. Ако система от вектори съдържа нулев вектор, то тя е линейно зависима.

Действително, ако в системата (*) векторът A1 = 0, Това е 1× 0 + 0× A2 + … + 0 × Аn = 0 .

20. Ако система от вектори съдържа два пропорционални вектора, то тя е линейно зависима.

Позволявам A1 = Л×a2. След това 1× A1 –l× A2 + 0× A3 + … + 0× А N= 0.

30. Крайна система от вектори (*) за n ³ 2 е линейно зависима тогава и само ако поне един от нейните вектори е линейна комбинация от останалите вектори на тази система.

Þ Нека (*) е линейно зависим. Тогава има ненулев набор от коефициенти a1, a2, …, an, за който a1× A1 + a2× A2 + … + an× Ан = 0 . Без загуба на общност можем да приемем, че a1 ¹ 0. Тогава съществува A1 = ×a2× A2 + … + ×an× А Н. И така, вектор A1 е линейна комбинация от останалите вектори.

Ü Нека един от векторите (*) е линейна комбинация от останалите. Можем да приемем, че това е първият вектор, т.е. A1 = B2 А2+ … + млрд А N, следователно (–1)× A1 + b2 А2+ … + млрд А N= 0 , т.е. (*) е линейно зависим.

Коментирайте. Използвайки последното свойство, можем да дефинираме линейната зависимост и независимост на безкрайна система от вектори.

Определение 15. Векторна система А1, а2, …, ан , … (**) е наречен Линейно зависим, Ако поне един от неговите вектори е линейна комбинация от някакъв краен брой други вектори. В противен случай се извиква системата (**). Линейно независим.

40. Крайна система от вектори е линейно независима тогава и само ако нито един от нейните вектори не може да бъде линейно изразен по отношение на останалите й вектори.

50. Ако една система от вектори е линейно независима, то всяка нейна подсистема също е линейно независима.

60. Ако някаква подсистема на дадена система от вектори е линейно зависима, то цялата система също е линейно зависима.

Нека са дадени две системи от вектори А1, а2, …, ан , … (16) и В1, В2, …, Вs, … (17). Ако всеки вектор от система (16) може да бъде представен като линейна комбинация от краен брой вектори от система (17), тогава се казва, че системата (17) е линейно изразена чрез система (16).

Определение 16. Двете векторни системи се наричат Еквивалентен , ако всеки от тях е линейно изразен през другия.

Теорема 9 (основна теорема за линейна зависимост).

Нека бъде – две крайни системи от вектори от Л . Ако първата система е линейно независима и линейно изразена през втората, тогава н£s.

Доказателство.Нека се преструваме, че н> С.Съгласно условията на теоремата

(21)

Тъй като системата е линейно независима, равенството (18) Û X1=x2=…=xN= 0.Нека заместим тук изразите на векторите: …+=0 (19). Следователно (20). Условия (18), (19) и (20) очевидно са еквивалентни. Но (18) е изпълнено само когато X1=x2=…=xN= 0.Нека намерим кога равенството (20) е вярно. Ако всичките му коефициенти са нула, то очевидно е вярно. Приравнявайки ги на нула, получаваме система (21). Тъй като тази система има нула, тогава тя

става Тъй като броят на уравненията повече бройнеизвестни, тогава системата има безкрайно много решения. Следователно, той има ненулево X10, x20, …, xN0. За тези стойности равенството (18) ще бъде вярно, което противоречи на факта, че системата от вектори е линейно независима. Така че нашето предположение е погрешно. следователно н£s.

Последица.Ако две еквивалентни системи от вектори са крайни и линейно независими, тогава те съдържат еднакъв брой вектори.

Определение 17. Векторната система се нарича Максимална линейно независима система от вектори Линейно пространство Л , ако е линейно независим, но при добавяне към него произволен вектор от Л , който не е включен в тази система, той става линейно зависим.

Теорема 10. Всякакви две крайни максимални линейно независими системи от вектори от Л Съдържат същия брой вектори.

Доказателствоследва от факта, че всеки две максимални линейно независими системи от вектори са еквивалентни .

Лесно е да се докаже, че всяка линейно независима система от пространствени вектори Л може да се разшири до максимална линейно независима система от вектори в това пространство.

Примери:

1. В множеството от всички колинеарни геометрични вектори всяка система, състояща се от един ненулев вектор, е максимално линейно независима.

2. В множеството от всички копланарни геометрични вектори всеки два неколинеарни вектора съставляват максимална линейно независима система.

3. В множеството от всички възможни геометрични вектори на тримерното евклидово пространство всяка система от три некомпланарни вектора е максимално линейно независима.

4. В множеството на всички полиноми степените не са по-високи от нС реални (комплексни) коефициенти, система от полиноми 1, x, x2, …, xnЕ максимално линейно независим.

5. В множеството от всички полиноми с реални (комплексни) коефициенти примери за максимална линейно независима система са

а) 1, x, x2, … , xn, … ;

б) 1, (1 – х), (1 – х)2, … , (1 – х)Н, ...

6. Набор от размерни матрици М´ не линейно пространство (проверете това). Пример за максимална линейно независима система в това пространство е матричната система E11= , E12 =, …, EМн = .

Нека е дадена система от вектори C1, c2, …, вж (*). Извиква се подсистемата от вектори от (*). Максимално линейно независим Подсистемасистеми ( *) , ако е линейно независим, но при добавяне на всеки друг вектор от тази система към него, той става линейно зависим. Ако системата (*) е крайна, тогава всяка от нейните максимални линейно независими подсистеми съдържа същия брой вектори. (Докажете го сами). Броят на векторите в максималната линейно независима подсистема на системата (*) се нарича Ранг Тази система. Очевидно еквивалентните системи от вектори имат еднакви рангове.

По-долу са дадени няколко критерия за линейна зависимост и съответно линейна независимост на векторните системи.

Теорема. (Необходими и достатъчно условиелинейна зависимост на векторите.)

Една система от вектори е зависима тогава и само тогава, когато един от векторите на системата е линейно изразен чрез останалите на тази система.

Доказателство. Необходимост. Нека системата е линейно зависима. Тогава, по дефиниция, той представя нулевия вектор нетривиално, т.е. има нетривиална комбинация от тази система от вектори, равна на нулевия вектор:

където поне един от коефициентите на тази линейна комбинация не е равен на нула. Позволявам , .

Нека разделим двете страни на предишното равенство на този ненулев коефициент (т.е. умножете по:

Нека означим: , където .

тези. един от векторите на системата се изразява линейно през останалите на тази система и т.н.

Адекватност. Нека един от векторите на системата е линейно изразен чрез други вектори на тази система:

Нека преместим вектора вдясно от това равенство:

Тъй като коефициентът на вектора е равен на , тогава имаме нетривиално представяне на нула чрез система от вектори, което означава, че тази система от вектори е линейно зависима и т.н.

Теоремата е доказана.

Последица.

1. Векторна система векторно пространствое линейно независима тогава и само ако нито един от векторите на системата не е линейно изразен чрез други вектори на тази система.

2. Система от вектори, съдържаща нулев вектор или два равен вектор, е линейно зависим.

Доказателство.

1) Необходимост. Нека системата е линейно независима. Нека приемем обратното и има вектор на системата, който е линейно изразен чрез други вектори на тази система. Тогава според теоремата системата е линейно зависима и стигаме до противоречие.

Адекватност. Нека никой от векторите на системата не е изразен чрез други. Да приемем обратното. Нека системата е линейно зависима, но тогава от теоремата следва, че има вектор на системата, който се изразява линейно чрез други вектори на тази система и отново стигаме до противоречие.

2a) Нека системата съдържа нулев вектор. Да приемем със сигурност, че векторът :. Тогава равенството е очевидно

тези. един от векторите на системата се изразява линейно чрез другите вектори на тази система. От теоремата следва, че такава система от вектори е линейно зависима и т.н.

Обърнете внимание, че този факт може да бъде доказан директно от линейно зависима система от вектори.

Тъй като , следното равенство е очевидно

Това е нетривиално представяне на нулевия вектор, което означава, че системата е линейно зависима.

2b) Нека системата има два равни вектора. Нека за. Тогава равенството е очевидно

Тези. първият вектор се изразява линейно чрез останалите вектори на същата система. От теоремата следва, че тази система е линейно зависима и т.н.

Подобно на предишното, това твърдение може да се докаже директно чрез дефиницията на линейно зависима система. Тогава тази система представя нулевия вектор нетривиално

откъдето следва линейната зависимост на системата.

Теоремата е доказана.

Последица. Система, състояща се от един вектор, е линейно независима тогава и само ако този вектор е различен от нула.