Определя се градиентът на функцията. Градиент на дадена функция. Екстремуми на функция на няколко променливи

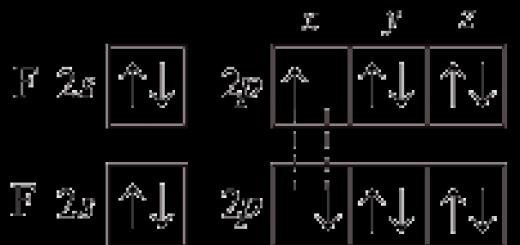
Лекция 15. „Диференциране на функция на няколко променливи”

Градиент на функция на две променливи и производна по посока.

Определение. Градиентна функция

наречен вектор

Както може да се види от дефиницията на градиента на функция, компонентите на градиентния вектор са частните производни на функцията.

Пример. Изчислете градиента на функция

в точка А(2,3).

Решение. Нека изчислим частните производни на функцията.

Най-общо градиентът на функцията има формата:

Нека заместим координатите на точка A(2,3) в изразите за частни производни

Градиентът на функцията в точка A(2,3) има формата:

По подобен начин можем да дефинираме концепцията за градиента на функция от три променливи:

Определение. Градиентна функция на три променливи

наречен вектор

В противен случай този вектор може да се запише по следния начин:

Определениепроизводна по посока.

Нека е дадена функция на две променливи

и произволен вектор

Нека разгледаме увеличението на тази функция, взето по даден вектор

Тези. векторът е колинеарен по отношение на вектора . Дължина на нарастване на аргумента

Производната в определена посока е границата на отношението на нарастването на функция по дадена посока към дължината на нарастването на аргумента, когато дължината на нарастването на аргумента клони към 0.

Формула за изчисляване на производната по посока.

Въз основа на дефиницията на градиента, производната на функцията по отношение на посоката може да се изчисли, както следва.

някакъв вектор. Вектор със същата посока, но единиченнека наречем дължината

Координатите на този вектор се изчисляват, както следва:

От определението за производна по посока, производната по посока може да се изчисли по следната формула:

Дясната страна на тази формула е скаларно произведениедва вектора

Следователно производната на посоката може да бъде представена като следната формула:

От тази формула следват няколко важни свойства на градиентния вектор.

Първото свойство на градиента следва от очевидния факт, че скаларното произведение на два вектора отнема най-висока стойност, когато векторите съвпадат по посока. Второто свойство следва от факта, че скаларното произведение на перпендикулярни вектори е равно на нула. В допълнение, първото свойство предполага геометричното значение на градиента - градиентът е вектор по посока, чиято производна по посока е най-голяма. Тъй като производната по посока определя тангенса на ъгъла на наклон на допирателната към повърхността на функцията, градиентът е насочен по най-големия наклон на допирателната.

Пример 2. За функция (от пример 1)

Изчислете производната на посоката

в точка А(2,3).

Решение. За да изчислите производната на посоката, трябва да изчислите вектора на градиента в определената точка и единичния вектор на посоката (т.е. да нормализирате вектора).

Градиентният вектор е изчислен в пример 1:

Изчисляваме единичния вектор на посоката:

Изчисляваме производната по отношение на посоката:

#2. Функции на максимум и минимум на няколко променливи.

Определение.функция

Има максимум в точка (т.е. при и ), ако

Определение.Точно по същия начин казват, че функцията

Има минимум в точка (т.е. при и ), ако

за всички точки, достатъчно близки до точката и различни от нея.

Максимумът и минимумът на функция се наричат екстремуми на функцията, т.е. казват, че функцията има екстремум в дадена точка, ако тази функция има максимум или минимум в дадена точка.

Например функцията

Има очевиден минимум z = -1 при x = 1 и y = 2.

Има максимум в точката при x = 0 и y = 0.

Теорема.(необходими условия за екстремум).

Ако функцията достигне екстремум при , тогава всяка частична производна от първи ред на z или изчезва за тези стойности на аргумента, или не съществува.

Коментирайте.Тази теорема не е достатъчна за изучаване на въпроса за екстремните стойности на функция. Можем да дадем примери за функции, които имат нулеви частични производни в някои точки, но нямат екстремум в тези точки.

Пример.Функция, която има нулеви частични производни, но няма екстремум.

Наистина:

Достатъчни условия за екстремум.

Теорема.Нека в някаква област, съдържаща точката , функцията има непрекъснати частни производни до трети ред включително; Нека освен това точката е критична точка на функцията, т.е.

Тогава когато ,

Пример 3.2. Разгледайте максималните и минималните функции

Да намерим критичните точки, т.е. точки, в които първите частни производни са нула или не съществуват.

Първо, изчисляваме самите частни производни.

Приравняваме частните производни на нула и решаваме следната система от линейни уравнения

Умножете второто уравнение по 2 и го добавете към първото. Резултатът е уравнение само в y.

Намираме и заместваме в първото уравнение

Да се трансформираме

Следователно точка () е критична.

Нека изчислим вторите производни от втори ред и заместим координатите на критичната точка в тях.

В нашия случай няма нужда да заместваме стойностите на критичните точки, тъй като вторите производни са числа.

В резултат на това имаме:

Следователно намерената критична точка е точка на екстремум. Освен това, тъй като

тогава това е минималната точка.

Градиент функции– векторна величина, чието определяне е свързано с определянето на частните производни на функцията. Посоката на градиента показва пътя на най-бързия растеж на функцията от една точка на скаларното поле до друга.

Инструкции

1. За решаване на проблема с градиента на функция се използват методи на диференциално смятане, а именно намиране на частични производни от първи ред по отношение на три променливи. Предполага се, че самата функция и всички нейни частни производни притежават свойството на непрекъснатост в областта на дефиниране на функцията.

2. Градиентът е вектор, чиято посока показва посоката на най-бързото нарастване на функцията F. За целта на графиката се избират две точки M0 и M1, които са краищата на вектора. Големината на градиента е равна на скоростта на нарастване на функцията от точка M0 до точка M1.

3. Функцията е диференцируема във всички точки на този вектор, следователно проекциите на вектора върху координатните оси са неговите частични производни; Тогава формулата на градиента изглежда така: grad = (?F/?x) i + (?F/?y) j + (?F/?z) k, където i, j, k са координатите на единичния вектор . С други думи, градиентът на функция е вектор, чиито координати са нейните частни производни grad F = (?F/?х, ?F/?y, ?F/?z).

4. Пример 1. Нека е дадена функцията F = sin(x z?)/y. Изисква се да се открие градиентът му в точката (?/6, 1/4, 1).

5. Решение.Определяме частните производни по всяка променлива: F'_y = sin(х z?) (-1) 1/(y?); '_z = 1/y cos(x z?) 2 x z.

6. Заменете известните координатни стойности на точката: F’_x = 4 сos(?/6) = 2 ?3; F’_y = sin(?/6) (-1) 16 = -8; F’_z = 4 cos(?/6) 2 ?/6 = 2 ?/?3.

7. Приложете формулата за градиент на функцията: grad F = 2 ?3 i – 8 j + 2 ?/?3 k.

8. Пример 2. Намерете координатите на градиента на функцията F = y arсtg (z/x) в точка (1, 2, 1).

9. Решение.F'_x = 0 arctg (z/x) + y (arctg(z/x))'_x = y 1/(1 + (z/x)?) (-z/x?) = -y z/ (x? (1 + (z/x)?)) = -1;F'_y = 1 аrсtg(z/х) = аrсtg 1 = ?/4;F'_z = 0 аrсtg(z/х) + y (arсtg(z/х))'_z = y 1/(1 + (z/х)?) 1/х = y/(х (1 + (z/х)?)) = 1.град = (- 1, ?/4, 1).

Градиентът на скаларното поле е векторна величина. По този начин, за да го намерите, е необходимо да се определят всички компоненти на съответния вектор, въз основа на познаването на разделението на скаларното поле.

Инструкции

1. Прочети в някой учебник по висша математика какво е градиент на скаларно поле. Както знаете, това векторно количество има посока, характеризираща се с максимална скоростзатихване на скаларната функция. Тази интерпретация на тази векторна величина е оправдана от израза за определяне на нейните компоненти.

2. Не забравяйте, че всеки вектор се определя от величините на неговите компоненти. Компонентите на вектора всъщност са проекции на този вектор върху една или друга координатна ос. Така, ако се счита триизмерно пространство, тогава векторът трябва да има три компонента.

3. Запишете как се определят компонентите на вектор, който е градиент на дадено поле. Всички координати на такъв вектор са равни на производната на скаларния потенциал по отношение на променливата, чиято координата се изчислява. Тоест, ако трябва да изчислите компонента „x“ на вектора на градиента на полето, тогава трябва да диференцирате скаларната функция по отношение на променливата „x“. Моля, обърнете внимание, че производната трябва да е частична. Това означава, че по време на диференцирането останалите променливи, които не участват в него, трябва да се считат за константи.

4. Напишете израз за скаларното поле. Както е известно, този термин предполага само скаларна функция на няколко променливи, които също са скаларни величини. Броят на променливите на една скаларна функция е ограничен от размерността на пространството.

5. Диференцирайте скаларната функция отделно по отношение на всяка променлива. В резултат на това ще получите три нови функции. Запишете произволна функция в израза за градиентния вектор на скаларното поле. Всяка от получените функции всъщност е индикатор за единичен вектор на дадена координата. Така крайният вектор на градиента трябва да изглежда като полином с експоненти под формата на производни на функцията.

Когато разглеждаме въпроси, включващи градиентно представяне, обичайно е да мислим за функциите като за скаларни полета. Поради това е необходимо да се въведе подходящо обозначение.

Ще имаш нужда

– бум;
- химилка.

Инструкции

1. Нека функцията е зададена с три аргумента u=f(x, y, z). Частичната производна на функция, например по отношение на x, се определя като производната по отношение на този аргумент, получена чрез фиксиране на останалите аргументи. Подобно за други аргументи. Нотацията за частичната производна е записана във формата: df/dx = u’x ...

2. Общият диференциал ще бъде равен на du=(дf/дх)dx+ (дf/дy)dy+(дf/дz)dz. Частичните производни могат да се разбират като производни по посоките на координатните оси. Следователно възниква въпросът за намиране на производната по отношение на посоката на даден вектор s в точката M(x, y, z) (не забравяйте, че посоката s се определя от единичния вектор s^o). В този случай вектор-диференциалът на аргументите (dx, dy, dz) = (дscos(алфа), dscos(бета), dscos(гама)).

3. Гледайки гледката пълен диференциал du, можем да заключим, че производната по посока s в точка M е равна на: (дu/дs)|M=((дf/дх)|M)сos(alpha)+ ((дf/дy)|M) сos (бета) +((df/dz)|M) cos(гама). Ако s= s(sx,sy,sz), тогава посоката е косинус (cos(алфа), cos(бета), cos(гама)) се изчисляват (виж фиг. 1а).

4. Дефиницията на производната по посока, разглеждайки точка M като променлива, може да бъде пренаписана под формата на скаларно произведение: (дu/дs)=((дf/дх, дf/дy,дf/дz), (cos(алфа) , cos(бета), cos (гама)))=(град u, s^o). Този изразще бъде обективен за скаларно поле. Ако една функция се разглежда лесно, тогава gradf е вектор с координати, съвпадащи с частните производни f(x, y, z).gradf(x,y,z)=((df/dh, df/dy, df/ dz )=)=(df/dx)i+(df/dy)j +(df/dz)k. Тук (i, j, k) са единичните вектори на координатните оси в правоъгълна декартова координатна система.

5. Ако използваме Хамилтоновия диференциален векторен оператор, тогава gradf може да се запише като умножение на този векторен оператор по скалара f (виж Фиг. 1b). От гледна точка на връзката между gradf и производната по посока, равенството (gradf, s^o)=0 е приемливо, ако тези вектори са ортогонални. Следователно gradf често се определя като посоката на най-бързата метаморфоза на скаларното поле. И от гледна точка на диференциалните операции (gradf е една от тях), свойствата на gradf точно повтарят свойствата на диференциращите функции. По-специално, ако f=uv, тогава gradf=(vgradu+u gradv).

Видео по темата

ГрадиентТова е инструмент, който в графичните редактори запълва силует с плавен преход от един цвят към друг. Градиентможе да придаде на силует резултат от обем, да имитира осветление, отблясъци от светлина върху повърхността на обект или резултат от залез на фона на снимка. Този инструмент се използва широко, така че за обработка на снимки или създаване на илюстрации е много важно да се научите как да го използвате.

Ще имаш нужда

Компютър, графичен редактор Adobe Photoshop, Corel Draw, Paint.Net или друг.

Инструкции

1. Отворете изображение в програмата или вземете ново. Направете силует или изберете желаната област в изображението.

2. Включете инструмента за градиент в лентата с инструменти на графичния редактор. Поставете курсора на мишката върху точката в избраната област или силует, където ще започне първият цвят на градиента. Щракнете и задръжте левия бутон на мишката. Преместете курсора до точката, където искате градиентът да се промени до крайния цвят. Пуснете левия бутон на мишката. Избраният силует ще бъде запълнен с градиентно запълване.

3. ГрадиентМожете да зададете прозрачност, цветове и тяхното съотношение в определена точка от запълването. За да направите това, отворете прозореца за редактиране на градиента. За да отворите прозореца за редактиране във Photoshop, щракнете върху примера за градиент в панела с опции.

4. Прозорецът, който се отваря, показва наличните опции за градиентно запълване под формата на примери. За да редактирате една от опциите, изберете я с щракване на мишката.

5. В долната част на прозореца се показва пример за градиент под формата на широка скала, върху която са разположени плъзгачи. Плъзгачите показват точките, в които градиентът трябва да има зададени съпоставки, а в интервала между плъзгачите цветът равномерно преминава от цвета, посочен в първата точка, към цвета на 2-рата точка.

6. Плъзгачите, разположени в горната част на скалата, задават прозрачността на градиента. За да промените прозрачността, щракнете върху желания плъзгач. Под скалата ще се появи поле, в което да въведете необходима степенпрозрачност като процент.

7. Плъзгачите в долната част на скалата задават цветовете на градиента. Като щракнете върху един от тях, ще можете да изберете желания цвят.

8. Градиентможе да има няколко преходни цвята. За да зададете друг цвят, щракнете върху свободното място в долната част на скалата. На него ще се появи друг плъзгач. Придайте му необходимия цвят. Скалата ще покаже пример за градиента с още една точка. Можете да местите плъзгачите, като ги задържите с левия бутон на мишката, за да постигнете желаната комбинация.

9. ГрадиентПредлагат се в няколко вида, които могат да придадат форма на плоски силуети. Например, за да придадете на кръг формата на топка, се използва радиален градиент, а за да придадете формата на конус, се използва конусообразен градиент. За да придадете на повърхността илюзия за изпъкналост, можете да използвате огледален градиент, а градиент с форма на диамант може да се използва за създаване на акценти.

Видео по темата

от училищен курсМатематиците знаят, че вектор в равнина е насочен сегмент. Началото и краят му имат две координати. Координатите на вектора се изчисляват чрез изваждане на началните координати от крайните координати.

Концепцията за вектор може да се разшири до n-мерно пространство (вместо две координати ще има n координати).

Градиент grad z на функцията z = f(x 1, x 2, ...x n) е векторът на частните производни на функцията в точка, т.е. вектор с координати.

Може да се докаже, че градиентът на функция характеризира посоката на най-бързо нарастване на нивото на функция в дадена точка.

Например за функцията z = 2x 1 + x 2 (виж Фигура 5.8), градиентът във всяка точка ще има координати (2; 1). Можете да го построите на самолет различни начини, приемайки всяка точка за начало на вектора. Например, можете да свържете точка (0; 0) с точка (2; 1), или точка (1; 0) с точка (3; 1), или точка (0; 3) с точка (2; 4), или така нататък. (Вижте Фигура 5.8). Всички вектори, конструирани по този начин, ще имат координати (2 – 0; 1 – 0) =
= (3 – 1; 1 – 0) = (2 – 0; 4 – 3) = (2; 1).

От фигура 5.8 ясно се вижда, че нивото на функцията нараства в посока на градиента, тъй като построените линии на ниво съответстват на стойностите на нивото 4> 3> 2.

Фигура 5.8 - Градиент на функция z = 2x 1 + x 2

Нека разгледаме друг пример - функцията z = 1/(x 1 x 2). Градиентът на тази функция вече няма да бъде винаги еднакъв в различни точки, тъй като нейните координати се определят от формулите (-1/(x 1 2 x 2); -1/(x 1 x 2 2)).

Фигура 5.9 показва линиите на нивото на функцията z = 1/(x 1 x 2) за нива 2 и 10 (правата линия 1/(x 1 x 2) = 2 е обозначена с пунктирана линия, а правата линия
1/(x 1 x 2) = 10 – плътна линия).

Фигура 5.9 - Градиенти на функцията z = 1/(x 1 x 2) в различни точки

Вземете например точката (0,5; 1) и изчислете градиента в тази точка: (-1/(0,5 2 *1); -1/(0,5*1 2)) = (-4; - 2). Обърнете внимание, че точката (0,5; 1) лежи на линията на нивото 1/(x 1 x 2) = 2, защото z = f(0,5; 1) = 1/(0,5*1) = 2. За да изобразите вектора ( -4; -2) на фигура 5.9 свързваме точката (0,5; 1) с точката (-3,5; -1), т.к.
(-3,5 – 0,5; -1 - 1) = (-4; -2).

Нека вземем друга точка на същата линия на ниво, например точка (1; 0,5) (z = f(1; 0,5) = 1/(0,5*1) = 2). Нека изчислим градиента в тази точка
(-1/(1 2 *0,5); -1/(1*0,5 2)) = (-2; -4). За да го изобразим на фигура 5.9, свързваме точката (1; 0.5) с точката (-1; -3.5), защото (-1 - 1; -3.5 - 0.5) = (-2; - 4).

Нека вземем друга точка на същата линия на ниво, но само сега в неположителна координатна четвърт. Например точка (-0,5; -1) (z = f(-0,5; -1) = 1/((-1)*(-0,5)) = 2). Градиентът в тази точка ще бъде равен на
(-1/((-0,5) 2 *(-1)); -1/((-0,5)*(-1) 2)) = (4; 2). Нека го изобразим на фигура 5.9, като свържем точката (-0,5; -1) с точката (3,5; 1), защото (3,5 – (-0,5); 1 – (-1)) = (4 ; 2).

1 0 Градиентът е насочен нормално към равната повърхност (или към линията на нивото, ако полето е плоско).

2 0 Градиентът е насочен към увеличаване на полевата функция.

3 0 Модулът на градиента е равен на най-голямата производна по посока в дадена точка от полето:

Тези свойства осигуряват инвариантна характеристика на градиента. Казват, че векторът gradU показва посоката и големината на най-голямата промяна в скаларното поле в дадена точка.

Забележка 2.1.Ако функцията U(x,y) е функция на две променливи, тогава векторът

лежи в окси равнината.

Нека U=U(x,y,z) и V=V(x,y,z) са диференцируеми в точката M 0 (x,y,z) функции. Тогава важат следните равенства:

а) grad()= ; б) град(УВ)=ВградУ+УградВ;

в) grad(U V)=gradU gradV; г) г) град = , V ;

д) gradU( = gradU, където , U=U() има производна по отношение на .

Пример 2.1.Дадена е функцията U=x 2 +y 2 +z 2. Определете градиента на функцията в точка M(-2;3;4).

Решение.Съгласно формула (2.2) имаме

Повърхнините на нивото на това скаларно поле са семейството от сфери x 2 +y 2 +z 2 , векторът gradU=(-4;6;8) е нормалният вектор на равнините.

Пример 2.2.Намерете градиента на скаларното поле U=x-2y+3z.

Решение.Съгласно формула (2.2) имаме

Повърхнините на нивото на дадено скаларно поле са равнини

x-2y+3z=C; векторът gradU=(1;-2;3) е нормалният вектор на равнините от това семейство.

Пример 2.3.Намерете най-голямата стръмност на издигането на повърхността U=x y в точка M(2;2;4).

Решение.Ние имаме:

Пример 2.4.Намерете единичния нормален вектор към повърхността на нивото на скаларното поле U=x 2 +y 2 +z 2 .

Решение.Нивелираните повърхности на дадена скаларна полева сфера x 2 +y 2 +z 2 =C (C>0).

Градиентът е насочен нормално към равната повърхност, така че

Определя нормалния вектор към повърхността на нивото в точка M(x,y,z). За единичен нормален вектор получаваме израза

Пример 2.5.Намерете градиента на полето U=, където и са постоянни вектори, r е радиус векторът на точката.

Решение.Позволявам

Тогава: . По правилото за диференциране на детерминантата получаваме

следователно

Пример 2.6.Намерете градиента на разстоянието, където P(x,y,z) е изследваната точка на полето, P 0 (x 0,y 0,z 0) е някаква фиксирана точка.

Решение.Имаме единичен вектор на посоката.

Пример 2.7.Намерете ъгъла между градиентите на функциите в точката M 0 (1,1).

Решение.Намираме градиентите на тези функции в точката M 0 (1,1), имаме

; Ъгълът между gradU и gradV в точка M 0 се определя от равенството

Следователно =0.

Пример 2.8.Намерете производната по посока, на която е равен радиус векторът

Решение.Намерете градиента на тази функция:

Замествайки (2.5) в (2.4), получаваме

Пример 2.9.Намерете в точка M 0 (1;1;1) посоката на най-голямата промяна в скаларното поле U=xy+yz+xz и величината на тази най-голяма промяна в тази точка.

Решение.Посоката на най-голямото изменение на полето се обозначава с вектора grad U(M). Намираме го:

А това означава... Този вектор определя посоката на най-голямото увеличение на това поле в точка M 0 (1;1;1). Големината на най-голямата промяна на полето в тази точка е равна на

Пример 3.1.Намерете векторните линии на векторното поле, където е постоянен вектор.

Решение.Имаме така че

Умножете числителя и знаменателя на първата дроб по x, на втората по y, на третата по z и добавете член по член. Използвайки свойството на пропорциите, получаваме

Следователно xdx+ydy+zdz=0, което означава

x 2 +y 2 +z 2 =A 1, A 1 -const>0. Сега като умножим числителя и знаменателя на първата дроб (3.3) по c 1, втората по c 2, третата по c 3 и добавим член по член, получаваме

Където от 1 dx+c 2 dy+c 3 dz=0

И следователно с 1 x+c 2 y+c 3 z=A 2 . A 2 -const.

Необходимите уравнения на векторни прави

Тези уравнения показват, че векторните линии се получават от пресичането на сфери с общ център в началото с равнини, перпендикулярни на вектора. От това следва, че векторните прави са окръжности, чиито центрове са на права линия, минаваща през началото по посока на вектор c. Равнините на окръжностите са перпендикулярни на посочената права.

Пример 3.2.Намерете линията на векторното поле, минаваща през точката (1,0,0).

Решение. Диференциални уравнениявекторни линии

Следователно имаме. Решаване на първото уравнение. Или ако въведем параметъра t, тогава ще имаме В този случай уравнението приема формата или dz=bdt, откъдето z=bt+c 2.

Разгледайте формулата за производната на скаларна функция u по посока λ

Вторите фактори са проекции на единичния вектор, насочен по протежение на лъча λ.

Да вземем вектор, чиито проекции върху координатните оси ще бъдат стойностите на частичните производни в избраната точка P(x, y, z).

Този вектор се нарича градиент на функцията u (x, y, z) и се означава градиент или

Определение. Градиентът на функция u(x, y, z) е вектор, чиито проекции са стойностите на частните производни на тази функция, т.е.

Производната на функция в дадена посока е равна на скаларното произведение на градиента на функцията и единичния вектор на тази посока.

Разширявайки скаларното произведение, получаваме

където φ е ъгълът между вектора дипломирани лъч λ.

Достига най-голяма стойност

Така че в дадено TR има най-голяма стойност на производната, а посоката grad u съвпада с посоката на лъча, излизащ от TR, по който функцията се променя най-бързо.

Нека установим връзка между посоката на градиента на функцията и повърхностите на нивото на скаларното поле.

Теорема. Градиентът на функцията u (x,y,z) във всяка точка съвпада с нормалата към повърхността на нивото на скаларното поле, минаващо през тази точка.

Доказателство. Нека изберем произволно t P 0 (x 0, y 0, z 0).

Уравнение на повърхността

преминаващо ниво

т.е. ще бъде u(x,y,z)= ,

u 0 = u (x 0, y 0, z 0)

Уравнението на нормалата към тази повърхност ще бъде

От това следва, че посоката нормален вектор, който има проекции , е градиентът на функцията u (x, y, z) в t P 0 и т.н.

По този начин градиентът във всяка точка е перпендикулярен на допирателната равнина към равнинната повърхност, преминаваща през нея тази точка, т.е. неговата проекция върху тази равнина е нула.

Следователно:Производната във всяка посока, допирателна към повърхността на нивото, минаваща през дадена точка, е равна на нула.

Основни свойства на градиентната функция:

2) град , където C – конст