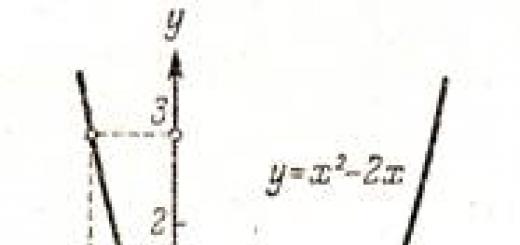На първо място, трябва да запомните, че детерминанти съществуват само за матрици квадратен вид, защото няма детерминанти за матрици от други типове. В теорията на системите линейни уравненияи в някои други въпроси е удобно да се използва понятието детерминант, или детерминант.

Изчисляване на детерминанти

Помислете за произволни четири числа, записани под формата на матрица от две в редове и две в колони, Определящоили детерминант, съставен от числата в тази таблица, е числото реклама-пр.н.е, се обозначава по следния начин: Такава детерминанта се нарича детерминанта от втори ред, тъй като за нейното компилиране е взета таблица от два реда и две колони. Числата, които съставляват определителя, се наричат ​​негови елементи; същевременно казват, че елементите аИ дгрим главен диагоналдетерминанта и елементите bИ ° Снеговият страничен диагонал. Вижда се, че детерминантата е равна на разликата на произведенията на двойки елементи, разположени на неговия главен и вторичен диагонал. Детерминантата на третия и всеки друг ред е приблизително една и съща, а именно: Да приемем, че имаме квадратна матрица. Детерминантата на следната матрица е следният израз: a11a22a33 + a12a23a31 + a13a21a32 - a11a23a32 - a12a21a33 - a13a22a31. Както можете да видите, изчислява се доста лесно, ако запомните определена последователност. С положителен знак са главният диагонал и триъгълниците, образувани от елементите, които имат страна, успоредна на главния диагонал, в случая това са триъгълници a12a23a31, a13a21a32.

Страничният диагонал и успоредните на него триъгълници са с отрицателен знак, т.е. a11a23a32, a12a21a33. По този начин могат да бъдат намерени детерминанти от всякакъв ред. Но има случаи, когато този метод става доста сложен, например, когато има много елементи в матрицата и за да изчислите детерминантата, трябва да отделите много време и внимание.

Има още лесен начинизчисляване на детерминанта от n-ти ред, където n2. Нека се съгласим да наричаме минор на всеки елемент Aij от матрица от n-ти ред детерминантата, съответстваща на матрицата, която се получава от матрицата в резултат на изтриването на i-тия ред и j-тата колона (редът и колоната в пресечната точка на който стои елементът Aij). Малкият елемент Aij ще бъде обозначен със символа. В тази нотация горният индекс обозначава номера на реда, долният индекс номера на колоната, а лентата отгоре Мозначава, че посоченият ред и колона са зачеркнати. Детерминанта на ред n, съответстващо на матрицата, наричаме числото, равно на и означено със символа .

Теорема 1.1Какъвто и да е номерът на ред i (i = 1, 2..., n), за детерминанта от n-ти ред формулата е валидна

Наречен разширяване на тази детерминанта в i-ти ред . Подчертаваме, че в тази формула степента, до която се повишава числото (-1), равно на суматаномера на реда и колоната, в пресечната точка на които се намира елементът Aij.

Теорема 1.2Какъвто и да е номерът на колона j (j = 1, 2..., n), формулата е валидна за детерминанта от n-ти ред

Наречен разширение на тази детерминанта в j-та колона.

ГЛАВА I. ЕЛЕМЕНТИ НА ТЕОРИЯТА НА ДЕТЕРМИНАНТИТЕ

Теорията на детерминантите възниква през 18 век във връзка с проблема за решаване на системи от линейни алгебрични уравнения. Впоследствие обаче детерминантите намират приложение в голямо разнообразие от клонове на математиката, по-специално във векторната алгебра, аналитична геометрияИ математически анализ.

§ 1. Детерминанти от втори ред

Да разгледаме система от две линейни алгебрични уравнения с две неизвестни и

,

Където
- числени коефициенти на системата (1).

Таблица, съставена от коефициентите на тази система

,

се нарича коефициентна матрица на система (1).

На матрица (2) е присвоено число, наречено детерминанта на матрицата
, което се обозначава
и се изчислява по правилото, т.е. детерминантът от втори ред е равен на разликата между произведението на елементите на главния диагонал и вторичния диагонал на матрицата. Детерминантата на матрицата се обозначава по следния начин

.

Нека намерим решение на система (1). Лесно е да се провери, че се изразява чрез коефициентите на системата, както следва (приемаме, че
):

;
.

Виждаме, че знаменателят на изразите за и съдържа детерминантата, а числителят също съдържа детерминантите, които означаваме с
и съответно, т.е.

,
.

Лесно се вижда, че детерминантата се получава от детерминантата , ако в него заместим колоната с коефициенти за (първата колона) с колона със свободни членове, а детерминантата
- ако втората колона на детерминантата се замени с колона със свободни членове. Тогава решението на система (4) може да се запише по следния начин:

,
(
).

Тези формули се наричат Формули на Крамер . И така, за да намерим решение на линейното алгебрична системаот втори ред е достатъчно да се преброят трите детерминанти , , и да се формира тяхното отношение.

Пример 1 . Намерете решение на линейна алгебрична система с помощта на формулите на Крамер

.

Решение . Нека изчислим детерминантите , , :

Според формулите на Крамер

.

Така,

.

Основни свойства на детерминантите от втори ред

1. Детерминантата няма да се промени, ако нейните редове се разменят със съответните колони, т.е.

2. При пренареждане на два реда (колони) детерминантата сменя знака на противоположния, т.е.

3. Общият множител на всички елементи на ред (колона) може да бъде изведен отвъд знака на детерминантата, т.е. , Например,

4. Детерминанта с еднакви редове (колони) е равна на нула, т.е.

5. Детерминанта с нулев ред (колона) е равна на нула, т.е. Например,

6. Ако към елементите на ред (колона) добавим съответните елементи на друг ред (колона), умножени по същото число, то детерминантата няма да се промени, т.е. Например

Всички тези свойства са доказани директно изчислениелявата и дясната част на изразите, включени в разглежданите равенства. Нека докажем, например, свойство 6.

За да направим това, изчисляваме детерминантата от лявата страна на равенството:

§ 2. Детерминанти от трети ред.

Да разгледаме квадратна матрица (таблица) от трети ред

.

Ако задраскате който и да е ред или колона в тази матрица, тогава останалите елементи образуват квадратна матрица от втори ред. От квадратна матрица от трети ред могат да се получат девет квадратни матрици от втори ред. Нека въведем няколко нови концепции.

Определение 1 . Второстепенен елемент матриците от трети ред са детерминантата на матрица от втори ред, която се получава от дадена матрица чрез изтриване -ти ред и та колона, т.е. редове и колони, в пресечната точка на които стои този елемент.

Второстепенният елемент на елемент се обозначава със символа
. Например второстепенният елемент
матрица (1) е детерминантата

.

Определение 2. Алгебрично събиране на елемент матриците от трети ред наричат ​​числото, равно на произведението на второстепенния на този елемент по
.

В противен случай: алгебричното допълнение на елемент е второстепенно, ако сумата от индексите
четно и второстепенно, взето с обратен знак, ако сборът от индексите е нечетен. Означава се алгебричното допълнение на елемент
, т.е. а-приорен
.

Пример 1. Изчисляване на алгебрични допълнения
И
матрици

.

;
.

Коментирайте . Можем също да говорим за минори и алгебрични допълнения на елементи от матрица от втори ред, ако под детерминанта на матрица, състояща се от един елемент (матрица от първи ред), имаме предвид число, равно на този елемент.

Определение 3. Определящо (детерминант ) квадратна матрица от трети ред (детерминанта от трети ред ) наричаме числото, равно на сумата от произведенията по двойки на елементите от първия ред и техните алгебрични допълнения. Тези. по дефиниция имаме

.

Пример 2 . Изчислете детерминанта на матрица

Коментирайте . Ако заместим изрази на алгебрични добавки чрез матрични елементи във формула (3), получаваме

В тази формула има шест члена и всеки от тях е продукт на три матрични елемента: по един от всеки ред и по един от всяка колона; три термина са включени със знак „+“, а три със знак „-“. Във висшите курсове по алгебра формула (4) се приема като дефиниция на детерминанта от трети ред.

§ 3. Основни свойства на детерминанти от 3-ти ред.

Лесно е да се провери, че всички свойства на детерминанти от 2-ри ред са валидни и за детерминанти от 3-ти ред. Но като по-сложен обект детерминантите от трети ред имат и допълнителни свойства. Нека формулираме и докажем напълно всички свойства.

1. Детерминантата не се променя, ако нейните редове се разменят със съответните колони, т.е.

.

Доказва се чрез разлагане на всяка детерминанта на елементите от първия ред. В резултат на това получаваме същия израз.

2. Детерминантата е равна на сумата от произведенията по двойки на елементи от всеки ред (колона) с техните алгебрични допълнения.

Нека докажем, например, равенството

Следователно, .

Това свойство се нарича свойство за разлагане на елемент на ред или колона.

3. При пренареждане на два реда детерминантата сменя знака на противоположния.

Доказателство . Нека първият и третият ред на матрица от трети ред са пренаредени. Нека покажем това

Развивайки детерминантата от лявата страна на равенството (3) в елементите на първия ред, получаваме

Разширявайки детерминантата от дясната страна на това равенство в елементите на третия ред, получаваме

тези. същият израз, но с обратен знак.

4. Детерминанта с два еднакви реда (колони) е равна на нула.

Доказателство . Нека е детерминанта на матрица с два еднакви реда. Ако тези редове се пренаредят, детерминантата трябва да промени знака. Но тъй като низовете са еднакви, детерминантата няма да се промени. Тези. ние имаме
, където
или

5. Ако всички елементи на който и да е ред от детерминантата се умножат по числото K, тогава цялата детерминанта ще бъде умножена по това число.

Доказателство . Нека да покажем например това

.

Нека разложим по елементи от втория ред. Тогава лява странаравенството може да се запише така:

където е детерминантата на матрицата.

Това свойство понякога се формулира по следния начин: общият фактор на всички елементи на низа може да бъде взет отвъд знака на детерминантата.

6. Детерминанта, чиито съответни елементи от два реда са пропорционални, е равна на нула.

Доказателство . Нека например елементите на третия ред са пропорционални на елементите на първия, т.е.

След това, използвайки свойство 5 и след това 4, имаме

7. Детерминанта, в която всички елементи на който и да е ред са сбор от два члена, е равна на сбора от два детерминанта, получени от дадения чрез замяна на елементите на въпросния ред съответно с първия и втория член.

Доказателство . нека например

8.Детерминантата не се променя, ако има елементиредовете добавят съответните елементи от всеки друг ред, умножени по общ множител

Доказателство . Нека добавим например към елементите на първия ред съответните елементи на третия ред, умножени по същото число . Тогава по свойство 7 и след това по свойство 6 ще имаме

9. Теорема за заместване. Сумата от произведенията на алгебрични добавки на произволен низ от числа ,И е равна на детерминантата на матрицата, получена от тази чрез заместване на разглежданите елементи съответно с числата , и .

Доказателство . Помислете например за сумата от продуктите на елементите от първия ред от алгебричните допълнения на елементите от третия ред:

и определящо

.

Разширявайки го в елементите на първия ред, получаваме , т.е. оригинален израз.

10. Сумата от произведенията на елементите на всеки ред и алгебричните допълнения на друг ред е нула.

Доказателство . Помислете например за сумата от продуктите на елементите от третия ред:

По теоремата за заместване (свойство 9) този израз е равен на детерминантата, чийто трети ред съдържа числата , И
:

.

Тази детерминанта е равна на нула по Свойство 4, тъй като първият и третият ред са еднакви.

Изброените свойства, особено свойство 8, позволяват значително да се опрости изчисляването на детерминантата, по-специално да се намали изчисляването на детерминанта от трети ред до изчисляването на една детерминанта от втори ред, вместо три.

Пример . Изчислителна детерминанта

Първо, отбелязваме, че елементите от втората колона имат общ коефициент 2, а елементите от третия ред имат общ коефициент 3. Следователно, като вземем тези фактори отвъд знака на детерминантата, получаваме

.

Сега като добавим третия ред към първия, имаме

.

Развивайки този детерминант в елементи от първия ред, в който само един елемент е различен от нула, получаваме

.

§ 4. Детерминанти от по-високи разряди

Детерминанти от по-високи порядъци, т.е. четвърти, пети и т.н., се определят с помощта на детерминанти от по-нисък порядък по точно същия начин, както беше дефиниран детерминантът от трети порядък.

Така детерминантата от четвърти ред е равна по дефиниция

,

където ,, и
са елементите на първия ред и
, ,
И
са съответните им алгебрични добавки. Минори и алгебрични добавки се дефинират точно по същия начин, както за детерминанти от трети ред. По този начин изчисляването на детерминанта от четвърти ред се свежда до изчисляване на четири детерминанти от трети ред.

Детерминанта на реда на-приорен

.

Както се вижда, детерминантата н- th редът се определя чрез н детерминанти н-1 ред, всеки от тях се определя чрез
детерминант н-2 и т.н. Привеждайки разширението до детерминанти от 2-ри ред и изчислявайки ги, откриваме, че детерминантата н- ти ред е алгебрична сума н! сположени.

Всички формулирани и доказани свойства за детерминанти от трети ред са валидни и за детерминанти
-та поръчка. И те се доказват по същия начин.

За да изчислим детерминантите на реда, използваме свойство 8. Използвайки това свойство, гарантираме, че в един от редовете или в една от колоните всички елементи с изключение на един са равни на нула. И така, изчисляване на детерминантата - от трети ред може да се сведе до изчисляване на единична детерминанта на реда.

Пример . Изчислете детерминанта от пети ред

Забелязваме, че в третата колона два елемента са равни на нула. Можете да получите още два нулеви елемента в тази колона, ако добавите пети ред към втория и четвъртия ред, умножени съответно по 3 и „-4“. Тогава получаваме

.

По този начин

За да изчислите получения детерминант от 4-ти ред, добавете към първия, третия и четвъртия ред втория ред, умножен съответно по 2, -3, -2. Получаваме

Сега като разширим детерминантата в елементите на първата колона, получаваме (като първо извадим фактора „-10“ за елементите на третия ред отвъд знака на детерминантата), че

Добавяйки трети ред към първия ред, имаме

Коментирайте . Има и друга дефиниция на детерминантата на матрицата на реда н : това е сумата от всички възможни произведения на елементи, взети по един от всеки ред, по един от всяка колона и подписани според определено правило. Можете да научите повече за теорията на детерминантите, например, от книгата на A.G. Курош „Курс по висша алгебра“.

§5. Изследване и решаване на системи от линейни алгебрични уравнения

Да разгледаме система от линейни алгебрични уравнения от трети ред

Елиминиране на променливите една по една , И , да преминем към формулите; не може да се изчисли, тъй като детерминантата на матрицата A е означена с detA. Определящон-...

Линейните проблеми, използващи теорията на матриците, са свързани с апарата на така наречените детерминанти, който е много ценен от гледна точка на широчината на приложения към теоретичните въпроси.

1. Насочващи съображения.

Нека разгледаме в общ изгледсистема от две линейни уравнения с две неизвестни

Нека приемем, че системата има решение и двойката x, y представлява решението, така че и двете уравнения вече са се превърнали в истински равенства. Нека умножим двете страни на първото равенство по второто и да извадим. Получаваме

Сега нека умножим първото равенство по второто и го съберем. Получаваме

Нека се преструваме, че. Тогава

Така, ако приемем, че решение съществува, успяхме да го намерим. Сега имаме алтернатива - или решението съществува и тогава е дадено с формули (2), или решението не съществува. За да се отървете от втората възможност, трябва само да установите, че формулите (2) наистина дават решение на системата, за което трябва да замените x и y от (2) в система (1). Хайде да го направим:

Виждаме, че и двете уравнения са станали истински равенства.

Ако иначе разсъжденията ни не доведат до пълен резултат, засега ще оставим този случай настрана.

Във формули (2) знаменателят е един и същ. Числителите са много подобни по форма на знаменателя.

Има специално име за израза

матрична детерминанта и специална нотация:

Използвайки нотация за детерминанти, формули (2) са записани във формата

Прилагайки, например, тези формули за решаване на системата

Разбира се, понятието детерминанта не би било необходимо, ако говорим само за системи от две уравнения с две неизвестни. Резултатът може да се обобщи за линейни системи от уравнения с неизвестни.

Нека разгледаме друг случай: нека системата е дадена

Нека веднага изключим неизвестните y и . За да направите това, умножете първото уравнение по второто по третото по и добавете. Получаваме

Ясно е, че коефициентите на y и z са равни на нула.

Коефициентът при играе тук същата роля, както при системите от втори ред. Нарича се детерминанта на матрицата и се означава:

В тази нотация, ако детерминантата не е нула,

по същия начин,

Нашето заключение има смисъл при предположението, че съществува решение. Въпреки това, ако заместите намерените изрази за x, y, z в оригиналната система, можете да се уверите, че и трите уравнения се превръщат в правилни равенства.

И така, ние показахме, че формулите за решението в общ вид линейни системиуравненията за и имат сходна структура и основна роля в тях играят детерминантите от втори ред

и трети ред

И двата израза са алгебрични суми на продукти на матрични елементи и тези продукти са съставени от един елемент от всеки ред и един от всяка колона. Всички такива продукти са включени в детерминанта. Творбите се обозначават със знаци + и - съгласно правилата

На тези фигури елементите на матрицата, които съставят продуктите, включени в детерминанта със знаци, са свързани с линии

Нека сега се обърнем към обобщение на детерминанта за квадратни матрици от всякакъв ред, въз основа на формата на тези изрази за

Тук е удобно да обозначим елементите на матрицата с една буква, като й присвоим два индекса - номера на реда и номера на колоната. Нека дадем формална дефиниция на детерминантата за квадратна матрица от ред, както следва:

Детерминантата на квадратна матрица от ред (или детерминанта от ред) се нарича алгебрична сумавсички възможни произведения на матрични елементи, взети по един от всеки ред, по един от всяка колона и оборудвани със знаци плюс и минус според някакво специфично правило.

Ще се обърнем към въпроса какво е това правило в близко бъдеще, но засега ще се опитаме да запишем символично формулираното по-горе определение. Във всеки член на детерминантата ще запишем факторите по реда на редовете. Номерата на колоните ще съберат всички числа от 1 до , в различни редове и във всички възможни редове, тъй като детерминантата, според това определение, се състои от всички произведения на елементите, взети по един от всеки ред и по един от всяка колона. В буквени обозначения:

Тук индексите преминават през всички възможни пермутации на числа. Всички пермутации трябва да бъдат разделени на два класа, така че единият клас да съответства на термини със знак "плюс", а другият - със знак "минус".

Метрични и нормирани пространства.

Евклидови и унитарни пространства.

Евклидови пространства. Скаларен продуктв евклидовото пространство и неговите свойства.

Дължина на вектор в евклидовото пространство, ъгъл между векторите. Неравенство на Коши-Буняковски и неравенство на триъгълник.

Ортогонални и ортонормални системи от вектори в евклидовото пространство. Точково произведение в ортонормална основа.

Процесът на Щурм за ортогонализиране на система от вектори.

Изоморфизъм на евклидовите пространства.

Унитарни пространства. Скаларното произведение в унитарно пространство и неговите свойства.

Дължина на вектор в унитарно пространство. Неравенство на Коши-Буняковски и неравенство на триъгълник.

Ортогонални и ортонормални системи в унитарно пространство. Точково произведение в ортонормална основа.

Ортогонално допълнение към подпространство. Свойства на ортогоналното допълнение.

Представяне на пространство като пряка сума от подпространство и неговото ортогонално допълнение.

Ортогонална проекция и ортогонална компонента на вектор върху подпространство.

Разстоянието между вектор и подпространство, вектор и многообразие.

Ъгълът между вектор и подпространство на евклидовото пространство, ъгълът между вектор и многообразие на евклидовото пространство.

Метрични пространства. Граница на последователност в метрично пространство.

Топки в метрично пространство. Ограничени множества. Гранични точки.

Пълнота метрични пространства. Теорема за вложените топки.

Нормализирани пространства. Връзка между нормирани и метрични пространства.

Координатна сходимост и нормална сходимост, връзката между тях. Пълнота на нормираните пространства.

Линейни функционали на линейно пространство. Пространство на линейните функционали.

Билинейни функционали върху линейно пространство. Симетрични и антисиметрични билинейни функционали.

Мултилинейни функционали върху линейно пространство. Симетрични, антисиметрични, абсолютно симетрични и абсолютно антисиметрични многолинейни функционали.

Детерминантата на квадратна матрица като мултилинеен абсолютно антисиметричен функционал. Формули за изчисляване на детерминанти от втори и трети ред.

Свойства на детерминантите.

Разлагане на детерминантата на елементите на ред или на елементите на колона.

Минори от ред, техните алгебрични допълнения. Теорема на Лаплас.

Метод за изчисляване на детерминантите на реда чрез редуцирането им до триъгълна форма.

Метод на избор линейни умножителипри изчисляване на детерминанти на реда. Детерминант Вандермонд.

Метод на рекурентните отношения при изчисляване на детерминантата на реда.

Метод за представяне на детерминанта като сбор от две детерминанти при изчисляване на детерминанти на ред.

Метод за промяна на елементите на детерминанта при изчисляване на детерминанти на ред.

СОУ No45.

град Москва.

Ученик от 10 клас „Б” Горохов Евгений

Курсова работа (чернова).

Въведение в теорията на матриците и детерминантите .

1. Матрици..................................................... ......... ................................................ ............... ................................. ................... ......

1.1 Понятие за матрица ............................................. ...... ............................................ ............ ...................................

1.2 Основни операции с матрици ............................................. ......................................................... ............. .

2. Детерминанти ............................................. ......... ................................................ ............... ................................. ........

2.1 Концепцията за детерминанта..................................... ......................................................... ............ ........................

2.2 Изчисляване на детерминантите ............................................. ...... ............................................ ............ ...............

2.3 Основни свойства на детерминантите............................................. ......................................................... .............

3. Системи линейни уравнения..................................... ......................................................... .............. .

3.1 Основни дефиниции ............................................. .... .............................................. .......... ........................

3.2 Условие за съвместимост за системи от линейни уравнения.................................................. .......... ...............

3.3 Решаване на системи от линейни уравнения по метода на Крамър.................................................. ........... ..........

3.4 Решаване на системи от линейни уравнения по метода на Гаус.................................................. ............ .............

4. Обратна матрица............................................. ...... ............................................ ............ ...................................

4.1 Концепция за обратна матрица..................................... ......................................................... ............. ................

4.2 Изчисляване на обратната матрица..................................... ......................................................... .......................

Библиография.................................................. ................................................. ..... ................................

Матрица е правоъгълна таблица с числа, съдържаща определено количество м редове и определен брой н колони. Числа м И н са наречени поръчкиматрици. Ако м = н , матрицата се нарича квадрат, а числото m = n -- нея в ред .

Основен аритметични операциинад матрици са умножение на матрица по число, събиране и умножение на матрици.

Нека да преминем към дефинирането на основните операции върху матрици.

Събиране на матрица: Сумата от две матрици, например: А И Б , с еднакъв брой редове и колони, с други думи, еднакви поръчки м И н наречена матрица C = ( СЪС ij )( i = 1, 2, …m; j = 1, 2, …n) същите поръчки м И н , елементи Cij които са равни.

Cij = Aij + Bij (i = 1, 2, …, m; j = 1, 2, …, n) (1.2 )

За означаване на сумата от две матрици се използва нотацията C = A + B. Операцията на сумиране на матрици се нарича техен допълнение

Така че по дефиниция имаме:

+ =

=

От дефиницията на сумата от матрици или по-точно от формулата ( 1.2 ) веднага следва, че операцията за добавяне на матрици има същите свойства като операцията за добавяне на реални числа, а именно:

1) комутативно свойство: A + B = B + A

2) комбиниране на собственост: (A + B) + C = A + (B + C)

Тези свойства ви позволяват да не се притеснявате за реда на членовете на матриците, когато добавяте две или Повече ▼матрици

Умножение на матрица по число :

Матричен продукт за реално число се нарича матрица C = (Cij) (i = 1, 2, …, m; j = 1, 2, …, n) , чиито елементи са равни

Cij = Aij (i = 1, 2, …, m; j = 1, 2, …, n). (1.3 )

За означаване на произведението на матрица и число се използва нотацията C= А или C=A . Операцията за съставяне на произведението на матрица по число се нарича умножаване на матрицата по това число.

Директно от формула ( 1.3 ) ясно е, че умножаването на матрица по число има следните свойства:

1) разпределително свойство по отношение на сумата от матрици:

( A + B) = A+ Б

2) асоциативно свойство по отношение на числов фактор:

() А= ( а)

3) разпределително свойство по отношение на сумата от числа:

( + ) А= А + А .

Коментирайте :Разлика на две матрици А И Б от еднакви порядки е естествено да наречем такава матрица ° С от същите поръчки, които в сумата с матрицата Б дава матрицата А . За да се обозначи разликата между две матрици, се използва естествена нотация: C = A – B.

Матрично умножение :

Матричен продукт A = (Aij) (i = 1, 2, …, m; j = 1, 2, …, n) , като поръчките са съответно равни м И н , на матрица B = (Bij) (i = 1, 2, …, n;

j = 1, 2, …, p) , като поръчките са съответно равни н И стр , се нарича матрица C= (СЪС ij) (i = 1, 2, … , m; j = 1, 2, … , p) , като поръчките са съответно равни м И стр , и елементи Cij , определени по формулата

Cij = (i = 1, 2, …, m; j = 1, 2, …, p) (1.4 )

За означаване на произведението на матрица А към матрицата Б използвайте запис

C=AB . Операцията по съставяне на матричен продукт А към матрицата Б Наречен умножениетези матрици. От горното определение следва, че матрица А не може да се умножи по никаква матрица Б : необходимо е броят на колоните на матрицата А беше равно наброй редове на матрицата Б . За да работи и двете AB И Б.А. са били не само дефинирани, но и са имали същия ред, е необходимо и достатъчно и двете матрици А И Б бяха квадратни матрици от един и същи ред.

формула ( 1.4 ) е правило за съставяне на матрични елементи ° С ,

което е произведение на матрицата А към матрицата Б . Това правило може да се формулира устно: елемент Cij , стоящ на кръстовището i ти ред и j- та колона на матрицата C=AB , е равно сумата от произведенията по двойки на съответните елементи i ти ред матрици А И j- та колона на матрицата Б . Като пример за приложението на това правило представяме формулата за умножение на квадратни матрици от втори ред

От формулата ( 1.4 ) следват следните свойства на матричното произведение: А към матрицата Б :

1) асоциативно свойство: ( AB)C = A(BC);

2) разпределително свойство по отношение на сумата от матрици:

(A + B) C = AC + BC или A (B + C) = AB + AC.

Има смисъл да се повдига въпросът за пермутационното свойство на произведение от матрици само за квадратни матрици от същия ред. Елементарни примери показват, че произведението на две квадратни матрици от един и същи ред, най-общо казано, няма свойството комутация. Всъщност, ако сложим

A = , B = , Че AB = , А BA =

Обикновено се наричат ​​същите матрици, за които произведението има свойството комутация пътуване до работното място.

Сред квадратните матрици изтъкваме класа на т.нар диагоналматрици, всяка от които има елементи, разположени извън главния диагонал, равни на нула. Сред всички диагонални матрици със съвпадащи елементи на главния диагонал две матрици играят особено важна роля. Първата от тези матрици се получава, когато всички елементи на главния диагонал са равни на единица, наречена матрица на идентичност н- д . Втората матрица се получава с всички елементи равни на нула и се нарича нулева матрица н- ред и се обозначава със символа О . Да приемем, че има произволна матрица А , Тогава

AE=EA=A , AO=OA=O .

Първата от формулите характеризира специалната роля на матрицата на идентичността д, подобно на ролята, която играе числото 1 при умножаване на реални числа. Що се отнася до специалната роля на нулевата матрица ОТНОСНО, то се разкрива не само от втората от формулите, но и от елементарно проверимо равенство: A+O=O+A=A . Концепцията за нулева матрица може да се въведе не за квадратни матрици.

На първо място, трябва да запомните, че детерминанти съществуват само за матрици от квадратен тип, тъй като няма детерминанти за матрици от други типове. В теорията на системите от линейни уравнения и в някои други въпроси е удобно да се използва понятието детерминант, или детерминант .

Нека разгледаме произволни четири числа, записани под формата на матрица от две в редове и две колони , Определящо или детерминант, съставен от числата в тази таблица, е числото ad-bc , означен по следния начин: .Такава детерминанта се нарича детерминанта от втори ред, тъй като за нейното компилиране е взета таблица от два реда и две колони. Числата, които съставляват определителя, се наричат ​​негови елементи; същевременно казват, че елементите а И д грим главен диагоналдетерминанта и елементите b И ° С неговият страничен диагонал. Вижда се, че детерминантата е равна на разликата на произведенията на двойки елементи, разположени на неговия главен и вторичен диагонал. Детерминантата на третия и всеки друг ред е приблизително една и съща, а именно: Да кажем, че имаме квадратна матрица . Детерминантата на следната матрица е следният израз: a11a22a33 + a12a23a31 + a13a21a32 – a11a23a32 – a12a21a33 – a13a22a31. . Както можете да видите, изчислява се доста лесно, ако запомните определена последователност. С положителен знак са главният диагонал и триъгълниците, образувани от елементите, които имат страна, успоредна на главния диагонал, в случая това са триъгълници a12a23a31, a13a21a32 .

Страничният диагонал и успоредните на него триъгълници са с отрицателен знак, т.е. a11a23a32 , a12a21a33 . По този начин могат да бъдат намерени детерминанти от всякакъв ред. Но има случаи, когато този метод става доста сложен, например, когато има много елементи в матрицата и за да изчислите детерминантата, трябва да отделите много време и внимание.

Има по-лесен начин за изчисляване на детерминантата н- о, ред, къде n2 . Нека се съгласим да наричаме всеки елемент второстепенен Aij матрици н- детерминанта от първи ред, съответстваща на матрицата, която се получава от матрицата в резултат на изтриване i ти ред и j- та колона (онзи ред и тази колона, в пресечната точка на които има елемент Aij ). Минорен елемент Aij ще се обозначава със символа. В тази нотация горният индекс обозначава номера на реда, долният индекс номера на колоната, а лентата отгоре М означава, че посоченият ред и колона са зачеркнати. Детерминанта на реда н , съответстващо на матрицата, наричаме числото равно на и се обозначава със символа .

Теорема 1.1 Какъвто и да е номерът на реда i ( i =1, 2..., n) , за определителя н- валидна е формулата от първи порядък

= det A =

Наречен аз- ти ред . Подчертаваме, че в тази формула показателят, до който се повишава числото (-1), е равен на сумата от номерата на реда и колоната, в пресечната точка на които се намира елементът Aij .

Теорема 1.2 Какъвто и да е номерът на колоната й ( j =1, 2..., n) , за определителя н формулата за th ред е валидна

= det A =

Наречен разширяване на тази детерминанта в j- та колона .

Детерминантите също имат свойства, които улесняват задачата за тяхното изчисляване. И така, по-долу установяваме редица свойства, които има произволен детерминант н -та поръчка.

1. Свойство за равенство на ред-колона . Транспониранена всяка матрица или детерминанта е операция, в резултат на която редовете и колоните се разменят, като се запазва редът им. В резултат на матрично транспониране А получената матрица се нарича матрица, наречена транспонирана по отношение на матрицата А и се обозначава със символа А .

Първото свойство на детерминантата се формулира по следния начин: по време на транспониране стойността на детерминантата се запазва, т.е. = .

2. Свойство на антисиметрия при пренареждане на два реда (или две колони). Когато два реда (или две колони) се разменят, детерминантата запазва своята абсолютна стойност, но променя знака на противоположния. За детерминанта от втори ред това свойство може да се провери по елементарен начин (от формулата за изчисляване на детерминанта от втори ред веднага следва, че детерминантите се различават само по знак).

3. Линейно свойство на детерминантата. Ще кажем, че някакъв низ ( а) е линейна комбинациядва други реда ( b И ° С ) с коефициенти и . Линейното свойство може да се формулира по следния начин: ако в детерминантата н някакъв ред i Редът е линейна комбинация от два реда с коефициенти и , тогава = + , къде

- определител, който има i -тият ред е равен на един от двата реда на линейната комбинация, а всички останали редове са същите като , a е детерминантата, за която аз- низът i е равен на втория от двата низа, а всички останали низове са същите като .

Тези три свойства са основните свойства на определителя, разкриващи неговата природа. Следните пет свойства са логични следствиятри основни свойства.

Следствие 1. Детерминанта с два еднакви реда (или колони) е равна на нула.

Следствие 2. Умножаване на всички елементи на някакъв ред (или някаква колона) на детерминанта по число а е еквивалентно на умножаване на детерминантата по това число а . С други думи, общият фактор на всички елементи на определен ред (или колона) на детерминанта може да бъде изваден от знака на тази детерминанта.

Следствие 3. Ако всички елементи на определен ред (или някаква колона) са равни на нула, то самата детерминанта е равна на нула.

Следствие 4. Ако елементите на два реда (или две колони) на детерминантата са пропорционални, то детерминантата е равна на нула.

Следствие 5. Ако към елементите на определен ред (или колона) на детерминанта добавим съответните елементи от друг ред (друга колона), умножени по произволен коефициент, тогава стойността на детерминантата не се променя. Следствие 5, както и линейно свойство, позволява по-обща формулировка, която ще дам за низове: ако към елементите на определен низ от детерминанта добавим съответните елементи на низ, който е линейна комбинация от няколко други низа от тази детерминанта (с всякакви коефициенти ), тогава стойността на детерминантата няма да се промени. Следствие 5 се използва широко при конкретното изчисляване на детерминанти.

Известно е, че с помощта на матрици можем да решаваме различни системи от уравнения и тези системи могат да бъдат с произволен размер и произволен брой променливи. С няколко извода и формули решаването на огромни системи от уравнения става доста бързо и по-лесно.

По-специално ще опиша методите на Крамер и Гаус. Най-лесният начин е методът на Крамер (за мен) или както още го наричат ​​формулата на Крамер. И така, да кажем, че имаме някаква система от уравнения

, В матрична форма тази система може да бъде записана по следния начин: А= , където отговорите на уравненията ще бъдат в последната колона. Сега ще въведем концепцията за фундаментална детерминанта; в този случай ще изглежда така:

= . Основният детерминант, както вече забелязахте, е матрица, съставена от коефициентите на променливите. Те също се появяват в ред на колони, т.е. първата колона съдържа коефициентите, които се намират в х , във втората колона при г , и така нататък. Това е много важно, тъй като в следващите стъпки ще заменим всяка колона с коефициенти за променлива с колона с отговори на уравнението. И така, както казах, заместваме колоната при първата променлива с колоната за отговор, след това при втората, разбира се всичко зависи от това колко променливи трябва да намерим.

1 = , 2 = , 3 = .

След това трябва да намерите детерминантите 1, 2, 3. Вече знаете как да намерите детерминанта от трети ред. А Тук прилагаме правилото на Крамър. Изглежда така:

x1 = , x2 = , x3 = – за този случай, но като цяло изглежда така: х аз = . Извиква се детерминанта, съставена от коефициенти за неизвестни детерминанта на системата .

1. В. А. Илин, Е. Г. Позняк “Линейна алгебра”

2. Г. Д. Ким, Е. В. Шикин “Елементарни трансформации в линейната алгебра”