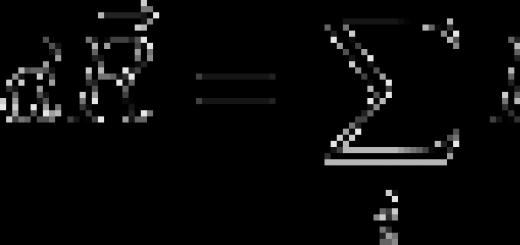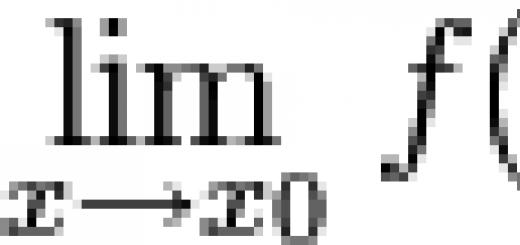ОБЩИНСКА АВТОНОМНА ОБЩО ОБРАЗОВАТЕЛНА ИНСТИТУЦИЯ СРЕДНО ОБРАЗОВАТЕЛНО УЧИЛИЩЕ № 2
Подготвени
Легкоконец Владислав, 10А ученик
Практическо приложение на теорията на графите
Ръководител
L.I. Носкова, учител по математика
ул.Брюховецкая
2011 г
1.Въведение……………………………………………………………………………………….………….3
2. Историята на възникването на теорията на графите………………………………………………………………..4
3.Основни дефиниции и теореми на теорията на графовете………………………………….………6
4. Задачи, решени с помощта на графики………………………………………..……………………..8
4.1 Известни задачи………………………………….…………………………………...8
4.2 Някои интересни задачи…………………………………………………………..9
5. Прилагане на графики в различни области от живота на хората…………………………………………11
6. Решаване на проблеми………………………………………………………………………………………………………...12
7. Заключение…………………………………………………………………………………………………….13
8. Списък на литературата……………………………………………………………………………………………………………………… ……………………………………………………………………………………………………………………………………………………………… ………………………………………………………………………………………………………………………………………….
9.Приложение………………………………………………………………………………………………15
Въведение
Родена в решаването на пъзели и забавни игри, теорията на графите вече се превърна в прост, достъпен и мощен инструмент за решаване на проблеми, свързани с широк спектър от проблеми. Графиките са буквално повсеместни. Под формата на графики можете например да интерпретирате пътни карти и електрически вериги, географски картии молекули химични съединения, връзки между хора и групи от хора. През последните четири десетилетия теорията на графите се превърна в един от най-бързо развиващите се клонове на математиката. Това се дължи на изискванията на бързо разширяваща се област на приложение. Използва се при проектирането на интегрални схеми и схеми за управление, при изучаване на автомати, логически схеми, програмни блок-схеми, в икономиката и статистиката, химията и биологията, в теорията на графика. Ето защо уместностТемата се дължи, от една страна, на популярността на графиките и свързаните с тях изследователски методи, а от друга страна на неразвитата, интегрална система за нейното прилагане.
Решаването на много житейски проблеми изисква дълги изчисления и понякога тези изчисления не носят успех. В това се състои изследователски проблем. Възниква въпросът: възможно ли е да се намери просто, рационално, кратко и елегантно решение за тяхното решение. По-лесно ли е да решавате проблеми, ако използвате графики? То определи тема на моето изследване: "Практическо приложение на теорията на графите"
целизследванията бяха с помощта на графики, за да се научат как бързо да решават практически проблеми.
Изследователска хипотеза.Графичният метод е много важен и широко използван в различни области на науката и човешкия живот.
Цели на изследването:
1. Да проучи литературата и интернет ресурси по този въпрос.
2. Проверете ефективността на графичния метод при решаване на практически задачи.
3. Направете заключение.
Практическо значениеизследванияе, че резултатите несъмнено ще предизвикат интереса на много хора. Никой от вас не се е опитвал да изгради родословно дърво на семейството си? И как да го направя правилно? Ръководителят на транспортна фирма вероятно трябва да реши проблема с по-изгодното използване на транспорта при превоз на стоки от дестинация до няколко населени места. Всеки ученик се изправи пред логически задачи за трансфузия. Оказва се, че лесно се решават с помощта на графики.
В работата се използват следните методи: наблюдение, търсене, подбор, анализ.
Историята на възникването на теорията на графите
Математикът Леонхард Ойлер (1707-1783) се счита за основоположник на теорията на графите. Историята на възникването на тази теория може да бъде проследена чрез кореспонденцията на великия учен. Ето превод на латински текст, който е взет от писмото на Ойлер до италианския математик и инженер Маринони, изпратено от Санкт Петербург на 13 март 1736 г.
„Веднъж ми поставиха проблем за остров, разположен в град Кьонигсберг и заобиколен от река, през която са прехвърлени седем моста.
[Приложение Фиг.1]Въпросът е дали някой може да ги заобикаля непрекъснато, минавайки само веднъж през всеки мост. И тогава ме информираха, че никой все още не е успял да направи това, но никой не е доказал, че е невъзможно. Този въпрос, макар и банален, ми се стори обаче, заслужава вниманиефактът, че нито геометрията, нито алгебрата, нито комбинаторното изкуство са достатъчни за неговото решение. След дълго мислене открих едно лесно правило, базирано на напълно убедително доказателство, с помощта на което във всички задачи от този вид може веднага да се определи дали такъв кръг може да се направи през произволно брой и произволно разположени мостове или не. Кьонигсбергските мостове са разположени така, че да могат да бъдат представени на следващата фигура [Приложение Фиг.2], където A означава остров, а B, C и D са части от континента, разделени една от друга с речни разклонения
По отношение на метода, който е открил за решаване на проблеми от този вид, Ойлер пише:
„Това решение по своята същност изглежда няма много общо с математиката и не ми е ясно защо това решение трябва да се очаква от математик, а не от който и да е друг човек, тъй като това решение се поддържа само от разума и няма нужда да се включват, за да се намери това решение, каквито и да било закони, присъщи на математиката. Така че не знам как се оказва, че въпросите, които имат много малко общо с математиката, е по-вероятно да бъдат разрешени от математиците, отколкото от други."
Така че възможно ли е да заобиколите мостовете на Кьонигсберг, като преминете само веднъж през всеки от тези мостове? За да намерим отговора, нека продължим писмото на Ойлер до Маринони:
„Въпросът е да се определи дали е възможно да се заобиколят всички тези седем моста, минавайки през всеки само веднъж, или не. Моето правило води до следното решение на този въпрос. Първо, трябва да погледнете колко отсечки са разделени от вода - такива, които нямат друг преход от един към друг, освен през моста. В този пример има четири такива секции - A, B, C, D. След това трябва да различите дали броят на мостовете, водещи към тези отделни участъци, е четно или нечетно.Така че в нашия случай пет моста водят до участък А, а три моста към останалите, т.е. решаване на проблема. Когато това е определено, прилагаме следното правило: ако броят на мостовете, водещи към всеки отделен участък, е четен, тогава байпасът, за който въпросният, би било възможно и в същото време би било възможно да започне това отклонение от всеки участък. Ако обаче две от тези числа бяха нечетни, тъй като само едно не може да бъде нечетно, тогава дори и тогава преходът би могъл да се осъществи, както е предписано, но само началото на байпаса трябва задължително да бъде взето от една от тези две секции, към които нечетен брой води.мостове. Ако в крайна сметка имаше повече от два участъка, до които води нечетен брой мостове, тогава такова движение като цяло е невъзможно ... ако тук могат да се цитират други, по-сериозни проблеми, този метод може да бъде още по-полезен и не трябва бъде пренебрегван“.
Основни дефиниции и теореми на теорията на графовете
Теорията на графите е математическа дисциплина, създадена с усилията на математиците, така че нейното представяне включва необходимите строги дефиниции. И така, нека преминем към организираното въвеждане на основните понятия на тази теория.
Определение 1.Графиката е колекция краен бройточки, наречени върхове на графиката, и свързващи по двойки някои от тези върхове на линиите, наречени ръбове или дъги на графа.
Тази дефиниция може да бъде формулирана по различен начин: графиката е непразен набор от точки (върхове) и сегменти (ръба), и двата края на които принадлежат на даден набор от точки
В бъдеще ще обозначаваме върховете на графиката с латински букви A, B, C, D. Понякога графиката като цяло ще бъде обозначена с единица Главна буква.
Определение 2.Върховете на графа, които не принадлежат на нито един ръб, се наричат изолирани.
Определение 3.Граф, състоящ се само от изолирани върхове, се нарича нула - броя .
Обозначение: O "- графика с върхове и без ръбове
Определение 4.Граф, в който всяка двойка върхове е свързана с ръб, се нарича пълна.
Обозначение: U" – граф, състоящ се от n върха и ребра, свързващи всички възможни двойки от тези върхове. Такава графика може да бъде представена като n-ъгълник, в който са начертани всички диагонали
Определение 5.Степента на върха е броят на ръбовете, на които принадлежи върхът.
Определение 6.Граф, чиито степени на всички k върхове са еднакви, се нарича хомогенен график от степен k .
Определение 7.Допълнението на дадена графа е графика, състояща се от всички ръбове и техните краища, които трябва да бъдат добавени към оригиналната графа, за да се получи пълен граф.
Определение 8.Граф, който може да бъде представен в равнина по такъв начин, че ръбовете му да се пресичат само във върховете, се нарича планарен.
Определение 9.Многоъгълник на планарен граф, който не съдържа върхове или ръбове на графа вътре, се нарича негово лице.
Понятията за плоска графика и графични лица се използват при решаване на задачи за "правилното" оцветяване на различни карти.
Определение 10.Път от A до X е поредица от ръбове, водещи от A до X, така че всеки два съседни ръба да имат общ връх и нито един ръб не се среща повече от веднъж.
Определение 11.Цикълът е път, при който началната и крайната точки са еднакви.
Определение 12.Прост цикъл е цикъл, който не преминава през нито един от върховете на графа повече от веднъж.
Определение 13.дълъг път , положени на примка , е броят на ръбовете на този път.
Определение 14.Два върха A и B в графа се наричат свързани (несвързани), ако в него съществува (не съществува) път, водещ от A до B.
Определение 15.Графът се нарича свързан, ако всеки два негов върха са свързани; ако графът съдържа поне една двойка несвързани върхове, тогава графът се нарича несвързан.
Определение 16.Дървото е свързана графика, която не съдържа цикли.
Триизмерен модел на граф-дърво е, например, истинско дърво с неговата сложно разклонена корона; реката и нейните притоци също образуват дърво, но вече плоско - на повърхността на земята.
Определение 17.Несвързана графа, състояща се само от дървета, се нарича гора.
Определение 18.Дърво, чиито n върхове са номерирани от 1 до n, се нарича дърво с преномерирани върхове.
И така, разгледахме основните дефиниции на теорията на графовете, без които би било невъзможно да се доказват теореми и следователно да се решават проблеми.
Проблеми, решени с помощта на графики
Известни предизвикателства
Проблемът с пътуващия продавач
Проблемът с пътуващия продавач е един от известните проблеми в теорията на комбинаториката. Поставен е през 1934 г. и най-добрите математици си счупиха зъбите за него.
Постановката на проблема е следната.
Пътуващият търговец (пътуващ търговец) трябва да напусне първия град, да посети градове 2,1,3..n веднъж в неизвестен ред и да се върне в първия град. Разстоянията между градовете са известни. В какъв ред трябва да се изминат градовете, така че затвореният път (обиколка) на продавача да е най-кратък?
Метод за решаване на проблема с продавача
Алчен алгоритъм
„Отидете до най-близкия (в който все още не сте влезли) град.“
Този алгоритъм се нарича „алчен“, защото в последните стъпки трябва да плащате скъпо за алчността.
Да разгледаме например мрежата на фигура [приложение фиг.3]представляващ тесен ромб. Нека продавачът започне от град 1. Алгоритъмът „отидете до най-близкия град” ще го отведе до град 2, след това 3, след това 4; на последната стъпка ще трябва да платите за алчност, връщайки се по дългия диагонал на ромба. Резултатът не е най-кратката, а най-дългата обиколка.
Проблемът с Кьонигсбергските мостове.
Задачата е формулирана по следния начин.
Град Кьонигсберг е разположен на брега на река Прегел и два острова. Различни части на града бяха свързани със седем моста. В неделя жителите на града се разхождаха из града. Въпрос: възможно ли е да се направи разходка по такъв начин, че, напускайки къщата, да се върнете, като сте минали точно веднъж през всеки мост.
Мостовете над река Прегел са разположени както на снимката[Приложение Фиг.1].
Помислете за графика, съответстваща на мостовата схема [приложение фиг.2].
За да се отговори на въпроса за задачата, е достатъчно да се установи дали графиката е Ойлерова. (Поне един връх трябва да има четен брой мостове). Невъзможно е, разхождайки се из града, да минеш през всичките мостове веднъж и да се върнеш.
Няколко интересни предизвикателства
1. „Маршрути“.
Задача 1
Както си спомняте, ловецът мъртви душиЧичиков посещава известни земевладелци по веднъж. Той ги посети в следния ред: Манилов, Коробочка, Ноздрев, Собакевич, Плюшкин, Тентетников, генерал Бетрищев, Петух, Констанжолго, полковник Кошкарев. Намерена е диаграма, на която Чичиков е скицирал взаимно урежданеимения и селски пътища, които ги свързват. Определете кое имение на кого принадлежи, ако Чичиков не е минал нито един от пътищата повече от веднъж [приложение фиг.4].
Решение:
По пътната карта се вижда, че Чичиков е започнал пътуването си с имението Е, а завършва с имението О. Забелязваме, че само два пътя водят до имотите В и В, така че Чичиков трябваше да кара по тези пътища. Нека ги отбележим с получер линии. Определят се участъците от маршрута, преминаващ през А: AC и AB. Чичиков не е пътувал по пътищата AE, AK и AM. Да ги зачеркнем. Нека отбележим с дебела линия ED ; зачертайте DK . Зачертайте MO и MN; маркирайте с удебелена линия MF ; зачертавам FO ; маркираме FH , NK и KO с удебелена линия. Нека намерим единствения възможен маршрут при даденото условие. И получаваме: имението E - принадлежи на Манилов, D - Коробочка, C - Ноздрев, A - Собакевич, V - Плюшкин, M - Тентетников, F - Бетрищев, N - Петух, K - Констанжолго, O - Кошкарев [приложение фиг.5].
Задача 2
Фигурата показва карта на района [приложение фиг.6].
Можете да се движите само в посоката на стрелките. Всяка точка може да се посети не повече от веднъж. По колко начина можете да стигнете от точка 1 до точка 9? Кой маршрут е най-краткият и кой най-дълъг.
Решение:
Последователно "стратифицирайте" схемата в дърво, започвайки от връх 1 [приложение фиг.7]. Да вземем дърво. номер възможни начинихитове от 1 до 9 е равно на броя на "висящите" върхове на дървото (има 14 от тях). Очевидно най-краткият път е 1-5-9; най-дългият е 1-2-3-6-5-7-8-9.
2 "Групи, запознанства"
Задача 1
Участниците в музикалния фестивал, след като се срещнаха, си размениха пликове с адреси. Докажи това:
а) общо са изпратени четен брой пликове;
б) броят на участниците, разменили пликове нечетен брой пъти, е четен.
Решение: Нека участниците във фестивала са A 1 , A 2 , A 3 . . . , И n са върховете на графиката, а ръбовете свързват двойки върхове, представляващи момчета, които са разменили пликове [Приложение Фиг.8]
Решение:
а) степента на всеки връх A i показва броя на пликовете, които участник A i е дал на приятелите си. Общ бройпрехвърлените обвивки N е равно на сумата от степените на всички върхове на графа N = стъпка. A 1 + стъпка. A 2 + +. . . + стъпка. И n -1 + стъпка. И n , N =2p , където p е броят на ръбовете на графа, т.е. N е четно. Поради това бяха изпратени четен брой пликове;
б) в равенството N = стъпка. A 1 + стъпка. A 2 + +. . . + стъпка. И n -1 + стъпка. И n сумата от нечетните членове трябва да е четна, а това може да бъде само ако броят на нечетните членове е четен. А това означава, че броят на участниците, разменили пликове нечетен брой пъти, е четен.
Задача 2
Веднъж Андрей, Борис, Володя, Даша и Галя се съгласиха да отидат на кино вечер. Решиха да се договорят за избора на киното и сесията по телефона. Също така беше решено, че ако не е възможно да се обади на някого, тогава пътуването до киното ще бъде отменено. Вечерта не всички се събраха в киното и затова посещението на киното пропадна. На следващия ден започнаха да откриват кой на кого се е обадил. Оказа се, че Андрей се обади на Борис и Володя, Володя вика Борис и Даша, Борис се обади на Андрей и Даша, Даша се обади на Андрей и Володя, а Галя се обади на Андрей, Володя и Борис. Кой не можа да се обади и следователно не дойде на срещата?
Решение:
Да начертаем пет точки и да ги обозначим с буквите A, B, C, D, E. Това са първите букви на имената. Нека свържем онези точки, които съответстват на имената на момчетата, които са се обадили.
[приложение фиг.9]
От снимката се вижда, че всяко от момчетата - Андрей, Борис и Володя - се обади на всички останали. Затова тези момчета дойдоха на кино. Но Галя и Даша не успяха да се обадят (точки D и D не са свързани с сегмент) и следователно, в съответствие със споразумението, не дойдоха на кино.
Използването на графики в различни области от живота на хората
В допълнение към дадените примери, графиките намират широко приложение в строителството, електротехниката, управлението, логистиката, географията, машиностроенето, социологията, програмирането, автоматизацията на технологичните процеси и индустрии, психологията и рекламата. И така, от всичко казано по-горе, неоспоримо следва практическата стойност на теорията на графите, доказателството на което беше целта на това изследване.
Във всяка област на науката и технологиите се срещате с графики. Графиките са прекрасни математически обекти, с които можете да решавате математически, икономически и логически задачи, различни пъзели и да опростявате условията на задачи по физика, химия, електроника, автоматизация. Удобно е да се формулират много математически факти на езика на графиките. Теорията на графите е част от много науки. Теорията на графите е една от най-красивите и визуални математически теории. Напоследък теорията на графите намира все повече приложения в приложните проблеми. Появи се дори компютърната химия – сравнително млада област на химията, базирана на приложението на теорията на графите.
Молекулни графики, използвани в стереохимията и структурната топология, химията на клъстерите, полимерите и др., са ненасочени графики, които показват структурата на молекулите [приложение фиг.10]. Върховете и ръбовете на тези графики съответстват на съответните атоми и химичните връзки между тях.
Молекулни графики и дървета: [приложение фиг.10] a, b - мултиграфи респ. етилен и формалдехид; in-mol. изомери на пентан (дървета 4, 5 са изоморфни на дърво 2).
В стереохимията на организмите най-много често се използват молекулярни дървета - основните дървета на молекулярните графики, които съдържат само всички върхове, съответстващи на C атоми. дърветата и установяването на техния изоморфизъм ви позволяват да определите кея. структури и намерете общ бройизомери на алкани, алкени и алкини
Протеинови мрежи
Протеинови мрежи - групи от физически взаимодействащи протеини, които функционират в клетката съвместно и по координиран начин, контролирайки взаимосвързаните процеси, протичащи в тялото [приложение фиг. единадесет].
Йерархична системна графиканаречено дърво. Отличителна чертана едно дърво е, че има само един път между всеки два от неговите върха. Дървото не съдържа цикли и цикли.
Обикновено дърво представлява йерархична система, се разпределя един главен връх, който се нарича корен на дървото. Всеки връх на дървото (с изключение на корена) има само един предшественик - обозначеният от него обект принадлежи към един клас от най-високо ниво. Всеки връх на дървото може да генерира няколко потомци - върхове, съответстващи на класове от по-ниско ниво.
За всяка двойка върхове на дървото има уникален път, който ги свързва. Това свойство се използва при намиране на всички предци, например по мъжка линия, на всяко лице, чието родословно дърво е представено под формата на родословно дърво, което е „дърво” и в смисъла на теорията на графите.
Пример за моето родословно дърво [приложение фиг.12].
Още един пример. Фигурата показва библейското родословно дърво [приложение фиг.13].
Разрешаване на проблем
1. Транспортна задача. Нека има база със суровини в град Краснодар, която трябва да бъде засадена в градовете Кримск, Темрюк, Славянск-на-Кубан и Тимашевск наведнъж, като същевременно харчите възможно най-малко време и гориво и се връщате обратно до Краснодар.
Решение:
Първо, нека създадем графика на всички възможни маршрути. [приложение фиг.14], като се вземат предвид реалните пътища между тези населени места и разстоянието между тях. За да решим този проблем, трябва да създадем друга графика, дърво [приложение фиг.15].
За удобство на решението обозначаваме градовете с числа: Краснодар - 1, Кримск - 2, Темрюк - 3, Славянск - 4, Тимашевск - 5.
Това доведе до 24 решения, но имаме нужда само от най-кратките пътища. От всички решения само две са доволни, това са 350 км.
По същия начин е възможно и според мен е необходимо да се изчисли реалния транспорт от едно населено място до друго.
Логическа задача за трансфузия.В една кофа има 8 литра вода, като има две тенджери с вместимост 5 и 3 литра. необходимо е да се излеят 4 литра вода в петлитрова тенджера и да се оставят 4 литра в кофа, тоест да се налее вода по равно в кофа и голяма тенджера.
Решение:
Ситуацията във всеки един момент може да се опише с три числа [приложение фиг.16].
В резултат получаваме две решения: едното на 7 хода, другото на 8 хода.
Заключение
Така че, за да се научите как да решавате проблеми, трябва да разберете какви са те, как са подредени, от какво съставни частите се състоят от това какви инструменти се използват за решаване на проблеми.
Решавайки практически задачи с помощта на теорията на графите, стана ясно, че на всяка стъпка, на всеки етап от тяхното решаване е необходимо да се прилага креативност.
От самото начало, на първия етап, се крие във факта, че трябва да можете да анализирате и кодирате състоянието на проблема. Вторият етап е схематична нотация, която се състои в геометрично представяне на графики, като на този етап елементът на творчеството е много важен, тъй като далеч не е лесно да се намерят съответствия между елементите на условието и съответните елементи на графиката .
При решаване на транспортна задача или задача за съставяне на родословно дърво, стигнах до извода, че графичният метод със сигурност е интересен, красив и визуален.
Бях убеден, че графиките се използват широко в икономиката, управлението и технологиите. Теорията на графите се използва и в програмирането.Това не беше обсъждано в тази статия, но мисля, че това е само въпрос на време.
В тази научна работа се разглеждат математическите графики, техните области на приложение, няколко проблема се решават с помощта на графики. Познаването на основите на теорията на графите е необходимо в различни области, свързани с управлението на производството, бизнеса (например диаграма на строителната мрежа, графици за доставка на поща). Освен това, докато работех върху научен труд, усвоих работата на компютър в текст WORD редактор. И така, задачи научна работазавършен.
И така, от всичко казано по-горе, неоспоримо следва практическата стойност на теорията на графите, доказателството на което беше целта на тази работа.
литература
Бердж К.Теория на графите и нейните приложения. -М.: ИИЛ, 1962г.
Кемени Дж., Снел Дж., Томпсън Дж.Въведение в крайната математика. -М.: ИИЛ, 1963г.
Оре О.Графики и тяхното приложение. -М.: Мир, 1965.
Харари Ф.Теория на графите. -М.: Мир, 1973.
Зиков А.А.Теория на крайните графи. -Новосибирск: Наука, 1969.
Березина Л.Ю.Графики и тяхното приложение. -М.: Образование, 1979. -144 с.
„Образователно списание Сорос” № 11 1996 г. (статия „Плоски графики”);
Гарднър М. "Математическо свободно време", М. "Мир", 1972 (глава 35);
Олехник С. Н., Нестеренко Ю. В., Потапов М. К. "Стари забавни проблеми", М. "Наука", 1988 (част 2, раздел 8; приложение 4);
Приложение

Приложение



П 
Ориз. 6


Ориз. 7
Ориз. 8
приложениеПриложение


Приложение

Приложение


П 

Ориз. четиринадесет
приложениеПриложение

Теорията на графите намира приложение, например, в географските информационни системи (ГИС). Съществуващите или новопроектирани къщи, сгради, квартали и др. се считат за върхове, а свързващите ги пътища, инженерни мрежи, електропроводи и др. - за ръбове. Използването на различни изчисления, направени на такава графика, позволява например да се намери най-краткият отклонен път или най-близкия магазин за хранителни стоки, да се планира най-добрият маршрут.
Теорията на графите съдържа голям брой нерешени проблеми и недоказани хипотези.
Основните области на приложение на теорията на графите:
В химията (за описание на структури, начини на сложни реакции, фазовото правило може да се тълкува и като проблем на теорията на графите); компютърната химия е сравнително млада област на химията, базирана на приложението на теорията на графите. Теорията на графите е математическата основа на хемоинформатиката. Теорията на графите дава възможност за точно определяне на броя на теоретично възможните изомери на въглеводороди и други органични съединения;
По информатика и програмиране (диаграма на алгоритъма);
В комуникационните и транспортните системи. По-специално, за маршрутизиране на данни в Интернет;
В икономиката;
в логистиката;
В схемотехниката (топологията на взаимовръзките на елементи на печатна платка или микросхема е графика или хиперграфа).
Има специален вид графика, дърво.дървое свързан ацикличен граф. Свързаността означава наличието на пътища между всяка двойка върхове, ацикличността означава липса на цикли и факта, че има само един път между двойки върхове. На Фиг.1.3подаден двоично дърво.
двоично дървое дървовидна структура от данни, в която всеки възел има най-много два потомци(деца). Обикновено се нарича първият родителски възели децата са кръстени левичарИ прави наследници.
Матрично представяне на графики. Матрицата на инцидентите.
Разработването на алгоритмични подходи за анализиране на свойствата на графиките изисква определени методи за описание на графики, които са по-подходящи за практически изчисления, включително тези с помощта на компютри. Помислете за трите най-често срещани начина за представяне на графики.
Да предположим, че всички върхове и всички ръбове на неориентиран граф или всички върхове и всички дъги (включително бримки) на насочен граф са номерирани, започвайки от единица. Граф (ненасочен или насочен) може да бъде представен като матрица от типа , където е броят на върховете и е броят на ръбовете (или дъгите). За неориентирана графа елементите на тази матрица са дадени, както следва:
За насочена графика матричните елементи са дадени, както следва:

Извиква се матрица на типа, дефинирана по този начин матрица на инцидентите.
Пример за получаване на матрица на честотата. За графиката, показана по-долу ( Ориз. 2.1 аФигура 2.1 b).


Фиг. 2.1 а Фиг. 2.1 б
Матрица на съседство.
Въпреки факта, че представянето на графика под формата на матрица на честотата играе много важна роля в теоретичните изследвания, на практика този метод е много неефективен. На първо място, има само два различни от нула елемента в матрицата във всяка колона, което прави този начин на представяне на графиката неикономичен с голям брой върхове. Освен това решаването на практически проблеми с помощта на матрицата на честотата е много трудоемко.
Нека оценим например времето, прекарано за решаване на такъв прост проблем в насочен граф, използвайки матрицата на инцидентите: за даден връх намерете неговата „среда“ – множеството от наследници и множеството от предшественици на върха, т.е. множеството от всички върхове, от които е пряко достъпно, и множеството от всички върхове, от които е пряко достъпен.
За да решите този проблем, върху матрицата на честотата на насочена графика, трябва да преминете по реда с числото, докато се появи ненулев елемент (+1 или -1). Ако се намери +1, в съответната колона трябва да намерите реда, в който е изписано числото -1. Номерът на реда, съдържащ това число, дава номера на върха, който може да се достигне директно от дадения връх. Ако се намери -1, в колоната трябва да намерите реда, в който е изписано 1, и да получите номера на върха, от който е директно достъпен даден връх. За да получите цялата "среда", трябва да извършите посоченото търсене за всички ненулеви елементи от k-тия ред. Най-отнемащата време процедура е да се намери ненулев елемент в колона. Броят на такива процедури за търсене е равен на степента на върха. В този случай ще кажем, че сложността на алгоритъма за анализиране на средата на даден връх е (от порядъка на).
Може да се види, че намирането на "околната среда" на всички върхове ще отнеме време от порядъка на произведението на броя на върховете на насочения граф, умножено на сумата от степени на всички върхове, което може да се покаже, че е пропорционално на броят на дъгите на насочения граф. По този начин сложността на алгоритъма за търсене на "среда" е, т.е. търсенето отнема време от реда на произведението на броя на върховете и броя на дъгите.
По-ефективна матрична структура, представляваща графика е матрица за съседство на върховете, или булева матрицаграфика. Това е квадратна матрица B от порядък н, чиито елементи са дефинирани, както следва:
за неориентирана графика: ![]()
за ориентирана графика: ![]()
За графиката, показана по-долу ( Ориз. 2.2 а) матрицата на честотата ще бъде матрицата, представена на ( Фигура 2.2 b).
Началото на теорията на графите единодушно се приписва на 1736 г., когато Л. Ойлер решава популярната по това време проблема за мостовете на Кьонигсбер. Този резултат обаче остава единственият резултат от теорията на графите повече от сто години. Едва в средата на 19 век електроинженерът Г. Кирхоф разработва теорията на дърветата за изучаване електрически вериги, а математикът А. Кейли, във връзка с описанието на структурата на въглеводородите, решава изброителни задачи за три вида дървета.
Роден по време на решаване на пъзели и забавни игри (проблеми за шах кон, за дами, “ пътуване около света“, проблеми за сватби и хареми и др.), теорията на графите вече се превърна в прост, достъпен и мощен инструмент за решаване на въпроси, свързани с широк спектър от проблеми. Графиките са буквално повсеместни. Под формата на графики може например да се интерпретират пътни диаграми и електрически вериги, географски карти и молекули на химични съединения, връзки между хора и групи хора. През последните четири десетилетия теорията на графите се превърна в един от най-бързо развиващите се клонове на математиката. Това се дължи на изискванията на бързо разширяваща се област на приложение. Използва се при проектирането на интегрални схеми и схеми за управление, при изучаване на автомати, логически схеми, програмни блок-схеми, в икономиката и статистиката, химията и биологията, в теорията на графика. До голяма степен чрез теорията на графиките сега се осъществява проникването на математическите методи в науката и техниката.
В тази статия ние разглеждаме не собствените проблеми на теорията на графите, а начина, по който тя се използва в училищен курсгеометрия.
Следователно, актуалността на изследователската тема се дължи, от една страна, на популярността на графиките и свързаните с тях изследователски методи, които органично проникват в почти цялата съвременна математика на различни нива, а от друга страна, на интегралната система за нейното прилагане в курсът на геометрията не е разработен.
Целта на изследването е да се проучи използването на графики в училищния курс по геометрия.
Обект е процесът на обучение по геометрия.
Предмет – класни и извънкласни дейности
Задачи: 1) определят същността и съдържанието на използването на графики в училищния курс по геометрия;
2) да се разработи ПМК за провеждане на уроци по геометрия в 7-9 клас.
Водеща тема е изграждането на графичен модел за доказване на геометрични теореми.
Теоретична основа:
1. Теорията на графиките, възникнала през 1736 г. (Леонхард Ойлер (1708-1783) се развива бързо, остава актуална и сега, тъй като през Ежедневиетовсе по-често се използват графични илюстрации, геометрични изображения и други техники и методи за визуализация.
1. Теорията на графите намира приложение в различни области на съвременната математика и многобройните й приложения (Липатов Е.П.)
2. Теорията на графите се използва в такива области на математиката като математическа логика, комбинаторика и др.
Теоретичното значение на работата се крие в:
Идентифициране на областите на приложение на теорията на графите;
Използване на теория на графите за изучаване на геометрични теореми и задачи;
Практическата значимост на работата се крие в използването на графики при доказването на геометрични теореми и при решаването на задачи.
В резултат на тази работа беше създадено следното:
Програмно-методически комплекс за провеждане на уроци по геометрия в 7-9 клас.
Най-трудното нещо при намирането на решение на проблем е да се установи верига от логически следствия, която води до доказуемо твърдение. За да се разсъждава логически компетентно, е необходимо да се развият уменията за такова мислене, което би помогнало за изграждането на различни геометрични факти в логически връзки.
Формите играят специална роля в развитието на уменията за култура на мислене. писанестуденти. Писмените форми на работа са най-важната дейност, която формира устойчиви умения за логически разсъждения при доказване на теореми и решаване на задачи. Формата на записване на условията на задачата, разумни съкращения и означения в изчисленията и доказателствата на проблеми дисциплинира мисленето и насърчава геометричното виждане. Както знаете, зрението поражда мисленето. Възниква проблемът: как да се установят логически връзки между различни геометрични факти и как да се подредят във формата на едно цяло. За да видите напредъка на доказването на теореми и решаването на задачи, методът на графичните схеми позволява, което прави доказателството по-визуално и ви позволява да изложите накратко и точно доказателствата на теоремите и решаването на проблеми.
За това се използва дървовидна графика.
Върховете на „дървото“ (условието на теорема или задача и последователност от логически връзки) са показани като правоъгълници с поставена в тях информация, които след това се свързват със стрелки. Краят на граф-схемата съдържа твърдението, което трябва да се докаже. Описаната форма за доказване на теореми и решаване на задачи е полезна и удобна за студентите, тъй като дава възможност лесно да се разграничат основните етапи на доказване на теорема, решаване на задача.
Изследователска част.
Раздел 1. Изучаване на историята на възникването на теорията на графите.
Математикът Леонхард Ойлер (1707-1783) се счита за основоположник на теорията на графите. Историята на възникването на тази теория може да бъде проследена чрез кореспонденцията на великия учен. Ето превод на латински текст, който е взет от писмото на Ойлер до италианския математик и инженер Маринони, изпратено от Санкт Петербург на 13 март 1736 г.
„Веднъж ми предложиха проблема за остров, намиращ се в град Кьонигсберг и заобиколен от река, през която са прехвърлени седем моста. Въпросът е дали някой може непрекъснато да ги заобикаля, минавайки само веднъж през всеки мост. досега не е успях да направя това, но никой не доказа, че е невъзможно. Този въпрос, макар и банален, ми се стори обаче достоен за внимание, защото нито геометрията, нито алгебрата, нито комбинаторното изкуство са достатъчни за решението му. След дълго обмисляне , намерих лесно правило, базирано на напълно убедително доказателство, с помощта на което при всички задачи от този вид може веднага да се определи дали такава схема може да се направи през произволно брой и произволно разположени мостове или не. те могат да бъдат представени на следващата фигура, на която A означава остров, а B, C и D са части от континента, разделени една от друга с разклонения на реката. мостовете са маркирани с букви a, b, c, d, e, f, g ".
Относно открития от него метод за решаване на проблеми от този вид, Ойлер пише
„Това решение по своята същност изглежда няма много общо с математиката и не ми е ясно защо това решение трябва да се очаква от математик, а не от който и да е друг човек, тъй като това решение се поддържа само от разума и няма нужда да се включват, за да се намери това решение, каквито и да било закони, присъщи на математиката. Така че не знам как се оказва, че въпросите, които имат много малко общо с математиката, е по-вероятно да бъдат разрешени от математиците, отколкото от други."
Така че възможно ли е да заобиколите мостовете на Кьонигсберг, като преминете само веднъж през всеки от тези мостове? За да намерим отговора, нека продължим писмото на Ойлер до Маринони:
„Въпросът е да се определи дали е възможно да се заобиколят всички тези седем моста, минавайки през всеки само веднъж, или не. Моето правило води до следното решение на този въпрос. Първо, трябва да погледнете колко отсечки са разделени от вода - такива, които нямат друг преход от един към друг, освен през моста. В този пример има четири такива секции - A, B, C, D. След това трябва да различите дали броят на мостовете, водещи към тези отделни участъци, е четно или нечетно.Така че в нашия случай пет моста водят до участък А, а три моста към останалите, т.е. решаване на проблема. Когато това е определено, прилагаме следното правило: ако броят на мостовете, водещи до всеки отделен участък, е четен, тогава въпросното отклонение би било възможно и в същото време би било възможно да се стартира това отклонение от който и да е раздел. би било нечетно, защото само един е нечетен не може, тогава дори и тогава преходът би могъл да се направи, както е предписано, но със сигурност трябва да се вземе само началото на обхода от един от тези два участъка, до които води нечетен брой мостове. Ако в крайна сметка имаше повече от два участъка, до които водят нечетен брой мостове, тогава такова движение като цяло е невъзможно; ако тук могат да бъдат цитирани други, по-сериозни проблеми, този метод може да бъде още по-полезен и не бива да се пренебрегва .
Обосновката за горното правило може да се намери в писмо от Л. Ойлер до неговия приятел Елер от 3 април същата година. По-долу ще преразкажем откъс от това писмо.
Математикът пише, че преходът е възможен, ако в разклонения участък на реката има не повече от две зони, до които води нечетен брой мостове. За да улесним да си представим това, ще изтрием вече преминатите мостове на фигурата. Лесно е да се провери, че ако започнем да се движим в съответствие с правилата на Ойлер, преминем един мост и го изтрием, тогава фигурата ще покаже участък, където отново има не повече от две области, до които водят нечетен брой мостове, и в наличието на зони с нечетен брой мостове ще се намираме в една от тях. Продължавайки да се движим така нататък, ще преминем през всички мостове веднъж.
Историята на мостовете на град Кьонигсберг има съвременно продължение.
Проблем На езерото има седем острова, които са свързани помежду си, както е показано на фигура 2. До кой остров трябва да отведе пътниците, за да могат да преминат през всеки мост и само веднъж? Защо пътниците не могат да бъдат отведени до остров А?
Решение. Тъй като този проблем е подобен на проблема с моста на Кьонигсберг, ние също ще използваме правилото на Ойлер, за да го решим. В резултат на това получаваме следния отговор: лодката трябва да отведе пътниците до остров E или F, за да могат да преминат през всеки мост веднъж. Същото правило на Ойлер предполага, че изискваното заобикаляне е невъзможно, ако тръгва от остров А.
По-късно Кьониг (1774-1833), Хамилтън (1805-1865) работят върху графики, сред съвременните математици - К. Берж, О. Оре, А. Зиков.
В исторически план теорията на графите се ражда преди повече от двеста години в хода на решаването на пъзели. Много дълго време тя беше далеч от основните посоки на изследване на учените, беше в областта на математиката в позицията на Пепеляшка, чиито таланти се разкриха напълно едва когато беше в центъра на всеобщото внимание.
Първата работа по теория на графите, на известния швейцарски математик Л. Ойлер, се появява през 1736 г. Тласъкът за развитието на теорията на графите е на границата на 19-ти и 20-ти век, когато броят на трудовете в областта на топологията и комбинаториката, с която има най-тесни връзки, нарасна драстично.родството. Графиките започват да се използват при конструирането на електрически схеми и молекулярни вериги. Като отделна математическа дисциплина теорията на графите е въведена за първи път в работата на унгарския математик Кьониг през 30-те години на ХХ век.
Напоследък графиките и свързаните с тях методи на изследване органично проникват в почти цялата съвременна математика на различни нива. Теорията на графите се разглежда като един от клоновете на топологията; тя също е пряко свързана с алгебрата и теорията на числата. Графиките се използват ефективно в теорията на планирането и управлението, теорията на планирането, социологията, математическата лингвистика, икономиката, биологията, медицината и географията. Графиките се използват широко в области като програмиране, теория на крайните автомати, електроника, при решаване на вероятностни и комбинаторни проблеми, най-кратко разстояниеи др. Математическите забавления и пъзелите също са част от теорията на графите. Теорията на графите се развива бързо, намирайки нови приложения.
Раздел 2. Основни видове, понятия и структура на графиките.
Теорията на графите е математическа дисциплина, създадена с усилията на математиците, така че нейното представяне включва необходимите строги дефиниции.
Графът е съвкупност от краен брой точки, наречени върхове на графиката и свързващи по двойки някои от тези върхове на линии, наречени ръбове или дъги на графиката.
№ Име на графиката Определение Фигура Пример за използването на този тип графика
1 Нулева графа Върхове на графа, които не принадлежат Проблем: Аркадий, Борис. Владимир, Григорий и Дмитрий на срещата не се ръкуваха с никого, всеки се ръкува с всеки по веднъж. Колко ръба са общо се наричат изолирани. ръкостискането беше направено? Ситуацията, съответстваща на момента, в който ръкостисканията все още не са извършени, е пунктирана диаграма, показана на фигурата.
Граф, състоящ се само от изолирани върхове, се нарича нулев граф.
Нотация: O" - графика с върхове и без ръбове
2 Пълни графи Графа, в която всяка двойка върхове Обърнете внимание, че ако пълната графа има n върха, тогава броят на ръбовете ще бъде. Всички ръкостискания са направени.
Обозначение: U" е графика, състояща се от n 10.
върхове и ръбове, свързващи всички възможни двойки от тези върхове. Такава графика може да бъде представена като n-ъгълник, в който са начертани всички диагонали
3 Непълни графики Графики, в които всички не са изградени Ситуацията, когато не всички ръкостискания все още са завършени, ръкуваните A и B, A и D, E и възможните ръбове се наричат непълни D, C и E.
4 Път в графиката. Цикъл. Път в графиката от един връх до друг В точка А има гараж за снегорин. Твърди се, че водачът на колата е бил инструктиран да почиства снега от улиците на частта от града, показана на снимката. Възможно ли е той да завърши работата си на кръстовището, където се намира гаражът, ако е възможно да прокара трасе между тези улици от неговия участък от града по всяка една от тях само веднъж?
върхове.
В този случай нито един ръб на маршрута не трябва да се появява повече от веднъж. Върхът от Това е невъзможен, тъй като затворен път, минаващ през всички ръбове на графа и по който е положен маршрутът, се извиква за всеки ръб само веднъж, ако степените на всички върхове на графа са четни.
началото на пътеката, върха в края на маршрута -
край на пътя. Цикълът е път, на фигурата с помощта на графика е показана диаграма на пътищата между населените места, в която началото и краят съвпадат. Прости точки.
цикълът е цикъл, който не преминава. Например, от точка А (горната част на графиката) до точка H може да се достигне по различни маршрути: ADGH, AEH, AEFCEH, ABCEH.
през един от върховете на графа повече от един Каква е разликата между маршрута AEH и маршрута AEFCEH?
пъти. Фактът, че във втория маршрут на "кръстовището" в точка Е посетихме два пъти.
Този маршрут е по-дълъг от AEH. Маршрут AEH може да бъде получен от маршрут
Ако цикълът включва всички ръбове, AEFCEH "изтрива" маршрута на FCE от последния.
графика веднъж, тогава такъв цикъл. Маршрутът AEH е път в графиката, но маршрутът AEFCEH не е път.
наречена линия на Ойлер.
Свързани и разединени графики. Определение 1: Възможно ли е да се направи рамка от куб с дължина на ръба от тел с дължина 12 dm
Два върха на графиката се наричат свързани, 1 dm, без да се разкъсва проводникът?
ако в графиката има път, който завършва в тези върхове. Ако няма такъв път, върховете се наричат несвързани.
Тъй като пътят, минаващ през всички ръбове на графиката и покрай всеки ръб само веднъж, съществува само в следните случаи:
1) когато степента на всеки връх е четна (пътят е затворен)
2) когато има само два върха с нечетна степен.
Определение 2:
Графът се нарича свързан, ако всяка двойка от неговите върхове е свързана.
Графът се нарича несвързан, ако има поне една несвързана двойка върхове.
6 Дървета Дървото е всяка свързана графа, Приложение № 1. Генеалогично дървоЖолмурзаева Томирис.
върхове. Несвързана графа, състояща се само от дървета, се нарича гора.
7 Изоморфни графики. Графиките, показани на фигурата, дават същата информация. Такива графики се наричат изоморфни (идентични).
8 Концепцията за планарна графика Графика, която може да бъде представена върху задача. В три различни къщи живеят три самолета в съседи, които са се скарали помежду си. Недалеч от мястото, където ребрата му се пресичат от къщите им, има три кладенеца. Възможно ли е само от върховете, се нарича всяка къща да лежи плоска до всеки от кладенците. път, така че да не се пресичат две от тях?
Решение: След като начертаете осем пътеки, можете да се уверите, че не е възможно да нарисувате деветия, който не се пресича с нито един от предварително начертаните пътища.
Изграждаме граф, чиито върхове
А, Б, В, 1, 2, 3
условията на задачата отговарят на къщите и кладенците и ще се опитаме да докажем, че деветият път - ръбът на графиката, който не пресича останалите ребра, не може да бъде начертан.
Начертани ръбове в графиката на фигурата
A1, A2, A3 и B1, B2, VZ (съответстващи на пътищата от къщи A и B до всички кладенци).
Построената графика разделя равнината на три области: X, Y, Z. Върхът B, в зависимост от местоположението му в равнината, попада в една от тези три области. Ако вземете предвид всеки от трите попадения във върха
B към една от областите X, Y или Z, след което се уверете, че всеки път един от върховете на графиката е 1, 2 или 3
(едно от кладенците) ще бъде „недостъпно“ за връх B (т.е. няма да е възможно да се начертае едно от ръбовете B1, B2 или B3, които няма да пресичат ръбовете, които вече са в графиката).
Отговорът на въпроса на задачата ще бъде: „Невъзможно е!“
Насочени графи Ръб на граф се нарича насочен ръб, ако един от неговите върхове се счита за начало, а другият за край на този ръб.
Граф, в който всички ребра са насочени, се нарича насочен граф.
И така, разгледах основните понятия на теорията на графовете, без които би било невъзможно да се доказват теореми и следователно да се решават проблеми.
Заключение за извършената работа:
Научих как да структурирам целия информационен материал в таблица;
Съставът на теоретичния материал допринася за нагледно представяне на видовете графики и тяхното приложение;
Тя разработи примери за прилагане на теорията на графите при съставянето на нейното родословно дърво.
Заявление No1.
ГЕНОЛОГИЧНО ДЪРВО
Изградете родословно дърво на Жолмурзаева Томирис.
Метод на решение.
Графичен начин за решаване на проблема.
Графичен начин за решаване на проблема е да се начертае „дърво на логическите условия“. "Дървото" изразява под формата на проста рисунка логическата връзка между роднините. Всяко поколение на дървото съответства на един клон.
Като пример взех моето родословно дърво.
Раздел 3. Прилагане на теорията на графите.
Срещаме се с графики по-често, отколкото е възможно, изглежда на пръв поглед. Примери за графики могат да бъдат всяка пътна карта, електрическа верига, чертеж на многоъгълници и т. н. Дълго време се смяташе, че теорията на графите се използва главно при решаване на логически задачи. При решаване на логически задачи често е трудно да се запомнят многобройните условия, дадени в задачата, и да се установи връзка между тях.Графиките помагат за решаването на такива задачи, което позволява да се визуализира връзката между данните на задачата. Самата теория на графите се разглеждаше като част от геометрията. Въпреки това, през двадесети век, широки приложения на теорията на графите са открити в икономиката, биологията, химията, електрониката, мрежовото планиране, комбинаториката и други области на науката и технологиите. В резултат на това тя започва да се развива бързо и се превръща в независима разклонена теория.Решаването на много математически задачи се опростява, ако може да се използват графики. Представянето на данните под формата на графика им дава видимост. Много доказателства също се опростяват и стават по-убедителни, ако се използват графики.
3. 1. Приложение на графики в геометрични проблемии теореми.
С помощта на графики може лесно да се установят вериги от логически следствия, които водят до доказуемо твърдение. Накратко и точно изложете доказателството на теоремата и решението на задачата.
Докажи това равнобедрен триъгълниксиметралите, изтеглени от върховете в основата, са равни.
Методи за решение.
Доказателство на проблема чрез разсъждения.
Нека ABC е равнобедрен триъгълник с
B1 A1 основа AB и ъглополовящи AA1 и BB1.
Да разгледаме ∆ABB1 и ∆BAA1. Те имат ∟B1AB=
∟A1BA като ъглите в основата на равнобедрения триъгълник ∆ABC. ∟ABB1= ∟A1AB
A B, тъй като AA1 и BB1 са ъглите на ъглите в основата на равнобедрен триъгълник. AB е общата страна. Средства
∆ABB1 = ∆BAB1 по протежение на страната и два ъгъла, съседни на нея. От равенството на триъгълниците следва равенството на техните страни AA1 и BB1.
Доказателство на проблема с помощта на графика.
Докажете: AA=BB
Нека използваме графика за разсъждения. Върховете на графа са условията на теоремата или задачата и етапите на доказателството.
Ръбовете на графиката са логически следствия. Краят на граф-схемата е твърдението, което трябва да се докаже.
Цветът се използва за подчертаване на компонентите. Условието на теоремата и задачата са сини. Твърдението, което трябва да се докаже, е червено. Стъпките за доказване са в черно.
Описаната форма за доказване на теореми и решаване на задачи е полезна и удобна за студентите, тъй като дава възможност да се отделят основните етапи на доказване на теорема и решаване на задача.
3. 2. Програмно-методически комплекс.
а) Ръководство за учителя.
Предложеното ръководство е съставено в съответствие с учебника по геометрия от 7-9 клас от A. V. Pogorelov. Основната му цел е да осигури процеса на изучаване на геометрията с необходимите средства за визуализация, да подпомогне учителя при преподаване на геометрия: да улесни процеса на доказване на теореми, усвояване на теоретичния материал в процеса на решаване на задачи. Графичните диаграми са многостранни и в зависимост от целите и формите на занятията могат да се използват по различни начини: като илюстративни, насочени към повишаване на видимостта при обяснение на нов теоретичен материал, при обобщаване и систематизиране на нов материал (графични диаграми с теореми); като карти, използвани при провеждане на индивидуални и фронтални проучвания (графични диаграми със задачи). Предлага се това ръководство работна книгаза студенти. Работната тетрадка може да се използва за организиране самостоятелна работаученици по време и след учебните часове.
б) Работна тетрадка за ученици.
Наръчникът е под формата на работна тетрадка. Помагалото включва 28 граф-схеми с теореми и 28 граф-схеми със задачи. Графичните диаграми съдържат основния програмен материал, който е представен с необходимата яснота и представлява рамката на решението. Учениците последователно попълват празните клетки с информация, която съставя решението на проблема.
Цветът се използва за подчертаване на компоненти. Условието на теоремата и задачата са сини, доказваното твърдение е червено, етапите на доказателството са черни.
Помагалото е полезно за ученици от 7-9 клас.
в) Електронно ръководство.
Резултатите от работата и тяхното обсъждане. Проектът е резултат от двугодишно изследване на използването на графики в училищния курс по математика.
Създаване програмно - методически комплекси изпълнението му е извършено в хода на:
Провеждане на занятия на клуб „Аристотел” на тема „Решаване на логически задачи с помощта на графики”.
Приложения на графики в доказателствата на геометрични теореми и задачи
На уроците по геометрия в 8.9 клас.
Изпълнения с проекта в училището научни и практическиконференции.
ЗАКЛЮЧЕНИЕ.
Обобщавайки резултатите от изследването на използването на графики в училищния курс по геометрия, стигнах до следното заключение:
1. Предимството на графичното доказателство на теореми и решаването на проблеми пред традиционното е илюстрирането на динамиката на доказване на теореми и задачи.
2. Въведение в процеса на доказване на геометрични теореми и задачи на метода граф-схема спомага за засилване на уменията на учениците за изграждане на доказателство.
3. Разработеният програмно-методически комплекс за изучаване на геометрия в 7-9 клас: а) ръководство за учителя; б) работна тетрадка за ученици; в) електронното помагало е полезно за ученици от 7-9 клас.
Изпратете вашата добра работа в базата от знания е лесно. Използвайте формуляра по-долу
Студенти, специализанти, млади учени, които използват базата от знания в своето обучение и работа, ще Ви бъдат много благодарни.
Подобни документи
Възстановяване на графики от дадени матрици за съседство на върхове. Построяване за всяка графика на матрицата на съседство на ръбове, честота, достижимост, контрадостижимост. Търсете състава на графиките. Определяне на локални степени на върховете на графа. Потърсете основата на графиките.
лабораторна работа, добавена на 01/09/2009
Теория на графите като клон на дискретната математика, който изучава свойствата на крайните множества с дадени връзки между техните елементи. Основни понятия от теорията на графите. Матрици на съседство и честота и техните практическа употребапри анализиране на решения.
резюме, добавен на 13.06.2011
Основни понятия от теорията на графите. Степен на върха. Маршрути, вериги, цикли. Свързаност и свойства на насочени и равнинни графи, алгоритъм за тяхното разпознаване, изоморфизъм. операции върху тях. Общ преглед на това как да дефинирате графики. Цикли на Ойлер и Хамилтонов.
презентация, добавена на 19.11.2013
Описание на даден граф чрез набори от върхове V и дъги X, списъци на съседство, матрица на инцидентност и съседство. Матрицата на теглото на съответния неориентиран граф. Определяне на дървото с най-къси пътища с помощта на алгоритъма на Дайкстра. Намиране на дървета върху графика.
курсова работа, добавена на 30.09.2014
Основни понятия от теорията на графите. Разстояния в графики, диаметър, радиус и център. Използването на графики в практически човешки дейности. Определяне на най-кратките маршрути. Ойлерови и Хамилтонови графики. Елементи от теорията на графите в факултативни часове.
дисертация, добавена на 19.07.2011г
Понятие и матрично представяне на графики. Насочени и неориентирани графи. Дефиниция на матрицата на съседство. Маршрути, вериги, цикли и техните свойства. Метрични характеристики на графиката. Приложение на теорията на графите в различни области на науката и технологиите.
курсова работа, добавена на 21.02.2009
Математическо описание на системата автоматично управлениес помощта на графики. Изготвяне на графика и нейната трансформация, отърваване от диференциали. Оптимизиране на насочени и неориентирани графи, съставяне на матрици на съседство и честота.
лабораторна работа, добавена 03/11/2012
Текстът на творбата е поставен без изображения и формули.
Пълна версияработата е достъпна в раздела "Работни файлове" в PDF формат
Нашият свят е пълен не само с букви и цифри, но и с голямо разнообразие от изображения. Това са картини и всякакви снимки, както и множество диаграми. Схеми се намират върху лога на компании и автомобили, пътни знации карти. Ако погледнете картата на метрото или автобусен маршрут, това са просто линии с точки. Такива схеми от линии (ръбове) и точки (върхове) се наричат графи.
Теорията на графиките се появи благодарение на един забавен проблем, който Леонхард Ойлер разреши. Историята казва, че през 1736 г. този брилянтен математик се отбива в Кьонигсберг. Градът е разделен от реката на 4 части, свързани със седем моста. Трябваше да се определи дали е възможно да се заобиколят всички мостове, като се премине през всеки точно веднъж. Ойлер установи, че е невъзможно да се реши проблемът. Кьонигсбергските мостове са разрушени по време на Втората световна война, но тази история поражда една красива математическа теория – теория на графите.
През 20-ти век теорията на графите получи невероятно развитие, намери множество приложения в планирането, архитектурата, инженерството и особено в компютърните науки и телекомуникациите. Графиките са свързани с комбинаториката, дискретната математика, топологията, теорията на алгоритмите и други клонове на математиката.
Какви възможности получава студентът, който притежава тази теория? Ще успее ли да постигне някакъв успех в обучението си или обикновен живот? Този проект е посветен на такива изследвания.
Цел на проекта:Покажете, че методите на теорията на графите дават на ученика инструмент за решаване на сложни олимпиадни задачи, а в живота - за организиране на предаването на спешна информация между хората.
Хипотези:
С помощта на графики можете лесно да решите много олимпиадни задачи
Теорията на графиките помага да се създаде система за спешно уведомяване на екипа
задачи:
Научете как да решавате проблеми с помощта на графики
Разработете уебсайт за тестване на олимпиадни задачи
Проектирайте система за спешни предупреждения в класната стая с помощта на графика
Изследователски обекти:олимпиадни проблеми, системи за предупреждение
Предмет на изследване:теория на графите, уеб програмиране.
Изследователски методи:
методи на теория на графите
методи за уеб програмиране
Изследователски план:
Научете за историята на теорията на графите
Научете правилата за решаване на олимпиадни задачи с помощта на графики
Вземете курса "Уеб-програмиране" училище Информационни технологии"ИСТИНСКИ"
Разработете сайт за тестване на олимпиадни задачи по теория на графите и го тествайте на приятели
Проектирайте система за спешно предупреждение в класната стая (SOK).
Проведете експеримент за тестване на системата SOC
Глава 1. Теория на графите в нашия живот
1.1. Приложение на теорията на графите в различни области
Графиките се използват в различни области: при проектирането на електрически вериги, телефонни мрежи, при търсене на маршрути между населени места, в икономиката.
В химията графиките се използват за представяне на различни съединения. За представяне могат да се използват графики прости молекулии доста сложни органични съединения.
Теорията на графите играе ключова роля в различни фази на архитектурни проекти. След като частите на проекта са дефинирани и преди да преминете от скици към чертежи, ще бъде полезно да се изгради графика на връзката на елементите на проекта. Анализът на графиките в обществени сгради ще помогне да се определи степента на достъпност на различни отдели, местоположението на помещенията (бюфет, библиотека и др.), както и пожарните стълби. Графиките ви позволяват значително да опростите анализа трудни ситуации.
В наше време, благодарение на Интернет – „мрежа от мрежи“, която свързва компютрите по целия свят, цифровата революция стана възможна. Мощността на компютрите непрекъснато нараства, но благодарение на мрежите беше възможно да се направи огромен скок към дигиталния свят. Графиките и телекомуникациите винаги са вървели ръка за ръка.
Фигура 1.1 показва различни схеми за свързване на компютри един към друг. Най-често има три начина за свързване на компютри към локална мрежа: "обща шина", "звезда" и "пръстен". Всяка диаграма има графика, така че се използва терминът "мрежова топология". Мрежовата топология е графична конфигурация, чиито върхове са компютри и рутери, а ръбовете са комуникационни линии (кабели) между тях. На фигура 1.2 всички топологии са показани като графики.
Дървото е много проста графика, в която има само един път между всеки два върха. Дърветата се използват в генетиката за илюстриране на семейни връзки (родословни дървета), както и при анализа на вероятностите за различни събития.
Фигура.1.1. Опции за изграждане на локални компютърни мрежи
Фигура 1.2. Опции за изграждане на локални компютърни мрежи
a - общ автобус, b - звезда, c - пръстен
Има много игри, в които трябва да изградите определена графика (лабиринт игри) или да използвате графиката, за да определите дали има печеливша стратегия.
GPS, карти и упътвания за шофиране в мрежата са друг чудесен пример за това как могат да се използват графики. Ръбовете в тях са улици и пътища, а върховете са селища. Върховете на такива графики имат имена, а ръбовете съответстват на числа, показващи разстоянието в километри. Така такава графика е етикетирана и претеглена. Графиките помагат да се визуализират моделите на обществения транспорт, което улеснява планирането на вашето пътуване.
Графиките се използват и в нефтената и газовата промишленост в системите за транспорт на нефт и газ. С помощта на графично-аналитични методи на газопреносни системи е възможно да се избере най-краткият вариант от всички възможни начини за заобикаляне на тръбопровода.
Развитието на компютърните науки доведе до факта, че много математически модели са били използвани в автоматичните процеси. Машината може лесно да се справи с изчисленията, но изборът на най-добрия вариант от набора при несигурност е много по-трудна задача. Появиха се нови алгоритми, които използват механизми, напомнящи биологична революция. Те използват графики като начин за визуализиране на процеси. Моделирането на невроните в човешкия мозък и принципът на тяхното действие са в основата нова теория- теории на невронните мрежи.
1.2. Заключения по глава.
Теорията на графите е намерила своето приложение в много области на науката, технологиите и ежедневието. Но въпреки широкото му приложение в различни области, в училищния курс по математика му се обръща само повърхностно внимание. В същото време различни експерименти в областта на образованието показват, че елементите на теорията на графите имат висока образователна стойност и следователно трябва да бъдат включени в училищната програма.
Наистина ще бъде много полезно за учениците от средното училище да научат основите на теорията на графите, тъй като те ще им помогнат при овладяването на основния курс по математика и особено при решаването на олимпиадни задачи по комбинаторика и теория на вероятностите.
Глава 2
2.1. Теория на графите в олимпиадни задачи
Различни математически олимпиади, като "Кенгуру", "Dino-Olympiad Uchi.ru", Международна евристична олимпиада "Owlet", също често включват проблеми в теорията на графите в различни формулировки.
Както знаете, децата много обичат всичко, свързано с компютрите и интернет, и не е толкова лесно да ги настаните на масата с книга по математика. За да предизвикат интереса на учениците към теорията на графите, авторите на статията, на базата на курсовете по уеб програмиране в Училището по информационни технологии "REAL-IT", разработиха онлайн симулатор, включващ тестване по теория на графите, намиращ се на страницата на тюменското частно училище „Evolventa »: evolventa-tmn.github.io . Учениците са поканени да решат шест задачи с различни нива на трудност, той въвежда отговорите в полетата и след това чрез натискане на бутона „Край“ се показва резултатът: броят на проблемите, които е решил правилно (Фигура 2.1).
Фигура 2.1. Фрагмент от екрана на сайта с тестови опции
Естествено, хитро дете веднага ще започне да търси отговори в търсачките, но няма да намери точно такива формулировки, а само подобни, например на уебсайта на научно-методическото електронно списание "Концепция". Следователно, за да получите желания резултат: 6 от 6 задачи ученикът ще трябва да разбере основни принципирешаване на проблеми с помощта на теория на графите. И в бъдеще придобитите знания ще му помогнат да решава успешно както училищни, така и олимпиадни задачи.
Когато сайтът беше напълно готов, тестван и публикуван в интернет, нашите съученици получиха линк към него. Интересът към сайта беше голям: съдейки по брояча на посещенията, той беше посетен повече от 150 пъти през първата седмица! Много момчета се опитаха да решат проблеми, но те им се сториха трудни. Дори някои родители с по-високи техническо образование, редица задачи объркани, това предполага, че теорията на графите дори не се изучава във всички по-високи образователни институции. Това означава, че подготвеното от нас тестване ще бъде полезно не само за ученици, но и за възрастни!
2.2. Теория на графите при проектиране на система за предупреждение за класове
В момента е дадена сферата на спешната система за управление на персонала в организациите голямо внимание, поради факта, че подобни системи играят съществена роля в организирането на всички дейности на служителите.
Първоначално системите за обществено обявяване и управление на евакуацията бяха замислени за спешно информиране на служителите, персонала и гостите за пожар в сграда, предоставяне на информация и излъчване на важна информация за бърза и успешна евакуация на хората. Днес подобни системи могат да се наблюдават не само в рамките на една организация или предприятие, но и в цялата ни страна, използвани за подобряване на безопасността на хората.
Трябва да се отбележи, че повечето от използваните предупредителни системи са насочени към възрастни. Но най-опасната възраст са децата. Децата също се нуждаят от собствени системи, които да предупреждават повечето от връстниците си във възможно най-кратък срок за предстояща опасност или промяна в ситуацията.
В училище всяко дете прекарва значителна част от времето си: пет до шест дни в седмицата по няколко часа. Ето защо създаването на система за предупреждение за деца би позволило да се организира всяко дете за бърза и компетентна реакция на променената ситуация.
Например, тази система би била много полезна при предаване на съобщение за опасност, информация за спешно събиране или за промяна на ситуацията, когато са в различни части на училището или като цяло в гората на ваканция (Фигура 2.2)
Фигура 2.2. Нашият клас на екскурзия до ГАУ ДО към „Регионален център за преднаборна подготовка и патриотично възпитание „Застава“
В тази работа беше направен опит да се създаде система за колективно уведомяване, използвайки примера на един клас образователна институция: MAOU SOSH No 89.
Тъй като децата сами трябва да разпространяват информация, те трябва да използват само наличните за тях видове комуникация - мобилни комуникации. Цялата ведомост на класа трябва да бъде уведомена, следователно, за да се анализира кое от децата е готово да уведоми кой от приятелите си, беше проведено проучване на класа. Във въпросниците първоначално беше поставено ограничение: всяко дете успява да се обади на максимум четирима приятели, а ако има време, още двама.
Проучването показа доста висока активност на момчетата: като цяло в класа ще бъдат направени около 118 обаждания. Почти невъзможно е да се анализира такъв обем информация в ума, затова беше решено да се използват информационни технологии. Моделът за уведомяване на екипа е най-добре представен като графика. Ръбовете в него са обаждания (или sms), а върховете са деца. Тъй като върховете на графиката имат имена, а ръбовете съответстват на числа, показващи вероятността за повикване (1 или 0,5), тогава такъв график е етикетиран и претеглен. Графиката помага да се визуализира схемата за уведомяване на екипа, което улеснява моделирането.
Беше решено да се визуализира графиката с помощта на инструмента RAMUS CASE, тъй като той ви позволява да работите с цвета на върховете и ръбовете, а също така ви позволява да премествате върхове на графика с ръбове, прикрепени към тях за яснота. Фигура 2.3 показва графика на RNS системата.
На 19 ноември 2017 г. беше изпробвана проектираната система SOK. Първоначално планирахме нотификацията да стане в рамките на три обиколки. За първия кръг (началото на известието) избрахме две деца, на които никой не иска да се обади, но са готови да се обадят, както и самите автори на Проекта (фиг. 2.3, розови блокчета). Допълнителна информация се предава на втория кръг на уведомяване (фиг. 2.4, жълти блокове). И на третия кръг за уведомяване (фиг. 2.4, зелени блокове) целият клас ще бъде информиран. Но по време на експеримента видяхме, че някои деца тренират 1,5-2 часа и не гледат телефона, други с отрицателен баланс следователно не могат да се обадят.
Фигура 2.3. графика за предупреждение за клас
Фигура 2.4. SOK кръгове за предупреждение
Следователно в действителност нашият клас беше уведомен само за 490 минути - това са 8 часа и 10 минути. Но всичко беше 100%. Важното тук е, че нашата система има структура не на дърво, а на графика. И в него няколко пътя водят от един връх до друг, така че във всеки случай всеки ще бъде уведомен!
Фигура 2.6 показва графика на сигналите за класа (брой алармирани хора) спрямо времето (в минути).
Фигура 2.6. график за предупреждения за клас
За да се улесни следенето на известията, по време на процеса на тестване децата трябваше да кажат на авторите на проекта любимата си тема, а те водеха запис кога и кой съобщава информацията.
Друг резултат от теста – проучване на любимите предмети (Фигура 2.7), показа, че децата в нашия клас обичат най-много математиката, информатиката и игрите на открито! А това означава, че те може да харесват теорията на графите точно толкова, колкото и ние.
Фигура 2.7. Кругова диаграма на любимите елементи от класа
2.3. Заключения по глава.
Тествахме и двете хипотези. Сайтът, който разработихме за тестване на олимпиадни задачи по теория на графите, помогна да се установи, че редица олимпиадни задачи просто не могат да бъдат решени без познания по теория на графите, дори и за възрастни инженери. Първата хипотеза беше потвърдена.
Втората хипотеза също се оказа вярна. Проектираната и изпробвана система за колективно известяване, на примера на един клас, даде възможност за уведомяване на целия детски екип за 8 часа и 10 минути. Чрез оптимизиране на графиката можете да постигнете по-бързи резултати.
Заключение.
Надяваме се, че след запознаване с теорията на графите и нейните многобройни приложения в различни области, студентите ще събудят интерес към теорията на графите и ще продължат да изучават самостоятелно този клон на математиката. Резултатът от проучването ще бъдат по-високи резултати на олимпиадите.
Относно приложението на теорията на графите в реалния живот, актуалността на разглежданата тема се подчертава от факта, че създаването на система за предупреждение за деца ще увеличи скоростта на предаване на спешна информация, ще обхване по-голямата част от детския екип, за който ще се използва тази система, ще намали времето за реакция на деца, а също така гарантират максимална безопасност за детския екип. Всичко това показва очевидните предимства от внедряването на проектираната система.
Библиография
Белобородова A.A. Развитие на пространственото мислене с помощта на лабиринтни игри / A.A. Белобородова // „Студентски научен форум“: материали от VIII Международен студентски електронен научна конференция.- 2017. https://www.site/2017/7/26746
Белобородова, A.A. Разработване на уеб симулатор за изучаване на теория на графите / A.A. Белобородова, С.В. Пахотин, А.А. Фролов // Нови информационни технологии в нефтената и газовата индустрия и образованието: материали от VII международна научно-техническа конференция; респ. изд. ТОЙ ЛИ Е. Кузяков. - Тюмен: ТИУ, 2017. - С. 156-159.
Белобородова A.A. Не се губете в математиката! / A.A. Белобородова // XVIII Всеруски детски конкурс за научни изследвания. и творчески разработки "Първи стъпки в науката": сборник с резюмета. - М.: NS Integration, Държавна дума на Федералното събрание на Руската федерация, Министерство на образованието и науката на Русия. - 2016. - С. 110-111 .
Генденщайн, Л.Е. Алиса в страната на математиката. Приказка-приказка / За младши. и средно училищна възраст - Харков: Изд. - търговски. предприятие "Паритет" ООД, 1994.-288 с., ил.
Давлетшин, М.И. Проучване на ефективността на методите за премахване на шума на изображението / M.I. Davletshin, K.V. Сизранцева // Енергоспестяване и иновативни технологиив горивно-енергийния комплекс: материали на междунар. научно-практически. конф. студенти, аспиранти, млади учени и специалисти. Т.1 / отв. редактор A.N. Халин. - Тюмен: ТИУ, 2016. - С. 25-29.
Карнаухова, А.А. Използването на теорията на графите при решаване на проблеми в икономиката / A.A. Карнаухова, А.Ф. Долгополова // Сборник с доклади от VII международна студентска електронна научна конференция „Студентски научен форум”. http://www.scienceforum.ru/2015/991.
Керн, Г. Лабиринти на света. Санкт Петербург: Издателство "Азбука-класика", 2007, 448с.
Краузе, М.В. Приложение на информационните технологии за проектиране на система за колективно уведомяване / М.В. Краузе, А.А. Белобородова, Е.И. Арбузова // Нови информационни технологии в нефтената и газовата индустрия и образованието: материали от VII международна научно-техническа конференция; респ. изд. ТОЙ ЛИ Е. Кузяков. - Тюмен: ТИУ, 2017. - С. 153-156.
Курс "Създаване на уебсайтове" Училище по информационни технологии "REAL-IT" http://it-schools.org/faculties/web/
Светът на математиката: в 40 т. V.11: Клауди Алсина. Карти на метрото и влакови мрежи. Теория на графите./ Пер. от испански - М.: De Agostini, 2014.- 144 с.
Москевич Л. В. Образователна олимпиада - една от формите на извънкласни дейности по математика / Л.В. Москевич // Научно-методическо електронно списание "Концепция". - 2015. - Т. 6. - С. 166-170. - URL: http://e-koncept.ru/2015/65234.htm.
Бележка за населението "Уведомяване на населението при заплаха и извънредна ситуация" http://47.mchs.gov.ru/document/1306125
Румянцев, В.О. Математическо моделиранена газопреносната система с помощта на теория на графите / В. О. Румянцев // Проблеми на геологията и развитието на минералите: сб. научен tr. / TPU. - Томск, 2017. - С. 340 - 342.
Уебсайт на Министерството на извънредните ситуации на Руската федерация http://www.mchs.gov.ru/dop/Kompleksnaja_sistema_jekstrennogo_opoves