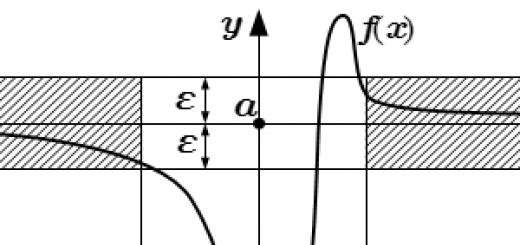
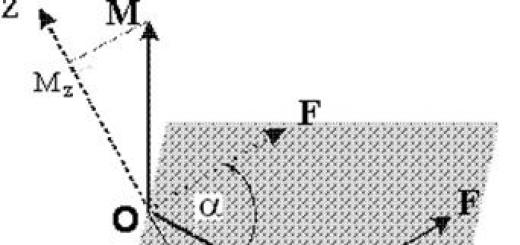
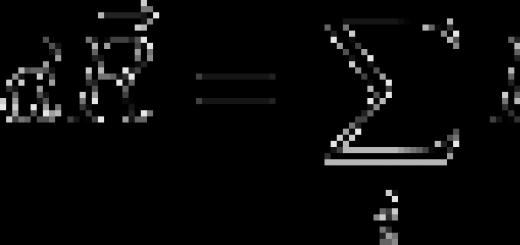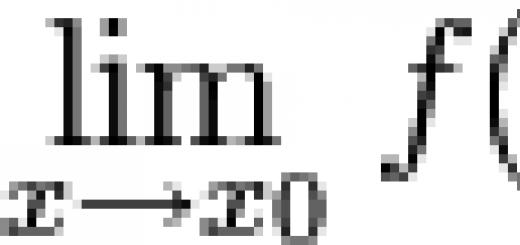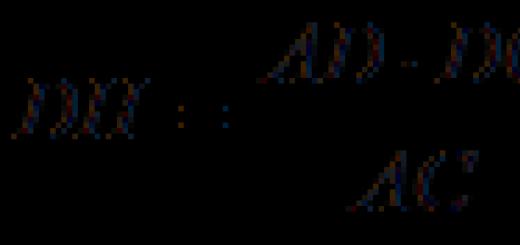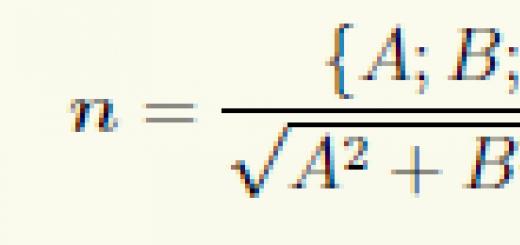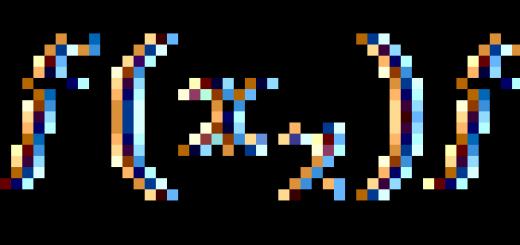Както знаете, математиката обича точността и краткостта - не е без причина една формула да заема абзац в словесна форма, а понякога и цяла страница от текст. По този начин графичните елементи, използвани по целия свят в науката, са предназначени да увеличат скоростта на писане и компактността на представянето на данните. В допълнение, стандартизирани графични изображенияможе да разпознае носител на всеки език, който има основни познания в съответната област.
Историята на математическите знаци и символи датира от много векове - някои от тях са изобретени на случаен принцип и са предназначени да обозначават други явления; други са се превърнали в продукт на дейността на учени, които целенасочено формират изкуствен език и се ръководят единствено от практически съображения.
Плюс и минус
Историята на произхода на символите, обозначаващи протозои аритметични операции, не е известно със сигурност. Съществува обаче доста вероятна хипотеза за произхода на знака плюс, който изглежда като кръстосани хоризонтални и вертикални линии. В съответствие с него символът за добавяне произхожда от латинския съюз et, който се превежда на руски като "и". Постепенно, за да се ускори процеса на писане, думата беше сведена до вертикално ориентиран кръст, наподобяващ буквата t. Най-ранният достоверен пример за такава редукция датира от 14 век.
Общоприетият знак минус се появи, очевидно, по-късно. През 14-ти и дори 15-ти век в научната литература са използвани редица символи, обозначаващи операцията на изваждане и само за XVI век"плюс" и "минус" в съвременната си форма започнаха да се появяват заедно в математическите работи.
Умножение и деление
По ирония на съдбата математическите знаци и символи за тези две аритметични операции не са напълно стандартизирани днес. Популярна нотация за умножение е диагоналният кръст, предложен от математика Оутред през 17 век, който може да се види например на калкулаторите. В уроците по математика в училище една и съща операция обикновено се представя като точка - този метод е предложен през същия век от Лайбниц. Друг начин за представяне е звездичката, която най-често се използва при компютърно представяне на различни изчисления. Беше предложено да се използва всичко в същия 17-ти век, Йохан Ран.
За операцията за разделяне са предвидени наклонена черта (предложена от Ougtred) и хоризонтална линия с точки отгоре и отдолу (символът е въведен от Йохан Ран). Първата версия на обозначението е по-популярна, но втората също е доста често срещана.
Математическите знаци и символи и техните значения понякога се променят с времето. Въпреки това и трите метода за графично представяне на умножението, както и двата метода за деление, са до известна степен последователни и актуални днес.
Равенство, идентичност, еквивалентност
Както при много други математически знаци и символи, нотацията за равенство първоначално е била словесна. От доста дълго време общоприетото обозначение беше съкращението ae от латинското aequalis („равен“). Въпреки това, през 16-ти век, уелски математик на име Робърт Рекорд предложи две хоризонтални линии, една под друга, като символ. Според учения е невъзможно да се измисли нещо по-равно помежду си от два успоредни сегмента.

Въпреки факта, че подобен знак беше използван за обозначаване на паралелизма на линиите, новият символ на равенство постепенно придоби популярност. Между другото, такива знаци като "повече" и "по-малко", изобразяващи разположени в различни страникърлежите се появяват едва през XVII-XVIII век. Днес те изглеждат интуитивни за всеки ученик.
Малко по-сложни знаци за еквивалентност (две вълнообразни линии) и идентичности (три хоризонтални успоредни линии) влизат в употреба едва през втората половина на 19 век.
Знак на неизвестното - "X"
Историята на появата на математически знаци и символи също познава много интересни случаи на преосмисляне на графиката с развитието на науката. Символът за неизвестното, днес наричан "x", произхожда от Близкия изток в зората на последното хилядолетие.
Още през 10-ти век, в арабския свят, известен със своите учени от този исторически период, понятието неизвестно се обозначава с дума, която буквално се превежда като „нещо“ и започва със звука „Sh“. За да се спести материали и време, думата в трактатите започва да се свежда до първата буква.

Много десетилетия по-късно писмените трудове на арабски учени се озовават в градовете на Иберийския полуостров, на територията на съвременна Испания. Научните трактати започнаха да се превеждат на националния език, но възникна трудност - в испанския няма фонема "Sh". Заетите арабски думи, започващи с него, се изписват по специално правило и се предхождат от буквата X. научен езикПо това време е имало латиница, на която съответният знак се нарича "X".
Така знакът, който на пръв поглед е само произволно избран символ, има дълбока история и първоначално е съкращение на арабската дума за „нещо“.
Обозначаване на други неизвестни
За разлика от "X", познатите ни от училище Y и Z, както и a, b, c, имат много по-прозаична история на произход.
През 17 век излиза книгата на Декарт, озаглавена „Геометрия“. В тази книга авторът предлага да се стандартизират символите в уравненията: в съответствие с неговата идея последните три букви от латинската азбука (започвайки от „X“) започнаха да означават неизвестни, а първите три – известни стойности.
Тригонометрични термини
Историята на такава дума като "синус" е наистина необичайна.
Съответните тригонометрични функции първоначално са наречени в Индия. Думата, съответстваща на концепцията за синус, буквално означаваше "низ". В разцвета на арабската наука индийските трактати са преведени и концепцията, която няма аналог в арабски, транскрибирано. По стечение на обстоятелствата случилото се в писмото приличаше на реалната дума „куха“, чиято семантика нямаше нищо общо с оригиналния термин. В резултат на това, когато арабските текстове бяха преведени на латински през 12 век, се появи думата "синус", което означава "депресия" и се фиксира като ново математическо понятие.

Но математическите знаци и символи за тангенс и котангенс все още не са стандартизирани - в някои страни обикновено се изписват като tg, а в други - като tan.
Някои други признаци
Както може да се види от описаните по-горе примери, появата на математически знаци и символи до голяма степен се случи през 16-17 век. В същия период се появяват и обичайните днес форми на запис на понятия като процент, квадратен корен, степен.
Процентът, т.е. една стотна, отдавна се обозначава като cto (съкратено от латински cento). Смята се, че общоприетият днес знак се е появил в резултат на печатна грешка преди около четиристотин години. Полученото изображение се възприема като успешен начин за намаляване и се вкоренява.

Основният знак първоначално е бил стилизирана буква R (съкратено от латинската дума radix, "корен"). Горният ред, под който днес е изписан изразът, служеше като скоби и беше отделен знак, отделен от корена. Скобите са измислени по-късно - те навлизат в широко разпространение благодарение на дейността на Лайбниц (1646-1716). Благодарение на собствената му работа интегралният символ е въведен и в науката, изглеждащ като удължена буква S - съкращение за думата "сума".
И накрая, знакът за степенуване е изобретен от Декарт и усъвършенстван от Нютон през втората половина на 17 век.
По-късни обозначения
Като се има предвид, че познатите графични изображения на „плюс“ и „минус“ бяха пуснати в обращение само преди няколко века, не изглежда изненадващо, че математическите знаци и символи, обозначаващи сложни явления, започнаха да се използват едва през предиминалия век.
Така факториалът, който има формата на удивителен знак след число или променлива, се появява само в началото на XIXвек. Приблизително по същото време главната буква "P" се появи, за да обозначи произведението и символа на границата.

Малко странно е, че знаците за числото пи и алгебрична сумасе появяват едва през 18 век - по-късно от например интегралния символ, въпреки че интуитивно изглежда, че са по-често срещани. Графичното представяне на съотношението на обиколката на кръг към неговия диаметър идва от първата буква на гръцките думи, означаващи „обиколка“ и „периметър“. А знакът "сигма" за алгебричната сума е предложен от Ойлер през последната четвърт на 18 век.
Имена на символи на различни езици
Както знаете, езикът на науката в Европа в продължение на много векове е латински. Физически, медицински и много други термини често са били заимствани под формата на транскрипции, много по-рядко под формата на паус. По този начин много математически знаци и символи на английски се наричат почти по същия начин, както на руски, френски или немски. Как по-твърда същностявления, толкова по-вероятно е това различни езицище има същото име.
Компютърна нотация на математически знаци
Най-простите математически знаци и символи в Word се обозначават с обичайната клавишна комбинация Shift + число от 0 до 9 в руската или английската подредба. За някои широко използвани знаци са запазени отделни клавиши: плюс, минус, равенство, наклонена черта.

Ако искате да използвате графични изображения на интеграла, алгебричния сбор или произведение, числото Pi и т.н., трябва да отворите раздела „Вмъкване“ в Word и да намерите един от двата бутона: „Формула“ или „Символ“. В първия случай ще се отвори конструктор, който ви позволява да изградите цяла формула в едно поле, а във втория - таблица със символи, където можете да намерите всякакви математически символи.
Как да запомня математически символи
За разлика от химията и физиката, където броят на символите за запаметяване може да надхвърли сто единици, математиката оперира с относително малък брой символи. Най-простите от тях научаваме в ранна детска възраст, като се учим да събираме и изваждаме, и само в университета в определени специалности се запознаваме с няколко сложни математически знака и символа. Снимките за деца помагат за няколко седмици да се постигне незабавно разпознаване на графичното изображение на необходимата операция, може да е необходимо много повече време, за да се овладее умението за самото изпълнение на тези операции и да се разбере тяхната същност.
По този начин процесът на запаметяване на знаци става автоматично и не изисква много усилия.
Най-накрая
Стойността на математическите знаци и символи се крие във факта, че те се разбират лесно от хора, които говорят различни езици и са носители на различни култури. Поради тази причина е изключително полезно да се разбират и могат да се възпроизвеждат графични изображения на различни явления и операции.
Високото ниво на стандартизация на тези знаци обуславя използването им в различни области: в областта на финансите, информационните технологии, инженерството и др. За всеки, който иска да прави бизнес, свързан с числа и изчисления, познаване на математически знаци и символи и техните значения се превръща в жизненоважна необходимост.
Безкрайност.Дж. Уолис (1655).
За първи път се среща в трактата на английския математик Джон Валис „За коничните сечения“.
База естествени логаритми. Л. Ойлер (1736).
Математическа константа, трансцендентално число. Даден номерпонякога се нарича не-Перовв чест на шотландцитеучен Напиер, автор на работата "Описание на удивителната таблица на логаритмите" (1614). Константата присъства мълчаливо за първи път в приложение към английския превод на гореспоменатата работа на Нейпиер, публикуван през 1618 г. Същата константа е изчислена за първи път от швейцарския математик Якоб Бернули в хода на решаването на проблема за пределната стойност на дохода от лихви.
2,71828182845904523...
Първата известна употреба на тази константа, където тя е обозначена с буквата б, намерен в писмата на Лайбниц до Хюйгенс, 1690-1691. писмо дзапочва да използва Ойлер през 1727 г., а първата публикация с това писмо е неговата Механика, или Науката за движението, изложена аналитично, 1736 г. респективно добикновено се нарича число на Ойлер. Защо е избрана буквата? д, не е точно известно. Може би това се дължи на факта, че думата започва с него експоненциален(„експоненциално“, „експоненциално“). Друго предположение е, че буквите а, б, ° СИ двече широко използвани за други цели и дбеше първото „безплатно“ писмо.
Съотношението на обиколката на кръга към неговия диаметър. У. Джоунс (1706), Л. Ойлер (1736).
Математическа константа, ирационално число. Числото "пи", старото име е числото на Лудолф. Както всяко ирационално число, π е представено с безкрайна непериодична десетична дроб:
π=3,141592653589793...
За първи път обозначението на това число с гръцката буква π е използвано от британския математик Уилям Джоунс в книгата „Ново въведение в математиката“ и става общоприето след работата на Леонхард Ойлер. Това обозначение идва от началната буква на гръцките думи περιφερεια – кръг, периферия и περιμετρος – периметър. Йохан Хайнрих Ламберт доказа ирационалността на π през 1761 г., а Адриен Мари Лежандър през 1774 г. доказа ирационалността на π 2 . Лежандър и Ойлер предположиха, че π може да бъде трансцендентално, т.е. не може да задоволи никакво алгебрично уравнение с цели коефициенти, което в крайна сметка беше доказано през 1882 г. от Фердинанд фон Линдеман.
въображаема единица. Л. Ойлер (1777, в печат - 1794).
Известно е, че уравнението x 2 = 1има два корена: 1 И -1 . Въображаемата единица е един от двата корена на уравнението x 2 \u003d -1, обозначава се с латинската буква и, друг корен: -i. Това обозначение е предложено от Леонхард Ойлер, който е взел първата буква на латинската дума за това имагинариус(въображаем). Той също така разшири всички стандартни функции към сложния домейн, т.е. набор от числа, представими във формата a+ib, където аИ бса реални числа. Терминът "комплексно число" е въведен в широка употреба от немския математик Карл Гаус през 1831 г., въпреки че преди това терминът е бил използван в същия смисъл от френския математик Лазар Карно през 1803 г.
Единични вектори. У. Хамилтън (1853).
Единичните вектори често се свързват с координатните оси на координатната система (по-специално с осите на декартовата координатна система). Единичен вектор, насочен по оста х, обозначено и, единичен вектор, насочен по оста Й, обозначено j, и единичният вектор, насочен по оста З, обозначено к. вектори и, j, ксе наричат ортове, те имат модули за идентичност. Терминът "орт" е въведен от английския математик и инженер Оливър Хевисайд (1892 г.), а нотацията и, j, кИрландският математик Уилям Хамилтън.
Цялата част от число, antie. К. Гаус (1808).
Цялата част от числото [x] на числото x е най-голямото цяло число, което не надвишава x. И така, =5, [-3,6]=-4. Функцията [x] се нарича още "антиера на x". Символът на функцията на цяло число е въведен от Карл Гаус през 1808 г. Някои математици предпочитат вместо това да използват обозначението E(x), предложено през 1798 г. от Лежандър.
Ъгъл на паралелизъм. Н.И. Лобачевски (1835).
На равнината на Лобачевски - ъгълът между линиятабпреминаване през точкатаОТНОСНОуспоредно на права линияа, без точкаОТНОСНО, и перпендикулярно отОТНОСНОна а. α е дължината на този перпендикуляр. Тъй като точката е премахнатаОТНОСНОот направо аъгълът на паралелизъм намалява от 90° на 0°. Лобачевски дава формула за ъгъла на паралелизъмP( α )=2arctg e - α /q , където qе някаква константа, свързана с кривината на пространството на Лобачевски.
Неизвестни или променливи количества. Р. Декарт (1637).
В математиката променливата е величина, характеризираща се с набор от стойности, които може да приеме. Това може да означава както реално физическо количество, временно разглеждано изолирано от неговия физически контекст, така и някакво абстрактно количество, което няма аналози в реалния свят. Концепцията за променлива възниква през 17 век. първоначално под влияние на изискванията на естествените науки, които извеждат на преден план изучаването на движението, процесите, а не само състоянията. Тази концепция изисква нови форми за изразяването си. Такива нови форми бяха буквалната алгебра и аналитична геометрияРене Декарт. За първи път правоъгълната координатна система и обозначението x, y са въведени от Рене Декарт в неговия труд „Беседа за метода“ през 1637г. Пиер Ферма също допринася за развитието на координатния метод, но работата му е публикувана за първи път след смъртта му. Декарт и Ферма използваха координатния метод само на равнината. координатен методза триизмерно пространство е използвано за първи път от Леонхард Ойлер още през 18 век.
вектор. О.Коши (1853).
От самото начало под вектор се разбира обект, който има величина, посока и (по избор) точка на приложение. Началото на векторното смятане се появява заедно с геометричния модел комплексни числав Гаус (1831). Разширените операции върху вектори са публикувани от Хамилтън като част от неговото кватернионно смятане (въображаемите компоненти на кватерниона образуват вектор). Хамилтън измисли термина вектор(от латинската дума вектор, носител) и описва някои операции за векторен анализ. Този формализъм е използван от Максуел в неговите работи върху електромагнетизма, като по този начин привлича вниманието на учените към новото смятане. Скоро следват „Елементите на векторния анализ“ на Гибс (1880-те), а след това Хевисайд (1903) придава на векторния анализ неговия модерен вид. Самият векторен знак е въведен от френския математик Огюстен Луи Коши през 1853 г.
Събиране, изваждане. Дж. Уидман (1489).
Знаците плюс и минус очевидно са измислени в немската математическа школа на "косистите" (тоест алгебраисти). Използвани са в учебника на Ян (Йоханес) Видман „Бързо и приятно преброяване за всички търговци“, публикуван през 1489 г. Преди това добавянето се означаваше с буквата стр(от лат плюс„повече“) или латинската дума et(съвет "и"), а изваждане - по буква м(от лат минус"по-малко, по-малко"). В Widman символът плюс замества не само събирането, но и съюза "и". Произходът на тези символи е неясен, но най-вероятно те са били използвани преди това в търговията като знаци за печалба и загуба. И двата символа скоро станаха често срещани в Европа – с изключение на Италия, която използва старите обозначения от около век.
Умножение. В. Аутред (1631), Г. Лайбниц (1698).
Знакът за умножение под формата на наклонен кръст е въведен през 1631 г. от англичанина Уилям Аутред. Преди него най-често използваното писмо М, въпреки че бяха предложени и други обозначения: символът на правоъгълника (френският математик Еригон, 1634 г.), звездичката (швейцарският математик Йохан Ран, 1659 г.). По-късно Готфрид Вилхелм Лайбниц заменя кръста с точка (края на 17 век), за да не се бърка с буквата х; преди него такава символика е открита от немския астроном и математик Региомонтанус (XV век) и английския учен Томас Хариът (1560 -1621).
дивизия. И. Ран (1659), Г. Лайбниц (1684).
Уилям Аутред използва наклонената черта / като знак за деление. Дебелото черво започна да обозначава Готфрид Лайбниц. Преди тях буквата също беше често използвана д. Като се започне от Фибоначи, се използва и хоризонталната линия на дроба, която е използвана от Херон, Диофант и в арабските писания. В Англия и Съединените щати символът ÷ (obelus), който беше предложен от Йохан Ран (вероятно с участието на Джон Пел) през 1659 г., стана широко разпространен. Опит на Американския национален комитет по математически стандарти ( Национален комитет по математически изисквания) премахването на обела от практиката (1923 г.) беше неубедително.
Процент. М. де ла Порт (1685).
Една стотна от цялото, взета като единица. Самата дума "процент" идва от латинското "pro centum", което означава "сто". През 1685 г. в Париж излиза книгата Наръчник по търговска аритметика от Матьо де ла Порт. На едно място ставаше дума за проценти, което тогава означаваше "cto" (съкратено от cento). Набирачът обаче обърка това "cto" за част и написа "%". Така че поради печатна грешка този знак влезе в употреба.
![]()
Градуси. Р. Декарт (1637), И. Нютон (1676).
Съвременната нотация за степента е въведена от Рене Декарт в неговата " геометрии“(1637 г.), обаче, само за естествени градусис експоненти, по-големи от 2. По-късно Исак Нютон разшири тази форма на нотация до отрицателни и дробни експоненти (1676), чиято интерпретация вече беше предложена по това време: фламандският математик и инженер Саймън Стивин, английският математик Джон Уолис и френският математик Албер Жирар.
аритметичен корен нстепен на реално число но ≥0, - неотрицателно число н-та степен на която е равна на но. Аритметичният корен от 2-ра степен се нарича корен квадратен и може да се запише без да се посочва степента: √. Аритметичният корен от 3-та степен се нарича кубичен корен. Средновековните математици (например Кардано) означават квадратния корен със символа R x (от лат. Radix, корен). Съвременното обозначение е използвано за първи път от немския математик Кристоф Рудолф от Косистката школа през 1525 г. Този символ идва от стилизираната първа буква на същата дума радикс. Линията над радикалния израз отначало липсваше; по-късно е въведена от Декарт (1637) с друга цел (вместо скоби) и скоро тази характеристика се слива със знака на корена. Кубичният корен през 16 век е обозначен както следва: R x .u.cu (от лат. Radix universalis cubica). Алберт Жирар (1629) започва да използва обичайната нотация за корен от произволна степен. Този формат е създаден благодарение на Исак Нютон и Готфрид Лайбниц.
Логаритъм, десетичен логаритъм, естествен логаритъм. И. Кеплер (1624), Б. Кавалиери (1632), А. Принсхайм (1893).
Терминът "логаритъм" принадлежи на шотландския математик Джон Нейпиър ( "Описание на невероятната таблица на логаритмите", 1614); възникнало е от комбинация от гръцките думи λογος (дума, отношение) и αριθμος (число). Логаритъмът на J. Napier е помощно число за измерване на съотношението на две числа. Съвременната дефиниция на логаритъма е дадена за първи път от английския математик Уилям Гардинър (1742). По дефиниция логаритъмът на число бпо разум а (а ≠ 1, a > 0) - степен м, до което числото трябва да се повиши а(наречена основа на логаритъма), за да получите б. Обозначава се log a b.Така, m = дневник а б, ако a m = b.
Първите таблици с десетични логаритми са публикувани през 1617 г. от професора по математика от Оксфорд Хенри Бригс. Следователно в чужбина десетични логаритмичесто наричани бриги. Терминът "естествен логаритъм" е въведен от Пиетро Менголи (1659) и Николас Меркатор (1668), въпреки че лондонският учител по математика Джон Спайдел състави таблица с естествени логаритми още през 1619 година.
До края на 19-ти век не е имало общоприето обозначение за логаритъма, основата апосочен отляво и над символа дневник, след това над него. В крайна сметка математиците стигнаха до извода, че най-удобното място за основата е под линията, след символа дневник. Знакът на логаритъма - резултат от намаляването на думата "логаритъм" - се появява в различни форми почти едновременно с появата на първите таблици от логаритми, напр. Дневник- И. Кеплер (1624) и Г. Бригс (1631), дневник- Б. Кавалиери (1632). Обозначаване вътрешенза естествения логаритъм е въведен от немския математик Алфред Прингсхайм (1893).
![]()
Синус, косинус, тангенс, котангенс. W. Outred (средата на 17 век), I. Bernoulli (18 век), L. Euler (1748, 1753).
Съкратената нотация за синус и косинус е въведена от Уилям Аутред в средата на седемнадесетивек. Съкращения за тангенс и котангенс: tg, ctgвъведени от Йохан Бернули през 18 век, те се разпространяват в Германия и Русия. В други страни се използват имената на тези функции. тен, креватчепредложено от Алберт Жирар още по-рано, в началото на XVIIвек. IN съвременна форматеорията на тригонометричните функции е изведена от Леонхард Ойлер (1748, 1753) и ние му дължим консолидирането на реалния символизъм.Терминът "тригонометрични функции" е въведен от немския математик и физик Георг Симон Клугел през 1770 г.
Синусовата линия на индийските математици първоначално се е наричала "арха джива"("полуструна", тоест половината от акорда), след това думата "арха"беше изхвърлен и синусоидната линия започна да се нарича просто "джива". Арабските преводачи не са превели думата "джива"арабска дума "ватар", обозначавайки тетивата и акорда, и се транскрибира с арабски букви и започва да нарича синусоида "джиба". Тъй като кратките гласни не са посочени на арабски, а дългите "и" в думата "джиба"обозначен по същия начин като полугласната "y", арабите започнаха да произнасят името на синусоида "насмешка", което буквално означава "куха", "пазна". Когато превеждаха арабски произведения на латински, европейските преводачи превеждаха думата "насмешка"латинска дума синус, имащи същото значение.Терминът "тангенс" (от лат.допирателни- трогателен) е въведен от датския математик Томас Финке в неговата Геометрия на кръга (1583).
![]()
Арксинус. К. Шерфер (1772), Ж. Лагранж (1772).
Обратните тригонометрични функции са математически функции, които са обратни на тригонометричните функции. Името на обратната тригонометрична функция се образува от името на съответната тригонометрична функция чрез добавяне на префикса "дъга" (от лат. дъга- дъга).Обратните тригонометрични функции обикновено включват шест функции: арксинус (арксин), арккосинус (арккос), арктангенс (arctg), арккотангенс (arcctg), арксеканс (арксеканс) и арккосеканс (арккосекант). За първи път специални символи за обратни тригонометрични функции са използвани от Даниел Бернули (1729, 1736).Начин на отбелязване на обратни тригонометрични функции с префикс дъга(от лат. arcus, arc) се появява при австрийския математик Карл Шерфер и се утвърждава благодарение на френския математик, астроном и механик Жозеф Луи Лагранж. Имаше се предвид, че например обичайният синус ви позволява да намерите хордата, която го стяга по дъгата на окръжност, и обратна функциярешава обратния проблем. До края на 19-ти век английските и немските математически школи предлагат друго обозначение: sin -1 и 1/sin, но те не са широко използвани.
Хиперболичен синус, хиперболичен косинус. В. Рикати (1757).
Историците откриват първата поява на хиперболични функции в писанията на английския математик Абрахам дьо Муавр (1707, 1722). Съвременната дефиниция и подробното им изследване е извършено от италианеца Винченцо Рикати през 1757 г. в работата "Opusculorum", той също предлага техните обозначения: ш,гл. Рикати изхожда от разглеждането на единична хипербола. Независимо откритие и по-нататъшно изследване на свойствата на хиперболичните функции е извършено от немския математик, физик и философ Йохан Ламберт (1768), който установява широк паралелизъм между формулите на обикновената и хиперболичната тригонометрия. Н.И. Впоследствие Лобачевски използва този паралелизъм, опитвайки се да докаже последователността на неевклидовата геометрия, в която обикновената тригонометрия се заменя с хиперболична.
Подобен на тригонометричен синуси косинус са координатите на точка на координатен кръг, хиперболичният синус и косинус са координатите на точка от хиперболата. Хиперболични функциисе изразяват чрез експонента и са тясно свързани с тригонометрични функции: sh(x)=0,5(e х-е-х) , ch(x)=0.5(e x +e -x). По аналогия с тригонометричните функции, хиперболичният тангенс и котангенсът се дефинират като съотношения на хиперболичен синус и косинус, косинус и синус, съответно.
![]()
![]()
Диференциал. Г. Лайбниц (1675, в печат 1684).
Основната, линейна част на функцията инкремент.Ако функцията y=f(x)една променлива x има при x=x0производна и приращениеΔy \u003d f (x 0 +? x)-f (x 0)функции f(x)може да се представи катоΔy \u003d f "(x 0) Δx + R (Δx) , където член Рбезкрайно малък в сравнение сΔx. Първи членdy=f"(x 0 )Δxв това разширение се нарича диференциал на функцията f(x)в точкатаx0. IN произведения на Готфрид Лайбниц, Якоб и Йохан Бернули дума"диференция"е използвано в смисъла на "приращение", И. Бернули го обозначи чрез Δ. Г. Лайбниц (1675 г., публикуван през 1684 г.) използва означението за "безкрайно малка разлика"д- първата буква на думата"диференциал", образувано от него от"диференция".
Неопределен интеграл. Г. Лайбниц (1675, в печат 1686).
Думата "интеграл" е използвана за първи път в печат от Якоб Бернули (1690). Може би терминът произлиза от латински цяло число- цяла. Според друго предположение основата е била латинската дума интегро- възстановяване, възстановяване. Знакът ∫ се използва за обозначаване на интеграл в математиката и е стилизирано представяне на първата буква на латинска дума сума-сума За първи път е използван от немския математик Готфрид Лайбниц, основателят на диференциалното и интегралното смятане, в края на 17 век. Друг от основателите на диференциалното и интегралното смятане, Исак Нютон, не предлага алтернативна символика на интеграла в своите произведения, въпреки че се опитва различни опции: вертикална лента над функция или квадратен символ, който предхожда или заобикаля функция. Неопределен интеграл за функция y=f(x)е съвкупността от всички първопроизводни на дадена функция.

Определен интеграл. Ж. Фурие (1819-1822).
Определен интеграл от функция f(x)с долна граница аи горна граница бможе да се определи като разликата F(b) - F(a) = a ∫ b f(x)dx , където F(x)- някои първопроизводна на функция f(x) . Определен интеграл a ∫ b f(x)dx числено равна на площфигура, ограничена от оста x, прави линии x=aИ x=bи функционална графика f(x). Дизайнът на определен интеграл в познатия ни вид е предложен от френския математик и физик Жан Батист Жозеф Фурие в началото на 19 век.
![]()
Производна. Г. Лайбниц (1675), Ж. Лагранж (1770, 1779).
Производна - основната концепция на диференциалното смятане, характеризираща скоростта на промяна на функция f(x)когато аргументът се промени х . Дефинира се като граница на съотношението на приращението на функция към приращението на нейния аргумент, тъй като приращението на аргумента клони към нула, ако съществува такава граница. Функция, която има крайна производна в дадена точка, се нарича диференцируема в тази точка. Процесът на изчисляване на производната се нарича диференциране. Обратният процес е интегрирането. В класическото диференциално смятане производната най-често се дефинира чрез концепциите на теорията на границите, но исторически теорията на границите се появява по-късно от диференциалното смятане.
Терминът "производна" е въведен от Жозеф Луи Лагранж през 1797 г.; dy/dx- Готфрид Лайбниц през 1675 г. Начинът за обозначаване на производната по отношение на времето с точка над буквата идва от Нютон (1691).Руският термин "производна на функция" е използван за първи път от руски математикВасилий Иванович Висковатов (1779-1812).
Частна производна. А. Лежандър (1786), Ж. Лагранж (1797, 1801).
За функции на много променливи се дефинират частични производни - производни по отношение на един от аргументите, изчислени при допускането, че останалите аргументи са постоянни. Нотация ∂f/ ∂ х, ∂ z/ ∂ гвъведена от френския математик Адриен Мари Лежандре през 1786 г.; ех",zx"- Жозеф Луи Лагранж (1797, 1801); ∂ 2z/ ∂ x2, ∂ 2z/ ∂ х ∂ г- частни производни от втори ред - немският математик Карл Густав Якоб Якоби (1837).
Разлика, увеличение. И. Бернули (края на 17 век - първата половина на 18 век), Л. Ойлер (1755).
Обозначаването на приращението с буквата Δ е използвано за първи път от швейцарския математик Йохан Бернули. Символът "делта" влезе в общата практика за използване на символа "делта" след работата на Леонхард Ойлер през 1755 г.
Сума Л. Ойлер (1755).
Сумата е резултат от добавяне на стойности (числа, функции, вектори, матрици и т.н.). За обозначаване на сумата от n числа a 1, a 2, ..., an се използва гръцката буква "sigma" Σ: a 1 + a 2 + ... + an = Σ ni=1 ai = Σ n 1 ai . Знакът Σ за сумата е въведен от Леонхард Ойлер през 1755 г.
Работете. К. Гаус (1812).
Продуктът е резултат от умножение. За означаване на произведението на n числа a 1, a 2, ..., a n се използва гръцката буква "pi" Π: a 1 a 2 ... a n = Π n i=1 a i = Π n 1 a i . Например, 1 3 5 ... 97 99 = ? 50 1 (2i-1). Символът Π за продукта е въведен от немския математик Карл Гаус през 1812 г. В руската математическа литература терминът "работа" се среща за първи път от Леонти Филипович Магнитски през 1703 г.
Факториален. К.Кръмп (1808).
Факториалът на число n (означава се n!, произнася се "en factorial") е произведението на всички естествени числа до и включително n: n! = 1 2 3 ... n. Например 5! = 1 2 3 4 5 = 120. По дефиниция 0! = 1. Факториалът е дефиниран само за неотрицателни цели числа. Факториалът на число n е равен на броя на пермутациите на n елемента. Например 3! = 6, наистина,
♣ ♦
♣ ♦
♣ ♦
♦ ♣
♦ ♣
♦ ♣
Всичките шест и само шест пермутации на три елемента.
Терминът "факториален" е въведен от френския математик и политическа фигураЛуи Франсоа Антоан Арбогаст (1800), обозначение n! - френски математик Кристиан Крамп (1808).
Модул, абсолютна стойност. К. Вайерщрас (1841).
Модул, абсолютната стойност на реалното число x - неотрицателно число, дефинирано както следва: |x| = x за x ≥ 0 и |x| = -x за x ≤ 0. Например, |7| = 7, |- 0,23| = -(-0,23) = 0,23. Модулът на комплексно число z = a + ib е реално число, равно на √(a 2 + b 2).
Смята се, че терминът "модул" е предложен да се използва от английския математик и философ, ученик на Нютон, Роджър Коутс. Готфрид Лайбниц също използва тази функция, която той нарече „модул“ и обозначи: mol x. Общо обозначение абсолютна стойноствъведена през 1841 г. от немския математик Карл Вайерщрас. За комплексните числа това понятие е въведено от френските математици Огюстен Коши и Жан Робер Арган в началото на 19 век. През 1903 г. австрийският учен Конрад Лоренц използва същата символика за дължината на вектор.
норма. Е. Шмид (1908).
Нормата е функционалност, дефинирана на векторно пространствои обобщаване на концепцията за дължината на вектор или модул на число. Знакът "норма" (от латинската дума "norma" - "правило", "проба") е въведен от немския математик Ерхард Шмид през 1908 г.
![]()
Лимит. S. Luillier (1786), W. Hamilton (1853), много математици (до началото на 20 век)
Лимит - едно от основните понятия на математическия анализ, което означава, че определена променлива в процеса на въпросната си промяна се доближава до определена стойност за неопределено време постоянна стойност. Концепцията за граница е използвана интуитивно още през втората половина на 17-ти век от Исак Нютон, както и от математиците от 18-ти век, като Леонард Ойлер и Джоузеф Луи Лагранж. Първите строги дефиниции на границата на последователност са дадени от Бернар Болцано през 1816 г. и Огюстен Коши през 1821 г. Символът lim (първите 3 букви от латинската дума limes - граница) се появява през 1787 г. при швейцарския математик Симон Антоан Жан Луийе, но използването му все още не прилича на съвременното. Изразът lim в по-позната за нас форма е използван за първи път от ирландския математик Уилям Хамилтън през 1853 г.Вайерщрас въведе обозначение, близко до съвременното, но вместо стрелката, с която сме свикнали, използва знака за равенство. Стрелката се появява в началото на 20-ти век с няколко математици наведнъж - например с английския математик Годфрид Харди през 1908 г.
Дзета функция, d Дзета функция на Риман. Б. Риман (1857).
Аналитична функция на комплексна променлива s = σ + it, за σ > 1, определена от абсолютно и равномерно сходящия ред на Дирихле:
ζ(s) = 1 -s + 2 -s + 3 -s + ... .
За σ > 1 е валидно представянето под формата на произведението на Ойлер:
ζ(s) = Πстр (1-p -s) -s ,
където произведението е взето върху всички прости числа p. Дзета функцията играе голяма роля в теорията на числата.Като функция на реална променлива, дзета функцията е въведена през 1737 г. (публикувана през 1744 г.) от Л. Ойлер, който посочва нейното разлагане в продукт. Тогава тази функция е разгледана от немския математик Л. Дирихле и особено успешно от руския математик и механик П.Л. Чебишев в изследването на закона за разпределението прости числа. Въпреки това, най-дълбоките свойства на дзета функцията са открити по-късно, след работата на немския математик Георг Фридрих Бернхард Риман (1859), където дзета функцията се разглежда като функция на комплексна променлива; той също така въвежда името "дзета функция" и обозначението ζ(s) през 1857 г.
Гама функция, Γ-функция на Ойлер. А. Лежандър (1814).
Гама функцията е математическа функция, която разширява понятието факториал до полето на комплексните числа. Обикновено се означава с Γ(z). Z-функцията е въведена за първи път от Леонхард Ойлер през 1729 г.; дефинира се по формулата:
Γ(z) = limn→∞ n! n z /z(z+1)...(z+n).
Изразено чрез G-функцията голям бройинтеграли, безкрайни произведения и суми от редове. Широко използван в аналитичната теория на числата. Името "гама функция" и обозначението Γ(z) са предложени от френския математик Адриен Мари Лежандър през 1814 г.
Бета функция, B функция, Ойлер B функция. Ж. Бине (1839).
Функция на две променливи p и q, дефинирани за p>0, q>0 от равенството:
B(p, q) = 0 ∫ 1 x p-1 (1-x) q-1 dx.
Бета функцията може да бъде изразена чрез Γ-функцията: В(p, q) = Γ(p)Г(q)/Г(p+q).Точно както гама функцията за цели числа е обобщение на факториала, бета функцията в известен смисъл е обобщение на биномните коефициенти.
Много свойства са описани с помощта на бета функцията.елементарни частициучастващи в силно взаимодействие. Тази особеност е забелязана от италианския физик-теоретикГабриеле Венецианопрез 1968г. Започнатеория на струните.
Името "бета функция" и обозначението B(p, q) са въведени през 1839 г. от френския математик, механик и астроном Жак Филип Мари Бине.
Оператор на Лаплас, лапласиан. Р. Мърфи (1833).
Линеен диференциален оператор Δ, който функционира φ (x 1, x 2, ..., x n) от n променливи x 1, x 2, ..., x n асоциира функцията:
Δφ \u003d ∂ 2 φ / ∂x 1 2 + ∂ 2 φ / ∂x 2 2 + ... + ∂ 2 φ / ∂x n 2.
По-специално, за функция φ(x) на една променлива, операторът на Лаплас съвпада с оператора на 2-ра производна: Δφ = d 2 φ/dx 2 . Уравнението Δφ = 0 обикновено се нарича уравнение на Лаплас; от тук идват имената "оператор на Лаплас" или "Лапласиан". Означението Δ е въведено от английския физик и математик Робърт Мърфи през 1833 г.
Хамилтонов оператор, оператор набла, хамилтонов оператор. О. Хевисайд (1892).
Векторен диференциален оператор на формата
∇ = ∂/∂x и+ ∂/∂y j+ ∂/∂z к,
където и, j, И к- координатни вектори. Чрез оператора nabla основните операции на векторния анализ, както и оператора на Лаплас, се изразяват по естествен начин.
През 1853 г. ирландският математик Уилям Роуън Хамилтън въвежда този оператор и измисля символа ∇ за него под формата на обърната гръцка буква Δ (делта). В Хамилтън точката на символа сочи наляво; по-късно, в трудовете на шотландския математик и физик Питър Гътри Тейт, символът придоби модерен вид. Хамилтън нарече този символ думата "atled" (думата "делта" се чете обратно). По-късно английските учени, включително Оливър Хевисайд, започват да наричат този символ "набла", след името на буквата ∇ във финикийската азбука, където се среща. Произходът на буквата се свързва с музикален инструмент като арфата, ναβλα (nabla) на старогръцки означава „арфа“. Операторът се наричал оператор на Хамилтън или оператор набла.
Функция. И. Бернули (1718), Л. Ойлер (1734).
математическа концепция, което отразява връзката между елементите на множествата. Можем да кажем, че функцията е "закон", "правило", според което на всеки елемент от едно множество (наречен домейн на дефиниция) се приписва някакъв елемент от друго множество (наречен домейн от стойности). Математическата концепция за функция изразява интуитивна идея за това как една величина напълно определя стойността на друга величина. Често терминът "функция" означава числова функция; тоест функция, която поставя едни числа в съответствие с други. Дълго време математиците дадоха аргументи без скоби, например, като това - φх. Тази нотация е използвана за първи път от швейцарския математик Йохан Бернули през 1718 г.Скобите се използват само ако има много аргументи или ако аргументът е сложен израз. Ехото от онези времена са често срещани и сега са записаниsin x, lg xи т.н. Но постепенно използването на скоби, f(x) , стана основно правило. И основната заслуга в това принадлежи на Леонхард Ойлер.
Равенство. R. Record (1557).
Знакът за равенство е предложен от уелския лекар и математик Робърт Рекорд през 1557 г.; очертанията на героя бяха много по-дълги от сегашните, тъй като имитираха изображението на два успоредни сегмента. Авторът обясни, че няма нищо по-равно в света от два успоредни сегмента с еднаква дължина. Преди това в древната и средновековната математика равенството се означаваше устно (напр. est egale). Рене Декарт през 17 век започва да използва æ (от лат. aequalis), но модерен знактой използва равенства, за да посочи, че коефициентът може да бъде отрицателен. Франсоа Виет обозначи изваждането със знак за равенство. Символът на Рекорда не се разпространи веднага. Разпространението на символа Рекорд беше възпрепятствано от факта, че от древни времена един и същ символ е бил използван за обозначаване на успоредността на линиите; в крайна сметка беше решено символът на паралелизма да бъде вертикален. В континентална Европа знакът "=" е въведен от Готфрид Лайбниц едва в началото на 17-18 век, тоест повече от 100 години след смъртта на Робърт Рекорд, който за първи път го използва за това.
Приблизително същото, горе-долу същото. А. Гюнтер (1882).
Знак " ≈" е въведен като символ на връзката "приблизително равно" от немския математик и физик Адам Вилхелм Зигмунд Гюнтер през 1882 г.
Повече по-малко. Т. Хариът (1631).
Тези два знака са въведени в употреба от английския астроном, математик, етнограф и преводач Томас Хариът през 1631 г., преди това са използвани думите „повече“ и „по-малко“.
![]()
Съпоставимост. К. Гаус (1801).
Сравнението е съотношението между две цели числа n и m, което означава, че разлика n-mот тези числа се дели на дадено цяло число a, наречено модул на сравнение; пише се: n≡m(mod a) и гласи "числата n и m са сравними по модул a". Например, 3≡11(mod 4), тъй като 3-11 се дели на 4; числата 3 и 11 са конгруэнтни по модул 4. Сравненията имат много свойства, подобни на тези на равенствата. Така че терминът в една част на сравнението може да се прехвърли с противоположен знак в друга част, а сравнения със същия модул могат да се добавят, изваждат, умножават, двете части на сравнението могат да се умножават по едно и също число и т.н. Например,
3≡9+2(mod 4) и 3-2≡9(mod 4)
В същото време верни сравнения. И от двойка верни сравнения 3≡11(mod 4) и 1≡5(mod 4) верността на следното:
3+1≡11+5(mod 4)
3-1≡11-5(mod 4)
3 1≡11 5 (мод 4)
3 2 ≡11 2 (мод 4)
3 23≡11 23 (мод 4)
В теорията на числата се разглеждат методи за решаване на различни сравнения, т.е. методи за намиране на цели числа, които удовлетворяват сравнения от един или друг вид.Сравненията по модули са използвани за първи път от немския математик Карл Гаус в неговата книга от 1801 г. „Аритметични изследвания“. Той също така предложи символиката, установена в математиката, за сравнение.
самоличност. Б. Риман (1857).
Идентичност - равенство на два аналитични израза, валидно за всеки разрешени стойностиписма, включени в него. Равенството a+b = b+a е валидно за всички числови стойности a и b и следователно е идентичност. За записване на идентичности в някои случаи от 1857 г. насам се използва знакът „≡“ (чете се „идентично равен“), чийто автор в тази употреба е немският математик Георг Фридрих Бернхард Риман. Може да се пише a+b ≡ b+a.
Перпендикулярност. П.Еригон (1634).
Перпендикулярност - взаимно урежданедве прави, равнини или права линия и равнина, в която посочените фигури образуват прав ъгъл. Знакът ⊥ за обозначаване на перпендикулярност е въведен през 1634 г. от френския математик и астроном Пиер Еригон. Концепцията за перпендикулярност има редица обобщения, но всички те, като правило, са придружени от знака ⊥ .
Паралелизъм. W. Outred (посмъртно издание от 1677 г.).
Паралелизъм – връзката между някои геометрични фигури; например прави линии. Дефинирани по различен начин в зависимост от различните геометрии; например в геометрията на Евклид и в геометрията на Лобачевски. Знакът на паралелизъм е познат от древни времена, използван е от Херон и Пап от Александрия. Първоначално символът беше подобен на текущия знак за равенство (само по-разширен), но с появата на последния, за да се избегне объркване, символът беше обърнат вертикално ||. Появява се в тази форма за първи път в посмъртно издание на трудовете на английския математик Уилям Аутред през 1677 г.
Пресечна точка, съюз. Дж. Пеано (1888).
Пресечната точка на множествата е множеството, към което принадлежат онези и само онези елементи, които принадлежат едновременно на всички дадени множества. Обединението от множества е множество, което съдържа всички елементи на оригиналните множества. Пресичане и обединение се наричат също операции върху множества, които присвояват нови множества на определени множества съгласно горните правила. Обозначава се съответно ∩ и ∪. Например, ако
A= (♠ ♣ )И B= (♣ ♦ ),
Че
A∩B= {♣ }
A∪B= {♠ ♣ ♦ } .
Съдържа, съдържа. Е. Шрьодер (1890).
Ако A и B са две множества и няма елементи в A, които не принадлежат на B, тогава те казват, че A се съдържа в B. Пишат A⊂B или B⊃A (B съдържа A). Например,
{♠}⊂{♠ ♣}⊂{♠ ♣ ♦ }
{♠ ♣ ♦ }⊃{ ♦ }⊃{♦ }
Символите "съдържа" и "съдържа" се появяват през 1890 г. с немския математик и логик Ернст Шрьодер.
Принадлежност. Дж. Пеано (1895).
Ако a е елемент от множеството A, тогава напишете a∈A и прочетете „a принадлежи на A“. Ако a не е елемент от A, напишете a∉A и прочетете „a не принадлежи на A“. Първоначално отношенията „съдържа“ и „принадлежи“ („е елемент“) не бяха разграничени, но с течение на времето тези понятия изискваха разграничение. Знакът за членство ∈ е използван за първи път от италианския математик Джузепе Пеано през 1895 г. Символът ∈ идва от първата буква на гръцката дума εστι - да бъде.
Универсалният квантор, екзистенциалният квантор. Г. Генцен (1935), К. Пиърс (1885).
Кванторът е общо име за логически операции, които показват областта на истинността на предикат (математическо твърдение). Философите отдавна обръщат внимание на логическите операции, които ограничават обхвата на истинността на предикат, но не ги отделят като отделен клас операции. Въпреки че кванторно-логическите конструкции се използват широко както в научната, така и в ежедневната реч, тяхното формализиране се извършва едва през 1879 г., в книгата на немския логик, математик и философ Фридрих Лудвиг Готлоб Фреге "Изчисление на понятията". Нотацията на Фреге изглеждаше като тромава графична конструкция и не беше приета. Впоследствие бяха предложени много по-успешни символи, но нотацията ∃ за екзистенциалния квантор (четете „съществува“, „има“), предложена от американския философ, логик и математик Чарлз Пиърс през 1885 г., и ∀ за универсалния квантор ( четете "всяко", "всеки", "всеки"), образувано от немския математик и логик Герхард Карл Ерих Генцен през 1935 г. по аналогия със символа на екзистенциалния квантификатор (обърнати първи букви английски думиСъществуване (съществуване) и Всяко (всяко)). Например вписването
(∀ε>0) (∃δ>0) (∀x≠x 0 , |x-x 0 |<δ) (|f(x)-A|<ε)
чете така: „за всяко ε>0 има δ>0 такова, че за всички x не е равно на x 0 и отговаря на неравенството |x-x 0 |<δ, выполняется неравенство |f(x)-A|<ε".
Празен комплект. Н. Бурбаки (1939).
Набор, който не съдържа никакъв елемент. Знакът празен набор е въведен в книгите на Никола Бурбаки през 1939 г. Бурбаки е колективен псевдоним на група френски математици, създадена през 1935 г. Един от членовете на групата Бурбаки е Андре Вейл, авторът на символа Ø.
Q.E.D. Д. Кнут (1978).
В математиката доказателство се разбира като последователност от разсъждения, основани на определени правила, показващи, че определено твърдение е вярно. Още от Ренесанса краят на едно доказателство се обозначава от математиците като „Q.E.D.“, от латинския израз „Quod Erat Demonstrandum“ – „Какво трябваше да се докаже“. При създаването на компютърната система за оформление ΤΕΧ през 1978 г., американският професор по компютърни науки Доналд Едуин Кнут използва символ: запълнен квадрат, така наречения „символ на Халмос“, кръстен на американския математик от унгарски произход Пол Ричард Халмос. Днес завършването на доказателство обикновено се обозначава със символа Халмос. Като алтернатива се използват други знаци: празен квадрат, правоъгълен триъгълник, // (две наклонени черти), както и руската абревиатура "ch.t.d.".
Търсете в инженерния наръчник на DPVA. Въведете вашата заявка:
Допълнителна информация от Инженерния наръчник на DPVA, а именно други подраздели на този раздел:
Когато хората взаимодействат дълго време в рамките на определена област на дейност, те започват да търсят начин да оптимизират комуникационния процес. Системата от математически знаци и символи е изкуствен език, който е предназначен да намали количеството графично предавана информация и в същото време да запази напълно значението, присъщо на съобщението.
Всеки език изисква учене и езикът на математиката в това отношение не е изключение. За да се разбере значението на формули, уравнения и графики, е необходимо предварително да има определена информация, да се разбират термините, обозначенията и т. н. При липса на такива знания текстът ще се възприема като написан на непознат чужд език.
В съответствие с изискванията на обществото, графичните символи за по-прости математически операции (например запис на събиране и изваждане) са разработени по-рано, отколкото за сложни понятия като интеграл или диференциал. Колкото по-сложно е понятието, толкова по-сложен знак обикновено се обозначава.
Модели за формиране на графични символи
В ранните етапи на развитието на цивилизацията хората свързваха най-простите математически операции с познатите си понятия, основани на асоциации. Например, в древен Египет събирането и изваждането се обозначаваха с модел на ходещи крака: линиите, насочени в посоката на четене, означаваха „плюс“, а в обратната посока - „минус“.
Числата, може би във всички култури, първоначално са били обозначени със съответния брой тирета. По-късно за запис започнаха да се използват конвенции - това спести време, както и място на материални носители. Често буквите се използват като символи: тази стратегия е широко разпространена в гръцки, латински и много други езици по света.
Историята на появата на математическите символи и знаци познава двата най-продуктивни начина за формиране на графични елементи.
Преобразуване на представяне на думи
Първоначално всяко математическо понятие се изразява с някаква дума или фраза и няма свое собствено графично представяне (различно от лексикално). Извършването на изчисления и писането на формули с думи обаче е продължителна процедура и заема неоправдано голямо пространство на материалния носител.
Често срещан начин за създаване на математически символи е да се трансформира лексикалното представяне на понятие в графичен елемент. С други думи, думата, обозначаваща понятие, се съкращава или трансформира по някакъв друг начин с течение на времето.

Например, основната хипотеза за произхода на знака плюс е неговото съкращение от латински et, чийто аналог на руски език е съюзът "и". Постепенно, при скоропис, първата буква престана да се пише и тсведен до кръст.
Друг пример е знакът "x" за неизвестното, който първоначално е бил съкращение за арабската дума за "нещо". По същия начин имаше знаци за квадратен корен, процент, интеграл, логаритъм и др. В таблицата с математически символи и знаци можете да намерите повече от дузина графични елементи, които се появиха по този начин.
Произволно присвояване на знаци
Вторият често срещан вариант на образуване на математически знаци и символи е присвояването на символ по произволен начин. В този случай думата и графичното обозначение не са свързани помежду си - знакът обикновено се одобрява в резултат на препоръка на един от членовете на научната общност.
Например знаците за умножение, деление и равенство са предложени от математиците Уилям Оутред, Йохан Ран и Робърт Рекорд. В някои случаи няколко математически знака могат да бъдат въведени в науката от един учен. По-специално, Готфрид Вилхелм Лайбниц предложи редица символи, включително интеграл, диференциал и производна.
Най-простите операции
Знаци като плюс и минус, както и символи за умножение и деление са познати на всеки ученик, въпреки че има няколко възможни графични знака за последните две споменати операции.
Спокойно е да се каже, че хората са знаели как да добавят и изваждат много хилядолетия преди Христа, но стандартизираните математически знаци и символи, които обозначават тези действия и са ни известни днес, се появяват едва през XIV-XV век.

Въпреки това, въпреки установяването на определено споразумение в научната общност, умножението в наше време може да бъде представено с три различни знака (диагонален кръст, точка, звездичка) и разделянето на две (хоризонтална линия с точки отгоре и отдолу или наклонена черта ).
писма
В продължение на много векове научната общност е използвала латински изключително за обмен на информация и много математически термини и знаци намират своя произход в този език. В някои случаи графичните елементи са се превърнали в резултат от съкращаване на думи, по-рядко - тяхното умишлено или случайно преобразуване (например поради печатна грешка).
Обозначаването на процента ("%"), най-вероятно, идва от погрешното изписване на съкращението Кой(центо, т.е. "стотна част"). По подобен начин се появи знакът плюс, чиято история е описана по-горе.
Много повече се образува чрез умишлено съкращаване на думата, въпреки че това не винаги е очевидно. Не всеки човек разпознава буквата в знака квадратен корен Р, т.е. първият знак в думата Radix („корен“). Интегралният символ също представлява първата буква на думата Summa, но интуитивно е подобен на главна буква. ебез хоризонтална линия. Между другото, в първата публикация издателите направиха точно такава грешка, като написаха f вместо този знак.
гръцки букви
Като графични символи за различни понятия се използват не само латински, но и в таблицата с математически символи можете да намерите редица примери за такова име.
Числото Pi, което е съотношението на обиколката на кръг към неговия диаметър, идва от първата буква на гръцката дума за кръг. Има няколко по-малко известни ирационални числа, обозначени с буквите на гръцката азбука.

Изключително често срещан знак в математиката е "делта", който отразява размера на промяната в стойността на променливите. Друг често срещан знак е "сигма", който действа като знак за сума.
Освен това почти всички гръцки букви се използват по един или друг начин в математиката. Тези математически знаци и символи и тяхното значение обаче са известни само на хората, които се занимават професионално с наука. В ежедневието и ежедневието това знание не се изисква от човек.
Признаци на логиката
Колкото и да е странно, много интуитивни символи са измислени едва наскоро.
По-специално, хоризонталната стрелка, заменяща думата "следователно", е предложена едва през 1922 г. Въведени са количествените показатели на съществуване и универсалност, т.е. знаците, четени като: "съществува ..." и "за всяко ..." съответно през 1897 и 1935 г.

Символите от областта на теорията на множествата са изобретени през 1888-1889 г. А зачеркнатият кръг, който днес е известен на всеки гимназист като знак за празен набор, се появява през 1939 г.
По този начин знаците за такива сложни понятия като интегралът или логаритъмът са измислени векове по-рано от някои интуитивни символи, които лесно се възприемат и усвояват дори без предварителна подготовка.
Математически символи на английски език
Поради факта, че значителна част от понятията са описани в научни трудове на латински, редица имена на математически знаци и символи на английски и руски език са еднакви. Например: плюс („плюс“), интеграл („интеграл“), делта функция („делта функция“), перпендикулярна („перпендикулярна“), успоредна („паралелна“), нула („нула“).
Някои от понятията на двата езика се наричат по различен начин: например деление е Деление, умножение е Умножение. В редки случаи английското име за математически знак получава известно разпространение на руски: например наклонената черта през последните години често се нарича "наклонена черта" (английски наклонена черта).
таблица със символи
Най-лесният и удобен начин да се запознаете със списъка с математически знаци е да разгледате специална таблица, която съдържа знаците на операциите, символите на математическата логика, теорията на множествата, геометрията, комбинаториката, математическия анализ, линейната алгебра. Тази таблица показва основните математически знаци на английски език.

Математически символи в текстов редактор
При извършване на различни видове работа често е необходимо да се използват формули, които използват знаци, които не са на клавиатурата на компютъра.
Подобно на графични елементи от почти всяка област на знанието, математическите знаци и символи в Word могат да бъдат намерени в раздела Вмъкване. Във версиите на програмата 2003 или 2007 има опцията „Вмъкване на символ“: когато щракнете върху бутона от дясната страна на панела, потребителят ще види таблица, която съдържа всички необходими математически символи, гръцки малки букви и главни букви, различни видове скоби и много други.
Във версиите на програмата, пуснати след 2010 г., е разработена по-удобна опция. Когато щракнете върху бутона "Формула", отивате в дизайнера на формули, който предвижда използването на дроби, въвеждане на данни под корена, промяна на главния регистър (за посочване на градуси или редови номера на променливите). Всички знаци от таблицата, представена по-горе, също можете да намерите тук.
Струва ли си да научите математически символи
Системата за математическа нотация е изкуствен език, който само опростява процеса на запис, но не може да донесе разбиране на обекта на външен наблюдател. По този начин запомнянето на знаци без изучаване на термини, правила, логически връзки между понятията няма да доведе до овладяване на тази област на знанието.

Човешкият мозък лесно научава знаци, букви и съкращения - математическите обозначения се запомнят сами по себе си при изучаване на предмета. Разбирането на значението на всяко конкретно действие създава толкова силно, че знаците, обозначаващи термините, а често и формулите, свързани с тях, остават в паметта в продължение на много години и дори десетилетия.
Най-накрая
Тъй като всеки език, включително изкуствен, е отворен за промени и допълнения, броят на математическите знаци и символи със сигурност ще нараства с времето. Възможно е някои елементи да бъдат заменени или коригирани, а други да бъдат стандартизирани по единствения възможен начин, който е от значение например за знаците за умножение или деление.
Способността за използване на математически символи на ниво пълен училищен курс е практически необходима в съвременния свят. В контекста на бурното развитие на информационните технологии и науката, широко разпространената алгоритмизация и автоматизация, притежаването на математически апарат трябва да се приема като даденост, а разработването на математически символи като неразделна част от него.
Тъй като изчисленията се използват и в хуманитарната сфера, и в икономиката, и в природните науки, и, разбира се, в областта на инженерството и високите технологии, разбирането на математическите понятия и познаването на символите ще бъде полезно за всеки специалист.
от две), 3 > 2 (три е по-голямо от две) и т.н.Развитие математическа символикабеше тясно свързана с общо развитиепонятия и методи на математиката. Първо Математически знациимаше знаци за изобразяване на числа - числа, появата на които, очевидно, е предшествала писането. Най-древните системи за номериране - вавилонска и египетска - се появяват още през 3 1/2 хилядолетия пр.н.е. д.
Първо Математически знацитъй като произволните стойности се появяват много по-късно (започвайки от 5-4 в. пр. н. е.) в Гърция. Количествата (площ, обеми, ъгли) бяха показани като отсечки, а произведението на две произволни еднородни величини - като правоъгълник, изграден върху съответните отсечки. в "Начала" Евклид (3 век пр. н. е.) количествата се обозначават с две букви - началната и крайната буква на съответния сегмент, а понякога дори и една. В Архимед (3 век пр. н. е.) последният метод става често срещан. Такова обозначение съдържаше възможностите за развитие на буквалното смятане. Въпреки това, в класическата древна математика буквалното смятане не е създадено.
Началото на представянето на буквите и смятането възниква в късната елинистическа епоха в резултат на освобождаването на алгебрата от геометричната форма. Диофант (вероятно 3-ти век) е записал неизвестен ( х) и неговите степени със следните знаци:
[ - от гръцкия термин dunamiV (dynamis - сила), обозначаващ квадрата на неизвестното, - от гръцкия cuboV (k_ybos) - куб]. Вдясно от неизвестното или неговите градуси, Диофант е написал коефициентите, например е изобразено 3x5
(където = 3). При събирането, Диофант приписва термини един на друг, за изваждане той използва специален знак; Диофант обозначава равенството с буквата i [от гръцки isoV (isos) - равен]. Например, уравнението
(х 3 + 8х) - (5х 2 + 1) =х
Диофант би го написал така:
(тук
означава, че единицата няма множител под формата на степен на неизвестното).
Няколко века по-късно индианците въвеждат различни Математически знациза няколко неизвестни (съкращения за имената на цветовете, обозначаващи неизвестни), квадрат, корен квадратен, извадено число. Така че уравнението
3х 2 + 10х - 8 = х 2 + 1
В записа Брахмагупта (7 век) ще изглежда така:
Ya va 3 ya 10 ru 8
Ya va 1 ya 0 ru 1
(ya - от yavat - tawat - неизвестен, va - от varga - квадратно число, ru - от rupa - монета рупия - свободен член, точка над числото означава числото, което трябва да се извади).
Създаването на съвременната алгебрична символика датира от 14-17 век; то се определя от успехите на практическата аритметика и изучаването на уравнения. В различни страни се появяват спонтанно Математически знациза някои действия и за мощности с неизвестна величина. Минават много десетилетия и дори векове, преди да се развие един или друг удобен символ. И така, в края на 15 и. Н. Шук и Л. Пачоли използвани знаци за събиране и изваждане
(от лат. плюс и минус), немските математици въведоха съвременния + (вероятно съкращение от лат. et) и -. Още през 17 век може да брои около десет Математически знациза операцията за умножение.
бяха различни и Математически знацинеизвестен и неговите степени. През 16 - началото на 17 век. повече от десет нотации се състезаваха само за квадрата на неизвестното, например се(от преброяване - латински термин, който служи като превод на гръцкото dunamiV, В(от квадрат), , A (2), , Aii, аа, а 2и т.н. По този начин уравнението
х 3 + 5 х = 12
италианският математик Г. Кардано (1545) ще има формата:
от немския математик М. Щифел (1544):
от италианския математик Р. Бомбели (1572 г.):
Френският математик Ф. Виета (1591 г.):
от английския математик Т. Хариът (1631):
През 16-ти и началото на 17-ти век Знаците за равенство и скоби влизат в употреба: квадрат (R. Бомбели , 1550 г.), кръг (Н. Тарталия, 1556), къдрава (Ф. viet, 1593 г.). През 16 век съвременната форма приема запис на дроби.
Значителна стъпка напред в развитието на математическия символизъм е въвеждането на Виета (1591 г.) Математически знациза произволен константипод формата на главни съгласни на латинската азбука B, D, което му даде възможност да пише за първи път алгебрични уравненияс произволни коефициенти и оперирайте с тях. Неизвестен Виет, представен от гласни главни букви A, E, ... Например вписването на Vieta
В нашите символи изглежда така:
х 3 + 3bx = д.
Виет е създателят на алгебричните формули. Р. Декарт (1637) придават на знаците на алгебрата съвременен вид, обозначавайки неизвестните с последните букви на лат. азбука x, y, z,и произволно дадени количества - с начални букви а, б, в.Той също така притежава текущия рекорд на степента. Нотацията на Декарт имаше голямо предимство пред всички предишни. Затова скоро получиха всеобщо признание.
По-нататъчно развитие Математически знацибеше тясно свързана със създаването на безкрайно малък анализ, за развитието на символиката, основата на която вече беше подготвена до голяма степен в алгебрата.
Дати на поява на някои математически знаци
| знак | смисъл | Кой въведе | Когато се въведе |
| Признаци на отделни обекти | |||
| ¥ | безкрайност | J. Wallis | 1655 |
| д | основа на естествени логаритми | Л. Ойлер | 1736 |
| стр | съотношение на обиколката към диаметъра | У. Джоунс Л. Ойлер | 1706 |
| и | корен квадратен от -1 | Л. Ойлер | 1777 г. (в печат 1794 г.) |
| i j k | единични вектори, орт | У. Хамилтън | 1853 |
| П (а) | ъгъл на паралелизъм | Н.И. Лобачевски | 1835 |
| Признаци на променливи обекти | |||
| x,y,z | неизвестни или променливи | Р. Декарт | 1637 |
| r | вектор | О. Коши | 1853 |
| Знаци отделни операции | |||
| + | допълнение | немски математици | Краят на 15 век |
| – | изваждане |
||
| ´ | умножение | W. Outred | 1631 |
| × | умножение | Г. Лайбниц | 1698 |
| : | дивизия | Г. Лайбниц | 1684 |
| a 2 , a 3 ,..., a n | степен | Р. Декарт | 1637 |
| I. Нютон | 1676 |
||
| | корени | К. Рудолф | 1525 |
| А. Жирар | 1629 |
||
| Дневник | логаритъм | И. Кеплер | 1624 |
| дневник | Б. Кавалиери | 1632 |
|
| грях | синус | Л. Ойлер | 1748 |
| cos | косинус |
||
| tg | допирателна | Л. Ойлер | 1753 |
| дъгов грях | арксинус | Ж. Лагранж | 1772 |
Ш | хиперболичен синус | В. Рикати | 1757 |
гл | хиперболичен косинус |
||
| dx, ddx, … | диференциал | Г. Лайбниц | 1675 г. (в печат 1684 г.) |
d2x, d3x,… |
|||
| | интегрална | Г. Лайбниц | 1675 г. (в печат 1686 г.) |
| | производно | Г. Лайбниц | 1675 |
| ¦¢x | производно | Ж. Лагранж | 1770, 1779 |
| y' |
|||
| ¦¢(x) |
|||
| Dx | разлика | Л. Ойлер | 1755 |
| | частична производна | А. Лежандър | 1786 |
| | определен интеграл | Ж. Фурие | 1819-22 |
| | сума | Л. Ойлер | 1755 |
| П | работа | К. Гаус | 1812 |
| ! | факториал | К. Кръмп | 1808 |
| |x| | модул | К. Вайерщрас | 1841 |
| lim | ограничение | У. Хамилтън, много математици | 1853, началото на 20 век |
| lim |
|||
| н = ¥ |
|||
| lim |
|||
| н ® ¥ |
|||
| х | дзета функция | Б. Риман | 1857 |
| г | гама функция | А. Лежандър | 1808 |
| IN | бета функция | J. Binet | 1839 |
| д | делта (оператор на Лаплас) | Р. Мърфи | 1833 |
| Ñ | nabla (оператор на Хамилтън) | У. Хамилтън | 1853 |
| Признаци на променливи операции | |||
| jx | функция | И. Бернули | 1718 |
| f(x) | Л. Ойлер | 1734 |
|
| Признаци на индивидуални взаимоотношения | |||
| = | равенство | R. Запис | 1557 |
| > | Повече ▼ | Т. Хариът | 1631 |
| < | по-малко |
||
| º | съпоставимост | К. Гаус | 1801 |
| | паралелизъм | W. Outred | 1677 |
| ^ | перпендикулярност | П. Еригон | 1634 |
И. Нютон в своя метод на флуксиите и плавността (1666 и следващите години) въвежда знаци за последователни флуксии (производни) на величина (под формата
и за безкрайно малко увеличение о. Малко по-рано Дж. Уолис (1655) предложи знака за безкрайност ¥.
Създателят на съвременната символика на диференциалното и интегралното смятане е Г. Лайбниц. Той, по-специално, принадлежи към използваните в момента Математически знацидиференциали
dx, d 2 х, г 3 х
и интегрална
Огромна заслуга в създаването на символиката на съвременната математика принадлежи на Л. Ойлер. Той въвежда (1734) в обща употреба първия знак на операцията с променливата, а именно знака на функцията е(х) (от лат. functio). След работата на Ойлер знаците за много отделни функции, като тригонометрични функции, придобиват стандартен характер. Ойлер притежава нотацията за константи д(база на естествените логаритми, 1736), p [вероятно от гръцки perijereia (periphereia) - кръг, периферия, 1736], въображаема единица
(от френски imaginaire - въображаем, 1777 г., публикуван през 1794 г.).
През 19 век нараства ролята на символиката. В този момент знаците на абсолютната стойност |x| (ДА СЕ. Вайерщрас, 1841), вектор (O. Коши, 1853), определител
(НО. Кейли, 1841) и др. Много теории, възникнали през 19 век, като тензорното смятане, не могат да бъдат развити без подходящ символизъм.
Заедно с посочения процес на стандартизация Математически знацив съвременната литература често може да се намери Математически знациизползвани от отделни автори само в рамките на това изследване.
От гледна точка на математическата логика, между Математически знацимогат да се очертаят следните основни групи: А) признаци на обекти, Б) признаци на операции, В) признаци на отношения. Например, знаците 1, 2, 3, 4 изобразяват числа, тоест обекти, изучавани от аритметика. Знакът за добавяне + сам по себе си не представлява никакъв обект; той получава предметно съдържание, когато е посочено кои числа са добавени: обозначението 1 + 3 изобразява числото 4. Знакът > (по-голям от) е знакът на връзката между числата. Знакът на връзката получава съвсем определено съдържание, когато се посочи между кои обекти се разглежда връзката. Към горните три основни групи Математически знацидо четвъртия долепва: Г) спомагателни знаци, които установяват реда на комбиниране на основните знаци. Достатъчна представа за такива знаци се дава от скоби, указващи реда, в който се извършват действията.
Знаците на всеки три групиА), Б) и В) са два вида: 1) индивидуални признаци на добре дефинирани обекти, операции и отношения, 2) общи признаци на „неповтарящи се“ или „неизвестни“ обекти, операции и отношения.
Примери за знаци от първия вид могат да служат (вижте също таблицата):
A 1) Записване на естествени числа 1, 2, 3, 4, 5, 6, 7, 8, 9; трансцедентални числа ди р; въображаема единица и
Б 1) Знаци на аритметични операции +, -, ·, ´,:; извличане на корени, диференциация
признаци на сбор (обединение) È и произведение (пресечна точка) Ç на множества; това включва и знаците на отделните функции sin, tg, log и др.
1) Знаци за равенство и неравенство =, >,<, ¹, знаки параллельности || и перпендикулярности ^, знаки принадлежности Î элемента некоторому множеству и включения Ì одного множества в другое и т.п.
Знаците от втория вид изобразяват произволни обекти, операции и отношения от определен клас или обекти, операции и отношения, подчинени на някои предварително определени условия. Например, когато пишете самоличността ( а + б)(а - б) = а 2 -б 2 букви ноИ бобозначават произволни числа; при изследване на функционалната зависимост в = х 2 букви хИ y -произволни числа, свързани с дадено съотношение; при решаване на уравнението
хобозначава всяко число, което отговаря на даденото уравнение (в резултат на решаването на това уравнение научаваме, че само две възможни стойности +1 и -1 отговарят на това условие).
От логическа гледна точка е законно да наричаме такива общи признаци знаци на променливи, както е обичайно в математическата логика, без да се страхуваме от факта, че „регионът на промяна“ на променлива може да се окаже, че се състои от един обект или дори „празен“ (например в случай на уравнения без решение). Други примери за такива знаци са:
A 2) Обозначаване на точки, прави, равнини и по-сложни геометрични фигури с букви в геометрията.
Б 2) Нотации е, , j за функции и нотация на операторно смятане, когато една буква Лизобразява, например, произволен оператор от формата:
![]()
Означението за "променливи съотношения" е по-рядко срещано и се използва само в математическата логика (вж. Алгебра на логиката ) и в относително абстрактни, предимно аксиоматични, математически изследвания.
букв.:Каджори, История на математическите означения, v. 1-2, Чи., 1928-29.
Статия за думата Математически знаци“ в Голямата съветска енциклопедия е прочетена 40088 пъти