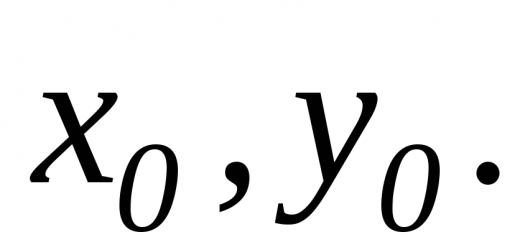Def. ስብስብ w መስመራዊ ቦታ እና ኤለመንት ተብሎ ይጠራል። - ቬክተሮች ከሆነ:
*ህግ በድመት መሰረት (+) ተገልጿል. ማንኛውም ሁለት ኤለመንቶች x፣ y ከ w ከተባለው ንጥረ ነገር ጋር ይያያዛሉ። ድምራቸው [x + y]
* ህግ ተሰጥቷል (* ለቁጥር ሀ) ፣ እንደ ድመት ንጥረ ነገር x ከ w እና a ፣ ከ w አንድ ንጥረ ነገር ይነፃፀራል ፣ የ x እና a [ax] ምርት ይባላል።
* ተጠናቅቋል
የሚከተሉት መስፈርቶች (ወይም axioms)
መከታተያ c1. ዜሮ ቬክተር (ctv 0 1 እና 0 2. በ a3: 0 2 + 0 1 = 0 2 and 0 1 + 0 2 = 0 1. በ a1 0 1 + 0 2 = 0 2 + 0 1 => 0 1 = 0 2.)
c2. .(ctv, a4)
c3. 0 ቬክት (a7)
c4. ሀ(ቁጥር)*0=0.(a6፣c3)
c5. x (*) -1 =0 ቬክተር፣ ከ x ተቃራኒ፣ i.e. (-1) x = -x. (a5,a6)
c6. በ w, የመቀነስ እርምጃ ይገለጻል: ቬክተር x የቬክተር ለ እና a ልዩነት ይባላል, x + a = b ከሆነ እና x = b - a.
ቁጥር nተብሎ ይጠራል ልኬት ሊን. ፕራ-አ ኤል ፣ ከገባ ኤል ስርዓት አለ nሊን. ነዛቭ vectors, እና ማንኛውም ሥርዓት n+1 ቬክተር - ሊን. ጥገኛ ደብዛዛ ኤል= n. ክፍተት ኤል n-dimensional ይባላል.
n መስመሮች የታዘዘ ስብስብ. ነዛቭ vectors n ልኬት ገለልተኛ. ቦታ - መሠረት
ቲዎረም. እያንዳንዱ ቬክተር X እንደ መስመር ልዩ በሆነ መንገድ ሊወከል ይችላል የመሠረት ቬክተሮች ጥምረት
(1) n-ልኬት መስመራዊ መሰረት ይሁን። pr-va ቪ፣ ማለትም እ.ኤ.አ. የመስመር ላይ ገለልተኛ የቬክተሮች ስብስብ. የቬክተሮች ስብስብ መስመራዊ ይሆናል. ጥገኛ, ምክንያቱም የእነሱ n+ 1.
እነዚያ። ሁሉም በተመሳሳይ ጊዜ ከዜሮ ጋር እኩል ያልሆኑ ቁጥሮች አሉ, ከእሱ ጋር ምን ግንኙነት አለው (አለበለዚያ (1) በመስመር ላይ ጥገኛ ናቸው).
ከዚያም የቬክተር መበስበስ የት ነው xበመሠረት (1) .
ይህ አገላለጽ ልዩ ነው, ምክንያቱም ሌላ አገላለጽ ካለ (**)
እኩልነትን (**) ከ (*) መቀነስ
እናገኛለን
ምክንያቱም በመስመር ላይ ገለልተኛ ናቸው ፣ ከዚያ . Chtd
ቲዎረም. ከሆነ - ሊን. የቦታ V እና እያንዳንዱ ቬክተር x ከ V በ በኩል ሊወከሉ ይችላሉ፣ ከዚያም እነዚህ ቬክተሮች የ V መሰረት ይመሰርታሉ።
ሰነድ፡ (1) -lin.independent =>ሰነዱ ከመስመር ነጻ የሆነ ሆኖ ይቀራል። በኮንቬንሽኑ መሰረት እያንዳንዱ ቬክተር ሀ በ (1) ይገለጻል፡ , ግምት , rang≤n => ከአምዶች መካከል ከ n የማይበልጡ በመስመር ነጻ ናቸው ነገር ግን m > n=> m አምዶች በመስመር ላይ ጥገኛ ናቸው => s=1, n
ማለትም ቬክተሮቹ ቀጥተኛ ጥገኛ ናቸው።
ስለዚህ, የቦታው V n-ልኬት እና (1) መሰረቱ ነው
№4ዲፍንዑስ ስብስብ L lin. ምርት ቪ ሊን ይባላል. cond በ V ውስጥ ከተገለጹት ኦፕሬሽኖች (+) እና (*a) አንፃር ፣ የንዑስ ክፍተቱ L መስመራዊ ቦታ ከሆነ ፣
Theorem የሕዋ V የቬክተር ስብስብ l መስመራዊ ነው። የዚህ ቦታ ንዑስ ቦታ ይሰራል
(ቅድመ) (1) እና (2) እንዲረኩ፣ ኤል ንዑስ ንዑስ እንዲሆን። pr-va.
(-x): -x+x=0 መ. a(x + y) = መጥረቢያ + ay;
(a-b) እና (e-h) ከ V ትክክለኛነት ይከተላሉ፤ እናረጋግጥ (ሐ)
(አስፈላጊነት) L lin ይሁን. የዚህ ቦታ ንዑስ ቦታ፣ ከዚያም (1) እና (2) በመስመሮች ፍቺ ምክንያት ይረካሉ። pr-va
ዲፍየሁሉም አይነት መስመሮች ስብስብ. የአንዳንድ ንጥረ ነገሮች ጥምረት (x j) lin. ምርቱ መስመራዊ ቅርፊት ይባላል
ቲዎረምየሁሉም መስመሮች የዘፈቀደ ስብስብ። የቬክተሮች V ከእውነተኛው ጋር ጥምረት. Coefficient lin ነው. subpr V (መስመራዊ ቅርፊት የተሰጠው የቬክተር ሊን ስርዓት. pr. የዚህ pr. ቀጥተኛ ንዑስ ክፍል ነው። )
ኦዲኤየኤል መስመር ቬክተሮች ባዶ ያልሆነ ንዑስ ስብስብ። ምርት ቪ ሊን ይባላል. ንዑስ ቦታ ከሆነ፡-
ሀ) የማንኛውም ቬክተር ድምር የኤል ነው።
ለ) የእያንዳንዱ ቬክተር ምርት በማንኛውም ቁጥር L ነው።
የሁለት ንዑስ ቦታዎች ድምርኤልእንደገና ንዑስ ቦታ ነው።ኤል
1) y 1 +y 2 (L 1 +L 2)<=>y 1 = x 1 +x 2፣ y 2 =x’ 1 +x’ 2፣ የት (x 1፣x’ 1) L 1፣ (x 2፣x’ 2) L 2። y 1 +y 2 =(x 1 +x 2)+(x' 1 +x' 2)=(x 1 +x' 1)+(x 2 +x' 2)፣ የት (x 1 +x' 1) ) L 1 , (x 2 +x' 2) L 2 => የመስመራዊ ንዑስ ቦታ የመጀመሪያ ሁኔታ ረክቷል።
ay 1 =ax 1 +ax 2፣ የት (ax 1) L 1፣ (ax 2) L 2 =>ምክንያቱም (y 1 +y 2) (L 1 +L 2)፣ (ly 1) (L 1 +L 2) => ሁኔታዎች ተሟልተዋል => L 1 +L 2 መስመራዊ ንዑስ ቦታ ነው።
የሁለት ክፍልፋዮች መገናኛ.ኤል 1 እናኤል 2 ሊን. pr-vaኤል በተጨማሪም subsp. ይህ ቦታ.
ሁለት የዘፈቀደ ቬክተሮችን ተመልከት x,y, የንዑስ ቦታዎች መገናኛ ንብረት እና ሁለት የዘፈቀደ ቁጥሮች ሀ,ለ:.
እንደ ዲፍ. የቅንጅቶች መገናኛዎች;
=> በመስመራዊ ቦታ ንዑስ ቦታ ፍቺ:,.
ቲ.ኬ. ቬክተር መጥረቢያ + በየብዙዎች ነው። ኤል 1, እና ብዙ ኤል 2, ከዚያም በትርጓሜው, የእነዚህ ስብስቦች መገናኛ ነው. ስለዚህም፡-
ኦዲኤ V የንዑስ ክፍሎቹ ቀጥተኛ ድምር ነው ይላሉ። ከሆነ እና ለ) ይህ መበስበስ ልዩ ነው
ለ))ለ) ከ b) ጋር እኩል መሆኑን እናሳይ።
መቼ ለ) እውነት ነው ለ)
ሁሉም ዓይነት (ኤም, ኤን) ከ በዜሮ ቬክተር ብቻ መቆራረጥ
እስቲ ∃ z ∈
ፍትሃዊ መመለስኤል=
ተቃርኖ
ቲዎረም ወደ (*) ለመሠረት አንድነት አስፈላጊ እና በቂ ነው ( የቦታ መሠረት ፈጠረ
(ያስፈልጋል)(*) እና ቬክተሮች የንዑስ ስብስቦች መሠረት ይሁኑ። እና ውስጥ መስፋፋት አለ; x በመሠረት L ላይ ተዘርግቷል፣ ያንን ለማስረገጥ (መሰረት ይሆናል፣ የመስመር ነፃነታቸውን ማረጋገጥ አስፈላጊ ነው፣ ሁሉም 0 0=0+...+0 ይይዛሉ። የ0 መስፋፋት ልዩ በመሆኑ በላይ፡ => የመሠረት መስመራዊ ነፃነት ምክንያት => (- መሠረት
(ቅጥ.)ልዩ የሆነ መበስበስ (**) ቢያንስ አንድ ብስባሽ ይኑር (የኤል መሰረቱን እንፍጠር) በልዩነት (*) => ልዩነት (**)
አስተያየት። የቀጥታ ድምር ልኬት ከንዑስ ቦታው ልኬቶች ድምር ጋር እኩል ነው።
ማንኛውም ነጠላ ያልሆነ ኳድራቲክ ማትሪክስ ከአንድ መሠረት ወደ ሌላ እንደ ሽግግር ማትሪክስ ሆኖ ሊያገለግል ይችላል።
በ n ልኬት ውስጥ ይሁን መስመራዊ ቦታ V ሁለት መሠረቶች አሉ እና
(1) =A፣ ንጥረ ነገሮች * እና ** ቁጥሮች ያልሆኑበት፣ ነገር ግን የተወሰኑ ስራዎችን በቁጥር ማትሪክስ ላይ ወደ እንደዚህ ረድፎች እናራዝማለን።
ምክንያቱም አለበለዚያ ቬክተሮች ** ቀጥተኛ ጥገኛ ይሆናሉ
ተመለስ።ከሆነ የ A ዓምዶች በቀጥታ ነጻ ናቸው =>መሰረት ይመሰርታሉ
መጋጠሚያዎች እና ከግንኙነት ጋር የተያያዘ ፣ የት የሽግግር ማትሪክስ አካላት
የ "አዲሱ" መሰረት የሆኑትን ንጥረ ነገሮች ወደ "አሮጌው" መበስበስ ይታወቅ
ከዚያ እኩልነቶቹ እውነት ናቸው
ነገር ግን የመስመራዊ ገለልተኛ አካላት ቀጥተኛ ጥምረት 0 ከሆነ =>
መሰረታዊ የመስመር ጥገኝነት ቲዎረም
ከሆነ (*) በቀጥታ የሚገለጸው በ (**) ያn<= ኤም
በ m ላይ በማስተዋወቅ እናረጋግጥ
m=1፡ ስርዓት (*) 0 እና ሊን ይዟል። አስተዳዳሪ - የማይቻል
ለ m=k-1 እውነት ይሁን
ለ m=k እናረጋግጥ
ይህ ሊሆን ይችላል 1) ፣ ማለትም እ.ኤ.አ. v-ry (1) lin.comb ናቸው። ሊን. ውስጠ-ዲች (2) ስርዓት (1) ሊኒያር የማይታመን፣ ምክንያቱም የlin.nezav አካል ነው። ስርዓቶች (*). ምክንያቱም በስርዓት (2) ውስጥ k-1 ቬክተሮች ብቻ አሉ ፣ ከዚያ በመነሻ መላምት k+1 እናገኛለን ለማ 1
: በመጠን ማትሪክስ ውስጥ n n ቢያንስ አንድ ረድፍ (አምድ) ዜሮ ከሆነ, ከዚያም የማትሪክስ ረድፎች (አምዶች) በመስመር ላይ ጥገኛ ናቸው. ማረጋገጫ፡-የመጀመሪያው መስመር ዜሮ ይሁን, ከዚያ
የት አንድ 10. የተፈለገውም ያ ነው። ፍቺ፡
ከዋናው ዲያግናል በታች የሚገኙት ንጥረ ነገሮች ከዜሮ ጋር እኩል የሆነ ማትሪክስ ይባላል ሦስት ማዕዘን፡
እና ij = 0, i>j. ለማ 2፡
የሶስት ማዕዘን ማትሪክስ ወሳኙ ከዋናው ዲያግናል ንጥረ ነገሮች ምርት ጋር እኩል ነው። ማረጋገጫው በማትሪክስ ስፋት ላይ በማስተዋወቅ ለማከናወን ቀላል ነው። ቲዎረም
ኦ የመስመር ነጻነትቬክተሮች. ሀ)አስፈላጊነት:
በመስመር ላይ ጥገኛ D=0 . ማረጋገጫ፡-እነሱ በመስመር ላይ ጥገኛ ይሁኑ ፣ j=, ማለትም፣ ሁሉም ከዜሮ ጋር እኩል ያልሆኑ j አሉ፣ j=,ምንድን a 1 A 1 + a 2 A 2 + ... a n A n =, A j –ማትሪክስ አምዶች ሀ.ለምሳሌ፡- አንድ n¹0. እና አለነ a j * = a j / a n , j£ n-1a 1 * A 1 + a 2 * A 2 + ... a n -1 * A n -1 + A n = . የመጨረሻውን የማትሪክስ አምድ እንተካው። ሀላይ A n * = a 1 * A 1 + a 2 * A 2 + ... a n -1 A n -1 + A n = . ከላይ በተረጋገጠው የመወሰኛ ንብረት መሰረት (ሌላ በቁጥር የሚባዛ ሌላ አምድ በማትሪክስ ውስጥ ካለ አምድ ላይ ቢጨመር አይቀየርም) የአዲሱ ማትሪክስ ወሳኙ ከዋናው መወሰኛ ጋር እኩል ነው። ነገር ግን በአዲሱ ማትሪክስ ውስጥ አንድ አምድ ዜሮ ነው, ይህም ማለት በዚህ አምድ ላይ ወሳኙን በማስፋት, እናገኛለን. D=0፣ጥ.ኢ.ዲ. ለ)በቂነት፡መጠን ማትሪክስ n nበመስመራዊ ገለልተኛ ረድፎችየመወሰኛውን ፍፁም ዋጋ የማይለውጡ ለውጦችን በመጠቀም ሁልጊዜ ወደ ሦስት ማዕዘን ቅርጽ መቀነስ ይቻላል. በተጨማሪም ፣ ከዋናው ማትሪክስ ረድፎች ነፃነት ፣ የሚወስነው ከዜሮ ጋር እኩል ነው። 1. በመጠን ማትሪክስ ውስጥ ከሆነ n nበመስመራዊ ገለልተኛ የረድፎች አካል ሀ 11ከዜሮ ጋር እኩል ነው, ከዚያም ዓምድ የማን አባል ነው አንድ 1 j¹ 0. በአቶ ለማ 1 መሰረት እንደዚህ ያለ አካል አለ። የተለወጠው ማትሪክስ ወሳኙ ከዋናው ማትሪክስ ወሳኙ በምልክት ብቻ ሊለያይ ይችላል። 2. ቁጥሮች ካላቸው መስመሮች እኔ>1በክፍልፋይ ተባዝቶ የመጀመሪያውን መስመር ቀንስ a i 1/a 11. ከዚህም በላይ ከቁጥሮች ጋር በረድፎች የመጀመሪያ ዓምድ ውስጥ እኔ>1ዜሮ ንጥረ ነገሮችን ያስከትላል. 3. በመጀመሪያው አምድ ላይ በመበስበስ የተገኘውን ማትሪክስ ወሳኙን ማስላት እንጀምር. ከመጀመሪያው በስተቀር ሁሉም ንጥረ ነገሮች ከዜሮ ጋር እኩል ናቸው. D አዲስ = አንድ 11 አዲስ (-1) 1+1 ዲ 11 አዲስ፣ የት መ 11 አዲስአነስተኛ መጠን ያለው ማትሪክስ የሚወስን ነው። በመቀጠል, ወሳኙን ለማስላት ዲ 11የመጨረሻው መወሰኛ የመጠን ማትሪክስ መወሰኛ እስኪሆን ድረስ እርምጃዎችን 1 ፣ 2 ፣ 3 ይድገሙ 1 1.
ደረጃ 1 የሚለወጠው የማትሪክስ መወሰኛ ምልክትን ብቻ ስለሚቀይር እና ደረጃ 2 የመለያውን ዋጋ በጭራሽ አይለውጥም ፣ ከዚያ እስከ ምልክቱ ድረስ ፣ በመጨረሻ የዋናውን ማትሪክስ መወሰኛ እናገኛለን። በዚህ ሁኔታ ፣ በዋናው ማትሪክስ ረድፎች መስመራዊ ነፃነት ምክንያት ፣ ደረጃ 1 ሁል ጊዜ ይረካል ፣ ሁሉም የዋናው ሰያፍ አካላት ከዜሮ ጋር እኩል ያልሆኑ ይሆናሉ። ስለዚህ, የመጨረሻው መወሰኛ, በተገለፀው ስልተ ቀመር መሰረት, በዋናው ዲያግናል ላይ ዜሮ ያልሆኑ ንጥረ ነገሮች ምርት ጋር እኩል ነው. ስለዚህ, የዋናው ማትሪክስ ወሳኙ ከዜሮ ጋር እኩል አይደለም. ጥ.ኢ.ዲ. አባሪ 2 ተግባሮቹ ተጠርተዋል ገለልተኛ ገለልተኛ ፣ከሆነ (በተመሳሳይ መልኩ ከዜሮ ጋር እኩል የሆነ ተራ የመስመር ላይ የተግባር ጥምረት ብቻ ነው የሚፈቀደው)። ከቬክተሮች መስመራዊ ነፃነት በተቃራኒ፣ እዚህ የመስመር ጥምር ከዜሮ ጋር ተመሳሳይ ነው፣ እና እኩልነት አይደለም። የመስመር ጥምር ከዜሮ ጋር ያለው እኩልነት ለማንኛውም የክርክር እሴት ማርካት ስላለበት ይህ ለመረዳት የሚቻል ነው። ተግባሮቹ ተጠርተዋል ቀጥተኛ ጥገኛ ፣ዜሮ ያልሆነ የቋሚ ቋሚዎች ስብስብ ካለ (ሁሉም ቋሚዎች ከዜሮ ጋር እኩል አይደሉም) እንደዚህ ያሉ (ከዜሮ ጋር እኩል የሆነ ተራ ያልሆነ የመስመር ጥምረት አለ)። ቲዎረም.ተግባራቶች ቀጥተኛ ጥገኛ እንዲሆኑ፣ አንዳቸውም በሌሎቹ በኩል (እንደ መስመራዊ ቅንጅታቸው የሚወከለው) በመስመር መገለጹ አስፈላጊ እና በቂ ነው። ይህንን ንድፈ ሃሳብ እራስዎ ያረጋግጡ፤ ስለ ቬክተሮች ቀጥተኛ ጥገኛነት ከተመሳሳይ ቲዎሪ ጋር በተመሳሳይ መልኩ የተረጋገጠ ነው። የ Vronsky መወሰኛ. የ Wronski ቆራጥ ለተግባሮች እንደ መወሰኛ አስተዋውቋል የማን ዓምዶች የእነዚህ ተግባራት መነሻዎች ከዜሮ (ተግባሮቹ እራሳቸው) ወደ n-1 ኛ ቅደም ተከተል ነው። ቲዎረም. ተግባራት ከሆነ ማረጋገጫ። ከተግባራት ጀምሮ ማንነቱ ሊለያይ ይችላል, ስለዚህ ከዚያም የWronski መወሰኛ የመጀመሪያው አምድ በቀሪዎቹ አምዶች በቀጥታ ይገለጻል፣ ስለዚህ የዊንስኪ መወሰኛ በተመሳሳይ መልኩ ከዜሮ ጋር እኩል ነው። ቲዎረም.ለተመሳሳይ ተመሳሳይነት መፍትሄዎች ልዩነት እኩልታ n ኛ ቅደም ተከተል በመስመር ላይ ጥገኛ ነበር ፣ አስፈላጊ እና በቂ ነው።. ማረጋገጫ። አስፈላጊነት ከቀዳሚው ጽንሰ-ሐሳብ ይከተላል. በቂነት። አንድ ነጥብ እናስተካክል. ጀምሮ፣ በዚህ ነጥብ ላይ የሚሰላው የወሳኙ አምዶች በመስመር ላይ ጥገኛ ናቸው። ወደ መስመራዊ ተመሳሳይነት ያለው እኩልታ የመፍትሄዎች መስመራዊ ጥምረት መፍትሄው ስለሆነ፣ የቅጹን መፍትሄ ማስተዋወቅ እንችላለን። ከተመሳሳዩ መጋጠሚያዎች ጋር የመፍትሄዎች መስመራዊ ጥምረት። ይህ መፍትሔ ዜሮ የመጀመሪያ ሁኔታዎችን እንደሚያሟላ ልብ ይበሉ, ይህ ከላይ ከተፃፈው የእኩልታዎች ስርዓት ይከተላል. ነገር ግን የመስመራዊ ተመሳሳይነት እኩልነት ቀላል መፍትሄ እንዲሁ ተመሳሳይ ዜሮ የመጀመሪያ ሁኔታዎችን ያሟላል። ስለዚህ፣ ከካውቺ ንድፈ ሐሳብ መረዳት እንደሚቻለው፣ የተዋወቀው መፍትሔ በተመሳሳይ መልኩ ከትንሹ ጋር እኩል ነው፣ ስለዚህም፣ ስለዚህ መፍትሄዎቹ በቀጥታ ጥገኛ ናቸው. መዘዝ።የWronski መወሰኛ ፣በቀጥታ ተመሳሳይነት ባለው እኩልታ መፍትሄዎች ላይ የተገነባው ቢያንስ በአንድ ነጥብ ላይ ከጠፋ፣ በተመሳሳይ መልኩ ከዜሮ ጋር እኩል ነው። ማረጋገጫ። ከሆነ, መፍትሄዎቹ በመስመር ላይ ጥገኛ ናቸው, ስለዚህም,. ቲዎረም.1. ለመፍትሄዎች ቀጥተኛ ጥገኛ አስፈላጊ እና በቂ ነው(ወይም). 2. ለመፍትሄዎች ቀጥተኛ ነፃነት አስፈላጊ እና በቂ ነው። ማረጋገጫ። የመጀመሪያው አረፍተ ነገር ከላይ ከተረጋገጠው ቲዎሪ እና አስተባባሪነት ይከተላል። ሁለተኛው መግለጫ በቀላሉ በተቃርኖ ሊረጋገጥ ይችላል። የመፍትሄ ሃሳቦች በቀጥታ ነጻ ይሁኑ። ከሆነ, መፍትሄዎቹ በመስመር ላይ ጥገኛ ናቸው. ተቃርኖ። ስለዚህም እ.ኤ.አ. .
ፍቀድ .
መፍትሄዎቹ በመስመር ላይ ጥገኛ ከሆኑ ታዲያ ,
ስለዚህ, ተቃርኖ. ስለዚህ, መፍትሔዎቹ በቀጥታ ነጻ ናቸው. መዘዝ።የWronski መወሰኛ መጥፋት ቢያንስ በአንድ ነጥብ ላይ የመፍትሄዎች ቀጥተኛ ጥገኝነት ወደ መስመራዊ ተመሳሳይ እኩልነት መስፈርት ነው። በWronski መወሰኛ እና ዜሮ መካከል ያለው ልዩነት ወደ መስመራዊ ተመሳሳይ እኩልታ የመፍትሄዎች ቀጥተኛ ነፃነት መስፈርት ነው። ቲዎረም.የ nth ቅደም ተከተል ወደ መስመራዊ ተመሳሳይነት ያለው እኩልታ የመፍትሄዎች ቦታ ልኬት ከ n ጋር እኩል ነው። ማረጋገጫ። ሀ) ለ n ኛ ቅደም ተከተል ቀጥተኛ ተመሳሳይነት ያለው ልዩነት እኩልታ በመስመር ላይ ገለልተኛ መፍትሄዎች እንዳሉ እናሳይ። መፍትሄዎችን እናስብ ........................................................... እንደዚህ ያሉ መፍትሄዎች አሉ. በእርግጥ, በካውቺ ቲዎሪ መሰረት, በነጥቡ በኩል እነዚህ መፍትሔዎች ከመስመር ነጻ ናቸው, ጀምሮ ለ) ቀጥተኛ ተመሳሳይነት ያለው እኩልታ ያለው ማንኛውም መፍትሔ በእነዚህ መፍትሄዎች በቀጥታ የሚገለጽ መሆኑን እናሳይ (የእነሱ መስመራዊ ጥምረት)። ሁለት መፍትሄዎችን እንመልከት። አንድ - ከመጀመሪያ ሁኔታዎች ጋር የዘፈቀደ መፍትሄ ቲዎሬም 1. (በኦርቶጎናል ቬክተሮች ቀጥተኛ ነፃነት ላይ).
ከዚያ የቬክተሮች ስርዓት በቀጥታ ገለልተኛ ነው. መስመራዊ ቅንጅት እንስራ ∑λ i x i =0 እና ስኬር ምርቱን እናስብ (x j , ∑λ i x i)=λ j ||x j || 2 =0፣ ግን ||x j || 2 ≠0⇒λ j =0። ፍቺ 1.
የቬክተር ስርዓት ፍቺ 2.
የዘፈቀደ ኤለመንት x የዘፈቀደ ማለቂያ የሌለው-ልኬት Euclidean ቦታ እና የዘፈቀደ orthonormal የንጥረ ነገሮች ስርዓት፣ በስርዓቱ ላይ ያለው የ ፎሪየር ተከታታይ ኤለመንት x በመደበኛነት የተዋቀረ ያልተወሰነ ድምር (ተከታታይ) የቅጹ ይባላል። አስተያየት።
(በተፈጥሮ, የዚህ ተከታታይ ውህደት በተመለከተ ጥያቄው ይነሳል. ይህንን ጉዳይ ለማጥናት የዘፈቀደ ቁጥር n እናስተካክለው እና ምን እንደሚለይ እንወቅ nth ከፊልየኦርቶዶክስ ስርዓት የመጀመሪያ n አካላት የማንኛውም ሌላ ቀጥተኛ ጥምረት የ Fourier ተከታታይ ድምር።) ቲዎሪ 2.
ለማንኛውም ቋሚ ቁጥር n፣ ከቅጹ ሁሉ ድምሮች መካከል፣ የአራተኛው ተከታታይ ንጥረ ነገር nth ከፊል ድምር በተሰጠው የዩክሊዲያን ቦታ ደንብ መሠረት ከኤለመንት x ትንሹ ልዩነት አለው። የስርዓቱን orthonormality እና የ Fourier Coefficient ፍቺን ከግምት ውስጥ በማስገባት, መጻፍ እንችላለን የዚህ አገላለጽ ዝቅተኛው በ c i =λ i ላይ ይገኛል, ምክንያቱም በዚህ ሁኔታ በቀኝ በኩል አሉታዊ ያልሆነው የመጀመሪያ ድምር ሁልጊዜ ይጠፋል, እና የተቀሩት ቃላቶች በ c i ላይ አይመሰረቱም. ለምሳሌ.
የትሪግኖሜትሪክ ስርዓትን አስቡበት በክፍል [-π,π] ላይ በሁሉም የ Riemann የተቀናጁ ተግባራት f(x) ቦታ። ይህ ONS መሆኑን ለመፈተሽ ቀላል ነው፣ እና ከዚያ የF (x) ተግባር ፎሪየር ሲሪየር ፎርም ያለው ነው። አስተያየት።
(የትሪጎኖሜትሪክ ፉሪየር ተከታታይ አብዛኛውን ጊዜ የሚፃፈው በቅጹ ነው። ተጨማሪ ግምቶች በሌለበት ማለቂያ በሌለው-ልኬት Euclidean ቦታ ላይ ያለ የዘፈቀደ ONS፣ በአጠቃላይ አነጋገር፣ የዚህ ቦታ መሰረት አይደለም። በማስተዋል ደረጃ፣ ጥብቅ ፍቺዎችን ሳንሰጥ የጉዳዩን ፍሬ ነገር እንገልፃለን። በዘፈቀደ ማለቂያ በሌለው-ልኬት Euclidean ቦታ ኢ፣ ONSን ያስቡ፣ (e i,e j)=δ ij የክሮኔከር ምልክት ነው። ኤም የዩክሊዲያን ጠፈር ንዑስ ቦታ ይሁን፣ እና k=M ⊥ ለኤም የሥሩ ጠፈር ኦርቶጎን ይሁን እንደዚህ Euclidean space E=M+M ⊥ . የቬክተር xE በንዑስ ጠፈር M ላይ ያለው ትንበያ ቬክተር ∈M ሲሆን እዚያም እነዚያን የማስፋፊያ ቅንጅቶች α k ለተቀረው (ካሬ ቀሪ) h 2 =||x-|| እንፈልጋለን። 2 ዝቅተኛው ይሆናል: ሸ 2 =||x-|| 2 =(x-,x-)=(x-∑α ከ k,x-∑α ከ k)=(x,x)-2∑α k (x, e k)+(∑α k e k,∑α k e k)= ||x|| 2 -2∑α k (x,e k)+∑α k 2 +∑(x,e k) 2 -∑(x,e k) 2 =||x|| 2 +∑(α k -(x፣e k)) 2 -∑(x፣e k) 2 . ይህ አገላለጽ አነስተኛውን እሴት በ α k =0 እንደሚወስድ ግልጽ ነው፣ ይህም ቀላል ነው፣ እና በ α k =(x,e k)። ከዚያም ρ ደቂቃ =||x|| 2 -∑α k 2 ≥0. ከዚህ የቤሴል እኩልነት ∑α k 2 ||x|| እናገኛለን 2. በ ρ=0 orthonormal of vectors (ONS) በስቴክሎቭ ስሜት (PONS) ውስጥ የተሟላ ኦርቶኖርማል ሥርዓት ይባላል።ከዚህ ስቴክሎቭ-ፓርሴቫል እኩልነት ∑α k 2 =||x|| ማግኘት እንችላለን። 2 - "የፓይታጎሪያን ቲዎሬም" ማለቂያ የሌላቸው የዩክሊዲያን ቦታዎች በስቴክሎቭ ስሜት የተሟሉ ናቸው. አሁን በጠፈር ላይ ያለ ማንኛውም ቬክተር በልዩ ሁኔታ በፎሪየር ተከታታይ መልክ ወደ እሱ በመገጣጠም ፣ የስቴክሎቭ-ፓርሴቫል እኩልነት እንዲኖር አስፈላጊ እና በቂ መሆኑን ማረጋገጥ አስፈላጊ ነው። የ vectors pic=""> ONB ቅጾች? ለምሳሌ.ትሪግኖሜትሪክ ስርዓት በሁሉም የ Riemann የሚገጣጠሙ ተግባራት f(x) በክፍል [-π,π] ላይ PONS ነው እና ONB ይመሰርታል።
.
በመስመር ላይ ጥገኛ ናቸው, ከዚያበመስመር ላይ ጥገኛ ናቸው ፣ ከዚያ አንዳቸውም በመስመር ላይ በሌሎች በኩል ይገለጣሉ ፣ ለምሳሌ ፣
, ግንኙነቶቹ ረክተዋል, የሚከተሉትን የመጀመሪያ ሁኔታዎች ማሟላት:
በአንድ ነጠላ ኩርባ ውስጥ ያልፋል - መፍትሄ። በነጥቡ በኩል 
መፍትሄው በነጥቡ ውስጥ ያልፋል
- መፍትሄ, በአንድ ነጥብ በኩል 
- መፍትሄ .
.
. ፍትሃዊ ጥምርታ
ወይም (e i,e j)=δ ij - የክሮኔከር ምልክት፣ orthonormal (ONS) ይባላል።
, በ ውስጥ ትክክለኛ ቁጥሮች λ i በሲስተሙ ውስጥ ያለው ኤለመንት x Fourier coefficients ተብሎ የሚጠራ ሲሆን λ i = (x, e i).
ከዚያም 
)
ከዚያም 
እንደ convergent ተከታታይ ጅራት. ስለዚህ የቬክተሮች ስርዓት PONS ነው እና ONB ይመሰርታል.
